1 Introduction

At different heat input levels, the weld undergoes various peak temperatures and heating rates, leading to different pAGSs in the heat-affected zone (HAZ). The variation of pAGS is expected to range from 5 to 100 μm and affects the subsequent microstructural evolution [1]. Due to the transient process of welding, it is impossible to capture the development of AGS in every position. Compared to the method of direct observation [2], Ashby and Easterling [3] proposed a general function to describe the grain growth of austenite. Later, Andersen and Grong [4] extended the model and assigned a limited value for the grain size. Leblond and Devaux [5] suggested another set of functions, in which the grain size was expected to grow even as the austenite began to decompose. In this sense, their approach did not comply with transformation kinetics proposed by Bhadeshia et al. [6,7,8,9,10]. Comparably, the grain growth model proposed by Andersen and Grong [4] was expressed explicitly, providing a flexible approach to predict the development of grain size. Therefore, it has been incorporated in several metallurgical models [11, 12]. The current work adopts this algorithm for the calculation of pAGS in the whole weldment. The values of pAGS are further imported to a metallurgical algorithm for predicting the microstructure. As a result, the models of grain growth and transformation kinetics are combined together.

The residual stress arises as a consequence of inhomogeneous heating and localised fusion [13]. Due to the non-isothermal process, the phase transformation becomes complex and makes the stress distribution even more complicated. Therefore, accurately predicting the microstructural evolution is critical to the forecast of residual stress [14]. The metallurgical model developed by Leblond and Devaux [5] was the first implemented in FE analysis for predicting residual stress. Later, the model proposed by Kirkaldy [15] was extended and applied in a coupled thermo-metallurgical analysis [16]. The model by Leblond and Devaux [5] needed to be calibrated before application. That is to say, as the chemical composition changes, the parameters in their model need to be determined again by metallurgical diagrams or experiments. The model by Kirkaldy [15] provided sufficient flexibility but rather coarse results [17]. The series of work done by Bhadeshia et al. [6,7,8,9] were able to predict the microstructural evolution without the necessity of calibrating parameters. This model only requires the input of chemical composition, pAGS and thermal histories. Compared to other models [18, 19], this model is able to treat the microstructural evolution locally and to include all the transformation products. Therefore, the metallurgical algorithm of Bhadeshia et al. [6,7,8,9] is implemented into the coupled FE model to evaluate the influence of pAGS on phase transformation and residual stress. It should be also mentioned that the grain growth algorithm has never been incorporated to Bhadeshia’s model before [10, 17]. It is the first time that the two models are joined together to provide a complete metallurgical simulation in FE analysis.

In the current research, the accuracy of Bhadeshia’s model is validated first by comparing its prediction with the experimental results of the S700 steel CCT diagram. The influence of pAGS is demonstrated by providing different values of pAGS to a separate metallurgical model, which has not yet been implemented in FE model. Then, the bead-on-plate arc welding process is conducted under three heating levels in order to achieve different microstructure distributions. The after-weld geometries, chemical composition and heat source are obtained by using the commercial software SimWeld. With these geometries, FE models are built in ABAQUS. The data of pAGS and phase volume fractions at each node are imported to the FE models by writing user subroutine. The material properties in the FE analysis are calculated by interpolating values of individual phase with its volume fractions [20]. For comparison, the simulations assuming constant value of pAGS are performed as well. By doing so, the influence of pAGS is manifested. Similarly, simulations with general material properties are conducted. Thereafter, resultant stress distributions predicted by models of interpolated and general properties are plotted with the phase distributions to analyse the influence of microstructure on residual stress. All the simulations were conducted using the traditional FE analysis. Other modified procedures, such as the singular edge-based smoothed FE [21] and isogeometric analysis [22], serve as promising techniques to predict residual stresses, and are to be discussed in future work.

2 Dependency of phase transformation on pAGS

The kinetic functions of austenite grain growth, reaustenization and austenite decomposition are briefly presented in the first sub-section. The transformation products, allotriomorphic ferrite, Widmannstätten ferrite, pearlite, bainite and martensite, are denoted as γ, α, α w , α p , α b and α′, respectively. In the second sub-section, the metallurgical model is run for different pAGSs. The results are compared to the CCT diagram for analysing the effect of grain size.

2.1 Transformation kinetics

In the presence of precipitate, the grain growth is retarded and hence is limited to a maximum value during a weld cycle. The grain growth occurs after precipitate dissolution [23]. It is a process where the larger grains expand at the expense of the shrinkage of smaller ones. Andersen and Grong [4] proposed an incremental function for the mean grain size \( \overline{D} \) as:

$$ \frac{\mathrm{d}\overline{D}}{\mathrm{d}t}={M}_o^{\ast}\exp \left(-\frac{Q_{\mathrm{app}}}{RT}\right){\left[\frac{1}{\overline{D}}-\frac{1}{{\overline{D}}_{\mathrm{lim}}}\right]}^{\left(\frac{1}{n}-1\right)} $$
(1)

where \( {M}_o^{\ast } \) is a physical constant related to the grain boundary mobility. n is a measure of the resistance to the mobility in the presence of impurity. Qapp is the apparent activation energy for grain growth. \( {\overline{D}}_{\mathrm{lim}} \) is the limiting grain size due to the existence of precipitating elements and is independent of the thermal cycle [4]. R is the gas constant and T is the temperature. This function is used to predict the prior austenite grain size, where reaustenization or melting occurs.

The base material is heated up first and then cooled down during welding. The region that does not melt but experiences superheating is reaustenized. The austenzied part will definitely affect the performance of welded structures. Under non-isothermal condition, the reaustenization begins as long as the additivity law is fulfilled [24]:

$$ \underset{0}{\overset{t_s}{\int }}\frac{\mathrm{d}t}{\tau_{\mathrm{i}}(T)}=1 $$
(2)

where ts is the time when the integration reaches at one and τi denotes the incubation time for a given transformation, such as γ to α transformation. The incubation time is estimated by Bhadeshia et al. [25] as:

$$ \ln \left\{\frac{\tau_{\mathrm{i}}{G_{\mathrm{max}}}^p}{T^z}\right\}=\frac{Q_{\mathrm{a}}}{RT}+{C}_g $$
(3)

Qa is an activation energy and C g , p and z are fitting constants determined by the chemistry [26]. The transformation finish time τf is determined in the same way but with different fitting constants. If decomposition transformation time (τf − τi) is assumed to be identical to the time of inverse transformation, the increment of γ is estimated as:

$$ \frac{\mathrm{d}{X}_{\gamma }}{1-{X}_{\gamma }}=\frac{\mathrm{d}t}{\tau_{\mathrm{f}}(T)-{\tau}_{\mathrm{i}}(T)} $$
(4)

where X γ is the volume fraction of γ.

Upon cooling, γ proceeds to decompose as long as the space inside austenite grain is not fulfilled. The grain boundary area O B of austenite is estimated as [27]:

$$ {O}_B=\frac{2}{\overline{L}} $$
(5)

where \( \overline{L} \) is the mean linear intercept for an equiaxed grain structure, which has the relationship with mean grain diameter [28]:

$$ \overline{D}=\frac{3}{2}\overline{L} $$
(6)

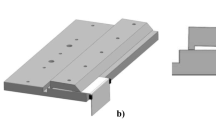
All the reconstructive products are assumed to grow layer by layer as shown in Fig. 1b).

Fig. 1
figure 1

Representative figure of α grain growth

Full size image

Then, the total increment of jth product in the extended area intersected with the plane at distance y from time t = 0 to t = m∆t, is summed up as [6]:

$$ {\Delta O}_{j,y}^e={O}_B{\sum}_{k=0}^m\left({I}_{j,k}\Delta \tau {A}_{j,k,y}\Delta t\right) $$
(7)

where Ij, k is the nucleation rate per unit area of jth product in time period from t = k∆τ to t = (k + 1)∆τ. To include the non-isothermal effect, Ij, k is defined as a temperature dependent value [6]. Aj, k, y is the change rate of intersection area at distance y of jth product, which nucleates at τ = k∆τ. However, the newly formed layers may intervene with each other as they grow up. To eliminate this effect, the increment of jth product in the real area intersected with the plane at distance y is estimated by modifying the extended area [6]:

$$ \Delta {O}_{j,y}=\left(1-\frac{\sum_{i=1}^n{O}_{i,y}}{O_B}\right){\Delta O}_{j,y}^e $$
(8)

where Oi, y is the total real area intersected by the ith product on the plane parallel to the boundary. Furthermore, the extended volume increment of jth phase on both sides of grain boundary can be written as [6]:

$$ {\Delta V}_j^e=2\Delta y{\sum}_{y=0}^{y={q}_j^{\mathrm{max}}}\Delta {O}_{j,y} $$
(9)

where \( {q}_j^{\mathrm{max}} \) is the maximum extended height of jth product in direction normal to the grain boundary and ∆y is the height of interval as shown in Fig. 1a. Finally, the volume increment of jth product with in time period ∆t is calculated as [6]:

$$ \Delta {V}_j=\left(1-\frac{\sum_{i=1}^n{V}_i}{V}\right){\Delta V}_j^e $$
(10)

where V i is the real volume of ith product and V is the total sample volume. Here, V is taken as one so that the volume increment ∆V j equals to the volume fraction increment dX j of the jth transformation product. In this way, the nucleation rates are updated during each time step ∆t and the fraction of each product is calculated accordingly. As the grain boundary area O B or the total volume V is fulfilled, the transformation ceases.

The growth of α are modelled as expansion and thickening of discs as presented in Fig. 1b. As it can be seen, the shape of newly formed α is approximated by laid-up round discs. Those discs are assumed to be able to grow on both sides of γ grain boundaries with the half-thickness q α as [6]:

$$ {q}_{\alpha }={v}_{\alpha }{\left(t-\tau \right)}^{1/2} $$
(11)

where v α is the constant parabolic thickening rate and τ the incubation time. Then, the rate of change of area intersected with a plane at a distance of y away from grain boundary at time t = m∆t is [6]:

(12)

where k denotes that the α nucleated at τ = k∆τ. During calculation, ∆τ and ∆t are taken numerically identical. η α is the ratio of disc radius to half-thickness. The growth of α p and α w is handled similarly as α but with different nucleation rates [6]. The growth mechanism is treated as lengthening of tetragonal rather than discs. The kinetics of α b growth is written in an incremental form as [9]:

$$ \frac{d\xi}{d t}=\frac{u{K}_1}{X_{\alpha_b,\max }}\left(1-\xi \right)\left(1+\beta {X}_{\alpha_b,\max}\xi \right){e}^{\left[-\frac{K_2}{RT}\left(1+\frac{\Delta {F}_{\mathrm{max}}}{C_e}\right)+\frac{K_2\left({\Delta F}_{\mathrm{max}}-\Delta {F}_N\right)}{C_e RT}\right]} $$
(13)

where \( ={X}_{\alpha_b}/{X}_{\alpha_b,\max } \) . \( {X}_{\alpha_b} \) is the volume fraction of α b and \( {X}_{\alpha_b,\max } \) is its maximum possible value. u is the volume of a bainitic subunit and \( \beta ={\lambda}_1\left(1-{\lambda}_2\overline{x}\right) \) with \( \overline{x} \) the carbon centration in steel. K1, K2, λ1, and λ2 are fitted constants. ΔFmax is the maximum molar energy difference between γ and α b . For α′, a new relationship was proposed to calculate its volume faction as [8]:

$$ -\frac{\ln \left(1-{X}_{\alpha^{\prime }}\right)}{X_{\alpha^{\prime }}}=1+{C}_f\left({M}_s-T\right) $$
(14)

\( {X}_{\alpha^{\prime }} \) is the volume fraction of α′ at T and C f is a fitted constant relating to the number of autocatalytic sites.

2.2 Influence of pAGS

From the metallurgical algorithm, it can be seen that the diffusional transformation is directly controlled by pAGS, while the displacive transformation is indirectly affected. To demonstrate the influence of pAGS, several values (100, 80, 50 and 20 μm) were tested in the metallurgical model at four cooling rates (3, 6, 12 and 20 K/s). The small values (3 and 6 K/s) are chosen because the minimum cooling rate in the HAZ close to the weld interface is about 5 K/s [29], which means that the transition to diffusional phases are possible. In the HAZ close to the base material, the cooling rate is even smaller. The based material (S700 steel), whose chemical composition is listed in Table 1, was used for the analysis. The CCT diagram, which was measured by dilatometric test at OCAS (OnderzoeksCentrum voor de Aanwending van Staal), is presented in Fig. 2. Since different phases possess different specific volumes, the transformation temperatures are determined by observing the point where a change in thermal expansion coefficient happens [30].

Table 1 The chemical composition of base material and filler
Full size table
Fig. 2
figure 2

CCT diagram of S700 steel

Full size image

When conducting the dilatometric test, the base material was heated up to 1300 °C and was held for 3 min, leading to an approximate pAGS of 100 μm [1]. This value was also used as the maximum pAGS in the grain growth algorithm [6]. With the chemical composition of S700, various values of pAGS were fed into the metallurgical model. The evolving diagrams of ferrite (including allotriomorphic and Widmannstätten ferrite) are presented in Fig. 3. The black horizontal line is the experimental resultant volume fraction of ferrite measured at the end of the test. It is seen that when the pAGS value is given 100 μm, the predicted volume fraction of ferrite is in a good agreement with the experimental results in all considered cooling rates. At low cooling rate (3 K/s), the austenite transforms completely to ferrite. Therefore, the ferrite volume fraction is not affected by the variation of pAGS. However, with respect to the transformation kinetics, it is seen that the finer pAGS is, the earlier decomposition begins. As the cooling rate increases (6 and 12 K/s), it is also found that finer grain size leads to an earlier start of decomposition. Moreover, the ferrite volume fraction acquired from the finer grain size has a higher value than that from coarser grain. These predictions are quite reasonable since the nucleation rate has an inverse relationship with the grain size [31]. A larger nucleation rate will definitely cause an earlier decomposition of austenite and higher possibility of nucleation. The same phenomenon was also verified by Jones and Bhadeshia [6]. Though small pAGS is beneficial to the formation of ferrite, the difference caused by pAGS becomes smaller as the cooling rate increases (20 K/s). It is due to the fact that the transition to Widmannstätten ferrite is displacive, and that its growth depends on the prior formed allotriomorphic ferrite and the carbon enriched untransformed austenite [6]. Therefore, a further increase of cooling rate favours the formation of Widmannstätten ferrite, which offsets the decrease of allotriomorphic ferrite.

Fig. 3
figure 3

The evolution of ferrite by changing pAGS and cooling rate

Full size image

Moreover, the volume fractions of all transformation products obtained at various cooling rates are plotted with the predictions in Fig. 4. It is seen that the volume fractions predicted by the metallurgical model are quite close to the measurements. To quantitatively estimate the metallurgical model, sensitivity analysis based on the research of Vu-Bac et al. [32] was conducted. It can be seen that at given cooling rates, the values of adjusted R-squared of all product phases are close to one, indicating that the metallurgical algorithm is robust in a wide range of cooling rate. In the next section, this metallurgical algorithm is implemented in the FE model to predict the microstructure in welding process.

Fig. 4
figure 4

Experimental and predicted volume fraction of product phases at various cooling rates

Full size image

3 Welding experimental setup

The samples of bead-on-plate weld were formed using gas metal arc welding (GMAW) process. Three heat inputs (low, medium and high) are used so that different microstructures are expected at the end of experiments. The input heat level was varied by changing the welding current and voltage as shown in Table 2. For GMAW, a constant voltage source is typically adopted and the electric arc is formed between the tip of the welding rod and the plate. As the tip-to-plate distance increases, a smaller current is acquired, leading to a different shape of weld pool and input power. During simulation, the welding arc was equated as an ellipsoid heat source. SimWeld was able to identify the heat source model from any combination of voltage and current, which will be discussed in Section 4. In the current research, the tip-to-plate distance is kept constant. Therefore, a larger current is obtained by applying a higher voltage. The welding speed was kept at constant value of 300 mm/min. The dimensions of the steel plate are 800 × 400 × 8 mm as shown in Fig. 5.

Table 2 The different currents and voltages used for bead-on-plate welding
Full size table
Fig. 5
figure 5

The plate dimension and the geometry of weld cross-section after welding

Full size image

4 Coupled FE model

The construction of the coupled FE model needs the pre-processing in several aspects. First, the parameters in the equivalent heat source need to be calibrated. According to Joshi et al. [33], three types of methods, namely, comparing with measured temperatures, residual stresses or FZ geometry, can be used for calibration. The current research adopts the third approach. The calibration was done by SimWeld, in which the power distribution q was simulated by the double ellipsoidal model [34]:

$$ q\left(x,y,z,t\right)=\frac{6\sqrt{3}{f}_{\mathrm{f}}{Q}_{inp}}{a_{\mathrm{f}} bc\pi \sqrt{\pi }}{e}^{-3{\left[x+v\left(\tau -t\right)\right]}^2/{a_{\mathrm{f}}}^2}{e}^{-3{y}^2/{b}^2}{e}^{-3{z}^2/{c}^2} $$
(15)

where ff is the fraction of front ellipsoid. Parameters af, b and c are the lengths of ellipsoid semi-axes. The distribution function in the rear quadrant has the same form but with different values for the semi-axis length ar and the power fraction fr satisfying ff + fr = 2. The right of Fig. 5 shows the dimensions of the weld cross-section predicted by SimWeld. The enclosure on the top of the plate is the area belonging to the FZ, which is analysed by computational fluid dynamics. Values of af, ar, b and c were estimated according to the geometry of FZ in Fig. 5 so that the ellipsoid has the same dimensions as the melt pool. Q inp was predicted using the voltage and the current in Table 2. The calibrated parameters in the three conditions (low, medium and high heat input) are listed in Table 3.

Table 3 The calibrated parameters of double-ellipsoidal model by SimWeld
Full size table

Due to the solidification and the addition of filler, the shape of plate did not recover and the geometry was changed. It is seen that with the higher heat input, the larger area of FZ is obtained. These 2D geometries were exported as ‘.igs’ files by SimWeld and were further imported to ABAQUS to create 3D models. Because the 2D-dimensional model imported by SimWeld was not symmetric, full 3D models were built for simulations in ABAQUS.

The thermal modelling is required for the metallurgical analysis. Therefore, a separate thermal analysis was conducted ahead of the coupled model in order to obtain the thermal history at every node. The thermal load was applied by writing user subroutine DFLUX. The temperature dependent thermal properties were plotted in Fig. 6. By doing so, the influence of the latent heat on the temperature is ignored. However, due to the fact that the magnitude of input heat is much higher than the latent heat, the ignorance of it is acceptable [18].

Fig. 6
figure 6

Temperature dependent thermal conductivity and heat capacity of S700 steel [35]

Full size image

The results of the prior thermal analysis were stored in ABAQUS output database (‘.odb’ files). Python scripts were written to subtract the nodal temperature history and to calculate the heating and cooling rates at every node. The calculation results were reserved in separate ‘.dat’ files for subsequent metallurgical analysis. Similarly, the value of pAGS at every node was calculated according to the algorithm in Section 2.1 and saved in the ‘.dat’ file.

The base material composes mainly bainite, and the SEM micrograph shows that bainite dominates 99% and the remaining percentage is ferrite [36]. Therefore, the initial values of bainite and ferrite in FE models were assigned as 0.01 and 0.99, respectively. The remaining phases were input as 0.00.

The prerequisite to conduct the metallurgical analysis has been prepared in separate file. Similar with other coupled models [5, 18, 23], the influence of stress on phase transformation was ignored. Therefore, the microstructural evolution could be calculated before the mechanical analysis. The volume fraction of each phase with respect to time was predicted and written to ABAQUS ‘.fil’ files using the metallurgical algorithm written in subroutine ABAMAIN. To analyse the effect of pAGS, metallurgical analysis assuming constant pAGS of 100 μm was also conducted.

With the information above, the thermo-metallo-mechanical model were built. The mechanical properties were calculated by linearly interpolating the temperature dependent properties of the single phase with its volume fraction. The general interpolation function can be written as [20]:

$$ P\left(T,t\right)=\sum \limits_i{X}_i\left(T,t\right){P}_i(T) $$
(16)

where P is the overall property, i.e. Elastic modulus, Poisson’s ratio, yield strength, etc. P i and X i are the properties and the volume fraction of the ith phase at temperature T and time t, respectively. The temperature and volume fraction were imported as predefined field variables (FV) by using keywords ‘*TEMPERATURE’ and ‘*FIELD’, respectively. The volume fractions of each phase are arranged in the sequence shown in Table 4.

Table 4 The different products shown in ABAQUS field variables
Full size table

The properties of each phase used in the coupled model are listed in Fig. 7. Moreover, the tangent modulus of all phases is considered to be 0.5% of the elastic modulus at corresponding temperature [35]. The increment of the total strain ∆ε is calculated as:

$$ \Delta \varepsilon =\Delta {\varepsilon}^e+\Delta {\varepsilon}^p+\Delta {\varepsilon}^T $$
(17)

where ∆εe is the elastic strain increment without the portion caused by the temperature change. ∆εp is the plastic strain increment and ∆εT the isotropic strain increment due to the temperature change. The von Mises stress is employed as the yield criterion. At each iteration, all material properties are updated to account for the change of microstructure and temperature.

Fig. 7
figure 7

Temperature dependent properties of individual phase and overall S700 steel [20, 35, 37]

Full size image

The element used for the mechanical analysis is C3D8 with the minimum size of 3 × 10−3 mm. The displacement vertical to the plate surface at four corners were constrained at first. This boundary condition was set to avoid rigid movement when the temperature field was applied. As the plate cools down, the constraint was removed gradually. The implementation procedure is summarised in Fig. 8.

Fig. 8
figure 8

The flow chart of the thermo-metallo-mechanical model

Full size image

The effect of phase transformation on residual stress is manifested by comparing the simulation results predicted by interpolated and overall material properties. Therefore, simulations of overall material properties shown in Fig. 7  were also performed. In total, nine FE models were established as summarised in Table 5.

Table 5 Simulation models created to analyse the influence of pAGS and phase transformation
Full size table

5 Results and discussion

The phase distributions at the end of simulation are plotted at all heat input levels (high, medium and low) in Fig. 9. It is clearly seen that different phase distributions have been achieved by changing the heat input. The results from the thermal analysis show that the cooling rate becomes smoother as the input power increases. Therefore, the high heat input process is more likely to produce α and α p , which is also manifested in Fig. 9a, c. The volume fraction of α contributes to a very small portion of the whole microstructure in all the three cases and its value increases as the heat input increases. Similar tendency is found in case of α w since α provides the initiation position for α w [6]. α w accounts for the main transformation product at high input. The transition to α p occurs only in case of high heat input, but the volume fraction remains much smaller than α. In contrary to the case of α and α p , α b occurs at rapid cooling rate. Therefore, it is noticed in Fig. 9d that γ decomposes into α b at low heat input. α′ exists in all the three cases and its volume fraction decreases with the increase of input power, which is also found in the experiments of Guo et al. [36].

Fig. 9
figure 9

The final volume fraction distributions of (a) α, (b) α w , (c) α p , (d) α b and (e) α′ at high (H), medium (M) and low (L) heat inputs considering the γ grain size by algorithm (GSA)

Full size image

Since the main constituent of base material is α_b (volume fraction 0.99) and γ does not decompose into α_b at high heat input (see Fig. 9d), then the HAZ can be roughly manifested by the area where α_b fraction changes. In Fig. 10, the distribution of α_b at a cross-section cut in the middle of the sample is presented. By comparing the configuration with the optical graph, it can be said that this coupled model is able to accurately capture the microstructural evolution during welding. The fractions of the product phases along the path (shown in dash green line) at the middle cross-section are also presented in Fig. 10. α_b is not plotted because it is not found at high heat input level. In the HAZ (about 5~8 mm from centreline), the volume fractions of α and α_p predicted by models considering the grain growth (H-GSA) are greater than the ones assuming constant grain size (H-CpAGS). It is caused by the fact that γ grain in HAZ has not grown up to its maximum limit size and small pAGS is beneficial to the reconstructive transformation as discussed in previous section. Consequently, the volume fractions of α_w and α^′ in HAZ decrease. In FZ (within 5 mm), the influence of pAGS vanishes because the temperature is high enough for the γ grains to grow until the maximum size. The phenomenon is in agreement with the discussion in Section 2.2.

Fig. 10
figure 10

The weld profile and predicted distributions of α, α w , α p and α′ along the path at high (H) heat input using constant prior γ grain size (CpAGS) and grain size by algorithm (GSA)

Full size image

The contour plots of residual stresses distributions are shown in Fig. 11. As the effect of grain growth is considered in simulation (H-GSA), the stresses in both x and z directions increase, while the area subjected to the tensile stress becomes smaller.

Fig. 11
figure 11

The distributions of residual stress at the weld cross-section predicted at high (H) heat input in cases of constant prior γ grain size (CpAGS) and grain size by algorithm (GSA)

Full size image

The stress distribution along the path in x direction (S11, the longitudinal residual stress) and z direction (S33) are plotted in Fig. 12. The results produced from high heat input are shown in blue and the ones of low heat input in black. Correspondingly, the distributions of product phases at the same path in both heat inputs are plotted in Fig. 13. The difference in volume fractions is caused by the magnitude of heat input. The boundary of FZ/HAZ was determined by SimWeld, where drastic change of α b  was found (see Fig. 13). The S11 distributions show that tensile stresses are formed in the centre and become compressive as it goes away from the centreline. This pattern conforms well with the typical distribution in butt weld [38]. Inside FZ, the stresses predicted by the GSA model stay lower than the ones predicted by OMP. Referring to Fig. 13, α′ is found to form in this zone, and with higher volume fraction of α′ (at low heat input), the difference in S11 stress between GSA and OMP cases becomes significant. Therefore, it can be said that the production of α′ leads to a release in the tensile stress, which is also validated by Deng et al. [18]. Moreover, at high heat input, the release of the tensile stress caused by phase transformation becomes significant in HAZ as compared to FZ. In the same region (HAZ) of Fig. 13, α w and α b are found to be the main transformation products. Hence, the transition to a combination of α w and α b can also lead to a decrease in the tensile stress, which needs further validation by experiments [39].

Fig. 12
figure 12

The predicted distributions of residual stresses along the path at high (H) and low (L) heat inputs using interpolated properties (with phase distributions considering the grain size by algorithm (GSA)) and overall material properties (OMP)

Full size image
Fig. 13
figure 13

The predicted distributions of α, α w , α b and α′ along the path at high (H) and low (L) heat inputs considering the grain size by algorithm (GSA)

Full size image

6 Conclusion

The current work investigated the effects of pAGS on phase transformation and the subsequent metallurgical influence on welding residual stress in case of bead-on-plate welding. FE models with or without consideration of the grain growth and phase transformation were constructed. By analysing the results, the following conclusions can be made:

  • A self-dependent metallurgical model can be implemented in FE analysis to predict the microstructural evolution and residual stress at high, medium and low heat inputs. The difference between the microstructure and stress distributions shows the importance of considering metallurgical analysis in welding simulation.

  • By running a separate metallurgical model, it is found that the smaller pAGS favours the generation of reconstructive products, which becomes evident at a medium cooling rate (e.g.12 K/s). By comparing the results with CCT diagram, the accuracy of the metallurgical model is also validated.

  • A grain growth algorithm can be integrated into the metallurgical model to evaluate the effect of pAGS for the first time. The comparison between the results of GSA and OMP shows that the small pAGS in HAZ increases the maximum value of residual stress and reduces the area that undergoes tensile stress. The distribution of phase volume fraction on the path also manifests the benefit of small pAGS to the formation of reconstructive phases.

  • The present coupled FE model is shown to be an efficient method to predict all aspects of information (temperatures, microstructure, stress, etc.) during welding. By aligning the residual stress with phase distribution, it can be concluded that α′ and the co-existence of α w and α b may account for the decrease of tensile stress in weld.