Introduction

Stabilizing natural and man-made slopes, e.g., cut slopes, is of great technical, safety, and economic importance. A variety of techniques, such as rigid retaining walls, sheet piles, bored pile walls, anchorage, nailing, etc. have been developed and are used to protect sloping grounds against failure and excessive deflection. Nailing was first used in the early 1960s by Austrian engineers to stabilize tunnel walls and received widespread attention afterward due to the relative simplicity of construction and reasonable overall cost. Many experimental, analytical, and numerical research works have been carried out to investigate the behavior of nail walls and the development of optimal design strategies.

To gain an insight into the behavior of soil nail walls, model tests in small scale [4, 9, 16, 25, 26], large scale [7, 36], and full scale [23, 29, 38] have been conducted on models of nail-reinforced slopes. Furthermore, the behavior of nailed slopes has been examined in detail by centrifuge model testing [20, 22, 28, 32, 37, 45]. Moreover, the seismic behavior of soil-nailed walls has been investigated using the shaking table test [42,43,44]. Varieties of numerical methods have been employed to analyze the behavior of nailed slopes. French method [30], German method [36], and Davis method [21] are examples of limit equilibrium-based approaches to design slopes reinforced with nails. More recently, a three-dimensional approach to analyze the nailed slopes by limit equilibrium method was proposed by Basudhar et al. [2]. Also, applying a modified pseudo-dynamic method, Sharma et al. [34] analyzed the effects of contributing factors to the static and dynamic stability of helical nailed walls. The upper bound limit analysis method has also been employed to solve nailing problems [14, 19]. In addition, numerical approaches like the finite element method [1, 8, 10, 25, 33, 35, 41, 46], finite difference method [5, 40], and discrete element method [15] have been used to analyze nailed earth structures.

Factors predominating the stability of nailed slopes include nail properties, length of nails, and arrangement of nails or nail spacing [6]. Additional shear resistance developed by nails is primarily due to the mobilization of tensile resistance rather than flexural or shear strengths [13]. Juran et al. [14] reported the effects of the inclination angle of parallel nail arrangement on the stability of slopes. In addition, Viswanadham and Rotte [39], using the finite difference method, reported the influences of nail inclination on the facings of reinforced slopes.

Although numerous research has been devoted to characterizing different aspects of nailing method, comparatively few studies on optimization of nail walls are available. Sabahit et al. [27] employed a generalized Janbu method [11] and determined the minimum total force in nails necessary to achieve a permissible factor of safety against overall failure. To do so, they considered nails' inclination angles and distribution of force in nails as control variables. In addition, they assumed the slip surface to be the same as that of the corresponding unreinforced slope. However, facing was neglected in their research work. Furthermore, taking advantage of the slice method and nonlinear optimization, Patra and Basudhar [24] tackled the problem of optimum soil nail wall in its general manner, considering all the relevant parameters as optimization variables. The problem solved by these researchers was a multi-objective problem which aimed to minimize the total volume of nails and the difference between the permissible and desired safety factor against overall failure. A significant assumption was that they determined the overall slip surface by analyzing the associated unreinforced model. However, this slip surface may not necessarily be the critical slip surface of the corresponding reinforced slope.

Optimization of the bonded length of anchors, pre-stress forces in nails, and the number of nails were carried out by Seo et al. [31], considering multi-face failures. Fan and Luo [6] employed the nonlinear finite element method and strength reduction approach to obtain the best nail inclination angle for different slope geometry by analyzing nailed slope models with no facing. They concluded that nails located in the lower 1/3 part of the slope have more contribution to the slope stability in comparison with those at the upper and middle 1/3 parts so that using shorter nails at this part of the wall gives rise to a significant reduction in the wall’s safety factor against overall stability. They also found out that, as long as the same length nails are used, and the positions of the uppermost and the lowermost nails are kept unchanged, the arrangement of the other nails has negligible influence on the stability of nailed slopes. Moreover, using FEM analysis, Sharma and Ramkrishnan [33] indicated that the nail length for the lower-third portion of the nailed wall could be reduced by 10–20% of their lengths compared with the upper-third and middle-third parts. It seems that in terms of the effect of the nails’ length at the lower 1/3 part of the wall, the findings of Fan and Lue [6] and Sharma and Ramkrishnan [33] contradict each other. Although using finite element method that involves displacement analysis may lead to more accurate and reasonable results than limit state methods, a parametric study to observe the influences of the contributing factors to the optimized design of the nail walls by this method would be extremely helpful time consuming and cumbersome. Furthermore, the Adaptive Network-based Fuzzy Inference System (ANFIS) was utilized by Jelusic and Zelender [12] to find the optimum inclination angles of nails in the soil nail walls. The required ANFIS inputs were provided by the optimum design of nailed walls using limit equilibrium method and nonlinear programming. They involved active earth pressure in calculating the overall stability safety factor, which is contrary to the recommendation in the literature and design procedure presented by Federal Highway of Administration (FHWA).

Although several numerical methods have been introduced for the design of soil nail walls, the design process presented by FHWA [3, 17], which is based on the limit equilibrium method, has maintained its popularity and is still widely used by engineers. In the present study, according to the relations presented in the FHWA manuals and using the nonlinear programming, the optimum nail inclination angles resulting in the best (maximum) values of the critical (minimum) safety factor against overall failure (FSmin)max, are obtained. Furthermore, the effects of main factors contributing to the optimum design of the nail wall are evaluated thoroughly. To ease generalization, results are presented through non-dimensional graphs.

Theory

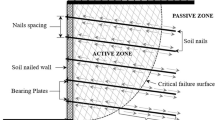
Soil nail walls are constructed in multiple phases through a top-to-bottom construction technique and are aimed to protect excavations against failure. Each stage consists of excavation to a certain depth, nail insertion and grouting, shotcrete (temporary facing), and permanent facing. The stability and serviceability of each phase should be provided to have a comprehensive design. Cross section and details of a typical soil nail wall are illustrated in Fig. 1.

Fig. 1
figure 1

Cross section of a typical soil nail wall [17]

Full size image

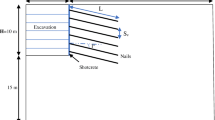
The geometrical properties of a typical sloping soil nail wall are illustrated in Fig. 2. As shown in Fig. 2, H is the slope height, Zn represents the nail length, and Sv refers to the vertical spacing of the adjacent nails. Sh denotes the horizontal spacing of the nails. In addition, α, β, η, and ν are representatives of the inclination angles of the slope, the ground, the nails, and the slip surface, respectively, as shown in Fig. 2. Furthermore, the uppermost nail is situated at Sv top below the slope crest, and the lowermost nail is located at Sv bot by the toe of the slope. The slope's surface is covered with a concrete facing to which the tips of the nails are attached through a bearing plate as shown in Fig. 1.

Fig. 2
figure 2

Geometrical properties of a typical sloping soil nail wall

Full size image

On the ground that the actual geometry of the slip surface is unknown, to evaluate the overall stability of a slope, a wide variety of shapes such as planar, piecewise, circular, parabolic, and logarithmic spiral slip surfaces may be assumed for the failure surface. However, in the present study, planar slip surface passing through the toe is assumed for convenience (Fig. 2).

Overall slip failure, nail pullout failure, tensile failure of the nails, and facing rupture are considered as the main failure modes in the present research. Of those four primary failure modes, three are associated with the possible rupture of the nails with the relations at the limit state as follows:

  1. (1)

    The tensile failure of a nail is a structural limit state and can be expressed by Eq. 1:

    where Rt is the resistance of the nail against tensile failure, dn is the nail diameter, fy denotes the yield strength of the nail, and SFT represents the factor of safety against tensile failure.

    $${\text{R}}_{{\text{t}}} = \frac{{{\uppi }.{\text{d}}_{{\text{n}}}^{2} }}{4} \times \frac{{{\text{f}}_{{\text{y}}} }}{{{\text{SF}}_{{\text{T}}} }}$$
    (1)
  2. (2)

    The pullout capacity of nails shown by the following equation is a geotechnical limit state:

    In Eq 2, Tp is the pullout capacity of nails, d denotes the hole diameter, qs is the ultimate adhesion between soil and nail, and SFP indicates safety factor against pullout failure.

    $${\text{T}}_{{\text{P}}} = \frac{{{\uppi }.{\text{d}}.{\text{q}}_{{\text{s}}} }}{{{\text{SF}}_{{\text{p}}} }}$$
    (2)
  3. (3)

    Nail-cap (Fig. 1) bearing capacity (Rf) is calculated based on the following equation:

    $$R_{f} = \left[ {Min\left( {R_{t} ,T_{p} .z_{n} } \right)} \right] \times \left[ {0.6 + 0.2 \times \left( {s_{\max } - 1} \right)} \right]$$
    (3)

In Eq 3, Zn is the length of a typical nail, and smax is the spacing of nails either in horizontal or vertical direction, whichever one is greater. It should be noted that in using Eq. 3, values of parameters must be introduced in SI units (i.e., KN, m). Equations 1 and 3 are based on the simplified distribution of forces along a typical nail as shown in Fig. 3.

Fig. 3
figure 3

Distribution of force along a typical nail

Full size image

As Fig. 3 shows, the tensile force of the nail grows from zero at the back end of the nail, with a constant slope (Tp) which is equal to the pullout capacity per unit length of nails, to its maximum possible amount, namely nail tensile strength Rt. Then, it gradually reduces to Rf on the front end of the nail, at the intersection with the bearing plate, with the constant rate of Tp. Maximum permissible tensile force in the nth typical nail (Tmax (n) or Fn) depends on the three bearing capacities illustrated by Eq. 1–3 and in Fig. 3 and can be formulated as follows:

$$F_{n} = Min\left( {T_{P} .x_{n} , R_{t} , R_{f} + T_{P} .y_{n} } \right)$$
(4)

where xn and yn are lengths of the nth nail in the back and front of the slip surface, respectively (Fig. 2).

The overall safety factor against the slope failure along a slip surface passing through the nails (Fig. 2) is presented by Eq. 5.

$$FS = \frac{{c.L + \left( {W.\cos \left( \nu \right) + \sum F.\sin \left( {\nu + \eta } \right)} \right).\tan \left( \varphi \right)}}{{\left( {W.\sin \left( \nu \right) - \sum F.\cos \left( {\nu + \eta } \right)} \right)}}$$
(5)

where,

$$\Sigma F = {F_1} + {F_2} + {F_3} + ............. + {F_n}$$
(6)

In Eq. 5, c and φ are soil strength parameters based on the Mohr–Coulomb failure criterion, and L and W are, respectively, the length of the slip surface and weight of the slipping block for unit width of the wall. Regarding Fig. 4, parameters like W, y, and x can be calculated using geometrical relations.

$${\text{W}} = {\text{S}} \times {\upgamma } \times 1$$
(7)

where \(\upgamma\) is the unit weight of the soil and S is the cross area of the slipping block that are obtained as follows.

$${\text{S}} = \sqrt {{\text{P}}\left( {{\text{P}} - {\text{A}}} \right) \times \left( {{\text{P}} - {\text{B}}} \right) \times \left( {{\text{P}} - {\text{L}}} \right)}$$
(8)
Fig. 4
figure 4

Critical safety factor versus nail inclination angle

Full size image

Looking at Fig. 2, the required parameters to calculate S in Eq. 8 can be determined using Eqs. 9,10,11 and 12.

$${\text{B}} = \frac{{\text{H}}}{{{\text{cos}}\left( {\upalpha } \right)}}$$
(9)
$${\text{A}} = \frac{{{\text{sin}}\left( {90 - \alpha - \nu } \right)}}{{{\text{sin}}\left( {{\upnu } - {\upbeta }} \right)}} \times {\text{B}}$$
(10)
$${\text{L}} = \frac{{{\text{sin}}\left( {90 + \alpha + {\upbeta }} \right)}}{{{\text{sin}}\left( {{\upnu } - {\upbeta }} \right)}} \times {\text{B}}$$
(11)
$${\text{P}} = \frac{{{\text{A}} + {\text{B}} + {\text{L}}}}{2}$$
(12)

Moreover, from Fig. 2 and having the length of a typical nail zn, height of the nail with respect to the toe (Hn), the length of the nail at the front of the slip surface (yn), and the back of the slip surface (xn) are obtained by the equations below:

$${\text{y}}_{{\text{n}}} = \frac{{\left( {1 - {\text{tan}}\left( {\upalpha } \right) \times {\text{tan}}\left( {\upnu } \right)} \right)}}{{{\text{sin}}\left( {{\upeta } + {\upnu }} \right)}} \times ({\text{H}}_{{\text{n}}} ) \times \cos \left( {\upnu } \right)$$
(13)
$$x_{{\text{n}}} = {\text{z}}_{{\text{n}}} - {\text{y}}_{{\text{n}}}$$
(14)

This study aims to determine the optimum combination of the parameters contributing to the overall stability of the nail walls so that the best or the maximum factor of safety against overall failure is obtained. To do so, for a reinforced slope with a given geometry and number and location of nails, the best inclination angle of the nails is obtained so that the safety factor against overall stability (FSmin) acquires the maximum value. In this regard, goal function is defined as the following:

$${\text{Objective Function}}:{\text{ Max }}\left( {{\text{Min }}\left( {{\text{FS}}} \right)} \right)$$
(15)

Therefore, first FSmin for each of different given angles of nail inclination (η), which are chosen inside a reasonable range, is calculated using Eq. 5–14. Then, the maximum critical safety factor is extracted from the precalculated set of FSmin. Accordingly, the optimum nail inclination angle corresponding to the optimum safety factor can be obtained as well.

Equations 1–14, excluding Eq. 5, compose constraints of the present optimization problem. To simplify this problem, all constraints have been introduced into Eq. 5 (or 15) to develop an unconstrained problem. Mathematically, the problem can be formulated like this:

$$\max_{{\text{x}}} \min_{{\text{i}}} {\text{f}}_{{\text{i}}} \left( {\text{x}} \right){ },{\text{ lb}} \le {\text{x}} \le {\text{ub }}$$
(16)

In Eq. 16, X is the vector of variables consisting of ν and η. Indeed, other parameters available in the associated equations must be defined in advance. As Eq. 16 indicates, a reasonable range should be defined for both ν and η. Here, nail inclination angle (η) was confined between zero and 50˚ and slip surface angle (ν) was limited to (0˚, 90˚-α). Since the objective function is not linear, nonlinear programming was utilized to solve this optimization problem. To do so, the optimization toolbox of the MATLAB [18] software was used. The fminimax function inside the optimization toolbox is designed to find the min(max) of an arbitrary function F(x). However, using the identity max (min F(x)) = -min (max -F(x)), the max (min F(x)) can be obtained.

Comparison with Available Results

In order to verify the current approach, results presented by Jelusic and Zlender (2013) [12] for an 8-m high vertical wall reinforced with five nails were utilized. The geometrical properties of the wall are illustrated in Table 1, and parameters required to define soil and reinforcement are shown in Table 2.

Table 1 Geometrical properties of the wall used for verification
Full size table
Table 2 Soil and nail properties of the wall used for verification
Full size table

Variation in critical overall stability safety factor against nail inclination angle is shown in Fig. 4. As Fig. 4 indicates, the optimum nail inclination angles obtained in both studies are almost the same (ηopt = 19.2˚), whereas the maximum critical safety factors are substantially different. The present study’s (SFmin)max is about 50% greater than that obtained by Jelusic and Zlender [12]. Such difference is due to the involvement of active pressure in the overall stability of the nail wall in the Jelusic and Zlender research work. In fact, on the ground that the overall slip surface does not intersect the wall facing and bypasses the wall by passing right beneath the facing toe, the active earth pressure acts as an internal force or an action–reaction between the wall and backfill soil and must not be introduced directly to the external equilibrium equations of the slipping block. In addition, it appears that even considering the active earth pressure in the overall stability of the soil nail wall; the resulting formulation would be different from that of Jelusic and Zelender. However, the results obtained by the present method through Eq. 5 are in complete compliance with the corresponding relation presented by the FHWA manual and hence reflect the physics of the problem more realistically.

Furthermore, the same example was analyzed for different values of z, α, β, and d, 18 cases altogether, as indicated in Table 3. Variations in FS and ηopt versus data number are shown in Fig. 5 and Fig. 6, respectively. As indicated in Fig. 5, because of the reasons discussed earlier, the safety factor and the nail inclination angle of the present study are always greater than that of Jelusic and Zlender [12] for all cases. However, the variation in these two parameters follows practically the same trend as Fig. 6 illustrates.

Table 3 Input data for verification of the present approach
Full size table
Fig. 5
figure 5

Safety factor versus different inputs for the present study and Jelusic and Zlender [12]

Full size image
Fig. 6
figure 6

Optimum nail inclination angle versus different inputs for the present study and Jelusic and Zlender [12]

Full size image

Problem Definition

Considering the Safety factor indicated by Eq. 5 and the associated constraints of the optimization process as discussed earlier, the safety factor of a nailed wall with a specified nailing arrangement and a given facing can be represented as a function of some dimensionless parameters as follows:

$$FS = f\left( {\frac{c}{\gamma H}{ },{ }\frac{{f_{y} }}{\gamma H}{ },{ }\frac{{q_{s} }}{\gamma H},\frac{z}{H},\frac{t}{H},\frac{{d_{n} }}{H},\frac{d}{H},\frac{{s_{v} }}{H},\frac{{s_{v,up} }}{H},\frac{{s_{v,bot} }}{H},n,\varphi ,\alpha ,\beta } \right)$$
(17)

To implement the present approach, a typical slope reinforced with five rows of nail, all having the same length, is analyzed to determine the optimum variables, nail inclination angle, and (FSmin)max. In addition, the effects of some of the primary dimensionless parameters concerning Eq. 17 and the effects of the nail arrangements on the overall safety factor are investigated. For all the performed analyses, safety factors against nail tensile rupture and pullout failure were assumed to be 1.5, and Sh was taken as 1 m.

Results and Discussion

Effects of nail diameter (dn/H)

Optimization analyses were performed to quantify the effect of nail diameter by varying the dn/H value in the range of 0.001 to 0.005. Other contributing parameters, as indicated in Eq. 17, were kept constant as shown on the margins of Figs. 7–9. As Fig. 7 shows, irrespective of the dn/H value, the safety factor against overall failure increases steadily as c/ϒH grows. Besides, an increase in dn/H results in a rise in the safety factor so that dn/H values between 0.001 and 0.0025 have the most significant effect on FS. However, dn/H higher than a specified value, here dn/H≈0.003125, caused a marginal change in the FS (Fig. 7). For instance, at c/ϒH = 0.47, FSmax for dn/H = 0.001, 0.0015. 0.0025 and 0.003125 is 2.56, 2.95, 3.65 and 3.74, respectively, and remains 3.74 for dn/H > 0.003125. This can be explained by considering Eq. 4, in which the maximum allowable tensile force in a nail is the minimum of three values and only one of them is dependent on dn, giving rise to restricted effect of dn on the FS, when tensile rupture of nails governs the overall failure.

Fig. 7
figure 7

Maximum critical factor of safety against overall failure versus c/ϒH for different values of dn/H

Full size image

Analogous to FS, nail inclination angle (η) also increases with improvement in dn/H and stops changing beyond dn/H≈0.003125 (Fig. 8). For dn/H smaller than 0.0025, the nail inclination angle (η) increases as c/ϒH develops until approximately c/ϒH = 1 and levels off after that. This trend is quite the reverse for the case dn/H being equal or greater than 0.0025. In other words, as Fig. 8 indicates, η experiences an initial decrease with the increase in c/ϒH before staying unchanged beyond c/ϒH≈1. It can be argued that since the tensile resistance of the nails against failure is proportional to dn2 as Eq. 1 suggests, for lower nail diameters (dn/H ≤ 0.0015), the nails should be inclined more to compensate for the low tensile resistance. However, other failure criteria dominate the overall stability of the nail wall for dn/H ≥ 0.0025, leading to a decrease in ηopt, as Fig. 8 shows. Furthermore, the value of ηopt tolerates a relatively broad range with respect to dn/H assumed herein so that it varies between 1.5° and 22.73° at c/ϒH = 0.002 and between 14.5° and 21.07° at c/ϒH ≥ 1.

Fig. 8
figure 8

Optimum nail inclination angle versus c/ϒH for different values of dn/H

Full size image

In addition, slip surface angle declines as dn/H increases and with improvement in c/ϒH until approximately dn/H≈0.003125 where ν stops developing further (Fig. 9). Besides, for a given dn/H, ν tends to a constant value for c/ϒH greater than unity. The constancy of both optimum nail and slip surface orientations beyond a certain c/ϒH implies that for high cohesive soils, cohesion dominates the stability as opposed to nails. Another important point is that the nail diameter as a parameter exclusive to nails, and not soil or slope, may have a significant effect on the slip surface angle determined through an optimization process. It shows clearly that assuming the critical slip surface of unreinforced situations to find the optimum parameters of nail walls may not be reasonable in general.

Fig. 9
figure 9

Angle of inclination of failure surface (ν) against overall failure versus c/ϒH for different values of dn/H

Full size image

Effects of Nail Length (z/H)

Effects of the length of the nails were studied by considering a wide range of z/H, between 0.375 and 7.5, for certain parameters depicted on the margins of Fig. 10 to Fig. 12. In general, an increase in both z/H and c/ϒH leads to a rise in safety factor, as Fig. 10 indicates. The most dramatic change in FS occurs when z/H alternates between 0.625 and 1.875. The rate of increase in FS with z/H then declines relatively between z/H = 1.875 and 3.75, and z/H greater than 3.75 has a minor influence on the FS (Fig. 10). For instance, for c/ϒH = 0.02, FS which is equal to 0.36 at z/H = 0.375 jumps to 7.85 at z/H = 1.875 and reaches 11.44 at z/H = 3.75. This finding can be argued considering the variation in slip surface angles with c/ϒH as shown in Fig. 12 where ν declines as z/H goes up and ceases to change beyond z/H = 1.875 corresponding to ν = 3˚. It can be concluded that nails may support the stability of slopes in two ways; firstly, if the length of nails is smaller than a specified amount, they raise the FS by intersecting the slip surface. On the other hand, if the length of nails is long enough, the slip surface is formed near or outside the ends of the nails so that the resulting wide slip surface leads to a great safety factor. The same logic may be employed to explain the alternating variations in nail inclination angle in Fig. 11.

Fig. 10
figure 10

Maximum critical factor of safety against overall failure versus c/ϒH for different values of z/H

Full size image
Fig. 11
figure 11

Optimum nail inclination angle versus c/ϒH for different values of z/H

Full size image

As Fig. 12 shows, η experiences an initial drop as z/H increases from 0.375 to 1 and then grows when z/H is increased from 1 to 1.875. Any further development of z/H beyond 1.875 results in a drop in η. In fact, in an optimized design, depending on the length of the nails, they should be inclined as much as possible to intersect the slip surface or have a slight orientation angle to create a wider slip surface, both aiming at developing a greater safety factor. The graphs shown in Fig. 13 imply that unlike the assumption made in the available research studies on the optimized design of soil nail walls or slopes, the orientation of the slip surface of a reinforced slope is directly affected by the nail length. That is, taking the same critical slip surface of an unreinforced slope to design a nail wall does not lead to an optimum design in general.

Fig. 12
figure 12

Angle of inclination of failure surface (ν) against overall failure versus c/ϒH for different values of z/H

Full size image
Fig. 13
figure 13

Maximum critical factor of safety against overall failure versus c/ϒH for different values of φ

Full size image

Effects of Soil Internal Friction Angle

The internal friction angle was changed within a broad range of 0˚ to 40˚ to see its effects on the optimum design of nailed walls with parameters shown on the margins of Fig. 13 to Fig. 15. For a given c/ϒH, an increase in φ always gives rise to the increase in the safety factor as indicated in Fig. 13. For example, at c/ϒH = 0.47, the optimum FS equals 2.8 for φ = 0˚ and grows to 4.98 for φ = 40˚. In addition, for a constant φ, the maximum possible 8 safety factor improves linearly as c/ϒH goes up.

Variations in the optimum nail inclination angle (η) and the angle of slip surface (ν) with c/ϒH are illustrated in Fig. 14 and Fig. 15, respectively. As these figures show, an increase in φ leads to a rise in both η and ν. Besides, as c/ϒH grows, for any value of φ except for φ = 0˚ both η and ν first experience a sharp decline prior to c/ϒH≈0.5, keep decreasing smoothly to c/ϒH = 3 and remain almost unchanged afterward. Furthermore, for φ = 0˚, a change in c/ϒH does not have any meaningful influence on η and ν. Generally, regarding Figs. 14 and 15, it is clear that optimum values of η and ν alternate in a limited range with change in φ, so that η changes between 21˚ and 21.8˚ and ν is confined between 34.2˚ and 38˚. It can be reasoned that since all the contributing parameters to the internal stability of the wall are assumed constant, the overall stability of the wall is only influenced by the internal friction angle of the soil. In this regard, since the nails’ tensile force is not affected with ϕ, the internal friction angle has a limited effect on the overall factor of safety (as Fig. 13 shows), leading to insignificant variations in η and ν.

Fig. 14
figure 14

Optimum nail inclination angle versus c/ϒH for different values of φ

Full size image
Fig. 15
figure 15

Angle of inclination of failure surface (ν) against overall failure versus c/ϒH for different values of φ

Full size image

Effects of slope angle (α)

Effects of the slope orientation with respect to the vertical line (α) on the optimum design were evaluated through altering α between 0° and 50°. At the same time, other contributing parameters were kept constant as given on the margins of Figs. 16–18. As Fig. 16 shows, for a constant c/ϒH, an increase in α leads to an almost linear rise in the optimum safety factor. Regardless of the small initial fluctuation in FS, the nail inclination angle grows practically from 22° to 42° as α is increased from 0° to 50° for all c/ϒH values considered herein (Fig. 17). The following linear relation holds between ηopt and α (in degree) for the given input parameters represented on the margin of Fig. 17. The expressions similar to Eq. 18 are possible to obtain for other sets of contributing factors.

$$\eta_{opt} = 0.389 \alpha + 21.75$$
(18)
Fig. 16
figure 16

Maximum critical factor of safety against overall failure versus c/ϒH for different values of α

Full size image
Fig. 17
figure 17

Optimum nail inclination angle versus c/ϒH for different values of α

Full size image

However, for a certain α value, except for a small initial change (about 8% for α = 0° and less than 4% for other α values), ηopt remains approximately constant and is not influenced by c/ϒH (Fig. 17).

Besides, as evident in Fig. 18, the slip surface angle (ν) follows a descending trend as α increases. In addition, for a given α, the angle of slip surface first experiences a small drop prior to c/ϒH≈0.5 (less than 12% for all α values) and practically levels off afterward. Moreover, the increase in the FSmax with flattening the wall as shown in Fig. 16 can be justified with the change in the slip surface and nail inclination angles. The increase in the wall inclination angle reduces the slip surface angle (ν) and the increase in the η (Fig. 17 and Fig. 18). Firstly, the rise in ν leads to the rise in cos (ν), cos (ν + η), and the length of slip surface (L), and on the other hand, a reduction in sin (ν). Secondly, the increase in η increases sin (ν + η). Taking these two together yields an increase in the numerator and a reduction in the denominator in the FS equation (Eq. 5h), hence increasing the FSmax.

Fig. 18
figure 18

Angle of inclination of failure surface (ν) against overall failure versus c/ϒH for different values of α

Full size image

Effects of Back Slope Angle (β)

The influence of the back slope angle on the optimum design of slope nail walls was investigated considering β equal to 0°, 10°, 20°, 30°, 40°, and 50° while other parameters were kept constant. Besides, the effects of back slope angle on the design parameters (FSmax and ηopt) were studied at different slope orientations angle (α). For a vertical wall, α = 0°, variation in FS with c/ϒH for different β shown in Fig. 19 follows an increasing linear trend. However, at a constant c/ϒH, FS declines with the rise in β until β = 40° and stay constant afterward. As Fig. 20 indicates, for all β values, optimum nail inclination angle initially falls steeply with the increase in c/ϒH until approximately c/ϒH = 0.5 and gradually tends to a constant value thereafter. Furthermore, while ηopt alternates between a practically narrow range for β = 0° to β = 30° (from 22.73° at β = 0° and c/ϒH = 0 to 18.8° at β = 30° and c/ϒH greater than 0.5), relatively large decline in ηopt occurs for β = 40° and in particular for β = 50° as Fig. 21 shows. Analogously, as shown in Fig. 21, while the inclination angles of slip surface (ν) differ slightly from one another for β ≤ 30° as c/ϒH increases (about 5°), ν experiences an abrupt amplification for β > 30°, e.g., at c/ϒH = 0.5, β jumps from 37°, at β = 30°, to 51° at β = 50°.

Fig. 19
figure 19

Maximum critical factor of safety against overall failure versus c/ϒH for different values of β

Full size image
Fig. 20
figure 20

Optimum nail inclination angle versus c/ϒH for different values of β

Full size image
Fig. 21
figure 21

Angle of inclination of failure surface (ν) against overall failure, versus c/ϒH for different values of β

Full size image

Figure 22 indicates that similar to straight walls (α = 0°), FS follows a decreasing trend with an increase in β. For the parameters depicted on the margin of Fig. 22 (as well as Figs. 23 and 24), at α = 50° for instance, FS declines from 3.98 for β = 0° to 1.53 for β = 20° (Fig. 22). Besides, for a certain β, the optimum factor of safety improves following an increase in α (Fig. 22). For a given β value, the optimum inclination angle of nails grows with the rise in the slope angle α, as illustrated in Fig. 23. In addition, at a certain α, ηopt first decreases from β = 0° to β = 10° and ceases changing with an increase in β, except for α < 10° (Fig. 23). The slip surface angle (ν) is also affected by the change in β and α, as Fig. 24 suggests. At a given α, ν increases slightly, about 2°, for each 10° rise in β (Fig. 24). However, for a constant β, the slip surface angle declines almost linearly with an increase in α. For instance, for β = 20°, ν declines from 39.6° at α = 0° to 15 at α = 50° as Fig. 24 shows.

Fig. 22
figure 22

Variation in the factor of safety against overall failure versus α for different values of β

Full size image
Fig. 23
figure 23

Optimum nail inclination angle versus α for different values of β

Full size image
Fig. 24
figure 24

Angle of inclination of failure surface (ν) against overall failure versus α for different values of β

Full size image

Effects of Nail Arrangement

It is a common practice to spread nails evenly between the top and toe of a wall or slope. However, as some research works suggest, other possible nail arrangements might be more efficacious [6]. In the present study, nail alignment parameters (Sv, Sv top, Sv bot) were altered to form three different patterns, namely all nails collected in the upper 1/3 part, middle 1/3 part, and lower 1/3 part of the slope. Then, the results of the corresponding analysis were compared to the even distribution of nails. All patterns of nail arrangements considered in the present study and their related geometrical properties and measures are illustrated in Fig. 25. As Fig. 25 indicates, all model slopes are 8 m in height and are reinforced with five rows of nails having the same length.

Fig. 25
figure 25

Different soil arrangements and their geometrical properties. Nails collected: (a) in the bottom one-third of the wall height, (b) in the top one-third of the wall height, (c) in the middle one-third of the wall height, and (d) evenly distributed over the height of the wall

Full size image

Figure 26 shows the influence of different nail arrangements on the optimum overall safety factor with respect to different c/ϒH values. Constant parameters of the problem are depicted on the margin of Figs. 26, 27, and 28. As shown in Fig. 26, placing the nails in the lower 1/3 section leads to the highest safety factor, whereas the 1/3-top pattern results in the lowest FS value. This finding is in agreement with the conclusion made by Fan and Luo (2008) that nails located in the lower 1/3 part have the most significant effect on the stability of nail walls. In addition, as Fig. 26 suggests, irrespective of the measure of the c/ϒH, there is almost no difference between safety factors of models reinforced in the middle 1/3 part and those reinforced by the uniformly distributed nails. It can be reasoned that some of the nails are placed in the lower 1/3 part by evenly distribution of nails, some in the middle 1/3 region and the rest in the upper 1/3 part. Hence, the wall gains benefit from the nails placed in the lower 1/3 part and those in the middle 1/3 region. However, the number of nails in the 1/3 middle part in the even distribution of nails is less than the 1/3 middle arrangement. Since the nails in the lower 1/3 part are the most beneficial as shown in Fig. 26, they can compensate for the lower number of nails in the middle 1/3 part in the evenly distributed arrangement leading to an almost identical safety factor for these two nail arrangements. Furthermore, regardless of the nail arrangement, the safety factor follows an increasing trend as c/ϒH grows. It should be noted that since in practice, soil nail walls are constructed in phases and stability of each phase needs to be provided, inserting no nail in the upper and middle parts of the slope is practically impossible and may leave these unreinforced regions of the slope vulnerable to instability. Therefore, it can be concluded that the results of this study confirm that, on the whole, evenly distribution of the nails over the height of slope can be considered as the most reasonable arrangement.

Fig. 26
figure 26

Maximum critical factor of safety against overall failure versus c/ϒH for different nail arrangements

Full size image
Fig. 27
figure 27

Optimum nail inclination angle versus c/ϒH for different nail arrangements

Full size image
Fig. 28
figure 28

Optimum nail inclination angle versus c/ϒH for different nail arrangements

Full size image

The effects of the diversity of nail arrangements on the optimum nail inclination angle are depicted in Fig. 27. For a specified amount of c/ϒH, as Fig. 27 shows, η is the least if nails are embedded in the lower 1/3 part of the slope and takes its highest value if nails are performed in the top 1/3 section of the wall. It can be argued that since the nails positions in the upper part of the wall are in the furthest distance from the potential slip surface, they need to be inclined more, compared to other nail arrangements, to reach the slip surface to effectively contribute to the stability of slopes. Just as FS, whether nails are distributed evenly across the wall height or placed in the middle 1/3 part of the slope has little influence on η (Fig. 27). Besides, the nail inclination angle fluctuates only up to approximately c/ϒH = 0.5 and practically ceases to change afterward, as indicated in Fig. 27.

Variation in slip surface angle (ν) as shown in Fig. 28 suggests that ν increases as the levels of nails are changed from the lower 1/3 part to the upper 1/3 part of the wall such that the slip surface associated with the nails arranged in the middle 1/3 part are inclined at an angle ν between those of the lower and upper 1/3 height. In addition, as Fig. 28 indicates, inclination angles of slip surfaces associated with the uniform arrangement and middle 1/3 part arrangement are almost the same. Again, analogous to nail inclination angle, ν experiences changes up to about c/ϒH = 0.5 and levels off practically afterward (Fig. 28).

Summary and Conclusions

In the present study, taking advantage of the limit equilibrium approach and associated equations presented in FHWA code for soil nail walls, nail inclination angles were optimized to find the best (maximum) critical safety factor (SFmin) against overall slope failure. To achieve this, a combination of limit equilibrium relations and nonlinear programming has been employed. Effects of contributing factors such as nail diameter (dn), length of nails (z/H), soil internal friction angle, slope orientation with respect to the vertical line (α), back slope angle (β), and arrangement of nails on the optimum design parameters were investigated through extensive analyses. Results have been presented in the form of dimensionless parameters. Significant findings of the present study are as follows:

  1. (1)

    Analysis of the effect of nail diameter (dn) on the optimum design suggests that increasing dn/H up to a certain amount improves the stability (i.e., FS), and any further increase in dn beyond that would be practically inconclusive. Optimum nail inclination angle (ηopt) rises with the increase in dn/H and ceases to develop beyond a certain level of dn/H. Thus, regardless of the values of dn/H, FS is constantly increasing as c/ϒH goes up.

  2. (2)

    The increase in the length of nails (z) results in an abrupt rise in the safety factor up to z/H = 1.875 and is ineffective for z/H ≥ 5. It is argued that the increase in the overall safety factor of slopes is due to either intersection of nails and slip surface or the withdrawal of slip surface from the wall face, resulting in a broader failure surface. The same argument holds for the fluctuation of ηopt with change in z/H as well.

  3. (3)

    The increase in the internal friction angle of soil results in the rise in the safety factor against overall failure at any c/ϒH value. Furthermore, for a given φ, the safety factor grows linearly with c/ϒH. Results indicate that nail orientation angle increases with the rise in φ. Besides, for a constant φ, the nail inclination angle first declines sharply with an increase in c/ϒH and ceases changing at higher values of c/ϒH. Overall, variation in φ merely leads to a limited change in nail inclination angle. In addition, for frictionless soils (φ = 0), c/ϒH does not influence the ηopt value.

  4. (4)

    Steeper slopes have smaller optimum critical safety factors against overall failure. In addition, for a constant slope angle (α), an increase in c/ϒH leads to linear increase in FS. The nail inclination angle follows a growing linear trend as α goes up. Besides, except for a slight initial change, ηopt is practically constant for all c/ϒH values.

  5. (5)

    Steepening the back slope diminishes the factor of safety against overall failure as well as ηopt irrespective of the c/ϒH or α value. However, the decline in FS stops for β ≥ 40° while ηopt drops more extensively for β ≥ 40°.

  6. (6)

    Effects of nail arrangement in three different parts of the wall height: upper, middle, and lower 1/3 sections on the optimum design of the nail walls showed that embedding nails in the lower 1/3 part of the wall is the most beneficial layout. The lowest factor of safety is gained when nails are installed at the upper 1/3 part of the wall. Results indicate that uniform embedment of nails across the wall height and the middle 1/3-region arrangement leads to almost the same FS and ηopt. It is argued that since the soil nail walls are constructed in phases, evenly distribution of nails is the most effective layout in practice.

  7. (7)

    Dependency of the slip surface angle to the nail properties (diameter and length of the nails), as the results suggest, indicates that assuming the same critical slip surface of the unreinforced situation for analysis of reinforced slopes may lead to inaccurate results.

  8. (8)

    The constancy of the optimum nail inclination angle and the slip surface orientation beyond a certain c/ϒH value suggests that the stability of soil nail walls is dominated primarily by the cohesion of soil rather than the nails for short walls or highly cohesive soils.