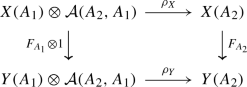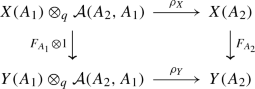Derived categories of NDG categories

Abstract

In this paper we study N-differential graded categories and their derived categories. First, we introduce modules over an N-differential graded category. Then we show that they form a Frobenius category and that its homotopy category is triangulated. Second, we study the properties of its derived category and give triangle equivalences of Morita type between derived categories of N-differential graded categories. Finally, we show that this derived category is triangle equivalent to the derived category of some ordinary differential graded category.

1 Preliminaries

The notion of N-complexes, that is, graded objects with N-differential d ($d^{N}=0$), was firstly considered by Mayer [13]. Afterwards it was formulated by Kapranov [8]. He also described the relation between an N-differential and a primitive N-th root q of unity. Dubois-Violette studied homological properties of N-complexes [2]. Yang and Ding showed that the homotopy category of N-complexes of an abelian category and its derived category are pretriangulated categories [18]. Afterwards, Iyama, Kato and Miyachi showed that they are triangulated categories [6]. Dubois-Violette and Kerner introduced N-differential ${\mathbb {N}}$-graded algebras, and studied homological properties [3, 4]. In this article, we study the derived category of an N-differential ${\mathbb {Z}}$-graded (NDG) category ${\mathcal {A}}$. In particular we study the homotopy category ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ of right NDG ${\mathcal {A}}$-modules and its derived category ${\mathsf {D}}_{Ndg}({\mathcal {A}})$.

Let k be a commutative ring, q a primitive N-th root of unity of k, U, V N-complexes of k-modules. Let $U\otimes _qV$ be the tensor product $(\coprod _{n \in {\mathbb {Z}}}(U{\otimes }V)^{n}, d_{U\otimes _qV}(u\otimes v))$ where $(U{\otimes }V)^{n}=\coprod _{r+s=n}U^r\otimes V^s$ with an N-differential $d_{U\otimes _qV}(u\otimes v)=d_U(u)\otimes v+q^r u\otimes d_V(v)$ for any $u \in U^r$ and $v\in V$. Then $U\otimes _qV$ is also an N-complex of k-modules [8]. An N-complex of k-modules $V\otimes _qU$ is also defined. But $V\otimes _qU$ is not isomorphic to $U\otimes _qV$ in the case of $N>2$ (Lemma 3.2). Moreover it is difficult to find the tensor product of NDG algebras [17]. This situation implies the difficulty to deal with NDG modules, especially NDG bi-modules as functors from NDG categories. Therefore we deal with NDG modules using module-theoretical language (Definitions 3.3, 3.7). In the language of monoidal categories (e.g. [10]), this difficulty is due to the fact that the category $C_{Ndg}(k)$ of N-complexes of k-modules is a non-symmetric biclosed monoidal category for $N>2$ (Remarks 3.3, 3.5).

In Sect. 2 we give some formulas on q-numbers. We use these formulas to describe NDG modules with complicated scalar multiplication of NDG categories.

In Sect. 3, we define an NDG category ${\mathcal {A}}$ with respect to q (=$N_q$DG category), and a right NDG ${\mathcal {A}}$-module, that is a graded module with right scalar multiplication of ${\mathcal {A}}$. In the language of enriched categories (e.g. [10]), an $N_q$DG category ${\mathcal {A}}$ is an enriched category over ${\mathcal {V}}=C_{Ndg}(k)$, and left NDG ${\mathcal {A}}$-modules are ${\mathcal {V}}$-functors (Remark 3.5). We show the following two results are obtained similar to the case of N-complexes [6]. First, we show that the category ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ of right NDG ${\mathcal {A}}$-modules is a Frobenius category (Corollary 3.2). Second, we show that the homotopy category ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ is an algebraic triangulated category (Theorem 3.1). In the case of $N>2$, ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ has two auto-equivalences: the shift functor $\theta _q$ of grading and the suspension functor $\Sigma$ as a triangulated category. Then the functor $\Sigma ^2$ is isomorphic to $\theta ^N_q$ as auto-equivalences of ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ (Theorem 3.2). Furthermore, we define an NDG ${\mathcal {B}}$-${\mathcal {A}}$-bimodule M, and we have triangle functors

$$\begin{aligned}\begin{aligned} {\text {Hom}}_{q, {{\mathcal {A}}}}(M, -): {\mathsf {K}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {K}}_{Ndg}({\mathcal {B}}),&-\otimes _{q, {{\mathcal {B}}}}M: {\mathsf {K}}_{Ndg}({\mathcal {B}}) \rightarrow {\mathsf {K}}_{Ndg}({\mathcal {A}}) , \end{aligned}\end{aligned}$$

such that $-\otimes _{q, {{\mathcal {B}}}} M$ is the left adjoint to ${\text {Hom}}_{q, {{\mathcal {A}}}}(M, -)$ (Theorems 3.3).

In Sect. 4, we describe the derived category ${\mathsf {D}}_{Ndg}({\mathcal {A}})$ of right NDG ${\mathcal {A}}$-modules, and the derived functors ${\mathbb {R}}{\text {Hom}}_{q, {{\mathcal {A}}}}(M, -): {\mathsf {D}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {D}}_{Ndg}({\mathcal {B}}), \ -\overset{{\mathbb {L}}}{\otimes }_{q, {{\mathcal {B}}}}M: {\mathsf {D}}_{Ndg}({\mathcal {B}}) \rightarrow {\mathsf {D}}_{Ndg}({\mathcal {A}}) .$ First, we show that the derived category ${\mathsf {D}}_{Ndg}({\mathcal {A}})$ is a compactly generated algebraic triangulated category (Theorems 4.1, 4.2). Second, we have the necessary and sufficient conditions for the above derived functors to be equivalences (Theorem 4.3). Finally, we show that the derived category ${\mathsf {D}}_{Ndg}({\mathcal {A}})$ is triangle equivalent to the derived category of some ordinary differential graded category (Theorem 4.4).

Throughout this note we fix a positive integer $N \ge 2$ and a commutative ring k with unity 1 and we assume that k has a primitive N-th root q of 1. We will write ${\text {Hom}}$ and $\otimes$ for ${\text {Hom}}_k$ and $\otimes _k$.

2 q-Numbers

In this section, we collect some formulas on q-numbers. We will omit proofs of some elementary facts. For a commutative ring k with unity 1 and a positive integer $N \ge 2$, we say that an element q of k is a primitive Nth root of 1 if $q^N-1=0$ and $q^l-1$ is a non-zero-divisor for any $1 \le l \le N-1$. Then $[m]=1+ q + \cdots + q^{m-1}$ is a non-zero-divisor for $1 \le m <N$, and $[N]=0$. We define q-numbers in the total quotient ring K of k. For any positive integer m, $[m]!=[m][m-1]\cdots [1]$ and $[0]!=1$. For $0 \le l \le m \le N$ with $(l, m)\ne (N, N)$ nor (0, N),

$$\begin{aligned} \begin{bmatrix} m \\ l \\ \end{bmatrix} =\frac{[m]!}{[l]![m-l]!} \end{aligned}$$

and

$$\begin{aligned} \begin{bmatrix} N \\ N \\ \end{bmatrix} = \begin{bmatrix} N \\ 0 \\ \end{bmatrix} =1. \end{aligned}$$

Then we have $\begin{bmatrix} m \\ l \\ \end{bmatrix}= \begin{bmatrix} m \\ m-l \\ \end{bmatrix}$.

By the following lemma, we can consider $\begin{bmatrix} m \\ l \\ \end{bmatrix}$ lies in k through the canonical injection $k \rightarrow K$.

Lemma 2.1

For $1 \le l < m \le N$,

$$\begin{aligned} \begin{bmatrix} m-1 \\ l-1 \\ \end{bmatrix} +\begin{bmatrix} m-1 \\ l \\ \end{bmatrix} q^{l} =\begin{bmatrix} m \\ l \\ \end{bmatrix}, \\ \begin{bmatrix} m-1 \\ l-1 \\ \end{bmatrix} q^{m-l} +\begin{bmatrix} m-1 \\ l \\ \end{bmatrix} =\begin{bmatrix} m \\ l \\ \end{bmatrix}. \end{aligned}$$

We show the following lemma for the lemma after the next.

Lemma 2.2

For $1 \le t \le N$.

$$\begin{aligned} \sum ^{t}_{j=0}(-1)^{j}q^{\frac{j(j-1)}{2}}\begin{bmatrix} t \\ j \\ \end{bmatrix}=0. \end{aligned}$$

Proof

Set $a_t=\sum ^{t}_{j=0}(-1)^{j}q^{\frac{j(j-1)}{2}}\begin{bmatrix} t \\ j \\ \end{bmatrix}$. We have that $a_1=1-1=0$. For any $2 \le t \le N$, by Lemma 2.1,

$$\begin{aligned} a_t&=\sum ^{t-1}_{j=0}(-1)^{j}q^{\frac{j(j-1)}{2}}\begin{bmatrix} t-1 \\ j \\ \end{bmatrix} +\sum ^{t}_{j=1}(-1)^{j}q^{\frac{j(j-1)}{2}}\begin{bmatrix} t-1 \\ j-1 \\ \end{bmatrix}q^{t-j}\\&=a_{t-1}-q^{t-1}a_{t-1}. \end{aligned}$$

Therefore $a_t=0$ for any $1\le t \le N$. $\square$

Lemma 2.3

Let n be an integer with $1 \le n \le N$ and X a k-module. For any morphisms $\phi$, $\psi \in {\text {Hom}}(X, X)$ with $\psi \phi = q\phi \psi$, the following hold.

• (1) $(\phi +\psi )^n= \sum _{l=0}^n \begin{bmatrix} n \\ l \\ \end{bmatrix}\phi ^{n-l}\psi ^l$,

• (2) $\phi ^n= \sum _{l=0}^n (-1)^lq^{\frac{l(l-1)}{2}}\begin{bmatrix} n \\ l \\ \end{bmatrix}(\phi +\psi )^{n-l}\psi ^l.$

Proof

Set $a_n=\sum _{l=0}^n \begin{bmatrix} n \\ l \\ \end{bmatrix}\phi ^{n-l}\psi ^l$. By Lemma 2.1,

$$\begin{aligned} a_n=&\sum _{l=0}^{n-1} \begin{bmatrix} n-1 \\ l \\ \end{bmatrix}\phi ^{n-l}\psi ^l+ \sum _{l=1}^{n} \begin{bmatrix} n-1 \\ l-1 \\ \end{bmatrix}q^{n-l}\phi ^{n-l}\psi ^l\\&= \phi \sum _{l=0}^{n-1} \begin{bmatrix} n-1 \\ l \\ \end{bmatrix}\phi ^{n-1-l}\psi ^l+ \psi \sum _{l=1}^{n} \begin{bmatrix} n-1 \\ l-1 \\ \end{bmatrix}\phi ^{n-l}\psi ^{l-1}\\&= (\phi +\psi )a_{n-1}\\&= (\phi +\psi )^n . \end{aligned}$$

Set $b_n=\sum _{l=0}^n (-1)^lq^{\frac{l(l-1)}{2}}\begin{bmatrix} n \\ l \\ \end{bmatrix}(\phi +\psi )^{n-l}\psi ^l$. By Lemma 2.3 (1),

$$\begin{aligned} b_n=&\sum _{l=0}^n (-1)^lq^{\frac{l(l-1)}{2}}\begin{bmatrix} n \\ l \\ \end{bmatrix} \sum _{j=0}^{n-l} \begin{bmatrix} n-l \\ j \\ \end{bmatrix}\phi ^{n-l-j}\psi ^j\psi ^l\\&= \sum _{l=0}^n\sum _{j=0}^{n-l}(-1)^lq^{\frac{l(l-1)}{2}}\begin{bmatrix} n \\ l \\ \end{bmatrix} \begin{bmatrix} n-l \\ j \\ \end{bmatrix}\phi ^{n-(l+j)}\psi ^{l+j}\\&= \sum _{l=0}^n\sum _{j=0}^{n-l}(-1)^lq^{\frac{l(l-1)}{2}}\begin{bmatrix} l+j \\ l \\ \end{bmatrix} \begin{bmatrix} n \\ l+j \\ \end{bmatrix}\phi ^{n-(l+j)}\psi ^{l+j}\\&= \sum _{t=0}^n\left( \sum _{l=0}^{t}(-1)^lq^{\frac{l(l-1)}{2}}\begin{bmatrix} t \\ l \\ \end{bmatrix}\right) \begin{bmatrix} n \\ t \\ \end{bmatrix}\phi ^{n-t}\psi ^{t}. \end{aligned}$$

By Lemma 2.2, $b_n=\phi ^n$. $\square$

We prepare the following lemma also, which will be used later.

Lemma 2.4

For any $1\le t \le N-1$ and $0 \le l \le N-t$,

$$\begin{aligned} (-1)^lq^{lt+\frac{l(l-1)}{2}}\begin{bmatrix} N-t \\ l\\ \end{bmatrix} =\begin{bmatrix} l+t-1 \\ l \\ \end{bmatrix} . \end{aligned}$$

In particular, $(-1)^{l}q^{\frac{l(l+1)}{2}} \begin{bmatrix} N-1 \\ l \\ \end{bmatrix}=1$ for $0 \le l \le N-1$.

Proof

Since $[j]+q^{j}[N-j]=[N]=0$ for any $1 \le j \le N-1$,

$$\begin{aligned}{}[t][t\!+\!1]\cdots [t\!+\!l\!-\!1]\!=\!(-1)^lq^{lt+\frac{j(j+1)}{2}}[N-t][N-(t+1)]\cdots [N-(t+l-1)] \end{aligned}$$

for $l \ge 1$. Hence

$$\begin{aligned} (-1)^lq^{lt+\frac{l(l-1)}{2}}\begin{bmatrix} N-t \\ l\\ \end{bmatrix} =\begin{bmatrix} l+t-1 \\ l \\ \end{bmatrix}. \end{aligned}$$

$\square$

3 NDG categories

In this section, we introduce N-differential graded (NDG) modules over an NDG category and give the definition of some categories.

We recall the definition of the category of ${\mathbb {Z}}$-graded k-modules. The category ${\mathsf {Gr}}(k)$ of ${\mathbb {Z}}$-graded k-modules is defined as follows:

• (1) An object is a ${\mathbb {Z}}$-graded k-module $U=\coprod _{i \in {\mathbb {Z}}}U^i$.

• (2) The morphism set between U and V is given by

  $$\begin{aligned} {\text {Hom}}_{{\mathsf {Gr}}(k)}(U, V):=\coprod _{i \in {\mathbb {Z}}}{\text {Hom}}^i(U, V) \end{aligned}$$

  where

  $$\begin{aligned} {\text {Hom}}^i(U, V):=\prod _{l \in {\mathbb {Z}}}{\text {Hom}}(U^l,V^{l+i}). \end{aligned}$$

  The composition

  $$\begin{aligned} {\text {Hom}}_{{\mathsf {Gr}}(k)}(V, W) \otimes {\text {Hom}}_{{\mathsf {Gr}}(k)}(U, V) \rightarrow {\text {Hom}}_{{\mathsf {Gr}}(k)}(U, W), \; f \otimes g \mapsto fg \end{aligned}$$

  is k-bilinear and homogeneous of degree 0.

The category ${\mathsf {Gr}}^0(k)$ is the subcategory of ${\mathsf {Gr}}(k)$ whose objects are same as ${\mathsf {Gr}}(k)$ and the morphism set between X and Y is given by

$$\begin{aligned} {\text {Hom}}_{{\mathsf {Gr}}^0(k)}(X, Y)={\text {Hom}}^0(X, Y). \end{aligned}$$

3.1 NDG k-modules

In this subsection we study N-differential graded (NDG) k-modules.

A sequence $X=(X, d_X)$ of k-modules is called an NDG k-module if a ${\mathbb {Z}}$-graded k-module X endowed with $d_X \in {\text {Hom}}_{{\mathsf {Gr}}(k)}^1(X, X)$ satisfying $d_X^{\{N\}}=0$. Here $d^{\{i\}}$ means the i-th power of d. The category ${\mathsf {C}}_{Ndg}(k)$ of NDG k-modules is defined as follows:

• (1) Objects are NDG k-modules.

• (2) The morphism set between $X=(X, d_X)$ and $Y=(Y,d_Y)$ is given by

  $$\begin{aligned} {\text {Hom}}_{{\mathsf {C}}_{Ndg}(k)}(X, Y)=\{ f \in {\text {Hom}}^0(X, Y) \mid f\circ d_X=d_Y\circ f\} \end{aligned}$$

  and the composition is given by the composition of maps.

Remark 3.1

It is easy to see that ${\mathsf {C}}_{Ndg}(k)$ and ${\mathsf {Gr}}^0(k)$ are abelian categories with ordinary exact sequences.

For NDG k-modules U and V, a sequence ${\text {Hom}}_q(U, V)$ is defined as follows.

$$\begin{aligned} {\text {Hom}}_q(U, V):={\text {Hom}}_{{\mathsf {Gr}}(k)}(U, V) \end{aligned}$$

and

$$\begin{aligned} d_{{\text {Hom}}_q(U, V)}(f)=d_V\circ f-q^rf\circ d_U \end{aligned}$$

for any $f \in {\text {Hom}}^r(U, V)$. A sequence $U\otimes _qV$ is defined as follows.

$$\begin{aligned} U\otimes _qV=\coprod _{i \in {\mathbb {Z}}}(U\otimes V)^{i} \end{aligned}$$

where

$$\begin{aligned} (U\otimes V)^{i} =\coprod _{l+m=i}U^l\otimes V^m \end{aligned}$$

for any $i \in {\mathbb {Z}}$, and

$$\begin{aligned} d_{U\otimes _qV}(u\otimes v)=d_U(u)\otimes v+q^su\otimes d_V(v) \end{aligned}$$

for any $u \in U^s$ and $v\in V$.

Then we have the following lemma.

Lemma 3.1

For any $n \in {\mathbb {N}}$ with $1\le n \le N$ and sequences of k-modules U and V, the following hold.

• (1) For any $f \in {\text {Hom}}^r(U, V)$,

  $$\begin{aligned} d_{{\text {Hom}}_q(U, V)}^{\{n\}}(f)=\sum ^{n}_{l=0}(-1)^lq^{lr+\frac{l(l-1)}{2}} \begin{bmatrix} n \\ l \\ \end{bmatrix}d^{\{n-l\}}_V\circ f\circ d^{\{l\}}_U. \end{aligned}$$

• (2) For any $u \in U^s$ and $v \in V$,

  $$\begin{aligned} d_{U\otimes _qV}^{\{n\}}(u\otimes v)=\sum ^n_{l=0}q^{ls} \begin{bmatrix} n \\ l \\ \end{bmatrix}d^{\{n-l\}}_U(u)\otimes d^{\{l\}}_V(v). \end{aligned}$$

Proof

For any $f \in {\text {Hom}}^r(U, V)$, set $\phi (f)=d_V\circ f$ and $\psi (f)=-q^rf\circ d_U$, then $d_{{\text {Hom}}_q(U, V)}(f)=(\phi +\psi )(f)$ and $\psi \phi (f)=q\phi \psi (f)$. By Lemma 2.3,

$$\begin{aligned} d_{{\text {Hom}}_q(U, V)}^{\{n\}}(f)=&(\phi +\psi )^n(f)\\&= \sum _{l=0}^n \begin{bmatrix} n \\ l \\ \end{bmatrix}\phi ^{n-l}\psi ^l(f)\\&= \sum ^{n}_{l=0}(-1)^lq^{lr+\frac{l(l-1)}{2}} \begin{bmatrix} n \\ l \\ \end{bmatrix}d^{\{n-l\}}_V\circ f\circ d^{\{l\}}_U. \end{aligned}$$

For any $u \in U^s$, $v \in V$, set $\phi (u\otimes v)=d_U(u)\otimes v$ and $\psi (u\otimes v)=q^su\otimes d_V(v)$, then $d_{U\otimes _qV}(u\otimes v)=(\phi +\psi )(u\otimes v)$ and $\psi \phi (u\otimes v)=q\phi \psi (u\otimes v)$. By Lemma 2.3,

$$\begin{aligned} d_{U\otimes _qV}^{\{n\}}(u\otimes v)=&(\phi +\psi )^n(u\otimes v)\\&= \sum _{l=0}^n \begin{bmatrix} n \\ l \\ \end{bmatrix}\phi ^{n-l}\psi ^l(u\otimes v)\\&= \sum ^n_{l=0}q^{ls} \begin{bmatrix} n \\ l \\ \end{bmatrix}d^{\{n-l\}}_U(u)\otimes d^{\{l\}}_V(v). \end{aligned}$$

$\square$

Corollary 3.1

([8]) For NDG k-modules U and V, the sequences ${\text {Hom}}_q(U, V)$ and $U\otimes _qV$ are NDG k-modules.

Proof

Since $0=[N]!=[l]![N-l]!\begin{bmatrix} N \\ l \\ \end{bmatrix}$ and $[l]![N-l]!$ is a non-zero-divisor for any $1 \le l \le N-1$, we have $\begin{bmatrix} N \\ l \\ \end{bmatrix}=0$ for any $1 \le l \le N-1$. By Lemma 3.1,

$$\begin{aligned} d_{{\text {Hom}}_q(U, V)}^{\{N\}}(f)=d^{\{N\}}_V\circ f+(-1)^{N}q^{\frac{N(N-1)}{2}}f\circ d^{\{N\}}_U=0 \end{aligned}$$

for any $f \in {\text {Hom}}(U, V)$. Similarly we have $d_{U\otimes _qV}^{\{N\}}=0$. $\square$

The following lemma is easy to check.

Lemma 3.2

For NDG k-modules U, V and W, the following hold.

• (1) We have the canonical isomorphism $(U\otimes _qV)\otimes _qW \simeq U\otimes _q(V\otimes _qW)$ in ${\mathsf {C}}_{Ndg}(k)$.

• (2) V induces the functors $V\otimes _q-: {\mathsf {C}}_{Ndg}(k) \rightarrow {\mathsf {C}}_{Ndg}(k)$, $- \otimes _qV: {\mathsf {C}}_{Ndg}(k) \rightarrow {\mathsf {C}}_{Ndg}(k)$.

• (3) V induces the functors ${\text {Hom}}_q(V, -) : {\mathsf {C}}_{Ndg}(k) \rightarrow {\mathsf {C}}_{Ndg}(k)$, ${\text {Hom}}_q(-, V): {\mathsf {C}}_{Ndg}(k) \rightarrow {\mathsf {C}}_{Ndg}(k)$.

• (4) We have the canonical isomorphism

  $$\begin{aligned} {\text {Hom}}_{{\mathsf {C}}_{Ndg}(k)}(U\otimes _qV,W) \simeq {\text {Hom}}_{{\mathsf {C}}_{Ndg}(k)}(U, {\text {Hom}}_q(V, W)). \end{aligned}$$

• (5) We have an isomorphism $U\otimes _qV \simeq V\otimes _{q^{-1}}U$ in ${\mathsf {C}}_{Ndg}(k)$.

• (6) We have an isomorphism

  $$\begin{aligned}{\text {Hom}}_{{\mathsf {C}}_{Ndg}(k)}(U\otimes _qV,W) \simeq {\text {Hom}}_{{\mathsf {C}}_{Ndg}(k)}(V, {\text {Hom}}_{q^{-1}}(U, W)). \end{aligned}$$

Proof

(1), (2), (3) It is easy.

(4) By the ordinary isomorphism ${\text {Hom}}(U^r\otimes V^s, W^{r+s}) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}(U^r {\text {Hom}}(V^s, W^{r+s}))$, it is easy to check.

(5) The morphism $U\otimes _qV \rightarrow V\otimes _{q^{-1}}U$ which is defined by $U^r\otimes V^s \rightarrow V^s\otimes U^r ~(u\otimes v \mapsto q^{-rs}v \otimes u)$ is an isomorphism in ${\mathsf {C}}_{Ndg}(k)$.

(6) By (4) and (5). $\square$

Remark 3.2

In the above $V\otimes _q-$ (resp., ${\text {Hom}}_q(V,-)$) is left (resp., right) exact in the sense of Remark 3.1.

Remark 3.3

Since the canonical morphisms $k\otimes _qV \rightarrow V$ and $V\otimes _qk \rightarrow V$ are obviously isomorphisms, by Lemma 3.2${\mathcal {V}}:=C_{Ndg}(k)$ is a non-symmetric biclosed monoidal category with the internal-homs ${\text {Hom}}_q(-,-)$ and ${\text {Hom}}_{q^{-1}}(-,-)$ for $N>2$.

3.2 NDG categories

In this subsection, we give the definition of an N-differential graded (NDG) category with respect to a primitive N-th root q of 1 and the definition of the homotopy category of an NDG category.

Definition 3.1

An $N_q$DG category ${\mathcal {A}}$ is defined by the following datum.

• (1) A class of objects $Ob{\mathcal {A}}$.

• (2) The morphism set

  $$\begin{aligned} {\mathcal {A}}(A, B)=\coprod _{i \in {\mathbb {Z}}}{\mathcal {A}}^i(A, B) \end{aligned}$$

  which is an NDG k-module for any A and B in $Ob{\mathcal {A}}$, and the composition

  $$\begin{aligned}\begin{array}{rll} \mu : &{} {\mathcal {A}}(B,C)\otimes _q{\mathcal {A}}(A,B) \rightarrow {\mathcal {A}}(A,C) &{} \text{ in }~{\mathsf {C}}_{Ndg}(k). \\ &{} (f \otimes g \mapsto fg) \end{array}\end{aligned}$$

  That is, $\mu \circ (\mu \otimes 1)=\mu \circ (1\otimes \mu )$ in ${\mathsf {C}}_{Ndg}(k)$.

The above condition that $\mu$ lies in ${\mathsf {C}}_{Ndg}(k)$ is equivalent to that $\mu$ lies in ${\mathsf {Gr}}^0(k)$ and satisfies $d_{{\mathcal {A}}(A,C)}\circ \mu =\mu \circ d_{{\mathcal {A}}(B,C)\otimes _q{\mathcal {A}}(A,B)},$ namely,

$$\begin{aligned} d(fg)=d(f)g+q^rfd(g) \end{aligned}$$

for any $f \in {\mathcal {A}}^r(B,C)$ and $g \in {\mathcal {A}}(A,B)$.

Example 3.1

Let $N_qdg(k)$ (resp., $N_{q^{-1}}dg(k)$) be the category of NDG k-modules of which morphism sets are ${\text {Hom}}_q(X, Y)$ (resp., ${\text {Hom}}_{q^{-1}}(X,Y)$) for all NDG k-modules X, Y. Then $N_qdg(k)$ (resp., $N_{q^{-1}} dg(k)$) is a $N_q$DG (resp., $N_{q^{-1}}$DG) category.

In the language of enriched categories, by Remark 3.3${\mathcal {V}}_q=N_qdg(k)$ and ${\mathcal {V}}_{q^{-1}}=N_{q^{-1}}dg(k)$ are enriched categories over ${\mathcal {V}}$ induced by the internal-homs ${\text {Hom}}_q(-,-)$ and ${\text {Hom}}_{q^{-1}}(-,-)$, respectively. Since ${\mathcal {V}}$ is non-symmetric for $N>2$, ${\mathcal {V}}_q$ is not equivalent to ${\mathcal {V}}_{q^{-1}}$ in general.

We give the definitions of right NDG modules over an $N_q$DG category and morphisms between these modules.

Definition 3.2

Let ${\mathcal {A}}$ be a $N_q$DG category. A right graded ${\mathcal {A}}$-module $X=(X ; \rho _X)$ is a collection of a graded k-module X(A) for any object A in ${\mathcal {A}}$ with a homogeneous morphism of degree 0 as a scalar multiplication

$$\begin{aligned}\begin{array}{rll} \rho _X : &{} X(A_1)\otimes {\mathcal {A}}(A_2, A_1) \rightarrow X(A_2) &{} \hbox { in}\ {\mathsf {Gr}}^0(k) \\ &{} ( x\otimes f \mapsto xf) \end{array}\end{aligned}$$

satisfying

• (1) $x1_{A}=x$ for any $A \in {\mathcal {A}}$, $x \in X(A)$ and $1_{A} \in {\mathcal {A}}(A, A)$.

• (2) $\rho _X\circ (1\otimes \mu )=\rho _X\circ (\rho _X\otimes 1)$ in ${\mathsf {Gr}}^0(k)$.

Namely, we have $x(fg)=(xf)g$ for any $x \in X(A_1)$, $f \in {\mathcal {A}}(A_2, A_1)$, $g\in {\mathcal {A}}(A_3, A_2)$ and any $A_1, A_2, A_3 \in {\mathcal {A}}$.

The category ${\mathsf {Gr}}^0({\mathcal {A}})$ of right graded ${\mathcal {A}}$-modules is defined by the following datum:

• (3) objects are right graded ${\mathcal {A}}$-modules.

• (4) For right graded ${\mathcal {A}}$-modules$X=(X; \rho _X), Y=(Y; \rho _Y)$, a morphism $F:X \rightarrow Y$ is defined by a collection of morphisms $F_A: X(A) \rightarrow Y(A)$ in ${\mathsf {Gr}}^0(k)$ such that

  

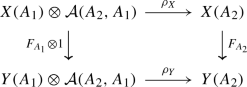
  is commutative in ${\mathsf {Gr}}^0(k)$.

Definition 3.3

A right NDG ${\mathcal {A}}$-module $X=(X, d_X; \rho _X)$ is a collection of an NDG k-module $X(A)=(X(A), d_{X(A)})$ for any object A of ${\mathcal {A}}$ with a homogeneous morphism of degree 0 as a scalar multiplication

$$\begin{aligned}\begin{array}{rll} \rho _X : X(A_1)\otimes _q{\mathcal {A}}(A_2, A_1) \rightarrow X(A_2)&\hbox { in}\ {\mathsf {C}}_{Ndg}(k) \end{array}\end{aligned}$$

satisfying

• (1) $x1_{A}=x$ for any $A \in {\mathcal {A}}$, $x \in X(A)$ and $1_{A} \in {\mathcal {A}}(A, A)$.

• (2) $\rho _X\circ (1\otimes \mu )=\rho _X\circ (\rho _X\otimes 1)$ in ${\mathsf {C}}_{Ndg}(k)$.

The category ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ of right NDG ${\mathcal {A}}$-modules is defined by the following datum:

• (3) objects are right NDG ${\mathcal {A}}$-modules.

• (4) For right NDG ${\mathcal {A}}$-modules$X=(X, \rho _X), Y=(Y, \rho _Y)$, a morphism $F:X \rightarrow Y$ is defined by a collection of morphisms $F_A: X(A) \rightarrow Y(A)$ in ${\mathsf {C}}_{Ndg}(k)$ such that

  

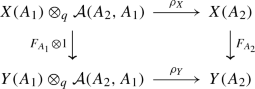
  is commutative in ${\mathsf {C}}_{Ndg}(k)$.

Similarly, left graded ${\mathcal {A}}$-modules and left NDG ${\mathcal {A}}$-modules are defined.

Remark 3.4

As well as Remark 3.1, it is easy to see that ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ and ${\mathsf {Gr}}^0({\mathcal {A}})$ are abelian categories with ordinary exact sequences.

Remark 3.5

For ${\mathcal {V}}=C_{Ndg}(k)$, by Lemma 3.2 we know that the above definition of left NDG ${\mathcal {A}}$-modules is equivalent to covariant ${\mathcal {V}}$-functors from ${\mathcal {A}}$ to ${\mathcal {V}}_q$ (see Example 3.1). But by the language of ${\mathcal {V}}$-functors, right NDG ${\mathcal {A}}$-modules are defined by contravariant ${\mathcal {V}}$-functors from ${\mathcal {A}}$ to ${\mathcal {V}}_{q^{-1}}$, because the opposite category ${\mathcal {A}}^{op}$ of an $N_q$DG category ${\mathcal {A}}$ is an $N_{q^{-1}}$DG category. Therefore in the case of $N >2$ it is difficult to define contravariant ${\mathcal {V}}$-functors, especially ${\mathcal {V}}$-bifunctors on the same ground (see also Definition  3.7).

Example 3.2

For any $N_q$DG category ${\mathcal {A}}$ and any object A of ${\mathcal {A}}$, $A\,\hat{}={\mathcal {A}}(-, A)$ is a right NDG ${\mathcal {A}}$-module and $\;\hat{}A={\mathcal {A}}(A, -)$ is a left NDG ${\mathcal {A}}$-module.

Let ${\mathcal {A}}$ be an $N_q$DG category. A homogeneous morphism $F : X \rightarrow Y$ of degree n between right graded ${\mathcal {A}}$-modules X and Y is a collection of $F_A$ in ${\text {Hom}}^n(X(A), Y(A))$ for any object A of ${\mathcal {A}}$ satisfying

$$\begin{aligned} F_{A_2}(xf)=F_{A_1}(x)f \end{aligned}$$

for any $x \in X(A_1)$ and $f \in {\mathcal {A}}(A_2, A_1)$.

We denote by ${\text {Hom}}_{{\mathcal {A}}}^n(X, Y)$ the set of homogeneous morphisms of degree n between right graded ${\mathcal {A}}$-modules X and Y. For $F \in {\text {Hom}}_{{\mathcal {A}}}^n(X, Y)$ and $G \in {\text {Hom}}_{{\mathcal {A}}}^m(Y, Z)$, we define $(GF)_A=G_AF_A$, so $GF \in {\text {Hom}}_{{\mathcal {A}}}^{n+m}(X, Z)$.

Definition 3.4

Let ${\mathcal {A}}$ be an $N_q$DG category. The category ${\mathsf {Gr}}({\mathcal {A}})$ of right graded ${\mathcal {A}}$-modules is defined as follows.

• (1) Objects are right graded ${\mathcal {A}}$-modules.

• (2) The morphism set between X and Y is given by

  $$\begin{aligned} {\text {Hom}}_{{\mathsf {Gr}}({\mathcal {A}})}(X, Y)=\coprod _{i \in {\mathbb {Z}}}{\text {Hom}}_{{\mathcal {A}}}^i(X, Y). \end{aligned}$$

To give the definition of a homotopy category ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ of an $N_q$DG category ${\mathcal {A}}$, we show the following three lemmas.

Lemma 3.3

Let ${\mathcal {A}}$ be an $N_q$DG category, X, Y right NDG ${\mathcal {A}}$-modules. For any $F\in {\text {Hom}}_{{\mathcal {A}}}^{i}(X, Y)$ and $i \in {\mathbb {Z}}$, we have

$$\begin{aligned} d_Y\circ F-q^iF\circ d_X \in {\text {Hom}}_{{\mathcal {A}}}^{i+1}(X, Y) . \end{aligned}$$

Therefore, $(\coprod _{i\in {\mathbb {Z}}}{\text {Hom}}_{{\mathcal {A}}}^i(X, Y), (d_Y\circ (-) -q^i(-)\circ d_X)_{i \in {\mathbb {Z}}})$ is an NDG k-module. We denote $(\coprod _{i\in {\mathbb {Z}}}{\text {Hom}}_{{\mathcal {A}}}^i(X, Y), (d_Y\circ (-) -q^i(-)\circ d_X)_{i \in {\mathbb {Z}}})$ by

$$\begin{aligned}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)=({\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y), d_{{\text {Hom}}_{q, {{\mathcal {A}}}}(X,Y)}) . \end{aligned}$$

Proof

Given $F \in {\text {Hom}}_{{\mathcal {A}}}^i(X, Y)$, for any $x \in X^s(A_1)$ and $f \in {\mathcal {A}}(A_2, A_1)$,

$$\begin{aligned} (d_{{\text {Hom}}_{q, {{\mathcal {A}}}} (X, Y)}(F))_{A_2}(xf) =&\, (d\circ F_{A_2}-q^iF_{A_2}\circ d)(xf)\\ =&\, d(F_{A_1}(x)f)-q^iF_{A_2}(d(x)f+q^sxd(f))\\ =&\, d(F_{A_1}(x))f+q^{s+i}F_{A_1}(x)d(f)\\&-q^i(F_{A_1}(d(x))f+q^sF_{A_1}(x)d(f))\\ =&\, d(F_{A_1}(x))f-q^iF_{A_1}(d(x))f\\ =&\, (d_{{\text {Hom}}_{q, {{\mathcal {A}}}} (X, Y)}(F))_{A_1}(x)f. \end{aligned}$$

Hence we have $d_{{\text {Hom}}_{q, {{\mathcal {A}}}}(X,Y)} \in {\text {Hom}}_{{\mathcal {A}}}^{i+1}(X,Y)$. $\square$

In the case that ${\mathcal {V}}$ is a symmetric monoidal category, there is “Yoneda’s lemma” for covariant ${\mathcal {V}}$-functors. We have also “Yoneda’s lemma” for right NDG ${\mathcal {A}}$-modules.

Lemma 3.4

For any right NDG ${\mathcal {A}}$-module X and any object A of ${\mathcal {A}}$,

$$\begin{aligned} {\text {Hom}}_{q, {{\mathcal {A}}}}(A\,\hat{}, X)\simeq X(A) ~\text{ in }~ {\mathsf {C}}_{Ndg}(k). \end{aligned}$$

In particular, ${\text {Hom}}^{n}_{{\mathcal {A}}}(A\,\hat{}, X)\simeq X(A)^n$ for any n.

Proof

Define $\phi : {\text {Hom}}_{q, {{\mathcal {A}}}}(A\,\hat{}, X) \rightarrow X(A)$ by

$$\begin{aligned} \phi (F)=F_A(1_A) \end{aligned}$$

for any $F \in {\text {Hom}}^i(A\,\hat{},X)$, and $\psi : X(A) \rightarrow {\text {Hom}}_{q, {{\mathcal {A}}}}(A\,\hat{}, X)$ by

$$\begin{aligned} \psi (x)_B(a)=xa \end{aligned}$$

for any $x \in X(A)^i$, $a \in A\,\hat{}\,(B)$ and $B \in {\mathcal {A}}$.

$$\begin{aligned}\begin{aligned}\phi (d_{{\text {Hom}}_{q, {{\mathcal {A}}}}(A\,\hat{}, X)}(F))&= (d_X\circ F -q^i Fd_{A\, \hat{}})_A(1_A) \\&= d_X(F_A(1_A)) - q^i Fd_A(1_A) \\&= d_X(F_A(1_A)) \\&= d_X(\phi (F)), \\ d_X(\psi (x))_B(a)&= (d_X\circ \psi (x) -q^i \psi (x)d_{A\, \hat{}})_B(a) \\&= d_X(xa) - q^i xd(a) \\&= d_X(x)a+q^i xd(a) - q^i xd(a) \\&= \psi (d(x))_B(a). \end{aligned}\end{aligned}$$

Since $\phi \psi =id$, $\psi \phi =id$, we have ${\text {Hom}}_{q, {{\mathcal {A}}}}(A\,\hat{}, X)\simeq X(A) ~\text{ in }~ {\mathsf {C}}_{Ndg}(k)$. $\square$

Definition 3.5

Let X be an NDG k-module. For $0< r<N$ and $i\in {\mathbb {Z}}$, we define the following k-modules:

$$\begin{aligned}\begin{aligned} {\text {Z}}^i_{(r)}(X)&:={\text {Ker}}(d_X^{i+r-1}\cdots d_X^i),&{\text {B}}^i_{(r)}(X)&:={\text {Im}}(d_X^{i-1}\cdots d_X^{i-r}), \\ {\text {C}}^i_{(r)}(X)&:={\text {Cok}}(d_X^{i-1}\cdots d_X^{i-r}),&{\text {H}}^i_{(r)}(X)&:={\text {Z}}^i_{(r)}(X)/{\text {B}}^i_{(N-r)}(X) . \end{aligned}\end{aligned}$$

Lemma 3.5

Let ${\mathcal {A}}$ be an $N_q$DG category and X, Y and Z right NDG ${\mathcal {A}}$-modules.

• (1) For any $F \in {\text {Z}}^m_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)$ and $G \in {\text {Z}}^n_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(Y, Z)$, we have that $GF \in {\text {Z}}^{m+n}_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Z)$.

• (2) For any $F \in {\text {B}}^m_{(N-1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)$ and $G \in {\text {Z}}^n_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(Y, Z)$ we have that $GF \in {\text {B}}^{m+n}_{(N-1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Z)$.

• (3) For any $F \in {\text {B}}^m_{(N-1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(Y, Z)$ and $G \in {\text {Z}}^n_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y))$ we have that $FG \in {\text {B}}^{m+n}_{(N-1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Z)$.

Proof

For any $F \in {\text {Z}}^m_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)$ and $G \in {\text {Z}}^n_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(Y, Z)$, we have that $d(GF)=d(G)F+q^nGd(F)=0$. Therefore $GF \in {\text {Z}}^{m+n}_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Z)$.

For any $F \in {\text {B}}^m_{(N-1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)$ and $G \in {\text {Z}}^n_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(Y, Z)$, we have that $F=d^{\{N-1\}}(F')$ for some $F' \in {\text {Hom}}_{{\mathcal {A}}}^{m-N+1}(X, Y)$ and $d\circ G=q^nG\circ d$. By Lemma 3.1 and Lemma 2.4,

$$\begin{aligned} GF&= G\circ d^{\{N-1\}}(F')\\&= G\circ \sum _{l=0}^{N-1}(-1)^lq^{l(m-N+1)+\frac{l(l-1)}{2}} \begin{bmatrix} N-1\\ l \end{bmatrix}d^{\{N-l-1\}}\circ F' \circ d^{\{l\}}\\&=\sum _{l=0}^{N-1}(-1)^lq^{l(m-N+1)+\frac{l(l-1)}{2}-n(N-l-1)} \begin{bmatrix} N-1\\ l \end{bmatrix}d^{\{N-l-1\}}\circ GF' \circ d^{\{l\}}\\&= q^nd^{\{N-1\}}(GF'). \end{aligned}$$

Hence $GF \in {\text {B}}^{m+n}_{(N-1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Z)$.

Similarly (3) is obtained. $\square$

For an $N_q$DG category ${\mathcal {A}}$, it is easy to see that

$$\begin{aligned} {\text {Hom}}_{{\mathsf {C}}_{Ndg}({\mathcal {A}})}(X, Y)={\text {Z}}^0_{(1)} {\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y) \end{aligned}$$

for any $X, Y \in {\mathsf {C}}_{Ndg}({\mathcal {A}})$.

Definition 3.6

For an $N_q$DG category ${\mathcal {A}}$, the homotopy category ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ of right NDG ${\mathcal {A}}$-modules is defined as follows.

• (1) Objects are the right NDG ${\mathcal {A}}$-modules.

• (2) The morphism set between X and Y is given by

  $$\begin{aligned} {\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(X, Y)={\text {H}}^0_{(1)} {\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y) \end{aligned}$$

  and the composition is given by the composition of maps (see Lemma 3.5).

Remark 3.6

For $S \in {\text {Hom}}_{{\mathcal {A}}}^{1-N}(X, Y)$, by Lemmas 2.4, 3.1

$$\begin{aligned}\begin{aligned} d^{\{N-1\}}(S) =&\sum _{l=0}^{N-1}(-1)^lq^{l(-N+1)+\frac{l(l-1)}{2}} \begin{bmatrix} N-1\\ l \end{bmatrix}d^{\{N-l-1\}}\circ S \circ d^{\{l\}} \\&= \sum _{l=0}^{N-1}d^{\{N-l-1\}}\circ S \circ d^{\{l\}} . \end{aligned}\end{aligned}$$

Then the above definition of morphisms is equivalent to the definition of homotopy relation in the sense of [8].

3.3 Shift functor and suspension functor

In this subsection, we show that the homotopy category ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ is an algebraic triangulated category and study the relationship between the shift functor and the suspension functor on ${\mathsf {K}}_{Ndg}({\mathcal {A}})$.

Let r be an integer and ${\mathcal {A}}$ an $N_q$DG category. We define the functor

$$\begin{aligned} U_r : {\mathsf {C}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {Gr}}^0({\mathcal {A}}) \end{aligned}$$

by $U_rX(A)^n=X(A)^{n+r}$ and $U_r(F_A)^n=F_A^{n+r}$ for any right NDG ${\mathcal {A}}$-module X and $F \in {\text {Hom}}_{{\mathsf {C}}_{Ndg}({\mathcal {A}})}(X, Y)$. For any $a \in {\mathcal {A}}(B, A)$ and integer n, we denote by $(a^n_{st})_{l}$ an $l \times l$ matrix whose s, t-entry is

$$\begin{aligned} a_{st}^n=0~(s>t)~\text{ and }~ \begin{bmatrix} t-1 \\ s-1 \end{bmatrix} q^{n(t-s)}d^{\{t-s\}}(a)~(s\le t). \end{aligned}$$

We define the functor

$$\begin{aligned}Q_r : {\mathsf {Gr}}^0({\mathcal {A}}) \rightarrow {\mathsf {C}}_{Ndg}({\mathcal {A}}) \end{aligned}$$

by

for any right graded ${\mathcal {A}}$-module X, $x \in (Q_rX)(A)^n$ and $a \in {\mathcal {A}}(B, A)$ (see Lemma 3.6 below),

$$\begin{aligned} Q_r(F)^n=\begin{pmatrix} F^{r+n-N+1}&{}&{} \\ &{}\ddots &{} \\ &{}&{}F^{r+n} \end{pmatrix} : Q_r(X)^n \rightarrow Q_r(Y)^n \end{aligned}$$

for any $F \in {\text {Hom}}_{{\mathsf {Gr}}^0({\mathcal {A}})}(X, Y)$.

Lemma 3.6

Let ${\mathcal {A}}$ be an $N_q$DG category. For any right graded ${\mathcal {A}}$-module X, $Q_rX$ is a right NDG ${\mathcal {A}}$-module.

Proof

Since

$$\begin{aligned} d(xa) ={}^t({}^tx(a^{n}_{st})_N{}^tJ) \end{aligned}$$

and

$$\begin{aligned} d(x)a+q^nxd(a) ={}^t({}^tx{}^tJ(a^{n+1}_{st})_N) +q^n{\;}^t({}^tx(d(a)^n_{st})_N) \end{aligned}$$

for any $a \in {\mathcal {A}}(A,B)$ and $x \in X(B)^n$, we show that

$$\begin{aligned} (a^{n}_{st})_N{}^tJ={}^tJ(a^{n+1}_{st})_N+q^n(d(a)^n_{st})_N. \end{aligned}$$

The i, j-entry

$$\begin{aligned} ((a^{n}_{st})_N{}^tJ)_{i\,j}=a^n_{i\, j+1}~\text{ where } \text{ we } \text{ set }~a^m_{i\, N+1}=0 \end{aligned}$$

and

$$\begin{aligned} ({}^tJ(a^{n+1}_{st})_N)_{i\,j}=a^{n+1}_{i-1\, j}~\text{ where } \text{ we } \text{ set }~a^m_{0\, j}=0. \end{aligned}$$

In the case that $i=1$,

$$\begin{aligned} a^{n+1}_{i-1\, j}+q^nd(a)^n_{i\,j}=q^nd(a)^n_{i\,j}=a^n_{i\, j+1}. \end{aligned}$$

In the case that $1\le j< i \le N$,

$$\begin{aligned} a^{n+1}_{i-1\, j}+q^nd(a)^n_{i\,j}=a^{n+1}_{i-1\, j}=a^n_{i\, j+1}. \end{aligned}$$

In the case that $2\le i\le j \le N$,

$$\begin{aligned} a^{n+1}_{i-1\, j}+q^nd(a)^n_{i\,j}&= \begin{bmatrix} j-1 \\ i-2 \end{bmatrix} q^{(n+1)(j-i+1)}d^{\{j-i+1\}}(a)\\&\quad +q^n\begin{bmatrix} j-1 \\ i-1 \end{bmatrix} q^{n(j-i)}d^{\{j-i\}}(d(a))\\&= (q^{j-i+1}\begin{bmatrix} j-1 \\ i-2 \end{bmatrix}+\begin{bmatrix} j-1 \\ i-1 \end{bmatrix}) q^{n(j-i+1)}d^{\{j-i+1\}}(a)\\&= \begin{bmatrix} j \\ i-1 \end{bmatrix} q^{n(j+1-i)}d^{\{j+1-i\}}(a)\\&= a^n_{i\, j+1}. \end{aligned}$$

Since $(xa)b={}^t({}^tx(a^n_{st})_N(b^{n+m}_{st})_N)$ and $x(ab)={}^t({}^tx((ab)^n_{st})_N)$ for any $a \in {\mathcal {A}}^m(B,C)$, $b \in {\mathcal {A}}(A,B)$ and $x \in X(C)^n$, we show that $(a^n_{st})_N(b^{n+m}_{st})_N=((ab)^n_{st})_N$. The i, j-entry

$$\begin{aligned} ((a^n_{st})_N(b^{n+m}_{st})_N)_{i\, j}&=\sum _{l=0}^{N}a^n_{i\,l}b^{n+m}_{l\, j}\\&=\sum _{l=i}^{j}\begin{bmatrix} l-1 \\ i-1 \end{bmatrix} q^{n(l-i)}d^{\{l-i\}}(a) \begin{bmatrix} j-1 \\ l-1 \end{bmatrix} q^{(n+m)(j-l)}d^{\{j-l\}}(b)\\&= \sum _{l=i}^{j}q^{n(j-i)+m(j-l)}\begin{bmatrix} l-1 \\ i-1 \end{bmatrix} \begin{bmatrix} j-1 \\ l-1 \end{bmatrix}d^{\{l-i\}}(a)d^{\{j-l\}}(b)\\&= \sum _{u=0}^{j-i}q^{n(j-i)+mu}\begin{bmatrix} j-u-1 \\ i-1 \end{bmatrix} \begin{bmatrix} j-1 \\ j-u-1 \end{bmatrix}d^{\{j-u-i\}}(a)d^{\{u\}}(b)\\&= \sum _{u=0}^{j-i}q^{n(j-i)+mu}\begin{bmatrix} j-1 \\ i-1 \end{bmatrix} \begin{bmatrix} j-1 \\ u \end{bmatrix}d^{\{j-u-i\}}(a)d^{\{u\}}(b)\\&= \begin{bmatrix} j-1 \\ i-1 \end{bmatrix} q^{n(j-i)} \sum _{u=0}^{j-i}q^{mu}\begin{bmatrix} j-i \\ u \end{bmatrix}d^{\{j-i-u\}}(a)d^{\{u\}}(b)\\&= \begin{bmatrix} j-1 \\ i-1 \end{bmatrix} q^{n(j-i)}d^{\{j-i\}}(ab)~\text{(see } \text{ Lemma }~3.7 \text {below.)}\\&= ((ab)^n_{st})_N)_{i\, j}. \end{aligned}$$

$\square$

Lemma 3.7

For any $f \in {\mathcal {A}}^r(B,C)$ and $g \in {\mathcal {A}}(A,B)$,

$$\begin{aligned} d^{\{n\}}(fg)=\sum _{l=0}^nq^{lr}\begin{bmatrix} n \\ l \\ \end{bmatrix}d^{\{n-l\}}(f)d^{\{l\}}(g). \end{aligned}$$

Proof

Let $\rho : {\mathcal {A}}(B,C)\otimes _{q} {\mathcal {A}}(A,B) \rightarrow {\mathcal {A}}(A,C)$ in ${\mathsf {C}}_{Ndg}(k)$ be the composition of ${\mathcal {A}}$. By Lemma 3.1,

$$\begin{aligned} d^{\{n\}}(fg)&= d^{\{n\}}(\rho (f\otimes g))\\&= \rho (d^{\{n\}}(f\otimes g))\\&= \rho (\sum _{l=0}^nq^{lr}\begin{bmatrix} n \\ l \\ \end{bmatrix}d^{\{n-l\}}(f)\otimes d^{\{l\}}(g))\\&= \sum _{l=0}^nq^{lr}\begin{bmatrix} n \\ l \\ \end{bmatrix}d^{\{n-l\}}(f)d^{\{l\}}(g). \end{aligned}$$

$\square$

To show Proposition 3.1, we prepare the following lemmas.

Lemma 3.8

For $x \in (Q_rX)^n(A)$ and $a \in {\mathcal {A}}(B, A)$,

$$\begin{aligned} d^{\{i\}}(xa)=&\sum _{l=0}^{i}d^{\{i-l\}}(x)a^n_{i-l+1\;i+1}\\ d^{\{N-i\}}(x)a=&\sum _{l=0}^{N-i}d^{\{N-i-l\}}(xa^{n-i}_{i\;i+l}) \end{aligned}$$

Proof

Let $\rho : (Q_rX)(A)\otimes _q{\mathcal {A}}(B, A) \rightarrow (Q_rX)(B)$ in $C_{Ndg}(k)$ be the scalar multiplication of a right NDG ${\mathcal {A}}$-module $Q_rX$. By Lemma 3.1,

$$\begin{aligned} d^{\{i\}}(xa)&= d^{\{i\}}(\rho (x\otimes a))\\&= \rho (d^{\{i\}}(x\otimes a))\\&= \rho \left( \sum _{l=0}^{i}q^{ln}\begin{bmatrix} i \\ l \\ \end{bmatrix}d^{\{i-l\}}(x)\otimes d^{\{i\}}(a)\right) \\&= \rho \left( \sum _{l=0}^{i}d^{\{i-l\}}(x)\otimes a^n_{i-l+1\;i+1}\right) \\&= \sum _{l=0}^{i}d^{\{i-l\}}(x)a^n_{i-l+1\;i+1}\\ \end{aligned}$$

Set $\phi (x\otimes a)=d(x)\otimes a$ and $\psi (x\otimes a)=q^nx\otimes d(a)$, then $\phi +\psi =d_{(Q_rX)(A)\otimes _q{\mathcal {A}}(B, A)}$ and $\psi \phi =q\phi \psi$. By Lemma 2.3 (2) and Lemma 3.1,

$$\begin{aligned} d^{\{N-i\}}(x)a&= \rho (\phi ^{N-i}(x\otimes a))\\&= \rho \left( \sum _{l=0}^{N-i} (-1)^lq^{\frac{l(l-1)}{2}}\begin{bmatrix} N-i \\ l \\ \end{bmatrix}(\phi +\psi )^{N-i-l}\psi ^l(x\otimes a)\right) \\&= \rho \left( \sum _{l=0}^{N-i} (-1)^lq^{\frac{l(l-1)}{2}}\begin{bmatrix} N-i \\ l \\ \end{bmatrix}d^{\{N-i-l\}}(q^{ln}x\otimes d^{\{l\}}(a))\right) \\&= \rho \left( \sum _{l=0}^{N-i} \begin{bmatrix} l+i-1 \\ l \\ \end{bmatrix}d^{\{N-i-l\}}(q^{l(n-i)}x\otimes d^{\{l\}}(a))\right) \\&= \sum _{l=0}^{N-i}d^{N-i-l}(xa^{n-i}_{i\;i+l}). \end{aligned}$$

$\square$

Lemma 3.9

The following morphisms

$$\begin{aligned} \pi _X : Q_{-r}U_rX \rightarrow X, \;\pi _{X(A)^m}(x)= (d^{\{N-1\}} \cdots \;\;d \;\;1)x, \;\; x \in Q_{-r}U_rX(A)^m \end{aligned}$$

and

$$\begin{aligned} \eta _X : X \rightarrow Q_{-r+N-1}U_rX, \;\eta _{X(A)^m}(x)={}^t(1 \;\; d \;\; \cdots \;\; d^{\{N-1\}})x, \;\; x \in X(A)^m \end{aligned}$$

lie in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$.

Proof

By a direct calculation, both morphisms lie in ${\mathsf {C}}_{Ndg}(k)$. By Lemma 3.8,

$$\begin{aligned} {}^t\eta _X(xa)&=(xa, d(xa), \ldots , d^{\{N-1\}}(xa)) \\&=(x, d(x), \ldots , d^{\{N-1\}}(x))(a^m_{st})_N\\&={}^t\eta _X(x)a, \end{aligned}$$

hence $\eta _X \in {\mathsf {C}}_{Ndg}({\mathcal {A}})$. For $x={}^t(x_1, \ldots , x_N) \in Q_{-r}U_rX(A)^m$, by Lemma 3.8,

$$\begin{aligned} \pi _X(x)a&=\Sigma _{i=1}^Nd^{\{N-i\}}(x_i)a \\&=\Sigma _{i=1}^N\Sigma ^{N-i}_{l=0} d^{\{N-i-l\}}(x_ia^{m}_{i\,i+l}) \\&=\pi _X(xa), \end{aligned}$$

hence $\pi _X \in {\mathsf {C}}_{Ndg}({\mathcal {A}})$. $\square$

Proposition 3.1

For any integer r, $Q_{-r}$ is the left adjoint to $U_r$, and $U_r$ is the left adjoint to $Q_{-r+N-1}$.

Proof

Let X be a right NDG ${\mathcal {A}}$-module and Y a right graded ${\mathcal {A}}$-module. The morphisms

$$\begin{aligned} \pi _X : Q_{-r}U_rX \rightarrow X, \;\pi _{X(A)^m}(x)= (d^{\{N-1\}} \cdots \;\;d \;\;1)x, \;\; x \in Q_{-r}U_rX(A)^m \end{aligned}$$

in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ and

$$\begin{aligned} \xi _Y : Y \rightarrow U_rQ_{-r}Y, \;\eta _{Y(A)^m}(y)={}^t(0 \;\; \cdots \;\; 0 \;\; 1)y, \;\; y \in Y(A)^m \end{aligned}$$

in ${\mathsf {Gr}}^0({\mathcal {A}})$ imply $Q_{-r}$ is the left adjoint to $U_r$, on the other hand, the morphisms

$$\begin{aligned} \zeta _Y : U_{r}Q_{-r+N-1}Y \rightarrow Y, \ \zeta _{Y(A)^m}(y)= (1 \;\; 0 \;\; \cdots \;\; 0)y, \;\; y \in U_rQ_{-r+N-1}Y(A)^m \end{aligned}$$

in ${\mathsf {Gr}}^0({\mathcal {A}})$ and

$$\begin{aligned} \eta _X : X \rightarrow Q_{-r+N-1}U_rX, \;\eta _{X(A)^m}(x)={}^t(1 \;\; d \;\; \cdots \;\; d^{\{N-1\}})x, \;\; x \in X(A)^m \end{aligned}$$

in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ imply that $U_r$ is the left adjoint to $Q_{-r+N-1}$. $\square$

Let ${\mathcal {A}}$ be an $N_q$DG category, $\mathcal {E}_{{\mathcal {A}}}$ the collection of exact sequence $0\rightarrow X\rightarrow Y\rightarrow Z\rightarrow 0$ in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ such that $0\rightarrow U_0X\rightarrow U_0Y\rightarrow U_0Z\rightarrow 0$ is a split exact sequence in ${\mathsf {Gr}}^0({\mathcal {A}})$, equivalently $0\rightarrow U_rX\rightarrow U_rY\rightarrow U_rZ\rightarrow 0$ is a split exact sequence in ${\mathsf {Gr}}^0({\mathcal {A}})$ for any integer r.

Corollary 3.2

$( {\mathsf {C}}_{Ndg}({\mathcal {A}}), {\mathcal {E}}_{{\mathcal {A}}})$ is a Frobenius category.

Proof

For any exact sequence $0\rightarrow X \rightarrow Y \rightarrow X \rightarrow 0$ in ${\mathcal {E}}_{{\mathcal {A}}}$, any right graded ${\mathcal {A}}$-module W and any integer r, we have the following exact sequence

$$\begin{aligned} 0\rightarrow {\text {Hom}}_{{\mathsf {Gr}}^0({\mathcal {A}})}(U_{r}(Z), W) \rightarrow {\text {Hom}}_{{\mathsf {Gr}}^0({\mathcal {A}})}(U_{r}(Y), W) \rightarrow {\text {Hom}}_{{\mathsf {Gr}}^0({\mathcal {A}})}(U_{r}(X), W)\rightarrow 0. \end{aligned}$$

By Proposition 3.1, we have the following exact sequence

$$\begin{aligned} 0\rightarrow {\text {Hom}}_{{\mathsf {C}}_{Ndg}({\mathcal {A}})}(Z, Q_{-r}(W))\rightarrow {\text {Hom}}_{{\mathsf {C}}_{Ndg}({\mathcal {A}})}(Y, Q_{-r}(W))\rightarrow {\text {Hom}}_{{\mathsf {C}}_{Ndg}({\mathcal {A}})}(X, Q_{-r}(W))\rightarrow 0. \end{aligned}$$

Hence $Q_n(W)$ is injective in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ for any integer n. Similarly one can show that $Q_n(W)$ is projective in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ for any integer n. For any projective object X and injective object Y of ${\mathsf {C}}_{Ndg}({\mathcal {A}})$, we have that $\rho _X : Q_{0}U_0X \rightarrow X$ is a split epimorphism and $\eta _Y : Y \rightarrow Q_{N-1}U_0Y$ is a split monomorphism. Hence any object of ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ is projective if and only if it is injective. $\square$

Theorem 3.1

The stable category of the Frobenius category $( {\mathsf {C}}_{Ndg}({\mathcal {A}}), {\mathcal {E}}_{{\mathcal {A}}})$ is the category ${\mathsf {K}}_{Ndg}({\mathcal {A}})$. In particular, ${\mathsf {K}}_{Ndg({\mathcal {A}})}$ is an algebraic triangulated category.

Proof

It is enough to show that $F \in B^0_{N-1}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)$ if and only if F factors through the $\eta _X$ in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$. For any $F \in B^0_{N-1}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)$, $F=d^{\{N-1\}}(H)$ for some $S \in {\text {Hom}}_{{\mathcal {A}}}^{1-N}(X, Y)$. By Remark 3.6,

$$\begin{aligned} d^{\{N-1\}}(S) = \sum _{l=0}^{N-1}d^{\{N-l-1\}}\circ S \circ d^{\{l\}} = \pi _Y Q_{N-1}(S)\eta _X. \end{aligned}$$

Hence F factors through the $\eta _X$.

For any $F \in {\text {Hom}}_{{\mathsf {C}}_{Ndg}({\mathcal {A}})}(X, Y)$, we assume that F factors through $\eta _X$, namely, $F=\sum _{l=0}^{N-1}F_l\circ d^{\{l\}}$ for some $(F_0, \ldots , F_{N-1}) \in {\text {Hom}}_{{\mathsf {C}}_{Ndg}({\mathcal {A}})}(Q_{N-1}U_0(X), Y)$. By the adjointness ${\text {Hom}}_{{\mathsf {C}}_{Ndg}({\mathcal {A}})}(Q_{N-1}U_0(X), Y)\simeq {\text {Hom}}_{{\mathsf {Gr}}^0({\mathcal {A}})}(U_0(X), U_{1-N}(Y))$, we have that $(F_0, \ldots , F_{N-1})=\zeta _YQ_{N-1}(F')$ for some $F' \in {\text {Hom}}_{{\mathcal {A}}}^{1-N}(X, Y)$. Hence $F=\zeta _Y Q_{N-1}(F')\eta _X=d^{\{N-1\}}(F')$. $\square$

In the rest of this subsection, we study the shift functor and the suspension functor on ${\mathsf {K}}_{Ndg({\mathcal {A}})}$. We define the shift functor $\theta _q : {\mathsf {C}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {C}}_{Ndg}({\mathcal {A}})$ by

$$\begin{aligned} \theta _q(X)(A)^m=X(A)^{m+1}, \\d_{\theta _q(X)(A)}=q^{-1}d_{X(A)} \end{aligned}$$

for any right NDG ${\mathcal {A}}$-module (X, d) and any object A of ${\mathcal {A}}$. One can check that $d_{\theta _q(X)(B)}(xf)=d_{\theta _q(X)(A)}(x)f+q^mxd(f)$ for any $x \in \theta _q(X)(A)^m$ and $f \in {\mathcal {A}}(B, A)$.

We define functors $\Sigma ~(~\text{ resp. }~ \Sigma ^{-1}) : {\mathsf {C}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {C}}_{Ndg}({\mathcal {A}})$ by

$$\begin{aligned} (\Sigma X)^m = \coprod _{i=m+1}^{m+N-1} X^i ~\left( \text{ resp. }~(\Sigma ^{-1} X)^m = \coprod _{i=m-N+1}^{m-1} X^i \right) , \\ xa={}^t({}^tx(a^m_{st})_{N-1})\end{aligned}$$

and

$$\begin{aligned} d_{\Sigma X}^m ~(\text{ resp. }~d_{\Sigma ^{-1} X}^m)= \left( \begin{array}{c|ccccc} 0&{}1&{}0&{}0&{}\cdots &{}0\\ &{}0&{}\ddots &{}\ddots &{}\ddots &{}\vdots \\ \vdots &{}\vdots &{}\ddots &{}\ddots &{}\ddots &{}0\\ &{}&{}&{}\ddots &{}\ddots &{}0\\ 0&{}0&{}\cdots &{}\cdots &{}0&{}1\\ \hline -d^{\{N-1\}}&{}-d^{\{N-2\}}&{}\cdots &{}\cdots &{}\cdots &{}-d\\ \end{array} \right) \end{aligned}$$

for any right NDG ${\mathcal {A}}$-module (X, d), $x \in \Sigma X(A)^m~(resp.~x \in \Sigma ^{-1} X(A)^m)$ and $a \in {\mathcal {A}}(B, A)$. Then we have functors $\Sigma$ and $\Sigma ^{-1}$ by the next lemma.

Lemma 3.10

We have the following short exact sequences which belong to $\mathcal {E}_{{\mathcal {A}}}$ in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$:

where

$$\begin{aligned} (\epsilon _X )^m= & {} \left( \begin{array}{cccc} 1&{}0&{}\cdots &{}0\\ 0&{}\ddots &{}\ddots &{}\vdots \\ \vdots &{}\ddots &{}\ddots &{}0\\ 0&{}\cdots &{}0&{}1\\ -d^{\{N-1\}}&{}\ldots &{}\ldots &{}-d \\ \end{array} \right) , \quad (\pi _X )^m = \left( \begin{array}{cccc} d^{\{N-1\}}&\cdots&d&1 \end{array} \right) , \\ (\eta _X )^m= & {} \left( \begin{array}{c} 1\\ d\\ \vdots \\ d^{\{N-1\}}\\ \end{array} \right) ~\text{ and }~ (\delta _X )^m = \left( \begin{array}{ccccc} -d&{}1&{}0&{}\cdots &{}0\\ 0&{}\ddots &{}\ddots &{}\ddots &{}\vdots \\ \vdots &{}\ddots &{}\ddots &{}\ddots &{}0\\ 0&{}\ldots &{}0&{}-d&{}1 \\ \end{array} \right) . \end{aligned}$$

Proof

By a direct calculation, the short exact sequences lie in ${\mathsf {C}}_{Ndg}(k)$. By Lemma 3.9, $\pi _X$ and $\eta _X$ are in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$. For $x={}^t(0, \ldots ,0 , x_i, 0, \ldots , 0) \in (\Sigma X)^m\;\; (x_i \in X^{m+i-1})$ and $a \in {\mathcal {A}}$, the t-entry

$$\begin{aligned} \delta _X(xa)_t&= -d(x_ia^m_{i\,t})+x_ia^m_{i\,t+1}\\&=-d(x_i)a^m_{i\,t}-q^{m+i-1}x_id(a^m_{i\,t})+x_ia^m_{i\,t+1}\\&=-d(x_i)a^m_{i\,t}+x_ia^m_{i-1\,t}\\&= (\delta _X(x)a)_t, \end{aligned}$$

therefore $\delta _X(xa)=\delta _X(x)a$.

For $x={}^t(0, \ldots ,0 , x_i, 0, \ldots , 0) \in (\Sigma ^{-1} X)^m\;\; (x_i \in X^{m-(N-i)})$ and $a \in {\mathcal {A}}$, the t-entry

$$\begin{aligned} (\epsilon _X(x)a)_t&= x_ia^m_ {i\;t}-d^{N-1}(x_i)a^m_{N\;t},\\ (\epsilon _X(xa))_t=&\, x_ia^m_{i\;t}~(t \ne N)~\text{ and } -\sum _{l=1}^{N-1}d^{N-l}(x_ia^m_{i\;l})~(t=N). \end{aligned}$$

By Lemma 3.8, $\epsilon _X(x)a=\epsilon _X(xa)$. $\square$

The shift functor $\theta _q : {\mathsf {C}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {C}}_{Ndg}({\mathcal {A}})$ induces the shift functor $\theta _q : {\mathsf {K}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {K}}_{Ndg}({\mathcal {A}})$ which is a triangle functor. Moreover, $\Sigma$ and $\Sigma ^{-1}$ induces the suspension functor and its quasi-inverse of the triangulated category ${\mathsf {K}}_{Ndg}({\mathcal {A}})$. Then we have the following observation.

Theorem 3.2

We have $\Sigma \simeq \Sigma ^{-1} \theta ^N_q \simeq \theta ^N_q \Sigma ^{-1}$ as auto-functors of ${\mathsf {C}}_{Ndg}({\mathcal {A}})$. Especially, we have $\Sigma ^2 \simeq \theta ^N_q$ as auto-equivalences of ${\mathsf {K}}_{Ndg}({\mathcal {A}})$.

Proof

In Lemma 3.10, we have $\Sigma X=\Sigma ^{-1}\theta _q^{N}X$. $\square$

We remark that $\Sigma ^{-1}$ is not the inverse functor of $\Sigma$ on ${\mathsf {C}}_{Ndg({\mathcal {A}})}$.

3.4 Bimodules and triangle functors

In this subsection, we give the definition of bimodules over NDG categories and show the adjoint relation between the tensor functor and the hom functor.

Definition 3.7

Let ${\mathcal {A}}$ and ${\mathcal {B}}$ be $N_q$DG categories. An NDG ${\mathcal {B}}$-${\mathcal {A}}$-bimodule M is defined by

• (1) $(M(A, -), d_{M(A, -)}; \rho _M)$ is a left NDG ${\mathcal {B}}$-module for any $A \in {\mathcal {A}}$,

• (2) $(M(-, B), d_{M(-, B)}; \lambda _M)$ is a right NDG ${\mathcal {A}}$-module for any $B \in {\mathcal {B}}$,

• (3) we have the following commutative diagram in ${\mathsf {C}}_{Ndg}(k)$:

  

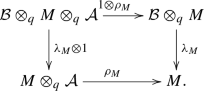
Namely, we have a collection of NDG k-modules $(M(A, B), d_{M(A, B)}; \lambda _M, \rho _M)$ for any $A \in {\mathcal {A}}$ and $B \in {\mathcal {B}}$ satisfying that $(M(A, -), d_{M(A, -)}; \rho _M)$ is a left NDG ${\mathcal {B}}$-module for $A \in {\mathcal {A}}$, $(M(-, B), d_{M(-, B)}; \lambda _M)$ is a right NDG ${\mathcal {A}}$-module for $B \in {\mathcal {B}}$ and $f(mg)=(fm)g$ for $f \in {\mathcal {B}}(B_1, B_2)$, $m \in M(A_1, B_1)$ and $g \in {\mathcal {A}}(A_2, A_1)$. One can check that $d(f(mg))=d((fm)g)$.

Example 3.3

Let ${\mathcal {A}}$ be an $N_q$DG category. Then ${\mathcal {A}}$ is an NDG ${\mathcal {A}}$-${\mathcal {A}}$-bimodule. We take k as an $N_q$DG category with one object $*$ and the morphism set $k(*, *)=k^0(*, *)=k$. Any right (resp. left) NDG ${\mathcal {A}}$-module X is an NDG k-${\mathcal {A}}$-bimodule (resp. NDG ${\mathcal {A}}$-k-bimodule).

Let ${\mathcal {A}}$ and ${\mathcal {B}}$ be small $N_q$DG categories, X a right NDG ${\mathcal {B}}$-module, Y a right NDG right ${\mathcal {A}}$-module and M an NDG ${\mathcal {B}}$-${\mathcal {A}}$-bimodule. We define a right NDG ${\mathcal {B}}$-module ${\text {Hom}}_{q, {{\mathcal {A}}}}(M, Y)$ by

$$\begin{aligned} {\text {Hom}}_{q, {{\mathcal {A}}}}(M, Y)(B)={\text {Hom}}_{q, {{\mathcal {A}}}}(M(-, B), Y) \end{aligned}$$

and

$$\begin{aligned} \rho : {\text {Hom}}_{q, {{\mathcal {A}}}}(M, Y)(B_1)\otimes _q{\mathcal {B}}(B_2, B_1) \rightarrow {\text {Hom}}_{q, {{\mathcal {A}}}}(M, Y)(B_2) \\\rho (F\otimes b)_A(m)=F_A(bm) \end{aligned}$$

for any B, $B_1$ and $B_2 \in {\mathcal {B}}$, $m \in M(A, B_2)$ and $A \in {\mathcal {A}}$. One can check that $\rho$ is in $C_{Ndg}(k)$. We define a right NDG ${\mathcal {A}}$-module $X\otimes _{q, {{\mathcal {B}}}}M$ by

$$\begin{aligned} (X\otimes _{q, {{\mathcal {B}}}}M)(A)=\mathrm{Cok}\,\nu _A \end{aligned}$$

in $C_{Ndg}(k)$ for any A in ${\mathcal {A}}$ where

$$\begin{aligned} \nu _A : \coprod _{B_1, B_2 \in {\mathcal {B}}}X(B_2)\otimes _q{\mathcal {B}}(B_1, B_2)\otimes _qM(A, B_1) \rightarrow \coprod _{B_3 \in {\mathcal {B}}}X(B_3)\otimes _qM(A, B_3), \\ \nu _A(x\otimes b\otimes m)=xb\otimes m-x\otimes bm \end{aligned}$$

and

$$\begin{aligned} \rho : X(B)\otimes _{q, {{\mathcal {B}}}}M(A_1, B)\otimes _q{\mathcal {A}}(A_2, A_1) \rightarrow X(B)\otimes _{q, {{\mathcal {B}}}}M(A_2, B)\\ \rho (x \otimes m \otimes a)=x \otimes ma \end{aligned}$$

for any $A_1$, $A_2 \in {\mathcal {A}}$ and $B \in {\mathcal {B}}$. One can check that $\mu _A$ and $\rho$ are in $C_{Ndg}(k)$. Similarly, a left NDG ${\mathcal {A}}$-module $M\otimes _{q, {{\mathcal {B}}}}Y$ is defined for any left NDG ${\mathcal {B}}$-module Y.

It is easy to see the following Remark and Lemmas.

Remark 3.7

${\text {Hom}}_{q, {{\mathcal {A}}}}(M,-): {\mathsf {C}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {C}}_{Ndg}({\mathcal {B}})$ (resp., ${\text {Hom}}_{{\mathsf {Gr}}({\mathcal {A}})}(M,-): {\mathsf {Gr}}^0({\mathcal {A}}) \rightarrow {\mathsf {Gr}}^0({\mathcal {B}})$) is left exact between abelian categories in the sense of Remark 3.6. And $-\otimes _{q, {{\mathcal {B}}}}M : {\mathsf {C}}_{Ndg}({\mathcal {B}}) \rightarrow {\mathsf {C}}_{Ndg}({\mathcal {A}})$ (resp., $(-\otimes _{q, {{\mathcal {B}}}}M)\mid _{{\mathsf {Gr}}^0({\mathcal {B}})} : {\mathsf {Gr}}^0({\mathcal {B}}) \rightarrow {\mathsf {Gr}}^0({\mathcal {A}})$) is right exact between abelian categories, where $(-\otimes _{q, {{\mathcal {B}}}}M)\mid _{{\mathsf {Gr}}^0({\mathcal {B}})}$ is the restriction of $-\otimes _{q, {{\mathcal {B}}}}M$ to ${\mathsf {Gr}}^0({\mathcal {B}})$.

Lemma 3.11

Let ${\mathcal {A}}$ and ${\mathcal {B}}$ be small $N_q$DG categories, X a right NDG ${\mathcal {B}}$-module, and M an NDG ${\mathcal {B}}$-${\mathcal {A}}$-bimodule. For any $n\in {\mathbb {Z}}$, we have the canonical isomorphism in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$:

$$\begin{aligned} (\theta _qX)\otimes _{q, {{\mathcal {B}}}}M_{{\mathcal {A}}} \simeq \theta _q(X\otimes _{q, {{\mathcal {B}}}}M_{{\mathcal {A}}}) \end{aligned}$$

Lemma 3.12

Let A (resp., B) be an object of ${\mathcal {A}}$ (resp., ${\mathcal {B}}$), M an NDG ${\mathcal {B}}$-${\mathcal {A}}$-bimodule. Then the following hold.

• (1) $B\,\hat{}\otimes _{q, {{\mathcal {B}}}}M \simeq M(-, B)$ as right NDG ${\mathcal {A}}$-modules.

• (2) $M\otimes _{q, {{\mathcal {A}}}}\hat{}A \simeq M(A, -)$ as left NDG ${\mathcal {B}}$-modules.

Proof

(1) It is easy to see that

$$\begin{aligned} \coprod _{B_1, B_2 \in {\mathcal {B}}}{\mathcal {B}}(B_2,B)\otimes _q{\mathcal {B}}(B_1,B_2)\otimes _qM(-, B_1) \xrightarrow {\nu } \coprod _{B_1 \in {\mathcal {B}}}{\mathcal {B}}(B_1,B)\otimes _qM(-, B_1) \xrightarrow {\pi } M(-, B) \end{aligned}$$

is a composition of morphisms in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$, where $\nu =1\otimes \lambda _M -\mu _{{\mathcal {B}}}\otimes 1$, $\pi =\Sigma \lambda ^{B_1}_{B}$ with $\lambda ^{B_1}_{B}:{\mathcal {B}}(B_1,B)\otimes _qM(-, B_1)\rightarrow M(-, B)$. Then it suffices to show that the following sequence is exact in ${\mathsf {C}}_{Ndg}(k)$:

$$\begin{aligned} \coprod _{B_1, B_2 \in {\mathcal {B}}}{\mathcal {B}}(B_2,B)\otimes _q{\mathcal {B}}(B_1,B_2)\otimes _qM(A, B_1) \xrightarrow {\nu } \coprod _{B_1 \in {\mathcal {B}}}{\mathcal {B}}(B_1,B)\otimes _qM(A, B_1) \xrightarrow {\pi } M(A, B) \rightarrow 0 \end{aligned}$$

for any $A \in {\mathcal {A}}$. It is trivial that $\pi =\Sigma \lambda ^{B_1}_{B}$ is an epimorphism. Since $\lambda ^{B_1}_{B}\circ (\mu _{{\mathcal {B}}}\otimes 1)=\lambda ^{B_2}_{B}\circ (1\otimes \lambda ^{B_1}_{B})$, we have $\pi \circ \nu =0$. Then there is an epimorphism $\alpha$ such that $\pi =\alpha \circ {\text {cok}}(\nu )$. For any finite set $\{B_1, \ldots , B_{n}\}$ of objects of ${\mathcal {B}}$ with $B_1=B$, consider an $n\times n$ matrix ring $\Lambda ={}^{t}({\mathcal {B}}(B_i,B_j))_{1\le i, j \le n}$, a left $\Lambda$-module ${\tilde{M}}=\coprod _{i=1}^{n}M(A, B_i)$, then $M(A, B)=e_1\Lambda \otimes _{\Lambda }{\tilde{M}}$, where $e_1$ is the idempotent corresponding to $B_1$. Then we have the following exact sequence

$$\begin{aligned} \coprod _{1 \le i, j \le n}{\mathcal {B}}(B_j,B)\otimes _q{\mathcal {B}}(B_i,B_j)\otimes _qM(A, B_i) \xrightarrow {\tilde{\nu }} \coprod _{1 \le i \le n}{\mathcal {B}}(B_i,B)\otimes _qM(A, B_i) \xrightarrow {\tilde{\pi }} M(A,B) \rightarrow 0 \end{aligned}$$

where $\tilde{\nu }$ is a restriction of $\nu$. Since $\coprod _{B_1 \in {\mathcal {B}}}{\mathcal {B}}(B_1,B)\otimes _qM(A, B_1)$ is the inductive limit $\underset{\rightarrow }{\lim } \coprod _{B_i \in {\mathsf {B}}}{\mathcal {B}}(B_i,B)\otimes _qM(A, B_i)$ where ${\mathsf {B}}$ is a finite set of objects which contains B, there is an epimorphism $\beta$ such that ${\text {cok}}(\nu )=\beta \circ \pi$. Hence we have the above exact sequence in ${\mathsf {C}}_{Ndg}(k)$.

(2) Similarly. $\square$

Theorem 3.3

Let ${\mathcal {A}}$ and ${\mathcal {B}}$ be small $N_q$DG categories. The following hold for a right NDG ${\mathcal {B}}$-module X, a right NDG ${\mathcal {A}}$-module Y and an NDG ${\mathcal {B}}$-${\mathcal {A}}$-bimodule M.

• (1) ${\text {Hom}}_{q, {{\mathcal {A}}}}(X\otimes _{q, {{\mathcal {B}}}} M, Y) \simeq {\text {Hom}}_{q, {{\mathcal {B}}}}(X, {\text {Hom}}_{q, {{\mathcal {A}}}}(M, Y))$ in ${\mathsf {C}}_{Ndg}(k)$.

• (2) ${\text {Hom}}_{{\mathsf {C}}_{Ndg}({\mathcal {A}})}(X\otimes _{q, {{\mathcal {B}}}} M, Y) \simeq {\text {Hom}}_{C_{Ndg({\mathcal {B}})}}(X, {\text {Hom}}_{q, {{\mathcal {A}}}} (M, Y))$.

• (3) ${\text {Hom}}_{K_{Ndg({\mathcal {A}})}}(X\otimes _{q, {{\mathcal {B}}}} M, Y) \simeq {\text {Hom}}_{K_{Ndg({\mathcal {B}})}}(X, {\text {Hom}}_{q, {{\mathcal {A}}}} (M, Y))$.

Proof

Define $\alpha : {\text {Hom}}_{q, {{\mathcal {A}}}}(X\otimes _{q, {{\mathcal {B}}}} M, Y) \rightarrow {\text {Hom}}_{q, {{\mathcal {B}}}}(X, {\text {Hom}}_{q, {{\mathcal {A}}}} (M, Y))$ as

$$\begin{aligned} (\alpha (F)_B(x))_A(m)=F_A(x \otimes m) \end{aligned}$$

for any $F \in {\text {Hom}}_{q, {{\mathcal {A}}}}(X\otimes _{q, {{\mathcal {B}}}} M, Y)$, $x \in X(B)$ and $m \in M(A, B)$. For any $F \in {\text {Hom}}_{{\mathcal {A}}}^{s}(X\otimes _{q, {{\mathcal {B}}}} M, Y)$, any $g \in {\mathcal {B}}(B',B)$,

$$\begin{aligned}\begin{array}{rcl} (\alpha (F)_{B'}(xg))_A(m) &{} = &{}F_A(xg\otimes m) = F_A(x\otimes gm) \\ &{} = &{}\alpha (F)_B(x)(gm) = ((\alpha (F)_B(x))_Ag)(m) . \end{array}\end{aligned}$$

Therefore $\alpha (F) \in {\text {Hom}}_{{\mathcal {B}}}^s(X, {\text {Hom}}_{q, {{\mathcal {A}}}}(M, Y))$.

For any $F \in {\text {Hom}}_{{\mathcal {A}}}^{s}(X\otimes _{q, {{\mathcal {B}}}}M, Y)$, $x\in X(B)^t$ and $m \in M(A, B)$,

$$\begin{aligned}\begin{array}{lll} (\alpha (d(F))_B(x))_A(m) &{} = &{}(\alpha (d\circ F - q^s F\circ d)_B(x))_A(m) \\ &{} = &{}(d\circ F-q^s F\circ d)_A(x\otimes m) \\ &{} = &{} d\circ F_A(x\otimes m)-q^s F_A(d(x)\otimes m+q^tx\otimes d(m)) \\ &{} = &{} d\circ F_A(x\otimes m)-q^s F_A(d(x)\otimes m)-q^{s+t}F_A(x\otimes d(m)), \\ \\ (d(\alpha (F))_B(x))_A(m) &{} = &{} d(\alpha (F)_B(x))_A(m)-q^s(\alpha (F)_B(d(x)))_A(m) \\ &{} = &{} d\circ F_A(x\otimes m) -q^{s+t}F_A(x\otimes d(m))-q^sF_A(d(x)\otimes m). \end{array}\end{aligned}$$

Then $\alpha \circ d=d\circ \alpha$, so that $\alpha$ is in $C_{Ndg}(k)$, and $\alpha$ is well defined. Therefore it suffices to show that $\alpha : {\text {Hom}}_{{\mathsf {Gr}}({\mathcal {B}})}(X\otimes _{q, {{\mathcal {B}}}} M, Y) \rightarrow {\text {Hom}}_{{\mathsf {Gr}}({\mathcal {A}})}(X, {\text {Hom}}_{q, {{\mathcal {A}}}} (M, Y))$ is an isomorphism in ${\mathsf {Gr}}^0(k)$. Let $X=\theta _q^iB\,\hat{}$. By Lemmas 3.11, 3.12, $\alpha$ is an isomorphism:

$$\begin{aligned}\begin{aligned} {\text {Hom}}_{{\mathsf {Gr}}({\mathcal {A}})}(\theta _q^iB\,\hat{}\otimes _{q, {{\mathcal {B}}}}M,Y)&\xrightarrow {\sim } {\text {Hom}}_{{\mathsf {Gr}}({\mathcal {A}})}(\theta _q^iM(-, B),Y) \\&\xrightarrow {\sim } {\text {Hom}}_{{\mathsf {Gr}}({\mathcal {B}})}(\theta _q^iB\,\hat{},{\text {Hom}}_{q, {{\mathcal {A}}}}(M,Y)). \end{aligned}\end{aligned}$$

According to Lemma 3.4, we have a projective presentation of X in ${\mathsf {Gr}}^0({\mathcal {B}})$:

$$\begin{aligned} \coprod _{i_1 \in {\mathbb {Z}}}\coprod _{B_1}\theta _q^{i_1}{B_1}\,\hat{}\ {}^{(I_{i_1})} \rightarrow \coprod _{i_0 \in {\mathbb {Z}}}\coprod _{B_0}\theta _q^{i_0}{B_0}\,\hat{}\ {}^{(I_{i_0})} \rightarrow X \rightarrow 0 . \end{aligned}$$

By applying $-\otimes _{q, {{\mathcal {B}}}}M$ to the above, we have an exact sequence in ${\mathsf {Gr}}^0({\mathcal {A}})$:

$$\begin{aligned} \coprod _{i_1 \in {\mathbb {Z}}}\coprod _{B_1}\theta _q^{i_1}{B_1}\,\hat{}\ {}^{(I_{i_1})} \otimes _{q, {{\mathcal {B}}}}M \rightarrow \coprod _{i_0 \in {\mathbb {Z}}}\coprod _{B_0}\theta _q^{i_0}{B_0}\,\hat{}\ {}^{(I_{i_0})} \otimes _{q, {{\mathcal {B}}}}M \rightarrow X \otimes _{q, {{\mathcal {B}}}}M \rightarrow 0 . \end{aligned}$$

Since ${\text {Hom}}_{{\mathsf {Gr}}({\mathcal {B}})}(-, {\text {Hom}}_{q, {{\mathcal {A}}}} (M, Y))$ and ${\text {Hom}}_{{\mathsf {Gr}}({\mathcal {A}})}(-, Y)$ preserve the left exactness of the above exact sequences, by Remark 3.7 and Lemmas 3.11, 3.12,

$$\begin{aligned} \alpha : {\text {Hom}}_{{\mathsf {Gr}}({\mathcal {A}})}(X\otimes _{q, {{\mathcal {B}}}} M, Y) \xrightarrow {\sim } {\text {Hom}}_{{\mathsf {Gr}}({\mathcal {B}})}(X, {\text {Hom}}_{q, {{\mathcal {A}}}}(M, Y)) \end{aligned}$$

is an isomorphism. Thus one can show (2) and (3). $\square$

Corollary 3.3

Let ${\mathcal {A}}$ and ${\mathcal {B}}$ be small $N_q$DG categories. The following hold for an NDG ${\mathcal {B}}$-${\mathcal {A}}$-bimodule M.

• (1) ${\text {Hom}}_{q, {{\mathcal {A}}}}(M, -):{\mathsf {K}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {K}}_{Ndg}({\mathcal {B}})$ is a triangle functor.

• (2) $-\otimes _{q, {{\mathcal {B}}}} M:{\mathsf {K}}_{Ndg}({\mathcal {B}}) \rightarrow {\mathsf {K}}_{Ndg}({\mathcal {A}})$ is a triangle functor.

Proof

By Proposition 4.3, it suffices to show the above functors send projective objects to projective objects. Consider

$$\begin{aligned} {\text {Hom}}_{K_{Ndg({\mathcal {A}})}}(X\otimes _{q, {{\mathcal {B}}}} M, Y) \simeq {\text {Hom}}_{K_{Ndg({\mathcal {B}})}}(X, {\text {Hom}}_{q, {{\mathcal {A}}}} (M, Y)) \end{aligned}$$

If $Y =0$ in ${\mathsf {K}}_{Ndg}({\mathcal {A}})$, then the left side is equal to 0 for any $X \in {\mathsf {K}}_{Ndg}({\mathcal {B}})$. Therefore ${\text {Hom}}_{q, {{\mathcal {A}}}}(M,Y)=0$ in ${\mathsf {K}}_{Ndg}({\mathcal {B}})$. Similarly $X\otimes _{q, {{\mathcal {B}}}} M=0$ in ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ if $X= 0$ in ${\mathsf {K}}_{Ndg}({\mathcal {B}})$. $\square$

4 Derived categories of NDG modules

In this section, we study the derived category of NDG modules and establish triangle equivalences of Morita type for NDG categories. Furthermore, we show that any derived category of NDG modules have a set of symmetric generators, and then describe derived equivalences induced by NDG bimodules.

Definition 4.1

For an $N_q$DG category ${\mathcal {A}}$, let ${\mathsf {Z}}^0_{(1)}{\mathcal {A}}$ be the category whose objects are the same as ${\mathcal {A}}$ and the morphism set between $A_1$ and $A_2$ is given by ${\mathsf {Z}}^0_{(1)}{\mathcal {A}}(A_1,A_2)={\text {Z}}^0_{(1)}{\mathcal {A}}(A_1, A_2)$, ${\mathsf {Mod}}({\mathsf {Z}}^0_{(1)}{\mathcal {A}})$ the category of contravariant k-linear functors from ${\mathsf {Z}}^0_{(1)}{\mathcal {A}}$ to the category of k-modules. For $0< r<N$ and $i\in {\mathbb {Z}}$, we define the following covariant functors from ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ to ${\mathsf {Mod}}({\mathsf {Z}}^0_{(1)}{\mathcal {A}})$:

$$\begin{aligned}\begin{aligned} {\text {Z}}^i_{(r)}(X)&:={\text {Ker}}(d_X^{i+r-1}\cdots d_X^i),&{\text {B}}^i_{(r)}(X)&:={\text {Im}}(d_X^{i-1}\cdots d_X^{i-r}), \\ {\text {C}}^i_{(r)}(X)&:={\text {Cok}}(d_X^{i-1}\cdots d_X^{i-r}),&{\text {H}}^i_{(r)}(X)&:={\text {Z}}^i_{(r)}(X)/{\text {B}}^i_{(N-r)}(X) . \end{aligned}\end{aligned}$$

We call X in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ an N-acyclic if ${\text {H}}^i_{(r)}(X)=0$ in ${\mathsf {Mod}}({\mathsf {Z}}^0_{(1)}{\mathcal {A}})$ for any $i \in {\mathbb {Z}}$, $1\le r \le N-1$. According to [8, Proposition 1.5], this is enough for $r=1$. We call a morphisms $F : X\rightarrow Y$ in ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ a quasi-isomorphism if F induces an isomorphism ${\text {H}}^i_{(r)}(F):{\text {H}}^i_{(r)}(X){\mathop {\rightarrow }\limits ^{\sim }}{\text {H}}^i_{(r)}(Y)$ in ${\mathsf {Mod}}({\mathsf {Z}}^0_{(1)}{\mathcal {A}})$ for any $i \in {\mathbb {Z}}$, $1\le r \le N-1$. By the following Lemma, this is enough for $r=1, N-1$. We denote by ${\mathsf {K}}_{Ndg}^{\phi }({\mathcal {A}})$ the full subcategory of ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ consisting of N-acyclic right NDG ${\mathcal {A}}$-modules. According to the hexagon of homologies in [2] (see Lemma 4.1), ${\mathsf {K}}_{Ndg}^{\phi }({\mathcal {A}})$ is a full triangulated subcategory of ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ which is closed under direct summands. The derived category of right NDG ${\mathcal {A}}$-modules is defined by the quotient category

$$\begin{aligned}{\mathsf {D}}_{Ndg}({\mathcal {A}})={\mathsf {K}}_{Ndg}({\mathcal {A}})/K^{\phi }_{Ndg}({\mathcal {A}}). \end{aligned}$$

Lemma 4.1

The following hold in ${\mathsf {K}}_{Ndg}({\mathcal {A}})$.

• (1) For a triangle $X \xrightarrow {F} Y \xrightarrow {G} Z \rightarrow \Sigma X$ we have the following exact sequence

  $$\begin{aligned} \begin{array}{llll} \cdots &{} \rightarrow &{}{\text {H}}^{i}_{(r)}(X) \rightarrow {\text {H}}^{i}_{(r)}(Y) \rightarrow {\text {H}}^{i}_{(r)}(Z)&{}\\ &{} \rightarrow &{} {\text {H}}^{i+r}_{(N-r)}(X)\rightarrow {\text {H}}^{i+r}_{(N-r)}(Y) \rightarrow {\text {H}}^{i+r}_{(N-r)}(Z)&{}\\ &{}\rightarrow &{}{\text {H}}^{i+N}_{(r)}(X)\rightarrow \cdots .&{} \end{array} \end{aligned}$$

• (2) ${\text {H}}^{i}_{(r)}\Sigma X \simeq {\text {H}}^{i+r}_{(N-r)}X$ for any i, $1 \le r < N$.

• (3) A morphism $F: X \rightarrow Y$ is a quasi-isomorphism if and only if ${\text {H}}^i_{(1)}(F)$ and ${\text {H}}^i_{(N-1)}(F)$ are isomorphisms for any i.

Proof

(1) By the hexagon of homologies in [2].

(2) Since $X \rightarrow Q_{N-1}U_0(X) \rightarrow \Sigma X \xrightarrow {1} \Sigma X$ is a triangle, and ${\text {H}}^i_{(r)}Q_{N-1}U_0(X) = 0$ for any i, $1 \le r < N$, ${\text {H}}^{i}_{(r)}\Sigma X \simeq {\text {H}}^{i+r}_{(N-r)}X$.

(3) In the triangle of (1), if ${\text {H}}^i_{(r)}(F)$ is an isomorphism for any i, $r=1, N-1$, then ${\text {H}}^i_{(r)}Z=0$ for any i, $r=1, N-1$. According to [8, Proposition 1.5], ${\text {H}}^i_{(r)}Z=0$ for any i, $1 \le r < N-1$. $\square$

Example 4.1

Since ${\mathsf {C}}_{Ndg}(k)$ is the category ${\mathsf {C}}_{N}({\mathsf {Mod}}k)$ of complexes of k-modules, ${\mathsf {K}}_{Ndg}(k)$ is the homotopy category ${\mathsf {K}}_{N}({\mathsf {Mod}}k)$ of N-complexes of k-modules. Then we have ${\mathsf {D}}_{Ndg}(k)={\mathsf {D}}_{N}({\mathsf {Mod}}k)$. In this case, we have the following pull-back square $(D_{(r)}^{n})$ (see [6]):

Lemma 4.2

In an abelian category for a commutative diagram

where all rows and columns are exact. Via an isomorphism $\left( {\begin{matrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} f \\ 0 &{} 0 &{} 1 \end{matrix}}\right) : V_1\oplus V_2\oplus V_3 \rightarrow V_1\oplus V_2\oplus V_3$, we can replace f by 0 in the above.

Proposition 4.1

If k is a field, then ${\mathsf {D}}_{Ndg}(k)={\mathsf {K}}_{Ndg}(k)$.

Proof

It suffices to show that every NDG k-module X of which all homologies are null is a zero object of ${\mathsf {K}}_{Ndg}(k)$. Since ${\text {Z}}_{(r)}^{i}(X)={\text {B}}_{(N-r)}^{i}(X)$ for any i, $1 \le r \le N-1$, we have an exact square

where all rows (resp., columns) are monic (resp., epic) for any n, $1 \le r < N$. Here ${\text {Z}}_{(0)}^{n+1}(X) = 0$ and ${\text {Z}}_{(N)}^{n+1}(X) = X^n$. By applying Lemma 4.2 to the above diagram for $1\le r < N$, it is easy to see that X is isomorphic to $(Y, d_Y)$ in ${\mathsf {C}}_{Ndg}(k)$, where $Y^n=\coprod _{i=0}^{N-1}{\text {Z}}_{(1)}^{n+i}(X)$, $d_Y$ is an $N\times N$ matrix $\begin{pmatrix} 0&{}1&{}&{} \\ &{}\ddots &{}\ddots &{} \\ &{}&{}\ddots &{}1 \\ &{}&{}&{}0 \end{pmatrix}$. Therefore X is a zero object of ${\mathsf {K}}_{Ndg}(k)$. $\square$

Proposition 4.2

For any right NDG ${\mathcal {A}}$-module X, Y and any object A of ${\mathcal {A}}$,

• (1) ${\text {Hom}}_{K_{Ndg({\mathcal {A}})}}(\theta ^{-n}_qX, Y)\simeq {\text {H}}^n_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y),$

• (2) ${\text {Hom}}_{K_{Ndg({\mathcal {A}})}}(\theta ^{-n}_qX, \Sigma Y)\simeq {\text {H}}^n_{(N-1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y).$

In particular, by Lemma 3.4,

$$\begin{aligned} {\text {Hom}}_{K_{Ndg({\mathcal {A}})}}(\theta ^{-n}_qA\,\hat{}, X)\simeq {\text {H}}^n_{(1)}X(A). \end{aligned}$$

Proof

We have that $Z^0_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(\theta ^{-n}_qX, Y)=Z^n_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)$ because F is in $Z^0_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(\theta ^{-n}_qX, Y)$ if and only if $d_Y\circ F=F\circ d_{\theta ^{-n}_qX}=q^{n}F\circ d_X$ if and only if F is in $Z^n_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)$.

For any $F \in {\text {B}}^n_{(N-1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)$ we have $F=d^{\{N-1\}}_{{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)}(F')$ for some $F' \in {\text {Hom}}^{n+1-N}_{{\mathcal {A}}}(X, Y)={\text {Hom}}^{1-N}_{{\mathcal {A}}}(\theta ^{-n}_qX, Y)$. By Lemmas 3.1, 2.4,

$$\begin{aligned} d^{\{N-1\}}_{{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)}(F')&= \sum _{l=0}^{N-1}(-1)^lq^{l(n+1-N)+\frac{l(l-1)}{2}} \begin{bmatrix} N-1\\ l \end{bmatrix}d^{\{N-l-1\}}_Y\circ F' \circ d^{\{l\}}_X \\&= \sum _{l=0}^{N-1}d^{\{N-l-1}\}_{Y}\circ F'\circ q^{nl}d^{\{l\}}_X \\&= \sum _{l=0}^{N-1}d^{\{N-l-1\}}_{Y}\circ F' \circ d^{\{l\}}_{\theta ^{-n}_qX} \\&= d^{\{N-1\}}_{{\text {Hom}}_{q, {{\mathcal {A}}}}(\theta ^{-n}_qX, Y)}(F'). \end{aligned}$$

Therefore ${\text {B}}^0_{(N-1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(\theta ^{-n}_qX, Y)={\text {B}}^n_{(N-1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)$. Hence

$$\begin{aligned} {\text {Hom}}_{K_{Ndg({\mathcal {A}})}}(\theta ^{-n}_qX, Y)={\text {H}}^0_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(\theta ^{-n}_qX, Y) ={\text {H}}^n_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y). \end{aligned}$$

One can show that ${\text {H}}^n_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, \Sigma Y)\simeq {\text {H}}^n_{(N-1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, Y)$. Thus (2) is proved. $\square$

Krause introduced the notion of symmetric generators [11]. Let E be an injective cogenerator of k-modules and ${\mathcal {A}}$ an $N_q$DG category. For a left NDG ${\mathcal {A}}$-module X, we denote by ${\mathbb {D}}X$ a right NDG ${\mathcal {A}}$-module defined by ${\mathbb {D}}X(A)={\text {Hom}}_q(X(A), E)$ for any $A \in {\mathcal {A}}$.

Definition 4.2

A set ${\mathsf {U}}$ of objects in a triangulated category $\mathcal {D}$ is called a set of symmetric generators for $\mathcal {D}$ if the following hold:

• (1) ${\text {Hom}}_{\mathcal {D}}({\mathsf {U}}, X)=0$ implies $X=0$.

• (2) There is a set ${\mathsf {V}}$ of objects in $\mathcal {C}$ such that for any $X \rightarrow Y$ in $\mathcal {D}$ the induced morphism ${\text {Hom}}_{\mathcal {D}}(U,X) \rightarrow {\text {Hom}}_{\mathcal {D}}(U,Y)$ is surjective for any $U \in {\mathsf {U}}$ if and only if ${\text {Hom}}_{\mathcal {D}}(Y,V) \rightarrow {\text {Hom}}_{\mathcal {D}}(X,V)$ is injective for any $V \in {\mathsf {V}}$.

Theorem 4.1

Let ${\mathcal {A}}$ be a small $N_q$DG category, ${\mathsf {U}}$ the set $\{ \Sigma ^i \theta ^j_q A\,\hat{}\; |\; A\in {\mathcal {A}}, 1-N \le j \le 0, i \in {\mathbb {Z}} \}$. Then the following hold.

• (1) ${\mathsf {U}}$ is a set of compact generators for ${\mathsf {D}}_{Ndg}({\mathcal {A}})$.

• (2) ${\mathsf {U}}$ is a set of symmetric generators for ${\mathsf {D}}_{Ndg}({\mathcal {A}})$.

Proof

(1) For any $n \in {\mathbb {Z}}$, by Theorem 3.2, $\theta ^n_q A\,\hat{}=\Sigma ^i \theta ^j_q A\,\hat{}$ for some $i \in {\mathbb {Z}}$ and $1-N \le j \le 0$. By Proposition 4.2, ${\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(\theta ^n_q A\,\hat{}, X)=0$ for any N-acyclic X. Thus, for any $Y\in {\mathsf {D}}_{Ndg}({\mathcal {A}})$,

$$\begin{aligned} {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {A}})}(\theta ^n_q A\,\hat{}, Y)&\simeq {\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(\theta ^n_q A\,\hat{}, Y)\\&\simeq {\text {H}}^{-n}_{(1)}(Y)(A) \end{aligned}$$

and, for any $Y_i \in {\mathsf {D}}_{Ndg}({\mathcal {A}})\;(i \in I)$,

$$\begin{aligned} {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {A}})}(\Sigma ^m\theta ^n_q A\,\hat{}, \coprod _{i\in I}Y_i)&\simeq {\text {H}}^{-n}_{(1)}(\Sigma ^{-m}\coprod _{i\in I}Y_i)(A)\\&\simeq \coprod _{i\in I}{\text {H}}^{-n}_{(1)}(\Sigma ^{-m}Y_i)(A)\\&\simeq \coprod _{i\in I}{\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {A}})}(\Sigma ^{m}\theta ^n_q A\,\hat{}, Y_i). \end{aligned}$$

Hence (1) is proved.

(2) Consider ${\mathsf {V}}=\{ \Sigma ^i \theta ^j_q {\mathbb {D}}~\hat{}A\; |\; A\in {\mathcal {A}}, 0 \le j \le N-1, i \in {\mathbb {Z}}\}$. For any $n \in {\mathbb {Z}}$, by Theorem 3.2, $\theta ^n_q {\mathbb {D}}~\hat{}A=\Sigma ^i \theta ^j_q {\mathbb {D}}~\hat{}A$ for some $i \in {\mathbb {Z}}$ and $0 \le j \le N-1$. By Proposition 4.2 and Lemma 3.12,

$$\begin{aligned} {\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(X, \theta ^n_q {\mathbb {D}}~\hat{}A)&\simeq {\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(\theta ^{-n}_q X, {\mathbb {D}}~\hat{}A)\\&\simeq {\text {H}}^n_{(1)}{\text {Hom}}_{q, {{\mathcal {A}}}}(X, {\text {Hom}}_q(\;\hat{}A, E))\\&\simeq {\text {H}}^n_{(1)}{\text {Hom}}_q(X\otimes _{q, {{\mathcal {A}}}}\hat{}A, E)\\&\simeq {\text {H}}^n_{(1)}{\text {Hom}}_q(X(A), E)\\&\simeq {\text {Hom}}({\text {H}}^n_{(1)}X(A), E). \end{aligned}$$

Therefore ${\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(X, \theta ^n_q {\mathbb {D}}~\hat{}A)=0$ for any N-acyclic X. Thus, for any $Y \in {\mathsf {D}}_{Ndg}({\mathcal {A}})$,

$$\begin{aligned} {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {A}})}(Y, \theta ^n_q {\mathbb {D}}~\hat{}A)&\simeq {\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(Y, \theta ^n_q {\mathbb {D}}~\hat{}A)\\&\simeq {\text {Hom}}({\text {H}}^n_{(1)}Y(A), E). \end{aligned}$$

For a morphism $X \rightarrow Y$ in ${\mathsf {D}}_{Ndg}({\mathcal {A}})$, ${\text {H}}_{(1)}^nX(A)\rightarrow {\text {H}}_{(1)}^nY(A)$ is surjective if and only if ${\text {Hom}}({\text {H}}_{(1)}^nY(A), E)\rightarrow {\text {Hom}}({\text {H}}_{(1)}^nX(A), E)$ is injective. Hence (2) is proved. $\square$

Let ${\mathcal {A}}$ be an $N_q$DG category. We denote by ${\mathsf {K}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}})$ (resp. ${\mathsf {K}}_{Ndg}^{{\mathbb {I}}}({\mathcal {A}})$) the smallest full triangulated subcategory of ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ consisting of $\theta _q^nA\,\hat{}$ (resp. $\theta ^n_q {\mathbb {D}}~\hat{}A$) for all $n \in {\mathbb {Z}}$ and $A \in {\mathcal {A}}$ which is closed under taking coproducts (resp. products).

Theorem 4.2

For an $N_q$DG category ${\mathcal {A}}$, the following hold.

• (1) ${\mathsf {D}}_{Ndg}({\mathcal {A}}) \simeq {\mathsf {K}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}}).$

• (2) ${\mathsf {D}}_{Ndg}({\mathcal {A}}) \simeq {\mathsf {K}}_{Ndg}^{{\mathbb {I}}}({\mathcal {A}}).$

Proof

(1) This is essentially the Brown Representability Theorem. Since

${\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(\theta _q^nA\,\hat{}, N)=0$ for any $N \in {\mathsf {K}}_{Ndg}^{\phi }({\mathcal {A}})$, we have ${\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(P, N)=0$ and then ${\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(P, Y) \simeq {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {A}})}(P, Y)$ for any $P \in {\mathsf {K}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}})$, any $Y \in {\mathsf {K}}_{Ndg}({\mathcal {A}})$. According to [11, Theorem A], there is a sequence $X_0 \rightarrow X_1 \rightarrow \cdots$ in ${\mathsf {K}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}})$ of which the homotopy colimit $\underset{\longrightarrow }{{\mathsf {hocolim}}}X_i$ has a morphism $\underset{\longrightarrow }{{\mathsf {hocolim}}}X_i \rightarrow X$ in ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ such that ${\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(P, \underset{\longrightarrow }{{\mathsf {hocolim}}}X_i) \simeq {\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(P, X)$ for any $P \in {\mathsf {K}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}})$. Then ${\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(P, Z) =0$ for any $P \in {\mathsf {K}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}})$, where $\underset{\longrightarrow }{{\mathsf {hocolim}}}X_i \rightarrow X \rightarrow Z \rightarrow \Sigma ( \underset{\longrightarrow }{{\mathsf {hocolim}}}X_i)$ is a triangle in ${\mathsf {K}}_{Ndg}({\mathcal {A}})$. Therefore we have $Z \in {\mathsf {K}}_{Ndg}^{\phi }({\mathcal {A}})$. Since $\underset{\longrightarrow }{{\mathsf {hocolim}}}X_i \in {\mathsf {K}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}})$, (1) is proved.

(2) By Theorem 4.1, ${\text {Hom}}_{{\mathsf {K}}_{Ndg}({\mathcal {A}})}(X, I) \simeq {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {A}})}(X, I)$ for any $I \in {\mathsf {K}}_{Ndg}^{{\mathbb {I}}}({\mathcal {A}})$, any $X \in {\mathsf {K}}_{Ndg}({\mathcal {A}})$. And $\{ \Sigma ^i \theta ^j_q A\,\hat{}\; |\; A\in {\mathcal {A}}, 1-N \le j \le 0, i\in {\mathbb {Z}} \}$ is a set of symmetric generators for ${\mathsf {D}}_{Ndg}({\mathcal {A}})$. According to [11, Theorem B], we similarly have the statement. $\square$

By the above proof, we can check that $({\mathsf {K}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}}), {\mathsf {K}}_{Ndg}^{\phi }({\mathcal {A}}))$ and $({\mathsf {K}}_{Ndg}^{\phi }({\mathcal {A}}), {\mathsf {K}}_{Ndg}^{{\mathbb {I}}}({\mathcal {A}}))$ are stable t-structures in ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ (see [6]). Hence the canonical quotient $Q:{\mathsf {K}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {D}}_{Ndg}({\mathcal {A}})$ has the left adjoint $\mathbf{p} : {\mathsf {D}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {K}}_{Ndg}({\mathcal {A}})$ and the right adjoint $\mathbf{i} : {\mathsf {D}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {K}}_{Ndg}({\mathcal {A}}).$ Therefore we have a recollement

where $i_{*}$ is the canonical embedding (see [1, 14]).

Let ${\mathcal {A}}$ and ${\mathcal {B}}$ be small $N_q$DG categories. For any NDG ${\mathcal {B}}$-${\mathcal {A}}$-bimodule M, we define the functor $-\overset{{\mathbb {L}}}{\otimes }_{q, {{\mathcal {B}}}}M : {\mathsf {D}} _{Ndg}({\mathcal {B}}) \rightarrow {\mathsf {D}} _{Ndg}({\mathcal {A}})$ by

$$\begin{aligned} X\overset{{\mathbb {L}}}{\otimes }_{q, {{\mathcal {B}}}}M=\mathbf{p}X\otimes _{q, {{\mathcal {B}}}}M \end{aligned}$$

for any right NDG ${\mathcal {B}}$-module X and the functor ${\mathbb {R}}{\text {Hom}}_{q, {{\mathcal {A}}}}(M, -) : {\mathsf {D}} _{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {D}} _{Ndg}({\mathcal {B}})$ by

$$\begin{aligned} {\mathbb {R}}{\text {Hom}}_{q, {{\mathcal {A}}}}(M, Y)={\text {Hom}}_{q, {{\mathcal {A}}}}(M, \mathbf{i}Y) \end{aligned}$$

for any right NDG ${\mathcal {A}}$-module Y.

Definition 4.3

Consider a bifunctor ${\text {Hom}}_{q, {{\mathcal {A}}}}(-,-): {\mathsf {C}}_{Ndg}({\mathcal {A}})^{op} \times {\mathsf {C}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {C}}_{Ndg}(k)$. By Corollary 3.3, ${\text {Hom}}_{q, {{\mathcal {A}}}}(X,P)$ is a projective object of ${\mathsf {C}}_{Ndg}(k)$ for any $X \in {\mathsf {C}}_{Ndg}({\mathcal {A}})$ and any projective object P of ${\mathsf {C}}_{Ndg}({\mathcal {A}})$.

In the case that k is a field, by Proposition 4.1, ${\text {Hom}}_{q, {{\mathcal {A}}}}(P,X)$ is a projective object of ${\mathsf {C}}_{Ndg}(k)$ because ${\text {Hom}}_{q, {{\mathcal {A}}}}(P,X)$ is an NDG k-module of which all homologies are null by Proposition 4.2. Therefore the above functor induces a triangle bi-functor

$$\begin{aligned} {\text {Hom}}_{q, {{\mathcal {A}}}}(-,-): {\mathsf {K}}_{Ndg}({\mathcal {A}})^{op} \times {\mathsf {K}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {K}}_{Ndg}(k) \end{aligned}$$

and hence we have the derived functor

$$\begin{aligned} {\mathbb {R}}{\text {Hom}}_{q, {{\mathcal {A}}}}(-,-): {\mathsf {D}}_{Ndg}({\mathcal {A}})^{op} \times {\mathsf {D}}_{Ndg}({\mathcal {A}}) \rightarrow {\mathsf {D}}_{Ndg}(k). \end{aligned}$$

Remark 4.1

If k is not a field, then ${\text {Hom}}_{q, {{\mathcal {A}}}}(P,X)$ maybe not projective in ${\mathsf {C}}_{Ndg}(k)$ in the case of $N>2$.

Theorem 4.3

Let ${\mathcal {A}}$ and ${\mathcal {B}}$ be small $N_q$DG categories. The following hold for an NDG ${\mathcal {B}}$-${\mathcal {A}}$-bimodule M.

• (1) The functor $-\overset{{\mathbb {L}}}{\otimes }_{q, {{\mathcal {B}}}}M : {\mathsf {D}} _{Ndg}({\mathcal {B}}) \rightarrow {\mathsf {D}} _{Ndg}({\mathcal {A}})$ is the left adjoint to the functor ${\mathbb {R}}{\text {Hom}}_{q, {{\mathcal {A}}}}(M, -)$.

• (2) The following are equivalent.

  • 1. $-\overset{{\mathbb {L}}}{\otimes }_{q, {{\mathcal {B}}}}M$ is a triangle equivalence.

  • 2. ${\mathbb {R}}{\text {Hom}}_{q, {{\mathcal {A}}}}(M, -)$ is a triangle equivalence.

  • 3. $\{ \Sigma ^i \theta ^{-n}_q B\,\hat{}\otimes _{q, {{\mathcal {B}}}}M\; |\; B\in {\mathcal {B}}, 0 \le n \le N-1, i \in {\mathbb {Z}}\}$ is a set of compact generators for ${\mathsf {D}} _{Ndg}({\mathcal {A}})$, and the canonical morphism

    $$\begin{aligned} {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {B}})}(\theta ^{j}B_1\hat{}, \Sigma ^{i} B_2\hat{}) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {A}})}(\theta ^{j}B_1\hat{} \otimes _{q, {{\mathcal {B}}}}M, \Sigma ^{i} B_2\hat{} \otimes _{q, {{\mathcal {B}}}}M) \end{aligned}$$

    is an isomorphism for $i=0,1$, any j and any $B_1, B_2 \in {\mathcal {B}}$.

  If k is a field, then the above are equivalent to

  • (d) $\{ \Sigma ^i \theta ^{-n}_q B\,\hat{}\otimes _{q, {{\mathcal {B}}}}M\; |\; B\; \mathrm{and}\; \in {\mathcal {B}}, 0 \le n \le N-1, i \in {\mathbb {Z}}\}$ is a set of compact generators for ${\mathsf {D}} _{Ndg}({\mathcal {A}})$, and the canonical map

    $$\begin{aligned} {\mathcal {B}}(B_1, B_2) \rightarrow {\mathbb {R}}{\text {Hom}}_{q, {{\mathcal {A}}}}(B_1\hat{} \otimes _{q, {{\mathcal {B}}}}M, B_2\hat{} \otimes _{q, {{\mathcal {B}}}}M) \end{aligned}$$

    is an isomorphism in ${\mathsf {D}}_{Ndg}(k)$ for any $B_1, B_2 \in {\mathcal {B}}$.

Proof

(a) $\Leftrightarrow$ (b) For any right NDG ${\mathcal {B}}$-module X and right NDG ${\mathcal {A}}$-module Y,

$$\begin{aligned} {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {A}})}(X\overset{{\mathbb {L}}}{\otimes }_{q, {{\mathcal {B}}}}M, Y)&\simeq {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {A}})}(\mathbf{p}X\otimes _{q, {{\mathcal {B}}}}M, Y)\\&\simeq {\text {Hom}}_{K_{Ndg}({\mathcal {A}})}(\mathbf{p}X\otimes _{q, {{\mathcal {B}}}}M, \mathbf{i}Y)\\&\simeq {\text {Hom}}_{K_{Ndg}({\mathcal {B}})}(\mathbf{p}X, {\text {Hom}}_{q, {{\mathcal {A}}}}(M, \mathbf{i}Y))\\&\simeq {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {B}})}(X, {\text {Hom}}_{q, {{\mathcal {A}}}}(M, \mathbf{i}Y))\\&\simeq {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {B}})}(X, {\mathbb {R}}{\text {Hom}}_{q, {{\mathcal {A}}}}(M, Y)). \end{aligned}$$

Thus $-\overset{{\mathbb {L}}}{\otimes }_{q, {{\mathcal {B}}}}M$ is the left adjoint of ${\mathbb {R}}{\text {Hom}}_{q, {{\mathcal {A}}}}(M, -)$, so that $-\overset{{\mathbb {L}}}{\otimes }_{q, {{\mathcal {B}}}}M$ is a triangle equivalence if and only if so is ${\mathbb {R}}{\text {Hom}}_{q, {{\mathcal {A}}}}(M, -)$.

(a) $\Leftrightarrow$ (c) Note that $\Sigma ^i \theta ^{-m}_q B\,\hat{}\overset{{\mathbb {L}}}{\otimes }_{q, {{\mathcal {B}}}}M \simeq \Sigma ^i \theta ^{-m}_q B\,\hat{}\otimes _{q, {{\mathcal {B}}}}M$. Since ${\mathsf {D}}_{Ndg}({\mathcal {B}})$ has a set of compact generators $\{ \Sigma ^i \theta ^{-m}_q B\,\hat{}\; |\; B\in {\mathcal {B}}, 0 \le m \le N-1, i \in {\mathbb {Z}} \}$, by Theorem 4.5, $-\overset{{\mathbb {L}}}{\otimes }_{q, {{\mathcal {B}}}}M$ is a triangle equivalence if and only if $\{ \Sigma ^i \theta ^{-n}_q B\,\hat{}\otimes _{q, {{\mathcal {B}}}}M\; |\; B\in {\mathcal {B}}, 0 \le n \le N-1, i \in {\mathbb {Z}}\}$ is a set of compact generators for ${\mathsf {D}}_{Ndg}({\mathcal {A}})$ and the canonical map

$$\begin{aligned} {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {B}})} (\Sigma ^i \theta ^{-m}_qB_1\hat{}, \Sigma ^j \theta ^{-n}_qB_2\hat{}\;) \rightarrow {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {A}})} (\Sigma ^i \theta ^{-m}_qB_1\hat{} \otimes _{q, {{\mathcal {B}}}}M, \Sigma ^j \theta ^{-n}_qB_2\hat{} \otimes _{q, {{\mathcal {B}}}}M) \end{aligned}$$

is an isomorphism for any $i, j \in {\mathbb {Z}}$, $0 \le m, n \le N-1$ and $B_1, B_2 \in {\mathcal {B}}$. By Theorem 3.2, we have the statement.

(c) $\Leftrightarrow$ (d) For any $B_1, B_2 \in {\mathcal {B}}$, the canonical map

$$\begin{aligned} \alpha : {\mathcal {B}}(B_1, B_2) \rightarrow {\mathbb {R}}{\text {Hom}}_{q, {{\mathcal {A}}}}(B_1\hat{} \otimes _{q, {{\mathcal {B}}}}M, B_2\hat{} \otimes _{q, {{\mathcal {B}}}}M) \end{aligned}$$

induces

$$\begin{aligned}\begin{aligned} {\text {H}}_{(1)}^n{\mathcal {B}}(B_1, B_2)&\xrightarrow {{\text {H}}_{(1)}^{n}(\alpha )} {\text {H}}_{(1)}^n{\text {Hom}}_{q, {{\mathcal {A}}}} (B_1\hat{} \otimes _{q, {{\mathcal {B}}}}M, B_2\hat{} \otimes _{q, {{\mathcal {B}}}}M)\\ {\text {H}}_{(N-1)}^n{\mathcal {B}}(B_1, B_2)&\xrightarrow {{\text {H}}_{(N-1)}^{n}(\alpha )} {\text {H}}_{(N-1)}^n{\text {Hom}}_{q, {{\mathcal {A}}}} (B_1\hat{} \otimes _{q, {{\mathcal {B}}}}M, B_2\hat{} \otimes _{q, {{\mathcal {B}}}}M) \end{aligned}\end{aligned}$$

for any n. By Lemma 4.1, $\alpha$ is an isomorphism in ${\mathsf {D}}_{Ndg}(k)$ if and only if ${\text {H}}_{(1)}^{n}(\alpha )$ and ${\text {H}}_{(N-1)}^{n}(\alpha )$ are isomorphisms for any n. By Proposition 4.2, this is equivalent to

$$\begin{aligned} {\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {B}})}(\theta _q^{n}B_1\hat{}, \Sigma ^{i} B_2\hat{}\;) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{{\mathsf {D}}_{Ndg}({\mathcal {A}})}(\theta _q^{n}B_1\hat{} \otimes _{q, {{\mathcal {B}}}}M, \Sigma ^{i} B_2\hat{} \otimes _{q, {{\mathcal {B}}}}M) \end{aligned}$$

is an isomorphism for $i=0,1$ and any n. $\square$

Finally, we show that the derived category ${\mathsf {D}}_{Ndg}({\mathcal {A}})$ of right NDG ${\mathcal {A}}$-modules is triangle equivalent to the derived category of some ordinary DG category (see also Remark 4.2).

Theorem 4.4

For any $N_q$DG category ${\mathcal {A}}$, there exists a DG category ${\mathcal {B}}$ such that ${\mathsf {D}} _{Ndg}({\mathcal {A}})$ is triangle equivalent to the derived category ${\mathsf {D}} _{dg}({\mathcal {B}})$.

Proof

By Theorem 3.1, ${\mathsf {K}}_{Ndg}({\mathcal {A}})$ is an algebraic triangulated category. By Theorems 4.2, 4.1, ${\mathsf {D}}_{Ndg}({\mathcal {A}})$ is a compactly generated algebraic triangulated category with a set $\{ \Sigma ^i \theta ^j_q A\,\hat{}\; |\; A\in {\mathcal {A}}, 1-N \le j \le 0, i \in {\mathbb {Z}} \}$ of compact generators (see Appendix for definition) . According to [12, 7.5 Theorem], there are a DG category ${\mathcal {B}}$ and a triangle equivalence $F:{\mathsf {D}} _{Ndg}({\mathcal {A}}) {\mathop {\rightarrow }\limits ^{\sim }}{\mathsf {D}} _{dg}({\mathcal {B}})$. $\square$

Remark 4.2

We denote by $F: {\mathsf {C}}_{Ndg}({\mathcal {A}})\rightarrow {\mathsf {K}}_{Ndg}({\mathcal {A}})$ the canonical projection. Let ${\mathsf {C}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}})$ be the full subcategory of ${\mathsf {C}}_{Ndg}({\mathcal {A}})$ consisting of objects M with F(M) in ${\mathsf {K}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}})$. Then ${\mathsf {C}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}})$ is a Frobenius category. Let ${\mathsf {C}}^{\phi }({\mathsf {C}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}}))$ be the category of ordinary complexes X satisfying that ${\text {B}}^i(X)={\text {Z}}^i(X)$ for all i, and that $0 \rightarrow {\text {Z}}^i(X) \rightarrow X^i \rightarrow {\text {Z}}^{i+1}(X) \rightarrow 0 \in \mathcal {E}_{{\mathsf {C}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}})}$. Consider the DG category ${\mathcal {B}}$ of complexes $X \in {\mathsf {C}}^{\phi }({\mathsf {C}}_{Ndg}^{{\mathbb {P}}}({\mathcal {A}}))$ with ${\text {Z}}^0(X)=\theta ^j_q A\,\hat{}$ for any $A\in {\mathcal {A}}$ $(1-N \le j \le 0)$, according to [12, Theorem 7.5] it satisfies the above theorem.

5 Appendix

In this section, we give the following results concerning Frobenius categories and triangulated categories. Let $\mathcal {C}$ be an exact category with a collection $\mathcal {E}$ of exact sequences in the sense of Quillen [16]. An exact sequence $0 \rightarrow X \xrightarrow {f} Y \xrightarrow {g} Z \rightarrow 0$ in $\mathcal {E}$ is called a conflation, and f and g are called an inflation and a deflation, respectively. An additive functor $F: \mathcal {C} \rightarrow \mathcal {C}'$ is called exact if it sends conflations in $\mathcal {C}$ to conflations in $\mathcal {C}'$. An exact category $\mathcal {C}$ is called a Frobenius category provided that it has enough projectives and enough injectives, and that any object of $\mathcal {C}$ is projective if and only if it is injective. In this case, the stable category $\underline{\mathcal {C}}$ of $\mathcal {C}$ by projective objects is a triangulated category (see [5]). This stable category is called an algebraic triangulated category.

Proposition 4.3

([7] Proposition 7.3) Let $(\mathcal {C}, \mathcal {E}_{\mathcal {C}}), (\mathcal {C}, \mathcal {E}_{\mathcal {C}'})$ be Frobenius categories, $F: \mathcal {C} \rightarrow \mathcal {C}'$ an exact functor. If F sends projective objects of $\mathcal {C}$ to projective objects of $\mathcal {C}'$, then it induces the triangle functor ${\underline{F}} : \underline{\mathcal {C}} \rightarrow \underline{\mathcal {C}}'$.

Let $\mathcal {D}$ be a triangulated category with arbitrary coproducts. An object U in $\mathcal {D}$ is compact if the canonical morphism $\coprod _{i}{\text {Hom}}_{\mathcal {D}}(U, X_i)\rightarrow {\text {Hom}}_{\mathcal {D}}(U, \coprod _{i }X_i)$ is an isomorphism for any set $\{X_i \}$ of objects in $\mathcal {D}$. A triangulated category $\mathcal {D}$ is called compactly generated if there is a set ${\mathsf {U}}$ of compact objects such that ${\text {Hom}}_{\mathcal {D}}({\mathsf {U}}, X) = 0$ implies $X=0$ in $\mathcal {D}$.

Theorem 4.5

Let $\mathcal {D}$ be a compactly generated triangulated category with a set ${\mathsf {U}}$ of compact generators for $\mathcal {D}$. Let $F: \mathcal {D} \rightarrow \mathcal {D}'$ be a triangle functor between triangle categories such that F preserves coproducts. Then the following are equivalent.

• (1) F is a triangle equivalence.

• (2)

  • 1. $F({\mathsf {U}})$ is a set of compact generators for $\mathcal {D}'$.

  • 2. ${\text {Hom}}_{\mathcal {D}}(U, V) \rightarrow {\text {Hom}}_{\mathcal {D}'}(FU,FV)$ is an isomorphism for any $U, V \in {\mathsf {U}}$.

Proof

(1) $\Rightarrow$ (2) Trivial.

(2) $\Rightarrow$ (1) We may assume that ${\mathsf {U}}=\Sigma {\mathsf {U}}$. Let $\mathcal {U}$ be the full subcategory of coproducts of objects U in ${\mathsf {U}}$. Let $<\mathcal {U}>_0:=\mathcal {U}$. For $n \ge 1$ let $<\mathcal {U}>_n$ be the full subcategory of $\mathcal {D}$ consisting of objects X such that there is a triangle $U \rightarrow V \rightarrow X \rightarrow \Sigma U$ with $U \in <\mathcal {U}>_0$, $V \in <\mathcal {U}>_{n-1}$. Given $U \in {\mathsf {U}}$, for any $U_i \in {\mathsf {U}}$ $(i \in I)$, we have a commutative diagram

such that all vertical arrows are isomorphisms. Therefore, for any $V \in \mathcal {U}$ we have the canonical morphism ${\text {Hom}}_{\mathcal {D}}(U, V) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{\mathcal {D}'}(FU, FV)$ is an isomorphism. For any $W\in <\mathcal {U}>_n$ we have a triangle $U' \rightarrow V \rightarrow W \rightarrow \Sigma U$ with $U' \in <\mathcal {U}>_0$, $V \in <\mathcal {U}>_{n-1}$. Applying ${\text {Hom}}_{\mathcal {D}}(U, -)$ to this triangle, by the induction the five lemma implies that the canonical morphism ${\text {Hom}}_{\mathcal {D}}(U, W) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{\mathcal {D}'}(FU, FW)$ is an isomorphism. According to Brown’s representability theorem (e.g. [15]), for any $Y \in \mathcal {D}$, there is a sequence $Y_0 \rightarrow Y_1 \rightarrow \cdots$ with $Y_i \in <\mathcal {U}>_i$ which has a triangle

$$\begin{aligned} \coprod _{i}Y_i \xrightarrow {1-\text {shift}} \coprod _{i}Y_i \rightarrow Y \rightarrow \Sigma \coprod _{i}Y_i \end{aligned}$$

Applying ${\text {Hom}}_{\mathcal {D}}(U, -)$ to this triangle, the five lemma implies that the canonical morphism ${\text {Hom}}_{\mathcal {D}}(U, Y) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{\mathcal {D}'}(FU, FY)$ is an isomorphism. Similarly, by the induction on n for any $W \in <\mathcal {U}>_n$, any $Y \in \mathcal {D}$ the canonical morphism ${\text {Hom}}_{\mathcal {D}}(W, Y) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{\mathcal {D}'}(FW, FY)$ is an isomorphism. Brown’s representability theorem implies that the canonical morphism ${\text {Hom}}_{\mathcal {D}}(X, Y) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{\mathcal {D}'}(FX, FY)$ is an isomorphism for any $X. Y \in \mathcal {D}$. Then F is fully faithful. Therefore we have $<F(\mathcal {U})>_i= F(<\mathcal {U}>_i)$ for any i. Since $F({\mathsf {U}})$ is a set of compact generator for $\mathcal {D}'$, for any $Z \in \mathcal {D}'$, there is a sequence $Z_0 \xrightarrow {\beta _0} Z_1 \xrightarrow {\beta _1} \cdots$ with $Z_i \in <F(\mathcal {U})>_i$ which has a triangle

$$\begin{aligned} \coprod _{i}Z_i \xrightarrow {1-\text {shift}} \coprod _{i}Z_i \rightarrow Z \rightarrow \Sigma \coprod _{i}Z_i \end{aligned}$$

Then there is a morphism $\alpha _i:X_i \rightarrow X_{i+1}$ such that $F\alpha _i=\beta _i$ for any i. Let X be the homotopy colimit of the sequence $X_0 \xrightarrow {\alpha _0} X_1 \xrightarrow {\alpha _1} \cdots$, then we have a commutative diagram

where the first, second, fourth vertical arrows are isomorphisms. Then the third vertical arrow is an isomorphism. Therefore F is dense, and hence a triangle equivalence. $\square$