Introduction

Polymer matrix composites (PMCs) have efficiently served several structural applications for over half a century. However, scientists still hesitate to replace the traditional material with PMCs due to its complexity, anisotropy, the absence of universal failure theory, and commonly accepted life prediction tool. Structures used in aircraft or wind turbine blades are vulnerable to cyclic stress because the live load is greater than the dead load [1]. Common issues plague PMCs, including susceptibility to moisture ingress [2,3,4,5,6,7,8], resulting mechanical property degradation [9,10,11,12,13], inadequate resistance against sliding wear [14,15,16,17], and vulnerability to dynamic loading conditions [18,19,20,21]. Moisture ingress is a persistent concern, compromising structural integrity and triggering a gradual decline in mechanical properties. Moreover, PMCs often exhibit insufficient resistance to sliding wear, heightening the risk of surface damage and material deterioration over time. The weakness against dynamic loading conditions further underscores the need for robust material formulations and engineering solutions to enhance resilience under varying stress environments. Addressing these multifaceted challenges necessitates a nuanced understanding of composite behavior and the development of innovative strategies to bolster resistance to moisture, wear, and dynamic loads. Consequently, ongoing research and advancements in composite materials science aim to overcome these obstacles and unleash the full potential of PMCs across diverse applications.

Modern synthetic fiber-reinforced composites are thought to be less susceptible to fatigue than metallic materials, but it is unavoidable that some properties may deteriorate over time. The theory currently used to predict the lifespan of conventional materials cannot be directly applied to composite materials. An accurate life forecast of composite structural components under fatigue loading circumstances is essential for design engineers. The stress versus the number of cycles to failure (S–N curve) results are the prerequisite for the macroscopic or microscopic fatigue life prediction models. Localized damage accumulation, such as matrix cracking, fiber-matrix debonding, delamination, fiber rotation, buckling, and other phenomena, is quantified by microscopic models until final breakage [22]. To make more accurate forecasts, models correlate these damage metrics and their growth with the fatigue lifecycle. Macroscopic life prediction, however, does not consider damage mechanisms or its expansion under continuous cyclic loading. Macroscopic Prediction is based on probabilistic, empirical, theoretical, or experimental analysis, including modified S–N curves, residual strengths, stiffness, CLDs, and S–N curves for varied R ratios. For effective life prediction, numerous researchers have recently used genetic algorithms, neuro-fuzzy interference, artificial intelligence, rain flow approaches, artificial neural networks, etc. [23, 24].

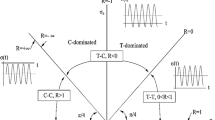
As the safe life envelopes fluctuate with fiber orientation, adopting multidirectional laminates in structural applications to decrease anisotropy made the Prediction considerably more challenging. The CLD is a projection of the ultimate tensile strength (UTS) and ultimate compressive strength (UCS) results generated by linearly interpolating the available S–N curves [25]. It is a fatigue life prediction tool that can forecast the safe life envelope and S–N curve for any stress ratio or stacking sequence while saving time and money. The mean (m) and alternating stress (a) sensitivities are considered in this combined plot with UTS, UCS, and S–N curve data. The most straightforward Goodman diagram was the earliest fatigue analysis tool primarily utilized for conventional materials [26]. The anisotropic laminate, however, was not symmetrical about the completely reversed stress ratio, or R = − 1, due to its differing UTS and UCS. Like the Goodman approach, even the CLD points (pair of mean and amplitude stresses) were not along a straight line. However, the asymmetric shifted, and inclined Goodman diagrams ideally addressed the static strength nonlinearity by repositioning the peak with respect to the zero-mean axis. A significant innovation that separated the diagram into subintervals was the half-spider web-shaped piecewise defined linear CLD diagram [27,28,29]. A nonlinear interpolation method and a piecewise-defined function were used in an asymmetric and shifted Gerber diagram with a parabolic envelope. The CLD discussed up to this point discussed peak shifting to the right or left, but the trend was unsolved before Kawai and colleagues developed the groundbreaking Anisomorphic CLD [30, 31]. They defined a characteristic stress ratio termed critical stress ratio (CRS) (χ), where alternating stress acquires the most considerable possible value for any arbitrary Nf. CSR was the ratio of compressive to tensile strength, where (UCS < 0) and (UTS > 0). The UTS/UCS of any laminate determines whether the peak shifts to the left (UTS < UCS) or right (UTS > UCS) of the zero-mean line.

While these nonlinear CLDs can be formulated using any S–N curves and static data as input, linear CLDs require many S–N curves and static data as input. This saves time, work, and money, but it might not be appropriate for a certain stacking and produce subpar predictions. Modern laminate curing procedures and improved fiber manufacturing methods, particularly following the advent of prepregs, have significantly changed the properties of laminates. To demonstrate the importance of CSR, it is necessary to evaluate further the experimental validity of various nonlinear CLDs for different laminates. This study produced extensive experimental constant amplitude fatigue data for a [+ 45, − 45]3S (CFRP45) laminate. Investigations were conducted into the impact of CSR and its importance in assessing the life prediction accuracy of various nonlinear CLDs available in the literature.

Experimental

IMA/ M21 carbon fiber epoxy prepreg was used to manufacture the [+ 45, − 45]3S orientation carbon fiber reinforced polymer (CFRP) composite laminate, which was autoclave-cured at 180° C with a heating rate of 2° C per minute and a dwell time of 120 min. The laminate is termed CFRP45 further, and during layup, prepreg sheets were meticulously organized in alternate directions of + 45° and − 45° to ensure they were stacked in the correct orientation and produced the best possible mechanical properties. Next, the layup composite structure was placed into a vacuum bag with 1 bar pressure and sealed to remove air, consolidate the layers, and promote uniform resin distribution while minimizing voids. Then, the vacuum-bagged composite laminate was subjected to 180° C heat and 7 bar pressure in an autoclave, initiating the cross-linking of the epoxy matrix and solidifying the composite structure. This controlled curing process ensured the formation of a strong and durable composite material with consistent mechanical properties. The basic properties of the IMA/M21 prepreg are attached to Table 1. The average fiber volume fraction and thickness of the sixteen-layered, 300 × 450 mm laminate were 59% and 3.1 mm, respectively. The static and fatigue test specimens were made with a diamond cutter, and rectangular glass fiber tabs were attached to both ends with Araldite (Epoxy: AV-138, Hardener: HY-998). The end tabs were meticulously trimmed to be close to the gauge length to lessen the effects of tabbing tension.

Table 1 Physical and mechanical properties of IMA/M21 prepreg
Full size table

The static tensile and compressive tests were carried out with a servo-hydraulic universal testing machine, as shown in Fig. 1 (Make: Instron, Model: 8802), following ASTM standards D3039 and D3410, respectively. A crosshead speed of 1 mm/min was employed per standard. Then, room temperature load-controlled constant amplitude fatigue tests were carried out at 2 Hz. Experimentally produced fatigue stress ratios include Tension–Tension (T-T) 0.1 and 0.5, Tension–Compression (T-C) − 1, and Compression–Compression (C–C) 5 stress ratios. The tests were run up to 106 cycles, or until failure, and were referred to as runout samples. At least three samples were evaluated to verify the fatigue life at a specific stress level. Figure 2 displays a detailed layout of the specimen geometry and a picture of the specimen utilized in static and fatigue tests [18, 20, 30, 31].

Fig. 1
figure 1

Fatigue experimental setup

Full size image
Fig. 2
figure 2

CFRP45 static and fatigue test specimen geometry and actual test specimen

Full size image

Results and Discussion

Tensile and Compression Test

Tensile and compressive tests on the CFRP45 laminate were performed at room temperature with a 1 mm/min crosshead speed. It was discovered that the UTS and UCS were 270 ± 10 and 168 ± 7 MPa, respectively. As previously reported, the results showed a nonlinear stress–strain response attributed to stress relaxation caused by fiber rotation and orientation [32,33,34,35]. These values were also used to calculate fatigue stress levels and formulate nonlinear CLDs. The CSR was calculated as χ = UCS/UTS = − 0.64.

Constant Amplitude Fatigue and S–N Curve

The CFRP45 CFRP laminate's experimental constant amplitude fatigue data under T–T (R = 0.1 and 0.5), T–C (R = − 1 and χ), and C–C (R = 5) loading was generated. The plot between σmax and Nf is shown in Fig. 3, where the arithmetic mean of at least three comparable fatigue life data corresponding to five stress levels was plotted for all R ratios. The estimated Basquin's constants, i.e., fatigue strength coefficient (FSC, f) and fatigue strength exponent (FSE, b), are shown in Table 2. The solid line shows the S–N curve was fitted using Basquin's law according to Eq. 1 [22]. These constants are useful in the mathematical computation of the required Nf or equivalent for any stress ratio.

$$\sigma = \sigma{\prime}_{f} \left( {N_{f} } \right)^{b}$$
(1)
Fig. 3
figure 3

Constant amplitude S–N curve for CFRP45 laminate

Full size image
Table 2 Experimental Basquin's constants of CFRP45 laminate
Full size table

The UTS/UCS lifespan typically ranged between 30–80%. The lower positioning of the T-T S–N curve at R = 0.1 compared to R = 0.5 confirms the previously proven phenomenon that the higher the stress range (σmax—σmin), the lower the fatigue life will be [36, 37]. The fact that the slope of 0.1 is steeper than that of 0.5 further supports the effect of mean stress and stress range in T-T loading. The R = − 1 S–N curve with the steepest slope and a 20–50% lifespan of UCS was the most critical. The S–N curves indicate that T-C loading caused damage more effectively and sensitively than T-T or C–C loading [38].

Constant Life Diagrams

The CLD determines a safe stress envelope within which the composite laminate may withstand more than a specific number of cycles with constant amplitude. CLD can be linear or nonlinear to the alternating stress axis based on interpolation technique or fitting equations. Asymmetric CLDs have distinct UTS and UCS values, while symmetric CLDs have the same values. With CFRP45 laminate having different UTS and UCS values, a few asymmetric nonlinear CLDs from the literature were analyzed in the following sections. The basic Goodman approximation assumes that the largest amplitude stress lies at zero mean stress, i.e., in the completely reversed stress ratio (R = −1). The current experimental results observed the highest alternating stress for CSR rather than R = −1. This experimental shift of the highest alternating stress to the left or right of R = −1 is called radial peak shift. Numerous researchers documented this radial peak shift [39,40,41,42,43,44,45,46], but Kawai et al. recently defined the shift's quantification [30, 31].

Nonlinear Asymmetric CLDs

Researchers have focused on modified nonlinear Goodman or Piecewise diagrams, which are more precise, practical, and time-saving. When using a particular nonlinear analytical function, parabolic or bell-shaped nonlinear CLDs were usually plotted with fewer input nodes. For the current CFRP45 experimental data, a few CLDs from the literature were plotted, and the accuracy was checked.

Asymmetric Gerber CLD

Initially, the nested parabolic-shaped asymmetric Gerber diagram was plotted using a Piecewise-defined parabolic function in Eq. 2, where σa = amplitude stress and σm = mean stress [47]. According to this equation, the peak will appear at R = − 1, and the underlying equation will be chosen based on a lower UTS or UCS value. The Gerber diagram derives the T-T, T-C, and C–C zones with a single equation. Currently, for CFRP45 laminate with UCS lower than UTS, the 2nd part of Eq. 2 was employed to plot the Gerber diagram, as shown in Fig. 4, with input stress ratio R = − 1. The figure demonstrates that the overall prediction accuracy of this CLD for R- 0.1, 0.5, and 5 was inferior if compared with the experimental data projected in the S–N curve.

Fig. 4
figure 4

Asymmetric Gerber CLD for CFRP45 laminate

Full size image
$$\begin{array}{c}-\frac{{\sigma }_{a}-{{\sigma }_{a}}^{R=-1}}{{{\sigma }_{a}}^{R=-1}}={\left(\frac{{\sigma }_{m}}{UTS}\right)}^{2},(0\le {\sigma }_{m}\le UTS)\\ -\frac{{\sigma }_{a}-{{\sigma }_{a}}^{R=-1}}{{{\sigma }_{a}}^{R=-1}}={\left(\frac{{\sigma }_{m}}{UCS}\right)}^{2},(UCS\le {\sigma }_{m}\langle 0)\end{array}$$
(2)

Shifted Gerber CLD

Gerber CLD did not address the experimental peak lying about non-zero mean stress. Later, this peak shift was addressed by shifted Gerber parabolic CLD where traditional Gerber CLD shifts to a non-zero mean (χ) following a Piecewise-defined function as given in Eq. 3. Here, σM is a constant denoting the mean of UTS and UCS whereas σA is a function Nf. The parabola with two different foci in the tension and compression zone was smoothly connected along with an unknown stress ratio (χ), as shown in Fig. 5. This R ratio was conveyed as Eq. 4 without any quantification till Kawai and coworker solved this recently [30, 31]. The prediction accuracy of the shifted Gerber CLD was comparatively more acceptable than traditional Gerber CLD, but the consideration of the unknown stress ratio was unsolved.

$$- \frac{{\sigma_{a} - \sigma_{A} }}{{\sigma_{A} }} = \begin{array}{*{20}c} {\left( {\frac{{\sigma_{m} - \sigma_{M} }}{{UTS - \sigma_{M} }}} \right)^{2} ,\sigma_{M} \le \sigma_{m} \le \sigma_{T} } \\ {\left( {\frac{{\sigma_{m} - \sigma_{M} }}{{UCS - \sigma_{M} }}} \right)^{2} ,\sigma_{C} \le \sigma_{m} < \sigma_{M} } \\ \end{array}$$
(3)
$$\chi = \frac{{\left( {\sigma_{M} - \sigma_{A} } \right)}}{{\left( {\sigma_{M} + \sigma_{A} } \right)}}$$
(4)
Fig. 5
figure 5

Shifted asymmetric Gerber CLD for CFRP45 laminate

Full size image
$$Where,{\sigma }_{M}=\frac{UTS+UCS}{2}$$

The shifted symmetric Gerber diagram showed acceptable prediction accuracy for carbon/Kevlar hybrid composites [40] and carbon fiber composites [43, 44]. The innovative bell-shaped CLD and inclined Gerber diagram were also developed because of this shifted Gerber diagram, and their correctness has been examined in the literature. Much research has been done on the bell-shaped diagram for different CFRP and GFRP composite laminates [22, 25]. Using nonlinear regression and material functions based on fatigue data, this method is complicated. This CLD can be extended mathematically to fit the bell-shaped CFL diagram. Eventually, Kawai and colleagues created a unique anisomorphic nonlinear CLD employing all these databases.

Anisomorphic Nonlinear CLD

The Anisomorphic CLD mathematically described the radial peak shift line as Eq. 5, where χ stands for the CSR. The T–T and C–C fatigue failure modes split the CLD into two halves along this radial line. Equation 6 only requires the CSR S–N curve values, UTS, and UCS to create the tension and compression side curves. In this case, UCS is negative, UTS is positive, the exponent "ψ(R=χ)" represents the function of Nf, and " σBχ " stands for a constant reference strength to be found for the CSR. The range of (2- ψ(R=χ)) in Eq. 6 is constrained between one and two, i.e., 1 ≤ 2- ψ(R=χ) ≥ 2. This is because the variable exponent "ψ(R=χ)" always resides between zero and one, i.e., 0 ≤ ψ(R=χ) ≥ 1. This CLD produces nested parametric curves whose shape gradually changes from a straight line to a parabola as fatigue life increases [48].

$$\frac{{\sigma }_{a}}{{\sigma }_{m}}=\frac{1-\chi }{1+\chi }$$
(5)
$$-\frac{{\sigma }_{a}-{{\sigma }_{a}}^{R=\chi }}{{{\sigma }_{a}}^{R=\chi }}=\begin{array}{c}{\left(\frac{{\sigma }_{m}-{{\sigma }_{m}}^{R=\chi }}{UTS-{{\sigma }_{m}}^{R=\chi }}\right)}^{2-{\psi }_{(R=\chi )}},\left({{\sigma }_{m}}^{R=\chi }\le {\sigma }_{m}\le UTS\right)\\ {\left(\frac{{\sigma }_{m}-{{\sigma }_{m}}^{R=\chi }}{UCS-{{\sigma }_{m}}^{R=\chi }}\right)}^{2-{\psi }_{(R=\chi )}},\left(UCS\le {\sigma }_{m}\le {{\sigma }_{m}}^{R=\chi }\right)\end{array}$$
(6)
$${Where, \psi }_{(R=\chi )}=\frac{{{\sigma }_{max}}^{R=\chi }}{{{\sigma }_{B}}^{R=\chi }}$$

The same equation was used to create four different CLDs using different experimental CFRP45 stress ratios, namely R = 0.1, 0.5, − 1, and 5, before creating the suggested CLD utilizing the CSR data, as shown in Fig. 6a–d. For the remainder of experimental S–N curves, the prediction accuracy of the R = 0.5 and R = 5 Anisomorphic CLD was less than optimal. On the other hand, R = 0.1 and R = − 1 demonstrated superior prediction accuracy for the T-T and C–C zones, respectively. Notably, for R = 5, the R = 0.1 anisomorphic CLD's prediction accuracy was close to the experiments' outcomes. The optimal stress ratio was R = − 1 based on the CLD peak and overall Prediction.

Fig. 6
figure 6

CFRP45 anisomorphic CLDs formulated with input stress ratios (R) of a 0.1, b 0.5, c − 1, and d 5

Full size image

The associated radially and correlated σ Mean and σ Amplitude, as given in Eq. 5–6, were resolved using the anisomorphic CLD diagram, as shown in Fig. 7 [48]. This represents the CLD after considering experimental fatigue data points of CSR (χ = − 0.64). The curve's apex has shifted to the right, which also denotes an ultimate tensile-dominated failure of the CFRP45 laminate. Any stress ratio within the life envelope can be predicted using the plotted CLD. The anisomorphic CLD plotted using critical stress as input offered the highest accuracy out of all the experimental CLDs.

Fig.7
figure 7

CFRP45 anisomorphic CLD plotted using static and CSR data

Full size image

Table 3 displays the inaccuracy % between experimental and anamorphic CLD prediction. The T-T S–N curves have errors below 10%. However, the C–C and fully reversed stress ratios exhibited close to 20% inaccuracy. As the CFRP45 failed under the dominance of tensile loading, the prediction in the T-T domain was better than that in the C–C domain. Researchers designed the three-segment anisomorphic CLD with an additional input node to broaden the anisomorphic CLD and address this problem of poor prediction based on the mode of failure [49].

Table 3 Error in experimental and anamorphic prediction
Full size table

This study addresses a crucial gap in knowledge by highlighting the limitations of linear CLDs and the importance of CSR in accurately predicting the fatigue life of composite laminates. While nonlinear CLDs offer a streamlined approach requiring fewer input parameters, linear CLDs may yield subpar predictions, especially for complex laminate configurations. The evolution of laminate curing procedures and fiber manufacturing methods necessitates a reassessment of CLD validity across different laminates. Focused on a [+ 45, − 45]3S laminate, the study generates extensive experimental fatigue data to evaluate the impact of CSR on the predictive accuracy of various nonlinear CLDs, bridging the gap between theory and practical application in composite materials engineering.

Conclusions

Nonlinear CLDs are a practical tool for estimating the fatigue life of composite materials with various orientations and stacking configurations. This study specifically investigated the predictive accuracy of several nonlinear CLDs for a laminated Carbon Fiber Reinforced Polymer composite with [+ 45, − 45]3S layup. Comparing experimental findings with anisomorphic CLD projected values revealed exciting insights. Experimental and theoretical error percentages were lower for T-T stress ratios but higher for C–C stress ratios. Introducing a transitional zone, i.e., critical stress ratio in the anisomorphic CLD, notably enhanced forecast accuracy. This innovative approach simplifies the predictive process and minimizes the required testing. By integrating a transitional zone, the anisomorphic CLD effectively mitigates mean stress sensitivity and offers accurate predictions with minimal input data, primarily comprising Ultimate Tensile Strength (UTS), Ultimate Compressive Strength (UCS), and CSR. Implementing these nonlinear CLDs can streamline labor-intensive and costly testing processes, saving valuable resources like time, effort, and financial investments. Future research can lead to refining and validating CLDs across different composite materials and configurations and exploring the impact of environmental factors on predictions. Overall, nonlinear CLDs hold promise for streamlining testing procedures and improving efficiency in composite material design and evaluation.