Introduction

The bulge test has been carried out to determine the biaxial flow stress curve of sheet metals under the equi-biaxial tension. Different techniques are experimented to get the biaxial flow stress curve of the materials, but the flow stress curves are not the same for all the techniques due to the effects of stress state, selection of yield criteria, anisotropy coefficient, experimental errors, temperature fluctuation, and general weakness of the modelling [1]. Among these techniques, a high plastic strain of the sheet metal has been achieved by the bulge test, which promotes the hardening law without extrapolation of the tensile test result, especially in the plastic deformation region [2]. Hydraulic pressure helps to deform the sheet metal that nullifies the friction between the tool and workpiece. It also simplifies the analytical solutions for the calculation of biaxial stresses and strains. Draw-beads or too high blank holder force has been applied on the sheet metal’s circumference region to obstruct the movement into the radial direction [3], and the hydraulic pressure is applied at an increasing rate (before the burst pressure) on the inner surface of the sheet. Under these conditions, the dome shape is formed and the biaxial in-plane stresses occur at the top of the dome [4].

In this experimental study, a hydraulic bulge test setup with a hemispherical die cavity is used to carry out the stepwise measurements of the hydraulic bulge test at room temperature. Aluminum 1xxx series alloys are considered commercial pure aluminum and have wondrous formability, high corrosion resistance, flexibility, and cost-effectiveness. This series of alloys have moderate strength, but it is increased by proper hardening processes. Commercial pure aluminum (AA1100 H18) sheet metal of 0.68 mm thickness is taken to study the biaxial stresses and strains under anisotropic behavior. Equivalent stress and strain of bulge test are calculated with the help of Hill’48 [5] and von Mises yield criteria and compared with the uniaxial tensile test result fitted by Swift hardening law [6]. A procedure is presented to measure the deformation and calculate in-plane principal strains (\({\upvarepsilon }_{1},\) \({\upvarepsilon }_{2}\)) of the top of the dome with help of the tool maker’s microscope. Bulge test important parameters, which influence the biaxial stresses and strains, are also measured and compared with various approaches.

Experimental Setup and Procedure

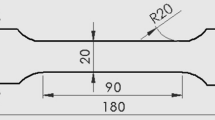
The bulge test is conducted by using the setup, which is developed at Blue Earth Machine Shop, Jadavpur University, Kolkata, and is demonstrated in Fig. 1. The test setup consists of the fluid container, die holder, hemispherical die, motor-driven reciprocating pump, manually operated pump, and control panel. In this experiment, sheet metal is clamped between the die holder and fluid container properly to prevent the material flow radially. As the fluid pressure is increased gradually by a motor-driven or manually operated pump, the metal starts to bulge and make a dome shape. The hydraulic circuit diagram of the manually operated pump and the motor-driven pump is presented in Fig. 2. The die set’s design parameters are the die cavity radius (rd), die corner radius (rf), and allowable sheet diameter (dsheet). The geometry and photographic view of the sheet metal (before and after the bulge test) are presented in Figs. 3 and 4, respectively. Circular grids on the sheet metal are made of the screen-printing process [7] to measure the deformation during the bulge test. The grid pattern is printed directly onto the metal sheet using a suitable ink that is resistant to the metal-forming process. After the deformation, the circular grids are changed to elliptical shapes. Commercial pure aluminum sheet (AA1100 H18) of 0.68 mm thicknesses (density 2.71 g/cc) is selected according to the setup capacity (allowable fluid pressure 75 kg/cm2) [8]. The chemical compositions of AA1100 have been found by spectroscopy, and the values are tabulated in Table 1.

Fig. 1
figure 1

A photographic view of the bulge test specimen

Full size image
Fig. 2
figure 2

Schematic diagram of the hydraulic circuit

Full size image
Fig. 3
figure 3

The geometry of the dome shape

Full size image
Fig. 4
figure 4

A photographic view of the bulge test specimen

Full size image
Table 1 Chemical compositions of AA1100 H18
Full size table

The water pressure is increased gradually to find out the burst pressure for that particular thickness. Maximum experimental pressure is considered about 95% of burst pressure (60 kg/cm2) because the study is concerned with the plastic zone. So, the experimental pressure range has been chosen from 4 to 57 kg/cm2, to continue the study.

Uniaxial Tensile Test

The uniaxial tensile tests are performed in the “INSTRON 8801” universal testing machine (shown in Fig. 5) at room temperature with a grip speed of 0.02600 mm/s, corresponding to a strain rate of 0.0010 s−1. The test sample is prepared by machining according to ASTM B557 with a gauge length of 25 and 6 mm width, for the three different directions relative to the rolling direction (0°, 45°, and 90°) to find out the anisotropy coefficients. Tables 2 and 3 present some important mechanical properties and anisotropy coefficients obtained from the uniaxial tensile test, respectively. The hardness value has been measured as 46 HV by using the microhardness tester (UHL VMHT).

Fig. 5
figure 5

Instron 8801 universal testing machine

Full size image
Table 2 Mechanical properties of AA1100
Full size table
Table 3 Anisotropy coefficients of AA 1100
Full size table

Using the experimental values of the tensile test (0 deg. To the rolling direction), the fitted curve is plotted (shown in Fig. 10) with the help of the Swift hardening law [9]. The Swift hardening law can be expressed by the equation

$$\overline{\sigma } = K \, \left( { \epsilon_{0} + \overline{ \epsilon }_{p} } \right)^{n}$$
(1)

where \(\overline{\sigma }\) is effective stress, εp: effective plastic strain, K: strain hardening coefficient, n: strain hardening exponent, ∈0: pre-strain.

Formulation of Bulge Test

The calculation of the biaxial stresses at the pole of the deformed sheet metal can be executed by using the membrane theory (Eq. 2) [10] when the ratio of the initial sheet thickness and the diameter of the die cavity should be smaller than 1/33 according to ISO 16808:2014 [11].

$$\frac{{\sigma_{1} }}{{R_{1} }} + \frac{{\sigma_{2} }}{{R_{2} }} = \frac{P}{t}$$
(2)

where σ1 and σ2 are the principal stresses in the surface and R1 and R2 are the corresponding radii of the curvature, P is the fluid pressure, and t is the final sheet thickness at the top of the dome. In the case of the hemispherical die and isotropic materials, the principal stresses (σ1 = σ2 = σ), principal strains (\(\epsilon_{1} = \epsilon_{2} = \epsilon\)) and corresponding curvature radii (R1 = R2 = R), which simplifies the membrane Eq. (2) as follows:

$$\sigma_{1} = \sigma_{2} = \sigma = \frac{PR}{{2t}}$$
(3)

Therefore, the von Mises equivalent stress (\(\tilde{\sigma }\) Mises) and equivalent strain (\({\overline{\epsilon }}_{\mathrm{Mises}}\)) under the plane stress condition (through-thickness stress negligible) are described by Eqs. 4 and 5 (assuming material incompressibility), respectively.

$$\overline{\sigma }_{{{\text{Mises}}}} = \sqrt {{\upsigma }_{2}^{2} + {\upsigma }_{1}^{2} - {\upsigma }_{1} {\upsigma }_{2} } = \frac{PR}{{2t}}$$
(4)
$$\overline{\epsilon}_{{{\text{Mises}}}} = \sqrt {\frac{4}{3}\left( {\epsilon_{2}^{2} +\epsilon_{1}^{2} +\epsilon_{1}\epsilon_{2} } \right)} = \ln \left( {\frac{{t_{o} }}{t}} \right)$$
(5)

In a practical scenario, the materials are anisotropic that’s why the Hill’48 yield criterion [5] can be used to calculate the equivalent stress and strain rather than the von Mises yield criterion. The following equations (Eqs. 6, 7) can be used to evaluate the Hill’48 equivalent stress (\({\tilde{\sigma }}_{\mathrm{Hill}}\)) and equivalent strain (\({\overline{\epsilon }}_{\mathrm{Hill}}\)) under the plane stress condition,

$$\overline{\sigma }_{{{\text{Hill}}}} = \sqrt {\left( {G + H} \right)\sigma_{1}^{2} + \left( {F + H} \right)\sigma_{2}^{2} - 2H\sigma_{1} \sigma_{2} }$$
(6)
$$\overline{\epsilon}_{{{\text{Hill}}}} = \sqrt {\frac{{\left( {F + H} \right)\epsilon_{1}^{2} + \left( {G + H} \right)_{2}^{2} + 2H\epsilon_{1}\epsilon_{2} }}{FG + GH + HF}}$$
(7)

where F, G, and H are the material parameters used to calculate the anisotropy behavior of the metal sheet (r0 = H/G, r90 = H/F). Now the equivalent stress and strain can be calculated by using the measurement and calculation of dome top thickness (t), dome radius of curvature (R), pressure (P), and anisotropy coefficients (r0, r45, r90). Many researchers have promoted their approaches and equations to calculate the bulge radius (R) (Eqs. 8, 9) and dome top thickness (t) (Eq. 10) to (Eq. 12) analytically, i.e.,

Hill [12]

$$R = \frac{{h^{2} + r_{d}^{2} }}{2h}$$
(8)

Panknin [13]

$$R = \frac{{\left( {r_{d} + r_{f} } \right)^{2} + h^{2} - 2r_{f} h}}{2h}$$
(9)

Hill [12]

$$t = t_{0} \left[ {\frac{1}{{1 + \left( {\frac{h}{{r_{d} }}} \right)^{2} }}} \right]^{2}$$
(10)

Chakrabarty [14]

$$t = t_{0} \left[ {\frac{1}{{1 + \left( {\frac{h}{{r_{d} }}} \right)^{2} }}} \right]^{2 - n}$$
(11)

Krughlov’s modification [7]

$$t = t_{0} \left( {\frac{\sin \alpha }{\alpha }} \right)^{2(1 + c\alpha )}$$
(12)

where \(c = \frac{{{\text{ln}}\sqrt {\frac{{t_{0} }}{{t_{{{\text{min}}{.}}} }}} {-} \ln \left( {\frac{{\alpha_{{{\text{max}}}} }}{{{\text{sin}}\alpha_{{{\text{max}}}} }}} \right)}}{{\alpha_{\max } {\text{ln}}\left( {\frac{{\alpha_{{{\text{max}}}} }}{{{\text{sin}}\alpha_{{{\text{max}}}} }}} \right)}}.\)

Results and Discussions

Measurement and Calculation of Bulge Radius of Curvature

To determine whether the dome radii varied along with the rolling (X) and transverse (Y) directions, the contours of the dome shape, i.e., the height of the dome, are measured against the distance from the center. In Fig. 6, two pressure values from the lower and upper range have been selected, respectively, to demonstrate the changes of the dome height with respect to the distance from the center. It is observed from Fig. 6 that irrespective of the fluid pressure (kg/cm2), the profiles along both directions coincide almost. It implies that the measuring directions (X, Y) have no influence on the radius of curvature at the top of the dome irrespective of anisotropic or isotropic material, which has validated Resis’s [15] numerical model. From this experimental result (Fig. 6), it has been implied that the dome shape is spherical and the radius of curvature can be considered as R1 = R2 = R for further calculation.

Fig. 6
figure 6

Dome height changes with the distance from the center at different pressures

Full size image

The radius of curvature of a dome shape is an important parameter to calculate the biaxial stress. It is measured by the three-axis CMM (Model—6.4.5 ACCURATE). It has been observed that the radius of the curvature increases nonlinearly with decreasing the dome height (shown in Fig. 7). The experimental results are also compared with the analytical approaches (Fig. 7). It is shown that the measured values follow Panknin’s equation in most of the cases.

Fig. 7
figure 7

Comparison of the bulge radius of curvature

Full size image

As the value of the die corner radius (rf = 1 mm) is small, the deviation between the Hill and Panknin approaches (see Eqs. 8 and Eq. 9) is not too much. Among the different parameters, it is notified that dome height is the controlling parameter for the bulge radius of curvature.

Biaxial Strains and Dome Top Thickness Calculation

The anisotropy behavior of sheet metals has been observed from the uniaxial tensile test result. So, biaxial strains along the principal axes are not equal to each other. After the bulging process, the printed circular grids on the sheet metal are converted to ellipses due to biaxial stretching. The initial and final grid diameter (after deformation) are measured by Tool Makers’ Microscope, and the calculation procedure of principal strains (\({\epsilon}_{1}\) and \({\epsilon}_{2}\)) with the help of the grid diameter deformation is described below with a simplified geometry of the top grid of the dome shape (Fig. 8).

Fig. 8
figure 8

Schematic 2D view of the dome shape and printed grid

Full size image

Arc ABC represents the maximum deformed length of the top grid. Here, \(\overline{QB }\)= dome height (h), \(\overline{OB }\) = \(\overline{OC }\)= radius of curvature (R), Tool maker’s microscope gives the length of \(\stackrel{-}{A{^{\prime}}BC{^{\prime}}}\) which is the top view projection of the arc ABC and the length is equal to \(\overline{AEC }\) . From \(\Delta\) OEC,\(\overline{OE }=\sqrt{{\overline{OC} }^{2}-{\overline{CE} }^{2}}\) and \(\Delta\) BEC,

$$\overline{BC} = \sqrt {\overline{BE}^{2} + \overline{EC}^{2} }$$
(13)

[where \(\overline{\text{BE} }=\overline{\text{OB} }-\overline{\text{OE} }\) ].

Now,

$${\text{Arc}}\;BC = \theta \times \overline{OC } = \sin^{ - 1} \left( {\frac{{\overline{BC} }}{{\overline{OB} }}} \right) \times \, R \, \times \, (\pi /{18}0)$$
(14)
$${\text{Arc}}\;ABC = {\text{Arc }}AB + {\text{Arc }}BC$$
(15)

From Fig. 8, it is clear that Arc BC = Arc AB. So, Principal Strain = ln (Arc ABC/Initial Grid Diameter) can be calculated finally by using the equations (Eqs. 13–15). This procedure can be followed to calculate the principal strains (\({\upepsilon }_{1}\) and \({\upepsilon }_{2}\)) along the principal axes, respectively.

The final thickness (t) at the top of the dome is an important parameter to calculate the biaxial stresses and strains. Assuming material incompressibility, the sum of the principal strains is zero, i.e., \({\epsilon }_{1}+{\epsilon }_{2}+{\epsilon }_{3}=0\). Now, the normal strain can be expressed as:

$$\epsilon_{3} = \ln \left( {\frac{t}{{t_{0} }}} \right)$$
$${\text{or,}} \;t = t_{0} {\text{exp}}\left[ { - \left( {\epsilon_{1} +\epsilon_{2} } \right)} \right]$$
(16)

where \({\epsilon }_{3}\) is the normal (through-thickness) strain, t0 is the initial thickness and t is the final thickness at the top of the dome at a particular pressure.

The calculated dome top thickness value to the dome height is plotted in Fig. 9. It is observed that the dome top thickness decreases nonlinearly with increases in the dome height and follows the latest approach to dome top thickness, i.e., Krughlov’s modification (Eq. 12), and the deviation is more prominent in the case of the Hill (1950) due to the absence of the strain hardening exponent (n). Furthermore, the formability of sheet metal has increased with increasing strain hardening exponent.

Fig. 9
figure 9

Comparison of the dome top thickness

Full size image

Biaxial Stress Calculation

In the case of anisotropic material, the equi-biaxial stresses and strains cannot be imposed. So, the normality condition, i.e., the associated flow rule with the yield surface, is applied in the case of the Hill criterion, which promotes the following equation (under plane stress condition) [15]

$$\frac{{d_{1} }}{{d_{2} }} = \frac{{\sigma_{1} \left( {G + H} \right) - \sigma_{2} H}}{{\sigma_{2} \left( {F + H} \right) - \sigma_{1} H}}$$
(17)

So the biaxial stresses (σ1, σ2) for the anisotropic material at particular pressure can be evaluated by using Eqs. 17 and 2. Now for the comparison with the uniaxial tensile test result (fitted by Swift hardening law), equivalent stress and strain of bulge test are calculated according to the von Mises (Eqs. 4, 5) and the Hill’48 (Eqs. 6, 7) yield criteria. From Fig. 10, it is observed that equivalent plastic strain (before necking) under biaxial loading is almost 15 times than uniaxial tensile test. Besides these, the bulge test gives over a broad range of plastic strain values, which helps to increase the feasibility of the simulation model. Due to anisotropic consideration, the flow stress curve according to Hill’48 follows more closely to the uniaxial tensile test result than the von Mises criterion. Moreover, the anisotropic yield criterion Hill’48 is considered to show the deviation of the equivalent stress–strain from the von Mises criteria, which will be more prominent with increasing anisotropic nature of the material.

Fig. 10
figure 10

Equivalent stress–strain curves of AA 1100

Full size image

Conclusions

The bulge test of the commercially pure aluminum has been done with help of the developed setup. The bulge parameters, i.e., dome height, dome radius of curvature, and dome top thickness value, are also compared with the benchmark equations, and the result is satisfactory. The following important conclusions can be summarized as follows:

  1. 1.

    The dome radius of the curvature along with the orthotropic directions coincides with each other at a particular pressure, which is not influenced by the anisotropy nature of the sheet metal.

  2. 2.

    Among all the analytical approaches, Krughlov’s modification approach is more effective to calculate the dome top thickness analytically for both of the thicknesses.

  3. 3.

    In this experimental work, different process and calculation steps have been elaborated to calculate the biaxial strains, which can be conducted without any expensive setup.

  4. 4.

    The difference is observed in the plastic strain between the uniaxial tensile test and bulge test. The value of plastic strain is more in the case of the bulge test and it helps to gather more information about the plasticity behavior of the material without the extrapolation of the uniaxial tensile test result.

  5. 5.

    The equivalent stress–strain curves by using the Hill’48 and von Mises yield criteria differ from each other, and the Hill’48 yield criterion is closer to the Swift hardening curve due to the anisotropic behavior of the sheet metal.