A History of Autocatalytic Sets

Abstract

This year we celebrated Stuart Kauffman’s 80th birthday. Kauffman has contributed many original ideas to science. One of them is that of autocatalytic sets in the context of the origin of life. An autocatalytic set is a self-sustaining chemical reaction network in which all the molecules mutually catalyze each other’s formation from a basic food source. This notion is often seen as a “counterargument” against the dominant genetics-first view of the origin of life, focusing more on metabolism instead. The original notion was introduced back in 1971, but it has taken several decades for this idea to really catch on. Thanks to theoretical as well as experimental progress in more recent research on autocatalytic sets, especially over the past 15 years, the idea now seems to be gaining significant interest and support. In this tribute to Kauffman’s work and ideas, a brief history of research on autocatalytic sets is presented.

1971

In 1971, Stuart Kauffman introduced the idea of autocatalytic sets. In a paper mostly about another one of his long-lasting contributions, now known as random Boolean networks, there is an appendix about self-replication. In this appendix, Kauffman succinctly states his idea: “Replication is the property of a complex dynamic system, not a single molecule. More fundamentally, self-replication is an autocatalytic process in which a set of molecules catalyzes the formation of a nearly identical second set. No molecule need catalyze its own formation” (Kauffman 1971, p. 90).

He then goes on to argue what it would take to get such a set of collectively and autocatalytically reproducing molecules, focusing mostly on peptides. He even refers to some results from computer simulations (in 1971!) to support his ideas. His computer model consisted of hypothetical polymers up to length five, consisting of two types of building blocks (A and B), and where polymers can be joined together into longer ones or broken apart into smaller ones. In addition, there was a probability P that a given peptide catalyzes a given reaction (i.e., the joining or breaking of peptides), with this probability varying between 0.0005 and 0.15. In Kauffman’s words: “Autocatalytic sets began to emerge when the probability of a molecule affecting a reaction was about 0.003 to 0.005” (Kauffman 1971, pp. 94–95).

Kauffman then ends the appendix (and paper) with the following bold and far-reaching conclusion: “If macromolecules can be supposed to be catalysts, these arguments sketch a view in which self-replication, homeostasis, and epigenesis may be the expected behavior of a particular class of matter. These global behaviors of macromolecular systems should underlie all organisms, no matter how evolution selected the surviving forms” (Kauffman 1971, p. 95).

Although Kauffman’s random Boolean network model was eventually adopted as a standard tool for studying the dynamics of genetic regulatory networks, his appendix on autocatalytic sets seems to have gone largely unnoticed. This may have been due, at least in part, to a rather influential paper that was published in the same year.

Nobel laureate Manfred Eigen discusses almost exactly the same idea in his seminal paper in which he introduced the concept of hypercycles. Eigen specifically considers reaction networks of proteins, where some proteins are able to catalyze the formation of others. If such a network contains a closed loop, then it forms what he calls a “catalytic network.” He illustrates his idea with a figure, which is reproduced here in Fig. 1 (Eigen 1971, p. 499).

Fig. 1

(From Eigen (1971, p. 499))

A catalytic network of proteins, including a closed loop: $E_1,\ldots ,E_{15}$. Each dot represents a different protein sequence, and arrows indicate which proteins catalyze the formation of which others

Eigen then asks the question: “How great is the probability that such cycles can form by themselves?” (Eigen 1971, p. 502). He seems to be willing to consider this to be quite plausible. However, he then basically dismisses the idea based on an evolutionary rather than a probabilistic argument: “For evolutionary behavior, however, unspecified autocatalytic growth is not sufficient. The system can improve only by utilizing selective advantages and that requires specification of sequences” (Eigen 1971, p. 502).

In other words, (auto)catalytic networks of proteins may have a high probability of forming, but they lack evolvability, which is a requirement for life. Eigen then goes on to introduce his idea of a hypercycle which, at least in its original conception, combines nucleic acids (as information carriers) and proteins (as catalysts). I will return to this “lack of evolvability” criticism later on.

1982

A little more than ten years later, physicist Freeman Dyson introduced a statistical model for the origin of life, describing the transition from “disorder” to “order” in a population of mutually catalytic molecules undergoing random mutations (Dyson 1982). Although he never uses the term explicitly, his “ordered” state basically constitutes an autocatalytic set (or catalytic network).

Dyson worked out a detailed, but highly abstract, mathematical model which gives the probability (given certain model parameters) that a population of monomers, possibly combined into polymers in an initially random way, can transform under mutation into a mutually catalytic set of molecules with high efficiency. He concludes from his model that under reasonable assumptions (such as using ten monomer species with a moderate catalytic specificity) in a population of about 2000 monomers, it would not require “a miracle” to make the transition from the disordered to the ordered (autocatalytic) state.

Interestingly, he also describes a scenario in which these autocatalytic molecule sets could be (or become) evolvable, which already provides a first step towards answering Eigen’s earlier criticism. Dyson then asks the question: “Does there exist a concrete realization of the model, for example a population of a few thousand amino-acids forming an association of polypeptides which can catalyze each other’s synthesis with 80% efficiency? Can such an association maintain itself in homeostatic equilibrium?” (Dyson 1982, p. 350). However, he had to wait another two decades for at least a partial answer to this question.

Finally, it is noteworthy that Dyson does cite and acknowledge Eigen, but not Kauffman—another indication that Kauffman’s ideas about autocatalytic sets were probably not very widely known yet. Dyson presents his ideas and model in more detail in a book a few years later (Dyson 1985).

1986

Fifteen years after the publication of his initial ideas, Kauffman published a more detailed account, including a simple model of a polymer-based reaction network (based on his computer simulations from back in 1971), and a mathematical argument to go with it. His main goal is stated early on: “Catalytic ‘closure’ must be achieved and maintained. That is, it must be the case that every member of the autocatalytic set has at least one of the possible last steps in its formation catalyzed by some member of the set, and that connected sequences of catalyzed reactions lead from the maintained ‘food set’ to all members of the autocatalytic set” (Kauffman 1986, pp. 2–3).

He then develops an argument for his claim that such catalytic closure may be “highly probable.” For this, he first presents a more formal description of his earlier computer model. Assume a set of abstract polymers up to (and including) length M, built up of two monomer types, A and B. Next, assume there are two types of chemical reactions possible between these different polymers: (1) condensation of two polymers into a longer one, and (2) cleavage of a polymer into two shorter ones. Note that the maximum length M is maintained, i.e., polymers longer than length M cannot be formed. Finally, assume that there is a probability P that an arbitrary polymer catalyzes an arbitrary (bidirectional) condensation/cleavage reaction. In other words, for each possible pair of a polymer and a reaction, decide with probability P whether that polymer catalyzes that reaction.

Next, given an instance of this polymer model, construct a “catalyzed reaction graph” as follows. Take a set of N nodes, where each node corresponds to a polymer type. For each possible pair of nodes, place an edge between these nodes if there is a catalyzed reaction that has one of the two corresponding polymer types as a reactant and the other as a product.

Finally, Kauffman invokes theoretical results by Erdős and Rényi (1959, 1960) on random graphs (I will refer to these as “E–R graphs”). Imagine a collection of N nodes, where (undirected) edges are placed between pairs of nodes with a given probability p. In other words, each pair of nodes is considered in turn, and with (independent) probability p it is decided whether to put an edge between the current pair of nodes or not. This gives rise to a random (E–R) graph with N nodes and, on average, $E=pN(N-1)/2$ edges.

What Erdős and Rényi showed is that for a low value of p, such a random graph mostly consists of many disconnected small components, where a “component” is a set of connected nodes (i.e., it is possible to go from any node in the component to any other node in the same component by traveling along existing edges). On the other hand, when p is large, the random graph is likely to contain a “giant connected component,” where almost all of the N nodes are connected. However, most interestingly, there is a sharp phase transition between these two regimes. When the ratio E/N between the number of edges E and the number of nodes N crosses the threshold 1/2, suddenly giant connected components start showing up.

Given that a catalyzed reaction graph constructed as described above is very similar to such E–R graphs, one can expect to see a similar phase transition towards the occurrence of giant connected components. As Kauffman shows, the ratio of the number of (catalyzed) reactions (i.e., edges) to the number of polymer types (i.e., nodes) grows linearly with increasing maximum polymer length M. In other words, given a fixed probability of catalysis P, if M is steadily increased, at some point the threshold will be reached where giant connected components start to show up. And such a giant connected component in the catalyzed reaction graph is likely to achieve the desired catalytic closure.

As Kauffman himself admits, the similarity between E-R graphs and his catalyzed reaction graph is only tenuous: “Peptide reaction graphs are strongly non-isotropic, since there are many more reactions forming small rather than large peptides. Thus, the results of Erdos and Renyi on isotropic graphs do not apply directly” (Kauffman 1986, p. 9). However, based on at least a qualitative correspondence, he concludes: “If the general ideas are right, and robust with respect to the idealizations of the model, then the formation of autocatalytic sets of polypeptide catalysts is an expected emergent collective property of sufficiently complex sets of polypeptides, amino acids, and other small molecules. This could have substantial implications for the origin of life” (Kauffman 1986, pp. 11–12).

That same year, Kauffman teamed up with physicists Doyne Farmer and Norman Packard. In their joint paper, these scientists investigate a dynamic version of Kauffman’s polymer model to get more insight into the probability of autocatalytic sets forming spontaneously (Farmer et al. 1986). The main idea was illustrated with an example that is reproduced here in Fig. 2.

As before, the molecules are abstract polymers made up of a given set of monomers, here simply a and b. These are presented as ovals with labels corresponding to polymer sequences. The food set is indicated with double ovals. There are again two types of reactions: condensation (or ligation) combining two polymers into a longer one; and the opposite, cleavage splitting a polymer into two shorter ones. These (bidirectional) reactions are represented by black dots, with solid lines going from the reaction to its reactants and products. Finally, catalysis is represented by dotted arrows going from the catalyst (a polymer) to a reaction.

Fig. 2

(From Farmer et al. (1986, p. 53))

A typical example of a graph that might describe an autocatalytic set. The reactions are represented by nodes connecting cleavage products with the corresponding condensate. Dotted lines indicate catalysis pathways, and point from the catalyst to the reaction being catalyzed

The dynamic model now works as follows. Start with a food set of polymers up to length L, and consider all the ligation and cleavage reactions that can be performed with this initial set of molecules. Randomly select a subset of these possible reactions (where each reaction is selected with independent and identical probability P), and for each selected reaction assign a random catalyst from the current set of molecules. Then add all newly created molecules through catalyzed reactions to the current set of molecules.

Next, consider all the new reactions that can now be performed with this larger molecule set. Again, select a fraction P of them and assign catalysts from the current molecule set, and add all newly created molecules through catalyzed reactions to the current molecule set. Repeat this procedure for a certain number of steps. As long as new molecular species (polymers) are being created at each step, this dynamic catalyzed reaction graph continues to grow. Whether or not such a graph grows indefinitely depends strongly on P.

As these researchers argue: “For sufficiently small P, it is virtually guaranteed to stop growing, and the graph is subcritical. For sufficiently large P, it is virtually guaranteed to grow without bound, and it is supracritical. The value of P on the boundary between subcritical and supracritical behavior is the critical value” (Farmer et al. 1986, p. 54; italics in original). They then show the existence of these three regimes with results from computer simulations of their dynamic catalyzed reaction graphs, and conclude that supracritical behavior is due to the corresponding graph containing an autocatalytic set.

However, as they argue next: “The existence of a supracritical graph is not sufficient to guarantee the generation of an autocatalytic set. Once chemical kinetics are taken into account competition for resources limits growth. Differences in efficiency can produce drastic differentials in concentration, so that many species are effectively not present in the system at all. Thus, even though it complicates matters considerably, a consideration of kinetics is essential for a realistic assessment of the potential to generate autocatalytic sets” (Farmer et al. 1986, p. 58).

They then present a kinetic extension to their model, where actual molecular concentrations are calculated over time using a set of (dynamic) differential equations. Furthermore, a constant influx of food molecules and outflux of all molecules is included, and newly created polymers can only start acting as catalysts once they have reached a given minimum concentration. In this model version growth cannot be unlimited, due to the constant outflux. However, as they observe from their simulations, there remains “a marked qualitative distinction between supracritical and subcritical behavior” (Farmer et al. 1986, p. 60).

The paper concludes with the following statement: “Our results suggest that autocatalytic properties may have played a major role in supplying the complex chemical prerequisites needed for the origin of life” (Farmer et al. 1986, p. 62). However, despite Kauffman’s theoretical results (Kauffman 1986) and the extensive simulation results of Farmer et al. (1986), this conclusion still did not seem to have much of an impact. As with the original idea, this is probably (at least partly) due to a highly influential paper published in the same year.

In early 1986, a one-page “News & Views” paper was published in Nature by another Nobel laureate, Walter Gilbert. The title of the paper was short and simple: “The RNA world.” Based on the (then) recent discovery that RNA molecules can catalyze chemical reactions such as splicing of other RNA molecules, it was suggested that protein enzymes would not have been necessary for the origin of life. In Gilbert’s words: “One can contemplate an RNA world, containing only RNA molecules that serve to catalyse the synthesis of themselves” (Gilbert 1986). This set the stage for a new paradigm that came to dominate origin of life research for at least the next three decades. And in this elegant but somewhat simplistic paradigm there was no need for such a thing as an autocatalytic set, especially not since, after all, they only existed on paper and in computer models.

1991

Another five years later, a pair of companion papers with first author Richard Bagley appeared in the proceedings of the second Conference on Artificial Life (Bagley and Farmer 1991; Bagley et al. 1991). These papers were based on Bagley’s Ph.D. dissertation in which an enhanced version of the dynamic model introduced earlier by Farmer et al. (1986) was studied in detail (Bagley 1990).

Next to an enhancement in the computational methods for dynamically simulating the catalyzed reaction graph, some other additions and variations to the original model were introduced. For example, next to assigning catalysts to reactions purely randomly (uniformly), a string matching rule was used. In analogy with base-pair complements in nucleic acids, a polymer has a higher catalytic efficiency if it matches the reaction site of a ligation reaction more closely. For example, for the ligation reaction $aaa + bbb \rightarrow aaabbb$, a polymer bbaa would be a more efficient catalyst (forming a perfect complementary match around the ligation site) than a polymer bbab, which has only a partial complementary match.

Bagley then performed a detailed study of the dependency of the emergence of autocatalytic sets on network topology, (kinetic) parameter values, and the composition of the food set. As the first paper concludes: “We have demonstrated that under appropriate conditions an autocatalytic set can concentrate much of the mass of its environment into a focused set, with concentrations orders of magnitude above equilibrium” (Bagley and Farmer 1991, p. 133). However, the authors follow this up with a word of warning: “Autocatalytic metabolisms can be highly sensitive to both the topology of the reaction network and the kinetic parameters of individual reactions” (Bagley and Farmer 1991, p. 134). They end the first of the two papers with an explicit stab at the recently introduced notion of an RNA world: “This model adds support to the idea that the emergence of a metabolism may have preceded the emergence of a self-replicator based on templating machinery” (Bagley and Farmer 1991, p. 134).

The second paper provides preliminary results of an investigation into the possible evolution of autocatalytic sets. The main idea is that once an autocatalytic set has emerged and settles down into a (dynamically) stable state (i.e., no new chemical species are being produced), with some probability a new species is introduced into the reaction network. This simulates the occurrence of occasional “spontaneous” reactions. In other words, any chemical reaction can happen without a catalyst as well, but will do so at a much lower rate compared to when the reaction is catalyzed. However, such spontaneous reactions in the “shadow” of an already existing autocatalytic set may actually produce a new catalyst that allows the existing set to grow and include even more chemical species before it settles down into a (new) stable state.

As the authors show with some preliminary numerical results: “Random variations, which play the role of mutations, are generated by spontaneous reactions. Some of these variations have no effect, and simply die out. Others have large effects, generating several new chemical species and perhaps causing others to die out, substantially altering the composition of the autocatalytic metabolism” (Bagley et al. 1991, p. 155). This result was a first step towards answering Eigen’s lack of evolvability criticism.

In conclusion, these two companion papers provided substantial computational support for the emergence and potential evolution of autocatalytic sets, perhaps even as a possible path towards the (or an) origin of life.

1993

Two years later, a highly mathematical paper was published by the trio Peter Stadler, Walter Fontana (who was also a co-author on the second of the 1991 companion papers), and John Miller (Stadler et al. 1993). These authors consider a system S of n types of molecules, where two molecules i and j interact to produce one or more types of molecules $k_l,\ldots ,k_r$. These reaction products are assumed to be in S as well, and the molecule types i and j are retained, thus playing the role of catalysts (a buffered food source is implicitly assumed). Now let $x_i$ denote the (relative) concentration of molecule type i. The system S can then be described in terms of ordinary differential equations as follows (Stadler et al. 1993):

$$\begin{aligned} {\dot{x}}_k = \sum _{i=1}^n \sum _{j=1}^n \alpha _{ij}^k x_i x_j - x_k \Phi (t), \;\; k=1,\ldots ,n, \end{aligned}$$

with second order rate constants $\alpha _{ij}^k$ for the reactions $i+j \rightarrow i+j+k$, and with $\Phi (t)$ being a dilution flux that keeps the total number of particles constant.

They then show that this “catalytic network equation” has several important special cases, including the well-known replicator equation, by setting the rate constants $\alpha _{ij}^k$ appropriately, and they derive various mathematical properties of the system. Finally, the authors investigate numerically the effects of interconnectedness on the behavior of the catalytic network equation. In particular, they study a random network where each (i, j) interaction has only one unique product k, and where the rate constants are assigned randomly. This is similar to Kauffman’s original (but more elaborate) binary polymer model. Indeed, the authors report that “in almost all of several hundred numerical integrations […] for n between 5 and 20 the system converged to a globally stable fixed point” (Stadler et al. 1993, p. 385).

The authors conclude their paper by stating that their research “indicates that the typical behavior of random networks is extremely robust” (Stadler et al. 1993, p. 390) and that they “showed that the systems always reduce their dimension to a self-maintaining subset of types” (Stadler et al. 1993, p. 391). Thus, these independent investigations also supported Kauffman’s earlier claims about the emergence of autocatalytic sets.

The year 1993 also saw the publication of Kauffman’s now classic book The Origins of Order (Kauffman 1993).¹ This book is packed with a detailed overview of his most notable work up to then, presented in three separate parts. The first part is about fitness landscapes in the context of evolutionary biology. The third part is about random Boolean networks as a model of gene regulatory networks, as already referred to above. Sandwiched in between, the second part is based on the notion of autocatalytic sets.

In particular, in Chap. 7 of the book, entitled “The Origins of Life: A New View,” Kauffman presents his ideas, theory, and results in great detail, placing them firmly within the context of the origin of life. As he summarizes: “The core of the theory is this: As the complexity of a collection of polymer catalysts increases, a critical complexity threshold is reached. Beyond this threshold, the probability that a subsystem of polymers exists in which the formation of each member is catalyzed by other members of the subsystem becomes very high. Such sets of polymers are autocatalytic and reproduce collectively. Thus the new view I shall propose is disarmingly simple. Life is an expected, collectively self-organized property of catalytic polymers” (Kauffman 1993, p. 289). The rest of the chapter than builds mostly on the models and results from the earlier papers (Kauffman 1971, 1986; Farmer et al. 1986; Bagley and Farmer 1991; Bagley et al. 1991).

At the end of the chapter, Kauffman also addresses the lack of experimental evidence for autocatalytic sets: “we must consider the experimental construction of autocatalytic sets of peptides or RNA ribozymes. I suspect this construction is feasible if we are bold enough to reach the needed complexity and meet the thermodynamic requirements” (Kauffman 1993, p. 337). As it turns out, Kauffman did not have to wait very long for such an experimental construction, and it took much less than the “needed complexity” his models seemed to suggest.

1994

A year after Kauffman’s book was published, a paper appeared in Nature reporting on the cross-catalytic replication of a pair of short nucleotide sequences (Sievers and von Kiedrowski 1994). The basic building blocks (or food set) are the trimers A = CCG and B = CGG, which form each other’s base-pair complement when read in opposite directions. The hexamers AA and BB now serve as templates to which the complementary trimers can attach by forming C–G base-pair bonds. For example, two B trimers can attach to an AA template, allowing these trimers to ligate (chemically join) into a fully formed BB hexamer. After strand separation, the original AA template is regained, plus a new BB template. In a similar way, such a BB template can facilitate the ligation of another AA template from two A trimers. This chemical reaction network is shown schematically in Fig. 3.

Fig. 3

(From Patzke and von Kiedrowski (2007))

The chemical reaction network of two cross-catalytic nucleotide-based oligomers AA and BB

The authors conclude their paper with the following statement: “Our results may have important implications for theories of the origin of life, including those that invoke self-organization of complex reaction systems involving collective replication of oligonucleotides” (Sievers and von Kiedrowski 1994, p. 224), with a reference to Kauffman’s recently published book. This result provided the first experimental example of a simple autocatalytic set. Kauffman had earlier promised to buy a bottle of champagne for the first person to succeed in producing such an experimental example. Living up to his promise, he and Von Kiedrowski shared that bottle together.

Ten years later, a similar experimental system of two cross-catalytic RNA sequences (in this case of more than 70 bases each) was constructed by Kim and Joyce (2004). These RNA sequences were subsequently subjected to mutations to increase their catalytic efficiency (Lincoln and Joyce 2009).

Also in 1994 another article by Fontana, together with co-author Leo Buss, was published (Fontana and Buss 1994b). In this article, the authors introduce and study a more abstract but formal model of chemistry based on $\lambda$-calculus. In $\lambda$-calculus, objects (e.g., molecules) are defined inductively in terms of nonlinear combinations of other objects, starting from primitives. In other words, each object can also act as a function (which can be interpreted as a catalyst).

From studying this formal model, the authors derive several main conclusions: “(i) hypercycles of self-reproducing objects arise, (ii) if self-replication is inhibited, self-maintaining organizations arise, and (iii) self-maintaining organization, once established, can combine into higher-order self-maintaining organizations” (Fontana and Buss 1994b, p. 757). Furthermore, they acknowledge the relationship of their formal model and results to that of earlier work: “Our level 1 organizations recall three different lines of research. […] The second and third research traditions are work on autocatalytic sets and on autopoietic systems” (Fontana and Buss 1994b, p. 759). A much longer and more detailed analysis of their formal model was published that same year (Fontana and Buss 1994a).

1997

In contrast to the computational and now also experimental support for the emergence and existence of autocatalytic sets, a rather strong criticism of Kauffman’s ideas appeared in 1997. In a paper on the origin of life stressing the need for taking (natural) selection into account, author Shneior Lifson includes an appendix reviewing the mathematics behind Kauffman’s binary polymer argument (Lifson 1997). As Lifson writes: “There are many problems with the model, but they need not all be discussed because of a major error which renders its conclusions wrong anyhow” (Lifson 1997, p. 7). A few paragraphs later, Lifson points out what this major error is: “Kauffman’s error was to increase M at constant P” (Lifson 1997, p. 7).

Recall that in Kauffman’s argument, if the maximum polymer length M is increased, given a fixed probability of catalysis P, then at some point a phase transition is reached where giant connected components (and thus autocatalytic sets) start showing up in the catalyzed reaction graph. Mathematically this might be correct, but the problem, according to Lifson, lies in the fact that one cannot increase M independently of P. As he points out: “When M increases, the number of sequences increases exponentially and the number of bonds increases even faster” (Lifson 1997, p. 7). In other words, increasing M while keeping P fixed causes each molecule to catalyze an exponentially increasing number of reactions, which may not be a realistic assumption. Basically what Lifson is saying is that what should be kept constant, instead, is the average number of reactions catalyzed per molecule. In that case, it is not clear at all whether autocatalytic sets are guaranteed to emerge. Lifson therefore concludes: “Thus, the derivation of reflexively autocatalytic sets collapses” (Lifson 1997, p. 7).

Despite this strong criticism, and largely thanks to the publication of Kauffman’s two books, the notion of autocatalytic sets finally started to catch on. Several independent papers appeared that study autocatalytic sets in various mathematical and computational models, but all inspired by Kauffman’s earlier work.

One such paper was by two physicists from New Zealand, Peter Wills and Leah Henderson (Wills and Henderson 1997). These authors were particularly interested in “structure-function relationship,” i.e., the correspondence between polymer sequences and their catalytic properties. Note that in Kauffman’s original model, each molecule type has the same probability of catalyzing any reaction, regardless of structure. The model extension studied by Bagley, using a (partial) template matching rule, already introduced more biological realism. Wills and Henderson go even further: “Our guiding principle comes from what is known about the structure-function relationship in protein sequence space: very specific structural features are usually required to build good catalysts which specifically differentiate different substrates and thus selectively catalyse just one or a few members of a class of reactions” (Wills and Henderson 1997).

Using a similar binary polymer model as that of Kauffman, with ligation and cleavage reactions, they divide the reactions up into different classes, such as the ligation of a polymer ending with a and one beginning with b, or $\cdots a + b \cdots \rightarrow \cdots ab \cdots$, represented as {$a-b$}. Now imagine, for example, a situation where polymers with structure $aa \dots aa$ catalyze the class of reactions {$b-b$} (and not any other) and polymers with structure $bb \ldots bb$ catalyze the class of reactions {$a-a$} (but not any other). This would generate an autocatalytic set where all a-polymers catalyze the formation of b-polymers and vice versa. They then look at different such structure-function combinations to see which ones could form autocatalytic sets and which could not.

They conclude by stating “that the selection of progressively more complex collectively autocatalytic sets of polymers is possible in systems whose structure-function relationship satisfies certain constraints. By examining simple ligation/cleavage systems we illustrate what is likely to be a general precondition for the evolutionary emergence of refined biological functions: structures which carry out refined functions should be differentiated in specialized ways through the presence or absence of the refined structural features which the refined functions selectively produce.” The authors realize the complicated structure of their own conclusion, as they end their paper with: “…the logic of functional evolution is strangely circular…” (Wills and Henderson 1997).

This conference proceedings paper was republished more formally a few years later (Wills and Henderson 2000), and the Wills-Henderson model was revisited in more detail almost two decades later (Hordijk et al. 2014b).

1998

Another independent autocatalytic sets paper was published by two physicists from India, Sanjay Jain and Sandeep Krishna (Jain and Krishna 1998). Their model consists of a directed graph with s nodes, each node representing a chemical species. A link from node j to node i means that species j catalyzes the production of i. Such a graph can be described by its adjacency matrix$C = (c_{ij})$, where $c_{ij}=1$ if there is a link from j to i in the graph, and $c_{ij}=0$ otherwise. Initially links are included in the graph at random with a certain probability p.

With each node (or species) i a “population” $y_i$ is associated, of which the dynamics is given by

$$\begin{aligned} {\dot{y}}_i = \sum _{j=1}^s c_{ij} y_j - \phi y_i, \end{aligned}$$

where $\phi$ is a dilution flux. This dynamics is run until a stable state is reached. In other words: “The ith species grows via the catalytic action of all species j that catalyze its production and declines via a common death rate $\phi$” (Jain and Krishna 1998, p. 5685).

Next, once a stable state is reached, the species k with the lowest population size $y_k$ is replaced with a new species with completely new and random catalytic links with the other species. In other words, the kth row and column of C are replaced by random entries but with the same probability p. The dynamics is then run again until a (new) stable state is reached, and the species with the lowest population is once more replaced with a new one with random catalytic links, and so on for many generations.

What Jain and Krishna observed in their model is the following: Initially the total number of links fluctuates around the expected value for a random graph. But at some (random) time, this number increases rapidly until it stabilizes again at a much higher value than it started out. They explain this rapid increase by the sudden appearance of an autocatalytic set. By removing nodes with low population size (due to a lower than average connectivity) and replacing them with nodes with new but random links, at some point catalytic closure occurs in a subset of the nodes (i.e., a cycle appears), giving rise to an autocatalytic set. This autocatalytic set then starts growing in size, as its current members will all have a high population size and thus never be removed, until eventually it encompasses (close to) the entire graph.

Fig. 4

(From Jain and Krishna (2002))

An example of an autocatalytic set (black and gray nodes) in a graph with $s=100$ nodes

Figure 4 shows an example of such an autocatalytic set existing within a graph with $s=100$ nodes after a certain number of generations. The nodes in black form the “core” of the autocatalytic set, i.e., they form a cycle (or catalytic closure). The nodes in gray form the “periphery” of the autocatalytic set, i.e., those nodes that are catalyzed by other nodes in the set, but that do not feed back into the core. The white nodes are not part of the autocatalytic set. The authors then also show that it can be derived mathematically whether the graph contains an autocatalytic set, and if so which nodes are part of it, by calculating the eigenvalues and eigenvectors of the adjacency matrix C (Jain and Krishna 1998).

Unlike the other models, the Jain–Krishna model explicitly includes selection. As the authors conclude: “this model provides an example of how selection for fitness at the level of individual species results, over a long time scale, in increased complexity of interaction of the collection of species as a whole. […] when selection is operative, the system ‘cashes in’ upon the novelty provided by an [autocatalytic set] that arises by chance” (Jain and Krishna 1998, p. 5687). This work was followed up with several further papers investigating the model and its results in more detail (Jain and Krishna 2001, 2002; Giri and Jain 2012).

In the same year (1998), a pair of papers appeared by a group of researchers from the Weizmann Institute of Science in Israel, introducing yet another model of autocatalytic sets called Graded Autocatalysis Replication Domain, or GARD (Segré et al. 1998a, b). This model assumes a collection of N types of molecules D that are chemically interconvertible via common precursors M, and that are contained in a spatial “vesicle” with a given volume. The membrane of the vesicle is permeable to the precursors M, but not to the molecule types D. Over time the vesicle can grow, increasing its volume to contain a larger number of molecules.

In addition, the molecule types D can mutually catalyze each other’s formation from the precursors M. However, contrary to Kauffman’s binary polymer model and the Jain–Krishna model, catalysis is not an “all or nothing” event, but actually has an efficiency associated with it. In particular, catalytic efficiencies are represented by an $N \times N$ matrix $\beta =(\beta _{ij})$, where $\beta _{ij}$ is the efficiency with which molecule type $D_j$ catalyzes the formation of molecule type $D_i$. The matrix entries $\beta _{ij}$ are drawn from an appropriate random distribution. Figure 5 shows a schematic overview of this GARD model.

Fig. 5

(From Segré et al. (1998a))

A schematic overview of the GARD model

This model is then analyzed mathematically in the first paper (Segré et al. 1998a) and with computer simulations in the second one (Segré et al. 1998b), using a set of differential equations very similar to the Jain–Krishna model. In these computer simulations, a large population of small GARD vesicles is considered, each with N molecule types randomly sampled from a number $N_G \gg N$ of chemically allowed species. Furthermore, changes in the $\beta$ matrix are induced by replacing one of the species by a randomly chosen one. This amounts to changing one row and one column in the $\beta$ matrix, again very similar to the Jain–Krishna model. However, in the GARD model such changes are accepted only if they give rise to a vesicle with higher self-replication capacity.

Given the similar features of the GARD model and the Jain–Krishna model, similar results are obtained. Indeed, as the authors observe: “While at the initial steps in this simulated process few instances of strong mutual catalysis are present, the later stages result in the formation of a chemical network that is well-connected in terms of mutual catalysis.” Furthermore: “Cycles of any size constitute powerful catalytic domains capable of catalyzing a number of other species in branched stems” (Segré et al. 1998b, p. 561). Such “catalytic domains” (cycles) are similar to the black nodes (core) in Fig. 4, while the “branched stems” are similar to the gray nodes (periphery).

Over the years, the GARD model has been studied in great detail and in different versions, an extensive review of which can be found in Lancet et al. (2018). Together, the results from the Wills-Henderson model, the Jain–Krishna model, and the GARD model formed another step towards answering Eigen’s lack of evolvability criticism, by explicitly considering a selection process.

2000

A few years later a short and highly mathematical paper was published by Mike Steel, a mathematician from New Zealand (Steel 2000). Steel addresses Lifson’s criticism of Kauffman’s model. Remember that for Kauffman’s argument to hold, each molecule needs to catalyze, on average, an exponentially increasing number of reactions with increasing maximum polymer length M to reach the phase transition where autocatalytic sets start to emerge.

Steel first generalizes and formalizes Kauffman’s notion of a connected, reflexively autocatalytic (CRA) set. He next considers Kauffman’s binary polymer model, using the variable n for the maximum polymer length (where Kauffman had used M). Steel then proves mathematically that “if each polymer catalyses on average $n^2$ reactions in total, then it becomes increasingly certain that the entire system of reactions is a CRA” (Steel 2000, p. 94). So, instead of an exponential growth rate in the level of catalysis (with increasing n), only a quadratic growth rate is sufficient to get autocatalytic sets with high probability.

This is certainly a significant improvement on Kauffman’s original result, although still not the constant level of catalysis that Lifson insisted on. In fact, Steel also shows mathematically that if the level of catalysis, i.e., the average number of reactions catalyzed per molecule, is smaller than $1/3e^{-1}$, then the probability of autocatalytic sets is basically equal to zero (for increasing n). However, he ends the paper with the conjecture that there is some sub-quadratic growth rate in the level of catalysis for which there still is a high probability of autocatalytic sets existing (Steel 2000). It took a few more years, though, before this conjecture was confirmed.

2004

The year 2004 saw two significant advances in research on autocatalytic sets, one theoretical and one experimental. On the theoretical side, a paper appeared in the Journal of Theoretical Biology that would become the foundation for a formal theory of autocatalytic sets, while on the experimental side a paper appeared in PNAS that would answer Kauffman’s and Dyson’s question of whether an autocatalytic set of peptides could indeed form and maintain itself.

The theoretical paper, by Wim Hordijk and Mike Steel, builds on Steel’s earlier formalism of autocatalytic sets, generalizing and extending it even further, including a novel computer algorithm (Hordijk and Steel 2004). This formalism was simplified and streamlined further in subsequent work (Hordijk et al. 2011, 2015). This later version of the formalism is presented here, as it does not change any of the earlier theoretical or computational results, but is easier to follow.

First, the authors define a chemical reaction system (CRS) as a tuple $Q = \{X,R,C,F\}$, where:

• $X = \{x_1, x_2, \ldots , x_n\}$ is a set of molecule types.

• $R = \{r_1, r_2, \ldots , r_m\}$ is a set of reactions. A reaction r is an ordered pair $r=(A,B)$ where $A, B \subset X$. The (multi)set $A = \{a_1, \ldots , a_s\}$ are the reactants and the (multi)set $B= \{b_1, \ldots , b_t\}$ are the products.

• $C \subseteq X \times R$ is a set of catalysis assignments. A catalysis assignment is a pair (x, r) with $x \in X$ and $r \in R$, denoting that molecule type x can catalyze reaction r.

• $F \subset X$ is a food set, i.e., molecule types that can be assumed to be available from the environment.

Next, given a CRS Q, a subset $R'$ of R, and a subset $X'$ of X, they define the closure of $X'$ relative to $R'$, denoted $\mathrm{cl}_{R'}(X')$, to be the (unique) minimal subset W of X that contains $X'$ and that satisfies the condition that, for each reaction $r=(A,B)$ in $R'$,

$$\begin{aligned} A \subseteq X' \cup W \Longrightarrow B \subseteq W. \end{aligned}$$

Informally, $\mathrm{cl}_{R'}(X')$ is $X'$ together with all molecules that can be constructed from $X'$ by the repeated application of reactions from $R'$.

Finally, given a CRS $Q=\{X,R,C,F\}$ and a subset $R'$ of R, $R'$ is a reflexively autocatalytic and food-generated (or RAF) set if for each $r=(A,B) \in R'$:

• 1. (RA) $\exists x \in \mathrm{cl}_{R'}(F): (x,r) \in C$, and

• 2. (F) $A \subseteq \mathrm{cl}_{R'}(F)$.

In other words, a subset of reactions $R'$ is a RAF set if for each of its reactions at least one catalyst and all reactants are in the closure of the food set relative to $R'$. A RAF set thus formalizes Kauffman’s original notion of an autocatalytic set.

Hordijk and Steel also introduce an efficient computer algorithm for detecting RAF sets in arbitrary chemical reaction systems. Note that the eigensystem calculation method of Jain and Krishna (1998) only works when all catalysts are produced directly from the food set, i.e., in just one reaction step. However, this method breaks down in the more general case where catalysts may require several reaction steps to be produced from the food set.

The RAF algorithm, presented formally in Algorithm 1, works as follows. Starting with the full set of reactions $R'=R$, the algorithm repeatedly calculates the closure of the food set relative to the current reaction set $R'$, and then removes from $R'$ all reactions that have none of their catalysts or not all of their reactants in this closure. This is repeated until no more reactions can be removed. If upon termination of the algorithm $R'$ is non-empty, then $R'$ is the unique maximal RAF set (maxRAF) contained in R, i.e., a RAF that contains every other RAF in R as a subset. If $R'$ is empty, then R does not contain a RAF set.

Computing the closure of the food set relative to the current reaction set $R'$ is the most expensive step in the RAF algorithm. It is presented formally in Algorithm 2.

A naive computational complexity analysis of the RAF algorithm gives a worst-case running time of $\mathcal {O}(|X||R|^3)$, i.e., polynomial in the size of the (full) reaction set. With some additional bookkeeping (such as keeping track of all reactions that each molecule is involved in), this can be reduced even further. In fact, the average running time on instances of Kauffman’s binary polymer model is subquadratic (Hordijk and Steel 2004).

After deriving some mathematical properties of RAF sets, Hordijk and Steel then apply the RAF algorithm to many instances of Kauffman’s binary polymer model with various values for the maximum polymer length n and probability of catalysis p, using as food set all monomers and dimers. What they find is that the level of catalysis (i.e., the average number of reactions catalyzed per molecule) needs to increase only linearly with increasing n to find RAF sets frequently (Hordijk and Steel 2004). This confirmed Steel’s earlier conjecture of a subquadratic growth rate in the level of catalysis being sufficient (Steel 2000). Moreover, this required level of catalysis is less than two reactions per molecule (on average) for n at least up to 20. Chemically this is not unrealistic at all.

Thus, the RAF formalism, algorithm, and results not only put the notion of autocatalytic sets on a firm theoretical basis, but also put to rest the earlier criticism of Lifson.

The experimental paper, by a team of scientists from the Scripps Research Institute in California, describes an experimentally constructed autocatalytic set made up of nine peptides (Ashkenasy et al. 2004). As with the nucleic acid autocatalytic sets of Sievers and von Kiedrowski (1994) and Kim and Joyce (2004), each peptide is formed through a ligation reaction between two shorter peptide fragments, catalyzed by one or more of the other (fully formed) peptides.

Starting from a known autocatalytic peptide (32 amino acids long), several single-site substitutions were introduced to generate a set of 81 sequences. Appropriate amino acid substitutions can alter the aggregate stability of substrates, reactive intermediates, and products, and thereby influence the template-directed replication, cross-catalytic selectivity, and efficiencies of these peptides. These catalytic efficiencies were then theoretically estimated by calculating the differences in the stability ($- \Delta \Delta G$) of all $81 \times 81$ possible catalyst-product ensembles. Using a given threshold value for the minimum required stability difference, this resulted in a network of 25 peptides and their mutually catalytic interactions (Ashkenasy et al. 2004, Fig. 2).

A subset of nine peptides was then selected from this network, and analyzed experimentally. From these experiments, the theoretically estimated catalytic interactions could be reconstructed with high accuracy (apart from a few minor exceptions). A schematic overview of this 9-peptide autocatalytic set is shown in Fig. 6.

Fig. 6

(From Ashkenasy et al. (2004))

A schematic overview of the experimental 9-peptide autocatalytic set. Arrows indicate which peptides catalyze the formation of which other peptides. Numbers along the arrows indicate the calculated $- \Delta \Delta G$ values (a proxy for catalytic efficiency)

These results formed a beautiful experimental confirmation of Kauffman’s original ideas about autocatalytic sets of proteins. As the authors conclude: “The studies presented here highlight a synthetic chemical approach toward the rational de novo design of complex self-organized molecular systems. […] Furthermore, since the functional characteristics of each network component can be estimated and/or experimentally assessed, the approach may also provide more accurate data facilitating various mathematical approaches used to model network behavior” (Ashkenasy et al. 2004). Indeed, the experimental peptide autocatalytic set was recently analyzed in more detail using the formal RAF framework (Hordijk et al. 2018b).

2005

Recall that the numerical results of Hordijk and Steel (2004) showed that a linear growth rate in the level of catalysis (with increasing maximum polymer length n) is sufficient for autocatalytic (RAF) sets to emerge in the binary polymer model. However, this was shown only for n up to 20, due to computational constraints (it had already taken several weeks of running the simulations on a large computer cluster to get these results). This left open the question of whether this trend still holds for larger n.

Inspired by the numerical results, Steel teamed up with another mathematician, Elchanan Mossel, and together they managed to prove theoretically as well that such a linear growth rate is indeed sufficient, for any n (Mossel and Steel 2005). In particular, what these authors showed is that such a linear growth rate suffices to guarantee that (1) a RAF set contains all molecules in X, and (2) only forward (ligation) reactions are required in the binary polymer model, i.e., an even stronger assumption than in the general case, for which a linear growth rate is therefore more than sufficient.

As a consequence, the actual slope of the linear relationship between the level of catalysis and the maximum polymer length n that was proved theoretically to be sufficient, was about two orders of magnitude larger than the slope obtained from the earlier numerical results. In later work, though, it was shown that this difference in slopes is due to those two stronger assumptions, by repeating the simulations with one or both of those assumptions included (Hordijk et al. 2011; Hordijk and Steel 2016). So, under more general assumptions (as in the original simulations), a very small slope already suffices to get RAF sets to emerge with increasing n. In other words, the level of catalysis only needs to increase by a very small amount with increasing n, still requiring no more than two reactions catalyzed per molecule (on average) for RAF sets to emerge in the binary polymer model even for $n=50$ (Hordijk 2013).

Also in 2005, Kauffman teamed up with physicists Rudolf Hanel and Stefan Thurner to study a mathematical model of catalytic networks very similar to that of Stadler et al. (1993) described earlier. Moreover, they also put this model and its results in the context of economics, in particular technological evolution: “We study catalytic random networks with respect to the final outcome diversity of products. […] We demonstrate the existence of a phase transition from a practically unpopulated regime to a fully populated and diverse one” (Hanel et al. 2005, p. 1). The authors also relate their findings directly to those of Stadler et al. (1993). This work was followed up by a study of the model in an evolutionary context (Hanel et al. 2007).

2007

A 2007 paper by Bill Marin and Mike Russell presents a model for the origin of biochemistry at an alkaline hydrothermal vent (Martin and Russell 2007). A lengthy argument is laid out, involving much and rather detailed geo- and biochemistry, but a reference is also made to some of the theoretical work on autocatalytic sets. As the authors state: “The series of arrows in Fig. 5 are drawn to look like a chemical hypercycle (Eigen 1992), and recent theoretical work indicates that autocatalytic networks may be much simpler to evolve than one might have thought (Hordijk and Steel 2004; Mossel and Steel 2005), provided that there is a sustained source of carbon and energy” (Martin and Russell 2007, p. 1910).

With that, the authors acknowledge that autocatalytic sets indeed may have played an important role in the origin of biochemistry. The relevant part of their Fig. 5 is reproduced here in Fig. 7, together with the original caption.

Fig. 7

(Figure and caption from Martin and Russell (2007))

a Schematic of the circumstance that in some micro-organisms TPP (thiamine pyrophosphate) and PLP are required for their own synthesis (see text), but also positively feedback into their own synthesis in the sense of a chemical hypercycle (Hordijk and Steel 2004)

This recognition of the (still largely theoretical) notion of autocatalytic sets in the context of actual (and early) biochemistry was certainly a big step forward, and would eventually lead to important new work (Sousa et al. 2015; Xavier et al. 2019; see also below).

2010

Of course autocatalytic sets are not one of a kind. In fact, as was already pointed out earlier, other similar notions have been proposed, such as Eigen’s hypercycles (Eigen 1971) and Dyson’s mutually catalytic sets of proteins (Dyson 1982). In 2010, a group of researchers mostly from Chile pointed out a close connection between RAF sets and a formalism known as (M, R) systems (Jaramillo et al. 2010). This formalism was introduced by Robert Rosen back in the 50s and 60s (Rosen 1991), but has been difficult to understand due to its rather abstract formulation.

Jaramillo et al. (2010) try to make the concept of (M, R) systems more clear by rephrasing it in terms of RAF sets: “An important unresolved matter is to make explicit how Rosen’s equations can be fulfilled using concepts and definitions imported from RAF sets” (Jaramillo et al. 2010, p. 99). However, they also note some differences. For example, in (M, R) systems all catalysts are supposed to be produced by reactions from the system itself, whereas in RAF sets catalysts could, in principle, also come from the food set, not necessarily being produced by any of the reactions. In short, (M, R) systems are specific instances of RAF sets, but in some cases additional features need to be taken into account to conform to Rosen’s formalism.

Incidentally, several years earlier Pier Luigi Luisi had also noted, in passing, a similarity between autocatalytic sets and the notion of autopoietic systems (Luisi 2003). This similarity was explored to some extent later on (Hordijk and Steel 2015).

Also in 2010, another strong criticism towards autocatalytic sets appeared. Following up on Eigen’s original criticism, researchers Vera Vasas, Eörs Szathmáry, and Mauro Santos questioned the evolvability of autocatalytic sets (Vasas et al. 2010). Although Kauffman was referred to as well, the criticism was mostly directed at the GARD model and its claims about evolvability.

The authors present a detailed analysis of (a later version of) the GARD model, both mathematically and with computer simulations, especially investigating its ability to generate selectable heritability, which, in this case, constitutes “compositional inheritance”. As they conclude: “If (and what a big IF) there can be in the same environment distinct, organizationally different, alternative autocatalytic cycles/networks, […] then these can also compete with each other and undergo some Darwinian evolution. But, even if such systems exist(-ed), they would in all probability have limited heredity only and thus could not undergo open-ended evolution. Note that the conditions ‘distinct, organizationally different, alternative’ have been shown to apply only to a very limited extent in the GARD model.” They add: “We now feel compelled to abandon compositional inheritance as a jumping board toward real units of evolution” (Vasas et al. 2010, p. 1475).

Perhaps Eigen was right after all? Despite this strong criticism, though, even more scientists became interested in the concept of autocatalytic sets.

2011

In 2011 a group of researchers in Italy published a paper presenting results from computer simulations, similar to those of Farmer et al. (1986), which also showed the emergence of autocatalytic sets (Filisetti et al. 2011). These authors used the standard binary polymer model as well, but the kinetics were simulated using a stochastic method known as the Gillespie algorithm (Gillespie 1976, 1977), rather than the deterministic differential equations method used by Farmer et al. (1986) and Bagley et al. (1991).

The authors then studied the influence of the size and composition of the food set and of the initial molecule concentrations on the emergence of autocatalytic sets. They did indeed observe autocatalytic sets (ACS) forming, but they were unstable, and only existed for a relatively short amount of time. As the authors state: “It is noteworthy that our results highlight a dynamical structural fragility of ACSs, due to the presence of rarely occurring reactions that prevent the autocatalytic closure over a reasonable time span” (Filisetti et al. 2011, p. 9).

As it turned out, the actual reason for this fragility is that the authors had used a slightly different definition of autocatalytic sets, where they only considered catalytic closure, i.e., autocatalytic cycles. They did not take into account that autocatalytic sets need a food source. In terms of RAF sets, they had looked for reflexively autocatalytic (RA) sets without also checking for the food-generated (F) requirement. This shortcoming was rectified later on, and truly self-sustaining autocatalytic (RAF) sets were subsequently observed in their simulations (Filisetti et al. 2014).

This work was followed up by many more simulation studies, including the emergence and dynamics of autocatalytic sets within so-called protocells, i.e., small compartments with internal chemistry; a schematic representation is provided in Fig. 8. In this case it was shown that synchronization takes place between the rate of replication of the internal reaction network and that of the container, provided that the set of reactions contains a RAF set (Serra et al. 2014; Villani et al. 2014; Serra and Villani 2017); see also Piedrafita et al. (2017).

Fig. 8

(From Serra et al. (2014))

A schematic representation of a protocell, a lipid membrane that is permeable to food molecules (monomers and dimers), but not to larger polymers. Autocatalytic sets forming within compartments remain intact, whereas outside of the compartment they dilute away

However, further studies showed that this synchronization depends on several additional factors (Serra and Villani 2019). For instance, especially when multiple RAF subsets (see next section) exist within a given reaction network, it depends on which molecules (from which RAF subset) are coupled to the growth of the container. In some cases no synchronization occurs at all, while in other cases only one RAF subset survives and synchronizes with the container growth. Furthermore, it also depends on how molecules diffuse across the membrane. If this diffusion is instantaneous (i.e., at an infinite rate), the behavior is different from when the diffusion has a finite (small) rate. In the latter case, different RAF subsets may actually coexist within the protocell. As the authors conclude: “These observations stress the importance of a dynamic analysis whose results may lead to conclusions that are widely different from those suggested by a naive look at the static topology” (Serra and Villani 2019, Sect. 5), echoing a concern already raised by Farmer et al. (1986).

2012

The year 2012 saw several major advances, from the resolution of the (lack of) evolvability in autocatalytic sets issue, to additional experimental support for autocatalytic sets.

After their strong criticism of a lack of evolvability in autocatalytic sets and feeling compelled to abandon the idea of compositional inheritance altogether, Vasas et al. (2010) revisited their own criticism and came up with a solution to this conundrum, one they had already alluded to in their earlier paper. With Christantha Fernando and Stuart Kauffman himself added to the team, they investigated several scenarios using the binary polymer model, and “discovered that if general conditions are satisfied, the accumulation of adaptations in chemical reaction networks can occur” (Vasas et al. 2012, p. 1).

First, the authors make a distinction between the “core” of an autocatalytic set (i.e., a closed catalytic loop), and its “periphery” (i.e., catalyzed reactions branching out from the core), just as Jain and Krishna (1998) had defined earlier. Next, as Bagley et al. (1991) had done as well, they also allow spontaneous (uncatalyzed) reactions to happen with low probability, which occasionally generates a new catalyst that could even give rise to an entirely new core coming into existence. Finally, they assume that the autocatalytic sets are contained within compartments (e.g., lipid membranes) that grow and divide, distributing the internal molecules between the offspring compartments randomly. In other words, “‘Mutation’ happens either when uncatalyzed reactions result in the emergence of a novel core, or when molecular components of a viable core are stochastically lost after compartment splitting” (Vasas et al. 2012, p. 10).

Their investigations then lead them to state: “We conclude that only when a chemical reaction network consists of many such viable cores, can it be evolvable. When many cores are enclosed in a compartment there is competition between cores within the same compartment, and when there are many compartments, there is between-compartment competition due to the phenotypic effects of cores and their periphery at the compartment level. Acquisition of cores by rare chemical events, and loss of cores at division, allows macromutation, limited heredity and selectability, thus explaining how a poor man’s natural selection could have operated prior to genetic templates” (Vasas et al. 2012, p. 1).

Such compositional inheritance may only allow for a limited form of evolution, but could very well have been a necessary step towards true open-ended evolution. As the authors state: “However, a viable core constitutes one bit of heritable information and therefore the number of possible selectable attractors is relatively small, meaning that autocatalytic networks may not be able to sustain open-ended evolution. While we think this to be the case, the potential role of these autocatalytic networks as a route to nucleotide-based template self-replicating systems should not be underestimated” (Vasas et al. 2012, p. 10).

So, after Lifson’s criticism about the required level of catalysis was already resolved, Eigen’s original criticism of the lack of evolvability was now also resolved. However, it still left open the question of how many autocatalytic cores one could expect to exist within a given reaction network. Around the same time Kauffman had also teamed up with the duo Hordijk and Steel. Independently, they published a paper in 2012 as well, which provided at least a partial answer to this still open question.

First recall that the RAF algorithm of Hordijk and Steel (2004) finds the maxRAF, i.e., the largest RAF that is present in a given reaction network. However, a maxRAF may contain smaller subsets that in themselves are also RAF sets. Indeed, using the example of a small (5-reaction) RAF set that was found by their RAF algorithm in an instance of the binary polymer model, Hordijk et al. (2012) show that this RAF set consists of several smaller RAF subsets, or subRAFs. Moreover, these subRAFs form a hierarchical structure known as a partially ordered set (or poset) in mathematical terms. The example maxRAF and its poset of subRAFs is reproduced in Fig. 9.

Fig. 9

(From Hordijk et al. (2012))

Top: A maxRAF as found in an instance of the binary polymer model, with the food set consisting of the monomers and dimers (i.e., bit strings of lengths one and two). Bottom: The poset of its subRAFs

Next, note that the two subRAFs at the bottom of the poset ($\{r_1,r_2\}$ and $\{r_3\}$) do not contain any smaller RAF subsets. They are therefor called irreducible RAFs, or irrRAFs. Hordijk et al. (2012) then show (by construction) that a given maxRAF can, in principle, contain an exponentially large number of irrRAFs. In particular, they provide an example of a RAF set consisting of 2k reactions, and which contains $2^k$ irrRAFs.

Finally, note that the notion of an irrRAF corresponds closely to that of a (viable) core of Vasas et al. (2012). In other words, a given reaction network that contains a large enough RAF set could thus (potentially) contain a very large number of autocatalytic cores, i.e., sufficient diversity to enable an evolutionary process to take place.

In later work, empirical estimates of the (average) number of irrRAFs in instances of the binary polymer were presented (Steel et al. 2013; Hordijk et al. 2015). The issue of evolvability was also further investigated (Hordijk and Steel 2014; Villani et al. 2014; Hordijk 2016; Serra and Villani 2017).

Next to these theoretical advances, a paper with additional experimental support from a group of scientists in the US appeared in Nature that year (Vaidya et al. 2012). This time it involved autocatalytic sets constructed with ribozymes, i.e., catalytic RNA molecules.

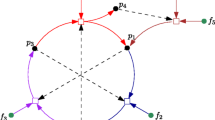
These researchers took a well-studied ribozyme (of about 200 nucleotides long) that can catalyze its own formation from smaller RNA fragments. This ribozyme has a 3nt “guide sequence” and also a 3nt “target sequence,” which form each other’s base-pair complement. They then varied the middle nucleotide in both the guide and target sequences, effectively creating 16 different ribozymes. As a consequence, ribozyme $\hbox {E}_1$ can catalyze the formation of ribozyme $\hbox {E}_2$ if $\hbox {E}_1$’s guide sequence is the base-pair complement of $\hbox {E}_2$’s target sequence. A simple example of a cycle of three mutually catalytic ribozymes is reproduced in Fig. 10.

Fig. 10

(From Vaidya et al. (2012))

An example of a three-membered autocatalytic set of RNA molecules. The ribozymes $\hbox {E}_1$, $\hbox {E}_2$, and $\hbox {E}_3$ are formed from smaller fragments, and each one catalyzes (curved arrows) the formation of the next one in the cycle

The researchers then studied various aspects of such autocatalytic sets, including the formation of the full 16-member network from a solution containing only the RNA (food) fragments. They conclude: “The three-membered cycle shown here resembles a hypercycle as envisioned previously, but without hyperbolic growth. We prefer to focus on the observation that the cycle can be derived from simpler cycles and has the potential to expand to more complex ones as evidence that RNA molecular coalitions can show spontaneous order-producing dynamics, which already has theoretical support” (Vaidya et al. 2012, p. 77). The “theoretical support” they mention includes a reference to the Hordijk and Steel (2004) paper.

So, next to the experimental peptide autocatalytic set of Ashkenasy et al. (2004), there is now also an experimental RNA autocatalytic set. This RNA network was subsequently investigated in more detail using the formal RAF framework (Hordijk and Steel 2013; Hordijk et al. 2014a). Note, though, that in both experimental systems the catalysts (fully formed peptides or ribozymes) are produced directly from the food set (fragments), as in the Jain–Krishna model. However, recently a more elaborate version of the RNA autocatalytic set was constructed in the laboratory where the catalysts require multiple reaction steps to be produced from the food set (Arsène et al. 2018), resembling more Kauffman’s original polymer model.

2013

It should be noted that both Martin and Russell (2007) and Vaidya et al. (2012) refer to their figures as representing hypercycles (Eigen and Schuster 1979). However, this rests on a confusion between the concepts of hypercycles and autocatalytic sets. In fact, this confusion appears to be more widespread, which led evolutionary biologist Eörs Szathmáry to publish a rather explicit criticism in 2013.

As he explains right from the start: “The molecular hypercycle as proposed by Eigen and elaborated by Eigen and Schuster is a system in which autocatalytic replicators also heterocatalytically aid each other’s replication so that replication of each member is catalyzed by at least one other member” (Szathmáry 2013; italics in original). In other words, in a hypercycle each member is an autocatalytic self-replicator and, in addition, also catalyzes the self-replication of the next member in the cycle. In contrast, as Kauffman had already stated from the beginning, in an autocatalytic set “no molecule need catalyze its own formation” (Kauffman 1971, p. 90).

Szathmáry then presents a long list of quotes from the scientific literature where similar confusions have occurred. In fact, such confusion also exists between the concepts of autocatalytic sets and autocatalytic cycles. The difference may seem trivial, but is far from it. These different confusions were further clarified in another paper several years later (Hordijk 2017). Suffice it to say here that hypercycles are actually a special subclass of autocatalytic sets. However, each member also needing to catalyze its own formation seems a rather strong requirement, which is perhaps why there are (so far) no known experimental chemical examples of hypercycles.

2014

In 2014, Shinpei Tanaka, Harold Fellermann, and Steen Rasmussen published a paper using a simplified version of the binary polymer model to study the relationship between structure and selection in autocatalytic networks (Tanaka et al. 2014). Their model contains three types of reactions between polymers (or strands): “decomposition of a strand into any two substrands with rate $c_0$, random ligation of two strands with rate $c_1$, and autocatalytic ligation with rate $c_2$. Formally

$$\begin{aligned}&l.m \,{\mathop {\longrightarrow }\limits ^{c_o}} \,l + m, \\&l + m \,{\mathop {\longrightarrow }\limits ^{c_1}} \,l.m, \\&l + m + l \cdot m \, {\mathop {\longrightarrow }\limits ^{c_2}} \, 2\; l \cdot m, \end{aligned}$$

where l·m represents the concatenation of strands l and m” (Tanaka et al. 2014, p. 28004-p2).

They then performed a theoretical analysis using a differential equation approach and a dynamical analysis using the Gillespie algorithm. What they found is that highly ordered populations with particular sequence patterns are dynamically selected out of a vast number of possible states. Some examples of such highly ordered patterns are reproduced in Fig. 11.

Fig. 11

(From Tanaka et al. (2014))

Two examples of highly ordered patterns that emerge dynamically from the model, referred to as a bootlace and b pinecone

As the authors conclude: “to our knowledge, it has not been reported previously that the selection of specific sequence patterns arises spontaneously out of the autocatalytic dynamics. This intrinsic selection is important for the study of the origin of complex and functional polymers” (Tanaka et al. 2014, p. 28004-p6). This work was followed by a more detailed study a few years later (Fellermann et al. 2017).

2015

Another major advance was made in 2015. Autocatalytic sets (or RAFs) have always been considered an essential property of life. “However, despite their appeal, the relevance of RAFs for real biochemical networks that exist in nature has, so far, remained virtually unexplored” (Sousa et al. 2015, p. 1). When Bill Martin (of the hydrothermal vent theory) and (then) postdoctoral researcher Filipa Sousa teamed up with Hordijk and Steel, they entered this virtually unexplored terrain by searching for autocatalytic sets (using the RAF algorithm) in the metabolic network of Escherichia coli (Fig. 12).

Fig. 12

(Produced with iPath (Darzi et al. 2018))

The metabolic network of E. coli, which contains a large autocatalytic set when cofactors are considered as the catalysts

Escherichia coli is the most-studied single-celled organism, and its reconstructed metabolic network is the most complete of any organism. So this seemed a reasonable place to start. However, next to the (still) missing data even for E. coli, another hurdle had to be overcome. In the metabolism of living systems, all reactions are catalyzed by enzymes, i.e., genetically encoded proteins. In other words, the catalysts in the metabolic network are not directly produced by the network itself, which would thus not form a RAF.

The solution Sousa et al. (2015) came up with was to consider cofactors as catalysts. Most enzymes contain one or more small molecules (often referred to as cofactors), such as various metals like iron, zinc, or magnesium, or organically produced molecules like ATP, flavin, or CoA, which actually perform the catalysis. The complicated three-dimensional structure of the protein largely serves to hold everything (the reactants and the cofactor catalyst) in the right place. The protein thus makes the cofactor a more specific and more efficient catalyst. As the authors observe: “The critical role of cofactors in the E. coli RAFs might point to an interesting aspect of early chemical evolution. We see here that the size, hence in some respects the complexity, of RAFs within the E. coli metabolic network are dependent upon cofactors: a small number of catalysts that promote a large number of reactions each” (Sousa et al. 2015, p. 16).

Indeed, the RAFs found in the metabolic network of E. coli only have a small number of (cofactor) catalysts, just over 40, that together catalyze the close to 1800 reactions in the network. Moreover, these RAFs contain a modularity that corresponds closely to functional groups in metabolism in general. This modularity was discovered by investigating the influence of single molecules or reactions on the size of the RAF, by removing molecules or reactions from the network one at a time. Finally, the authors also applied a stochastic search method to find the smallest food set on which the full RAF set can still survive.

As they conclude: “The existence of RAF sets within a microbial metabolic network indicates that RAFs capture properties germane to biological organization at the level of single cells” (Sousa et al. 2015, p. 1). This is a rather crucial indication that was a first of its kind.

The same year, a review paper appeared by a group of authors including Kauffman and Lehman. Using the notion of autocatalytic sets as a fundamental concept, this paper suggests six key parameters in prebiotic network evolution. As the authors state: “we examine specifically the evolvability of prebiotic networks with an eye to plausible chemistry. As a result, our intent is to make network evolution a prebiotic plausibility and set the stage for empirical studies in the laboratory that can support, refine, or refute our conclusions” (Nghe et al. 2015, p. 3207). The six parameters are: (1) viable cores, (2) connectivity kinetics, (3) information control, (4) scalability, (5) resource availability, and (6) compartmentalization.

These parameters are described and analyzed mostly theoretically, but the authors include an overview of previous work, and suggestions for future work, for how these parameters and their influence on prebiotic network (autocatalytic set) evolution can be studied and tested empirically. They then end with a prediction: “One main prediction that we can make is that there is a process analogous to ecological succession in the evolution of networks. ‘Weedy’ sets such as irrRAFs, should form easily, but not be robust to environmental fluctuations. The addition of new nodes by a set of (as of yet not fully known) rules such as preferential attachment will then create more robust networks that are more resilient; these are capstone species in early chemical evolution” (Nghe et al. 2015, p. 3215).

2017

In 2017, Hordijk and Steel published another review article summarizing the main aspects and results of their RAF theory (Hordijk and Steel 2017). In that paper they also argue that RAF theory could be applied beyond chemistry and origin of life, for example to the economy (as was already suggested by Kauffman earlier), and to ecosystems. They illustrate this with a simple example: “one could think of economic production functions as the equivalent of chemical reactions. Inputs such as wood and nails are transformed into outputs such as tables in an economic production function, just as reactants are transformed into products in a chemical reaction. Furthermore, some of those outputs, such as hammers, can act as ‘catalysts’ in that they speed up the rate at which certain goods are produced, without being used up in that process. With this analogy in place, one could think of the economy as a whole as a catalytically closed and self-sustaining autocatalytic set” (Hordijk and Steel 2017, p. 8).

The idea of viewing the economy as an autocatalytic set was originally made by Kauffman himself (Kauffman 2011). Current work is under way, with the help of economists, to make this idea more explicit and formal.

The idea of viewing ecosystems as autocatalytic sets was worked out and published in detail with the help of ecologist Cazzolla Gatti et al. (2017, 2018). The main idea is as follows. As Sousa et al. (2015) had shown, organisms can be represented by the RAF sets that exist within their metabolism. Furthermore, as Hordijk et al. (2012) had shown, RAF sets can often be broken down into an entire hierarchy of smaller and smaller subRAFs, some of which may be dependent on each other. In other words, some RAF sets may need certain reactants or catalysts that are not present in the food set, but that are produced by other RAF sets.

Carrying this idea over to ecosystems, Cazzolla Gatti et al. (2017) argue that each species (or “guild” of similar species) can be represented by a RAF set, with mutual dependencies between such RAF sets. In other words, the RAF sets of some species will generate products that are required as food or catalysts by the RAF sets of other species. As the authors conclude: “We have argued that biodiversity can be viewed as a system of autocatalytic sets, and that this view offers a possible answer to the fundamental question of why so many species can coexist in the same ecosystem” (Cazzolla Gatti et al. 2017, pp. 74–75). The answer exists in the fact that each appearance of a new species (RAF) enables the coming into existence of yet other new species (RAFs) by generating additional products that can serve as food or catalysts. In other words, niche space is a (potentially exponentially) increasing system.

Furthermore, the argument was later extended to viewing the actual network of species relationships itself as a (higher-level) autocatalytic set. A simple example is given in Fig. 13, which is reproduced from Cazzolla Gatti et al. (2018). Solid arrows represent the equivalent of chemical reactions (one species being converted into another species by being eaten) and dashed arrows represent the equivalent of catalysis (e.g., aphids producing a sweet substance that is harvested by ants which in return provide protection against ladybugs).

Fig. 13

(From Cazzolla Gatti et al. (2018))

A simple example of an ecosystem that not only consists of RAF sets (the individual species) but also forms a RAF set itself

Interestingly, almost simultaneously another paper was published arguing for viewing cognition in terms of autocatalytic sets (Gabora and Steel 2017). In particular: “We suggest that, much as models of self-sustaining, autocatalytic networks have been useful for understanding how the origin of life, and thus biological evolution, could have come about, they are also useful for understanding how the origin of the kind of cognitive structure that makes cultural evolution possible could have come about. Mental representations (such as memories, concepts, and schemas) play the role of ‘reactants’ and ‘catalysts’, and relationships amongst them (such as associations, remindings, and causal relationships) are the ‘reactions’ ” (Gabora and Steel 2017, p. 93).

As the authors argue: “In the pre-cultural ‘episodic’ mind, such reactions are catalyzed only by external stimuli. As cranial capacity increases, representations become richer (more features or properties are encoded), and thus reactions become more plentiful, leading to streams of thought. Streams of thought cause the reaction network to become even denser. Eventually, it becomes almost inevitable that a percolation threshold is surpassed, and collectively the representations form an integrated autocatalytic set. At this point, the mind can combine representations and adapt them to specific needs and situations, and thereby become a contributor to culture” (Gabora and Steel 2017, p. 93).

In short, while the concept of autocatalytic sets and its formalization (RAF theory) were originally developed in the context of prebiotic chemistry, they have by now become a general tool to study all kinds of phenomena, including the economy, ecosystems, and even cognition.

Finally, the year 2017 also saw the publication of a book entitled Modelling Protocells, which summarizes in detail the mathematical and computational work that the Italian researchers have done on autocatalytic sets over the years (Serra and Villani 2017).

2018

Some similarities between autocatalytic (RAF) sets and other formalisms were already pointed out above. Another such similarity exists with chemical organization theory (COT) (Dittrich and Speroni di Fenizio 2007). A formal and explicit derivation of this similarity between RAFs and COT was published in 2018 (Hordijk et al. 2018c).

Given a set of molecules X and a set of reactions R, a chemical organization is a subset $X' \subseteq X$ of molecules that is (Dittrich and Speroni di Fenizio 2007):

• 1. Closed None of the reactions in R that can be applied to molecules in $X'$ produce any molecules not already in $X'$; and

• 2. Self-maintaining All molecules in $X'$ are produced by reactions in R at least as fast as they are consumed.

What Hordijk et al. (2018c) show is that there is a close mathematical correspondence between chemical organizations and so-called closed RAFs.

A closed RAF is a RAF set in which all reactions that can happen catalyzed are included. Another way of stating it is that to go from a closed RAF A to any larger RAF B that contains A as a proper subset ($A \subset B$) requires one or more reactions to happen spontaneously (i.e., the catalysts for these reactions are not part of A but they are part of B). For example, in the maxRAF of Fig. 9, the subset $\{r_3,r_4\}$ is, by definition, a RAF. However, it is not a closed RAF, given that $r_5$ can also happen catalyzed (i.e., $r_3$ and $r_4$ create the required reactant and catalyst for $r_5$). The subRAF $A = \{r_3,r_4,r_5\}$ is a closed RAF though. To go to the next larger RAF B that contains A as a proper subset (where in this case B is the maxRAF), either $r_1$ or $r_2$ has to happen spontaneously at least once to create the required catalysts.

Given this correspondence between RAFs and COT, it is possible to find closed subRAFs within a maxRAF by computing the chemical organizations in that maxRAF (note that a maxRAF itself is, by definition, always a closed RAF). From a dynamical point of view it is exactly these closed RAFs that are of interest, as they form the “stable states” of the reaction network (requiring rare spontaneous reactions to move from one to the other), whereas any non-closed RAF will only be transient (Hordijk et al. 2018c).

That same year, Hordijk teamed up with several researchers (including Fellermann) at Newcastle University, UK, who had recently developed an agent-based simulation toolkit, called Simbiotics, for studying the collective behavior of single-celled organisms such as bacteria (Naylor et al. 2017). Realizing that this toolkit could also be used to study the emergence and dynamics of autocatalytic sets in populations of compartments, together these researchers developed a simulation module to do just that (Hordijk et al. 2018a).

The overall setup is as follows. A population of (static) compartments exists in a two-dimensional spatial environment that has a constant influx of food molecules (monomers and dimers) that diffuse throughout the system, and a constant outflux of all molecules types. However, compartments are permeable to food molecules but not to larger molecule types, just as in the earlier simulations of Villani et al. (2014). So, when autocatalytic sets are formed inside compartments, they can be maintained (whereas in the outside environment they would dilute away). The authors then used an instance of the binary polymer model that contains several closed subRAFs, and watched what happened over time.

As expected, different combinations of closed subRAFs started to appear in different compartments. The emergence of these closed subRAFs require one or more spontaneous reactions to happen (at low rates), which are stochastic events. So, in one compartment a “blue” subRAF may appear at some point, while in another compartment a “red” subRAF may appear at some later time. Sometime later still, a compartment already containing a “blue” subRAF may also acquire a “red” subRAF, turning the compartment “purple” (i.e., both red and blue together), and so on. Figure 14, reproduced from Hordijk et al. (2018a), presents four snapshots over time, clearly showing how the compartment colors (representing the particular combinations of closed subRAFs they contain) change over time.

Fig. 14

(From Hordijk et al. (2018a))

Four snapshots over time (from left to right) from a dynamical simulation with a population of compartments

As the authors conclude: “Our simulations show that the main requirements for autocatalytic sets to be evolvable are met when encapsulating them into compartment populations: the existence of different combinations of autocatalytic subsets (i.e., closed RAFs) in a population of compartments, giving rise to different ‘cell types’ and competition between them” (Hordijk et al. 2018a, p. 12). They then also studied several additional scenarios, such as one closed subRAF generating a molecule that is “toxic” to another closed subRAF, or certain “inducer” molecules being allowed to diffuse between compartments, thereby increasing the chances that other compartments will also produce autocatalytic sets. The next steps will be to include growth and division in these compartments, to get a real (if only rudimentary) evolutionary process going.

2019

In 2019, Hordijk, Steel, and Kauffman published a paper together that could provide theoretical support for an origin of life scenario proposed a few years earlier by researchers Bruce Damer and David Deamer (Hordijk et al. 2019). Damer and Deamer propose that protocells originated not in deep sea vents, but in pools on land, subject to evaporation and refilling by rain or terrestrial sources such as streams. They suggest that lipid vesicles underwent successive wet-dry cycles on the margins of such pools. Central to this scenario is the idea that the lipid vesicles each contain a vast library of peptide or RNA polymers (Damer and Deamer 2015; Deamer 2019). They then speculate that this process will lead to vesicles with sets of polymers that can reproduce themselves: “selection of vesicles encapsulating these polymers leads to stepwise increments toward the emergence of functional systems capable of growth, reproduction, and evolution” (Damer and Deamer 2015, p. 873). Furthermore: “An important aspect of the scenario is that the polymers are not constant, but instead are in a steady state system in which hydrolysis is balanced by synthesis. Therefore, the system is continuously experimenting, trending towards combinations of polymers that are more stable than other combinations, and polymers that have specific functions, the most important being those that can catalyze their own reproduction” (Damer and Deamer 2015, p. 880).

Noting that Damer and Deamer seem to be implicitly referring to the formation of autocatalytic sets of polymers, Hordijk et al. (2019) then asked what the minimum size of such polymer libraries would need to be to have a high probability of an autocatalytic set to form. Using both mathematical arguments and results from computer simulations (using the binary polymer model and the Jain–Krishna model), they derived that such a minimum size might be on the order of a few thousand polymer types. They then conclude: “It is quite plausible that such diversities of polymers […] would have been found in the lipid vesicles undergoing the plastein reactions in the Damer and Deamer scenario, randomly shuffling the polymer libraries in each vesicle on each wet dry cycle. […] We therefore believe our results can provide strong theoretical support for the original Damer and Deamer scenario for the origin of protocells” (Hordijk et al. 2019).

While the current article was under review, several relevant papers with exciting new results were posted on different preprint archives. The first of these preprints examines the evolvability of autocatalytic sets experimentally (Ameta et al. 2019). Using variants of the RNA autocatalytic sets originally reported by Vaidya et al. (2012), the dynamical behavior of these sets was studied using microfluidics. This technology consists of microscopic water droplets (“microdroplets”) suspended in oil, as a way of experimentally simulating compartments.

As the authors conclude: “We have shown experimentally that a diversity of network behaviour can be generated from a small set of interactions, and that these networks can possess Darwinian properties” (Ameta et al. 2019). However, true evolvability depends on different trade-offs within these networks and their dynamics, in particular trade-offs between growth and variation, and between variation and robustness. These recent results form an exciting experimental validation of the earlier computational studies on the evolvability of autocatalytic sets.

The second preprint reports on an experimental autocatalytic set consisting entirely of inorganic molecules (Miras et al. 2019). These molecules are all based on molybdenum, with various auto- and cross-catalytic interactions. The results are supported by stochastic computer simulations of various dynamical aspects of the system. As the authors conclude: “The results presented here show that the formation of an autocatalytic set driven by molecular information can form with a simple inorganic system. […] All previous information-rich autocatalytic sets known are derived from known biology, but this study shows how information-rich autocatalytic sets, based on simple inorganic salts, can spontaneously emerge which are capable of collective self-reproduction outside of biology” (Miras et al. 2019).

The third preprint is a follow-up on the work by Sousa et al. (2015). Joana Xavier, another postdoctoral researcher with Bill Martin, decided to search for autocatalytic sets in more primitive organisms than E. coli. She chose one bacterium (Moorella thermoacetica) and one archaeon (Methanococcus maripaludis). These microbes represent primitive lineages that live on the simplest source of carbon and energy known, and are assumed to be closely related to some of the earliest living organisms, shortly after the origin of life. Not only did Xavier show that the metabolic networks of these organisms do contain RAF sets, but also that their intersection contains one. This autocatalytic set is interpreted as the RAF of LUCA: “RAFs uncover elements of metabolic evolution that go even further back in time before the divergence of archaea and bacteria from the last universal common ancestor, LUCA” (Xavier et al. 2019).

As with the original E. coli study, cofactors were used as catalysts, rather than complete enzymes. However, even with these small-molecule catalysts (several of which are naturally occurring inorganic elements), the “RAF of LUCA” is able to produce some amino acids and nucleotides. Hence the bold title and main conclusion of this recent work: “Autocatalytic chemical networks preceded proteins and RNA in evolution” (Xavier et al. 2019). Moreover, these microbial autocatalytic sets are compatible with hydrothermal vent chemistry.

Although several collaborations like this have already taken place between different researchers, most of the work on autocatalytic sets described here has been done relatively independently by various groups in different places. However, in 2019 a group of researchers including Kauffman received seed funding to organize themselves into a more formal collaboration and develop a detailed research strategy for a structural investigation into the emergence and evolution of autocatalytic sets, combining theoretical, computational, and experimental studies (COOLscience Club 2019). This funding comes from the ATTRACT initiative, which itself is funded by the European Union’s Horizon 2020 research and innovation program. It is expected that this seed funding will provide a boost to research on autocatalytic sets and the dissemination of its main ideas and results.

Finally, Kauffman’s latest book was published this year (Kauffman 2019). The main theme (and subtitle) of this book is “the emergence and evolution of life.” Not surprisingly, Kauffman uses the concept of autocatalytic sets and some of the, by now, large body of theoretical and experimental support for them to argue about a possible origin of life.

The Future

The large body of theoretical and experimental results on autocatalytic sets reviewed here is starting to suggest a very different scenario for a possible origin of life than that of the RNA world hypothesis. Instead of life starting with single self-replicating RNA molecules (for which there still is no experimental evidence), perhaps it started with simple autocatalytic sets that form quite easily, and that initially used molecules like metals and small self-produced organics (modern-day cofactors) as their catalysts. However, these initial autocatalytic sets were able to produce the basic building blocks for RNA and proteins. Once these polymers came into existence, they could have started taking over the role of the initial catalysts, or incorporated them as their cofactors, making them more efficient. This, in turn, would allow for the formation of yet other molecules, in an upward spiral of complexity and diversity, all the way to the first real metabolic networks.

It has been a long road since 1971, but after almost 50 years the future looks promising. More and more people, scientists and nonscientists alike, are catching on to the idea. Perhaps the days of the dominant RNA world paradigm are numbered in favor of a metabolism-oriented view of the origin of life in which autocatalytic sets play an important role. And not only in the origin of life, but also in other areas such as economics, ecology, cognition, and who knows where else.

Final Notes

In this history I have classified events by the year in which a relevant paper or book was published. Of course this does not necessarily mean that the actual work was done in that same year, but this seemed the most logical choice for putting a time stamp on events. Also, it may give the impression that all of these events formed one logical and continuous flow, whereas many of the research results described here were often achieved completely independently. Finally, no history is ever complete. Obviously there were other relevant events, papers, and researchers that have been left out for the sake of brevity, or simply because I did not know about them. I apologize for any such omissions.