A theoretical study on the dynamics of the gas phase reaction of NH₂(²B₁) with HO₂(²A″)

Abstract

Quasi-classical trajectory calculations and stochastic one-dimensional chemical master equation simulation methods are used to study the dynamics of the reaction of amidogen radical [NH₂(²B₁)] with hydroperoxyl radical [HO₂(²A″)] on the lowest singlet electronic state. The title complex reaction takes place on a multi-well multichannel potential energy surface consisting of three deep potential wells and one van der Waals complex. In quasi-classical trajectory calculations a new analytical potential energy surface based on CCSD(T)/aug-cc-pVTZ//MPW1K/6-31+G(d,p) ab initio method was driven and used to study the dynamics of the title reaction. In quasi-classical trajectory calculations, the reactive cross sections and reaction probabilities are determined for 200–2000 K relative translational energies to calculate the rate constants. The same ab initio method was used to have the necessary data for solving the one-dimensional chemical master equation to calculate the rate constants of different channels. In solving the master equation, the Lennard-Jones potential model was used to form the collision between the collider gases. The fractional populations of different intermediates and products in the early stages of the reaction were examined to determine the role of the energized intermediates and the van der Waals complex on the dynamics of the title reaction. Although the calculated total rate constants from both methods are in good agreement with the reported experimental values in the literature, the quasi-classical trajectory simulation predicts the formation of NH₂O + OH as the major channel in the title reaction in accordance with the previous studies (Sumathi and Peyerimhoff, Chem. Phys. Lett., 263:742–748, 1996), while the stochastic master equation simulation predicts the formation of HNO + H₂O as the major products.

Introduction

The presence of different radicals and reactive species in the atmosphere and combustion process causes some complexity in their chemistry. In many cases complex reactions proceed through the formation of energized adduct(s) to form chemically activated specie(s) that play important roles in the chemistry of those systems. Two key radical species that are involved in considerable number of cycles in the upper atmosphere are NH₂ and HO₂ [1, 2].

One of the important concerns about the role of these radicals in the upper atmosphere is their effects on the concentration of nitrogen oxides and consequently on the depletion of ozone layer [3–5]. Nitrogen oxides can be diminished in the atmosphere by reacting with NH₂ or HO₂ according to reactions (a) or (b). On the other hand, NH₂ has been considered as one of the three major natural sources for nitric oxide, reaction (c) [2].

$${\text{NH}}_{ 2} + {\text{ NO}} \to {\text{N}}_{ 2} + {\text{ H}}_{ 2} {\text{O}};{\text{ k}} = { 1}.0 2 { } \times { 1}0^{ 10}\, {\text{L}}\;{\text{mol}}^{ - 1} \;{\text{s}}^{ - 1}$$

(a)

$${\text{HO}}_{ 2} + {\text{ NO}} \to {\text{NO}}_{ 2} + {\text{ H}}_{ 2} {\text{O}};{\text{ k }} = { 6}.0 2 { } \times { 1}0^{ 8}\, {\text{L}}\;{\text{mol}}^{ - 1} \;{\text{s}}^{ - 1}$$

(b)

$${\text{NH}}_{ 2} + {\text{ O}}_{ 2} \to {\text{NO }} + {\text{ H}}_{ 2} {\text{O}}$$

(c)

Although the kinetics of the title reaction has been studied experimentally and theoretically in some extent, its dynamics still needs more elaboration. Cheskis and Sarkisov [6] in a flash photolysis study and in a separate experimental study Lesclaux [7] used laser spectroscopy technique to study the reactivity of gas phase ammonia and reported the total rate constant for the loss of NH₂ in the title reaction as 1.5 × 10¹⁰ L mol⁻¹ s⁻¹ and 3.0 × 10¹⁰ L mol⁻¹ s⁻¹, respectively.

Pouchan et al. [8] studied the kinetics of the title reaction and focused only on the formation of HNO + H₂O. Bozzelli and Dean [9] studied the effect of temperature and pressure on the kinetics of the title reaction in various bath gases. They predicted formation of chemically energized NH₂OOH adduct that dissociates into NH₂O and OH. They predicted that essentially 100 % of the energized NH₂OOH* adduct from the NH₂ + HO₂ reaction dissociates to the low-energy exit channel NH₂O + OH. They have suggested that stabilization or isomerization of the energized complex to dissociate to HNO + H₂O does not occur to any significant extent. This result suggests that NH₂ + HO₂ → NH₂O + OH should be included in the kinetic models for ammonia oxidation. They reported the following rate expression for the total rate of the title reaction, k(total) = 2.95 × 10^{1 3} × exp[−30.022 (kcal/mol)/RT]. Their study was limited just to HNO + H₂O and NH₂O + OH exit channels. They used the bimolecular version of Quantum Rice–Ramsperger–Kassel (QRRK) theory to predict the rate constants.

Sumathi and Peyerimhoff [1] studied the kinetics of the title reaction on an extended potential energy surface. They predicted the formation of three energized intermediates NH₂OOH, NH₂(OH)O and HN(OH)₂ along the reported potential energy surface with the dominant contribution of NH₂OOH for the formation of NH₂O + OH. They emphasized on the stabilization process of NH₂OOH as a dominant process beyond l0 atm pressure. Their calculated total rate constant in the pressure range of 0.001–10 atm in nitrogen bath varied from 2.43 × 10¹⁰ L mol⁻¹ s⁻¹ to 9.66 × 10⁹ L mol⁻¹ s⁻¹ in the temperature range of 300–2000 K. Lozovskii et al. [10] reported a value of 3.67 × 10¹⁰ L mol⁻¹ s⁻¹ as the rate constant for the loss of the reactants in the title reaction.

A quick look at the reported data on the kinetics of the title reaction in the literature indicates clear divergence between the reported mechanism and rate expressions for the title reaction (see Table S1 in the supplementary materials). This study is a theoretical attempt to provide more detailed information on the mechanism and dynamics of the title reaction using two different methods to determine the rate constants.

Quantum mechanical calculations

Gaussian 09 program [11] was employed to perform the quantum mechanical calculations. Since MPW1K hybrid density functional method consists of improved electron correlation functions to provide saddle point geometries and energies more accurately [12], the stationary point geometries were optimized at the MPW1K/6-31+G(d,p) level of theory as shown in Fig. 1. The relative energies of the stationary points were refined by applying CCSD(T)/aug-cc-pVTZ [13, 14] single point calculations. To destroy the spin contamination and spatial symmetries, mixed HOMO and LUMO option was considered in the ab initio calculations. Also, the zero-point energies, moments of inertia and vibrational frequencies were calculated at the MPW1K/6-31+G(d,p) level of theory as listed in Table 1S. The vibrational term values are scaled by a factor of 0.9515 [12]. Figure 2 shows a schematic of the calculated PES at the CCSD(T) level that the energies of the stationary points are corrected for the zero-point energies. Based on our ab initio calculations, our suggested mechanism for the title reaction is shown in Scheme 1.

Fig. 1

Optimized stationary point geometries at the MPW1K/6-31+G(d,p) level

Fig. 2

The ZPE corrected potential energy surface for the reaction of NH₂(²B₁) with HO₂(²A″) at the CCSD(T)/aug-cc-pVTZ//MPW1K/6-31+G(d,p) level of theory

Scheme 1

Suggested mechanism for the reaction of NH₂(²B₁) with HO₂(²A″)

Potential energy surface

As shown in Scheme 1 and Fig. 2, two initiation channels are predicted for the reaction of NH₂(²B₁) with HO₂(²A″) at the CCSD(T)/aug-cc-pVTZ//MPW1K/6-31+G(d,p) level. The main channel in this PES passes through a barrier-less path to form vibrationally energized intermediate NH₂OOH with −163.1 kJ mol⁻¹ energy relative to the reactants. This intermediate can undergo collisional stabilization (RW1 in Scheme 1) or dissociative or isomerization processes (channels R2, R8, and R10). By surmounting the saddle point TS2 with 19.7 kJ mol⁻¹ barrier height, the energized intermediate NH₂OOH isomerizes to another intermediate H₂N(OH)O that is −213.5 kJ mol⁻¹ more stable than the reactants by transferring the OH group from oxygen to nitrogen. The other path for NH₂OOH is the formation of a similar structure H₂NO–OH by passing over a shallow saddle point TS5 with only 4.5 kJ mol⁻¹ barrier height. The other possible path for disappearance of energized NH₂OOH is its dissociation to NH₃ + O₂, reaction R10. This path passes over saddle point TS9 with 161.1 kJ mol⁻¹ barrier height. Ammonia and molecular oxygen are 49.0 kJ mol⁻¹ more stable than the reactants. Energized intermediate NH₂O-OH can later dissociate into NH₂O and OH that are 92.8 kJ mol⁻¹ more stable than the reactants.

Dissociation of energized intermediate H₂N(OH)O by surmounting TS7 with −157.3 kJ mol⁻¹ energy relative to the reactants produces HNO and H₂O, the most stable products in this system with 321.7 kJ mol⁻¹ energy release. Another path for the loss of energized intermediate H₂N(OH)O is the formation of another energized molecule HN(OH)₂ by surmounting the saddle point TS3 with 72.2 kJ mol⁻¹ energy relative to the total energy of the reactants. Stabilized HN(OH)₂ is 281.7 kJ mol⁻¹ more stable than the reactants.

The chemically activated HN(OH)₂ specie can either undergo stabilization process via channel RW3 or dissociate into HNOH and OH that is 65 kJ mol⁻¹ more stable than the reactants, its conversion to HNO + H₂O, or formation of NOH + H₂O. The products of these last two channels are more stable than the reactants by 321.7  and 146.1 kJ mol⁻¹, respectively.

The other possible channel for the title reaction is the formation of HNOH + OH (channel R11) by passing over saddle point TS11 with 103.7 kJ mol⁻¹ barrier height. This path is not important in this system and its effect on the kinetics of the title reaction is ignored.

Rate constant calculations

In the present study, two methods were used to predict the rate constant for different channels of the title reaction. The first method was the chemical master equation simulation through MESMER program to calculate the fractional concentration of different species as a function of time at different translational temperatures. In the second method, quasi-classical trajectory calculations were carried out to predict the effective cross section for the title reaction as a function of relative translational energy to calculate the rate constants.

Master equation simulation

The kinetics of this multi-well complex reaction is investigated by means of master equation (ME) solver program MESMER 3.0 [15, 16]. MESMER uses matrix techniques to formulate and solve the Energy Grained Master Equation (EGME) for unimolecular systems composed of an arbitrary number of wells, transition states, sinks, and reactants. The form of the EGME in MESMER is the one-dimensional ME, wherein the total rovibrational energy of the system, E, is the only independent variable rather than the two-dimensional formulation in terms of both E and J (total angular momentum) [15]. The ab initio data including geometrical information, symmetry numbers, vibrational frequencies and classical rotor moments of inertia (see Table 1S) and zero-point energies (ZPE) at the CCSD(T)/aug-cc-pVTZ//MPW1K/6-31+G(d,p) level of theory were used to calculate the temperature and pressure dependence of the fractional concentrations of different species in early stages of the reaction.

The population of rovibronic energy levels of the intermediates (denoted by subscript i) on the PES were divided into energy grains, characterized by an average energy, E _i , and the population in each grain, n _i (E _i , t), was described by a set of coupled differential equations that accounted for collisional energy transfer within each intermediate as well as isomerization, dissociation and product formation [17, 18]. The general form of the time-dependent concentration of different species might be written as

$$\begin{aligned} \frac{d}{dt}n_{i} (E_{i} ,t) = \omega \int\limits_{{E_{i} ,0}}^{\infty } {P(\left. {E_{i} } \right|} E_{i}^{'} )n_{i} (E_{i}^{'} ,t)dE_{i}^{'} - \omega n_{i} (E_{i} ,t) \hfill \\ - \sum\limits_{j \ne i}^{M} {k_{ji} } (E_{i} )n_{i} (E_{i} ,t) + \sum\limits_{j \ne i}^{M} {k_{ij} } (E_{j} )n_{j} (E_{j} ,t) - k_{Pi} (E_{i} )n_{i} (E_{i} ,t) \hfill \\ - k_{Ri} (E_{i} )n_{i} (E_{i} ,t) + k_{Ri} (E_{i} )K_{Ri}^{eq} \frac{{\rho_{i} (E_{i} )e^{{ - \beta E_{i} }} }}{{Q_{i} (\beta )}}n_{R} n_{m} \hfill \\ \end{aligned}$$

(1)

The first term represents the probability of n _i (E _i , t) to be populated by collisional energy transfer via activating/deactivating bath gas collisions. Nitrogen bath gas was used in this study (with σ = 3.74 Å and ε/k _B  = 82.0 K). ω is the Lennard-Jones collision frequency [19] and (E _i |E′) is the probability that collision with bath gas will result in a transition between a grain with energy E′ _i and a grain with energy E _i . The second term represents the loss from grain E _i via collisional energy transfer. The third term stands for the loss from grain E _i via reaction to give other isomers, denoted by subscript j. k _ji (E _i ) is the microcanonical rate constant for loss from isomer i to isomer j. The fourth term defines the population of grain E _i by reactions from isomer i that give isomer j with the grains E _i and E _j spanning the same range of energy. The fifth term represents the rate of loss from grain E _i via dissociation channel with k _Pi (E _i ) as the corresponding rate of loss. Because the re-association of the products of unimolecular dissociations is generally negligible on an experimental time scale, dissociation to products was treated via an infinite sink approximation (i.e., re-association is not considered in this scheme). The final two terms are associated with the reactants bimolecular source term and only apply to the wells that populate via bimolecular association. By assuming that the reactants are thermalized via bath gas collisions in a Boltzmann distribution and that a pseudo-first order approximation is appropriate, by choosing one of the reactants (NH₂) as the deficient reactant, then the sixth and seventh terms include the rate at which two reactants associate to populate grain E _i and the rate of loss from that grain via re-dissociation to the reactants, respectively. k _Ri (E _i ) represents the rate constant at which E _i re-dissociates to give reactants, R, and K ^eq _Ri is the equilibrium constant between isomer i and the reactants. The expression $Q_{i} (\beta ) = \sum\nolimits_{{E_{i} }} {\rho_{i} (E_{i} )e^{{ - \beta E_{i} }} }$ is the rovibronic partition function for the molecular species corresponding to isomer i [20].

The microcanonical rate coefficients for the unimolecular reactions occurring in each energy grain (E _i ) were calculated from the PES data pertaining to the reagents and transition states via the microcanonical transition state/RRKM theory expression [21–24] [Eq. (2)] by relying on the ergodicity assumption.

$$k\left( E \right) = \frac{{\sigma_{r}^{{}} }}{{\sigma_{{}}^{ \ne } }}\frac{1}{h}\frac{{G_{{}}^{ \ne } \left( {E_{i} } \right)}}{{\rho \left( {E_{i} } \right)}}$$

(2)

In Eq. (2), σ ^≠ and σ _r are the symmetry numbers of the transition state and the reactant, respectively; h is the Planck’s constant; G ^≠(E _i ) is the transition state sum of states; and ρ(E _i ) is the density of states of the reactant molecule.

The calculated microcanonical rate coefficients were implemented in Eq. (3) to extract canonical rate coefficients from the chemically significant eigenvalues using a procedure similar to that described by Bartis and Widom [25]:

$$k(T) = \frac{1}{Q(\beta )}\int\limits_{{E_{i} }} {k(E_{i} )\rho (E_{i} )e^{{ - \beta E_{i} }} dE_{i} }$$

(3)

In this procedure, Eckart tunneling through an unsymmetrical barrier [26] was incorporated into the calculations and the k _Ri (E _i ) values for the barrier-less association reaction and the reaction paths possessing bottleneck were computed by the inverse Laplace transform (ILT) method [27, 28].

The reaction of NH₂ with HO₂ proceeds through a chemically activated mechanism with the entrance channel being a barrier-less recombination reaction R1 to form energized intermediate NH₂OOH*. As expected for complex reactions like the title reaction, the rate constant for each individual channel is correlated to the rate constants for the other channels. The net rate constant for the formation of each species, k(T _trans, P), might be calculated from relative population of different species (molar fractions; f _i ) that are present in the system multiplied by the total rate constant (k _{reactant loss}) that are functions of translational temperature (T _trans) and total pressure P, as shown in Eq. (4) [29, 30].

$$k(T_{\text{trans}} ,\,P) = f_{i} (T_{\text{trans}} ,\,P)k_{{{\text{NH}}_{ 2} {\text{loss}}}} (T_{\text{trans}} ,\,P)$$

(4)

Here, the values of f _i are the average relative molar populations for a specific collision period. In this study, the values of f _i are calculated for a time interval of 10 ps to 7.9 × 10⁻⁵ s. The fractional populations of the main contributors in this system are shown in Figs. 3 and 4 at two different translational temperatures of 298 and 3000 K, respectively. A quick glance through Figs. 3 and 4 reveals that by increasing the translational temperature the fractional concentrations tend to decrease as expected for barrier-less complex reactions. The fractional populations of different species are used to calculate the rate constants by means of Eq. (4). The Arrhenius plot for different products for reaction time of up to 1.0 × 10⁷ ps is shown in Fig. 5. Based on the reported results in Fig. 5, a non-linear least squares fitting procedure provided the following bimolecular rate expressions in units of kJ mol⁻¹ for the energy and Lmol⁻¹ s⁻¹ for the pre-exponential factor.

Fig. 3

Time evolutions of fractional concentrations of different species during the early (a) and extended (b) stages of the title reaction at 298 K and 1 atm

Fig. 4

Time evolutions of fractional concentrations of different species during the early (a) and extended (b) stages of the title reaction at 3000 K and 1 atm

Fig. 5

Arrhenius plot for different paths of the reaction of NH₂ + HO₂ calculated by solving the chemical master equation at 1 atm

$$k_{\text{total}} = 5.94 \times 10^{21} T^{ - 3.91} e^{{ - \frac{7.8}{RT}}}$$

$$k_{W1} = 4.39 \times 10^{27} T^{ - 7.96} e^{{ - \frac{16.7}{RT}}}$$

$$k_{W2} = 1.10 \times 10^{28} T^{ - 8.28} e^{{ - \frac{17.5}{RT}}}$$

$$k_{W3} = 3.87 \times 10^{25} T^{ - 8.28} e^{{ - \frac{0.10}{RT}}}$$

$$k_{4} = 3.74 \times 10^{30} T^{ - 6.95} e^{{ - \frac{18.3}{RT}}}$$

$$k_{5} = 2.45 \times 10^{18} T^{ - 4.47} e^{{ - \frac{10.0}{RT}}}$$

$$k_{7} = 3.25 \times 10^{21} T^{ - 4.94} e^{{ - \frac{11.3}{RT}}}$$

$$k_{W8} = 1.06 \times 10^{28} T^{ - 8.10} e^{{ - \frac{17.2}{RT}}}$$

$$k_{9} = 1.06 \times 10^{26} T^{ - 6.04} e^{{ - \frac{15.0}{RT}}}$$

$$k_{10} = 1.52 \times 10^{8} T^{ - 1.04} e^{{ - \frac{3.9}{RT}}}$$

Quasi-classical trajectory calculations

The dynamics of the system is analyzed through the time evolution of the Monte Carlo quasi-classical trajectory calculations using the general chemical dynamics computer program VENUS96 [31, 32] to generate the reactive cross sections and probabilities. The potential energy in VENUS program is first formulated in terms of curvilinear internal coordinates and then transformed to a Cartesian coordinate frame. With this procedure the Hamiltonian of the system depends only upon the potential energy since no terms are neglected in the kinetic energy expression [33]. In our dynamical calculations, a Born–Oppenheimer analytical potential energy function based on our DFT calculations at the MPW1K/6-31+G(d,p) level of theory was constructed, as defined below.

The analytical PES for this system is shown in Eq. (5). In order to obtain a more accurate system model at all regions of the PES, a few switching functions were used which could smoothly vary several parameters as a species dissociates or transits to a further structure.

$$\begin{aligned} V = V ( {\text{R}}_{\text{N1 - H2}} ) + V (R_{\text{N1 - H3}} ) + V (R_{\text{O4 - O5}} ) + V (R_{\text{O5 - H6}} ) + V (R_{\text{N1 - O4}} )\hfill \\ + V (R_{\text{N1 - O5}} ) + V (R_{\text{H2 - O4}} ) + V (R_{\text{H3 - O4}} ) + V (R_{\text{H2 - O5}} ) + V (R_{\text{H3 - O5}} )\hfill \\ + V (R_{\text{O4 - H6}} ) + V (R_{\text{N1 - H6}} ) + V (\theta_{{{\text{H2}}\,{\text{N1}}\,{\text{H3}}}} ) + V (\theta_{{{\text{O4}}\,\,{\text{O5}}\,{\text{H6}}}} ) + V (\theta_{{{\text{H2}}\,{\text{N1}}\,{\text{O4}}}} )\hfill \\ + V (\theta_{{{\text{H3}}\,{\text{N1}}\,{\text{O4}}}} ) + V (\theta_{{{\text{N1}}\,{\text{O4}}\,{\text{O5}}}} ) + V (\theta_{{{\text{H3}}\,{\text{N1}}\,{\text{O5}}}} ) + V (\theta_{{{\text{N1}}\,{\text{O5}}\,{\text{H6}}}} ) + V (\theta_{{{\text{O4}}\,{\text{N1}}\,{\text{O5}}}} )\hfill \\ + V (\theta_{\text{H3O5H6}} ) + V (\theta_{{{\text{H2}}\,{\text{O5}}\,{\text{H6}}}} ) + V (\theta_{{{\text{H2}}\,{\text{O4}}\,{\text{H6}}}} ) + V (\theta_{{{\text{H3}}\,{\text{O4}}\,{\text{H6}}}} ) + V (\theta_{{{\text{H2}}\,{\text{N1}}\,{\text{O5}}}} )\hfill \\ + V (\theta_{{{\text{N1}}\,{\text{O4}}\,{\text{H2}}}} ) + V (\theta_{{{\text{N1}}\,{\text{O4}}\,{\text{H3}}}} ) + V (\theta_{{{\text{H2}}\,{\text{N1}}\,{\text{H6}}}} ) + V (\theta_{{{\text{H3}}\,{\text{N1}}\,{\text{H6}}}} )\hfill \\ \end{aligned}$$

(5)

In this potential function, the harmonic bending interactions were described by

$$V(\theta ) = 1/2K(\theta - \theta_{\text{eq}} )^{2} ,$$

(6)

where θ and θ _eq correspond to instantaneous and equilibrium bending angles, respectively. The bond stretching function was represented by a modified Morse function:

$$V_{\text{bond}} = V + D_{e} \times {\text{SW1}} \times [(1 - \exp ( - \beta (r - r_{\text{eq}} ))]^{2} - D_{e} \times {\text{SW1}}$$

(7)

In this equation, D _e is the bond dissociation energy, β is an expansion of tentative displacement [Δr in Eq. (8)], V is the Morse function [Eq. (9)], and SW1 is the switching function that includes switching parameter for corresponding bond [C _i , Eq. (10)]. R and R _eq are bond lengths for the switched bond at time t and its equilibrium value, respectively.

$$\beta = c_{1} + c_{2} \Delta r + c_{3} \Delta r^{2} + c_{4} \Delta r^{3}$$

(8)

$$V = D[1 - \exp ( - \beta \Delta r)]^{2}$$

(9)

$${\text{SW1}} = 1 - \exp ( - Ci \times [(R - R_{\text{eq}} )^{2} ]$$

(10)

The Morse stretch, harmonic bend parameters and switching function parameters are reported in Tables 2S to 4S. Figure 1S shows the numbering of the atoms.

Batches of 1000 trajectories were run at a variety of collisional energies. Calculations have been done for a bimolecular six-atom system with translational temperature over the range of 200–2000 K. The trajectories were integrated numerically for 10,000 steps with a time step size of 0.2 fs. This integration step size guaranteed a conservation of the total energy better than 1 in 10⁵. The maximum impact parameter (b _max) was determined empirically to include more than 95 % of the reactive trajectories [34].

The initial conditions for the reaction of NH₂ + HO₂ were sampled by VENUS96 program to calculate the thermal rate constants from effective cross sections according to Eq. 11, which were corrected for the tunneling factor (κ) according to a model suggested by Brown [35], where a hydrogen atom approaches to a one-dimensional unsymmetrical Eckart barrier [36, 37].

$$k = \kappa \left( {\frac{{8k_{B} T}}{\pi \mu }} \right)^{1/2} \pi b_{\hbox{max} }^{2} \frac{{N_{r} }}{{N_{t} }}$$

(11)

In Eq. 11, N _r and N _t are the numbers of reactive and total 1000 trajectories, respectively, μ is the reactants’ reduced mass, k _B is the Boltzmann constant, b _max is the maximum impact parameter.

Based on Eq. (11), rate constants are directly related to the squared of b _max values. As shown in Table 1, our results indicate that increasing the translational temperature from 200 to 2000 K causes an increase in the impact parameter b _max by 25 %. As expected, increasing the translational energy causes a decrease on the formation of the products with no effective barrier height and also causes a decrease on the rate of stabilization processes for the energized intermediates (see Table 2). As it can be implied from Table 2, the values of N _r are only significant for the formation of the first chemically activated intermediate NH₂OOH and formation of the most probable product NH₂O + OH. For species with higher energy barrier (formation of NH₃ + O₂ and HNOH + OH) no significant number of reactive trajectories N _r was generated.

Table 1 Variation of maximum impact parameter (b _max) as a function of translational temperature (T _trans)

Table 2 Variation of the reactive trajectories (N _r ) for the formation of the different species as a function of translational temperature (T _trans)

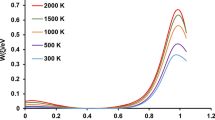
Figure 6 shows the Arrhenius plot for different channels based on Eq. (11). We were not able to have a reasonable number of reactive trajectories for the formation of energized intermediate NH₂O–OH, HNOH + OH, and NOH + H₂O. In Fig. 6 we have also shown the Arrhenius plot for the reported rate constants by Sumathi and Peyerimhoff [1]. Channels R5 (formation of HNOH + OH) and R6 (formation of NOH + H₂O) are in competition with channel R4 (formation of HNO + H₂O). Therefore, we do not expect to have considerable amount of the products of channels R5 and R6 at lower translational energies compared to the products of channel R4. Also we do not expect to have a significant amount of NH₃ + O₂ at lower temperatures as this channel needs more energy to surmount the barrier heights TS10 or TS11. In Fig. 6, the trend for the formation of NH₃ + O₂ is evident from the rate constants for the other species since its variation is apparently ascending with temperature (in accordance with the reported data by Sumathi and Peyerimhoff [1]), while for most of the other channels the rate constants decrease with temperature increase (as we expected for barrier-less reactions). Based on the reported results in Fig. 6, non-linear least squares fitting procedure provided the following bimolecular rate expressions in kJ mol⁻¹ for the energy and L mol⁻¹ s⁻¹ for the pre-exponential function.

Fig. 6

Arrhenius plot for different paths calculated from quasi-classical trajectory calculations. The asterisk indicates the rate constants from [1]

$$k_{\text{total}} = 2.38 \times 10^{11} T^{ - 0.13} e^{{ - \frac{0.01}{RT}}}$$

$$k_{W1} = 1.85 \times 10^{10} T^{ - 0.11} e^{{ - \frac{0.3}{RT}}}$$

$$k_{W2} = 1.42 \times 10^{12} T^{ - 0.83} e^{{ - \frac{0.05}{RT}}}$$

$$k_{W3} = 1.63 \times 10^{12} T^{ - 1.10} e^{{ - \frac{0.02}{RT}}}$$

$$k_{4} = 6.44 \times 10^{22} T^{ - 5.22} e^{{ - \frac{7.7}{RT}}}$$

$$k_{9} = 2.37 \times 10^{8} T^{ - 0.49} e^{{ - \frac{0.22}{RT}}}$$

$$k_{10} = 4.16 \times 10^{3} T^{1.91} e^{{ - \frac{0.13}{RT}}}$$

Results and discussion

A comparison between the reported rate constants from chemical master equation simulation in Fig. 5 and those from qausi-classical trajectory calculations in Fig. 6 reveals some similarities and some discrepancies. The total rates for the loss of the reactants are in reasonable agreement (5.49 × 10¹⁰ L mol⁻¹ s⁻¹ from solving the master equation and 3.33 × 10¹⁰ L mol⁻¹ s⁻¹ from quasi-classical trajectory calculations at 298 K). These values might be compared with the reported experimental and theoretical values of 1.5 × 10¹⁰ L mol⁻¹ s⁻¹ from [6], 3.67 × 10¹⁰ L mol⁻¹ s⁻¹ from [7], and 2.34 × 10¹⁰ Lmol⁻¹ s⁻¹ from [1], at 300 K and 1 atm. In Table 3 we compared our calculated rate constants for different channels with the available data reported in the literature at 300 K and 1 atm.

Table 3 A brief comparison between the calculated rate constants for different paths from present work with the available data for this system in the literature at 300 K and 1 atm

Our results from chemical master equation simulation indicate that the rate constant for the formation of NH₃ + O₂ (in Fig. 5) is not very sensitive to the temperature as suggested by Sumathi and Peyerimhoff [1] (shown in Fig. 6). As shown in Fig. 2, the saddle point for channel R10 is still 2 kJ mol⁻¹ less than the total energy of the reactants to prove our results from chemical master equation simulations. Also our results from chemical master equation simulations indicate that HNO and H₂O are the major products as path R7 is energetically more favorable than path R8 (formation of NH₂O + OH) in agreement with reported rate constant by Sarkisov et al. [37] and contrary to the reported data by Sumathi and Peyerimhoff [1]. Also, we do not expect the rate of formation of energized intermediates should be that much high as reported by Sumathi and Peyerimhoff [1] at low pressure. One of the important issues for this system is the knowledge of how fast the intra-molecular vibrational redistribution (IVR) process occurs for the energized intermediates in this system. To the best of our knowledge no data is available on the IVR for this system.

Our quasi-classical trajectory calculations predict the total rate constant for the title reaction is in good agreement with the results from our master equation simulation results and also with the reported data in the literature, but was not able to predict the rate constants for the formation of energized intermediates in agreement with the results from the other methods or experimental data. It seems in our quasi-classical trajectory calculations as soon as the energized intermediates are formed in deep potential wells, the system is not able to overcome the potential barriers and stays in those potential wells for a long period of time. This situation causes many trajectories end while the system is trapped in those wells and is not able to find its way out of those deep wells. This kind of behavior was also observed in the study on the dynamics of combustion of methanol [34].

In our dynamics study, no considerable number of trajectories is ended to the formation of HNOH and OH products, while in master equation solution method a noticeable amount of these two products is estimated to be formed.

It was not the intention of the present study for considering the possible secondary reactions that may occur in this system, for instance, the possible reactions between the energized intermediates or the products with each other or with the reactants. To the best of our knowledge, no kinetics study is reported for the reaction of the energized intermediates that are produced in this system with the reactants. It could be concluded that these energized intermediates prefer to undergo the unimolecular dissociation or isomerization reactions but not bimolecular reactions. The reaction of HNO (the most probable product in this system based on MESMER results) with one of the reactants (NH₂) [39] and ozone [40] to produce NO (one of the key species in NOx cycle) is studied by M.C. Lin’s group.

Conclusion

Detailed mechanism for the gas phase reaction of NH₂(²B₁) with HO₂(²A″) has been studied at the CCSD(T)/aug-cc-pVTZ//MPW1K/6-31+G(d,p) level of theory and the rate constants for each individual path is predicted by solving one-dimensional chemical master equation and also quasi-classical trajectory calculations. Both methods predict the total rate constant for the title reaction in reasonable agreement with the reported experimental and theoretical available data in the literature with some discrepancies between the calculated individual rate constants. The dynamical calculations predict an upper bound rate constant for stabilization of the energized intermediates and formation of NH₂O + OH as the major path in this system in agreement with reported results by Sumathi and Peyerimhoff [1]. The chemical master equation simulation predicts the formation of HNO + H₂O as the major path in accordance with our reported PES and in agreement with the reported value of the rate constant for this channel by Sarkisov et al. [38]. We were not able to predict any reasonable pressure dependence for the formation of the energized intermediates in this system. It seems that more accurate experimental studies on the kinetics and dynamics of the title reaction need to be done to verify a more reliable mechanism to judge the results of the present work.