Introduction

Dental composites have excellent esthetic properties compared to their metal-based competitors and have currently become popular dental restorative materials. The polymeric matrix of the composites is usually reinforced by incorporating of particulate and/or short fibrous fillers to improve their physical and mechanical properties [1, 2]. Particle size of the reinforcing fillers varies from a few nanometers to several micrometers [3, 4] which significantly affects mechanical properties of dental composite resins [5, 6].

The effect of particle size or volume fraction of the fillers on the flexural strength and flexural modulus of the resin-based composites have been investigated before [7–9]. The flexural properties of the composites have also been studied and predicted using analytical models [9–11]. It has been shown that incorporating of nanoparticles into dental composites may improve some properties like wear resistance, gloss retention [12], modulus [13], flexural strength, diametral tensile strength [14, 15], and fracture toughness properties [16–18]. In the composites, the main mechanism suggested for interactions occurring between the filler surface and their surrounding resin matrix is chemical bonding of the matrix monomer and the filler surface functional groups. The functional groups which present on the filler surface are usually the methacrylates originating from the silane coupling agent bonded onto the filler surface through condensation of the silanol functional groups of prehydrolyzed silane and the hydroxyl groups on the particle surface [19].

Different models have been proposed to predict the effect of parameters such as filler particle size, filler geometry and shape, interfacial interactions, etc. on the mechanical properties of composites. The models may be classified according to the characteristics of the matrix resin and/or filler [20].

Although nanoparticles have been widely used to improve the properties of polymeric matrix of dental composites [21], less attention has been devoted to compare the reinforcing effect of the particles in the nano-scale range. Therefore, the present study aims to compare the mechanical properties of experimental dental nanocomposites containing two silica nanoparticles, with 12 and 40 nm diameters, as reinforcing fillers. The amorphous silica nanoparticles were surface treated by silanization to improve interactions between the fillers and matrix resin. The effects of filler size and filler volume fraction on the mechanical properties of the composites were then investigated. The experimental results were also compared with some predicting models.

Experimental

Materials

2,2′-Bis-[4-(2-hydroxy-3-methacryloyloxy-propoxy)phenyl]-propane (bis-GMA) and triethyleneglycol dimethacrylate (TEGDMA) were prepared from Evonik (Germany). Camphor quinone (CQ), N-N′-dimethylaminoethyl methacrylate (DMAEMA), and 3-(methacryloxy)propyl trimethoxy silane (γ-MPS) were procured from Sigma-Aldrich (Germany). Amorphous, fumed silica with a primary particle size of 12 nm (surface area of 200 m2/g, Aerosil® 200, ASN12 in abbreviation) and 40 nm (surface area of 50 m2/g, Aerosil® OX50 ASN40, in abbreviation) in diameter were obtained from Evonik (Germany). Acetic acid was purchased from Merck (Germany).

Methods

Preparation of the nanocomposites

The ASN12 and ASN40 were surface treated by silanization in the presence of 5 and 10 wt% γ-MPS, respectively. γ-MPS was prehydrolyzed for 0.5 h in an aqueous solution of ethanol (70 wt%). The pH of ethanol solution was adjusted to 3–4 using acetic acid. The fillers were added to the solution and left for 1 week at room temperature. The fillers were separated, washed with ethanol, and dried. The nanoparticles were then incorporated into the matrix phase (a mixture of bis-GMA/TEGDMA, 70/30 wt/wt) and ethanol as solvent. The nanoparticles were thoroughly mixed and sonicated to obtain a homogeneous suspension. The solvent was then evaporated under reduced pressure to produce a homogeneous paste. Afterwards 0.5 wt% of camphor quinone and 0.5 wt% N-N′-dimethylaminoethyl methacrylate, respectively, as photoinitiator and accelerator, were dissolved in the paste under sub-ambient light. The compositions of the nanocomposites are tabulated in Table 1, where A represents nanocomposites containing ASN12 nanoparticles and O denotes nanocomposites containing ASN40 nanoparticles.

Table 1 The composition of the experimental composites
Full size table

Diametral tensile strength (DTS)

DTS test was performed according to American National Standard Institute/American Dental Association (ANSI/ADA) specification No. 27 for light-cured resins. The nanocomposite pastes were inserted into cylindrical stainless-steel molds with an internal diameter of 6 mm and height of 3 mm and cured for 40 s from both sides using a light-curing unit (LE Demetron, Kerr Corp., USA). The specimens were removed from the mold and stored in artificial saliva for 1 day at 37 °C prior to the test. A universal testing machine (UTM 2, Azmoon Gostar Co., Iran) was utilized for the test at a cross-head speed of 10 mm.min−1 (seven repeats). The DTS (MPa) was then calculated according to the following equation:

$${\text{DTS }}\; = \;2P/\pi DL,$$
(1)

where P is the load at fracture (N), D (mm) and L (mm) are diameter and height of specimens, respectively.

Flexural strength (FS) and flexural modulus (FM)

Flexural strength (FS) of the nanocomposites was determined according to the ISO specification No.4049/2000 [22] for polymer-based restorative materials which is widely employed in dental research [23, 24]. To this end, rectangular-shaped specimens (2 mm × 2 mm × 25 mm) (seven repeats) were prepared in stainless-steel molds. An overlapping regime was applied during photo-irradiation to the whole specimens on both sides (40 s for each irradiation). All specimens were stored in artificial saliva at 37 °C for 1 day prior to any further testing. The flexural strength was determined using the universal testing machine at a cross-head speed of 1 mm min−1 according to the following equation:

$${\text{FS}} \; = \;3PL/2bd^{2} ,$$
(2)

where P is the maximum load at the point of fracture (N), L is the span length (20 mm), and b and d are the width and thickness of the specimens in mm, respectively. The flexural modulus (FM) was also determined from the slope of the initial linear region of the stress-strain curve. The FM of the unfilled matrix resin was also measured in the same manner.

Theoretical models

A number of theories and equations have been developed and reported to describe the elastic modulus of particulate composites. We utilized some of these equations to predict and compare the elastic modulus of our experimental nanocomposites. The equations predict the modulus based on the volume fraction of the ingredients. Therefore, the volume fraction of the fillers and the matrix phase of the nanocomposites were calculated according to the following equation [25]:

$$V_{f} = W_{f} /\left[ {W_{f} + \left( {\frac{{\rho_{f} }}{{\rho_{m} }}} \right)\left( {1 - W_{f} } \right)} \right],$$
(3)

where v f , w f , and ρ f are the volume fraction, weight fraction, and density of the filler, respectively, and ρ m is density of the matrix. The density of the fillers was 2.2 g cm−3 and density of the matrix was determined as 1.13 g cm−3 considering density of bis-GMA (1.16 g cm−3) and TEGDMA (1.075 g cm−3) [10] and their volume fraction according to the “rule of mixtures”.

Scanning electron microscopy (SEM)

The fractured surfaces of the specimens were examined for determining the mode of fracture using Evo® 40 (Zeiss, UK) scanning electron microscopy. The samples were gold-coated by a sputter coater (INCA x-sight, polaron SC 7620, UK) prior to SEM observations.

Transmission electron microscope (TEM)

Transmission electron microscopy (Philips, CM30, The Netherlands) was used to observe dispersion pattern of the particles. Ultramicrotomy was performed at room temperature (OmU3, Reichert, Austria) for sample preparation. The layer was placed on a carbon-coated copper grid for TEM observations.

Fourier-transform infrared (FTIR) spectroscopy

FTIR spectroscopy (Bruker, Vertex 80, Germany) was performed to characterize the silanized fumed silica nanoparticles. The nanoparticles were mixed with KBr powder in 1:100 weight ratio. Aliquots of the mixture were compressed to form discs (10 mm dia.). The infrared spectra of discs were collected on FTIR spectrometer at 4 cm−1 resolution and 16 scans.

Thermal gravimetric analysis (TGA)

The extent of silane grafting on the fumed silica fillers surface was measured by thermogravimetric analysis (TGA/DSC1, Mettler Toledo, Switzerland) at a heating rate of 10 °C min−1 under nitrogen atmosphere.

Statistical analysis

The results were analyzed and compared using one-way ANOVA and the Tukey’s test at the significance level of 0.05. The reported values are at least the average of seven independent measurements for mechanical tests.

Results and discussion

The effects of particle size and volume fraction of the fillers on the mechanical properties of composites have already been reported in the literature [1, 2]. The studies have mostly focused on micron-sized particles. Characterizing and modeling of the mechanical properties of nanocomposites have attracted considerable attention due to the unique properties of the composites [26]. Therefore, this study focuses on the mechanical properties of nanocomposites and their modeling.

Surface treatment

An agglomeration of nanoparticles may end up in micrometric particles. The formation of these micrometer-sized agglomerates is a cause for deteriorating the mechanical properties. The particles thus need surface modification to reduce clustering and improve their dispersion throughout the resin matrix. In dentistry, silica nanoparticles are usually preferred because of their high biocompatibility and pleasing tint [27].

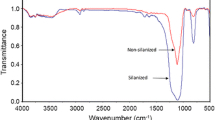
After treating with γ-MPS, the surface functionalized particles were characterized by FTIR spectroscopy. Figures 1 and 2 represent FTIR spectra of the modified and unmodified silica nanoparticles (ASN12 and ASN40, respectively). Both spectra confirm silanization of the nanoparticles. Grafting of γ-MPS onto the silica nanoparticles provides a new peak appeared in the range of 1705–1710 cm−1 due to the stretching vibration of carbonyl groups originating from γ-MPS. The reaction chemically begins with the hydrolysis of the OH groups of γ-MPS into silanols (Si-OH) which can condense with OH functional groups positioned on the silica surface forming siloxane bonds. A γ-MPS surface layer on the silica nanoparticles encourages better dispersion within the resin matrix. The emerging peak positioned at 1630–1637 cm−1 is also attributed to the methacrylate double bond of γ-MPS.

Fig. 1
figure 1

FTIR spectra of modified and unmodified silica nanoparticles (ASN12)

Full size image
Fig. 2
figure 2

FTIR spectra of modified and unmodified silica nanoparticles (ASN40)

Full size image

The extent of silanization of the nanoparticles was investigated by TGA as shown in Fig. 3. In the TGA curves the weight loss up to 200 °C is due to the evaporation of physically adsorbed water. The further weight loss between 200 and 600 °C is due to the thermal degradation of the organic modifier and was considered as the silane grafting percentage. Figure 3 shows that 2.0 and 4.5 % weight losses occur for ASN40 and ASN12 nanoparticles, respectively. ASN12 nanoparticles possess higher surface area than ASN40 and, consequently, more hydroxyl functional groups for bonding with γ-MPS. So, the extent of γ-MPS functionalization at the surface of ASN12 is more than the ASN40.

Fig. 3
figure 3

TGA curves of silanized nanoparticles

Full size image

TEM images of the nanocomposites are also shown in Fig. 4. In panels (a) and (b) nanocomposites with 15 and 30 wt% of ASN12 nanoparticles and in panels (c) and (d), nanocomposites with 50 and 53 wt% of ASN40 nanoparticles are shown. TEM imaging showed good dispersion of the fillers in the resin matrix. The interface effect in nanocomposites is more important than in composites containing micron-sized filler, due to the higher specific surface area of the nanoparticulate fillers [1]. Chemical coupling agents can influence dispersion and improve bonding between inorganic nanoparticles and the resin matrix [28]. The agglomerates, however, still form, as shown in TEM images, i.e., Figure 4. Since, ASN12 nanoparticles are smaller in size than ASN40; they possess higher specific surface area and surface energy resulting in more agglomerates. This phenomenon is recognizable in panels (a) and (b).

Fig. 4
figure 4

TEM images of group of composites: A2 (a), A5 (b), O4 (c) and O5 (d)

Full size image

Mechanical properties

DTS of dental composites depends on the filler content [29]. In general, the enhancement in DTS can be achieved when the particles are well bonded to the resin matrix. Figure 5 shows diametral tensile strength of the composites with no significant differences between nanocomposites of different compositions (p > 0.05). However, increasing in the silica filler content beyond the optimal value (20 wt% in nanocomposites containing of ASN12 and 25 wt% in nanocomposites containing of ASN40) resulted in reduced DTS. The findings are in accordance with those of Ekworapoj et al. [29] report. They reported that the composites showed better strength at lower filler content. Figure 6 depicts flexural strength of the nanocomposites. According to the results, flexural strength of the neat resin specimen and nanocomposites containing ASN12 were not different (p > 0.05), while flexural strength of the neat resin and the specimens containing ASN40 filler are significantly different (p < 0.05). The chemical bonding of the silane coupling agent, γ-MPS, prevents the crack propagation through the filler–matrix interface resulting in higher flexural strength. The flexural strength in nanocomposites containing ASN40 increases at higher rate than that of nanocomposites containing of ASN12. Figures 7 and 8 show flexural modulus of the nanocomposites. The results in these figures are summarized in Table 2. The statistical comparison between the nanocomposites from the same category (ASN40 or ASN12) showed a statistically significant (p < 0.05) difference in flexural modulus due to the varying filler content. The elastic modulus of a particulate-polymer composite is generally determined by the elastic properties of its particle and matrix components [30]. Since the inorganic particulate fillers generally have higher stiffness, the modulus of the polymeric matrix of dental composites is improved by incorporation of the rigid fillers.

Fig. 5
figure 5

Diametral tensile strength (DTS) of composites containing different filler contents: a ASN12 and b ASN40

Full size image
Fig. 6
figure 6

Flexural strength of the composites containing different filler contents: a ASN12 and b ASN40

Full size image
Fig. 7
figure 7

The experimental elastic modulus and the model prediction for ASN12 nanocomposites: a models for rigid particles in non-rigid matrix and b models for rigid particles in rigid matrix

Full size image
Fig. 8
figure 8

The experimental elastic modulus and the model prediction for ASN40 nanocomposites: a models for rigid particles in non-rigid matrix and b models for rigid particles in rigid matrix

Full size image
Table 2 The experimental and predicted elastic modulus (GPa) using different models
Full size table

SEM micrographs of the fractured surface of the specimens are shown in Fig. 9. This figure illustrates the details on the surface of the fractured specimens. The smooth surface without any remnant is representative of a brittle fracture.

Fig. 9
figure 9

SEM micrographs of the fracture surface of groups A4 (a) and O1 (b)

Full size image

Prediction of the elastic modulus

According to the rigidity of the particle and matrix, the models might be categorized in two classes: rigid particles in non-rigid matrix and rigid particles in rigid matrix [20]. In the following, the experimental results of elastic modulus are fitted to the models and compared. The good of fitness is reported by the R square of the least square analysis.

Models for rigid particles in non-rigid matrices

Einstein’s equation for prediction of the Young’s modulus of particulate composite is [31] as follows:

$$\frac{{E_{c} }}{{E_{m} }}\; = \;1\; + \;2.5V_{f} ,$$
(4)

where E c and E m are Young’s modulus of composite and matrix, and V f is particle volume fraction. As Figs. 7 and 8 show the prediction of the modulus of the nanocomposites by Einstein’s equation is far from the experimental values (R 2 = 0.09). Einstein’s equation was originally derived for the effective shear viscosity of dilute suspensions of rigid spheres and was extended to study the effective viscosity of concentrated suspensions of mono-sized spheres [32].

Guth [33] added a particle interaction term in the Einstein’s equation as follows:

$$\frac{{E_{c} }}{{E_{m} }}\; = \;1\; + \;2.5V_{f} \; + \;14.1V_{f}^{2} ,$$
(5)

where the linear term is the stiffening effect of individual particles and the second power term stands for contribution of the particles interaction. The Guth prediction is in agreement with the experimental data (R 2 = 0.86) (Fig. 7; Table 2). Halpin and Tsai found that the modulus of particulate composites can be predicted by a semi-empirical relationship [4, 34]:

$$\frac{{E_{c} }}{{E_{m} }} = \frac{{1 + ABV_{f} }}{{1 - BV_{f} }},$$
(6)

where A and B are constants for a given composite. A is a function of the particle shape and matrix Poisson’s ratio, and B is related to the modulus of the particle (E f ) and matrix (E m ).

$$A = K_{E} - 1,$$
(7)

where K E is Einstein’s coefficient.

$$B = \frac{{\frac{{E_{f} }}{{E_{m} }} - 1}}{{\frac{{E_{f} }}{{E_{m} }} + A}}$$
(8)

Another equation for estimating the modulus of a composite, containing spherical particles in a matrix, proposed by Kerner [35]:

$$\frac{{E_{c} }}{{E_{m} }} = 1\; + \;\left[ {\frac{{V_{f} }}{{1\; - \;V_{f} }}\frac{{15\left( {1\; - \;\vartheta_{m} } \right)}}{{\left( {8\; - \,10\vartheta_{m} } \right)}}} \right]$$
(9)

where υ m is the Poisson’s ratio of matrix. Poisson’s ratio was considered as ν m  = 0.35 in the present study [36]. The prediction of the Kerner equation does not cover the experimental values (Figs. 7, 8). Nielsen [34, 37, 38] used Eqs. (6) and (7) and suggested the following equation:

$$\frac{{E_{c} }}{{E_{m} }}\; = \;\frac{{1\; + \;ABV_{f} }}{{1\; - \;\psi BV_{f} }},$$
(10)

where ψ is related to particle packing fraction and constants A and B are as described before. The factor A is calculated as A = 1.168 for our experimental nanocomposites (K E  = 2.168 as suggested in the Ref. [38] for a matrix with Poisson’s ratio of 0.35). The elastic modulus of fillers may be considered as E f  = 70 GPa [39]

$$\psi = 1\; + \;\frac{{\left( {1\; - \;\varphi_{m} } \right)V_{f} }}{{\varphi_{m}^{2} }}.$$
(11)

The factor φ is related to the maximum packing fraction of the filler. For the studied systems with nearly spherical particles (aspect ratio of the particles is close to 1.0), a random close packing with φ = 0.63 [20, 38] was considered. The Nielsen’s equation prediction is found lower than the experimental values (Figs. 7, 8). Mooney [40] suggested another modification to the Einstein’s equation as follows:

$$\frac{{E_{c} }}{{E_{m} }} = { \exp }\left( {\frac{{2.5V_{f} }}{{1\; - \;sV_{f} }}} \right),$$
(12)

where s is a crowding factor (the ratio of the apparent volume occupied by the filler to its true volume). For close packed spheres s is equal 1.35 [20]. This model predicts values close to the experimental data (R 2 = 0.74). The Mooney equation predicts considerably more reinforcing efficiency than the Kerner equation and a modulus that tends to infinity at high volume fraction of filler. The equation assumes that υ m  = 0.5 and that the modulus of the filler is infinitely greater than the matrix, both of which are not correct for a rigid matrix thus restricting the applicability of this model for filled rigid thermosetting polymeric matrices [20, 38]. According to Fig. 8, the prediction of Halpin-Tsai equation is not in agreement with the experimental values (R 2 = 0.04).

Models for rigid particle in rigid matrices

Voigt and Reuss calculated the effective modulus in fiber composites in the fiber direction and in the transverse direction, respectively, as [26, 41] follows:

$$E_{c}^{L} = E_{m} V_{f} \; + \;E_{m} \left( {1\; - \;V_{f} } \right)$$
(13)

and

$$E_{c}^{T} = \frac{{E_{f} E_{m} }}{{\left[ {E_{f} \left( {1\; - \;V_{f} } \right)\; + \;E_{m} V_{f} } \right]}},$$
(14)

where V f is the volume fraction of fiber and E f and E m represent modulus for fiber and matrix, respectively. The superscripts L and T point to the longitudinal and transverse directions, respectively. Eqs. 13 and 14 can be used for any two-phase composites regardless of the shape of filler. Eq. 13 is also called the “rule of mixtures” and Eq. 14 is called “inverse rule of mixtures” [26]. The modulus of real composites lies between these two boundaries. These equations are upper- and lower-bound models and are applicable to particulate micro- and nanocomposites. Generally, the modulus of composites should be lower than upper-bound predicted by Eq. 13 and higher than the lower-bound by Eq. 14 [26, 42]. For two-phase materials Counto [43] proposed a simple model by assuming perfect bonding between filler and matrix. The composite modulus is given by

$$\frac{1}{{E_{c} }} = \frac{{1 - V_{f}^{{\frac{1}{2}}} }}{{E_{m} }} + \frac{1}{{\left[ {\frac{{1 - V_{f}^{{\frac{1}{2}}} }}{{V_{f}^{{\frac{1}{2}}} }}} \right]E_{m} + E_{f} }}$$
(15)

This model predicts moduli in good agreement with a wide range of testing data. Ishai and Cohen [44] and Paul [45] assumed that the fillers and matrix are subjected to the same uniform stress and there is a perfect adhesion between filler and matrix. When a uniform stress is applied on the boundary, the elastic modulus of the particulate composite is given by

$$\frac{{E_{c} }}{{E_{m} }} = 1 + \frac{{1 + \left( {k - 1} \right)V_{f}^{2/3} }}{{1 + \left( {k - 1} \right)\left( {V_{f}^{2/3} - V_{f} } \right)}},$$
(16)

which is another upper-bound solution. Using the same model, with uniform strain applied at the boundary, Ishai and Cohen [44] obtained a lower-bound solution:

$$\frac{{E_{c} }}{{E_{m} }} = 1\; + \;\frac{{V_{f} }}{{\frac{K}{K\; - \;1}\; - \;V_{f}^{1/3} }}$$
(17)

where K = E f /E m .

The predicted and experimental results (Figs. 7, 8) indicate that there is a good agreement between experimental values and models which have been developed for rigid particles in non-rigid matrix especially that of Guth model.

Prediction of the strength

Prediction of the strength for composite materials is difficult because it is determined by the fracture behaviors which are associated with the parameters as interface adhesion, stress concentration, and defect size/spatial distribution. Numerous theories have been developed to describe strength in composites but there is no universally accepted theory to date [26]. In the case of poor filler-matrix interface adhesion the stress cannot be transferred from the matrix to the filler. The strength of particulate-filled polymer composite is, therefore, determined from the effective sectional area of load-bearing matrix in the absence of the particles, an equation for the composite strength is [46, 47]:

$$\sigma_{c} = \sigma_{m} \left( {1\; - \;V_{f} } \right),$$
(18)

where, σ c and σ m designate the strength of the composite and the matrix and V f is filler volume fraction. This equation predicts that the strength of a particulate-filled composite decreases linearly with increases in filler volume fraction, but the results (Fig. 6) show an increasing trend up to the optimum filler content.

For strong particle–matrix interfacial bonding, such as the present study, Pukanszky et al. [48, 49] suggested an empirical relationship:

$$\sigma_{c} = \left[ {\frac{{\left( {1 - V_{f} } \right)\sigma_{m} }}{{1 + 2.5V_{f} }}} \right]\exp \left( {BV_{f} } \right),$$
(19)

where B is an empirical constant, which depends on the surface area of particles, particle density, and interfacial bonding energy [41]. Fitting to the experimental values in Eq. 19, the parameter B was calculated which was in the range of 2.3–5.4 for ASN12 and ASN40 samples, respectively. The higher value of B shows stronger interfacial adhesion between filler and matrix [49]. Figure 4 depicts a better distribution of the particles in the nanocomposite containing ASN40 in comparison with ASN12-contained nanocomposites which might be due to the formation of agglomerates of ASN12 leading to formation of local defects and weaker strength.

According to the experiments (Fig. 6), the flexural strength increased up to filler content of 14.5 vol% (25 wt%) in nanocomposites containing ASN12 nanoparticles and 29.5 vol% (45 wt%) in nanocomposites containing ASN40 nanoparticles. When the filler content increases, there would be further agglomeration which results in weaker load transfer at the interface of filler and the matrix and reduction in flexural strength. This occurs in nanocomposites containing ASN40 by up to 29.5 vol%, which is due to the difference in particle size of the filler. The large particles do not tend to aggregate in the resin matrix [6, 8].

In nanocomposites with equal volume fraction of particles, the flexural strength increases as the particle size decreases.

Conclusion

This study reports the effect of particle diameter and volume fraction of nanoparticles on mechanical properties (DTS, FS, FM) of spherical-silica-particle-filled composites. Particle diameters were 12 and 40 nm and the volume fraction ranged from 0 to 0.36.

The results indicate that stiffness of composite depends significantly on particle loading, since the fillers have much larger modulus than the matrix. In nanocomposites with an equal volume fraction of particles, the particle size affects flexural modulus. In this case, flexural modulus increases as the particle size is dropped.

The flexural strength increases as the volume fraction increases by up to 14.5 vol% (25 wt%) in nanocomposites containing of ASN12 and 29.5 vol% (45 wt%) in nanocomposites containing of ASN40 nanoparticles.

The predication of the theoretical values was compared with the experimental results. It can be concluded that the model which has been developed for the prediction of the modulus in the composites with rigid particle in non-rigid matrix presented a better agreement with the experimental values.