1 Introduction

This paper introduces a new variant of the VRPSTW trying to overcome the practitioners’ difficulty in using soft time windows routing algorithms. Quantifying customer inconvenience as opposed to routing costs is typically challeging in practice.

Route planning is a critical task in the logistic industry and it has been estimated to account for up to 20% of the overall logistic cost (Toth and Vigo 2002). The vehicle routing problem (VRP) was proposed more than 50 years ago (Dantzig and Ramser 1959) and it is a challenging combinatorial optimization problem. “Rich” VRP variants have been proposed to respond to the variety of operational constraints arising in the distribution industry (i.e. multiple depots, heterogeneous fleet, multi-trips, \(\ldots\)). Academics propose effective exact and heuristic algorithms responding to the needs of the distribution industry (Toth and Vigo 2002; Golden et al. 2008; Vidal et al. 2012).

One of the real-world features attracting remarkable attention from researchers and practitioners are the so called time windows constraints (Schrage 1981; Gendrau and Tarantilis 2010). Customers receiving goods often demand delivery within a time interval or time window. Time windows are classified as hard, if customers must be visited within the specified time interval, and soft, if time windows can be violated at the expense of customer inconvenience. In the first case, the problem is usually refereed to as the vehicle routing problem with hard time windows (VRPHTW), and in the latter as the vehicle routing problem with soft time windows (VRPSTW).

The VRPHTW was first proposed by Pullen and Webb (1967) and since then it has been widely studied. An interested reader may refer to the surveys of Cordeau et al. (2002), Bräysy and Gendreau (2005a, b), Kallehauge (2008), Gendrau and Tarantilis (2010), Desaulniers et al. (2010), Baldacci et al. (2012) and Desaulniers et al. (2014) for comprehensive literature reviews on the VRPHTW. The VRPHTW has been solved effectively both by exact and heuristic algorithms and high-quality solutions are achieved in relatively limited computing times.

Time window violations are often accepted in practical applications due to the potential routing cost saving. Figure 1 depicts an instance where the cost of traversing arcs (1, 3) and (2, 4) is 2 units, whereas all other arcs have cost 1 unit. The vehicle departs from the depot (the square vertex in the figure) at time zero and should visit each customer within the corresponding time window (minimum and maximum arrival times at a customer's location are reported in square brackets). We assume zero service time at the customers' locations. The time window of customer 2 imposes visits at earliest at time 4 and this forces the vehicle to a costly routing solution, when hard time windows constraints are imposed (figure on the left). The same instance may result in a much more convenient routing solution, if customer 2 is visited two units before the desired time window. Practitioners may favour the soft time windows solution (given two units routing cost saving) or the hard time window solution (if inconvenience at customer 2 is not acceptable).

Fig. 1
figure 1

Time windows violation at customer 2

Full size image

A survey and critical discussion of the VRPSTW literature will be presented in Sect. 2; the VRPSTW received less attention and there is not a unique interpretation of time windows violations. Customer inconvenience for being visited too late and (possibly) too early with respect to the desired time window is quantified and the VRPSTW’s objective function is typically modelled as a weighted combination of routing costs and a measure of the customer inconvenience. However, how to measure customer inconvenience and how to quantify the relative weight of routing and customer inconvenience are still open research questions.

Our previous collaborations with logistic companies made us realize that the VRPSTW objective functions often do not reflect the standard practice in handling soft time windows constraints. In Ruinelli et al. (2012), the handmade routing plans presented a large number of time windows violations and practitioners privileged routing cost optimization versus customer satisfaction. Moreover, the experience of human planners and their knowledge about customer needs allowed them to discriminate among sensible time-windows violations and routing benefits associated with each violation. Finally, regarding the practice of objective function weighting in multi-objective optimization, the planner is often

“not aware of which weights are the most appropriate to retrieve a satisfactorily solution, he/she does not know in general how to change weights to consistently change the solution” Caramia and Dell’ Olmo (2008).

In this paper, we model soft time windows constraints trying to overcome the difficulties of practitioners in comparing routing costs and customer’s inconvenience. A base of comparison is established, by setting as benchmark the optimal solution of the hard time windows problem. The planner sets a desired mileage saving with respect to the nominal solution. The exact algorithm minimizes the time window violations to achieve this goal. Therefore, we model the opportunity cost of solutions with smaller routing cost, that is, the incurred customer inconvenience due to time windows violations. This new variant makes VRPSTW software more intuitive for planners. The parameter they are asked to define is simply a measure of the desired mileage saving. Moreover, the iterative use of the software allows practitioners to generate solutions with the desired routing costs and to compare scenarios in which customer satisfaction is privileged with respect to routing costs and vice versa.

The exact algorithms we propose are both based on BCP. The first is a standard implementation, the second is a BCP nested in a bisection framework. The solutions obtained are compared with those produced by similar algorithms for the VRPHTW and the VRPSTW.

The reminder of the paper is as follows. Section 2 presents a comprehensive literature review on the VRPSTW. In Sect. 3, we provide a mathematical model for our problem variant. We propose an exact algorithm based on branch-and-price-and-cut in Sect. 4. Section 5 presents computational experiments performed on a test set derived from the well-known Solomon’s data set for the VRPTW (Desaulniers et al. 1997). Final remarks and future research directions are reported in Sect. 6.

2 VRPSTW: literature review

Early VRPSTWs have been presented in the pioneering articles by Sexton and Bodin (1985a, b) and Sexton and Choi (1986). Ferland and Fortin (1989) proposed a heuristic adjusting time windows of pairs of customers so to reduce the overall cost. Min (1991) modelled the problem of goods distribution among libraries using a multi-objective mixed integer linear programming model. In these articles, extra mileage with respect to the ideal TSP for each route should be counterbalanced by a suitable reduction in the inconvenience for late arrival or early departure at the customers' locations. More precisely, customer inconvenience is included in the objective function as a linear weighted penalization. Dumas et al. (1990) modelled customer inconvenience as a convex function and proposed an algorithm for optimizing departure and arrival time at each customer in a single route. The complexity of the resulting scheduling problems when costs are convex, linear and quadratic is discussed.

Koskosidis et al. (1992) presented a cluster-first route-second heuristic for the VRPSTW in which linear penalizations apply for early and late arrival at customer locations. Balakrishnan (1993) studied a variant in which the service at a customer's location can start early and tardy, but within an outer time window. Linear penalizations apply when the visit is early/tardy with respect to the inner time window. If the vehicle is early with respect to the outer time window, waiting time at a customer is allowed but bounded. Fast constructive heuristics are proposed, namely a nearest neighbour, a saving heuristic and a space–time heuristic.

In Chang and Russell (2004), a Tabu search is developed for the same problem studied in Balakrishnan (1993). Taillard et al. (1997) also proposed a Tabu Search for a VRPSTW, in which linear penalizations are applied only to late visits. Calvete et al. (2004) applies goal programming to the VRPSTW with linear penalizations for early and tardy visits.

A ship scheduling pickup and delivery problem with soft time windows is presented in Fagerholt (2001), in which the concept of maximum violation of a time window is introduced. Customer visits are allowed both before and after an “inner” time window; however, earliness and tardiness are bounded within an outer time window (comprising the inner window). Customer visits falling within the outer time window are penalized according to a linear, quadratic or constant function. The problem is solved by first enumerating a large set of feasible routes and than picking the most suitable subset using a set partitioning formulation.

The same problem with linear penalizations is studied in Ioannou et al. (2003), in which an iterative heuristic is developed. At each iteration, a percentage of the soft time windows is retained and the remaining windows are assumed to be hard. The resulting problem is solved by means of a nearest-neighbour heuristic.

Ibaraki et al. (2005) extend the concept of time window and measure customer’s inconvenience as a non-convex, piecewise linear and time-dependent function. The authors propose a dynamic programming algorithm to optimize the arrival time at each customer in each route and devise three local search-based metaheuristics (multi-start local search, iterated local search, adaptive multi-start local search). A faster algorithm is developed in Ibaraki et al. (2008) by assuming the inconvenience measure to be a nonnegative, convex, piecewise linear, time-dependent function.

Fu et al. (2008) acknowledge the need of a unified approach that model penalties associated with time windows. The variants modelled in Taillard et al. (1997), Koskosidis et al. (1992), Balakrishnan (1993), Chang and Russell (2004), and Fagerholt (2001) are all solved by a single Tabu search heuristic. Figliozzi (2010) propose an iterative route construction and improvement algorithm for the same variant and compares its results with Balakrishnan (1993), Fu et al. (2008) and Chang and Russell (2004). Taş et al. (2014b) study flexible time windows, similarly to Balakrishnan (1993), Chang and Russell (2004), Fu et al. (2008), Figliozzi (2010). The authors propose a Tabu search heuristic, in which a linear programming model defines the earliness and tardiness of arrival at the customers' locations.

Among the exact algorithms for VRPSTWs, it is worth referring to Qureshi et al. (2009). In this article, the authors solve by column generation a problem with semi-soft time windows, such as the problem in which penalizations are applied only for late arrival at the customers' locations and the maximum delay is bounded. Bhusiri et al. (2014) extend this algorithm to the variant in which both early and late arrival of a customer are penalized, but the arrival time is bounded in an outer time window. Liberatore et al. (2011) solves the VRPSTW with unbounded penalization of early and late arrival at the customers' locations using a BCP technique. Bettinelli et al. (2014) consider the same kind of time-window penalizations when solving a pickup and delivery routing problem with heterogeneous fleet. Taş et al. (2014a) solve a soft time windows problem, in which stochastic travel times are considered. A BCP algorithm is proposed to solve the problem to optimality.

Stochastic travel times are considered in Jabali et al. (2015) and Vareias et al. (2018). In Jabali et al. (2015), disruptions might occur on a leg of a route. The decision maker has to set suitable time buffers so that the drivers can reach customers on time even if a disruption occurs. A good trade-off between customer inconvenience and duration of the planned route has to be achieved. The authors propose a heuristic algorithm to sequence the customers and a linear programme to set buffers. Vareias et al. (2018) extend the problem of Jabali et al. (2015) considering both disruptions of continuous random duration on each arc and discrete travel times on each arc. An Adaptive Large Neighbourhood Search algorithm defines routes minimising the distance travelled, and then mathematical programming models set the customers’ time windows so that the sum of the expected overtime at the customers' locations, the duration of the routes and the length of the time windows are minimized.

Figure 2 presents a summary of the penalization functions presented in the literature. Light grey lines identify the (inner) time window and dark grey lines the maximum allowed earliness/tardiness (or the outer time window). When a single light grey line is present, only tardy arrival is admitted and penalized. Waiting time is represented with a dashed line (as in Balakrishnan 1993, Chang and Russell 2004, Fu et al. 2008, Figliozzi 2010, Taş et al. 2014b).

Penalizations have been modelled with a variety of functions in the literature to represent customer’s inconvenience. The most sophisticated penalizations involve five parameters per customer (i.e. Balakrishnan 1993, Chang and Russell 2004, Fu et al. 2008, Figliozzi 2010, Taş et al. 2014b) or even more for piecewise linear or convex functions (i.e. Dumas et al. 1990, Ibaraki et al. 2005,Ibaraki et al. 2008). These models are more flexible and rich. On the other hand, defining the penalization parameters for each customer and setting the relative weight of customer inconvenience is challenging for practitioners. Moreover, objective functions weighting routing costs and customer inconvenience suffer of typical drawbacks of weighted-sum multi objective optimization problems. Adjusting the weighting parameter between routing costs and customers inconvenience is often a time consuming task and this parameter often requires to be separately tuned for different instances.

Fig. 2
figure 2

Penalization functions

Full size image

3 Branch-and-cut-and-price algorithms

In what follows, we define the Opportunity Cost VRPSTW (OC-VRPSTW), by first introducing notation and recalling the definitions of the VRPSTW and of the VRPHTW.

A graph G(V, A) is given, where the set \(V = N \cup \{0\}\) is composed of a special vertex 0 representing the depot and a set of N customers. Non-negative weights \(t_{ij}\) and \(c_{ij}\) are associated with each arc \((i, j) \in A\) representing the traveling time and the transportation cost, respectively. Traveling times satisfy the triangle inequality. A positive integer demand \(d_i\) is associated with each vertex \(i \in N\) and Q is the capacity of each vehicle. The fleet is composed of K vehicles. A non-negative integer service time \(s_i\) and a time window \([a_i, b_i]\), defined by two non-negative integers, are also associated with each vertex \(i \in N\).

The VRTSTW asks to find a set of routes with cardinality at most |K|, visiting all customers exactly once and respecting time windows and vehicles’ capacity constraints. The objective is to minimize a combination of routing costs and customer inconvenience. In the VRPHTW, the vehicle has to wait until the opening of the time window \(a_i\), in case of early arrival at customer’s i location. However, both in the VRPHTW and in the VRPSTW, vehicles are allowed to wait at no cost before serving the customer.

In the OC-VRPSTW, the model assumes that the optimal routing cost of the underlying VRPHTW, \(z^*\), is known and is strictly positive. A cost saving is imposed by the planner as a maximum percentage \(\beta < 1\) of \(z^*\). The objective is to minimize the overall time windows violation. The model reads as follows:

$$\begin{aligned}&g_{\Theta } = \mathrm{minimize}{ }\sum _{r \in \Theta } v^r x^r, \end{aligned}$$
(1)
$$\begin{aligned}&\mathrm{s.t.} \sum _{r \in \Theta } f^r_i x^r \ge 1 \quad \forall i \in N, \end{aligned}$$
(2)
$$\begin{aligned}&\sum _{r \in \Theta } c^r x^r \le \beta \cdot z^*, \end{aligned}$$
(3)
$$\begin{aligned}&\sum _{r \in \Theta } x^r \le |K|, \end{aligned}$$
(4)
$$\begin{aligned}&x^r \in \{0,1\} \quad \forall r \in \Theta , \end{aligned}$$
(5)

where \(\Theta\) is the set of feasible routes in which the vehicle’s capacity is not exceeded, \(v^r\) is the overall time window violation of route r and each customer is served at most once. Constraints (2) impose that all customers are visited at least once; here, \(f^r_i\) represents the number of times route r visits customer i. Constraint (3) states that the routing cost must be not greater than a fraction of the cost of the optimal VRPHTW solution; here, \(c^r\) represents the routing cost of route r. Constraint (4) imposes that no more than |K| vehicles are used.

The routing cost improvement \(\beta\) is the only parameter required. Planners are likely to be comfortable defining parameter \(\beta\) as it directly relates to monetary savings, and alternative scenarios allow for a direct comparison between solutions in which customer convenience is more or less sacrificed in favour of routing cost savings.

4 Exact algorithms for the OC-VRPSTW

Model (1)–(5) contains a number of variables which grows exponentially with the size of the instance and cannot be dealt with explicitly. Therefore, to compute valid lower bounds, we solve the linear relaxation of the model recurring to a column generation procedure. To obtain feasible integer solutions we embed the column generation bounding procedure into an enumeration tree (Desaulniers et al. 2005; Vanderbeck and Wolsey 1996).

At each column generation iteration, the linear relaxation of the restricted master problem (RMP, i.e. the models (1)–(5) where a subset of variables is considered) is solved. We search for new columns with a negative reduced cost:

$$\begin{aligned} \overline{v}^r = v^r - \sum _{i \in N} f^r_i {\pi _{i}} - c^r \rho - \gamma , \end{aligned}$$
(6)

where \(\pi _i\) is the nonegative dual variable associated with the ith constraint of the set (2), \(\rho\) is the nonpositive dual variable associated with the threshold constraint (3) and \(\gamma\) is the nonpositive dual variable associated with constraint (4). The pricing problem can be modelled as a resource constrained elementary shortest path problem (RCESPP) and is solved by dynamic programming. In our implementation, we extend the algorithms presented in Righini and Salani (2006, 2008), Liberatore et al. (2011) and make use of some acceleration techniques presented in Salani and Vacca (2011).

After some preliminary computational experiments, we observed that the solution of models (1)–(5) required a substantially greater amount of computational time in comparison with the time required to solve the original counterpart without time windows violation. In some instances, the time required was of the order of several magnitudes higher. The reasons for this increased computational effort are the following:

  • The set of feasible columns is larger than in the corresponding VRPHTW, as it contains also routes violating time windows constraints.

  • For all routes r feasible for the corresponding VRPHTW instance \(v_r = 0\). This increases both the complexity of the column generation procedure and the pricing algorithm. In the dynamic programming algorithm, many more labels are non-dominated.

  • Proving the infeasibility of a node in the search tree, in particular with respect to constraint (3), is hard and requires computational effort. Indeed, a linear relaxation of the RMP may satisfy constraint (3), but no integral solution does.

Therefore, we propose an alternative formulation and an alternative exact solution algorithm based on bisection search inspired by the \(\epsilon\)-constraint method for multi-objective optimization.

At each iteration of the bisection search, we solve the models (7)–(11) which prescribes the minimization of the overall routing cost subject to a maximal permitted time windows violation. In the bisection search algorithm, the permitted time windows violation is then updated according to the value of the optimal solution of the model. Briefly: when the routing costs satisfy the savings prescribed by the planner, then the permitted time windows violation is reduced. When the routing costs do not satisfy the savings prescribed by the planner, then the permitted time windows violation is increased.

The model is solved with BCP and reads as follows:

$$\begin{aligned}&h_{\Theta } = \mathrm{minimize}{ }\sum _{r \in \Theta } c^r y^r, \end{aligned}$$
(7)
$$\begin{aligned}&\mathrm{s.t.} \sum _{r \in \Theta } f^r_i y^r \ge 1 \quad \forall i \in N, \end{aligned}$$
(8)
$$\begin{aligned}&\sum _{r \in \Theta } v^r y^r \le g_\mathrm{max}, \end{aligned}$$
(9)
$$\begin{aligned}&\sum _{r \in \Theta } y^r \le |K|, \end{aligned}$$
(10)
$$\begin{aligned}&y^r \in \{0,1\} \quad \forall r \in \Theta , \end{aligned}$$
(11)

where \(g_\mathrm{max}\) represents the maximal permitted time windows violation. Note that we model the overall time windows violation as the sum of violations of each selected route in constraint (9).

Problems (7)–(11) is defined over the same set of feasible routes \(\Theta\) as problem (1)–(5) and at each iteration of the bisection algorithm, in our implementation, we use a BCP algorithm, given that this is the most commonly employed algorithm to solve exactly routing problems with soft time windows. This problem can however be solved by any exact black box algorithm for the VRPSTW that can incorporate constraints (9). An advantage of the BCP framework over other implementations is that the set of feasible routes \(\Theta\) can be used as a warm start at each iteration of the bisection algorithm.

In the column generation process, the pricing problem searches for columns minimizing the following reduced cost:

$$\begin{aligned} \overline{c}^r = c^r - \sum _{i \in N} f^r_i \pi _i - v^r \psi - \gamma , \end{aligned}$$
(12)

where \(\pi _i\) is the nonegative dual variable associated with the ith constraint of the set (8), \(\psi\) is the nonpositive dual variable associated with the time windows violation (9) and \(\gamma\) is the nonpositive dual variable associated with constraint (10). The pricing problem associated with this formulation is equivalent to that studied by Liberatore et al. (2011), where the linear penalty for earliness and tardiness is adjusted by means of the dual variable of constraint (9). We choose, therefore, to exploit algorithms presented in Liberatore et al. (2011) and Salani and Vacca (2011). Relevant information about our implementation is reported in Sect. 4.1.

The overall exact algorithm is based on a bisection search on the value of the permitted violation \(g_\mathrm{max}\). If an optimal solution of (1)–(5) exists (denoted with \(g^*_{\Theta }\)), we prove that \(g_\mathrm{max}\) is either an upper or a lower bound to \(g^*_{\Theta }\). Let us denote with \(h^*_{\Theta }(g_\mathrm{max})\) the optimal solution of (7)–(11) associated with a given value of \(g_\mathrm{max}\).

Proposition 1

If \(h^*_{\Theta }(g_\mathrm{max}) > \beta \cdot z^*_{\Omega }\) then \(g_\mathrm{max}\) is a valid lower bound to \(g^*_{\Theta }\), if \(h^*_{\Theta }(g_\mathrm{max}) \le \beta \cdot z^*_{\Omega },\) then \(\sum _{r \in \Theta } v^r y^r\) is a valid upper bound to \(g^*_{\Theta }\).

Proof

We observe that the set of routes \(\Theta\) is the same for problems (1)–(5) and (7)–(11). The set of feasible solutions is determined in both problems by routes satisfying the same covering (2) and (8) and fleet (4) and (10) constraints. Therefore, the feasible sets of the two problems differ with respect to constraints (3) and (9) only.

Solutions for problems (7)–(11) with \(h^*_{\Theta }(g_\mathrm{max}) > \beta \cdot z^*_{\Omega }\) do not satisfy constraint (3) and are therefore infeasible for problem (1)–(5). To obtain a feasible solution for the original problems (1)–(5), the search space of (7)–(11) must be necessarily enlarged as \(h^*_{\Theta }(g_\mathrm{max})\) is the optimal solution of (7)–(11), i.e. no feasible solution with value strictly lower than \(h^*_{\Theta }(g_\mathrm{max})\) exists for the given \(g_\mathrm{max}\). Therefore, to enlarge the feasible set, the only possible action is to increase the value of \(g_\mathrm{max}\). This proves that \(g_\mathrm{max}\) is a valid lower bound to \(g^*_{\Theta }\). If \(h^*_{\Theta }(g_\mathrm{max}) \le \beta \cdot z^*_{\Omega }\), then the solution of (7)–(11) is feasible for (1)–(5) and therefore \(\sum _{r \in \Theta } v^r y^r\) is a valid upper bound to \(g^*_{\Theta }\). \(\square\)

The algorithm requires the existence of a feasible solution and the value of an upper bound \(g_\mathrm{UB}\) to \(g^*_{\Theta }\). To prove the existence of a feasible solution, the associated capacitated vehicle routing problem (CVRP), in which time windows are neglected, is solved. Assume that \(z^*_\mathrm{CVRP}\) is the optimal solution of the associated CVRP, if \(\beta \cdot z^* \ge z^*_\mathrm{CVRP}\) then a feasible solution to (1)–(5) exists.

We report in Algorithm 1 the pseudo code of the bisection algorithm.

figure a

At each iteration, the range of possible values for the violation of time windows \((g^{it}_{\mathrm{LB},\Theta }, g^{it}_{\mathrm{UB},\Theta })\) is halved. The algorithm stops when the gap between the lower and the upper bounds is less than \(\epsilon\). The value \(\epsilon\) is strictly positive and is determined using the instance data.

4.1 Branch-and-cut-and-price algorithm for problems (7)–(11)

We briefly recall the main features of our algorithm derived from Liberatore et al. (2011) and Salani and Vacca (2011) and literature referenced therein.

  • The algorithm iteratively solves the linear relaxation of problems (7)–(11) to compute valid lower bounds.

  • To build rapidly a representative set of routes \(\Theta\), several pricing algorithms of increasing complexity are devised: a greedy pricing, a randomized greedy pricing and a heuristic dynamic programming pricing. When the lower complexity pricing fails in finding new columns, the next is executed. If no column is produced, the exact pricing is solved and eventually the optimality is proven.

  • The exact pricing algorithm assigns states to each vertex: each state of vertex i represents a path from the source (i.e. the depot 0) to i. Each state has an associated resource consumption vector R and each component of R accounts for the consumption of a different resource along the path. R encodes the set of visited items as a binary vector which ensures paths elementarity. Each state has an associated cost C computed according to (12) which is represented as a piecewise linear function as described in Liberatore et al. (2011).

  • The exact pricing implements bidirectional search and decremental state space relaxation.

  • Dual space stabilization and valid 2-path inequalities are implemented (Rousseau et al. 2007).

  • Our branching scheme follows the following steps:

    • if the number of vehicles corresponding to the left hand side of constraint (10) is fractional, two children nodes are generated by rounding up and down the minimum and maximum number of vehicles used,

    • if there is an arc visited a fractional number of times, two children nodes are generated by rounding up and down the minimum and maximum number of times the arc is visited.

Implemented extensions with respect to known literature are:

  • The routes in \(\Theta\) are used to initialize the BCP algorithm. The pool of routes is then updated after each call to the BCP within Algorithm 1.

  • A new heuristic dynamic pricing algorithm has been devised: when a vehicle arrives at the location of customer i before the time windows opening time, two new states are generated. The first state models early visit decision, and the second state models the decision of waiting until the opening of the time window. Therefore, only two states are generated. Those two states are representative: the first state models the minimization of resource consumption (time) and the second the minimization of the penalty (time windows violation).

5 Computational results

We performed our experiments using the well-known Solomon’s data set (Solomon 1983). For 17 instances of classes R1 and RC1, we considered the first \(n=25\) customers. For each instance, we required a percentage improvement with respect to the nominal solution of 1, 5 and 10% (i.e. \(\beta\) equal to 0.99, 0.95, 0.90, respectively). The overall number of runs amounts therefore to 51. A time limit of 1 h was imposed on all runs. The computational time required to compute the reference value \(z^*\) of the underlying VRPHTW is not reported as it is negligible.

All tests were performed on a PC equipped with an Intel Core i7 2.67 GHz 2 Cores processor with 3 GB RAM. The branch-and-price-and-cut is coded in ANSI-C and the linear relaxation solver is IBM-Cplex 12.0.

We compare our results with those obtained with an exact method for the VRPSTW. We recall that in the VRPSTW the violation of time windows is permitted and penalized in the objective function. Each time unit of violation is penalized by a constant factor. To perform our comparison, we set the penalty for time windows violation equal to 1 as done in the tests reported by Liberatore et al. (2011). For the comparison, we executed the exact branch-and-price procedure over the same set of instances.

Table 1 illustrates the exact solution of both models (1)–(5) and (7)–(11) and it is organized as follows. Each row is dedicated to one instance and the name of the instance is given in the first column; three groups of three columns follow. Each group provides the results associated with a specific value of \(\beta\). Column \(g^*\) contains the opportunity cost (i.e. time windows violation) associated with the set cost saving. An asterisk (\(*\)) means that no feasible solution exists for the instance and the desired value of \(\beta\). Column t(s) contains the overall computational time required by the standard BCP algorithm, whereas column \(t'(s)\) provides information on the overall computational time required by the bisection algorithm. The last column \(z^*_{\Theta } (s)\) reports the overall computational time required by the algorithm for VRPSTW.

A dashed line \((-)\) in the cell related to the computational time means that the corresponding procedure did not converge within the time limit.

Table 1 Computational comparison between two exact algorithms for the OC-VRPSTW and VRPSTW with constant penalty
Full size table

The results in Table 1 show that the bisection algorithm was able to find an optimal solution or prove that no one exists for all instances, while the standard branch-and-price-and-cut procedure failed on 12 instances out of 51. Considering the instances solved by both algorithms, the bisection algorithm is on average faster than the standard-branch-and-price-and-cut. In many cases, the improvement is of two orders of magnitude. In few instances, the standard branch-and-price-and-cut is faster, but the order of magnitude of computational time is the same for the two algorithms. Our final observation is that infeasible instances are quickly detected by both algorithms.

For most instances, the computational effort required by the bisection algorithm is comparable with that of VRPSTW. We recall that the bisection algorithm solves to optimality a VRPSTW instance at each iteration. We observe that for some instances and for some settings of \(\beta ,\) the bisection algorithm is much slower. In particular, instance RC101 with \(\beta =99\) and \(\beta =95\) and instance R108 with \(\beta =95\) show convergence problems. We first note that convergence issues occur when the optimal violation is rather small (2.3 for instance R108, 3.4 and 4.3 for instance RC101). We also observe that, for these instances and for some iterations of the bisection algorithm, the linear relaxation of the master problems (7)–(11) is feasible for constraint (3), but no integer feasible solution exists for that constraint. This makes solving the associated VRPSTW particularly hard.

5.1 Comparison with VRPSTW

In this section, we present a comparison of OC-VRPSTW and VRPSTW from a managerial point of view: we are interested in the values of time windows violation and the corresponding value of the primary objective when a method based on soft-constraints is used, i.e. a linear combination of primary objective and time windows violation.

Results are summarized in Table 2 which is organized as follows: the first column contains the instance name followed by the optimal value without time windows violation \(z^*_{\Omega }\); the following two columns are dedicated to the optimal solution of VRPSTW and they contain the value of the violation of time windows, \(g_{\Theta }\) and the primary objective value, \(z_{\Theta }\). We recall that their sum is optimal for the model with soft time windows. Subsequent columns illustrate the minimal time windows violation, \(g^*_{\Theta }\), and the value of the routing cost objective corresponding to the optimal solution, \(z(g^*_{\Theta })\), for the opportunity cost approach (OC) with requested cost saving of 1, 5 and 10%. As above, when column \(g^*_{\Theta }\) contains an asterisk \((*)\), it means that the corresponding instance is infeasible.

We observe that the soft constraints method always produces a solution. For 3 out of 17 instances, the solution is the same as for the VRPHTW. For some other instances (e.g. r101 and r102), the time windows violation is larger than that necessary to obtain a 10% improvement over the optimal VRPHTW solution.

We recall that the reported solutions have been obtained by setting the same penalty to all customers. Different penalties would indeed lead to different solutions. This fluctuating behaviour of the algorithm is undesirable for planners. They cannot rely on these results as the same settings for the parameters lead to substantially different solutions in structurally similar instances.

Table 2 Comparison of VRPSTW with penalty 1 and OC-VRPSTW with \(\beta\) equal 99, 95 and 90%.
Full size table

The results reported in Table 2 are also plotted in Fig. 3. We report instances in which the solution of OC (\(\beta = 0.95\)) exists; therefore, a total of 14 instances are plotted. The x-axis reports normalized routing costs, and the y-axis standardized time window violations or customer inconvenience. Each dot type represents a different configuration: round dots, crossed round dots, diamonds and stars represent solutions to the VRPSTW, OC (\(\beta = 99\%\)), OC (\(\beta = 95\%\)) and OC (\(\beta = 90\%\)), respectively. We observe that solutions to the VRPSTW appear in the entire plot: some solutions have the lowest customer inconvenience and no routing savings (bottom right of the plot) and others the highest customer inconvenience and highest routing savings (top left of the plot). OC solutions are more clustered: solutions with \(\beta = 99\%\) are mostly in the bottom right corner of the plot (low savings, low violations), solutions with \(\beta = 90\%\) are mostly in the top centre of the plot (high savings, high violations), solutions with \(\beta = 95\%\) are less clearly clustered but are grouped in the central portion of the savings space.

Fig. 3
figure 3

Routing cost and customer inconvenience

Full size image

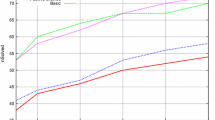
From the test bed, we selected instance R105 and conducted an in-depth analysis by solving OC with decreasing values of \(\beta\) ranging from 100 (no savings) to 83 (the highest possible saving for the instance). Results are reported in Table 3 where the first column is the required saving (1-\(\beta\)) with respect to the VRPHTW solution, the second column (\(g^*_{\Theta }\)) the optimal customer inconvenience, the third column (\(h(g^*_{\Theta })\)) the corresponding routing costs and the last column (\(\%\) Savings) the corresponding savings.

Results for the Instance R105 are also plotted in Fig. 4, where the customer inconvenience for subsequent 1% increases in routing savings is depicted. We plot the cumulative or overall customer inconvenience, the increase of customer inconvenience when an additional 1% routing saving is imposed, and the corresponding best fit lines (using the best fit polynomial line of order 2 in Excel). We observe a quasi-linear progression in customer inconvenience with increasing required savings. It is noticeable that savings of more than 16% substantially increase the overall customer inconvenience, and passing from a saving of 10–11% also increases quite substantially the customer inconvenience. Similar analyses conducted on other instances provide practitioners an appreciation of which are the worth opportunity costs for varying routing savings.

Table 3 Instance R105, customer inconvenience for decreasing values of \(\beta\)
Full size table
Fig. 4
figure 4

Instance R105, customer inconvenience as a function of the routing savings

Full size image

6 Conclusions

We introduced a new variant of the VRPSTW, in which practitioners are allowed to set a desired routing cost saving with respect to the VRPHTW solution. The opportunity cost of cheaper solutions is quantified by minimising the customer inconvenience due to time windows violations. This problem definition does not require practitioners to define a weighting coefficient between routing cost and time window violations, and allows for the analysis of alternative scenarios with increasing routing savings and decreasing customer satisfaction. Furthermore, customer dissatisfaction can be quantified with alternative measures (i.e. minimization of the maximum time window violations, minimization of the number of time window violations).

We propose two BCP algorithms. The second algorithm is embedded within a bisection framework and takes advantage of an easier pricing algorithm. Despite its iterative nature, this algorithm outperforms the first and it is capable of generating a larger number of optimal solutions.

Our results support the idea that BCP is an effective technique for solving complex routing problems exactly. Even if a “standard” implementation of the BCP algorithm may not seem adequate to solve the problem at hand (see for example model (1)–(5)), there may be an alternative way to exploit the effectiveness of BCP. Nesting a BCP within a bisection algorithm proved successful in our implementation. Even if our results are not sufficient to prove its general applicability and effectiveness, we think that this approach is worth considering for other problems as well.

Our computational results showcase that scenarios of decreasing routing cost and increasing time window violations can be easily obtained using smaller values of \(\beta\). The opportunity cost solutions obtained by iteratively decrementing \(\beta\) allow for an overview of the possible alternative solutions that can be obtained by prioritising routing cost versus customer inconvenience.