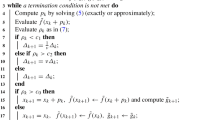On the construction of quadratic models for derivative-free trust-region algorithms

Abstract

We consider derivative-free trust-region algorithms based on sampling approaches for convex constrained problems and discuss two conditions on the quadratic models for ensuring their global convergence. The first condition requires the poisedness of the sample sets, as usual in this context, while the other one is related to the error between the model and the objective function at the sample points. Although the second condition trivially holds if the model is constructed by polynomial interpolation, since in this case the model coincides with the objective function at the sample set, we show that it also holds for models constructed by support vector regression. These two conditions imply that the error between the gradient of the trust-region model and the objective function is of the order of $\delta _k$, where $\delta _k$ controls the diameter of the sample set. This allows proving the global convergence of a trust-region algorithm that uses two radii, $\delta _k$ and the trust-region radius. Preliminary numerical experiments are presented for minimizing functions with and without noise.

1 Introduction

We consider the nonlinear programming problem

$$\begin{aligned} \begin{array}{ll} \text {minimize} &{} \ f(x)\\ \text {subject to} &{} x \in \Omega , \end{array} \end{aligned}$$

(1)

where $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ is a continuously differentiable function and $\Omega \subset {\mathbb {R}}^n$ is a non-empty closed convex set. Although the objective function is smooth, we assume its derivatives are not available.

We are interested in derivative-free trust-region methods, which have been applied to unconstrained problems by Conn et al. (1997, 2009a, b, c), Ferreira et al. (2015), Powell (2006, 2012), and Scheinberg and Toint (2010), to box-constrained problems by Powell (2009) and Gratton et al. (2011), to linearly constrained problems by Gumma et al. (2014) and Powell (2015), to convex constrained problems by Conejo et al. (2013), to general constrained problems by Bueno et al. (2013), Conejo et al. (2015), Conn et al. (1998), and Ferreira et al. (2016), and to composite non-smooth optimization by Grapiglia et al. (2016) and Garmanjani et al. (2016).

Derivative-free trust-region algorithms make use of quadratic models that approximate the objective function relying only on zero-order information. In this work, we discuss conditions on the models to ensure global convergence of an algorithm. These conditions are relaxed versions of classical hypotheses (Conn et al. 2009c) and will allow us to move beyond the polynomial interpolation models that are largely used in derivative-free frameworks (Conn et al. 2008a, b, 2009c; Powell 2006). The support vector regression (Drucker et al. 1996; Smola and Schölkopf 2004), which is a well-known machine learning technique, is a motivating framework for constructing the models which may have a superior performance on noisy problems. We state that not all practical and theoretical aspects of support vector regression have yet been explored here, but we show that this technique can be useful and theoretically justified.

We consider the following assumptions on the objective function.

A1

The function f is continuously differentiable, and $\nabla f$ is Lipschitz continuous with constant $L_g > 0$ in a sufficiently large open bounded domain ${\mathcal {X}}\subset {\mathbb {R}}^n$.

A2

The function f is bounded below in $\Omega$.

1.1 Structure of the paper

In Sect. 2, we propose a derivative-free trust-region algorithm which extends the ideas of Conejo et al. (2013) considering two radii, one that defines the trust region and another that controls the diameter of the sample set used to construct the trust-region models. The global convergence is proven under classical hypotheses on the problem and the assumption that the error between the gradient of the trust-region model and the objective function is of the order of $\delta _k$, where $\delta _k$ controls the diameter of the sample set. Section 3 shows that this assumption is implied by two conditions on the sample set, one on its geometry and another on the error between the trust-region model and the objective function at the points of this set. In Sect. 4, we prove that the first condition is fulfilled if the sample set is $\varLambda$-poised (Conn et al. 2009c) for some $\varLambda >0$. Section 5 shows that models constructed by quadratic interpolation or support vector regression satisfy the second condition. Numerical experiments are presented in Sect. 6.

1.2 Notation

Throughout the paper, the symbol $\Vert \cdot \Vert$ denotes the Euclidean norm and $B(x^k,r)=\{x\in {\mathbb {R}}^n\mid \Vert x-x^k\Vert \le r\}$.

2 Trust-region algorithm

In this section, we present a derivative-free trust-region algorithm based on Conejo et al. (2013) and we prove its global convergence under reasonable assumptions.

At each iteration $k \in {\mathbb {N}}$, we consider the current iterate $x^k \in \Omega$ and the quadratic model

$$\begin{aligned} m_k(x) = b_k + g_k^\top (x - x^k) + \dfrac{1}{2} (x - x^k)^\top H_k (x - x^k), \end{aligned}$$

(2)

where $b_k \in {\mathbb {R}}$, $g_k = \nabla m_k(x^k) \in {\mathbb {R}}^n$ and $H_k \in {\mathbb {R}}^{n \times n}$ is a symmetric matrix.

We define the stationarity measure at $x^k$ for the problem of minimizing the model $m_k$ over the set $\Omega$ by

$$\begin{aligned} \pi _k = \Vert P_\Omega (x^k - g_k) - x^k\Vert , \end{aligned}$$

where $P_\Omega$ denotes the orthogonal projection onto $\Omega$. Note that $x^*\in \Omega$ is stationary for the original problem (1) when

$$\begin{aligned} \Vert P_\Omega (x^* - \nabla f(x^*))-x^*\Vert = 0. \end{aligned}$$

Given the radius $\Delta _k > 0$, the trust-region computation solves approximately the subproblem

$$\begin{aligned} \begin{array}{ll} \text {minimize} &{} \ m_k(x^k + d)\\ \text {subject to} &{} x^k + d \in \Omega \\ &{} \Vert d\Vert \le \Delta _k. \end{array} \end{aligned}$$

(3)

We accept as an approximate solution of (3) any feasible direction $d^k$ satisfying the efficiency condition

$$\begin{aligned} m_k(x^k) - m_k(x^k + d^k) \ge \theta _1 \pi _k \min \left\{ \dfrac{\pi _k}{1 + \Vert H_k\Vert }, \Delta _k, 1\right\} , \end{aligned}$$

(4)

where $\theta _1 > 0$ is a constant independent of k. Similar conditions are common in trust-region approaches and used by several authors in different contexts as by Conn et al. (2000, 2009c), Nocedal and Wright (2006), and Gratton et al. (2011).

The point $x^k+d^k$ is accepted as the new iterate when the ratio between the actual and the predicted reductions

$$\begin{aligned} \rho _k = \dfrac{f(x^k) - f(x^k + d^k)}{m_k(x^k) - m_k(x^k + d^k)} \end{aligned}$$

(5)

is greater than or equal to a fixed constant $\eta > 0$. In this case, we define $x^{k+1} = x^k + d^k$ and repeat the process. Otherwise, the step $d^k$ is rejected and the radius $\Delta _k$ is reduced.

The model is updated at the beginning of each iteration, and its quality is controlled by a second radius $\delta _k>0$. We assume that the following assumption holds.

A3

There exists a constant $\kappa _m > 0$ such that, for all $k \in {\mathbb {N}}$,

$$\begin{aligned} \Vert \nabla f(x) - \nabla m_k(x) \Vert \le \kappa _m \delta _k \end{aligned}$$

for all $x \in {\mathcal {X}} \cap B(x^k, \delta _k)$.

Incorporating the radius $\delta _k$ is the main difference between our algorithm and the one proposed in Conejo et al. (2013), where it is proven that the radius $\Delta _k$ goes to zero. The motivation for such modification is the fact that, from a theoretical point of view, it is necessary that the term that controls the model quality converges to zero, but in practice it is desirable that the trust-region radius is as large as possible. The usage of two radii is not new. It was considered, for example, by Powell (2006, 2009), but without convergence analysis.

We present now the derivative-free trust-region algorithm.

When $\pi _k$ is small, the iterate is probably close to a solution of the problem of minimizing the model $m_k$ within the feasible set $\Omega$. On the other hand, if $\delta _k$ is large, we cannot guarantee that the model represents the objective function accurately enough. Hence, when $\delta _k > \beta \pi _k$, the radius $\delta _k$ is reduced in the attempt of finding a more accurate model. Although we could always set $\beta = 1$, this parameter might be used to balance the magnitude of $\pi _k$ and $\delta _k$, according to the problem.

2.1 Convergence analysis

We start the convergence analysis proving that the Hessian of the model is bounded.

Lemma 1

Suppose that Assumptions A1 and A3 hold. Then there exists $\kappa _H > 1$ such that, for all $k \in {\mathbb {N}}$,

$$\begin{aligned} \Vert H_k \Vert \le \kappa _H-1. \end{aligned}$$

Proof

Consider an arbitrary direction $d \in {\mathbb {R}}^n$ with $\Vert d\Vert = \delta _k$. By the definition of the model (2), the triangle inequality and the hypotheses we have that

$$\begin{aligned} \Vert H_k d \Vert= & {} \Vert \nabla m_k(x^k + d) - \nabla m_k(x^k) \Vert \\\le & {} \Vert \nabla m_k(x^k + d) - \nabla f(x^k + d) \Vert + \Vert \nabla f(x^k + d) - \nabla f(x^k) \Vert + \Vert \nabla f(x^k)\\&- \nabla m_k(x^k) \Vert \\\le & {} (2 \kappa _m + L_g ) \delta _k . \end{aligned}$$

Thus,

$$\begin{aligned} \Vert H_k \Vert = \max _{\Vert d\Vert = \delta _k} \left\| H_k \frac{d}{\Vert d\Vert } \right\| = \frac{1}{\delta _k} \max _{\Vert d\Vert = \delta _k} \Vert H_k d \Vert \le 2 \kappa _m + L_g. \end{aligned}$$

Defining $\kappa _H = 2 \kappa _m + L_g +1$, we complete the proof.

As a consequence of the previous lemma and Assumption A3, the Hypotheses H3 and H4 of Conejo et al. (2013) hold. Although the convergence analysis of Algorithm 1 is similar to the one presented in Conejo et al. (2013), the inclusion of the radius $\delta _k\le \Delta _k$ demands some modifications on the proofs that justify their presentation here.

Consider the following sets of indices

$$\begin{aligned} {\mathcal {S}} = \left\{ k \in {\mathbb {N}}\ | \ \rho _k \ge \eta \right\} \qquad \text {and} \qquad \overline{{\mathcal {S}}} = \left\{ k \in {\mathbb {N}}\ | \ \rho _k \ge \eta _1 \right\} . \end{aligned}$$

The set ${\mathcal {S}}$ is the set of successful iterations and $\overline{{\mathcal {S}}} \subset {\mathcal {S}}$.

The following lemma states that if the trust-region radius is small enough, then the iteration is successful.

Lemma 2

(Conejo et al. 2013, Lemma 3.1) Suppose that Assumptions A1 and A3 hold. Let $L_g$, $\kappa _m$, $\kappa _H$, and $\theta _1$ be the constants given in A1, A3, Lemma 1, and (4), respectively. Consider the set

$$\begin{aligned} {\mathcal {K}} = \left\{ k \in {\mathbb {N}}\ | \ \Delta _k \le \min \left\{ \dfrac{\pi _k}{\kappa _H}, \dfrac{(1 - \eta _1) \pi _k}{c}, \beta \pi _k, 1 \right\} \right\} , \end{aligned}$$

where $c = \dfrac{L_g + \kappa _m + \dfrac{\kappa _H}{2}}{\theta _1}$. If $k \in {\mathcal {K}}$, then $k \in \overline{{\mathcal {S}}}$.

From Assumption A3, we can see that the smaller $\delta _k$, the better the model locally represents the objective function. Thus, it is reasonable to expect that $\delta _k$ goes to zero. This is proven in the following lemma.

Lemma 3

Suppose that Assumptions A1–A3 hold. Then the sequence $\left\{ \delta _k \right\}$ converges to zero.

Proof

If $\overline{{\mathcal {S}}}$ is finite, from the mechanism of the algorithm, there exists $k_0 \in {\mathbb {N}}$ such that for all $k \ge k_0$, $\delta _{k+1} = \tau _1 \delta _k$. Thus, the sequence $\{\delta _k\}$ goes to zero. Henceforth, consider that $\overline{{\mathcal {S}}}$ is infinite. For any $k \in \overline{{\mathcal {S}}}$, we have that $\rho _k$ is computed and consequently, $\delta _k \le \beta \pi _k$. Using this, the definition of $\rho _k$, (4), Lemma 1 and the fact that $\delta _k \le \Delta _k$,

$$\begin{aligned} f(x^k) - f(x^{k+1}) \ge \displaystyle \eta _1 \theta _1 \pi _k \min \left\{ \dfrac{\pi _k}{\kappa _H},\Delta _k, 1\right\} \ge \displaystyle \eta \theta _1 \dfrac{\delta _k}{\beta }\min \left\{ \dfrac{\delta _k}{\beta \kappa _H},\delta _k, 1 \right\} . \end{aligned}$$

Once $\{f(x^k)\}$ is non-increasing by the mechanism of the algorithm and bounded below by Assumption A2, the left-hand side of the expression above goes to zero. Then,

$$\begin{aligned} \lim _{k \in \overline{{\mathcal {S}}}} \delta _k = 0. \end{aligned}$$

(6)

Consider the set

$$\begin{aligned} {\mathcal {U}} = \left\{ k \in {\mathbb {N}}\ | \ k \notin \overline{{\mathcal {S}}} \right\} . \end{aligned}$$

If ${\mathcal {U}}$ is finite, by (6) we have that $\displaystyle \lim \nolimits _{k \rightarrow \infty } \delta _k = 0$. Now suppose that ${\mathcal {U}}$ is infinite. For $k \in {\mathcal {U}}$, define $\ell _k$ as the last index in $\overline{{\mathcal {S}}}$ before k. By the algorithm, $\delta _k \le \tau _2 \delta _{\ell _k}$, which implies that

$$\begin{aligned} \lim _{k \in {\mathcal {U}}} \delta _k \le \tau _2 \lim _{k \in {\mathcal {U}}} \delta _{\ell _k} = \tau _2 \lim _{\ell _k \in \overline{{\mathcal {S}}}} \delta _{\ell _k}. \end{aligned}$$

By (6), it follows that $\displaystyle \lim \nolimits _{k \in {\mathcal {U}}} \delta _k = 0$, concluding the proof.

The next lemma shows that $\{\pi _k\}$ has a subsequence that converges to zero.

Lemma 4

Suppose that Assumptions A1–A3 hold. Then $\displaystyle \liminf \nolimits _{k \rightarrow \infty } \pi _k = 0.$

Proof

Suppose by contradiction that there exist $\varepsilon > 0$ and an integer $K > 0$ such that $\pi _k \ge \varepsilon$ for all $k \ge K$. Let $\eta _1$, $\beta$, $\kappa _H$, and c be the constants given in the algorithm and Lemmas 1 and 2. Take

$$\begin{aligned} \tilde{\Delta } = \min \left\{ \dfrac{\varepsilon }{\kappa _H}, \dfrac{(1 - \eta _1) \varepsilon }{c}, \beta \varepsilon , 1 \right\} . \end{aligned}$$

Consider $k \ge K$. If $\Delta _k \le \tilde{\Delta }$, by Lemma 2, $k \in \overline{{\mathcal {S}}}$ and thus $\Delta _{k+1} \ge \Delta _k$. It follows that the radius $\Delta _k$ can only decrease if $\Delta _k >\tilde{\Delta }$. In this case, if $\delta _k > \beta \pi _k$, we have that

$$\begin{aligned} \Delta _{k+1} \ge \delta _{k+1} = \tau _1 \delta _k > \tau _1 \beta \pi _k \ge \tau _1 \beta \varepsilon \ge \tau _1 \tilde{\Delta }. \end{aligned}$$

On the other hand, if $\delta _k \le \beta \pi _k$, by the algorithm

$$\begin{aligned} \Delta _{k+1} \ge \tau _1 \Delta _k > \tau _1 \tilde{\Delta }. \end{aligned}$$

In both cases, for all $k \ge K$,

$$\begin{aligned} \Delta _k \ge \min \left\{ \tau _1 \tilde{\Delta }, \Delta _K \right\} . \end{aligned}$$

(7)

Take $k \in \overline{{\mathcal {S}}}$ with $k \ge K$. By the definition of $\rho _k$ given in (5), the condition (4), the contradiction hypothesis, and (7), it follows that

$$\begin{aligned} f(x^k) - f(x^{k+1})\ge & {} \eta _1 \theta _1 \pi _k \min \left\{ \dfrac{ \pi _k}{\kappa _H},\Delta _k, 1 \right\} \\\ge & {} \eta _1 \theta _1 \varepsilon \min \left\{ \dfrac{\varepsilon }{\kappa _H}, \min \left\{ \tau _1 \tilde{\Delta }, \Delta _K \right\} , 1 \right\} . \end{aligned}$$

By Assumption A2, the sequence $\{ f(x^k) \}$ is bounded below, and since it is monotonically non-increasing, $f(x^k) - f(x^{k+1}) \rightarrow 0$. As the right-hand side of the inequality above is a positive constant, the set $\{ k \in \overline{{\mathcal {S}}} \mid k \ge K \}$ is finite. Thus, for all k sufficiently large, $\delta _k > \beta \pi _k$ or $\rho _k < \eta _1$. However, by Lemma 3, $\delta _k \rightarrow 0,$ and since $\pi _k \ge \varepsilon$ for all $k \ge K$, it follows that $\rho _k < \eta _1$ for all k sufficiently large, which implies that $\Delta _{k+1} = \tau _1 \Delta _k$. Consequently, $\Delta _k \rightarrow 0$, contradicting (7) and concluding the proof.

Assuming a sufficient decrease in the objective function, i.e., setting $\eta > 0$ in Algorithm 1, we prove that not only there exists a subsequence of $\{\pi _k\}$ converging to zero, but that the convergence prevails for the whole sequence.

Lemma 5

Suppose that Assumptions A1–A3 hold and $\eta > 0$. Then

$$\begin{aligned} \lim _{k \rightarrow \infty } \pi _k = 0. \end{aligned}$$

Proof

Suppose by contradiction that for some $\varepsilon >0$, the set

$$\begin{aligned} {\mathbb {N}}'=\left\{ k \in {\mathbb {N}}\ | \ \pi _k \ge \varepsilon \right\} \end{aligned}$$

is infinite. Given $k \in {\mathbb {N}}'$, consider $\ell _k$ the first index such that $\ell _k > k$ and $\pi _{\ell _k} \le {\varepsilon }/{2}.$ The existence of $\ell _k$ is ensured by Lemma 4. So, $\pi _k - \pi _{\ell _k} \ge \dfrac{\varepsilon }{2}.$ Using the definition of $\pi _k$, the triangle inequality, and the linearity and contraction properties of the projection operator, we have

$$\begin{aligned} \dfrac{\varepsilon }{2}\le & {} \Vert P_\Omega (x^k - g_k) - x^k \Vert - \Vert P_\Omega (x^{\ell _k} - g_{\ell _k}) - x^{\ell _k} \Vert \\\le & {} \Vert P_\Omega (x^k - g_k) - x^k - P_\Omega (x^{\ell _k} - g_{\ell _k}) + x^{\ell _k} \Vert \\\le & {} \Vert P_\Omega (x^k - x^{\ell _k}+g_{\ell _k}- g_k)\Vert +\Vert x^k-x^{\ell _k} \Vert \\\le & {} 2 \Vert x^k - x^{\ell _k}\Vert +\Vert g_k - g_{\ell _k}\Vert . \end{aligned}$$

Using again the triangle inequality and Assumptions A1 and A3, for $k \in {\mathbb {N}}'$,

$$\begin{aligned} \nonumber \dfrac{\varepsilon }{2}\le & {} 2\Vert x^k - x^{\ell _k}\Vert + \Vert g_k - \nabla f(x^k)\Vert + \Vert \nabla f(x^k) -\nabla f(x^{\ell _k})\Vert + \Vert \nabla f(x^{\ell _k}) - g_{\ell _k} \Vert \\\le & {} (2 + L_g) \Vert x^k - x^{\ell _k}\Vert + \kappa _m(\delta _k + \delta _{\ell _k}). \end{aligned}$$

(8)

On the other hand, by Lemma 3, $\delta _k \rightarrow 0$. Thus, there exists $k_0 \in {\mathbb {N}}$ such that for $k \ge k_0$, $\delta _k < \frac{\varepsilon }{8 \kappa _m}$, where $\kappa _m$ is the constant given in Assumption A3. Consequently, for $k \in {\mathbb {N}}'$, $k \ge k_0$,

$$\begin{aligned} \kappa _m (\delta _k + \delta _{\ell _k}) \le \dfrac{\varepsilon }{4}. \end{aligned}$$

(9)

Applying this in (8), it follows that

$$\begin{aligned} \Vert x^k - x^{\ell _k}\Vert \ge \dfrac{\varepsilon }{4 (2 + L_g)}. \end{aligned}$$

(10)

For $k \in {\mathbb {N}}'$, $k \ge k_0$, consider the set

$$\begin{aligned} C_k = \left\{ j \in {\mathcal {S}} | k \le j < \ell _k \right\} , \end{aligned}$$

which is non-empty. In fact, if $C_k=\emptyset$, then $x^k = x^{\ell _k}$, which means that $x^i \notin {\mathcal {S}}$ for $k \le i < \ell _k$. In this case, by Assumption A3,

$$\begin{aligned} \dfrac{\varepsilon }{2}\le & {} 2 \Vert x^k - x^{\ell _k}\Vert + \Vert g_k - g_{\ell _k}\Vert \\= & {} \Vert g_k - g_{\ell _k}\Vert \\\le & {} \Vert g_k - \nabla f(x^k) \Vert + \Vert \nabla f(x^{\ell _k}) - g_{\ell _k}\Vert \\\le & {} \kappa _m (\delta _k + \delta _{\ell _k}), \end{aligned}$$

which contradicts (9). So, by the definition of $C_k$, (4) and Lemma 1,

$$\begin{aligned} f(x^k) - f(x^{\ell _k}) = \sum _{j \in C_k} \left( f(x^j) - f(x^{j+1})\right) \ge \sum _{j \in C_k} \eta \theta _1 \pi _j \min \left\{ \dfrac{ \pi _j}{\kappa _H},\Delta _j, 1 \right\} . \end{aligned}$$

From the definition of $\ell _k$, we have that $\pi _j > \varepsilon /2$ for all $j \in C_k$. Thus,

$$\begin{aligned} f(x^k) - f(x^{\ell _k}) \ge \sum _{j \in C_k} \eta \theta _1 \dfrac{\varepsilon }{2} \min \left\{ \dfrac{\varepsilon }{2 \kappa _H},\Delta _j, 1 \right\} \ge \eta \theta _1 \dfrac{\varepsilon }{2} \min \left\{ \dfrac{\varepsilon }{2 \kappa _H}, \sum _{j \in C_k} \Delta _j, 1 \right\} . \end{aligned}$$

(11)

But, from (10),

$$\begin{aligned} \dfrac{\varepsilon }{4 (2 + L_g)} \le \Vert x^k - x^{\ell _k}\Vert \le \sum _{j \in C_k} \Vert x^j - x^{j+1}\Vert \le \sum _{j \in C_k} \Delta _j. \end{aligned}$$

So, as $\eta > 0$, it follows that the right-hand side of (11) is a positive constant. On the other hand, by Assumption A2, the sequence $\{ f(x^k) \}$ is bounded below, and by the algorithm, it is monotonically non-increasing. Consequently, $f(x^k) - f(x^{\ell _k}) \rightarrow 0$, which is a contradiction, completing the proof.

Now we present the main result of this section.

Theorem 1

Suppose that Assumptions A1–A3 hold. Then

• (i) If $\eta = 0$, $\displaystyle \liminf \nolimits _{k \rightarrow \infty } \Vert P_\Omega (x^k - \nabla f(x^k)) - x^k\Vert = 0$.

• (ii) If $\eta > 0$, $\displaystyle \lim \nolimits _{k \rightarrow \infty } \Vert P_\Omega (x^k - \nabla f(x^k)) - x^k\Vert = 0$.

Proof

By the triangle inequality, the projection operator properties, and Assumption A3, we have that

$$\begin{aligned}&\Vert P_\Omega (x^k - \nabla f(x^k)) -x^k\Vert \\&\quad = \Vert P_\Omega (x^k - \nabla f(x^k)) - P_\Omega (x^k - g_k) + P_\Omega (x^k - g_k) - x^k\Vert \\&\quad \le \Vert P_\Omega (x^k - \nabla f(x^k)) - P_\Omega (x^k - g_k)\Vert + \Vert P_\Omega (x^k - g_k) - x^k\Vert \\&\quad \le \Vert \nabla f(x^k) - g_k\Vert + \Vert P_\Omega (x^k - g_k) - x^k\Vert \\&\quad \le \kappa _m \delta _k + \pi _k. \end{aligned}$$

Using Lemmas 3, 4, and 5, we conclude the proof.

By Theorem 1, we conclude that if $\eta > 0$ and Algorithm 1 generates a sequence $\{x^k\}$ with an accumulation point $x^*$, then $x^*$ is a stationary point of first order (Conn et al. 2000). One way to ensure the existence of an accumulation point is to assume that the level set $\left\{ x \in {\mathbb {R}}^n \mid f(x)\le f(x^0) \right\}$ is bounded.

3 Ensuring Assumption A3

In this section, we discuss hypotheses in the construction of the models to ensure Assumption A3.

Let ${\mathcal {P}}_n^a$ be the space of polynomials of degree less than or equal to a in ${\mathbb {R}}^n$, whose dimension is

$$\begin{aligned} \dim {\mathcal {P}}_n^a = \frac{(n+a)!}{n! a!}. \end{aligned}$$

In particular, $\dim {\mathcal {P}}_n^1 = n + 1$ and $\dim {\mathcal {P}}_n^2 =(n+1) (n+2) / 2$.

Consider the set $X = \{x^0, x^1, \ldots , x^p\} \subset B(x^0, \delta )$, where $p=\dim {\mathcal {P}}_n^a - 1$. Assume that the function value in each point of X is known. Our task is to build a linear or quadratic model $m\in {\mathcal {P}}_n^a$ that approximates the function f in $B(x^0, \delta )$. The quality of the model depends on the geometry of the set X as we will discuss ahead.

In the linear case, $p=n$ and we define the matrix

$$\begin{aligned} L_{\ell } = \left( \begin{array}{c} (x^1 - x^0) ^\top \\ \vdots \\ (x^n - x^0)^\top \end{array} \right) = \left( \begin{array}{ccc} x^1_1 - x^0_1 &{} \cdots &{} x^1_n - x^0_n \\ \vdots &{} \ddots &{} \vdots \\ x^n_1 - x^0_1 &{} \cdots &{} x^n_n - x^0_n \end{array} \right) , \end{aligned}$$

(12)

and the scaled matrix

$$\begin{aligned} \widehat{L}_\ell = \frac{1}{\delta } L_\ell . \end{aligned}$$

(13)

In the quadratic case, $p=q$ with $q=(n^2+3n)/2$ and we define the matrix

$$\begin{aligned} L_q = \left( \begin{array}{c} \left( \bar{\varphi }(x^1 - x^0)\right) ^\top \\ \vdots \\ \left( \bar{\varphi }(x^q - x^0)\right) ^\top \end{array} \right) , \end{aligned}$$

(14)

where

$$\begin{aligned} \bar{\varphi }(x) = \left( x_1, x_2, \ldots , x_n, \frac{1}{2} x_1^2, x_1 x_2, x_1 x_3, \ldots , x_1 x_n, \frac{1}{2} x_2^2, \ldots , x_{n-1} x_n, \frac{1}{2} x_n^2\right) ^\top \end{aligned}$$

is the vector whose elements are the polynomials of the natural basis, as defined in Section 3.1 of Conn et al. (2009c). We also consider the scaled matrix

$$\begin{aligned} \widehat{L}_q = L_q \begin{pmatrix} D_\ell ^{-1} &{}\quad 0 \\ 0 &{}\quad D_q^{-1} \end{pmatrix}, \end{aligned}$$

(15)

where $D_\ell = \delta I_{n \times n}$ and $D_{q} = \delta ^2 I_{(q-n) \times (q-n)}$.

In the previous sections, we state some assumptions to prove convergence of a trust-region method. To achieve Assumption A3, assume that the following assumptions hold.

A4

If the model to be constructed is linear, then the matrix $L_{\ell }$ is non-singular and there exists a constant $\kappa _\ell >0$ such that $\Vert \widehat{L}_\ell ^{-1}\Vert \le \kappa _\ell$. If the model is quadratic, then the matrix $L_{q}$ is non-singular and there exists a constant $\kappa _q>0$ such that $\Vert \widehat{L}_q^{-1}\Vert \le \kappa _q$.

A5

There is a constant $\kappa \ge 0$ such that for all $x^i \in X\subset B(x^0, \delta )$,

$$\begin{aligned} |m(x^i) - f(x^i)| \le \kappa \delta ^2. \end{aligned}$$

Assumption A5 is weaker than asking that the model interpolates the objective function in the sample set, as required in theoretical analysis from Conn et al. (2009c). Our task is to prove a similar result assuming this weaker hypothesis. Before proving it, we state an auxiliary lemma proven in Dennis Jr and Schnabel (1996).

Lemma 6

(Dennis Jr and Schnabel 1996, Lemma 4.1.12) Assume that A1 holds. Then for all $x \in {\mathcal {X}}$ and $d\in {\mathbb {R}}^n$ such that $x + d \in {\mathcal {X}}$,

$$\begin{aligned} | f(x + d) - f(x) - \nabla f(x)^\top d | \le \frac{1}{2} L_g \Vert d\Vert ^2. \end{aligned}$$

Theorem 2

Suppose that Assumptions A1, A2, A4, and A5 hold. Then there exist constants $\kappa _H, \kappa _g, \kappa _f \ge 0$ such that, for all $x \in {\mathcal {X}} \cap B(x^0,\delta )$,

$$\begin{aligned} \Vert \nabla ^2 m(x) \Vert\le & {} \kappa _H, \end{aligned}$$

(16)

$$\begin{aligned} \Vert \nabla f(x) - \nabla m(x) \Vert\le & {} \kappa _g \delta \end{aligned}$$

(17)

and

$$\begin{aligned} | f(x) - m(x) | \le \kappa _f \delta ^2. \end{aligned}$$

(18)

Proof

There are two cases to be considered.

Linear case If the model is linear, it can be written as $m(x) = w^\top x + b$, with $w \in {\mathbb {R}}^n$ and $b \in {\mathbb {R}}$. In this case, we can set $\kappa _H=0$.

By the triangle inequality, the fact that $\nabla m(x) = w,$ Lemma 6 and Assumption A5, for all $i = 1, \ldots , n$, and $x \in {\mathcal {X}} \cap B(x^0,\delta )$,

$$\begin{aligned} \begin{array}{lll} \Vert \left( \nabla f(x^0) - \nabla m(x) \right) ^\top (x^i - x^0) \Vert &{} \le &{} | \nabla f(x^0)^\top (x^i - x^0) + f(x^0) - f(x^i)| + \\ &{} &{}+ |f(x^i) - w^\top x^i - b| + |w^\top x^0 + b - f(x^0) | \\ &{} \le &{}\dfrac{1}{2} L_g \delta ^2 + 2 \kappa \delta ^2. \end{array} \end{aligned}$$

By the definition of matrix $L_{\ell }$ in (12), we have

$$\begin{aligned} \left\| L_\ell \left( \nabla f(x^0){-}\nabla m(x) \right) \right\| \le \sqrt{n} \left\| L_\ell \left( \nabla f(x^0) {-} \nabla m(x) \right) \right\| _\infty \le \sqrt{n}\left( \frac{1}{2} L_g {+} 2 \kappa \right) \delta ^2. \end{aligned}$$

Then, by (13) and Assumption A4,

$$\begin{aligned} \left\| \nabla f(x^0) - \nabla m(x) \right\| \le \Vert L_\ell ^{-1}\Vert \left\| L_\ell \left( \nabla f(x^0) - \nabla m(x) \right) \right\| \le \kappa _\ell \sqrt{n} \left( \frac{1}{2} L_g + 2 \kappa \right) \delta . \end{aligned}$$

(19)

From the triangle inequality and Assumption A1, it follows that, for all $x \in {\mathcal {X}} \cap B(x^0,\delta )$,

$$\begin{aligned} \Vert \nabla f(x) - \nabla m(x) \Vert\le & {} \Vert \nabla f(x) - \nabla f(x^0)\Vert + \Vert \nabla f(x^0) - \nabla m(x)\Vert \\\le & {} \left( L_g + \kappa _\ell \sqrt{n} \left( \frac{1}{2} L_g + 2\kappa \right) \right) \delta . \end{aligned}$$

Defining $\kappa _g=L_g + \kappa _\ell \sqrt{n} \left( \frac{1}{2} L_g + 2\kappa \right)$, we obtain (17).

By the Taylor expansion of m around $x^0,$ the triangle inequality, Lemma 6, Assumption A5, the Cauchy–Schwarz inequality and (19), we can see that, for all $x \in {\mathcal {X}} \cap B(x^0,\delta )$,

$$\begin{aligned} | f(x) - m(x) |\le & {} |f(x) - f(x^0) - \nabla f(x^0)^\top (x - x^0)| + |f(x^0) - m(x^0)|\\&|\left( \nabla f(x^0) - \nabla m(x^0)\right) ^\top (x - x^0)|\\\le & {} \left( \frac{1}{2} L_g + \kappa + \left( \frac{1}{2} L_g + 2 \kappa \right) \sqrt{n} \kappa _\ell \right) \delta ^2. \end{aligned}$$

Defining $\kappa _f = \frac{1}{2} L_g + \kappa + \left( \frac{1}{2} L_g + 2 \kappa \right) \sqrt{n} \kappa _\ell$, we obtain (18).

Quadratic case If the model is quadratic, for all $i = 0,1, \ldots , q$ and for all $x \in {\mathcal {X}} \cap B(x^0,\delta )$,

$$\begin{aligned} m(x^i) = m(x) + \nabla m(x)^\top (x^i - x) + \frac{1}{2} (x^i - x)^\top H (x^i - x) \end{aligned}$$

(20)

with $H\in {\mathbb {R}}^{n\times n}$ symmetric.

By the mean value theorem, for all $i = 0,1, \ldots , q$, there exists $y^i \in [x^0, x^i] \subset B(x^0, \delta )$ such that

$$\begin{aligned} f(x^i) = f(x^0) + \nabla f(y^i)^\top (x^i - x^0). \end{aligned}$$

Therefore, by (20),

$$\begin{aligned} m(x^i) - f(x^i)= & {} m(x) + \nabla m(x)^\top (x^i - x) + \frac{1}{2} (x^i - x)^\top H(x^i - x) - f(x^0)\nonumber \\&- \nabla f(y^i)^\top (x^i - x^0), \end{aligned}$$

(21)

for all $i = 0,1, \ldots , q$.

Taking $i = 0$ in (21) and subtracting from (21), for $i = 1,...,q$, we have that

$$\begin{aligned}&m(x^i) - f(x^i) + f(x^0) - m(x^0) + \nabla f(y^i)^\top (x^i - x^0)\\&\quad =\nabla m(x)^\top (x^i - x^0) + \frac{1}{2} (x^i - x)^\top H (x^i - x) - \frac{1}{2} (x^0 - x)^\top H (x^0 - x)\\&\quad = \nabla m(x)^\top (x^i - x^0) + \frac{1}{2} (x^i - x^0)^\top H (x^i - x^0) - (x^i - x^0)^\top H (x - x^0). \end{aligned}$$

Subtracting $\nabla f(x)^\top (x^i - x^0)$ on both sides, we get

$$\begin{aligned}&m(x^i) - f(x^i) + f(x^0) - m(x^0) + (\nabla f(y^i) - \nabla f(x))^\top (x^i - x^0) \\&\quad = \left( \nabla m(x) - \nabla f(x) - H (x - x^0) + \frac{1}{2} H (x^i - x^0) \right) ^\top (x^i - x^0). \end{aligned}$$

By the triangle inequality, the Cauchy–Schwarz inequality, and Assumptions A1 and A5, we have that, for all $x \in {\mathcal {X}} \cap B(x^0,\delta )$, and for $i = 1, \ldots , q$,

$$\begin{aligned} \left| \left( \nabla m(x) - \nabla f(x) - H (x - x^0) + \frac{1}{2} H (x^i - x^0) \right) ^\top (x^i - x^0) \right| \le 2(\kappa + L_g) \delta ^2, \end{aligned}$$

since $\Vert y^i - x\Vert \le 2 \delta$. Defining

$$\begin{aligned} r^g(x) = \nabla m(x) - \nabla f(x) - H (x - x^0) \end{aligned}$$

(22)

and $r^H(x)$ as a vector in ${\mathbb {R}}^{q-n}$ that stores the elements $H_{kk}$, $k = 1, \ldots , n$ and $H_{k\ell }$, $1 \le \ell < k \le n$, from the definition of $L_g$ in (14), it follows that

$$\begin{aligned} \left\| L_q \begin{pmatrix} r^g(x) \\ r^H(x) \end{pmatrix} \right\| \le \sqrt{q} \left\| L_q \begin{pmatrix} r^g(x) \\ r^H(x) \end{pmatrix} \right\| _\infty \le 2\sqrt{q} (\kappa + L_g) \delta ^2. \end{aligned}$$

Using (15) and Assumption A4,

$$\begin{aligned} \left\| \begin{pmatrix} D_\ell r^g(x) \\ D_{q} r^H(x) \end{pmatrix} \right\|\le & {} \left\| \widehat{L}_q^{-1} \right\| \; \left\| \widehat{L}_q \begin{pmatrix} D_\ell r^g(x) \\ D_{q} r^H(x) \end{pmatrix} \right\| = \left\| \widehat{L}_q^{-1} \right\| \; \left\| L_q \begin{pmatrix} r^g(x) \\ r^H(x) \end{pmatrix} \right\| \\\le & {} 2 \kappa _q \sqrt{q} (\kappa + L_g) \delta ^2. \end{aligned}$$

Consequently,

$$\begin{aligned} \Vert r^g(x) \Vert \le \Vert D_\ell ^{-1} \Vert \Vert D_\ell r^g(x) \Vert \le 2 \kappa _q \sqrt{q}(\kappa + L_g) \delta , \end{aligned}$$

(23)

and

$$\begin{aligned} \left\| H \right\| \le \left\| H \right\| _F \le \sqrt{2} \Vert r^H(x) \Vert \le \sqrt{2} \Vert D_q^{-1} \Vert \Vert D_q r^H(x) \Vert \le 2\kappa _q \sqrt{2q} (\kappa + L_g) . \end{aligned}$$

(24)

Defining $\kappa _H = 2 \kappa _q \sqrt{2q} (\kappa + L_g)$, we obtain (16).

By (22), (23), and (24),

$$\begin{aligned} \Vert \nabla m(x) - \nabla f(x) \Vert \le \Vert r^g(x)\Vert + \left\| H\right\| \Vert x - x^0\Vert \le 2 \kappa _q \sqrt{q} (1 +\sqrt{2})(\kappa + L_g) \delta . \end{aligned}$$

Defining $\kappa _g = 2 \kappa _q \sqrt{q} (1 +\sqrt{2})(\kappa + L_g),$ we obtain (17).

Finally, note that, for all $x \in {\mathcal {X}} \cap B(x^0,\delta )$,

$$\begin{aligned} m(x) = m(x^0) + \nabla m (x^0)^\top (x - x^0) + \frac{1}{2} (x - x^0)^\top H (x - x^0). \end{aligned}$$

Thus, by the triangle inequality, the Cauchy–Schwarz inequality, Lemma 6, and Assumption A5,

$$\begin{aligned} |f(x) - m(x)|\le & {} |f(x) - f(x^0) - \nabla f(x^0)^\top (x - x^0)| + |f(x^0) - m(x^0)| \\&+\,|\left( \nabla f(x^0) - \nabla m(x^0) \right) ^\top (x - x^0)| + \frac{1}{2} |(x - x^0) H (x - x^0)|.\\\le & {} \left( \frac{1}{2} L_g + \kappa +\kappa _q \sqrt{q}(\kappa + L_g) (2 + 3\sqrt{2})\right) \delta ^2. \end{aligned}$$

Defining $\kappa _f =\frac{1}{2} L_g + \kappa +\kappa _q \sqrt{q}(\kappa + L_g) (2 + 3\sqrt{2}),$ we obtain (18), which concludes the proof.

Theorem 2 states that if the function f satisfies A1–A2, Assumptions A4 and A5 imply A3. Thus, we show that the quadratic model provides sufficient first-order accuracy. It is worth mentioning that it is possible to prove second-order error bounds for the quadratic models, similarly to Theorem 3.16 of Conn et al. (2009c), if A4 and A5 are made appropriately stronger. However, we do not focus on the second-order error bounds here, because we do not need them for our first-order convergence results. In the next sections, we will discuss how A4 and A5 can be ensured.

4 Sample set geometry

The main task of this section is to establish conditions on the sample set to ensure Assumption A4. First we define a measure of poisedness for a set of points.

Definition 1

(Conn et al. 2009c, Definition 3.6) Let $\phi = \{\phi _0(x), \phi _1(x), \ldots , \phi _p(x)\}$ be a basis in ${\mathcal {P}}_n^a$ and consider $\varLambda > 0$. A set $X =\{x^0, \ldots , x^p\} \subset {\mathcal {X}}$ is $\varLambda$-poised in $B(x^0,\delta )$ with respect to the base $\phi$ if for each $x \in B(x^0,\delta )$ there exists $\lambda (x) \in {\mathbb {R}}^{p+1}$ such that

$$\begin{aligned} \sum _{i=0}^p \lambda _i(x) \phi _j(x^i) = \phi _j(x) \quad \text {for all}\quad j=0,\ldots ,p, \qquad \text {with} \qquad \Vert \lambda (x)\Vert _\infty \le \varLambda . \end{aligned}$$

Note that these conditions can be written as

$$\begin{aligned} M(\phi ,X)^\top \lambda (x) = \phi (x) \qquad \text {with} \qquad \Vert \lambda (x)\Vert _{\infty } \le \varLambda , \end{aligned}$$

(25)

where

$$\begin{aligned} M(\phi , X) = \left( \begin{array}{ccccc} \phi _0(x^0) &{} \phi _1(x^0) &{} \phi _2(x^0) &{} \cdots &{} \phi _p(x^0) \\ \phi _0(x^1) &{} \phi _1(x^1) &{} \phi _2(x^1) &{} \cdots &{} \phi _p(x^1) \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ \phi _0(x^p) &{} \phi _1(x^p) &{} \phi _2(x^p) &{} \cdots &{} \phi _p(x^p) \end{array} \right) \quad \text {and}\quad \phi (x) = \left( \begin{array}{c} \phi _0(x) \\ \phi _1(x) \\ \vdots \\ \phi _p(x) \end{array} \right) . \end{aligned}$$

The definition of $\varLambda$-poisedness is independent of the choice of the basis. In fact, given $[I]_A^B$ the change in basis matrix from $\phi ^A$ to $\phi ^B$, the solution $\lambda (x)$ of (25) does not depend of the basis $\phi$, once

$$\begin{aligned} M(\phi ^A,X)^\top \lambda (x) = \phi ^A(x) \Rightarrow [I]_A^B M(\phi ^A,X)^\top \lambda (x) = [I]_A^B \phi ^A(x) \end{aligned}$$

which implies that $M(\phi ^B,X)^\top \lambda (x) = \phi ^B(x).$

The poisedness constant $\varLambda$ does not depend on the scaling of the sample set and is invariant with respect to shifts of coordinates (Conn et al. 2009c, Lemmas 3.8 and 3.9).

Now we state an auxiliary lemma.

Lemma 7

(Conn et al. 2009c, Lemma 3.13) Let $v \in {\mathbb {R}}^n$ be a unitary right singular vector corresponding to the largest singular value of a non-singular matrix $A \in {\mathbb {R}}^{n \times n}$. Then, for any vector $z \in {\mathbb {R}}^n$,

$$\begin{aligned} |v^\top z| \Vert A\Vert \le \Vert Az\Vert . \end{aligned}$$

The following result ensures that Assumption A4 holds when the model to be constructed is linear.

Lemma 8

Let $X =\{x^0, x^1, \ldots , x^n\}$ be a $\varLambda$-poised set in $B(x^0, \delta )$ with respect to the basis $\phi$ in ${\mathcal {P}}_n^1$ and $\widehat{L}_\ell$ be the matrix defined in (13). Then

$$\begin{aligned} \Vert \widehat{L}_\ell ^{-1}\Vert \le \varLambda \sqrt{n}. \end{aligned}$$

Proof

Consider v a unitary right singular vector of $\widehat{L}_\ell ^{-1}$ associated with the largest singular value $\sigma _1$. There exists a unitary vector $u \in {\mathbb {R}}^n$ such that $\widehat{L}_\ell ^{-1} v = \sigma _1 u$. Consequently,

$$\begin{aligned} \Vert \widehat{L}_\ell ^{-1} v\Vert = \sigma _1 \Vert u\Vert = \sigma _1 = \Vert \widehat{L}_\ell ^{-1}\Vert . \end{aligned}$$

(26)

Since the $\varLambda$-poisedness does not depend on the scaling of the sample set and is invariant with respect to a shift of coordinates, it follows that

$$\begin{aligned} \widehat{X} = \left\{ 0 , \frac{x^1 - x^0}{\delta }, \ldots , \frac{x^n - x^0}{\delta } \right\} \end{aligned}$$

is $\varLambda$-poised in B(0, 1). So there exists $\lambda (v) \in {\mathbb {R}}^n$ with $\Vert \lambda (v)\Vert _{\infty } \le \varLambda$ such that $\widehat{L}_\ell \lambda (v) = v$. Thus $\lambda (v) = \widehat{L}_\ell ^{-1} v.$ Using this, (26) and the fact that X is a $\varLambda$-poised set, we have

$$\begin{aligned} \Vert \widehat{L}_\ell ^{-1}\Vert = \Vert \lambda (v)\Vert \le \sqrt{n} \Vert \lambda (v)\Vert _{\infty } \le \varLambda \sqrt{n}, \end{aligned}$$

which concludes the proof.

To prove a similar result for the quadratic case, we first state an auxiliary lemma.

Lemma 9

(Conn et al. 2009c, Lemma 6.7) Let $v^\top \bar{\phi }(x)$ be a quadratic polynomial, where $\Vert v\Vert _\infty = 1$ and $\bar{\phi }$ is the natural basis in ${\mathcal {P}}_n^2$. Then

$$\begin{aligned} \max _{x \in B(0,1)} |v^\top \bar{\phi }(x)| \ge \frac{1}{4}. \end{aligned}$$

Given $\bar{v} \in {\mathbb {R}}^{q+1}$ with $\Vert \bar{v}\Vert = 1$, there exist $\beta \in (0, \sqrt{q+1})$ and $v\in {\mathbb {R}}^{q+1}$ such that $\Vert v\Vert _\infty = 1$ and $v = \beta \bar{v}$. Then, by Lemma 9,

$$\begin{aligned} \max _{x \in B(0,1)} |\bar{v}^\top \bar{\phi }(x)| = \max _{x \in B(0,1)} \frac{1}{\beta } |v^\top \bar{\phi }(x)| \ge \frac{1}{\sqrt{q+1}} \max _{x \in B(0,1)} |v^\top \bar{\phi }(x)| \ge \frac{1}{4\sqrt{q+1}}. \end{aligned}$$

(27)

The following result ensures that the Assumption A4 holds when the model to be constructed is quadratic.

Lemma 10

Let $X =\{x^0, x^1, \ldots , x^q\}$ be a $\varLambda$-poised set in $B(x^0, \delta )$ with respect to the basis $\phi$ in ${\mathcal {P}}_n^2$ and $\widehat{L}_q$ be the matrix defined in (15). Then,

$$\begin{aligned} \Vert \widehat{L}_q^{-1}\Vert \le 4 \varLambda \sqrt{(q + 1)^3} . \end{aligned}$$

Proof

Consider $\widehat{X} = \left\{ 0, \frac{x^1 - x^0}{\delta }, \ldots , \frac{x^q - x^0}{\delta } \right\}$ which is $\varLambda$-poised in B(0, 1) with respect to $\bar{\phi }$ the natural basis in ${\mathcal {P}}_n^2$. Consider also $\widehat{M} = \widehat{M}(\bar{\phi },\widehat{X})$ the matrix of the linear system in (25) and $L_q$ defined in (15). Then

$$\begin{aligned} \widehat{M} = \begin{pmatrix} 1 &{}\quad 0 \\ e &{}\quad \widehat{L}_q \end{pmatrix} \qquad \text {and}\qquad \widehat{M}^{-1} = \begin{pmatrix} 1 &{}\quad 0 \\ -\widehat{L}_q^{-1}e &{}\quad \widehat{L}_q^{-1} \end{pmatrix}. \end{aligned}$$

By the equivalence between the Frobenius and the Euclidean norms,

$$\begin{aligned} \Vert \widehat{L}_q^{-1}\Vert \le \Vert \widehat{L}_q^{-1}\Vert _F \le \Vert \widehat{M}^{-1}\Vert _F \le \sqrt{q + 1} \Vert \widehat{M}^{-1}\Vert . \end{aligned}$$

(28)

For each $x \in B(0,1)$, the solution $\lambda (x) \in {\mathbb {R}}^{q+1}$ of (25) satisfies

$$\begin{aligned} \varLambda \ge \Vert \lambda (x)\Vert _\infty \ge \frac{1}{\sqrt{q+1}} \Vert \lambda (x)\Vert = \frac{1}{\sqrt{q+1}} \Vert \widehat{M}^{-\top } \bar{\phi }(x)\Vert . \end{aligned}$$

Let $\bar{v}$ be a unitary right singular vector associated with the largest singular value of $\widehat{M}^{-\top }$. Consider $x \in {\mathbb {R}}^n$ the maximizer of $|\bar{v}^\top \bar{\phi }(x)|$ in B(0, 1). By the inequality above, Lemma 7 and (27),

$$\begin{aligned} \sqrt{q+1} \; \varLambda \ge \Vert \widehat{M}^{-\top } \bar{\phi }(x)\Vert \ge |\bar{v}^\top \bar{\phi }(x)| \Vert \widehat{M}^{-\top }\Vert \ge \frac{1}{4 \sqrt{q+1}} \Vert \widehat{M}^{-1}\Vert . \end{aligned}$$

By (28),

$$\begin{aligned} \Vert \widehat{L}_q^{-1}\Vert \le \sqrt{q + 1} \Vert \widehat{M}^{-1}\Vert \le 4\varLambda \sqrt{(q + 1)^3}, \end{aligned}$$

which concludes the proof.

When the sample set is $\varLambda$-poised, Lemmas 8 and 10 ensure Assumption A4 in the linear and quadratic case, respectively.

5 Model building

In this section, we discuss techniques to construct the models in derivative-free context which ensure Assumption A5. The standard one is polynomial interpolation (Conn et al. 2008a, b, 2009b, c; Powell 2002, 2006, 2008, 2009, 2012), which trivially satisfies the hypothesis. Alternatively, the models can be constructed by support vector regression (Drucker et al. 1996), as we will see in details later in this section.

5.1 Polynomial interpolation

Let $\phi$ be a basis of the space ${\mathcal {P}}_n^a$ of polynomials with degree less than or equal to a in ${\mathbb {R}}^n$, which dimension is $s+1$. As any polynomial $m \in {\mathcal {P}}_n^a$ can be written as a linear combination of the elements of $\phi$, we have that

$$\begin{aligned} m(x) = \sum _{j=0}^s {\mu _j \phi _j(x)} = \mu ^\top \phi (x), \end{aligned}$$

where $\mu = (\mu _0, \mu _1, \ldots , \mu _s)^\top$ is a vector in ${\mathbb {R}}^{s+1}$ and $\phi (x) = (\phi _0(x), \ldots , \phi _s(x))^\top$ is the vector with the elements of $\phi$.

We say that m interpolates the function f at $\bar{x}$ when $m(\bar{x}) = f(\bar{x})$. If $m \in {\mathcal {P}}_n^a$ interpolates f in the set $X = \{x^0, x^1, \ldots , x^p\} \subset {\mathbb {R}}^n$, then the coefficients $\mu _0, \ldots , \mu _s$ can be found by the interpolation conditions

$$\begin{aligned} m(x^i) = \sum _{j=0}^s \mu _j \phi _j (x^i) = f(x^i), \quad i =0, \ldots , p, \end{aligned}$$

which can be written as the linear system

$$\begin{aligned} M(\phi ,X) \mu _{\phi } = f(X), \end{aligned}$$

(29)

where

$$\begin{aligned} M(\phi ,X)= & {} \left( \begin{array}{cccc} \phi _0(x^0) &{} \phi _1(x^0) &{} \cdots &{} \phi _s(x^0) \\ \phi _0(x^1) &{} \phi _1(x^1) &{} \cdots &{} \phi _s(x^1) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \phi _0(x^p) &{} \phi _1(x^p) &{} \cdots &{} \phi _s(x^p) \end{array} \right) ,\\ \mu _{\phi }= & {} \left( \begin{array}{c} \mu _0 \\ \mu _1 \\ \vdots \\ \mu _s \end{array} \right) \quad \text { and } \quad f(X) = \left( \begin{array}{c} f(x^0) \\ f(x^1) \\ \vdots \\ f(x^p) \end{array} \right) . \end{aligned}$$

The set X is said poised for polynomial interpolation when the linear system (29) has a unique solution. This occurs if, and only if, $p = s$ and the matrix $M(\phi ,X)$ is non-singular. Since all bases in a finite-dimensional vector space are equivalent, the poisedness is independent of the choice of the basis $\phi$. Some authors call a poised set for polynomial interpolation as unisolvent set (Quarteroni et al. 2007).

It is easy to see that a set X that is $\varLambda$-poised by Definition 1 is also poised for polynomial interpolation and that interpolation models satisfy Assumption A5. Therefore, polynomial interpolation in $\varLambda$-poised sets can be used to construct the models in the derivative-free trust-region algorithm presented in Sect. 2.

5.2 Support vector regression

We present an alternative way to build models for derivative-free trust-region methods. The idea is to construct an approximation of the function f, from a sample set $X=\{x^0,\ldots ,x^p\}$, by using the technique of support vector machines developed for pattern classification by Vapnik (1998) and extended to regression by Drucker et al. (1996).

5.2.1 Linear support vector regression

In this section, we discuss how to determine $w\in {\mathbb {R}}^n$ and $b\in {\mathbb {R}}$ for constructing a linear model $m(x) = w^\top x + b$ that approximates the function f within $\varepsilon > 0$ accuracy, if possible. Ideally, we would like to solve the following convex quadratic optimization problem

$$\begin{aligned} \begin{array}{cll} \underset{(w,b)}{\text {minimize}} &{} \dfrac{1}{2} w^\top w &{}\\ \text {subject to} &{} f(x^i) - w^\top x^i - b \le \varepsilon , &{}i = 0, \ldots , p \\ &{} w^\top x^i + b - f(x^i) \le \varepsilon ,\quad &{}i = 0, \ldots , p. \end{array} \end{aligned}$$

However, since this problem does not always have a feasible solution, we allow some error and penalize it in the objective function. Thus, as presented in Section 9.1 by Schölkopf and Smola (2002), we consider the problem

$$\begin{aligned} \begin{array}{cll} \underset{(w,b,\xi ,\xi ')}{\text {minimize}} &{} \dfrac{1}{2} w^\top w + C \displaystyle \sum _{i=0}^p \left( \xi _i + \xi _i' \right) &{} \\ \text {subject to} &{} f(x^i) - w^\top x^i - b \le \varepsilon + \xi _i, \qquad &{} i = 0, \ldots , p\\ &{} w^\top x^i + b - f(x^i) \le \varepsilon + \xi _i', \qquad &{} i = 0, \ldots , p\\ &{} \xi _i, \xi _i' \ge 0, &{} i = 0, \ldots , p, \end{array} \end{aligned}$$

(30)

where $\xi ,\xi '\in {\mathbb {R}}^p$ are the error vectors and $C>0$ is the penalty parameter. If $\xi$ and $\xi '$ are null, then m is considered an $\varepsilon$-approximation of f in X.

The dual problem of (30) is given by

$$\begin{aligned} \begin{array}{cl} \underset{z}{\text {minimize}} &{} \dfrac{1}{2} z^\top Q z + v^\top z \\ \text {subject to} &{} Az = 0 \\ &{} 0 \le z \le C, \end{array} \end{aligned}$$

(31)

where

$$\begin{aligned} Q = \left( \begin{array}{cc} PP^\top &{} -PP^\top \\ -PP^\top &{} PP^\top \end{array} \right) \quad \text {with} \quad P = \left( \begin{array}{c} (x^0)^\top \\ (x^1)^\top \\ \vdots \\ (x^p)^\top \end{array} \right) \quad \text {and} \quad v = \left( \begin{array}{c} - f(P) + \varepsilon e \\ f(P) + \varepsilon e \end{array} \right) \end{aligned}$$

(32)

and $A = \left( -e^\top , e^\top \right)$ with $e = \left( 1, 1, \ldots , 1 \right) ^\top$.

As suggested in Schölkopf and Smola (2002), from the dual solution $z^* = (\alpha , \alpha ')$, with $\alpha ,\alpha '\in {\mathbb {R}}^p$, we compute w and b that define the model as

$$\begin{aligned} w = P^\top (\alpha - \alpha ') \end{aligned}$$

and

$$\begin{aligned} b = f(x^i) - w^\top x^i - \varepsilon \qquad \text {or}\qquad b = f(x^j) - w^\top x^j + \varepsilon \end{aligned}$$

for any $i,j \in \{1, \ldots , p\}$ such that $0< \alpha _i,\alpha '_j < C$.

5.2.2 Quadratic support vector regression

For building a quadratic model q, we lift the data to a space of higher dimension, called feature space, and construct a linear model in it. Defining

$$\begin{aligned} \varphi (x) = (x_1^2, \sqrt{2} x_1 x_2, \sqrt{2} x_1 x_3, \ldots , x_2^2, \ldots , \sqrt{2} x_{n-1} x_n, x_n^2, x_1, x_2, \ldots , x_n)^\top , \end{aligned}$$

the quadratic model can be written as $q(x) = w^\top \varphi (x) + b$, which is linear in the feature space. Following the approach of the last section, we consider the dual problem (31), in which the matrix P is now given by

$$\begin{aligned} P= \left( \begin{array}{c} (\varphi (x^0))^\top \\ (\varphi (x^1))^\top \\ \vdots \\ (\varphi (x^p))^\top \end{array} \right) . \end{aligned}$$

The coefficient $\sqrt{2}$ in some terms of the definition of $\varphi$ provides a simple expression for the entries of $PP^\top$, which are obtained by $\varphi (x^i)^\top \varphi (x^j)=(x^i)^\top x^j + ((x^i)^\top x^j)^2$, implying that the mapping $\varphi$ does not have to be explicitly computed.

For using support vector regression models in the derivative-free trust-region algorithm presented in Sect. 2, we need to ensure that Assumptions A4 and A5 are fulfilled. If the sample set in each iteration is $\varLambda$-poised, we have by Lemmas 8 and 10 that Assumption A4 holds in the linear and quadratic cases, respectively. On the other hand, given $c_1, c_2 > 0$, the support vector regression model m can be constructed solving (30) with $\varepsilon = c_1 \delta ^2$ and C so that $\displaystyle \max \nolimits _{1 \le i \le p} \{\xi _i, \xi _i'\} \le c_2 \delta ^2$, which implies that the error $|f(x^i) - m(x^i)|$ is not greater than $(c_1 + c_2) \delta ^2$ for all $x^i\in X$ and A5 holds. The existence of such C is guaranteed by the fact that the interpolation model is a feasible solution of (30) with null error in the sample set. Thus, we can start with an arbitrary C and increase it if sufficient accuracy is not reached. So, if in each iteration the sample set is $\varLambda$-poised and C is sufficiently large, then, by Theorem 2, Assumption A3 holds.

6 Numerical experiments

In this section, we describe numerical experiments to illustrate the practical performance of the algorithm. The tests were performed in a notebook ACER Intel Core i7-5500U, CPU 2.40GHz, with 8GB RAM, 64-bit, using Matlab 2015a, v. 8.5.

Algorithm 1 was run with $\Delta _0 = \delta _0 = 1$, $\beta = 1$, $\tau _1 = 0.6$, $\tau _2 = 1.5$, $\eta = 0.1$, $\eta _1 = 0.3$, $\eta _2 = 0.6$, and $\Delta _{k+1} = \Delta _k$ whenever a new trust-region radius should be taken in the interval $[\delta _k,\Delta _k].$ The subproblems (3) were solved by the Matlab routine trust with default parameters. We declare success when the sample set radius became too small: $\Vert \delta _k\Vert \le 10^{-8}$, as suggested in Conejo et al. (2013).

Two variants of Algorithm 1 were considered. In the first one, the models were built by polynomial interpolation, as suggested in Sect. 5.1, while in the second one the models were constructed by support vector regression, as discussed in Sect. 5.2.

Independently of the chosen technique to build the models, the sample sets consisted of $(n+1)(n+2)/2$ points. The first set was constructed by taking steps of size $\delta _0$ from $x^0$ in the positive and negative coordinate directions, resulting in $2n+1$ points. The remaining points were obtained by Algorithm 6.2 of Conn et al. (2009c). The sample set was updated by replacing at most a point per iteration. A new iterate replaced the most distant sample point from it. In the iteration in which the trial point was rejected, it replaced the farthest sample point only if was closer to the current iterate. Otherwise, the sample set was kept unchanged for the next iteration. No safeguard was implemented to ensure the sample set well-poisedness.

When interpolation models were considered, they were obtained by solving the linear system (29). On the other hand, models constructed using support vector regression were obtained by solving problem (31), with $C = 10^8$, by the Matlab routine quadprog with default parameters. Several values for the parameter C were tested, such as $C=10^j$ with $j=1,\ldots , 10$ and also dynamical choices. Our tests showed that taking a fixed large C is more efficient than starting with a small value and increasing it when necessary. We adopted $C=10^8$, which provided the best performance.

The following stopping criteria, with the respective exit flags, were considered as follows:

(1):

The algorithm succeeded: $\Vert \delta _k\Vert \le 10^{-8}$.

($-1$):

The number of iterations exceeded 5000.

($-2$):

The predicted reduction became too small: $m_k(x_k)-m_k(x_k+d_k)\le 10^{-32}.$

($-3$):

The norm of the gradient of the model at the current point became too small: $\Vert g_k\Vert \le 10^{-32}.$

The set of test problems consisted of all 35 problems from the Moré, Garbow, and Hillstrom collection (Moré et al. 1981), with default starting point $x^0$. The numerical experiments are discussed in two sections. First, we consider the functions as presented in the collection, and then the same set of problems adding noise.

6.1 Functions without noise

In this section, we discuss the numerical experiments for the problems from the Moré, Garbow, and Hillstrom collection. We set $\varepsilon = 10^{-8}$ in (32).

Table 1 presents the results. The first three columns contain information about the problems that consist of minimizing the sum of the square of m functions in ${\mathbb {R}}^n$. The label $\text {P}$ indicates the number of the problem in the collection. The next columns display the number of function evaluations $\#f$, the minimum function value $f^*$ and the exit flag for each instance of the algorithm. Finally, the column $f_{MGH}$ displays the solution available in the collection.

Table 1 Numerical results for functions without noise

As suggested in Birgin and Gentil (2012), given $\varepsilon _f > 0$ we considered that an instance of the algorithm solved a problem if it found a point $\overline{x}$ such that

$$\begin{aligned} \dfrac{f(\overline{x})-f_{\min }}{\max \{1,|f_{\min }| \}} \le \varepsilon _f, \end{aligned}$$

(33)

where $f_{\min }$ is the smallest function value found among the instances that are being compared.

Figure 1 presents the performance profiles (Dolan and Moré 2009) related to the number of objective function evaluations, as usual in derivative-free optimization. In the figure on the left, we considered $\varepsilon _f = 10^{-4}$ in (33). Algorithm 1 with polynomial interpolation models solved all the 35 problems, while the algorithm using support vector regression models solved 22 problems, which represents $62.9\%$ of the total amount. The algorithm using polynomial interpolation models was the most efficient for $74.3\%$, versus $31.4\%$ achieved by the algorithm with support vector regression models. On the other hand, in the right figure, it was used $\varepsilon _f = 10^{-1}$. Algorithm 1 with polynomial interpolation models solved all problems being the most efficient in $57.1\%$ of the problems. When support vector regression models were used, the algorithm solved 29 problems, being the most efficient in $48.6\%$ of them.

Fig. 1

Performance profiles for functions without noise

6.2 Noisy functions

In this section, we discuss numerical results for the Moré, Garbow, and Hillstrom collection adding a uniform random noise between $-10^{-3}$ and $10^{-3}$ to the functions. Noisy optimization problems are common in applications, for example when the objective function is associated with a simulation. In this situation, the objective function values are often inaccurate and polynomial interpolation may be a bad choice for building the models. On the other hand, support vectors regression is likely to produce models that do not try to capture the noise accurately. We compare the two alternatives for constructing the models. For support vectors regression models, we set $\varepsilon = 10^{-3}$, the same order of the noise.

Table 2 presents the results, and Fig. 2 shows the performance profiles for noisy functions. In the figure on the left, we considered $\varepsilon _f = 10^{-4}$ in (33). Algorithm 1 with support vector regression models solved 25 problems ($71.4\%$ of the total amount), while the algorithm using polynomial interpolation models solved 17 problems ($48.6\%$). The algorithm using support vector regression models was the most efficient for $65.7\%$, versus $42.9\%$ achieved by the algorithm with polynomial interpolation models. On the other hand, in the right figure, it was used $\varepsilon _f = 10^{-1}$. When support vector regression models were used, the algorithm solved 32 problems, being the most efficient in $65.7\%$ of them. With polynomial interpolation models solved 27 problems, being the most efficient in $42.9\%$ of the problems.

Table 2 Numerical results for noisy functions

Fig. 2

Performance profiles for noisy functions

7 Conclusion

In this work, we discuss the global convergence of a derivative-free trust-region algorithm for minimizing a function on a closed convex set. The algorithm has a very simple structure and considers two radii: the trust-region radius and another one that controls the sample set. The global convergence is proven assuming that the gradient of the model is a good approximation for the gradient of the objective function at the current point. We proved that this property holds for models constructed by polynomial interpolation and by support vector regression. Preliminary numerical results are presented comparing the performance of the algorithm with the two techniques to construct the models. As expected, the tests showed that the algorithm with polynomial interpolation models is more robust and efficient for solving smooth problems. On the other hand, the algorithm with support vectors regression models is more robust and efficient for noisy problems, since they do not try to capture the noise accurately.