1 Introduction

Wave breaking of large amplitude electron plasma waves via phase mixing phenomenon [1-4] is a subject of interest in theoretical plasma physics due to its role in many applications, such as particle acceleration [5] and plasma heating [6].

Historically, the concept of wave breaking in plasma physics was expressed by Dawson [7] in an one-dimensional cold plasma system. After that, many efforts have been made to find the physical nature of wave breaking, theoretically and experimentally. In this regard, the physics of nonlinear evolution of the large amplitude plasma oscillations was well presented by Davidson and Schram [8], where they employed the Lagrangian coordinates method to obtain the exact analytical expression for the wave breaking phenomenon. In the following, using the analytical methods, Wang et al. [9] investigated the plasma response to the nonlinear plasma oscillations in the breaking regime. They showed that the creation of multi-stream structures and fast-electrons generation will be a consequence of propagating of a wave with initial amplitude greater than the critical value, called wave breaking amplitude. Besides the mentioned theoretical researches, the simulation methods including the PIC simulation [10], Vlasov simulation [11], sheet simulation [2], and the fluid simulation [12] have been also employed to investigate the wave breaking/phase mixing phenomenon in detail. In the Vlasov simulation, considering the nonlinear terms, the time-developing distribution function is studied. Using the Vlasov simulation, Bergmann and Mulser [13] showed that the periodic wave structure does not significantly change when a small fraction of the plasma electrons gets trapped, while in the case with a considerable amount of trapped electrons, the periodic structure eventually disappears. The plane sheet method deals with the evolution of the physical quantities in Lagrange coordinates, which is quite similar to the fluid simulation in the sense that it leads to nonphysical results after the sheet crossing [7]. As can be seen, to find the details of the nonlinear processes, the selective method is very substantial. One of the benefits of the PIC and Vlasov simulations over fluid simulation is that the incorporators are capable to elucidate the physics of wave–particle interactions, and hence, these numerical tools can be used to study the dynamics of the plasma species even beyond the wave breaking [14].

For a long time, plasma physicists believed that during the wave breaking all of the electrostatic wave energy is converted into the random kinetic energy of particles to heat the plasma [9]. In 2017, the PIC simulation results by Verma [14] have shown that in the cold plasma, after the wave breaking, all wave energy does not transfer to particles, and a fraction of energy always remains as BGK (Bernstein–Greene–Kruskal) modes. In this case, wave damping would stop, and the amplitude starts to oscillate around an almost constant value. BGK modes are nonlinear solutions of the Vlasov–Poisson equations defined by several trapped particles [15]. The main parameter for BGK mode formation is the ratio of trapped particles to non-trapped particles. More recently in 2021, an investigation of the role of suprathermal electrons on the wave breaking amplitude limit for electrostatic excitations propagating in an electronegative plasma has been studied. The authors specified the electric field amplitude and discussed its parametric dependence on plasma parameters. The maximum electric field was illustrated to decrease with an increase in the suprathermal electron component [16]. In the same year, using 1D PIC simulation, Rathee and coworkers studied the effect of the electron temperature in the propagation of nonlinear electrostatic waves in inhomogeneous unmagnetized plasma (space-dependent density) systems to find the critical value of electron temperature beyond which the wave does not break [17]. They showed that their simulation’s results are in agreement with the theoretical arguments presented by Trines [18].

Due to many observations of wave modulation in space plasmas and in applications using plasma [19], there has been renewed interest in the nonlinear behavior of electrostatic waves in magnetized plasmas [20-26]. Even though the magnetic field has not any role in the linear electrostatic wave propagation in 1D, the presence of a magnetic field has a significant effect on the propagation in nonlinear cases [27]. In the present study, the effect of particle thermal motions in the presence of an external magnetic field on the wave breaking threshold, particle trapping phenomenon, phase mixing time, and BGK mode appearance has been investigated in detail, using 1D3V PIC code [10, 28]. For this purpose, particle-in-cell simulation as a powerful tool to study plasma phenomena, especially those in which the magnetic field and thermal effect play a significant role, has been employed to investigate the time evolution of the nonlinear electrostatic waves and plasma response to the propagation of these modes in the warm electron–ion plasma system.

2 Simulation Box

In this section, the simulation parameters used in the study are presented. The number of grid points is \(\left(NG\right)=512\) with 512 particles in each grid cells and the time step is \(d=\pi /50\). The simulation results are obtained for a plasma of mobile electrons with massive ions providing a fixed neutralizing background. It is worth noting that results would not modify if the number of particles per cell and grid points change. Normalization is important in computational physics; these normalizations have been made in our simulation as \(x\to kx\),\(t\to {w}_{pe}t\),\({n}_{e}\to \nicefrac{{n}_{e}}{{n}_{0}}\), \({v}_{e}\to {v}_{e}/\left({w}_{pe}{k}^{-1}\right)\), \(E\to keE/\left(m{w}_{pe}^{2}\right)\), \({v}_{th}\to {v}_{th}/{w}_{pe}{k}^{-1}\), \(\varnothing \to \nicefrac{{k}^{2}e\varnothing}{m{w}_{pe}^{2}}\), and the amplitude of the external field \({B}_{0}\to \nicefrac{e{B}_{0}}{mc{w}_{pe}}=\nicefrac{{w}_{c}}{{w}_{pe}}\), in which \(\varnothing\) is the potential of the system, \({w}_{pe}\) is the plasma frequency, and\({ n}_{e}\), \({v}_{e}\), and \(E\) are electron number density, electron velocity, and the electric field, respectively. The normalized length of the simulation box is \(L=2\pi\). The nonlinear electrostatic waves are excited in the system by initial perturbation \(\xi =kA\mathrm{cos}{kx}_{eq}\) and \({v}_{e}\)=\({\omega }_{pe}{k}^{-1}A\mathrm{sin}k{x}_{eq}\). \(\xi\) represents the electron’s displacement of its equilibrium position \(\left({x}_{eq}\right)\), and it is important to note that A is considered the amplitude of perturbation. It must be mentioned that, although only the results of two values of A have been reported in the manuscript, more than five values of amplitude have been examined to lead to the conclusions. Moreover, considering the fixed number of grid points in the simulations, to avoid nonphysical noises in the simulation results in each simulation, the plasma density will be considered so that it satisfies the \(\Delta x\approx {\lambda }_{d}\), where the condition \(\Delta x\) in the size of the cells of the simulation and \({\lambda }_{d}\) the Debye length of the plasma system [10, 28, 29].

3 Wave Breaking, Plasma Heating, and BGK Modes in a Typical Unmagnetized Warm Plasma

Consider a typical warm plasma system consisting of particles with thermal velocity \({v}_{th}=0.2{ w}_{pe}{k}^{-1}\) perturbed by the method described in the previous section. At the first step, to estimate the time to reach the steady-state, the evolution of the plasma temperature during the absorption of the high amplitude EPW has been studied. For this purpose, the effective temperature is obtained from \(p=k{T}_{eff}\), where \(p={\int }_{-oo}^{+oo}{v}^{2}f\left(v\right){d}^{3}v\) is the electron pressure parameter and \(f(v)\) the distribution function of the electrons. For a typical warm plasma, the variation of the distribution function via time has been depicted in Fig. 1. As clearly can be seen in this figure, with respect to the equilibrium state (Fig. 1a), a considerable number of energetic electrons could be found in the tail of the distribution function at early times of nonlinear EPWs’ excitation in the system (Fig. 1b), which does not considerably change in later times (Fig. 1c and d). So regarding the effective electron temperature definition, one can expect that the electron temperature will initially increase to reach a saturation value. To verify this assertion, for the typical warm plasma under study, the variation of temperature respect to time for the system with the initial perturbation amplitude \(A=1.05\) and the thermal velocity \({v}_{th}=0.2{ w}_{pe}{k}^{-1}\) has been depicted in Fig. 2. This figure confirms that the temperature of the system initially increases, through nonlinear absorption of the excited EPWs in the system, to reach a saturation value (steady-state time), where the absorption of the waves in the system is stopped. It must be mentioned, to verify the obtained results, that the time evaluation for particle and wave energies also have been examined, which were in agreement with the results of Fig. 1 and 2.

Fig. 1
figure 1

Distribution function of electrons for the system with \(A=1.05\) and \({v}_{th}=0.2{\omega }_{pe}{k}^{-1}\) at (a) \({\omega }_{pe}t=0\), (b) \({\omega }_{pe}t=30\pi\), (c) \({\omega }_{pe}t=60\pi\), and (d) \({\omega }_{pe}t=195\pi /2\)

Full size image
Fig. 2
figure 2

The effective temperature of the system for \(A=1.05\) and \({v}_{th}=0.2{\omega }_{pe}{k}^{-1}\)

Full size image

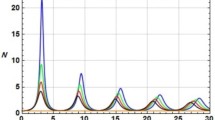
For this system, the absorption of the exciting harmonic modes with time can be followed by the spatial FFT diagram of the electric field depicted in Fig. 3a and b at \({\omega }_{pe}t=31.74\) and \({\omega }_{pe}t\)=195\(\pi /2\), respectively. The presence of high harmonics in the system after approaching the steady-state (\({\omega }_{pe}t\)=195\(\pi\)/2), related to BGK equilibrium, could be interesting in Fig. 3b. Great care must be taken here that all coherent energy has not disappeared and a fraction of it remains in the system as BGK modes. The amplitude of these modes crucially depends on the number of trapped particles in the potential well of the high amplitude EPWs, found as a vortex structure in the phase space.

Fig. 3
figure 3

FFT of the spatial profile of the electric field for \(A=1.05\) and \({v}_{th}=0.2{\omega }_{pe}{k}^{-1}\), at (a) \({\omega }_{pe}t=31.74\) and (b) \({\omega }_{pe}t=195\pi /2\)

Full size image

As a pioneering effort in investigating the plasma temperature effects on nonlinear EPWs in magnetized plasmas, in this part, the PIC simulation method has been employed to study the effect of the particle’s thermal motion on the wave breaking amplitude in a homogeneous, unmagnetized, and collisionless electron–ion plasma. It is well-known theoretically that the thermal effect has a significant influence on the wave breaking amplitude. In this regard, using the “water bag” model first introduced by Depackh [30] in analyzing the plasma systems, Coffey [31] theoretically calculated the maximum amplitude of periodic electric fields in a warm plasma system as \({E}_{\mathrm{max}}^{\%}\)=\(\left(1-1/3\beta -8/3{\beta }^{1/4}+2{\beta }^{1/2}\right)\)1/2, where \(\beta =3{V}_{th}^{2}/{u}_{0}^{2}\) in which \({u}_{0}\) (the phase velocity of the propagating wave) equals to \(\frac{\omega }{k}\). To determine the \({u}_{0}\), the frequency obeys the equation \({\omega }^{2}={\omega }_{pe}^{2}\)+\(\frac{3}{2}{k}^{2}{v}_{th}^{2}\), in which \({v}_{th}\) is the initial thermal velocity of electrons. For \(\beta \ne 0\), the thermal effects reduce the maximum amplitude of the periodic waves in the steady-state, while Dawson [7] showed that this parameter (\({E}_{\mathrm{max}}^{\%}\)) for a cold plasma system is constant and equal to 1.

To examine the wave breaking amplitude in a more realistic model, the PIC simulation results of the maximum amplitude of the EPW as a function of the initial thermal velocity of electrons have been illustrated in Fig. 4. As can be seen, similarly as in the water bag model, the wave breaking amplitude explicitly depends on the electron thermal velocity, and the inclusion of finite electron temperature significantly reduces the wave breaking amplitude.

Fig. 4
figure 4

Maximum electric field versus thermal velocity for \(A=1.05\) at \({\omega }_{pe}t=31.74\)

Full size image

Bernstein–Greene–Kruskal (BGK) modes [15] are undamped nonlinear electrostatic waves pervaded in unmagnetized collisionless plasma. Recently, using the PIC simulation method, the BGK mode formation in a cold plasma system has been investigated, where it has been shown that the trapped particles have the most important role in the stable propagation of these modes around the almost constant amplitude. In this part of our controversy, it is lucrative to speak about electron holes and \(\Delta {v}_{trap}\). The electron–hole is a region that represents trapped particles [32]. In the hole region, the electron density is lower than in the other parts of the plasma. Moreover, \(\Delta {v}_{trap}\) is the velocity band from which electrons are trapped in the wave potential.

In the first step to studying the thermal effects on these modes, in Fig. 5, simulation results have been used to demonstrate the value of normalized \(\Delta {v}_{trap}\) concerning initial normalized particle’s thermal velocity. As can be seen in this figure, by increasing the initial temperature of the system, the \(\Delta {v}_{trap}\) parameter drops down dramatically. Therefore, it is expected that the amplitude of the BGK modes, after the system approaches the steady-state conditions, decreases with the increase of the initial thermal velocity of the particles. To verify this assertion, in Fig. 6, the temporal evolution of the averaged electrostatic energy of the perturbed system has been plotted for three initial values of particle thermal velocity \({v}_{th}=0\) (cold plasma), \({v}_{th}=0.2\) \({\omega }_{pe}{k}^{-1}\), and \({v}_{th}=0.4\) \({\omega }_{pe}{k}^{-1}\).

Fig. 5
figure 5

\(\Delta {v}_{trap}\) versus thermal velocity for \(A=1.05\) at \({\omega }_{pe}t=301.44\)

Full size image
Fig. 6
figure 6

Temporal evolution of averaged electrostatic energy < ESE > for cold (green line), \({v}_{th}=0.2{\omega }_{pe}{k}^{-1}\) (red line), and \({v}_{th}=0.4{\omega }_{pe}{k}^{-1}\) (blue line) systems. In this figure \(A=1.05\)

Full size image

Consistent with our expectation, approaching the steady-state (saturation of the curves), the fraction of coherence energy remaining in the system decreases with the increase of the initial temperature of the system, due to reducing the \(\Delta {v}_{trap}\) parameter. So, we showed that the thermal effect can reduce the amplitude of the BGK modes appearing in the steady state.

The dependence of the BGK modes on the amplitude of the initial perturbation has also been investigated. The results obtained are shown in Fig. 7a and b, for the cold and warm plasmas, respectively. As a more interesting result, even though in the cold plasma system increasing the amplitude of the initial perturbation causes the decrease of the amplitude of the BGK modes, these results can be quite reversed for a warm plasma system.

Fig. 7
figure 7

a and b Temporal evolution of averaged electrostatic energy \(<LnESE>\) for \(A=1.05\) (orange line) and \(A=1.5\) (blue line), for the cold and warm systems, \({v}_{th}=0.2{\omega }_{pe}{k}^{-1}\), respectively

Full size image

4 Wave Breaking/Phase Mixing Phenomenon and BGK Modes in Magnetized Warm Plasma

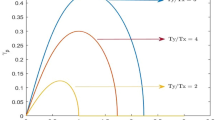
In this section, to examine the magnetic field effect on the phase mixing/wave breaking region and BGK mode behaviors, the evolution of an excited nonlinear electron plasma wave is investigated in cold and warm homogeneous collisionless magnetized plasma. In Fig. 8, the wave breaking amplitude (A) for the cold plasma systems with different applied magnetic fields has been illustrated. In this figure, as long as the magnetic field increases, the wave breaking amplitude will decrease considerably. It should be mentioned that wave breaking amplitude is \(A=1\) in a cold and unmagnetized system, in agreement with Verma [14]. Also, Fig. 8 shows that the variation gradient of wave breaking amplitude is greater at weaker magnetic fields.

Fig. 8
figure 8

Wave breaking amplitude of the cold system

Full size image

As an important simulation result, the BGK mode amplitude \(\left({E}_{\mathrm{max}}\right)\) versus magnetic field has been illustrated in Fig. 9a and b at \({\omega }_{pe}t=195\pi /2\), after saturating state, for both cold and warm plasma systems. In agreement with our results in the previous section, case B = 0, the thermal effects reduce the BGK mode amplitude. In the presence of external magnetic fields, for both cold and warm cases, the BGK mode amplitude decreases until that the magnetic field reaches a threshold value, named optimum magnetic field, and then increases. Wave energy absorption in an optimum amount of magnetic field has its maximum value. In this study, the optimum magnetic fields in the cold and warm systems are found to be 0.06 \(\frac{mc{\omega }_{pe}}{e}\) and 0.04 \(\frac{mc{\omega }_{pe}}{e}\) respectively. So, the optimum value of the magnetic field is lower for warm plasmas than for cold ones.

Fig. 9
figure 9

Maximum electric field for the cold (a) and warm (b) systems with \({v}_{th}=0.2{w}_{pe}{k}^{-1}\), respectively, at \({w}_{pe}t=\)195\(\pi /2\). In this figure, \(A=1.05\)

Full size image

Finally, at the last step of this report, we study the time evolution of the electrical potential of the cold and warm plasma systems in a fixed position for two cases with applied magnetic fields B = 0.1 \(\frac{mc{\omega }_{pe}}{e}\) and B = 1\(\frac{mc{\omega }_{pe}}{e}\); see Fig. 10. The thermal velocity of the warm plasma system is considered \(0.2{\omega }_{pe}{k}^{-1}\). Throughout this analysis, it is obvious that for the low value of the applied magnetic field, the potential will diminish with time progressing for both cold and warm cases. But, comparing Fig. 10a and c shows that considerable absorption of the wave occurs in the warm case earlier than in the cold case. Moreover, for B = 0.1\(\frac{mc{\omega }_{pe}}{e}\), the phase mixing time occurs at the time around \({\omega }_{pe}t=75\), while that value is lower for the warm case. So, the phase mixing time depends on the initial conditions of systems, like thermal velocity, in a low range of magnetic fields. For the systems with a high value of the applied magnetic field, e.g., B = 1 \(\frac{mc{\omega }_{pe}}{e}\) in Fig. 10b and d, the wave energy absorption rate and the phase mixing time do not significantly depend on the initial thermal velocity of the particles.

Fig. 10
figure 10

The evolution of the electrical potential in the cold (a) and warm (b) systems with different magnetic fields

Full size image

5 Conclusion

In this study, the PIC simulation method has been employed to investigate the evolution of nonlinear plasma waves and BGK modes in a thermal magnetized plasma. Regarding Verma’s study for a cold plasma system, after saturating the wave energy absorption, the remnant energy of the wave could be observed in the system in form of BGK modes.

Our PIC simulation results show that, for the thermal plasma systems, the effective temperature of the system initially increases in the system and then reaches a saturated value where the absorption of the wave is stopped. This steady-state occurs earlier than in cold plasma systems. Moreover, thermal effects reduce the maximum amplitude of the periodic waves in the steady-state. We also illustrated that trapped particles affect the propagation of BGK modes, and the amplitude of BGK waves depends on \(\Delta {v}_{trap}\) (the velocity interval in which electrons will be trapped in the wave). This parameter (\(\Delta {v}_{trap}\)) significantly drops by increasing the initial thermal velocity of the system. The effects of trapped particles on BGK modes in the thermal systems as well as the effects of the magnetic field and initial perturbation amplitude on the residual electrostatic energy value have been also investigated in this study. In this regard, our finding showed that the absorption of nonlinear electron plasma waves is very sensitive to the applied magnetic fields. Examining the range of magnetic field strength illustrated, the BGK mode amplitude tends to decrease with the increase of the magnetic field, up to an optimum value, and then increases for both cold and warm systems. So, as an interesting result of this study, we found an optimum value for the magnetic field strength in which the absorption of the nonlinear electron plasma waves is maximized in the system. Finally, we showed that the the phase mixing time is directly related to the thermal velocity of particles in a low range of magnetic fields.