Influence of the Axial-Vector Coupling Constant and the Energy Distribution Function on β-Decay Rates Within the Gross Theory of Beta Decay

Abstract

We evaluate the β-decay rates within the gross theory of beta decay (GTBD) and compare the results for different values of the axial-vector coupling constant, g_A = 0.76, g_A = 0.88, g_A = 1, g_A = 1.13, and g_A = 1.26, and also different energy distribution functions like Gaussian, exponential, Lorentzian, and modified Lorentzian ones. We use new sets of parameters as well as updated experimental mass defects and also an improved approximation for the Fermi function. We compare our calculated results for a set of 94 nuclei of interest in pre-supernova phase, with experimental data in terrestrial conditions and also with other theoretical models like the QRPA, the shell model (SM), and different versions of the GTBD. We show that best results are obtained with g_A = 1 using Gaussian and Lorentzian distributions, being the rates for the 74 and 80% of our sample, respectively, of the same order of magnitude that of experimental data. Finally, we show that the present results within the GTBD are better than those within the QRPA model and also older versions of the GTBD for the isotopes of cobalt and iron families, and comparable with SM for some elements.

1 Introduction

The gross theory of beta decay (GTBD) is a nuclear model proposed initially by Takahashi and Yamada in the end of the 1960s [1]. The GTBD is a parametrical model for nuclear disintegration rates, which combines arguments of independent particle associated with the Fermi gas model. Thus, it is a microscopic model which includes statistical arguments in a phenomenological way, through a convolution between the independent particle model β-amplitude and the density levels of the Fermi gas model corrected to take into account shell effects [2]. Within this formalism, the contributions of the Gamow-Teller resonance are included in a parametrical way.

The original version of the GTBD was not able to reproduce the experimental data with the same efficiency of that more sophisticated microscopical models like the QRPA or the shell model (SM). However, recent works [3, 4] indicate that improved versions of the GTBD provide models which allow to reproduce the experimental β-decay rates of the species available in the Letter of Nuclide as satisfactorily as the other models. The most remarkable feature of the GTBD is that it allows to perform systematic calculations very simple from the computational point of view, at difference of the other models. By these reasons, the GTBD version from ref. Ferreira and Dimarco [4] was applied to astrophysical studies on β and electron capture decay rates in massive stars in presupernova stage [5]. This motivates us to seek new improvements in the GTBD.

The dependence of the decay rates with the weak axial-vector coupling constant, g_A, has been analyzed in several works in the literature in the context of different models. In ref. Niu et al. [6], a value g_A < 1 is required for the evaluation of the rates within the continuum quasiparticle random phase approximation (CQRPA); in ref. Suhonen et al. [7], a great efficiency to reproduce the experimental data is obtained with g_A = 0.88 for the double β-decay using the CQRPA; in ref. Samana et al. [8], the value g_A = 1.13 is the most adequate to reproduce experimental data within the relativistic quasiparticle random phase approximation (RQRPA). This motivates us to ask what is the most appropriate value for g_A to reproduce the data within our GTBD. For this reason, we will compare here the results obtained within the GTBD for the values g_A = 0.76, g_A = 0.88, g_A = 1, g_A = 1.13, and g_A = 1.26.

Otherwise, within the GTBD, the parametrization of the nuclear matrix elements (NME) M_Ω(E) needed for the evaluation of the decay rates requires the use of an independent particle probability distribution function, D_Ω(E, ε). This is normalized as ${\int }_{-\infty }^{+\infty }D_{{\Omega }}(E, \varepsilon ) dE= 1$, being E the transition energy measured from the parent ground state, and ε the single-particle energy of the nucleon that undergoes a β-transition. The authors of the original version of the GTBD [1] have calculated the decay rates for different energy distribution functions: Gaussian, exponential, Lorentzian, and modified Lorentzian. With respect to those calculations, we must point out that (i) they were performed for nucleus in the mass region 12 < A < 250, leading to different parameters from the fits; (ii) the experimental error bars have not been considered in the calculation; (iii) not updated mass defect were used, which would lead to different Q values; (iv) a rough approximation was used for the Fermi function; (v) only the value g_A = 1.26 was adopted. Based on these arguments, we propose to compare here the β-decay rates calculated within the GTBD with Gaussian, exponential, Lorentzian, and modified Lorentzian distribution functions. We use in all cases updated parameters including the error bars in the fitting procedure, considering updated experimental mass defects in the calculation of the Q values, and using a better approximation discussed in ref. Ferreira and Dimarco [4] for the Fermi function, which is most efficient to represent the coulombian interaction between the electron and the parent nucleus.

Thus, we calculated the β-decay rates for a set of 94 nuclear species of the families of cobalt, copper, iron, manganese, chrome, scandium, and titanium that are of astrophysical interest in presupernova stage. We compared the results for different energy distribution functions and axial-vector constant g_A. Additionally, when available, we compared our results with the best choice of g_A and the energy distribution function, with other more sophisticated models like the QRPA, the SM [9], and some combinations like the extended Thomas-Fermi plus Strutinsky integral method plus GTBD generation 2 (ETFSI + GT2) [10], CQRPA + ETFSI [11], and also with the results of our GTBD with the parameters used in refs. Ferreira et al. [3, 4].

The paper is organized as follows. We summarize the formalism for the GTBD model of β-decay in Section 2, where we show the different energy distribution functions used in this work together with a description of the fitting method. In Section 3, we present and discuss our results. Final remarks are drawn in Section 4.

2 Formalism

2.1 Gross Theory of Beta Decay

The total decay rate for the nuclear β process $(Z,A)\rightarrow (Z + 1,A)+e^{-}+\bar {\nu }$ can be calculated within the GTBD as (in natural units $m_{e}=c=\hbar = 1$) [3]

$$ \lambda_{\beta} =\frac{{G_{F}^{2}}}{2\pi^{3}}{\int}_{-Q}^{0}|M(E)|^{2}f(-E)dE, $$

(1)

where G_F = (3.034545 ± 0.00006) × 10^− 12 is the Fermi weak coupling constant and M(E) is the NME being E the transition energy measured from the parent ground state, related to the true β-decay transition energy through the equation E_β = E_e + E_ν = −E > 0 with E_e and E_ν being the electron and antineutrino energies, respectively. f(−E) is the usual integrated dimensionless Fermi function defined as

$$\begin{array}{@{}rcl@{}} f(-E) &=&{\int}_{1}^{-E + 1}(-E + 1 - E_{e})^{2}E_{e}\sqrt{{E_{e}^{2}}-1}\\ &&\times F(Z,E_{e})dE_{e}, \end{array} $$

(2)

where F(Z, E_e) is the Fermi function that takes into account the coulombian interaction between the electron and the daughter nucleus. It is important to remark that for this Fermi function, we adopt here the proposal recipe from ref. [12] which, as discussed by ref. Ferreira and Dimarco [4], provides better results for the decay rates. Finally, the Q value represents the difference between neutral atomic masses of parent and daughter nuclei which, according to ref. [13], can be written as

$$ Q = m_{P} - m_{D} - 1, $$

(3)

with m_P and m_D the parent and daughter masses, respectively, which will be taken from the Letter of Nuclide [14]. Note that we use here updated values of the experimental mass defects, at difference of the previous version of the GTBD from ref. Ferreira et al. [3], where values taken from an old version of the Letter of Nuclide were used.

These β-decay rates receive contribution of different types of transitions like the allowed Fermi (F) and Gamow-Teller (GT) ones, the first forbidden transitions, the second forbidden ones, etc [15]. Neglecting the contribution of forbidden transitions, the total decay rate within the GTBD can be written as

$$\begin{array}{@{}rcl@{}} \lambda_{\beta} &=& \frac{{G_{F}^{2}}}{2\pi^{3}}{\int}_{-Q}^{0}\left[g_{V}^{2}|M_{F}(E)|^{2} + 3{g_{A}^{2}}|M_{GT}(E)|^{2}\right]\\ &&\times f(-E)dE. \end{array} $$

(4)

Here, g_V = 1 and g_A are, respectively, the vector and axial-vector effective coupling constants.¹ The value of g_A will be modified along this manuscript.

The NME can be evaluated by using the sum rule as described in ref. Ferreira et al. [3]. Thus, the NME reads |M_Ω(E)|² = |〈ψ_f|Ω|ψ_i〉|²ρ(E), where ψ_i and ψ_f represent the wave functions of the initial and final states, respectively, Ω ≡ 1 and Ω ≡σ are the F and GT nuclear operators, respectively, and ρ(E) is the final level energy density. Within the sum rule, the β-decay operator is a sum of independent particle operators [1]. Assuming the nucleons as independent particles, the energy E can be considered as the difference between the energies of the independent nucleon decay in daughter and parent nucleus. Therefore, the NME can be expressed as

$$ |M_{{\Omega}}(E)|^{2} = {\int}_{\epsilon_{0} (E)}^{\epsilon_{1}}D_{{\Omega}}(E,\epsilon) \frac{dN_{1}}{d\epsilon}W(E,\epsilon) d\epsilon $$

(5)

where 𝜖₁ is the energy of the highest occupied state and 𝜖₀(E) = max(𝜖_min, 𝜖₁ − Q − E) with 𝜖_min being the lowest single-particle energy of the parent nucleus. Pauli’s principle is considered in the lower limit of the integral and in the term W(E, 𝜖), which measures the probability of occupation of the final states (vacancy level). Equation (5) is valid for the special case of a step surface, where W(E, 𝜖) = 1, because 𝜖 + E > 1 − Q. In other cases, the term W(E, 𝜖) vanishes because 𝜖 + E ≤ 1 − Q. Within this approximation, the NME reads

$$ |M_{{\Omega}}(E)|^{2} = {\int}_{\epsilon_{0} (E)}^{\epsilon_{1}}D_{{\Omega}}(E,\epsilon) \frac{dN_{1}}{d\epsilon} d\epsilon. $$

(6)

Following the original version of the GTBD [1], the Fermi gas model was used to estimate the density of independent nucleon levels, $\frac {dN_{1}}{d\epsilon }$, as

$$ \frac{dN_{1}}{d\epsilon} = N_{1}\left[1-\left( 1-\frac{Q+E}{\epsilon_{F}}\right)^{\frac{3}{2}}\right], $$

(7)

where N₁ is the number of neutrons of the parent nuclei and 𝜖_F is the nucleon Fermi energy given by

$$ \epsilon_{F} = \frac{76.52}{\displaystyle \frac{M_{n}^{*}}{M_{n}}}\frac{1}{{r_{0}^{2}}}\left( \frac{N_{1}}{A}\right)^{\frac{2}{3}} \text{ MeV}, $$

(8)

being $M_{n}^{*}$ and M_n the effective and bare nucleon masses, respectively, and r₀ the nuclear radius. We used the relations r₀ = 1.25(1 + 0.65A^− 2/3), and for $\frac {M_{n}^{*}}{M_{n}} = 0.6 + 0.4A^{-1/3}$.

Finally, within the GTBD, the β-decay rate reads

$$\begin{array}{@{}rcl@{}} \lambda_{\beta} &=&\frac{{G_{F}^{2}}}{2\pi^{3}} {\int}_{-Q}^{0} \left[ {g_{V}^{2}} D_{F}(E,\epsilon) + 3{g_{A}^{2}} D_{GT}(E,\epsilon)\right]\\ &&\times N_{1}\left[1-\left( 1-\frac{Q+E}{\epsilon_{F}}\right)^{\frac{3}{2}}\right]f(-E)dE. \end{array} $$

(9)

The energy distribution functions D_Ω(E, 𝜖) will be discussed in the next subsection.

2.2 Energy Distribution Function

The energy distribution function, D_Ω(E, 𝜖), measures the probability that a nucleon with single-particle energy 𝜖 undergoes a β-transition. As in Takanahashi et al. [1], we neglect the 𝜖-dependence, i.e., it is assumed that all nucleons have the same decay probability, independent of their energies 𝜖, D_Ω(E, 𝜖) ≡ D_Ω(E). The GTBD characterizes this D_Ω(E) through their energy weight moments. Successive improvements of the GTBD have used Gaussian, exponential, and Lorentzian type functions for D_Ω(E). They are:

• 1. Gaussian function

  The Gaussian function is given by Takanahashi et al. [1]

  $$ D_{{\Omega}}(E)=\frac{1}{\sqrt{2\pi}\sigma_{{\Omega}}}e^{\frac{-(E-E_{{\Omega}})^{2}}{2\sigma_{{\Omega}}^{2}}}, $$

  (10)

  where E_Ω is the resonance energy and σ_Ω the standard deviation. Following the original work from ref. Takanahashi et al. [1], we assume the nuclei as a uniform charged sphere with radius $1.2\times A^{\frac {1}{3}}$ fm, which allows to consider the Coulombian (c) displacement of independent particle such as

  $$ E_{F} = E_{c}= \pm(1.44Z_{1}A^{-\frac{1}{3}}-0.7825)MeV, $$

  (11)
  $$ \sigma_{F} =\sigma_{c} = 0.157Z_{1}A^{-\frac{1}{3}}, $$

  (12)

  where Z₁ is the proton number of the daughter (parent) nuclei for β + and electron capture (β⁻) decay. For the GT resonance, we use the approximation [2, 16]

  $$ E_{GT} = E_{F} + \delta, $$

  (13)

  with

  $$ \delta = 26A^{-\frac{1}{3}}-\frac{18.5(N-Z)}{A} \text{MeV}, $$

  (14)

  and

  $$ \sigma_{GT} =\sqrt{{\sigma_{F}^{2}} + {\sigma_{N}^{2}}}, $$

  (15)

  with σ_N being a setting parameter which comes from the energy propagation produced by the forces dependent of the nuclear spin. The adjustment procedure of this parameter will be described below.

• 2. Exponential function

  The exponential distribution function proposed in ref. Takanahashi et al. [1] is

  $$ D_{{\Omega}}(E)=\frac{1}{\sqrt{2}\sigma_{{\Omega}}}e^{\frac{-\sqrt{2}|E-E_{{\Omega}}|}{\sigma_{{\Omega}}}}. $$

  (16)

  The values of E_F, E_GT, σ_F, and σ_GT are estimated as described previously in (11)–(15).

• 3. Lorentzian function

  The Lorentzian probability distribution function proposed in ref. Takanahashi et al. [1] is

  $$ D_{{\Omega}}(E)=\frac{{\Gamma}_{{\Omega}}}{2\pi}\left[\frac{1}{(E-E_{{\Omega}})^{2}} + \frac{1}{(\frac{{\Gamma}_{{\Omega}}}{2})^{2}}\right]. $$

  (17)

  For the F transition, we use

  $$ {\Gamma}_{F} = \frac{2(0.157 Z A^{-\frac{1}{3}})^{2}}{\gamma_{0}}, $$

  (18)

  with γ₀ = 220 MeV being an adjusted parameter which we adopted from ref. Takanahashi et al. [1]. Similarly, Γ_GT was calculated by the expression

  $$ {\Gamma}_{GT} = \sqrt{{\Gamma}_F^2 + {\Gamma}_N^2} $$

  (19)

  with Γ_N = σ_N. The values of E_F and E_GT were estimated from (11) and (13), respectively.

• 4. Modified Lorentzian function

  The Lorentzian modified probability function proposed in Takanahashi et al. [1] is

  $$\begin{array}{@{}rcl@{}} D_{{\Omega}}(E)&=&\frac{\sigma_{{\Omega}}^{2}+\gamma^{2}}{\pi}\frac{\frac{\sigma_{{\Omega}}^{2}}{\gamma}}{(E-E_{F})^{2}+\gamma^{2}}\\ &&\times\left[\frac{1}{(E-E_{{\Omega}})^{2}}+ \frac{1}{\left( \frac{\sigma_{{\Omega}}^{2}}{\gamma}\right)^{2}}\right], \end{array} $$

  (20)

  with γ = 100 MeV being an adjusted parameter taken from Takanahashi et al. [1], and E_F, E_GT, σ_F, and σ_GT were defined previously in (11)–(15).

  To set the value of the parameter σ_N, we need to choose the χ² function to minimize. In the original work from Takahashi and Yamada, they use Takanahashi et al. [1]

  $$ \chi^{2}=\sum\limits_{n = 1}^{N_{0}}\left[log(\tau^{cal}_{1/2}(n))/(\tau^{exp}_{1/2}(n))\right]^{2}, $$

  (21)

  where N₀ is the number of nuclides used in the calculation, and the superindexes cal and exp refer to “calculated” and “experimental” half lives, respectively. Instead of this expression, in the present work, we use Samana et al. [2]

  $$ \chi^{2}=\sum\limits_{n = 1}^{N_{0}}\left[ \frac{log(\tau^{cal}_{1/2}(n))/(\tau^{exp}_{1/2}(n))}{{\Delta} log(\tau^{exp}_{1/2}(n))}\right]^{2}, $$

  (22)

  where

  $$\begin{array}{@{}rcl@{}} {\Delta} log(\tau^{exp}_{1/2}(n)) &\equiv& |log [\tau^{exp}_{1/2}(n) + \delta \tau^{exp}_{1/2}(n)] - log [\tau^{exp}_{1/2}(n)]|,\\ \end{array} $$

  (23)

  and $\delta \tau ^{exp}_{\frac {1}{2}}(n)$ is the experimental error. Thus, this χ² function has the advantage of reinforcing the contribution of experimental data with small experimental errors.

3 Results and Discussions

3.1 Comparison for Different Distribution Functions

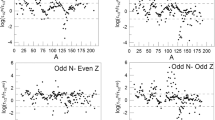
Firstly, we show the results for the adjusted parameter σ_N in Table 1. They have been obtained by fixing a value of g_A for each energy distribution function as described in the previous section, for a set of 94 nuclei belonging to the cobalt, copper, iron, manganese, chrome, scandium, and titanium families, of interest in astrophysics, in the region mass 46 ≤ A ≤ 70. To minimize the χ² function given in (22), we have separated the nuclei according to its parity: even-even (N₀ = 17), even-odd (N₀ = 20), odd-even (N₀ = 29), odd-odd (N₀ = 28). We present the adjusted values for the four distribution functions using g_A = 1.26 and, for reasons explained below, only for the Gaussian and Lorentzian functions when we take g_A = 1.13, 1.00, 0.88, and 0.76.

Table 1 Adjusted parameter σ_N (in units of MeV) for different values of g_A and energy distribution functions

We show in Fig. 1 our results for the logarithm of the ratio between the calculated and the experimental β-decay half lives, for the different energy distribution functions. As usually, we have added two horizontal lines to more easily visualize the nuclei whose half lives differ by less than an order of magnitude from the experimental results, which means those closer to the data. These results show that, for the Gaussian function, the 77.7% (88.3%) of our calculated half lives are in good agreement with the experimental data, because they differ by less than one (two) order of magnitude. Similarly, for the exponential function, we observed that 76.6% (91.5%) of our results agree with experimental ones up to one (two) order of magnitude. When the Lorentzian distribution is used, we obtain 79.8% (89.4%) of the nuclei that fall inside the bars corresponding to one (two) order of magnitude. The plot for the modified Lorentzian function exhibits the worst results with only the 6.4% (56.4%) of the nuclei differing by less than one (two) order of magnitude when compared with data. Thus, the better results are obtained with the Lorentzian distribution, which are comparable with those obtained using the Gaussian one. It is also interesting to mention here that, if we compare theoretical results with data up to the second order of magnitude, the exponential function is the more efficient distribution. On the contrary, the modified Lorentzian function describes the data with much less precision than the other energy distribution functions.

Fig. 1

Comparison of the β-decay rates for different energy distribution functions, using g_A = 1.26. Experimental data from Letter of Nuclide [14]

3.2 Comparison for Different Values of g _A

Next, using Gaussian and Lorentzian probability distribution functions, we calculate the β-decay rates for different values of the axial-vector coupling constant g_A: 0.76, 0.88, 1.00, 1.13, and 1.26. The results are shown in Figs. 2 and 3, respectively. For the Gaussian function, the best value is g_A = 1.00, with the 78.7% of the data being inside the band corresponding to differences of one order of magnitude compared with the experimental results. Otherwise, we obtain 72.3, 73.4, 75.5, and 77.7% of the nuclei inside that band when we use g_A = 0.76, 0.88, 1.13, and 1.26, respectively. Similarly, when the Lorentzian function is used, the best value is g_A = 1.00, which leads to 80.8% of the nuclear species well described with a difference less than one order of magnitude compared with experimental results, and 78.7, 78.7, 78.7, and 79.8% for g_A = 0.76, 0.88, 1.13, and 1.26, respectively.

Fig. 2

β-decay rates calculated using the Gaussian distribution function for different values of g_A. Experimental data from Letter of Nuclide [14]

Fig. 3

β-Decay rates calculated using the Lorentzian distribution function for different values of g_A. Experimental data from Letter of Nuclide [14]

Thus, we conclude that three of the four probability distribution functions tested here exhibit a good agreement with experimental data for nuclei in the mass region 46 ≤ A ≤ 70. Because the Gaussian function gives results close to zero when compared with the Lorentzian one, as shown in Figs. 2 and 3, from now on, we choose the first one to evaluate the β-decay rates within the GTBD described here, with a value of the axial-vector coupling constant g_A = 1.00, since we have shown that it is the more suitable to reproduce the data.

3.3 Comparison with Other Models

In Figs. 4, 5, 6, 7, 8, 9, and 10, we present our results for the β-decay rates within the GTBD described previously, which will be called GTBD1 from now on, for cobalt, copper, iron, manganese, chrome, scandium, and titanium families. We remark that within this GTBD1, we adopt a Gaussian distribution function and g_A = 1, an improved approximation for the Fermi function, and we use updated experimental mass defects and decay rates which lead to the values of the parameter σ_N given in Table 1. Our results are compared with experimental data and also with results obtained within other models like SM, QRPA, ETFSI + GT2, ETFSI + CQRPA, and the GTBD described in Ferreira and Dimarco [4] (GTBD2) which is essentially the same as GTBD1, but with g_A = 1.26, a different Fermi function and outdated experimental data for both the decay rates and the mass defects, which also means different values of the parameter σ_N.

Fig. 4

Comparison of β-decay half lives for the cobalt family: GTBD1 from (9), GTBD2 from Ferreira et al. [3], and QRPA and SM from ref. Kar et al. [17]

Fig. 5

Comparison of β-decay half lives for the copper family: GTBD1 from (9), GTBD2 from Ferreira et al. [3], and QRPA and SM from ref. Kar et al. [17]

Fig. 6

Comparison of β-decay half lives for the iron family: GTBD1 from (9), GTBD2 from Ferreira et al. [3], and QRPA from Marketin et al. [18] and SM from ref. Kar et al. [17]

Fig. 7

Comparison of β-decay half lives for the manganese family: GTBD1 from (9), GTBD2 from Ferreira et al. [3], ETFSI + GT2 from Takahashi et al. [10], and ETFSI + CQRPA from Borzov et al. [11]

Fig. 8

Comparison of β-decay half lives for the chrome family: GTBD1 from (9), GTBD2 from Ferreira et al. [3]

Fig. 9

Comparison of β-decay half lives for the scandium family: GTBD1 from (9) and GTBD2 from Ferreira et al. [3]

Fig. 10

Comparison of β-decay half lives for the titanium family: GTBD1 from (9) and GTBD2 from Ferreira et al. [3]

From Figs. 4 and 6, we observe that for cobalt and iron families, respectively, the GTBD1 gives better results than GTBD2 and QRPA for most employed isotopes. Besides, they are similar for some isotopes and still better for others than those obtained within the SM, which was not the case with the GTBD2. From Fig. 5, we observe that GTBD1 does not show better results than GTBD2 for copper, being the theoretical results obtained with the microscopic SM the more closer to the experimental data. For the isotopes of manganese, we can observe in Fig. 7 that the results obtained with the GTBD1 are closer to the experimental data than those calculated with GTBD2 and ETFSI + GT2. On the other hand, the half-lives evaluated within the ETFSI + CQRPA for the isotopes of manganese only with 63 ≤ A ≤ 69 are better than those obtained with our current GTBD1. For the isotopes of chrome, we note from Fig. 8 that GTBD1 is better than GTBD2 because all the results calculated in that case differ with the data in less than one order of magnitude. From the results exhibited in Fig. 10, similar comments can be performed for titanium family where most of the results calculated within the GTBD1 are closer to the data than those obtained within the GTBD2 model. Finally, the results for the scandium family, shown in Fig. 9, indicate that GTBD1 and GTBD2 do not show significative differences in this case.

4 Concluding Remarks

We have calculated the β-decay half lives within the GTBD model for a set of 94 nuclear species of astrophysical interest in presupernova stage, in terrestrial conditions. In order to improve previous results obtained in ref. Ferreira et al. [3], we have explored different options as changing the energy distribution function, D_Ω(E), variation of the value of the axial-vector coupling constant, g_A, using updated experimental mass defects in the calculation of the Q values, and using for the Fermi function appearing in (2) the approximation proposed in ref. [12] which, as discussed in ref. Ferreira and Dimarco [4], gives better results.

We have compared the results obtained with the Gaussian, exponential, Lorentzian, and modified Lorentzian probability distribution functions, for different values of the axial-vector coupling constant: g_A = 0.76, 0.88, 1.00, 1.13, and 1.26. We have shown that Gaussian and Lorentzian functions with g_A = 1.00 allow to reproduce adequately the experimental results, being the 78.7 and 80.1%, respectively, of the nuclei inside the band corresponding to differences of one order of magnitude compared with the data. It is interesting to mention here that this value of the axial-vector coupling constant agrees with the effective one usually adopted in calculations of double β-decay observables [19, 20]. Additionally, if we look for the number of nuclear species, which differs by less than two orders of magnitude when compared with data, we have observed that the exponential function gives the better results, in spite they are so disperse around the experimental values. On the other hand, we have concluded that the modified Lorentzian function is not a good choice for studies related to β-decay half lives within the GTBD because it leads to the worst results.

We have also compared our results within the present GTBD1 with those obtained within more sophisticated microscopical models, and with a previous version of GTBD2 which employs different parameters σ_N, mass defects, and another approximation for the Fermi function. This comparison was performed for the cobalt, copper, iron, manganese, chrome, scandium, and titanium families. We have concluded that GTBD1 gives better results than all the other models for most of the isotopes of iron and cobalt families. For the manganese family, the agreement with data obtained within the GTBD1 is better than that with the GTBD2 and ETFSI + GT2, in spite that the model which leads the results more closer to the data is the ETFSI + CQRPA, only for those isotopes available in the literature. For the copper family, the GTBD1 is not so efficient as GTBD2 and the SM, anyway is still giving satisfactory results. For the chrome, scandium, and titanium families the GTBD1 improves the results of GTBD2, but without significative differences.

In summary, we have shown that the present version of the GTBD, using the Gaussian or Lorentzian function and g_A = 1.00, the Fermi function as proposed by [12] and proved by Ferreira and Dimarco [4], with updated experimental mass defects and the σ_N fitting parameter, provides a model adequate to perform systematic calculations very simple from the computational point of view, recommended for applications in future researches in astrophysical environment in presupernova stage.