1 Introduction

It is important to study how MHD flow of an electric-conducting fluid is important in a lot of metal-working and metallurgical developments. Numerous researchers have focused on this sort of flow issue owing to its remarkable applicability in a variety of engineering difficulties, including plasma investigations, MHD generators, and extraction of geothermal energy. Additionally, hydromagnetic methods are utilized to separate molten metals from non-metallic impurities. MHD-free convection fluxes occur often in nature. In constructing flow examples for hydrometallurgical and chemical systems, the influences of chemical reactions on the fluid flow via a porous boundary layer are taken into account. For example, carbon dioxide emissions from vehicles are accounted for because they react chemically in the atmosphere and contribute to the development of photochemical smog. Many disciplines rely on the uses of hydromagnetic incompressible viscous flow in research and industrial, including heat transmission under the impact of chemical reactions. This is prevalent in the petrochemical industry, cooling and power systems, surface chemical vapour deposition, cooling of nuclear reactor, design of heat exchanger, geophysics, and MHD power generation systems. Nield and Bejan [1] conducted a thorough assessment of the research on convective heat transport mechanisms in porous media. The flow of a micropolar fluid over a fixed vertical plate with suction was studied by El-Amin [2]. Numerous authors have investigated MHD natural convection thermal transfer flows in porous media, including Raptis and Kafoussias [3] and Sattar [4].

It is now widely accepted that the study of MHD boundary layer flow with chemical reaction, thermal radiation, and mass transfer has been received in a variation of engineering, technological, and manufacturing applications, including the principles of flow calculation in piping systems, flow in various pumps, compressors, mass and heat transfer problems encountered in heat exchangers, boilers, and condensers, and applications. Thermal radiation has a considerable effect on the heat transfer and temperature area in the boundary layer flow of a sharing fluid at high temperatures. Thermal radiation and chemical reaction properties may be critical in regulating heat transmission in industries where the final product’s quality is somewhat dependent on heat-controlling elements. Apart from convective heat transmission, study of radiation heat transfer is critical, and so its significance cannot be avoided. Additionally, thermal radiation is critical in many engineering processes that occur at very extreme temperatures, as well as in the design of several modern energy power conversion systems and associated devices. In the energy equation, the radiative heat flow is defined using the Rosseland approximation. Pal and Talukdar [5] explored the analysis of unsteady MHD convective heat transport in a boundary layer slip flow across a permeable vertical plate accompanied by radiation. Ibrahim [6] analysed the implications of radiation and heat generation on mass transport in a highly porous media with chemical reaction. Veera Krishna and Ali J. Chamkha [7] examined the Hall and ion slip effects on the MHD rotating boundary layer flow of nanofluid across an infinite vertical plate contained in a porous medium. Veera Krishna and Ali J. Chamkha [8] investigated the influence of Hall and ion slip on the unsteady MHD convective rotating flow of nanofluids in biomedical engineering. Bag Ali et al. [9] analysed the impact of suction/injection, gravity modulation, heat radiation, and magnetohydrodynamics on the dynamics of a micropolar fluid subjected to an inclined sheet using the finite element method. Bagh Ali et al. [10] conducted a finite element study on the transient MHD 3D rotational flow of Maxwell and tangent hyperbolic nanofluid via a bidirectional stretching sheet using the Cattaneo Christov heat flux model. VeeraKrishna and Ali J. Chamkha [11] examined the Hall and ion slip effects on the MHD rotational flow of an elastico-viscous fluid through a porous media. Veera Krishna [12] investigated the Hall and ion slip effects on the MHD-free convective rotating flow confined by a semi-infinite vertical porous surface. Numerous researches have proposed a mathematical model for the impact of linear/nonlinear radiation on non-Newtonian/Newtonian fluids by including a variety of physical characteristics [13,14,15,16].

The effects of viscous dissipation, which are often quantified by the Eckert number, are significant in geophysical fluid flows and also in some industrial uses, such as the movement of oil products via ducts. When an internal heat source or absorption happens, the study of heat transfer in hydrodynamic boundary layer flow across a porous stretched sheet becomes more intriguing. Viscosity dissipation is a critical element in fluid dynamics and is sometimes difficult to include into mathematical models. Duwairi [17] investigated the influence of viscous dissipation on forced convection flow emanating from radiate isothermal surfaces. Das et al. [18] inspected the outcomes of Joule heating MHD mixed convective slip flow over an inclined permeable plate with viscous dissipation. Babu et al. [19] investigated a vertically moving porous plate immersed in a porous fluid exhibiting viscous dissipation. Numerous studies, on the other hand, investigated viscous dissipation impact on hydromagnetic flow through a saturated permeable media and provided a new mathematical model based on a variety of criteria. Ali et al. [20] examined using finite element modelling the significance of Lorentz and Coriolis forces on the dynamics of water-based silver nanoparticles. Danial Habib et al. [21] studied the time-dependent MHD nanofluid dynamics resulting from an expanding sheet with bioconvection and two thermal boundary conditions. Bagh Ali et al. [22] studied MHD impacts on rotating Casson nanofluid flow using the Cattaneo–Christov heat flux model. Ali et al. [23] analysed the influence of G-Jitter on magnetohydrodynamic non-Newtonian fluid on an inclined surface using finite element modelling. Magnetic dipole and heat radiation effects on hybrid base micropolar CNTs flow across a stretched sheet: finite element technique approach was studied by Bagh Ali et al. [24].

Mass transfer mediated by temperature gradients, on the other hand, is concerned to as the thermal diffusion (Soret) outcome. Thus, the Soret issue is used to refer to species differentiation that occurs when a homogeneous mixture is subjected to a temperature gradient, while the Dufour result is used to refer to the heat flux created by a concentration gradient. Every time there are temperature and species concentration discrepancies in a medium, or between media, thermosolutal or double diffusive convection takes place. Simultaneous heat and mass transmission gradients are regarded important in technical and engineering terms. As a result of this, they are used in many different thermal engineering branches, such as oil extraction and geothermal systems. Alam and Rahman [25] investigated the Dufour and Soret effects on a vertical porous plate submerged in a porous media. Chamkha and El Kabeir [26] conducted a theoretical investigation of the different influences on unsteady heat and mass transfer through mixed convection flow via a rotating vertical cone. Soret and radiation impact on mass transfer flow over porous materials with heat generation and chemical reaction was explored by Shankar and Shekar [27]. Sheikholeslami et al. [28] and Veeresh et al. [29] contemplated the effect of thermal diffusion on MHD flow past a vertical plate through porous medium. Enhanced heat transfer for bioconvective motion of Maxwell nanofluids across a stretched sheet with Cattaneo–Christov flux was explored by Sohaib et al. [30]. Sohaib et al. [31] investigated the Significance of chemical reaction with activation energy for Riga wedge flow of hyperbolic tangent nanofluid in the presence of a heat source. Hall and ion slip effects on radiative MHD rotating flow of Jeffreys fluid through an infinite vertical flat porous surface with ramping wall velocity and temperature were reported by Veera Krishna [32]. Veera Krishna [33] investigated the Hall and ion slip effects on the MHD flow of Casson hybrid nanofluid across an infinitely exponentially accelerated porous vertical surface. Many researchers [34,35,36,37,38,39] discussed the Soret impacts on MHD flow through a vertical plate.

The intention of this work is to determine the effect of the heat source and diffusion-thermo, on an unsteady radiative MHD boundary layer flow of a chemically reacting fluid across an infinite porous vertical plate. These numerical solutions provide a greater knowledge of the physical phenomena of the modelled problem, which are critical in industrial and technical domains. Due to the nonlinear nature of the fundamental equations and the additional mathematical problems connected with their solution, we chose the numerical technique. The converted non-dimensional governing equations are numerically elucidated applying the bvp4c scheme. The authors evaluate the impact of several physical factors on velocity, heat, and mass transmission and also on coefficient of friction factor, rate of heat transfer, and Sherwood number. The current study’s applications would also be beneficial in processing of magnetic materials, thermal systems, energy production, heat transfer, extrusion systems, computer devices, polymer processing, and chemical engineering systems etc.

2 Formulation of the problem

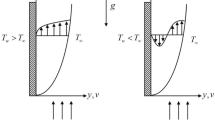
Let us assume that the viscous and electrically conducting mixed convection incompressible fluid flow with the \({x}^{*}-\) axis along with the plate surface and the \({y}^{*}\)-axis vertical to it in the way of applied magnetic field as presented in Fig. 1. A transverse magnetic field which is constant in the way of y*-direction is applied. Due to the two-dimensional nature of the motion and the length of the plate large, all physical variables are considered to be independent on axis \({x}^{*}\). A fluid and a concentration in which the rate of chemical reaction is directly proportional to the amount of a particular species’ concentration are being investigated for their homogenous first-order chemical reactions.

Fig. 1
figure 1

Schematic representation and physical model of the problem

Full size image

Based on the aforementioned scenarios, the flow estimates are:

  • ➢ Viscous, electrically conducting, incompressible fluid flow is deliberated.

  • ➢ In the momentum equation, mixed convection is deliberated.

  • ➢ Viscous dissipation, heat source/sink, and thermal radiation are considered in the interpretation of the energy equation.

  • ➢ The classical model is applied to the flow through a vertical surface with the limitations of limited porosity and low velocity range.

  • ➢ In interpreting the concentration equation, homogeneous first-order chemical processes are considered.

The resulting governing equations are as follows (Ref. [40] and [41]):

$${v}^{*}\frac{d{u}^{*}}{d{y}^{*}}=v\frac{{d}^{2}{u}^{*}}{d{y}^{{*}^{2}}}+g\beta \left({T}^{*}-{T}_{\infty }\right)+g{\beta }^{*}\left({C}^{*}-{C}_{\infty }\right)-\frac{\sigma {B}_{0}^{2}}{\rho }\left({u}^{*}-{U}_{\infty }\right)-\frac{v}{{k}^{*}}\left({u}^{*}-{U}_{\infty }\right)$$
(1)
$${v}^{*}\frac{d{T}^{*}}{d{y}^{*}}=\frac{k}{\rho {C}_{p}}\frac{{d}^{2}{T}^{*}}{d{y}^{*2}}-\frac{1}{\rho {C}_{p}}\frac{d\mathrm{q}}{d{y}^{*}}+\frac{v}{{C}_{p}}{\left(\frac{d{u}^{*}}{d{y}^{*}}\right)}^{2}+\frac{{Q}_{0}}{\rho {C}_{p}}\left({T}^{*}-{T}_{\infty }\right) +\frac{\sigma {B}_{0}^{2}}{\rho {C}_{p}}{u}^{{*}^{2}}$$
(2)
$${v}^{*}\frac{d{C}^{*}}{d{y}^{*}}=D\frac{{d}^{2}{C}^{*}}{d{y}^{{*}^{2}}}+{D}_{1}\frac{{d}^{2}{T}^{*}}{d{y}^{{*}^{2}}}-\mathrm{Kr}\left({C}^{*}-{C}_{\infty }\right)$$
(3)

The boundary circumstances are as follows (Ref. [40] and [41]):

$$\begin{array}{c}{y}^{*}=0:{u}^{*}=0;{T}^{*}={T}_{w};{C}^{*}={C}_{w}\\ {y}^{*}\to \infty :{u}^{*}\to 0;{T}^{*}\to {T}_{\infty };{C}^{*}\to {C}_{\infty }\end{array}$$
(4)

The following non-dimensional values are presented:

$$\begin{array}{c}y=\frac{{y}^{*}{v}_{0}}{v},u=\frac{{u}^{*}}{{\mathrm{U}}_{\infty } },Pr=\frac{v\rho {C}_{p}}{k},\theta =\frac{{T}^{*}-{T}_{\infty }}{{T}_{w}-{T}_{\infty }}\\ \phi =\frac{{C}^{*}-{C}_{\infty }}{{C}_{w}-{C}_{\infty }},Gr=\frac{\mathrm{\nu g}\beta \left({T}_{w}-{T}_{\infty }\right)}{{v}_{0}^{2}{\mathrm{U}}_{\infty }}, \delta =\frac{{\mathrm{Q}}_{0}v}{{v}_{0}^{2}}\\ Gm=\frac{v\mathrm{g}{\beta }^{*}\left({C}_{w}-{C}_{\infty }\right)}{{v}_{0}^{2}{\mathrm{U}}_{\infty }},Ec=\frac{{\mathrm{U}}_{\infty }}{{C}_{p}\left({T}_{w}-{T}_{\infty }\right)}\\ M=\frac{v\sigma {B}_{0}^{2}}{\rho {v}_{0}^{2}},\chi =\frac{v}{{k}^{*}{v}_{0}^{2}},v=\frac{\mu }{\rho }, N=\frac{16v\alpha \sigma {T}_{\infty }^{3}}{\rho {C}_{p}{\upnu }_{0}}\\ Sc=\frac{v}{D},Sr=\frac{{D}_{1}\left({T}_{w}-{T}_{\infty }\right)}{v\left({C}_{w}-{C}_{\infty }\right)},R=\frac{v\mathrm{Kr}}{{v}_{0}^{2}}.\end{array}$$
(5)

Using Eq. (5), the set of Eqs. (1)–(3) is converted into the dimensionless form as follows:

$$\frac{{\mathrm{d}}^{2}U}{d{\eta }^{2}}+\frac{\mathrm{d}U}{d\eta }+M\left(U-1\right)=-Gr\theta -Gm\phi -\chi \left(U-1\right)$$
(6)
$$\frac{{\mathrm{d}}^{2}\theta }{d{\eta }^{2}}+\mathrm{Pr}\frac{\mathrm{d}\theta }{d\eta }+\mathrm{Pr}Ec{\left(\frac{\mathrm{d}U}{d\eta }\right)}^{2}+\mathrm{Pr}Ec\mathrm{M }{u}^{2}+\mathrm{Pr}(N+\delta )\theta =0$$
(7)
$$\frac{{\mathrm{d}}^{2}\phi }{d{\eta }^{2}}+Sc\frac{\mathrm{d}\phi }{d\eta }-ScR\phi +SrSc{\theta }^{\mathrm{^{\prime}}\mathrm{^{\prime}}}=0$$
(8)

The associated dimensionless boundary constraints are simplified to

$$\left.\begin{array}{c}U=0;\theta =1;\phi =1\ as\ \eta =0\\ U\to 0;\theta \to 0;\phi \to 0\ at\ \eta \to \infty \end{array}\right\}$$
(9)

2.1 The quantities of physical interest

The velocity field may be used to determine the coefficient of skin friction, which is presented in non-dimensional form:

$$Cf={\left(\frac{\partial U}{\partial y}\right)}_{y=0}$$

By determining the temperature and concentration gradients, one may derive the coefficients of rate of mass and heat transfer, which are articulated in non-dimensional terms in terms of the Sherwood and Nusselt numbers:

\(Nu={\left(\frac{\partial \theta }{\partial y}\right)}_{y=0}\) and \(Sh={\left(\frac{\partial \phi }{\partial y}\right)}_{y=0}\)

3 Numerical solution

The nonlinear ODEs (Eqs. (6)–(8)) are integrated with the aid of the MATLAB function bvp4c, as are the boundary limits (Eqs. (9)). This is carried out by first transforming the set of ODEs to first-order ODEs by consecutive substitutions.

let’s just let \(\xi=\begin{bmatrix}U\;U^{'}&\theta\;\theta^{'}&\phi\;\phi^{'}\end{bmatrix}^T\) which gives the following:

  • Step 1

We now have a system of equations of the first order:

$$\begin{array}{c}\frac{d}{d\eta }\left(\begin{array}{c}\xi \left(1\right)\\ \xi \left(2\right)\\ \xi \left(3\right)\\ \xi \left(4\right)\\ \xi \left(5\right)\\ \xi \left(6\right)\end{array}\right)\\ =\left(\begin{array}{c}\xi \left(2\right)\\ \xi \left(1\right)-M\xi \left(1\right)-1-Gr\xi \left(3\right)-Gm\xi \left(5\right)-{\rm X}\left(\xi \left(1\right)-1\right)\\ \xi \left(4\right)\\ -(\mathrm{Pr}\xi \left(4\right)+\mathrm{Pr}Ec{\left(\xi \left(2\right)\right)}^{2}+\mathrm{Pr}Ec\mathrm{M }{\xi \left(4\right)}^{2}+\mathrm{Pr}\left(N+\delta \right)\xi \left(3\right))\\ \xi \left(6\right)\\ -Sc\xi \left(6\right)+ScR\xi \left(5\right)+SrSc(\mathrm{Pr}\xi \left(4\right)+\mathrm{Pr}Ec{\left(\xi \left(2\right)\right)}^{2}+\mathrm{Pr}Ec\mathrm{M }{\xi \left(4\right)}^{2}+\mathrm{Pr}\left(N+\delta \right)\xi \left(3\right))\end{array}\right)\end{array}$$

  • Step 2

The numerical solution is performed using the MATLAB built-in bvp4c solver and the boundary conditions stated above, as well as an appropriate fixed value for the far area boundary condition. This is considered as an issue of boundary values, (bvp), i.e. \(\eta \to \infty\) say \(\eta \to 10\).

The following initial constraints apply:

$$\left(\begin{array}{c}\xi a\left(1\right)\\ \xi a\left(3\right)\\ \xi a\left(5\right)\\ \xi b\left(1\right)\\ \xi b\left(3\right)\\ \xi b\left(5\right)\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 1\\ 0\\ 0\\ 0\end{array}\right)$$

The scaling factor is taken by \(\eta =0.01\), and the convergence requirements are described with fifth-decimal-place precision.

A stable asymptotic boundary constraint (Eq. (9)) was found at the border, and it was found to be 10−6 It’s usual practice in boundary layer analysis to use a value of η∞ = 8 in this method. Figure 2 depicts the numerical flowchart of the issue.

Fig. 2
figure 2

The numerical flowchart of the issue

Full size image

4 Results and discussion

Profiles of dimensionless velocity, temperature, and concentration distributions, together with the friction factor, rate of heat, and mass transfer, are determined numerically for several values of the various physical pertinent flow factors encountered in the problem. These parameters include the \(M\), Sc, K, Gm, Ec, Pr, Gr, \(\delta\), Kr, and \(So\). The following default parameter quantities are used for calculations in the current study: \(M=0.5; N=1; R=0.2; \delta =0.5;\chi =0.1; Pr=0.71; Gr=2;Gm=1; Ec=0.01; Sc=0.62;Sr=0.3.\)

Figure 3a portrays the impact of the Grashof number \((Gr)\) on the flow regime. The qualified influence of the thermal buoyancy energy on the hydrodynamic viscous force in the edge is represented by Gr. The velocity of the fluid rises as the Gr enhances. Physically, positive values of Gr mean that the plate is being cooled by natural convection. So, heat moves away from the vertical plate and into the fluid. This raises the temperature of the fluid, which makes it more buoyant. Also, it can be seen that the peak value of the speed goes up quickly near the plate as the thermal Grashof number goes up and then goes down smoothly to the speed of the free stream. As seen in Fig. 3b, the non-dimensional velocity rises as the mass Grashof number \((Gm)\) increases. The ratio of the species’ buoyancy force to its viscous hydrodynamic force is given by the solutal Grashof number Gc. The impact of the magnetic parameter M on non-dimensional transverse velocity and temperature is seen in Fig. 3c and d. It is observed that the velocity grows slowly and eventually approaches the transverse velocity. However, it is seen that enhancing values of \(M\) consequences in a reduction in the dimensionless transverse velocity. Due to when a transverse magnetic field is applied to an electrically conducting fluid, an impeding Lorentz force is produced. The force affects the velocity of the fluid in the boundary layer by slowing its motion and so raising its temperature. Temperature rises when the magnetic parameter is increased, as seen in Fig. 3d.

Fig. 3
figure 3

a Gr against velocity. b Gm against velocity. c M against velocity. d M against temperature. e χ against velocity. f \(Ec\) \(\mathrm{against}\) velocity

Full size image

Figure 3e illustrates the influence of the porosity parameter \(\chi\) on the velocity field. The velocity of the fluid rises when the permeability parameter \(\chi\) is enhanced. To put it another way, the increasing permeability of the porous material causes a rise in fluid flow. When the pores in the porous media are big, the active resistance on the medium might also be disregarded. Figure 3f depicts the distributions of velocity field with transverse coordinates for various Eckert numbers Ec. As predicted, a rise in \(Ec\) results in an upsurge in velocity values owing to the increased buoyancy force. The temperature profiles as a function of the Eckert number are shown in Fig. 4a. Friction and compression heating dominates the boundary layer fluid temperature at high Eckert numbers because of their ability to dissipate heat. Figure 4a illustrates the influence of Ec on temperature. \(Ec\) increases the temperature of the wall as a result of the heat provided by friction heating.

Fig. 4
figure 4

a Ec against temperature. b N against velocity. c N against temperature. d Pr against velocity. e \(Pr\) \(\mathrm{against}\) temperature

Full size image

Figure 4b and c depicts the relationship between the radiation parameter \((N)\) and a velocity and temperature profile. The velocity and temperature declines as \(N\) increases. This is due to a decrease in the mean absorption coefficient when the parameter \(N\) is raised. Figure 4d and e illustrates the influence of Prandtl number on the velocity and temperature profile. This graph shows that raising the value of \(Pr\) lowers the fluid temperature. \(Pr\) is the ratio of kinematic viscosity to thermal diffusivity, which is called the Prandtl number \((Pr).\)

The decrease in velocity and concentration as the chemical reaction factor increases is seen in Fig. 5a and b. This indicates that the destructive reaction results in decreases in the region of concentration that do not produce buoyancy impacts as a function of concentration slopes. The impact of the heat source on non-dimensional velocity, temperature, and concentration is shown in Fig. 5c–e. As seen in Fig. 5c, the influence of the heat source on fluid velocity is demonstrated by increasing the size of the heat source parameter \((\delta )\), which results in a reduced velocity distribution. Figure 5d and e shows the temperature and concentration distribution profiles for the enhanced heat source parameter \((\delta )\). As can be seen from these figures, when the suction parameter is increase, the width of the thermal boundary layer diminishes, and the concentration enhances.

Fig. 5
figure 5

a R against velocity. b R against temperature. c δ against velocity. d δ against temperature. e \(\updelta\) \(\mathrm{against}\) concentration

Full size image

The concentration and velocity patterns over the boundary layer are shown in Fig. 6a and b for different amounts of the Schmidt number Sc. \(Sc\) is the ratio of momentum to mass (species) diffusivity, i.e. it expresses the relationship between the width of the hydrodynamic boundary layer and the thickness of the concentration (mass transfer) boundary layer. The graphic demonstrates that rising Sc leads in a reduction in velocity and concentration, since decreasing Sc values correspond to increasing chemical molecule diffusivity.

Fig. 6
figure 6

a Sc against velocity. b Sc against concentration. c Sr against velocity. d \(Sr\) \(\mathrm{against}\) concentration

Full size image

Figure 6c and d exemplifies the velocity and concentration curves for various Soret numbers (Sr). It is ascertained that when the Soret number step ups, the velocity and concentration inside the boundary layer drop.

The influence of \(M, Gr, Gm, Ec, M, N, R, Sc,\) and \(Sc\) on friction factor, heat transmission, and mass transfer are shown in Tables 1, 2 and 3. As seen in Table 1, increasing \(M, Gr,\) and \(Gm\) increased skin friction for both mercury and electrolytic solution but lowered the rate of heat and mass transfer. Skin friction coefficient and Nusselt and Sherwood number values are enhanced for larger values of chemical reaction parameter. Table 2 illustrates the changes in the rate of heat transmission. The rate of heat transmission for both fluids decreases as \(Ec\) rises, but the heat transfer rate \(Nu\) for rises as N enhances. Table 3 illustrates the changes in the rate of heat and mass transport. In both situations when \(Pr=0.71\) and \(Pr=1\), the rate of mass and heat transfer rises as \(R, Sr,\) and \(Sc\) increase.

Table 1 Numerical computations of friction factor and the Nusselt and Sherwood numbers when \(N=1; R=0.2; \delta =0.5; Ec=0.01; Sc=0.62; Sr=0.3\)
Full size table
Table 2 Numerical calculation of Nusselt number when \(M=0.5;R=0.2; \chi =0.1; Gm=1;Sc=0.62;Sr=0.3\)
Full size table
Table 3 Numerical calculation of Nusselt and Sherwood numbers when \(M=0.5; N=1; \delta = 0.5; \chi =0.1; Pr=0.71; Gm=1; Ec=0.01\)
Full size table

5 Conclusions

This article discusses the Soret influence of mixed convection flow of heat and mass transmission via an infinite vertical plate under the impact of a heat source and chemical reaction. Numerous physical factors, including Joule heating and radiation, contribute to the flow regime of a fluid, as examined in this article. By applying similarity transformations, the PDEs are transformed to ordinary differential equations. A numerical built-in solver bvp4c technique is used to investigate the impacts of relevant physical flow factors, including thermal radiation, viscous dissipation, and magnetic field. The tables illustrate the impacts of different governing flow factors on the friction factor, rate of heat, and mass transfer. The features shown by these results are consistent and agree well with those that have been reported in the past [40, 41]. The following are the study’s major findings:

  • The fluid velocity of the flow field decreases when the parameters M and K are raised beyond their default values.

  • As the value of \(Sc\) increases, both the velocity and concentration distributions deteriorate.

  • Rise in \(Pr\) causes a drop in temperature.

  • As the heat source parameter \(Q\) rises, both the temperature and velocity enhance.

  • The velocity rises as the amount of Gr and Gm increases.

  • With a rise in \(Sr\) and \(Kr\), the velocity and concentration of the fluid drop.

  • Nusselt number \(Nu\) grows as \(Pr\) rises but reduces as \(Q\) increases.

  • The rate of mass transfer \(Sh\) rises when \(Kr\) and \(Sc\) increase and decline as \(Sr\) levels grow.

  • When \(Gr\) and \(Gm\) increase in value, \(Cf\) increases; however, a reversible tendency is seen for higher values of \(M\) and \(K\).

Incorporating nanoparticles into the fluid in order to examine their thermal increase beneath an infinite vertical plate for nanofluid and hybrid nanofluid might be viewed as a potential avenue for future research.