On stability and square integrability of solutions to some third order neutral differential equations

Abstract

In this paper, the asymptotic behavior of solutions for a class of non-autonomous third order neutral delay differential equations is studied. Results on the stability, the boundedness and the square integrability of solutions and their derivatives are obtained. An example to illustrate the results is included.

1 Introduction

Over the last several years, a great interest has been given to the asymptotic behavior of various classes of third-order differential equations [4, 7, 8, 17,18,19,20,21]. Being aware of the practical importance of third-order differential equations, the area of qualitative theory for such equations has attracted a large portion of research interest in the last decades. Neutral differential equations are differential equations in which the delayed argument occurs in the highest derivative of the state variable. These equations appear often in the modeling of networks containing lossless transmission lines [7, 8].

Based on the Lyapunov functional approach, we give new results on asymptotic behavior for some neutral differential equations. Precisely, sufficient conditions are given for the stability and square integrability of solutions for the following neutral delay differential equation

$$\begin{aligned}&\left( p(t)\left( q(t)(x(t)+\rho x(t-\sigma ))'\right) '\right) '+f(x(t),x'(t))x''(t)\nonumber \\&\quad +g(x(t),x'(t))x'(t)+h(x(t))=e(t), \end{aligned}$$

(1)

for all $t\ge t_1= t_0+\sigma$, and $0<\rho <1$. The functions $p(t),\ q(t),\ f(x(t),x'(t))), g(x(t),x'(t))$ and h(x(t)) are continuous in their respective arguments with $h(0)=0$. In addition, it is also supposed that the derivatives $f_u(u,v)=\frac{\partial f}{\partial u},p^{\prime }(t),q^{\prime }(t),q^{\prime \prime }(t)$ exist and are continuous.

By a solution of (1) we mean a continuous function $x : [t_x,\infty )\rightarrow {\mathbb {R}}$ such that $x(t)+\rho x(t-\sigma )\in C^3([t_x,\infty ),{\mathbb {R}})$ and which satisfies (1) on $[t_x,\infty )$.

The paper structure is as follows: In Sect. 2, we give stability results. In Sect. 3, we verify the stability result throughout an example. Finally, Subsections of Sect. 4 are devoted to the study of boundedness and square integrability of solutions.

2 Asymptotic stability

Asymptotic stability of solutions to Eq. (1) will be studied in the case $e(t)=0$. Before proceeding further, we start by making some assumptions and notations. Suppose there exist positive constants $p_i$, $q_i$, $f_i$, $g_i$, $h_i$, L and $\alpha$ for $i=0,1$, such that the following conditions are satisfied :

• (i) ${\left\{ \begin{array}{ll} 0<p_0\le p(t)\le p_1,\;-L\le p^{\prime }(t)\le 0,\\ 0<q_0\le q(t)\le q_1;\;-L\le q'(t)\le 0; \end{array}\right. }$

• (ii) $0<f_0\le f(u,v)\le f_1,\;vf_u(u,v)\le 0,\;0<g_0\le g(u,v)\le g_1$;

• (iii) $|h'(u)|\le h_1$, for all u and $\frac{h(u)}{u}\ge h_0$ for all $u\ne 0$;

• (iv) $2p_1h_1<\alpha <\frac{f_0}{2}$;

Define for each solution x(t) of (1) the equations:

$$\begin{aligned} Y(t)=qX'(t)=q(t)\left[ x(t)+\rho x(t-\sigma )\right] ', \end{aligned}$$

(2)

and

$$\begin{aligned} Z(t)=Y'(t)=\left( q(t)\left[ x(t)+\rho x(t-\sigma )\right] '\right) '. \end{aligned}$$

(3)

Also, to ease exposition of the paper, we make use of the following notation

$$\begin{aligned} r_0=\min \{p_0,q_0\},\quad r_1=\max \{p_1,q_1\}, \\ a =r_1(1+\rho )(r_1^2+r_1g_1+r_1h_1)+r_1^2h_1, \end{aligned}$$

and

$$\begin{aligned} b=\rho r_1\left( r_{1}+L\right) \left( f_{1}-\alpha \right) +r_1^3\left( 1+\rho \right) +r_1^2g_{1}+r_{1}L\left( f_{1}-\alpha \right) , \end{aligned}$$

which allows us rewrite Eq. (1) as the equivalent system

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}x'=y,\\ &{}y'=z,\\ &{}(p(t)Z)'=-f(x(t),y(t))z(t)-g(x(t),y(t))y(t)-h(x(t)). \end{aligned} \end{array}\right. } \end{aligned}$$

(4)

It can be seen from system (4) that

$$\begin{aligned} Y(t)=q(t)y(t)+\rho q(t)y(t-\sigma ), \end{aligned}$$

and

$$\begin{aligned} Z(t)=q'(t)y(t)+q(t)z(t)+\rho q'(t)y(t-\sigma )+\rho q(t)z(t-\sigma ). \end{aligned}$$

Now, we will give our main result on the asymptotic stability of solutions for system (4) :

Theorem 1

In addition to assumptions $(i)-(iv)$, assume the following hold :

• 1. $a+\rho r_1^2(2L(1+\rho )+h_1+r_1(1+\rho ))+\rho r_{1}L\left( f_{1}+g_{1}-\alpha \right) -2\alpha g_{0}<0,$

• 2. $b+\rho r_1^2(\left( f_{1}+g_{1}-\alpha \right) + r_{1}\left( 1+\rho \right) )+2r_0^2\left( \alpha -f_{0}\right) <0.$

Then the trivial solution of (4) is asymptotically stable.

Proof

Define a Lyapunov function W(t, x, y, z) by

$$\begin{aligned} \begin{aligned} W=\exp \left( -\frac{1}{\omega }\int _{0}^{t}\left( \left| p^{\prime }\left( s\right) \right| +\left| q^{\prime }\left( s\right) \right| \right) ds\right) V, \end{aligned} \end{aligned}$$

(5)

where

$$\begin{aligned} \begin{aligned} V&=\alpha \int _{0}^{x}h(s)ds+p(t)h(x)Y+\frac{p(t)}{2}Y^2+\frac{1}{2}(p(t)Z)^2+\alpha yp(t)Z\\&\quad \,\,+\alpha \int _{0}^{y}f(x,u)udu+\gamma _0\int _{t-\sigma }^{t}y^2(s)ds+\gamma _1\int _{t-\sigma }^{t}z^2(s)ds. \end{aligned} \end{aligned}$$

(6)

Here, $\gamma _0$ and $\gamma _1$ are positive constants to be determined later in the proof.

The first step is to show that V defined by (5) is positive definite. It is easy to see that $V(t,0)=0$. Recall that

$$\begin{aligned} 2\int _{0}^{x}h'(s)h(s)ds=h^2(x). \end{aligned}$$

In view of conditions (i), (iii) and (iv),

$$\begin{aligned}&\alpha \int _{0}^{x}h(u)du+p\left( t\right) h(x)Y+\frac{p\left( t\right) }{2} Y^{2}\\&\quad =\alpha \int _{0}^{x}h(u)du+p\left( t\right) \left( h(x)+\frac{1}{2} Y\right) ^{2}-p\left( t\right) h^{2}\left( x\right) +\frac{p\left( t\right) }{4}Y^{2} \\&\quad \ge \alpha \int _{0}^{x}h(u)du-2p\left( t\right) \int _{0}^{x}h^{\prime }(u)h(u)du+\frac{p\left( t\right) }{4}Y^{2} \\&\quad \ge \int _{0}^{x}(\alpha -2p_{1}h_{1})h(u)du+\frac{p_{0}}{4}Y^{2}. \end{aligned}$$

Hence

$$\begin{aligned} \alpha \int _{0}^{x}h(u)du+p\left( t\right) h(x)Y+\frac{p\left( t\right) }{2} Y^{2}\ge \frac{h_{0}(\alpha -2p_{1}h_{1})}{2}x^{2}+\frac{p_{0}}{4}Y^{2}. \end{aligned}$$

(7)

Since

$$\begin{aligned} \frac{1}{2}\left( p\left( t\right) Z\right) ^{2}+\alpha yp\left( t\right) Z+\alpha \int _{0}^{y}f(x,\xi )\xi d\xi \ge 2\left( \frac{1}{4}\left( p\left( t\right) Z\right) ^{2}\right) +\alpha yp\left( t\right) Z+\frac{ \alpha f_{0}}{2}y^{2}, \end{aligned}$$

we have

$$\begin{aligned} \frac{1}{4}\left( p\left( t\right) Z\right) ^{2}+\alpha yp\left( t\right) Z+ \frac{\alpha f_{0}}{2}y^{2}\ge & {} \frac{1}{8}\left( p\left( t\right) Z+2\alpha y\right) ^{2}+\frac{1}{4}\alpha f_{0}\left( \frac{1}{f_{0}}p\left( t\right) Z+y\right) ^{2}\\&+\left( f_{0}-2\alpha \right) \left( \frac{\alpha }{4}y^{2}+ \frac{1}{8f_{0}}\left[ p\left( t\right) Z\right] ^{2}\right) . \end{aligned}$$

Therefore

$$\begin{aligned} \frac{1}{2}\left( p\left( t\right) Z\right) ^{2}+\alpha yp\left( t\right) Z+\alpha \int _{0}^{y}f(x,\xi )\xi d\xi \ge \left( f_{0}-2\alpha \right) \left( \frac{\alpha }{4}y^{2}+\frac{p_0^2}{ 8f_{0}}Z ^{2}\right) +\frac{p_0^2}{4}Z^2.\nonumber \\ \end{aligned}$$

(8)

Using (7), (8) and the fact that $\gamma _0\int _{t-\sigma }^{t}y^{2}(s)ds+\gamma _{1}\int _{t-\sigma }^{t}z^{2}(s)ds\ge 0$, it follows that

$$\begin{aligned} V\ge k_0\left( x^2+y^2+Y^2+Z^2\right) , \end{aligned}$$

(9)

where $k_0=\frac{1}{2}\min \left\{ h_{0}(\alpha -2p_{1}h_{1}),\frac{p_0}{2},\frac{\alpha (f_0-2\alpha )}{2},\frac{p_0^2}{2}\left( 1+\frac{ f_0-2\alpha }{2f_0}\right) \right\} .$

It is clear that

$$\begin{aligned} {\bar{V}}(x,y,z)=k_0 \left( x^2+y^2+Y^2+Z^2 \right) =0\quad \text {iff}\quad x=y=z=0, \end{aligned}$$

(10)

and

$$\begin{aligned} V(t,x,y,z)\ge k_0 \left( x^2+y^2+Y^2+Z^2 \right) ={\bar{V}}(x,y,z)>0\quad \text {if}\quad (x,y,z)\ne (0,0,0). \end{aligned}$$

(11)

By condition (i), we conclude that

$$\begin{aligned} W\ge k(x^2+y^2+Y^2+Z^2), \end{aligned}$$

(12)

where $k=k_0\cdot \exp {\left( \frac{1}{\omega }\left( p_0-p_1+q_0-q_1 \right) \right) }$.

This shows that W is positive definite.

The next step is to show that the derivative of (5) is negative definite. Differentiating (5) along trajectories of (4) gives

$$\begin{aligned} W_{(4)}'=\exp {-\left( \frac{1}{\omega }\int _{0}^{t}\left( \left| p^{\prime }\left( s\right) \right| +\left| q^{\prime }\left( s\right) \right| \right) ds\right) }\cdot \left( V_{(4)}'-\frac{1}{\omega }\left( \left| p^{\prime }\left( t\right) \right| +\left| q^{\prime }\left( t\right) \right| \right) V\right) ,\nonumber \\ \end{aligned}$$

(13)

with

$$\begin{aligned} V_{(4)}'=U_1+U_2+U_3, \end{aligned}$$

(14)

where

$$\begin{aligned} U_{1}=p^{\prime }\left( t\right) h\left( x\right) Y+\frac{p^{\prime }\left( t\right) }{2}Y^{2}+\alpha y\int _{0}^{y}f_{x}(x,u)udu, \\ U_{2}=\left( \gamma _{0}-\alpha g(x,y)\right) y^{2}-\gamma _{0}y^{2}\left( t-\sigma \right) +\gamma _{1}z^{2}-\gamma _{1}z^{2}\left( t-\sigma \right) , \end{aligned}$$

and

$$\begin{aligned} U_{3}=p\left( t\right) h^{\prime }\left( x\right) yY+p\left( t\right) \left[ \alpha -f(x,y)\right] zZ+p\left( t\right) YZ-p\left( t\right) g(x,y)yZ. \end{aligned}$$

(15)

On applying conditions (ii) and (iii), we obtain

$$\begin{aligned} U_{1} \le p^{\prime }\left( t\right) h\left( x\right) Y+\frac{p^{\prime }\left( t\right) }{2}Y^{2} \le \frac{\left| p^{\prime }\left( t\right) \right| }{2} h_{1}^{2}x^{2}+\left| p^{\prime }\left( t\right) \right| Y^{2}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} U_{2}&=\left( \gamma _{0}-\alpha g(x,y)\right) y^{2}-\gamma _{0}y^{2}\left( t-\sigma \right) +\gamma _{1}z^{2}-\gamma _{1}z^{2}\left( t-\sigma \right) \\&\le \left( \gamma _{0}-\alpha g_{0}\right) y^{2}-\gamma _{0}y^{2}\left( t-\sigma \right) +\gamma _{1}z^{2}-\gamma _{1}z^{2}\left( t-\sigma \right) . \end{aligned} \end{aligned}$$

Developing the estimate (15) according to Eqs. (2), (3), and using the fact $2|uv|\le (u^2+v^2)$, besides conditions $(i)-(ii)$, one get

$$\begin{aligned} U_{3}\le & {} \frac{\left| q^{\prime }(t)\right| }{2}\left( 2r_1^2\left( 1+\rho \right) +r_{1}g_{1}\left( \rho +2\right) +r_{1}\left( f_{1}-\alpha \right) \right) y^{2} \\&+\frac{1}{2}\left( r_1^3\left( 1+\rho \right) +r_1^2g_{1}\left( 1+\rho \right) +r_1^2h_{1}\left( 2+\rho \right) \right) y^{2} \\&+\frac{1}{2}\left( \rho r_{1}\left( r_{1}+L\right) \left( f_{1}-\alpha \right) +r_1^3\left( 1+\rho \right) +r_1^2g_{1}+r_{1}L\left( f_{1}-\alpha \right) +2r_0^2\left( \alpha -f_{0}\right) \right) z^{2} \\&+\frac{1}{2}\left( 2\rho r_1^2L\left( 1+\rho \right) +\rho r_{1}L\left( f_{1}+g_1-\alpha \right) +\rho r_1^3\left( 1+\rho \right) +\rho r_1^2h_{1}\right) y^{2}(t-\sigma ) \\&+\frac{1}{2}\left( \rho r_1^3\left( 1+\rho \right) +\rho r_1^2\left( f_{1}-\alpha \right) +\rho r_1^2g_{1}\right) z^{2}(t-\sigma ). \end{aligned}$$

Combining the estimates on $U_1-U_3$, we get

$$\begin{aligned} V^{\prime }\le & {} \xi \left( \left| p^{\prime }\left( t\right) \right| +\left| q^{\prime }(t)\right| \right) \left( x^{2}+y^{2}+Y^{2}\right) \\&+\frac{1}{2}\left( r_1^3\left( 1+\rho \right) +r_1^2g_{1}\left( 1+\rho \right) +r_1^2h_{1}\left( 2+\rho \right) +2\gamma _{0}-2\alpha g_{0}\right) y^{2} \\&+\frac{1}{2}\left( \rho r_{1}\left( r_{1}+L\right) \left( f_{1}-\alpha \right) +r_1^3\left( 1+\rho \right) +r_1^2g_{1}+r_{1}L\left( f_{1}-\alpha \right) \right. \\&\left. +2r_0^2\left( \alpha -f_{0}\right) +2\gamma _{1}\right) z^{2} \\&+\frac{1}{2}\left( 2\rho r_1^2L\left( 1+\rho \right) +\rho r_{1}L\left( f_{1}+g_{1}-\alpha \right) +\rho r_1^3\left( 1+\rho \right) +\rho r_1^2h_{1}-2\gamma _{0}\right) y^{2}(t-\sigma ) \\&+\frac{1}{2}\left( \rho r_1^3\left( 1+\rho \right) +\rho r_1^2\left( f_{1}+g_{1}-\alpha \right) -2\gamma _{1}\right) z^{2}(t-\sigma ), \end{aligned}$$

where $\xi =\frac{1}{2}\max \left\{ 2,h_1^2,2r_1^2(1+\rho )+r_1g_1(2+\rho )+r_1(f_1-\alpha ) \right\}$.

Putting

$$\begin{aligned} 2\gamma _{0}=2\rho r_1^2L\left( 1+\rho \right) +\rho r_{1}L\left( f_{1}+g_{1}-\alpha \right) +\rho r_1^3\left( 1+\rho \right) +\rho r_1^2h_{1}, \end{aligned}$$

and

$$\begin{aligned} 2\gamma _{1}=\rho r_1^2\left( f_{1}+g_{1}-\alpha \right) +\rho r_1^3\left( 1+\rho \right) , \end{aligned}$$

we get

$$\begin{aligned} \begin{aligned} V^{\prime } \le&\,\xi \left( \left| p^{\prime }\left( t\right) \right| +\left| q^{\prime }(t)\right| \right) \left( x^{2}+y^{2}+Y^{2}\right) \\&+\frac{1}{2}\left( a+2\rho r_1^2L\left( 1+\rho \right) +\rho r_1^2h_{1} +\rho r_{1}L\left( f_{1}+g_{1}-\alpha \right) +\rho r_1^3\left( 1+\rho \right) -2\alpha g_{0}\right) y^{2} \\&+\frac{1}{2}\left( b+\rho r_1^2\left( f_{1}+g_{1}-\alpha \right) +\rho r_1^3\left( 1+\rho \right) +2r_0^2\left( \alpha -f_{0}\right) \right) z^{2}. \end{aligned} \end{aligned}$$

Therefore, there exists a positive constant K such that

$$\begin{aligned} \begin{aligned} V'_{(4)}&\le \xi \left( \left| p^{\prime }\left( t\right) \right| +\left| q^{\prime }(t)\right| \right) \left( x^{2}+y^{2}+Y^{2}\right) -K(y^2(t)+z^2(t))\\&\le \frac{\xi }{k_0} \left( \left| p^{\prime }\left( t\right) \right| +\left| q^{\prime }(t)\right| \right) V-K(y^2(t)+z^2(t)). \end{aligned} \end{aligned}$$

(16)

Finally, take $\frac{1}{\omega }=\frac{\xi }{k_0}$, to get

$$\begin{aligned} W'_{(4)}\le -K\exp \left( -\frac{\xi }{k_0}\int _{0}^{t}\left( \left| p^{\prime }\left( s\right) \right| +\left| q^{\prime }\left( s\right) \right| \right) ds\right) (y^2(t)+z^2(t))\le 0. \end{aligned}$$

(17)

From the properties of the Lyapunov function (5), namely (12) and (17), we conclude that the zero solution of the system (4) is asymptotically stable. This terminates the proof of Theorem 1. $\square$

3 Example

Consider the following neutral delay differential equation

$$\begin{aligned} \begin{aligned}&\left( \left( 0.8+\frac{1}{10+t^{2}}\right) \left( \left( 0.9+\frac{1}{20+t^{2}}\right) (x(t)+\rho x(t-\sigma ))'\right) '\right) '\\&\quad +\left( 20.5-\frac{1}{3\pi }\arctan (x(t)x'(t))\right) x''(t)\\&\quad +\left( 4.35-\frac{1}{10\pi }\arctan (x(t)x'(t))\right) x'(t)+\left( 0.2x+\frac{x}{10+\mid x\mid }\right) =0. \end{aligned} \end{aligned}$$

(18)

Observing the functions over the Eq. (18), one can deduce the following

$$\begin{aligned} f_{0}= & {} 20\le f(x,y)=20.5-\frac{1}{3\pi }\arctan (xy)\le 21=f_{1}.\\ g_{0}= & {} 4.3\le g(x,y)=4.35-\frac{1}{10\pi }\arctan (xy)\le 4.4=g_{1}.\\ yf_x(x,y)= & {} -\frac{1}{3\pi }\frac{y^2}{1+x^2y^2}\le 0.\\ p_{0}= & {} 0.8\le p\left( t\right) =0.8+\frac{1}{10+t^{2}}\le 0.9=p_{1}.\\ q_0= & {} 0.9\le q\left( t\right) =0.9+\frac{1}{20+t^{2}}\le 0.95=q_{1}.\\ -L= & {} -0.95\le p'(t)=\frac{-2t}{(10+t^2)^2}\le 0.\\ -L= & {} -0.95\le q'(t)=\frac{-2t}{(20+t^2)^2}\le 0.\\ e(t)= & {} 0.\\ h(x)= & {} 0.2x+\frac{x}{10+\mid x\mid }. \end{aligned}$$

It is clear, from the relation of h(x), that $h(0)=0$. Besides, since $\displaystyle 0\le \frac{1}{ 10+\mid x\mid }\le 1,$ for all x, we have that

$$\begin{aligned} \frac{h(x)}{x}\ge 0.2=h_0,\quad \text {for all }x\ne 0. \end{aligned}$$

Moreover

$$\begin{aligned} |h^{\prime }(x)|=\left| 0.2+\frac{10}{(10+\mid x\mid )^{2}}\right| \le 0.3=h_1. \end{aligned}$$

Furthermore,

$$\begin{aligned} 2p_1h_1=0.54<\alpha =0.7<10=\frac{1}{2}f_0, \end{aligned}$$

and for $\rho =0.01$, we have

$$\begin{aligned} \begin{aligned} -0.3&=r_1^3\left( 1+\rho \right) +r_1^2g_{1}\left( 1+\rho \right) +r_1^2h_{1}\left( 2+\rho \right) \\&\quad +2\rho r_1^2L\left( 1+\rho \right) +\rho r_1^2h_{1}+\rho r_{1}L\left( f_{1}+g_{1}-\alpha \right) \\&\quad +\rho r_1^3\left( 1+\rho \right) -2\alpha g_{0}, \end{aligned} \end{aligned}$$

also

$$\begin{aligned} \begin{aligned} -0.9=&\rho r_1\left( r_{1}+L\right) \left( f_{1}-\alpha \right) +r_1^3\left( 1+\rho \right) +r_1^2g_{1}+r_{1}L\left( f_{1}-\alpha \right) +\rho r_1^2\left( f_{1}+g_{1}-\alpha \right) \\ {}&+\rho r_{1}^{3}\left( 1+\rho \right) +2r_0^2\left( \alpha -f_{0}\right) . \end{aligned} \end{aligned}$$

Fig. 1

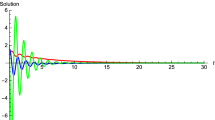
Numerical simulation of equation (18). $\sigma =0.2$

All the conditions of Theorem 1 hold, consequently the zero solution of (18) is asymptotically stable.

4 Square integrability

Our next results are stated with respect to $e(t)\ne 0$, hence Eq. (1) is rewriten as the following equivalent system

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}x'=y,\\ &{}y'=z,\\ &{}(p(t)Z)'=-f(x(t),y(t))z(t)-g(x(t),y(t))y(t)-h(x(t))+e(t). \end{aligned} \end{array}\right. } \end{aligned}$$

(19)

4.1 Boundedness of solutions

The main result of this section is the following lemma :

Lemma 1

Besides conditions of Theorem 1 being satisfied, suppose there exists a positive constant $e_1$ such that

• (v) $\int _{t_1}^{t}|e(s)|ds<e_1$,

hold. Then, every solution of (19) satisfies

$$\begin{aligned} |x(t)|\le N,\quad |y(t)|\le N,\quad \text {and}\quad |Z(t)|\le N, \end{aligned}$$

(20)

where N is a positive constant.

Proof

Over each solution (x(t), y(t), Z(t)) of (19), we have

$$\begin{aligned} W'_{(19)}=W'_{(4)}+\exp \left( -\frac{1}{\omega }\int _{t_1}^{t}(|p'(s)|+|q'(s)|)ds\right) \cdot (\alpha y+p(t)Z)e(t). \end{aligned}$$

From (17), we get

$$\begin{aligned} W'_{(19)}\le N_1(|y|+|Z|)|e(t)|, \end{aligned}$$

where $N_1=\exp \left( \frac{2\xi }{k_0}(p_1+q_1)\right) \max \{\alpha ,p_1\}$.

In view of inequality (12) together with the fact $|u|\le u^2+1$, we obtain

$$\begin{aligned} \begin{aligned} W'_{(19)}&\le N_1(y^2+Z^2+2)|e(t)|\\&\\&\le N_2|e(t)|W(t)+N_2|e(t)|, \end{aligned} \end{aligned}$$

(21)

where $N_2=\max \left\{ 2N_1,\frac{N_1}{k}\right\}$. Integrate from $t_1$ to t to arrive at

$$\begin{aligned} W(t)-W(t_1)\le N_2\int _{t_1}^{t}(|e(s)|W(s))ds+N_2\int _{t_1}^{t}|e(s)|ds. \end{aligned}$$

Thus

$$\begin{aligned} W(t)\le W(t_1)+e_1N_2+N_2\int _{t_1}^{t}(|e(s)|W(s))ds. \end{aligned}$$

Now, Gronwall inequality leads to

$$\begin{aligned} W(t)\le (W(t_1)+e_1N_2)\exp \left( N_2\int _{t_1}^{t}|e(s)|ds\right) \le N, \end{aligned}$$

(22)

where $N=(W(t_1)+e_1N_2)\exp \left( e_1N_2\right)$. This last inequality implies

$$\begin{aligned} |x(t)|\le N,\quad |y(t)|\le N,\quad \text {and}\quad |Z(t)|\le N, \end{aligned}$$

(23)

therefore, the proof is complete. $\square$

4.2 Square integrability of solutions

Our main result in this section is stated in the following Theorem and make use of Lemma 1:

Theorem 2

If conditions of Lemma 1 hold, then

$$\begin{aligned} \int _{t_0}^{\infty }\left( x''^2(s)+x'^2(s)+x^2(s)\right) ds<\infty . \end{aligned}$$

Proof

Define

$$\begin{aligned} G(t)=W(t)+\varepsilon \int _{t_{1}}^{t}(y^{2}(s)+z^{2}(s))ds\,for\,all\,t\ge t_{1}= t_{0}+\sigma \end{aligned}$$

(24)

where W is defined in (5) and $\varepsilon$ is to be determined, Differentiating (24) along solutions of (19) and using (17) and (21), we obtain

$$\begin{aligned} G'(t)\le & {} (\varepsilon -K)\exp \left( -\frac{\xi }{k_0} \int _{0}^{t}\left( \mid p'(s)\mid +\mid q'(s)\mid \right) \right) (y^{2}(t)+z^{2}(t))\\&+(N_{2}W(t)+N_{2})\mid e(t)\mid . \end{aligned}$$

Choosing $(\varepsilon -K)<0$ and using the fact that W(t) is bounded, we see that

$$\begin{aligned} G'(t)\le N_3\mid e(t)\mid , \end{aligned}$$

(25)

for some constant $N_{3}>0$. Integrating (25) from $t_{1}$ to t and using (i), we obtain

$$\begin{aligned} \int _{t_{1}}^{t}(y^{2}(s)+z^{2}(s))ds<\infty . \end{aligned}$$

That is, there exist positive constants $M_1$ and $M_2$ such that

$$\begin{aligned} \int _{t_{1}}^{t}y^2(s)ds\le M_1,\quad \text {and}\quad \int _{t_{1}}^{t}z^2(s)ds\le M_2. \end{aligned}$$

Hence

$$\begin{aligned} \int _{t_{1}}^{t}x'^2(s)ds\le M_1,\quad \text {and}\quad \int _{t_{1}}^{t}x''^2(s)ds\le M_2. \end{aligned}$$

(26)

Next, we show that $\int _{t_{1}}^{t} x^{2}(u)du<\infty$. Multiplying (1) by x(t) and integrating from $t_{1}$ to t, leads to

$$\begin{aligned} \int _{t_{1}}^{t} h(x(s))x(s)ds=L_{1}(t)+L_{2}(t)+L_{3}(t)+L_{4}(t), \end{aligned}$$

where

$$\begin{aligned}&L_{1}(t)=-\int _{t_{1}}^{t}(p(s)(q(s)(x(s)+\rho x(s-\sigma ))^{'})^{'})^{'}x(s)ds,\\&\quad L_{2}(t)=-\int _{t_{1}}^{t} f(x(s),x'(s))x''(s)x(s)ds,\\&\quad L_{3}(t)=-\int _{t_{1}}^{t} g(x(s),x'(s))x'(s)x(s)ds, \end{aligned}$$

and

$$\begin{aligned} L_{4}(t)=\int _{t_{1}}^{t} e(x(s))x(s)ds. \end{aligned}$$

Integrate $L_1$ by parts to get

$$\begin{aligned} \begin{aligned} L_{1}(t)=&-p(t)\left[ q'(t)\left[ x'(t)+\rho x'(t-\sigma )\right] +q(t)\left[ x''(t)+\rho x''(t-\sigma )\right] \right] x(t)\\&+p(t_{1})\left[ q'(t_{1})\left[ x'(t_{1})+\rho x'(t_{1}-\sigma )\right] +q(t_{1})\left[ x''(t_{1})+\rho x''(t_{1}-\sigma )\right] \right] x(t_{1})\\&+\int _{t_{1}}^{t}[p(t)[q'(s)x'(s)+q(s)x''(s)+\rho q'(s)x'(s-\sigma )+\rho q(s)x''(s-\sigma )]x'(s)]ds. \end{aligned} \end{aligned}$$

By condition (i) and inequalities (20) and (26), we have

$$\begin{aligned} L_{1}(t)\le \tau _1, \end{aligned}$$

where $\tau _1=p_{1}L(1+\rho )[2N^{2}+M_1]+p_{1}q_{1}(1+\rho )\left[ 2N^{2}+\frac{1}{2}(M_1+M_2)\right]$.

Next, by the use of inequality

$$\begin{aligned} \int _{t_1}^t f(s)g(s)ds\le \left( \int _{t_1}^t f^2(s)ds\right) ^{\frac{1}{2}}\left( \int _{t_1}^t g^2(s)ds\right) ^{\frac{1}{2}}, \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned} L_{2}(t)&=\int _{t_{1}}^{t}\mid f(x(s),x'(s))x''(s)x(s)\mid ds\\&\le \left( \int _{t_{1}}^{t}[f(x(s),x'(s))x''(s)]^{2}ds\right) ^{\frac{1}{2}}\left( \int _{t_{1}}^{t} x^{2}(s)ds\right) ^{\frac{1}{2}}, \end{aligned} \end{aligned}$$

and by condition (ii) and inequality (26), we get

$$\begin{aligned} L_2\le \tau _2\left( \int _{t_1}^{t}x^2(s)ds\right) ^{\frac{1}{2}}, \end{aligned}$$

where $\tau _2=f_1\sqrt{M_2}$. Similarly, we have

$$\begin{aligned} \begin{aligned} L_3(t)&=\int _{t_{1}}^{t}\mid g(x(s),x'(s))x'(s)x(s)\mid ds\\&\le \left( \int _{t_{1}}^{t}[g(x(s),x'(s))x'(s)]^{2}ds\right) ^{\frac{1}{2}}\left( \int _{t_{1}}^{t} x^{2}(s)ds\right) ^{\frac{1}{2}}\\&\le \tau _3\left( \int _{t_1}^{t}x^2(s)ds\right) ^{\frac{1}{2}}, \end{aligned} \end{aligned}$$

where $\tau _3=g_1\sqrt{M_1}$. Finally, applying (v) and (20), we obtain

$$\begin{aligned} L_{4}(t)\le \int _{t_{1}}^{t}\mid e(x(s))x(s)\mid ds\le Ne_{1}=\tau _4, \end{aligned}$$

On the other hand, from condition (iii), we have

$$\begin{aligned} \int _{t_{1}}^{t} h(x(s))x(s)ds\ge h_{0}\int _{t_{1}}^{t} x^{2}(s)ds, \end{aligned}$$

therefore,

$$\begin{aligned} h_{0}\int _{t_{1}}^{t} x^{2}(s)ds\le \tau _1+\tau _2\left( \int _{t_{1}}^{t} x^{2}(s)ds\right) ^{\frac{1}{2}}+\tau _3\left( \int _{t_{1}}^{t} x^{2}(s)ds\right) ^{\frac{1}{2}}+\tau _4. \end{aligned}$$

(27)

Suppose

$$\begin{aligned} \int _{t_{1}}^{t} x^{2}(s)ds\rightarrow \infty \quad as\quad t\rightarrow \infty , \end{aligned}$$

then dividing both ssides of (27) by $\left( \int _{t_{1}}^{t} x^{2}(s)ds\right) ^{\frac{1}{2}}$ immediately implies a contradiction. This completes the proof of Theorem 2. $\square$

4.3 Example

Consider again the neutral delay differential equation defined by (18) and choose $e(t)=\frac{1}{1+t^2}\ne 0$, namely

$$\begin{aligned}&\left( \left( 0.8+\frac{1}{10+t^{2}}\right) \left( \left( 0.9+\frac{1}{20+t^{2}}\right) (x(t)+\rho x(t-\sigma ))'\right) '\right) '\nonumber \\&\quad +\left( 20.5-\frac{1}{3\pi }\arctan (x(t)x'(t))\right) x''(t)\nonumber \\&\quad +\left( 4.35-\frac{1}{10\pi }\arctan (x(t)x'(t))\right) x'(t)+\left( 0.2x+\frac{x}{10+\mid x\mid }\right) =\frac{1}{1+t^2}. \end{aligned}$$

(28)

It is obvious that

$$\begin{aligned} \int _{t_1}^{\infty }\mid e(s)\mid ds<\infty , \end{aligned}$$

hence, all conditions of Theorem 2 are satisfied, the conclusions follow.