Bipolar soft rough sets and their applications in decision making

Abstract

In this study, concept of bipolar soft rough sets and set theoretical operations of bipolar soft rough sets are defined, and some of their properties are obtained. Also, a decision making method based on operations of bipolar soft rough sets is proposed to choose optimum element among alternatives. Finally, an illustrative example is given to show the method can be successfully applied to some problems.

1 Introduction

The concept of soft set was proposed by Molodtsov [17] in 1999 as a mathematical tool for dealing with uncertainty and vagueness. After Molodtsov [17], many researchers have made some contributions to the theory of soft sets. Maji et al. [15] introduced some novel concepts and operations on soft sets which are the soft subset, soft equality, soft union, soft intersection and soft complement. Ali et al. [3] proposed some new definitions related to intersection, union and difference. Çağman and Enginoğlu [5] redefined soft set operations to use effectively in decision making problems, and developed a decision making method called uni-int decision making method. Sezgin and Atagün [19] discussed basic operation of soft sets to make extending of theoretical aspect of soft set operations such as the intersection, extended intersection, restricted union and difference. Çağman [6] made some contributions to the theory of soft sets to fill gaps of former definition and operations.

Fuzzy sets [24] and intuitionistic fuzzy sets [4] are highly successful tools to model uncertainty and incomplete data encountered in decision making problems. A fuzzy set is identified by its membership function, and an intuitionistic fuzzy set is characterized by the membership and nonmembership functions. Intuitionistic fuzzy set is generalization of the fuzzy set. These sets have their own difficulties, which are pointed out in [17, 34], to construct a decision making method. To overcome these difficulties, the concept of bipolar fuzzy sets initiated by Zhang [34, 35] as a generalization of fuzzy sets. Bipolar fuzzy sets are an extension of fuzzy sets whose membership degree interval is $[-1,1]$. Abdullah et al. [1] introduced the notion of bipolar fuzzy soft sets by combining the soft sets and the bipolar fuzzy sets. Naz and Shabir [18] proposed the concept of fuzzy bipolar soft sets and investigated the algebraic structures of fuzzy bipolar soft sets. Also Shabir and Naz [20] defined bipolar soft sets and their operations. To construct algebraic and topological structures on bipolar soft sets Karaaslan and Karataş [11] redefined concept of bipolar soft sets and operations of bipolar soft sets which are based on bijective functions.

Pawlak [23] introduced rough set theory in 1982 as an alternative approach to the fuzzy set theory and tolerance theory, and applied successfully in many field such as pattern recognition, machine learning and data mining, etc. Dubois and Prade [7] defined lower and upper approximations of fuzzy set to extend concept of rough sets, and they proposed the concept of rough fuzzy set. Feng et al. [8] defined soft rough sets by combining the soft sets with rough sets. Feng et al. [9] introduced the soft rough approximations with their basic properties and gave an application of soft rough approximations in multi criteria group decision making problems. Meng et al. [16] proposed a new soft rough set model and obtained its properties, and established a more general model called soft rough fuzzy set. Ali [2] discussed concept of approximation space associated with each parameter in a soft set and defined an approximation space associated with the soft sets, and established connection between soft set, fuzzy soft set and rough sets. Zhang [26] presented a decision making method for intuitionistic fuzzy soft sets based on the rough set approach. Zhang [27] studied on parameter reduction fuzzy soft sets based on the soft fuzzy rough set and defined some new concepts such as lower soft fuzzy rough approximation operator and upper soft fuzzy rough approximation operator. To find approximations of a set, Shabir et al. [21] proposed concept of modified soft rough sets. Sun and Ma [22] proposed a new concept of soft fuzzy rough set by combining the fuzzy soft set and the fuzzy rough set. They also defined concept of the pseudo fuzzy binary relation and based on this concept they defined the soft fuzzy rough lower and upper approximation operators of any fuzzy subset in the parameter set. Karaaslan [12] introduced concept of soft class and soft class operations and defined soft rough class, and gave a decision making method determining effectiveness of decision makers. Some studies related to (fuzzy) soft rough sets, rough soft sets and their algebraic structures can be found in references [13, 14, 25, 28,29,30,31,32,33].

In this paper, we introduce for the first time concepts of soft P-lower positive, soft P-lower negative, soft P-upper positive and soft P-upper negative approximations considering both a subset of initial universe and complement of this subset. Later, we define concept of bipolar soft rough sets based on these approximations. We then propose a decision making method to select optimum element among the alternatives. Finally, we give an application of proposed decision making to show the method can be successfully applied to some problems containing uncertainty in the real world. The concept of bipolar soft rough set is more a general structure than soft rough set defined by Feng et al. [9]. With this point of view, bipolar soft rough set is an important tool for modeling of some problems in real life.

2 Preliminary

In this section, we present some basic concepts and properties of soft sets, bipolar soft sets, soft rough sets required in this study.

A soft set is a parameterized family of subsets of the universal set. Throughout the paper, U is an initial universe, $\mathcal {P}(U)$ is the power set of U and A is a subset of the parameter set.

Definition 1

[17] Let U be a set of objects, A be a set of parameters. Then, a mapping $F:A\rightarrow \mathcal {P}(U)$ is called a soft set over U and denoted by (F, A).

Example 1

Let $U=\{u_1,u_2,u_3,u_4,u_5,u_6,u_7,u_8\}$ be the universe containing eight houses and $A=\{a_1,a_2,a_3,a_4\}$ be the set of parameters where the parameters $a_i \, (i=1,2,3,4)$ stand for “modern”, “expensive”, “large” and “near to the city center” respectively. If a mapping $F:A\rightarrow \mathcal {P}(U)$ is given as; a set of houses $\{u_1,u_4,u_7,u_8\}$ is modern, a set of houses $\{u_1,u_3,u_4\}$ is expensive, a set of houses $\{u_1,u_2,u_3,u_8\}$ is large and a set of houses $\{u_1,u_2,u_3,u_8\}$ is near to the city center, then the soft set (F, A) can be written as $(F,A) = \big \{(a_1,\{u_1,u_3,u_4\}),(a_2,\{u_1,u_4,u_7,u_8\}),(a_3, \{u_1,u_2,u_3,u_8\}), (a_4, \{u_2, u_7\})\big \}$.

Definition 2

[15] Let A be a set of parameters. Then, NOT set of A, denoted by $\rceil A$, is defined by $\rceil A=\{\lnot a: a\in A\}$ where $\lnot a=\text { not } a$ for $a\in A$.

Example 2

If $A=\{a_1=good,\, a_2=cheap,\, a_3=modern\}$, then the NOT set of A is can be written by $\rceil A=\{\lnot a_1=not\, good,\, \lnot a_2=not\, cheap,\, \lnot a_3=not\, modern\}.$

Definition 3

[20] Let A be a parameter set and (F, A), $(G,\rceil A)$ be two soft sets over U such that $F(a)\cap G(\lnot a)=\emptyset$ for all $a\in A$. Then, a triplet (F, G, A) is called a bipolar soft set over U.

From now on, set of all bipolar soft sets over U will be denoted by $\mathcal {BS}_U$.

Definition 4

[20] Let $(F_1,G_1,A),(F_2,G_2,A)\in \mathcal {BS}_U$. $(F_1,G_1,A)$ is a bipolar soft subset of $(F_2,G_2,A)$, denoted by $(F_1,G_1,A)\tilde{\subseteq }(F_2,G_2,A)$, if $F_1(a)\subseteq F_2(a)$ and $G_2(\lnot a) \subseteq G_1(\lnot a)$ for all $a\in A$.

Definition 5

[20] Let $(F_1,G_1,A),(F_2,G_2,A)\in \mathcal {BS}_U$. $(F_1,G_1,A)$ is equal to $(F_2,G_2,A)$, denoted by $(F_1,G_1,A)=(F_2,G_2,A)$, if $(F_1,G_1,A)\tilde{\subseteq }(F_2,G_2,A)$ and $(F_2,G_2,A)\tilde{\subseteq }(F_1,G_1,A).$

Definition 6

[20] Let $(F,G,A)\in \mathcal {BS}_U$. Then, the complement of (F, G, A), denoted by $(F,G,A)^c$, is defined by $(F,G,A)^c = (F^c ,G^c ,A)$ where $F^c$ and $G^c$ are mappings given by $F^c (a) = G(\lnot a)$ and $G^c(\lnot a) = F(a)$ for all $a\in A$.

Definition 7

[20] Let $(F,G,A)\in \mathcal {BS}_U$. Then, (F, G, A) is called a relative null bipolar soft set, denoted by $(\Phi , \mathcal {U}, A)$, if $F(a)=\emptyset$ and $G(\lnot a)=U$ for all $a \in A$.

Definition 8

[20] Let $(F,G,A)\in \mathcal {BS}_U$. Then, (F, G, A) is called relative absolute bipolar soft set, denoted by $(\mathcal {U},\Phi , A)$, if $F(a)=U$ and $G(\lnot a)=\emptyset$ for all $a \in A$.

Definition 9

[9] Let U be a set of objects and A be a set of attributes. Then, (U, A) is called an information system, where each attribute $a\in A$ is a function $a:U\rightarrow V_a$, where $V_a$ is the set of values of attribute a.

If R is an equivalence relation on the universe U, then the pair (U, R) is called a Pawlak approximation space.

Definition 10

Let (F, A) be a soft set over U and (U, R) be a Pawlak approximation space. If R is taken as (F, A), then the Pawlak approximation space is called a soft approximation space and denoted by $P=(U,(F,A))$.

Definition 11

[9] Let (F, A) be a soft set over U, $X\subseteq U$ and $P=(U,(F,A))$ be a soft approximation space. Then,

$$\begin{aligned} \begin{aligned} \underline{S}_P(X)&= \{u\in U: \exists a\in A, [u\in F(a)\subseteq X]\}\\ \overline{S}_P(X)&=\{u\in U: \exists a\in A, [u\in F(a), F(a)\cap X\not =\emptyset ]\} \end{aligned} \end{aligned}$$

are called soft P-lower approximation and soft P-upper approximation of X, respectively.

Definition 12

[9] Let $\underline{S}_P(X)$ be the soft P-lower approximation and $\overline{S}_P(X)$ be the soft P-upper approximation of X. Then,

$$\begin{aligned} \begin{aligned} Pos_P(X)&= \underline{S}_P(X),\\ Neg_P(X)&=U{\setminus }\overline{S}_P(X),\\ Bnd_P(X)&=\overline{S}_P(X){\setminus }\underline{S}_P(X) \end{aligned} \end{aligned}$$

are called soft P-positive region, soft P-negative region and soft P-boundary region of X, respectively.

Definition 13

[9] Let $\underline{S}_P(X)$ be the soft P-lower approximation and $\overline{S}_P(X)$ be the soft P-upper approximation of X. If $\underline{S}_P(X)=\overline{S}_P(X)$, then X is said to be soft P-definable; otherwise X is called a soft P-rough set.

3 Bipolar soft rough sets

In this section, we define concept of bipolar soft rough sets and investigate their related properties.

We first show that information systems and bipolar soft sets are closely related.

Proposition 1

Each bipolar soft set is an information system.

Proof

Let us consider (F, G, A) be a bipolar soft set over U. If each $a\in A$ is an attribute, defined by $a:U\rightarrow V_a=\{-1,0,1\}$,

$$\begin{aligned} a(x)=\left\{ \begin{array}{ll} 1, &{} \quad if\;x\in F(a), \\ 0,&{} \quad if \;x \not \in F(a)\cup G(\lnot a)\\ -1, &{} \quad x\in G(\lnot a) \end{array} \right. \end{aligned}$$

then every bipolar soft set may be considered as an information system. $\square$

Definition 14

Let $(F,G,A)\in \mathcal {BS}_U$ and (U, R) be a Pawlak approximation space. If R is taken as (F, G, A), then the Pawlak approximation space is called a bipolar soft approximation space (BSA-space) and denoted by $P=(U,(F,G,A))$.

Definition 15

Let $(F,G,A)\in \mathcal {BS}_U$. Then, the mappings $F:A \rightarrow \mathcal {P} (U)$ and $G:\rceil A\rightarrow \mathcal {P}(U)$ are called positive soft set and negative soft set of (F, G, A), respectively.

Definition 16

Let $(F,G,A)\in \mathcal {BS}_U$ and $P=(U,(F,G,A))$ be a BSA-space. Then, the soft approximation spaces, denoted by $P^+=(U,(F,A))$ and $P^-=(U,(G,\rceil A))$, are called positive soft approximation space and negative soft approximation space of bipolar soft set (F, G, A), respectively.

After this, the complement of X in U is denoted by $\sim X$.

Definition 17

Let $(F,G,A)\in \mathcal {BS}_U$, $P=(U,(F,G,A))$ be a BSA-space and $X\subseteq U$. Then,

$$\begin{aligned} \underline{S}_{P^+}(X)= & {} \{u\in U:\exists a\in A, [u\in F(a)\subseteq X]\}, \\ \underline{S}_{P^-}(X)= & {} \{u\in U:\exists \lnot a\in \rceil A, [u\in G(\lnot a),G(\lnot a)\cap \sim X\ne \emptyset ]\}, \\ \overline{S}_{P^+}(X)= & {} \{u\in U:\exists a\in A, [u\in F(a),F(a)\cap X\ne \emptyset ]\}, \\ \overline{S}_{P^-}(X)= & {} \{u\in U:\exists \lnot a\in \rceil A, [u\in G(\lnot a)\subseteq \sim X]\} \end{aligned}$$

are called soft P-lower positive approximation $(SPL^+-approximation)$, soft P-lower negative approximation $(SPL^--approximation)$, soft P-upper positive approximation $(SPU^+-approximation)$ and soft P-upper negative approximation $(SPU^--approximation)$ of X, respectively.

In this definition, it is easy to see that $\underline{S}_{P^+}(X)\subseteq X$ and $\overline{S}_{P^-}(X)\subseteq \sim X$. However, $\underline{S}_{P^-}(X)\subseteq \sim X$ and $\overline{S}_{P^+}(X)\subseteq X$ don’t hold in generally.

Note that, it need not to be $\underline{S}_{P^+}(X)\cap \underline{S}_{P^-}(X)=\emptyset$. Also $\underline{S}_{P^+}(X)$ and $\overline{S}_{P^+}(X)$ are identical to soft P-lower and P-upper approximation of X defined by Feng et al. in [9], respectively.

Definition 18

Let $\underline{S}_{P^+}(X)$, $\underline{S}_{P^-}(X)$, $\overline{S}_{P^+}(X)$ and $\overline{S}_{P^-}(X)$ be $SPL^+-approximation$, $SPL^--approximation$, $SPU^+-approximation$ and $SPU^--approximation$ of X, respectively. Then,

$$\begin{aligned} \underline{BS}_{P}(X)= & {} \big (\underline{S}_{P^+}(X),\underline{S}_{P^-}(X)\big ), \\ \overline{BS}_{P}(X)= & {} \big (\overline{S}_{P^+}(X),\overline{S}_{P^-}(X)\big ) \end{aligned}$$

are called bipolar soft rough approximations of X.

Proposition 2

Let $(F,G,A)\in \mathcal {BS}_U$. Then,

• 1. $\underline{S}_{P^+}(X)\subseteq \overline{S}_{P^+}(X)$

• 2. $\overline{S}_{P^-}(X)\subseteq \underline{S}_{P^-}(X).$

Proof

• 1. Since $\underline{S}_{P^+}(X)$ and $\overline{S}_{P^+}(X)$ is identical to definitions of soft lower and upper approximations given in [9], the proof is clear.

• 2. Let $u\in \overline{S}_{P^-}(X)$. By Definition 17, $u\in G(\lnot a)\subseteq \sim X$ for some $\lnot a\in \rceil A$. Thus, it follows that $G(\lnot a)\cap \sim X\not =\emptyset$ and $u\in G(\lnot a)$. Therefore, we get $u\in \underline{S}_{P^-}(X)$. This show that $\overline{S}_{P^-}(X)\subseteq \underline{S}_{P^-}(X)$.

$\square$

Definition 19

Let $(F,G,A)\in \mathcal {BS}_U$, $P=(U,(F,G,A))$ be a BSA-space and $X,Y\subseteq U$. Then,

• 1. $\underline{BS}_{P}(X)\sqsubseteq \underline{BS}_{P}(Y) \Leftrightarrow \underline{S}_{P^+}(X)\subseteq \underline{S}_{P^+}(Y)$ and $\underline{S}_{P^-}(X)\supseteq \underline{S}_{P^-}(Y)$

• 2. $\overline{BS}_{P}(X)\sqsubseteq \overline{BS}_{P}(Y) \Leftrightarrow \overline{S}_{P^+}(X)\subseteq \overline{S}_{P^+}(Y)$ and $\overline{S}_{P^-}(X)\supseteq \overline{S}_{P^-}(Y).$

Corollary 1

If $X=Y$, then $\underline{BS}_{P}(X)\sqsubseteq \overline{BS}_{P}(X).$ Also, it is clear that $\underline{S}_{P^+}(X)\subseteq \overline{S}_{P^+}(X)$, $\overline{S}_{P^-}(X)\subseteq \underline{S}_{P^-}(X)$ for all $X\subseteq U$.

Definition 20

Let $(F,G,A)\in \mathcal {BS}_U$ and $P=(U,(F,G,A))$ be a BSA-space. If $\underline{BS}_{P}(X)\sqsubseteq \overline{BS}_{P}(X)$ and $\overline{BS}_{P}(X)\sqsubseteq \underline{BS}_{P}(X)$ , then

$$\begin{aligned} \underline{BS}_{P}(X)=\overline{BS}_{P}(X). \end{aligned}$$

Definition 21

Let $(F,G,A)\in \mathcal {BS}_U$, and $P=(U,(F,G,A))$ be a BSA-space. Then,

$$\begin{aligned} BPOS_P(X)= & {} \big (\underline{S}_{P^+}(X),\overline{S}_{P^-}(X)\big ), \\ BNEG_P(X)= & {} \big (\sim \overline{S}_{P^+}(X),\sim \underline{S}_{P^-}(X)\big ), \\ BBND_P(X)= & {} \big (\overline{S}_{P^+}(X){\setminus } \underline{S}_{P^+}(X), \underline{S}_{P^-}(X){\setminus }\overline{S}_{P^-}(X)\big ) \end{aligned}$$

are called bipolar soft P-positive region ($BSP^+-region$), bipolar soft P-negative region ($BSP^--region$) and bipolar soft P-boundary region ($BSB-region$) of X, respectively. If $\underline{BS}_{P}(X)=\overline{BS}_{P}(X)$, X is said to be bipolar soft P-definable; otherwise X is called a bipolar soft P-rough set.

Form Definition 17 and Proposition 2, we immediately have that $X\subseteq U$ is a bipolar soft P-definable set, if the bipolar soft P -boundary region $BBND_P(X)$ of X is $(\emptyset ,\emptyset )$.

Now, let us give an example to explain some definitions presented above by considering example of the bipolar soft set given in [20].

Example 3

Let U be the set of houses under consideration, and E be the set of parameters, $U = \{h_1,h_2,h_3,h_4,h_5\}$, $A = \{a_1,a_2,a_3,a_4\} = \{\textit{in the green surroundings, wooden,} \textit{cheap, in good repair}\}$. Then $\rceil A = \{\lnot a_1,\lnot a_2,\lnot a_3,\lnot a_4\} = \{\textit{in the commercial area,} \textit{marbled, expensive, in bad repair}\}$. The bipolar soft sets (F, G, A) describe the “requirements of the houses” which Mr. X going to buy. Suppose that

$$\begin{aligned} F(a_1)= & {} \{h_2, h_3\}, F(a_2) = \{h_2, h_5\}, F(a_3) = \{h_3\},F(a_4) = \{h_2, h_3, h_5\} \\ G(\lnot a_1)= & {} \{h_4, h_5\},G(\lnot a_2) = \{h_3, h_4\}, G(\lnot a_3) = \{h_2, h_4\},G(\lnot a_4) = \{h_4\}. \end{aligned}$$

For $X=\{h_1,h_2,h_3\}\subseteq U$, we have $SPL^+-approximation$ $\underline{S}_{P^+}(X)=\{h_2,h_3\}$ and $SPL^--approximation$ $\underline{S}_{P^-}(X)= \{h_2,h_3,h_4,h_5\}$. Thus

$$\begin{aligned} \underline{BS}_{P}(X)=\big (\{h_2,h_3\},\{h_2,h_3,h_4,h_5\}). \end{aligned}$$

(1)

Also we have $SPU^+-approximation$ $\overline{S}_{P^+}(X)\!=\!\{h_2,h_3,h_5\}$ and $SPU^--approximation$ $\overline{S}_{P^-}(X)=\{h_4,h_5\}$. Thus

$$\begin{aligned} \overline{BS}_{P}(X)=\big (\{h_2,h_3,h_5\},\{h_4,h_5\}). \end{aligned}$$

(2)

From (1) and (2)

$$\begin{aligned} \underline{BS}_{P}(X)\ne \overline{BS}_{P}(X) \end{aligned}$$

and so X is a bipolar soft P-rough set. Moreover, $BSP^+-region$, $BSP^--region$ and $BSB-region$ of X can be obtained, respectively, as follows:

$$\begin{aligned} BPOS_P(X)= & {} \big (\{h_2,h_3\},\{h_4,h_5\}\big ), \\ BNEG_P(X)= & {} \big (\{h_1,h_4\},\{h_1\}\big ), \\ BBND_P(X)= & {} \big (\{h_5\},\{h_2,h_3\}\big ). \end{aligned}$$

If $X_1=\{h_1\}\subseteq U$. Since $\underline{BS}_{P}(X_1)= \big (\emptyset , \{h_2,h_3,h_4,h_5\}\big )=\overline{BS}_{P}(X_1)$, $X_1$ is a bipolar soft P-definable set.

Here $X_1$ is a bipolar soft P-definable set since $X_1=\{h_1\}\subseteq U{\setminus } \{h_2,h_3,h_4,h_5\}$.

Proposition 3

Let $(F,G,A)\in \mathcal {BS}_U$ and $P=(U,(F,G,A))$ be a BSA-space. Then, for all $X\subseteq U$,

$$\begin{aligned} \underline{BS}_{P}(X)=\big (\bigcup _{a\in A}\{F(a):F(a)\subseteq X\},\bigcup _{\lnot a \in \rceil A }\{G(\lnot a):G(\lnot a)\cap \sim X\ne \emptyset \} \big ) \end{aligned}$$

and

$$\begin{aligned} \overline{BS}_{P}(X)=\big (\bigcup _{a\in A}\{F(a):F(a)\cap X\ne \emptyset \},\bigcup _{\lnot a \in \rceil A }\{G(\lnot a):G(\lnot a)\subseteq \sim X\} \big ). \end{aligned}$$

Proposition 4

Let $(F,G,A)\in \mathcal {BS}_U$ and $P=(U,(F,G,A))$ be a BSA-space. Then for any $X\subseteq U$, X is bipolar soft $P-$definable if and only if $\overline{S}_{P^+}(X)\subseteq X$ and $\underline{S}_{P^-}(X)\subseteq \sim X$.

Proof

Let X is bipolar soft $P-$definable. Then $\overline{S}_{P^+}(X)=\underline{S}_{P^+}(X)$ and $\underline{S}_{P^-}(X)=\overline{S}_{P^-}(X)$. Therefore $\overline{S}_{P^+}(X)=\underline{S}_{P^+}(X)\subseteq X$ and $\underline{S}_{P^-}(X)=\overline{S}_{P^-}(X)\subseteq \sim X$.

Conversely, let $\overline{S}_{P^+}(X)\subseteq X$ and $\underline{S}_{P^-}(X)\subseteq \sim X$. In order to show that X is bipolar soft $P-$definable, it is sufficient that $\overline{S}_{P^+}(X)\subseteq \underline{S}_{P^+}(X)$ and $\underline{S}_{P^-}(X)\subseteq \overline{S}_{P^-}(X)$, since $\underline{S}_{P^+}(X)\subseteq \overline{S}_{P^+}(X)$ and $\overline{S}_{P^-}(X)\subseteq \underline{S}_{P^-}(X)$. Let $u\in \overline{S}_{P^+}(X)$. Then $u\in F(a)$ and $F(a)\cap X\not =\emptyset$ for some $a\in A$. From Proposition 3 and hypothesis, $u\in F(a)\subseteq \overline{S}_{P^+}(X)\subseteq X$. Therefore $u\in \underline{S}_{P^+}(X)$, and so $\overline{S}_{P^+}(X)\subseteq \underline{S}_{P^+}(X)$. Also, let $u\in \underline{S}_{P^-}(x)$. Then $u\in G(\lnot a)$ and $G(\lnot a)\cap X\not =\emptyset$ for some $\lnot a \in \rceil A$. From Proposition 3 and hypothesis, $u\in G(\lnot a)\subseteq \underline{S}_{P^-}(X)\subseteq \sim X$. Thus $u\in \overline{S}_{P^-}(X)$, and so $\underline{S}_{P^-}(X)\subseteq \overline{S}_{P^-}(X)$. $\square$

Definition 22

Let $(F,G,A)\in \mathcal {BS}_U$, $P=(U,(F,G,A))$ be a BSA-space and $X,Y \subseteq U$. Then, union of bipolar soft P-lower approximations and bipolar soft P-upper approximations of sets X and Y are defined as, respectively,

$$\begin{aligned} \underline{BS}_{P}(X)\sqcup \underline{BS}_{P}(Y)= & {} \big (\underline{S}_{P^+}(X)\cup \underline{S}_{P^+}(Y), \underline{S}_{P^-}(X)\cap \underline{S}_{P^-}(Y) \big ) \\ \overline{BS}_{P}(X)\sqcup \overline{BS}_{P}(Y)= & {} \big (\overline{S}_{P^+}(X)\cup \overline{S}_{P^+}(Y), \overline{S}_{P^-}(X)\cap \overline{S}_{P^-}(Y) \big ). \end{aligned}$$

Definition 23

Let $(F,G,A)\in \mathcal {BS}_U$, $P=(U,(F,G,A))$ be a BSA-space and $X,Y \subseteq U$. Then, intersection of bipolar soft P-lower approximations and bipolar soft P-upper approximations of sets X and Y are defined as, respectively,

$$\begin{aligned} \underline{BS}_{P}(X)\sqcap \underline{BS}_{P}(Y)= & {} \big (\underline{S}_{P^+}(X)\cap \underline{S}_{P^+}(Y), \underline{S}_{P^-}(X)\cup \underline{S}_{P^-}(Y) \big ) \\ \overline{BS}_{P}(X)\sqcap \overline{BS}_{P}(Y)= & {} \big (\overline{S}_{P^+}(X)\cap \overline{S}_{P^+}(Y), \overline{S}_{P^-}(X)\cup \overline{S}_{P^-}(Y) \big ). \end{aligned}$$

Proposition 5

Let $(F,G,A)\in \mathcal {BS}_U$, $P=(U,(F,G,A))$ be a BSA-space and $X, Y\subseteq U$. Then,

• 1. $\underline{S}_{P^+}(\emptyset )=\overline{S}_{P^+}(\emptyset )= \emptyset$

• 2. $\underline{S}_{P^+}(U)=\overline{S}_{P^+}(U)=\cup _{a\in A}F(a)$

• 3. $\underline{S}_{P^+}(X\cap Y)\subseteq \underline{S}_{P^+}(X)\cap \underline{S}_{P^+}(Y)$

• 4. $\underline{S}_{P^+}(X\cup Y)\supseteq \underline{S}_{P^+}(X)\cup \underline{S}_{P^+}(Y)$

• 5. $\overline{S}_{P^+}(X\cap Y)\subseteq \overline{S}_{P^+}(X)\cap \overline{S}_{P^+}(Y)$

• 6. $\overline{S}_{P^+}(X\cup Y)=\overline{S}_{P^+}(X)\cup \overline{S}_{P^+}(Y)$

• 7. $X\subseteq Y \Rightarrow \underline{S}_{P^+}(X) \subseteq \underline{S}_{P^+}(Y)$

• 8. $X\subseteq Y \Rightarrow \overline{S}_{P^+}(X) \subseteq \overline{S}_{P^+}(Y)$

Proof

This proposition is similar to the proposition given by Feng et al. [8] where the soft approximation spaces $\underline{apr}_P(X)$ and $\overline{apr}_P(X)$ are used instead of $\underline{S}_{P^+}(X)$ and $\overline{S}_{P^+}(X)$, respectively. $\square$

Proposition 6

Let $(F,G,A)\in \mathcal {BS}_U$, $P=(U,(F,G,A))$ be a BSA-space and $X, Y\subseteq U$. Then,

• 1. $\underline{S}_{P^-}(\emptyset )=\overline{S}_{P^-}(\emptyset )= \cup _{\lnot a \in \rceil A }G(\lnot a)$

• 2. $\underline{S}_{P^-}(U)=\overline{S}_{P^-}(U)=\emptyset$

• 3. $\underline{S}_{P^-}(X\cap Y)= \underline{S}_{P^-}(X)\cup \underline{S}_{P^-}(Y)$

• 4. $\underline{S}_{P^-}(X\cup Y)\subseteq \underline{S}_{P^-}(X)\cap \underline{S}_{P^-}(Y)$

• 5. $\overline{S}_{P^-}(X\cap Y)\supseteq \overline{S}_{P^-}(X)\cup \overline{S}_{P^-}(Y)$

• 6. $\overline{S}_{P^-}(X\cup Y)= \overline{S}_{P^-}(X)\cap \overline{S}_{P^-}(Y)$

• 7. $X\subseteq Y \Rightarrow \underline{S}_{P^-}(Y) \subseteq \underline{S}_{P^-}(X)$

• 8. $X\subseteq Y \Rightarrow \overline{S}_{P^-}(Y) \subseteq \overline{S}_{P^-}(X).$

Proof

• 1. According to the definition of $SPL^--approximation$, $\underline{S}_{P^-}(\emptyset )=\bigcup _{\lnot e \in \rceil A} \{G(\lnot a):G(\lnot a)\cap \sim \emptyset \not =\emptyset \}$. Since $G(\lnot a)\cap U=G(\lnot a)$, $\underline{S}_{P^-}(\emptyset )=\bigcup _{\lnot a \in \rceil A }G(\lnot a)$. From definition of $SPU^--approximation$, $\overline{S}_{P^-}(\emptyset )=\bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\subseteq \sim \emptyset \}$. As $G(\lnot a)\subseteq U$ for all $\lnot a \in \rceil A$, $\overline{S}_{P^-}(\emptyset )=\bigcup _{\lnot a \in \rceil A }G(\lnot a)$.

• 2. From definition of $SPL^--approximation$, we know that $\underline{S}_{P^-}(U)=\bigcup _{\lnot a \in \rceil A}\{G(\lnot a): G(\lnot a)\cap \sim U\not =\emptyset \}$. But, since $G(\lnot a)\cap \emptyset =\emptyset$ for all $\lnot a\in \rceil A$, $\underline{S}_{P^-}(U)=\emptyset$. According to the definition of $SPU^--approximation$, $\overline{S}_{P^-}(U)=\bigcup _{\lnot a \in \rceil A}\{G(\lnot a): G(\lnot a)\subseteq \sim U \}$. Since $G(\lnot a)\subseteq \emptyset$, $G(\lnot a)=\emptyset$ for all $\lnot a \in \rceil A$ and so $\overline{S}_{P^-}(U)=\emptyset$.

• 3. Let $u\in \underline{S}_{P^-}(X\cap Y).$

  $$\begin{aligned} u\in \underline{S}_{P^-}(X\cap Y)\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a): G(\lnot a)\cap \sim (X\cap Y)\not =\emptyset \} \nonumber \\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a): G(\lnot a)\cap (\sim X\cup \sim Y)\not =\emptyset \} \nonumber \\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\cap \sim X\not =\emptyset \}\nonumber \\&\cup \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\cap \sim Y\not =\emptyset \}\nonumber \\\Rightarrow & {} u\in \underline{S}_{P^-}(X)\cup \underline{S}_{P^-}(Y)\nonumber \\ \underline{S}_{P^-}(X\cap Y)\subseteq & {} \underline{S}_{P^-}(X)\cup \underline{S}_{P^-}(Y). \end{aligned}$$

  (3)

  We prove the reverse inclusion as follows:

  $$\begin{aligned} u\in \underline{S}_{P^-}(X)\cup \underline{S}_{P^-}(Y)\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\cap \sim X\not =\emptyset \}\nonumber \\&\cup \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\cap \sim Y\not =\emptyset \}\nonumber \\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\cap (\sim X\cup \sim Y)\not =\emptyset \} \nonumber \\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\cap \sim (X\cap Y)\not =\emptyset \} \nonumber \\\Rightarrow & {} u\in \underline{S}_{P^-}(X\cap Y)\nonumber \\ \underline{S}_{P^-}(X)\cup \underline{S}_{P^-}(Y)\subseteq & {} \underline{S}_{P^-}(X\cap Y). \end{aligned}$$

  (4)

  From (3) and (4), we have $\underline{S}_{P^-}(X\cap Y)=\underline{S}_{P^-}(X)\cup \underline{S}_{P^-}(Y)$.

• 4. Let $u\in \underline{S}_{P^-}(X\cup Y).$

  $$\begin{aligned} u\in \underline{S}_{P^-}(X\cup Y)\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\cap \sim (X\cup Y)\not =\emptyset \} \\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a): G(\lnot a)\cap (\sim X\cap \sim Y)\not =\emptyset \} \\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\cap \sim X\not =\emptyset \}\\&\cap \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\cap \sim Y\not =\emptyset \}\\\Rightarrow & {} u\in \underline{S}_{P^-}(X)\cap \underline{S}_{P^-}(Y). \end{aligned}$$

  Then,

  $$\begin{aligned} \underline{S}_{P^-}(X\cup Y)\subseteq \underline{S}_{P^-}(X)\cap \underline{S}_{P^-}(Y). \end{aligned}$$

  Let us show by an example that reverse inclusion don’t held. Consider bipolar soft set given in Example 3 and subsets $X=\{h_1,h_2,h_3\}$ and $Y=\{h_2,h_4,h_5\}$ of $U=\{h_1,h_2,h_3,h_4,h_5\}$. Then, $\underline{S}_{P^-}(X)=\{h_2,h_3,h_4,h_5\}$ and $\underline{S}_{P^-}(Y)=\{h_1,h_3,h_4\}$. Since $\underline{S}_{P^-}(X\cup Y)=\emptyset$ and $\underline{S}_{P^-}(X) \cap \underline{S}_{P^-}(Y)=\{h_3,h_4\}$, $\underline{S}_{P^-}(X) \cap \underline{S}_{P^-}(Y)\not \subseteq \underline{S}_{P^-}(X\cup Y).$

• 5. Let $u\in \overline{S}_{P^-}(X\cap Y).$

  $$\begin{aligned} u\in \overline{S}_{P^-}(X)\cup \overline{S}_{P^-}(Y)\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A} \{G(\lnot a): G(\lnot a)\subseteq \sim X\}\\&\cup \bigcup _{\lnot a \in \rceil A}\{G(\lnot a): G(\lnot a)\subseteq \sim Y \}\\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A} \{G(\lnot a): G(\lnot a)\subseteq (\sim X\cup \sim Y)\} \\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A} \{G(\lnot a): G(\lnot a)\subseteq \sim (X\cap Y)\} \\\Rightarrow & {} u\in \overline{S}_{P^-}(X\cap Y). \end{aligned}$$

  Then, $\overline{S}_{P^-}(X)\cup \overline{S}_{P^-}(Y) \subseteq \overline{S}_{P^-}(X\cap Y).$

• 6. Let $u\in \overline{S}_{P^-}(X\cup Y).$

  $$\begin{aligned} u\in \overline{S}_{P^-}(X\cup Y)\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A} \{G(\lnot a): G(\lnot a)\subseteq \sim (X\cup Y)\} \nonumber \\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A} \{G(\lnot a):G(\lnot a)\subseteq (\sim X\cap \sim Y)\} \nonumber \\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A} \{G(\lnot a):G(\lnot a)\subseteq \sim X\}\nonumber \\&\cap \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\subseteq \sim Y \}\nonumber \\\Rightarrow & {} u\in \overline{S}_{P^-}(X)\cap \overline{S}_{P^-}(Y)\nonumber \\ \overline{S}_{P^-}(X\cup Y)\subseteq & {} \overline{S}_{P^-}(X)\cap \overline{S}_{P^-}(Y). \end{aligned}$$

  (5)

  We prove the reverse inclusion as follows:

  $$\begin{aligned} u\in \overline{S}_{P^-}(X)\cap \overline{S}_{P^-}(Y)\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a): G(\lnot a)\subseteq \sim X\}\nonumber \\&\cap \bigcup _{\lnot a \in \rceil A} \{G(\lnot a): G(\lnot a)\subseteq \sim Y \}\nonumber \\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a): G(\lnot a)\subseteq (\sim X\cup \sim Y)\} \nonumber \\\Rightarrow & {} u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\subseteq \sim (X\cap Y)\} \nonumber \\\Rightarrow & {} u\in \overline{S}_{P^-}(X\cup Y)\nonumber \\ \overline{S}_{P^-}(X)\cap \overline{S}_{P^-}(Y)\subseteq & {} \overline{S}_{P^-}(X\cup Y). \end{aligned}$$

  (6)

  From (5) and (6), $\overline{S}_{P^-}(X\cup Y)=\overline{S}_{P^-}(X)\cap \overline{S}_{P^-}(Y).$

  Let us show by an example that reverse inclusion don’t held. Consider bipolar soft set given in Example 3 and subsets $X=\{h_1,h_2,h_3\}$ and $Y=\{h_2,h_4,h_5\}$ of $U=\{h_1,h_2,h_3,h_4,h_5\}$. Then, $\overline{S}_{P^-}(X)=\{h_4,h_5\}$ and $\overline{S}_{P^-}(Y)=\emptyset$. Since $\overline{S}_{P^-}(X\cap Y)=\{h_3,h_4,h_5\}$ and $\overline{S}_{P^-}(X) \cup \overline{S}_{P^-}(Y)=\{h_4,h_5\}$, $\overline{S}_{P^-}(X\cup Y)\not \subseteq \overline{S}_{P^-}(X) \cup \overline{S}_{P^-}(Y).$

• 7. Let $u\in \underline{S}_{P^-}(Y)$, then $u\in \bigcup _{\lnot a \in \rceil A} \{G(\lnot a):G(\lnot a)\cap \sim Y\not =\emptyset \}$. Since $X\subseteq Y$, $\sim Y\subseteq \sim X$ and so $u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\cap \sim X\not =\emptyset \}$. Therefore $\underline{S}_{P^-}(Y) \subseteq \underline{S}_{P^-}(X)$.

• 8. Assume that $u\in \overline{S}_{P^-}(Y)$, then $u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\subseteq \sim Y\}$. Since $\sim Y\subseteq \sim X$, $u\in \bigcup _{\lnot a \in \rceil A}\{G(\lnot a):G(\lnot a)\subseteq \sim X\}$. Thus, $\overline{S}_{P^-}(Y) \subseteq \overline{S}_{P^-}(X)$.

$\square$

Proposition 7

Let $(F,G,A)\in \mathcal {BS}_U$, $P=(U,(F,G,A))$ be a BSA-space and $X,Y\subseteq U$. Then, the bipolar soft rough approximations held on the following properties:

• 1. $\underline{BS}_{P}(\emptyset )=\overline{BS}_{P}(\emptyset )=( \emptyset ,\bigcup _{\lnot a \in \rceil A }G(\lnot a))$

• 2. $\underline{BS}_{P}(U)=\overline{BS}_{P}(U)=(\bigcup _{a\in A}F(a),\emptyset )$

• 3. $\underline{BS}_{P}(X\cap Y)\sqsubseteq \underline{BS}_{P}(X)\sqcap \underline{BS}_{P}(Y)$

• 4. $\underline{BS}_{P}(X\cup Y)\sqsupseteq \underline{BS}_{P}(X)\sqcup \underline{BS}_{P}(Y)$

• 5. $\overline{BS}_{P}(X\cup Y)= \overline{BS}_{P}(X)\sqcup \overline{BS}_{P}(Y)$

• 6. $\overline{BS}_{P}(X\cap Y)\sqsubseteq \overline{BS}_{P}(X)\sqcap \overline{BS}_{P}(Y)$

• 7. $X\subseteq Y \Rightarrow \underline{BS}_{P}(X) \sqsubseteq \underline{BS}_{P}(Y)$

• 8. $X\subseteq Y \Rightarrow \overline{BS}_{P}(X) \sqsubseteq \overline{BS}_{P}(Y)$

Proof

• 1. Proof is clear from Proposition 5-1 and Proposition 6-1.

• 2. From Proposition 5-2 and Proposition 6-2, the proof is clear.

• 3. By Definition 17, $\underline{BS}_{P}(X\cap Y)= \big (\underline{S}_{P^+}(X\cap Y),\underline{S}_{P^-}(X\cap Y) \big )$. From Proposition 5 and Proposition 6, $\underline{S}_{P^+}(X\cap Y)\subseteq \underline{S}_{P^+}(X)\cap \underline{S}_{P^+}(Y)$ and $\underline{S}_{P^-}(X\cap Y)= \underline{S}_{P^-}(X)\cup \underline{S}_{P^-}(Y)$, respectively. Therefore,

  $$\begin{aligned} \underline{BS}_{P}(X\cap Y)\sqsubseteq & {} \big (\underline{S}_{P^+}(X)\cap \underline{S}_{P^+}(Y), \underline{S}_{P^-}(X)\cup \underline{S}_{P^-}(Y)\big )\\\sqsubseteq & {} \big (\underline{S}_{P^+}(X),\underline{S}_{P^-}(X)\big )\sqcap \big (\underline{S}_{P^-}(Y), \underline{S}_{P^-}(Y)\big )\\\sqsubseteq & {} \underline{BS}_{P}(X)\sqcap \underline{BS}_{P}(Y). \end{aligned}$$

• 4. From Definition 17, $\underline{BS}_{P}(X\cup Y)=\big (\underline{S}_{P^+}(X\cup Y),\underline{S}_{P^-}(X\cup Y) \big )$, by Proposition 5 and Proposition 6, $\underline{S}_{P^+}(X\cup Y)\supseteq \underline{S}_{P^+}(X)\cup \underline{S}_{P^+}(Y)$ and $\underline{S}_{P^-}(X\cup Y)\subseteq \underline{S}_{P^-}(X)\cap \underline{S}_{P^-}(Y)$, respectively. Thus,

  $$\begin{aligned} \underline{BS}_{P}(X\cup Y)\sqsupseteq & {} \big (\underline{S}_{P^+}(X)\cup \underline{S}_{P^+}(Y), \underline{S}_{P^-}(X)\cap \underline{S}_{P^-}(Y)\big )\\\sqsupseteq & {} \big (\underline{S}_{P^+}(X),\underline{S}_{P^-}(X)\big )\sqcup \big (\underline{S}_{P^-}(Y), \underline{S}_{P^-}(Y)\big )\\\sqsupseteq & {} \underline{BS}_{P}(X)\sqcup \underline{BS}_{P}(Y). \end{aligned}$$

• 5. From Definition 17, $\overline{BS}_{P}(X\cup Y)=\big (\overline{S}_{P^+}(X\cup Y),\overline{S}_{P^-}(X\cup Y) \big )$, by Proposition 5 and Proposition 6, $\overline{S}_{P^+}(X\cup Y)= \overline{S}_{P^+}(X)\cup \overline{S}_{P^+}(Y)$ and $\overline{S}_{P^-}(X\cup Y)= \overline{S}_{P^-}(X)\cap \overline{S}_{P^-}(Y)$, respectively. Thus,

  $$\begin{aligned} \overline{BS}_{P}(X\cup Y)= & {} \big (\overline{S}_{P^+}(X)\cup \overline{S}_{P^+}(Y), \overline{S}_{P^-}(X)\cap \overline{S}_{P^-}(Y)\big )\\= & {} \big (\overline{S}_{P^+}(X),\overline{S}_{P^-}(X)\big )\sqcup \big (\overline{S}_{P^-}(Y), \overline{S}_{P^-}(Y)\big )\\= & {} \overline{BS}_{P}(X)\sqcup \overline{BS}_{P}(Y). \end{aligned}$$

• 6. From Definition 17, $\overline{BS}_{P}(X\cap Y)=\big (\overline{S}_{P^+}(X\cap Y),\overline{S}_{P^-}(X\cap Y) \big )$, by Proposition 5 and Proposition 6, $\overline{S}_{P^+}(X\cap Y)\subseteq \overline{S}_{P^+}(X)\cap \overline{S}_{P^+}(Y)$ and $\overline{S}_{P^-}(X\cap Y)\supseteq \overline{S}_{P^-}(X)\cup \overline{S}_{P^-}(Y)$, respectively. Thus,

  $$\begin{aligned} \overline{BS}_{P}(X\cup Y)\sqsubseteq & {} \big (\overline{S}_{P^+}(X)\cup \overline{S}_{P^+}(Y), \overline{S}_{P^-}(X)\cap \overline{S}_{P^-}(Y)\big )\\\sqsubseteq & {} \big (\overline{S}_{P^+}(X),\overline{S}_{P^-}(X)\big )\sqcup \big (\overline{S}_{P^-}(Y), \overline{S}_{P^-}(Y)\big )\\\sqsubseteq & {} \overline{BS}_{P}(X)\sqcup \overline{BS}_{P}(Y). \end{aligned}$$

• 7. Let $X\subseteq Y$, by Proposition 5 and 6, $\underline{S}_{P^+}(X) \subseteq \underline{S}_{P^+}(Y)$ and $\underline{S}_{P^-}(Y) \subseteq \underline{S}_{P^-}(X)$. Then it is obvious that $\underline{BS}_{P}(X) \sqsubseteq \underline{BS}_{P}(Y).$

• 8. The proof can be made similar way to proof of 7.

$\square$

Definition 24

[8] Let $\mathcal {S}=(F,A)$ be a soft set over U. If for any $a_1,a_2\in A$, there exists $a_3\in A$ such that $F(a_3)=F(a_1)\cap F(a_2)$ whenever $F(a_1)\cup F(a_2)\not =\emptyset$, then $\mathcal {S}$ is called an intersection complete soft set.

Proposition 8

[8] Let $\mathcal {S}=(F,A)$ be an intersection complete soft set over U and $P=(F,\mathcal {S}=(F,A))$ be a soft approximation space. Then, we have $\underline{S}_{P}(X\cap Y)=\underline{S}_{P}(X)\cap \underline{S}_{P}(Y)$, for all $X,Y \subseteq U$.

Proposition 9

Let $(F,G,A)\in \mathcal {BS}_U$ and $P^+=(U,(F,A))$ and $P^-=(U,(G,\rceil A))$ be positive and negative soft approximation spaces of $P=(U,(F,G,A))$. If G is an intersection complete soft set, then for all $X, Y\subseteq U$,

$$\begin{aligned} \underline{BS}_{P}(X\cap Y)=\underline{BS}_{P}(X)\sqcap \underline{BS}_{P}(Y). \end{aligned}$$

Proof

Since positive soft approximation space is identical to soft approximation space given in [8], $\underline{S}_{P^+}(X\cap Y)=\underline{S}_{P^+}(X)\cap \underline{S}_{P^+}(Y)$. By Proposition 6-iii, $\underline{S}_{P^-}(X\cap Y)=\underline{S}_{P^-}(X)\cup \underline{S}_{P^-}(Y)$. Then we have $\underline{BS}_{P}(X\cap Y)=\underline{BS}_{P}(X)\sqcap \underline{BS}_{P}(Y)$. $\square$

Definition 25

Let $(F,G,A)\in \mathcal {BS}_U$, $P=(U,(F,G,A))$ be a BSA-space and $X\subseteq U$. Then, complements of bipolar soft P -lower approximation and bipolar soft P-upper approximation of X are defined, respectively as follows:

$$\begin{aligned} \underline{BS}^c_{P}(X)= & {} \big ( \underline{S}_{P^-}(X),\underline{S}_{P^+}(X)\big ) \\ \overline{BS}^c_{P}(X)= & {} \big (\overline{S}_{P^-}(X), \overline{S}_{P^+}(X)\big ). \end{aligned}$$

Example 4

Let us consider bipolar soft P-lower approximation and bipolar soft P -upper approximation of X given in Example 3. Then,

$$\begin{aligned} \underline{BS}^c_{P}(X)= & {} \big (\{h_2,h_3,h_4,h_5\},\{h_2,h_3\}),\\ \overline{BS}^c_{P}(X)= & {} \big (\{h_4,h_5\},\{h_2,h_3,h_5\}). \end{aligned}$$

Proposition 10

Let $(F,G,A)\in \mathcal {BS}_U$, $P=(U,(F,G,A))$ be a BSA-space and $X,Y\subseteq U$. Then,

• 1. $(\underline{BS}^c_P(X))^c=\underline{BS}_P(X)$

• 2. $(\overline{BS}^c_P(X))^c=\overline{BS}_P(X)$

• 3. $(\underline{BS}_P(X)\sqcup \underline{BS}_P(Y))^c=\underline{BS}^c_P(X) \sqcap \underline{BS}^c_P(Y)$

• 4. $(\overline{BS}_P(X)\sqcup \overline{BS}_P(Y))^c=\overline{BS}^c_P(X) \sqcap \overline{BS}^c_P(Y)$

• 5. $(\underline{BS}_P(X)\sqcap \underline{BS}_P(Y))^c=\underline{BS}^c_P(X) \sqcup \underline{BS}^c_P(Y)$

• 6. $(\overline{BS}_P(X)\sqcap \overline{BS}_P(Y))^c=\overline{BS}^c_P(X) \sqcup \overline{BS}^c_P(Y)$

• 7. $\underline{BS}_P(X) \sqsubseteq \underline{BS}_P(Y) \Leftrightarrow \underline{BS}^c_P(Y)\sqsubseteq \underline{BS}^c_P(X)$

• 8. $\overline{BS}_P(X) \sqsubseteq \overline{BS}_P(Y) \Leftrightarrow \overline{BS}^c_P(Y) \sqsubseteq \overline{BS}^c_P(X).$

Proof

The proof can be made by using definitions of union, intersection and complement of bipolar soft rough approximations of X and Y. $\square$

Definition 26

Let $(F,G,A)\in \mathcal {BS}_U$ and $P=(U,(F,G,A))$ be a BSA-space. If for all $a_i,a_j\in A$, $F(a_i)\cap G(\lnot a_j)=\emptyset$, then bipolar soft set (F, G, A) is called semi-intersection bipolar soft set, and denoted by $(F,G,A)_{\cap }$.

Example 5

Let $U=\{u_1,u_2,u_3,u_4,u_5,u_6,u_7,u_8\}$ be the universe and $A=\{a_1,a_2,a_3,a_4\}$ be a parameter set. Let us consider positive and negative soft sets as $F(a_1)=\{u_1,u_3\},F(a_2)=\{u_2,u_4\},F(a_3)=\{u_1,u_4\}$ and $G(\lnot a_1)=\{u_5\},G(\lnot a_2)=\{u_7,u_8\},G(\lnot a_3)=\{u_6,u_8\}$. Then, (F, G, A) is semi-intersection bipolar soft set.

Proposition 11

Let $(F,G,A)_{\cap }$ be a semi-intersection bipolar soft set over U, $X\subseteq U$ and $\underline{BS}_P(X)$, $\overline{BS}_P(X)$ be bipolar soft rough approximations of X. Then,

• 1. $\underline{S}_{P^+}(X) \cap \underline{S}_{P^-}(X)=\emptyset$

• 2. $\overline{S}_{P^+}(X) \cap \overline{S}_{P^-}(X)=\emptyset .$

Proof

For all $a_i\in A$ and $\lnot a_j\in \rceil A$, since $F(a_i)\cap G(a_j)=\emptyset$, it is clear that $\underline{S}_{P^+}(X) \cap \underline{S}_{P^-}(X)=\emptyset$ and $\overline{S}_{P^+}(X) \cap \overline{S}_{P^-}(X)=\emptyset$. $\square$

Proposition 12

Let $(F,G,A)_{\cap }\in \mathcal {BS}_U$ and $P=(U,(F,G,A))$ be a BSA-space. If

$$\begin{aligned} X\subseteq U{\Bigg \backslash } \left( \bigcup _{a\in A}F(a)\cup \bigcup _{\lnot a \in \rceil A}G(\lnot a)\right) \end{aligned}$$

then X is a bipolar soft P-definable set, namely

$$\begin{aligned} \underline{BS}_{P}(X)=\overline{BS}_{P}(X) \end{aligned}$$

Proof

We know that $\underline{S}_{P^+}(X)\subseteq \overline{S}_{P^+}(X)$ and $\overline{S}_{P^-}(X)\subseteq \underline{S}_{P^-}(X)$. Then we only need to prove that $\overline{S}_{P^-}(X)\subseteq \underline{S}_{P^+}(X)$ and $\underline{S}_{P^-}(X)\subseteq \overline{S}_{P^-}(X)$. Let $X\subseteq U{\setminus } \big (\bigcup _{a\in A}F(a)\cup \bigcup _{\lnot a \in \rceil A}G(\lnot a) \big )$. Then $\underline{S}_{P^+}(X)=\emptyset$, and so $\underline{S}_{P^+}(X)\subseteq \overline{S}_{P^+}(X).$ Let $u\in \underline{S}_{P^-}(X)$. Then $u\in G(\lnot a)$ and $G(\lnot a)\cap \sim X \not =\emptyset$. From hypothesis $X\cap G(\lnot a)=\emptyset$ for all $\lnot a \in \rceil A$ and so $u\in G(\lnot a)\subseteq \sim X$. It follows that $\underline{S}_{P^-}(X)\subseteq \overline{S}_{P^-}(X)$ as required. $\square$

Corollary 2

Let $(F,G,A)_{\cap }\in \mathcal {BS}_U$, $P=(U,(F,G,A))$ be a BSA-space and $X\subseteq U$. If $\bigcup _{a\in A}F(a)=X$ and $\bigcup _{\lnot a \in \rceil A }G(\lnot a)=\sim X$, then (F, G, A) is a bipolar soft P -definable set.

Definition 27

Let (F, G, A) be a bipolar soft set over U, $P=(U,(F,G,A))$ be a BSA-space. If $\bigcup _{a\in A}F(a)=U$ and $\bigcup _{\lnot a \in \rceil A }G(\lnot a)=U$ such that $X\subseteq U$, (F, G, A) is called full bipolar soft set and denoted by $(F,G,A)_f.$

Theorem 1

Let $(F,G,A)_f$ be a full bipolar soft set over U, $P=(U,(F,G,A))$ be a BSA-space. Then, the following conditions are equivalent:

• 1. (F, G, A) is a full bipolar soft set.

• 2. $\underline{BS}_{P}(U)=(U,\emptyset )$

• 3. $\overline{BS}_{P}(U)=(\emptyset ,U)$

• 4. $(X,\sim X)\sqsubseteq \overline{BS}_{P}(X)$ for all $X\in U$

• 5. $\underline{BS}_P(\{u\})\not =(\emptyset ,\emptyset ).$

Proof

The proofs are clear. $\square$

4 Multicriteira group decision making on bipolar soft rough sets

In this section, we construct a multicriteira group decision making method based on the bipolar soft rough sets.

Let $U=\{u_1,u_2,...,u_n\}$ be a set of objects, $A=\{a_1,a_2,...,a_m\}$ be a set of parameters and (F, G, A) be a bipolar soft set over U. Assume that $H=\{P_1,P_2,...,P_k\}$ is a set of experts, $E_1, E_2,...,E_k$ are subsets of U denote results of primary evaluations of experts $P_1,P_2,...,P_k$, respectively and $T_1, T_2,..., T_r \in \mathcal {BS}_U$ are real results that previously obtained for same or similar problems in different times or different places.

Definition 28

Let $\underline{BS}_{T_q}(E_j)=(\underline{S}_{T^+_q}(E_j), \underline{S}_{T^-_q}(E_j))$, $\overline{BS}_{T_q}(E_j)=(\overline{S}_{T^+_q}(E_j),$ $\overline{S}_{T^-_q}(E_j))$ be bipolar soft lower and upper approximations of $E_j (j=1,2,...,k)$ related to $T_q (q=1,2,...,r)$. Then,

$$\begin{aligned} \underline{b}= & {} \left( \begin{array}{cccc} \{\underline{w}^{1^{+}}_1,\underline{w}^{1^{-}}_1\} &{} \{\underline{w}^{1^{+}}_2,\underline{w}^{1^{-}}_2\} &{} \ldots &{} \{\underline{w}^{1^{+}}_k,\underline{w}^{1^{-}}_k\} \\ \{\underline{w}^{2^{+}}_1,\underline{w}^{2^{-}}_1\} &{} \{\underline{w}^{2^{+}}_2,\underline{w}^{2^{-}}_2\} &{} \ldots &{} \{\underline{w}^{2^{+}}_k,\underline{w}^{2^{-}}_k\} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \{\underline{w}^{r^{+}}_1,\underline{w}^{r^{-}}_1\} &{} \{\underline{w}^{r^{+}}_2,\underline{w}^{r^{-}}_2\} &{} \ldots &{} \{\underline{w}^{r^{+}}_k,\underline{w}^{r^{-}}_k\} \\ \end{array} \right) \\ \overline{b}= & {} \left( \begin{array}{cccc} \{\overline{w}^{1^{+}}_1,\overline{w}^{1^{-}}_1\} &{} \{\overline{w}^{1^{+}}_2,\overline{w}^{1^{-}}_2\} &{} \ldots &{} \{\overline{w}^{1^{+}}_k,\overline{w}^{1^{-}}_k\} \\ \{\overline{w}^{2^{+}}_1,\overline{w}^{2^{-}}_1\} &{} \{\overline{w}^{2^{+}}_2,\overline{w}^{2^{-}}_2\} &{} \ldots &{} \{\overline{w}^{2^{+}}_k,\overline{w}^{2^{-}}_k\} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \{\overline{w}^{r^{+}}_1,\overline{w}^{r^{-}}_1\} &{} \{\overline{w}^{r^{+}}_2,\overline{w}^{r^{-}}_2\} &{} \ldots &{} \{\overline{w}^{r^{+}}_k,\overline{w}^{r^{-}}_k\} \\ \end{array} \right) \end{aligned}$$

are called bipolar soft lower and upper approximations matrices, respectively, and denoted by $\underline{b}$ and $\overline{b}$. Here

$$\begin{aligned} \underline{w}^{q^{+}}_j= & {} \left( \underline{u}^{q^{+}}_{1j},\underline{u}^{q^{+}}_{2j},...,\underline{u}^{q^{+}}_{nj}\right) \\ \underline{w}^{q^{-}}_j= & {} \left( \underline{u}^{q^{-}}_{1j},\underline{u}^{q^{-}}_{2j},...,\underline{u}^{q^{-}}_{nj}\right) \\ \overline{w}^{q^{+}}_j= & {} \left( \overline{u}^{q^{+}}_{1j},\overline{u}^{q^{+}}_{2j},...,\overline{u}^{q^{+}}_{nj}\right) \\ \overline{w}^{q^{-}}_j= & {} \left( \overline{u}^{q^{-}}_{1j},\overline{u}^{q^{-}}_{2j},...,\overline{u}^{q^{-}}_{nj}\right) \end{aligned}$$

where

$$\begin{aligned} \underline{u}^{q^{+}}_{ij}=\left\{ \begin{array}{ll} 1, &{} \quad u_i\in \underline{S}_{T^+_q}(E_j) \\ 0, &{} \quad u_i\not \in \underline{S}_{T^+_q}(E_j) \end{array} \right. , \quad \underline{u}^{q^{-}}_{ij}=\left\{ \begin{array}{ll} -\frac{1}{2}, &{} \quad u_i\in \underline{S}_{T^-_q}(E_j) \\ 0, &{} \quad u_i\not \in \underline{S}_{T^-_q}(E_j) \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \overline{u}^{q^{+}}_{ij}=\left\{ \begin{array}{ll} \frac{1}{2}, &{} \quad u_i\in \overline{S}_{T^+_q}(E_j) \\ 0, &{} \quad u_i\not \in \overline{S}_{T^+_q}(E_j) \end{array} \right. , \quad \overline{u}^{q^{-}}_{ij}=\left\{ \begin{array}{ll} -1, &{} \quad u_i\in \overline{S}_{T^-_q}(E_j) \\ 0, &{} \quad u_i\not \in \overline{S}_{T^-_q}(E_j) \end{array} \right. \end{aligned}$$

Definition 29

Let $\underline{b}$ and $\overline{b}$ be bipolar soft lower and upper approximation matrices based on $\underline{BS}_{T_q}(E_j)=(\underline{S}_{T^+_q}(E_j), \underline{S}_{T^-_q}(E_j))$, $\overline{BS}_{T_q}(E_j)=(\overline{S}_{T^+_q}(E_j),$ $\overline{S}_{T^-_q}(E_j))$ for $q=1,2,...,r$ and $j=1,2,...,k$. Bipolar soft lower approximation vector (denoted by $\underline{w}$) and bipolar soft upper approximation vector (denoted by $\overline{w}$) are defined by, respectively,

$$\begin{aligned} \underline{w}= & {} \bigoplus _{j=1}^k\bigoplus _{q=1}^r \left( \underline{w}^{q^{+}}_j\oplus \underline{w}^{q^{-}}_j\right) \end{aligned}$$

(7)

$$\begin{aligned} \overline{w}= & {} \bigoplus _{j=1}^k\bigoplus _{q=1}^r \left( \overline{w}^{q^{+}}_j\oplus \overline{w}^{q^{-}}_j\right) . \end{aligned}$$

(8)

Here the operations $\bigoplus$ and $\oplus$ denote the vector summation,

Definition 30

Let $\underline{w}$ and $\overline{w}$ be bipolar soft $T_q-$lower approximation vector and bipolar soft $T_q-$upper approximation vector, respectively. Vector summation $\underline{w}\oplus \overline{w}=(w_1,w_2,...,w_n)$ is called decision vector.

Definition 31

Let $\underline{w}\oplus \overline{w}=(w_1,w_2,...,w_n)$ be the decision vector. Then each $w_i$ is called a weighted number of $u_i\in U$ and $u_i$ is called an optimum element of U if its weighted number is maximum of $w_i$ for all $i\in I_n$. In this case, if there are more then one optimum elements of U, chose one of them.

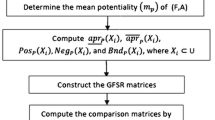
5 Algorithm

Let $U=\{u_1,u_2,...,u_n\}$, $A=\{a_1,a_2,...,a_m\}$ and (F, G, A) be a bipolar soft set over U. Assume that $H=\{P_1,P_2,...,P_k\}$ is a set of experts, $E_1, E_2,...,E_k$ are subsets of U denote results of primary evaluations of experts $P_1,P_2,...,P_k$, respectively and $T_1, T_2,..., T_r \in \mathcal {BS}_U$.

Step 1: :

Take primary evaluations $E_1,E_2,...,E_k$ of experts $P_1,P_2,...,P_k$

Step 2: :

Construct $T_1,T_2,...,T_r$ bipolar soft sets using the real results.

Step 3: :

Compute $\underline{BS}_{T_q}(E_j)$ and $\overline{BS}_{T_q}(E_j)$ for each $q=1,2,...,r$ and $j=1,2,...,k$.

Step 4: :

Construct bipolar soft lower and upper approximations matrices $\underline{b}$ and $\overline{b}$.

Step 5: :

Compute $\underline{w}$ and $\overline{w}$,

Step 6: :

Compute $\underline{w}\oplus \overline{w}$,

Step 7: :

Find $max_{i\in I_n}w_i$.

6 Illustrative example

In investment company three investment experts $P_1,P_2$ and $P_3$ want to make investment one of firms $u_1=\text {car company},u_2=\text {food company},u_3=\text {computer company},u_4=\text {arm company}$ and $u_5=\text {TV company}$ in stock market. Also $A=\{a_1=\text {appreciation} ,a_2=\text {economical growth},a_3=\text {marketshare} \}$ is parameter set.

Step 1: :

Primary evaluations of $P_1,P_2$ and $P_3$ are $E_1=\{u_1,u_2,u_3\},E_2=\{u_1,u_3,u_5\}$ and $E_3=\{u_2,u_4,u_5\}$, respectively.

Step 2: :

Real results in different three periods are expressed as bipolar soft sets as follows:

$$\begin{aligned} T_1= & {} \Big \{(a_1,\{u_1\},\{u_3,u_5\}),(a_2,\{u_1,u_5\},\{u_3\}),(a_3,\{u_4,u_5\},\{u_1,u_3\})\Big \}, \\ T_2= & {} \Big \{(a_1,\{u_2\},\{u_1,u_4\}),(a_2,\{u_2,u_4\},\{u_5\}),(a_3,\{u_3,u_4\},\{u_1,u_5\})\Big \} \end{aligned}$$

and

$$\begin{aligned} T_3=\Big \{(a_1,\{u_3,u_5\},\{u_1,u_2\}),(a_2,\{u_2\},\{u_4\}),(a_3,\{u_2,u_5\},\{u_1,u_3\})\Big \}. \end{aligned}$$

Step 3: :

$$\begin{aligned} \begin{array}{rcl} \underline{BS}_{T_1}(E_1)&{}=&{}\Big (\{u_1\},\{u_3,u_5\}\Big )\\ \overline{BS}_{T_1}(E_1)&{}=&{}\Big (\{u_1,u_5\},\{\}\Big ) \end{array},\quad \begin{array}{rcl} \underline{BS}_{T_1}(E_2)&{}=&{}\Big (\{u_1,u_5\},\{\}\Big )\\ \overline{BS}_{T_1}(E_2)&{}=&{}\Big (\{u_1,u_4,u_5\},\{\}\Big ) \end{array} \end{aligned}$$

$$\begin{aligned} \underline{BS}_{T_1}(E_3)= & {} \Big (\{u_4,u_5\},\{u_1,u_3,u_5\}\Big )\\ \overline{BS}_{T_1}(E_3)= & {} \Big (\{u_1,u_4,u_5\},\{u_1,u_3\}\Big ) \end{aligned}$$

$$\begin{aligned} \begin{array}{rcl} \underline{BS}_{T_2}(E_1)&{}=&{}\Big (\{u_2\},\{u_1,u_4,u_5\}\Big )\\ \overline{BS}_{T_2}(E_1)&{}=&{}\Big (\{u_2,u_3,u_4\},\{u_5\}\Big ) \end{array},\quad \begin{array}{rcl} \underline{BS}_{T_2}(E_2)&{}=&{}\Big (\{\},\{u_1,u_4\}\Big )\\ \overline{BS}_{T_2}(E_2)&{}=&{}\Big (\{u_3,u_4\},\{\}\Big ) \end{array} \end{aligned}$$

$$\begin{aligned} \underline{BS}_{T_2}(E_3)= & {} \Big (\{u_2,u_4\},\{u_1,u_4,u_5\}\Big )\\ \overline{BS}_{T_2}(E_3)= & {} \Big (\{u_2,u_3,u_4\},\{\}\Big ) \end{aligned}$$

and

$$\begin{aligned} \begin{array}{rcl} \underline{BS}_{T_3}(E_1)&{}=&{}\Big (\{u_2\},\{u_4\}\Big )\\ \overline{BS}_{T_3}(E_1)&{}=&{}\Big (\{u_2,u_3,u_5\},\{u_4\}\Big ) \end{array},\quad \begin{array}{rcl} \underline{BS}_{T_3}(E_2)&{}=&{}\Big (\{u_3,u_5\},\{u_1,u_2,u_4\}\Big )\\ \overline{BS}_{T_3}(E_2)&{}=&{}\Big (\{u_2,u_3,u_5\},\{u_4\}\Big ) \end{array} \end{aligned}$$

$$\begin{aligned} \underline{BS}_{T_3}(E_3)= & {} \Big (\{u_2,u_5\},\{u_1,u_2,u_3\}\Big )\\ \overline{BS}_{T_3}(E_3)= & {} \Big (\{u_2,u_3,u_5\},\{u_1,u_3\}\Big ) \end{aligned}$$

Step 4: :

Bipolar soft lower approximation matrix and bipolar soft upper approximation matrix are obtained as follows:

$$\begin{aligned} \underline{b}= & {} \left( \begin{array}{ccc} \big \{(1,0,0,0,0),(0,0,-\frac{1}{2},0,-\frac{1}{2})\big \} &{} \big \{(1,0,0,0,1),(0,0,0,0,0)\big \} &{} \big \{(0,0,0,1,1),(-\frac{1}{2},0,-\frac{1}{2},0,-\frac{1}{2})\big \} \\ &{} &{} \\ \big \{(0,1,0,0,0),(-\frac{1}{2},0,0,-\frac{1}{2},-\frac{1}{2})\big \} &{} \big \{(0,0,0,0,0),(-\frac{1}{2},0,0,-\frac{1}{2},0)\big \} &{} \big \{(0,1,0,1,0),(-\frac{1}{2},0,0,-\frac{1}{2},-\frac{1}{2})\big \} \\ &{} &{} \\ \big \{(0,1,0,0,0),(0,0,0,-\frac{1}{2},0)\big \} &{} \big \{(0,0,1,0,1),(-\frac{1}{2},-\frac{1}{2},0,-\frac{1}{2},0)\big \} &{} \big \{(0,1,0,0,1),(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},0,0)\big \} \\ \end{array} \right) \\ \overline{b}= & {} \left( \begin{array}{ccc} \big \{(\frac{1}{2},0,0,0,\frac{1}{2}),(0,0,0,0,0)\big \} &{} \big \{(\frac{1}{2},0,0,\frac{1}{2},\frac{1}{2}),(0,0,0,0,0)\big \} &{} \big \{(\frac{1}{2},0,0,\frac{1}{2},\frac{1}{2}),(-1,0,-1,0,0)\big \} \\ &{} &{} \\ \big \{(0,\frac{1}{2},\frac{1}{2},\frac{1}{2},0),(0,0,0,0,-1)\big \} &{} \big \{(0,0,\frac{1}{2},\frac{1}{2},0),(0,0,0,0,0)\big \} &{} \big \{(0,\frac{1}{2},\frac{1}{2},\frac{1}{2},0),(0,0,0,0,0)\big \} \\ &{} &{} \\ \big \{(0,\frac{1}{2},\frac{1}{2},0,\frac{1}{2}),(0,0,0,-1,0)\big \} &{} \big \{(0,\frac{1}{2},\frac{1}{2},0,\frac{1}{2}),(0,0,0,-1,0)\big \} &{} \big \{(0,\frac{1}{2},\frac{1}{2},0,\frac{1}{2}),(-1,0,-1,0,0)\big \} \\ \end{array} \right) \end{aligned}$$

Step 5: :

Using Eqs. (7) and (8), bipolar soft lower approximation vector and bipolar soft upper approximation vectors are obtained as follows:

$$\begin{aligned} \underline{w}= & {} \left( -1,3,-\frac{1}{2},-\frac{1}{2},2\right) \\ \overline{w}= & {} \left( -\frac{1}{2},\frac{5}{2},1,\frac{1}{2},2\right) . \end{aligned}$$

Step 6: :

Decision vector is obtained as $\underline{w}\oplus \overline{w}=(-\frac{3}{2},\frac{11}{2}, \frac{1}{2},0,4)$.

Step 7: :

Since $max_{i\in I_n}w_i=w_2=\frac{11}{2}$, optimum element is $u_2$.

7 Conclusion

In this paper, we defined the bipolar soft rough sets, and gave their set theoretical operations with basic properties. We also defined the soft P-lower positive, soft P-lower negative, soft P-upper positive and soft P-upper negative approximations, and then introduced the concept of bipolar soft rough sets. By using these new definitions and operations we constructed a decision making method. We finally gave an application to show the method can be successfully applied to some problems including uncertainty in the real world. In future, based on the defined concepts and operations in this paper, researchers may study on algebraic structures of bipolar soft rough sets such as bipolar soft rough lattices and rough bipolar soft groups. Also concept of bipolar soft rough sets may be extended to bipolar fuzzy soft rough sets and effective decision making methods may be developed.