1 Introduction

Performance-based earthquake engineering, seismic design for life safety, post-earthquake functional recovery, and seismic isolation systems are the approaches used for designing buildings that can withstand earthquakes [1]. Among these methods, seismic isolation is an effective design approach where a structure or a part of it is isolated from the devastating impacts of earthquakes. Thus, the primary goal of seismic isolation is to shift the fundamental frequency of a structure away from the prominent frequencies of earthquake motion and the fixed base-superstructure fundamental frequency [2]. Over the past few decades, the performance of base isolation devices against seismic action has been investigated. Some of the practical applications of base isolation on a structure based on retrofit or new design concepts are in barracks, fire stations, emergency control centers, hospitals, and other similar structures [3,4,5,6]. In addition, the base isolation devices are practically proven to protect the structure against near-fault (NF) excitation and also far-field (FF) excitation under consideration of a large displacement isolator [7,8,9,10]. The NF zone is expected to be within 20 km of the ruptured fault [11]. The base isolation plays a vital role in controlling the vibration of the structure under excitation. However, there are some limitations under NF ground excitation. In NF conditions, ground excitation necessitates considerable displacement at the base isolator. Hence, in NF, the ground excitation base isolator has to be restricted strictly and also requires high damping in NF motion. Based on previous research, an additional supplementary damper is added to the base isolator under NF excitation [7,8,9, 12, 13].

The vibration mitigation of structures using vibration control strategies such as active, passive, and semiactive devices has been investigated by several researchers [14,15,16,17]. An extensive review of the historical development of vibration isolation techniques is reported by Rivin [18] and Ibrahim [19]. Compared to other control systems, the passive control system is consistent and straightforward [20]. Several passive control systems can be installed. As an example, the base isolation system is a passive control system that is added between the structure and the vibration source, resulting in response control [21,22,23,24,25,26,27,28]. Other examples are the addition of energy dissipation devices into the bracing system (dampers) [29,30,31,32] and the introduction of a tuned mass damper where the frequencies of the structure are tuned [33,34,35,36,37,38]. Different passive damper systems can be used, including fluid-viscous, viscoelastic, frictional, metallic, etc. In addition, various tunning dampers can be utilized, such as tuned liquid column dampers (TLCD), tuned liquid sloshing dampers (TLSD), tuned mass dampers (TMD), etc. In this regard, the dynamic response of a structure is controlled by using both energy dissipation devices and a tuned damper [39,40,41,42,43,44,45].

The structural response under wind and seismic loads is reduced using conventional devices such as TMD attached to structures [46, 47]. The key parameters considered for the design of TMD are non-dimensional, such as mass ratio, damping ratio, and frequency ratio [48]. The earlier studies investigated the various optimization procedures for determining the optimum parameters of TMD, which include H2, H∞, and stabilization techniques [49]. The structure under harmonic loading is also considered by using the transfer function H∞ optimization technique [50]. Compared to the H∞ optimization technique, it is reported that the H2 optimization technique is effective in controlling the response under wide frequency band excitation (e.g., wind load and seismic load) [51,52,53]. The transfer function is also optimized by the H2-based technique for obtaining the optimum parameters in the closed-form of expressions for single degree of freedom (SDOF) systems with TMD [50], tuned mass damper inerter (TMDI) [54] or other inerter dampers [52, 54, 55]. Likewise, the H2 optimization technique is used for multiple degrees of freedom (MDOF) systems [56] or base isolation systems under seismic excitation [57,58,59]. Research conducted by Talley et al. [60] explored the use of CID to improve the seismic resistance of structures. However, most studies have focused on systems equipped with TMDI, NSADI, and CID only under uniaxial seismic excitation.

Several studies have also investigated the behavior of different structures under bi-directional seismic excitation. For instance, Tsourekas et al. [61] studied the mean square critical response of structures, while Banerjee et al. [62] focused on enhancing masonry structures. Vern et al. [63] explored the performance of liquid storage tanks with base-isolated structures, and Zeris et al. [64] investigated the performance of reinforced concrete walls considering the torsional effect. However, little attention has been paid to base-isolated structures with supplementary devices under bi-directional seismic excitation.

From the literature review presented above, it is found that researchers have studied base-isolated structures, damped structures, bridges, and benchmark structures with combinations of several inerter under uniaxial seismic load. To the best of the authors' knowledge, research on base-isolated damped structures incorporating hybrid vibration control has not yet been conducted. Furthermore, there are some gaps of information regarding the studies of SDOF systems with TMDI, negative stiffness amplifier damper inerter (NSADI), and clutching inerter damper (CID) for statistical response under a stationary random process by considering the frequency domain. Therefore, the objectives of the present study are: (i) The SDOF system damped with TMDI, NSADI, and CID under excitation of white noise for minimizing mean square response by formulating H2 optimization formulae was investigated. (ii) The trapezoidal rule, known for its simplicity, efficiency, and high accuracy, was employed as a numerical search technique for a base-isolated structure with TMDI, NSADI, and CID to obtain optimum parameters for controlling displacement and acceleration response of an isolated structure based on H2 optimum control. (iii) This was done by using a sequence of curve fitting techniques to obtain the optimum parameters of TMDI, NSADI, and CID using explicit formulae. (iv) The performance of a base-isolated structure with supplemental damping devices (TMDI, NSADI, and CID) under the combined effect of horizontal and vertical ground motion and comparisons were carried out. Thus, the paper is organized by presenting the structural modeling with various dampers in Sect. 2, followed by an optimization using H2 control white noise excitation in Sect. 3. Section 4 discusses the optimal parameter in the closed-form of expressions, and Sect. 5 applies the optimization concept to a base-isolated shear structure with different supplementary dampers, followed by numerical model verifications.

2 Modelling of SDOF System with Various Dampers

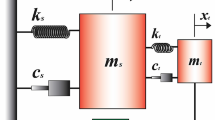
Figure 1 represents the SDOF shear frame of a single bay having mass m, stiffness k, and damping constant c. The TMD serves as a passive control mechanism designed to absorb energy unleashed during seismic activity. Integrating a mass component into the structure typically increases its overall mass. To counteract this, a lightweight inerter component is incorporated alongside the TMD, effectively reducing the mass of the system. This combined setup is referred to as the tuned mass damper inerter (TMDI). The TMDI comprises two flywheels positioned on either side and supported by chevron braces. Each flywheel features a ratchet mechanism between the gear and itself, with opposite orientations for the ratchets on each flywheel. This arrangement creates a clutching effect, enabling the flywheel to detach from the structure, thereby preventing it from exerting force in the opposite direction. This paper introduces a passive device called the negative stiffness amplifying damper (NSAD). This device incorporates a negative stiffness (NS) spring into flexibly-supported-viscous-damper systems, typically represented by a classical Maxwell damping element (MDE). Another passive control mechanism, the negative amplifier stiffness damper inerter (NSADI), combines the negative amplifier stiffness damper with an inerter. The study evaluates a single degree of freedom (SDOF) system with various supplementary dampers, including one TMDI, three NSADI setups, and one CID. Figure 2 provides a schematic representation of these supplemental dampers, illustrating their configurations.

Fig. 1
figure 1

SDOF structure with a supplementary damper

Full size image
Fig. 2
figure 2

Schematic reprsentation of diferent supplementary dampers: a TMDI; b NSADI-1; c NSADI-2; d NSADI-3; and e CID

Full size image

Different parameters of the damper are as follows: negative stiffness (kns), inertance (b), dashpot damping (cd), and positive stiffness (kp). Figures 1 and 2 consist of two terminals. Terminal 1 is connected to the SDOF mass, and terminal 2 is connected to the ground. The parameters used in the system are defined as follows:

$$\omega_{n} = \sqrt{\frac{k}{m}} \quad \& \quad \xi = \frac{c}{{2m\omega_{n} }}$$
(1)
$$\alpha = \frac{{k_{ns} }}{{k_{p} }};\beta = \frac{{k_{p} }}{k};\gamma = \frac{{c_{d} }}{c};\xi_{d} = \frac{{c_{d} }}{{2m\omega_{n} }};\;{\text{and}}\;\mu = \frac{b}{m}$$
(2)

where, negative stiffness ratio is \(\alpha\), positive stiffness ratio is \(\beta\), inertance to mass ratio is \(\mu\), the inherent damping ratio is \(\xi\) and supplemental damping ratio is \({\xi }_{d}\).

The governing equation of motion of the SDOF system with a supplementary damper exposed to earthquake excitation is given as:

$$m\ddot{x} + c\dot{x} + kx + f_{d} = - m\ddot{x}_{g}$$
(3)

where, displacement of the SDOF system relative to the ground is \(x\), control force generated from the supplemental damper at terminals 1 and 2 is fd, and the excitation of acceleration is \({\stackrel{..}{x}}_{g}\).

3 Optimization Using H2 Control Under White Noise Excitation

Since seismic stimulation is a stochastic/random input [59, 65], the performance of a system under the influence of Gaussian white noise input with a mean value of zero consisting of the H2 norm of the parameter root mean square (RMS) is preferable. The building's inherent frequency exceeds the frequency of earthquake excitation. This phenomenon plays a vital role. Assuming base excitation \({\stackrel{..}{x}}_{g}\) is the same as random white noise excitation, the resulting power spectral density function (PSDF) of base excitation is uniform (So). The displacement response's RMS is given below:

$$\sigma_{xx} = \left( {S_{o} \mathop \smallint \limits_{ - \infty }^{\infty } \left| {H\left( \omega \right)} \right|^{2} d\omega } \right)^{\frac{1}{2}} = \sqrt {S_{0} } \left\| H \right\|_{2}$$
(4)
$$H_{x} \left( \omega \right) = \frac{1}{\Delta m}\left( { - \omega^{2} + 2i\xi_{d} \omega_{t} \omega + \omega_{T}^{2} } \right)$$
(5)
$$H_{{\dot{x}}} \left( \omega \right) = \frac{1}{\Delta }\left( {i\frac{\omega }{{\omega_{T}^{2} }}\left( {\mu^{2} - \gamma^{2} } \right) - 2i\xi_{d} \omega_{t} \omega + \omega_{T}^{2} } \right)$$
(6)
$$\Delta = \omega^{4} - 2i\left[ {\omega_{d} \xi_{d} + \left( {1 + \mu } \right)\xi_{d} \omega_{d} } \right]\omega^{3} - \left[ {\omega^{2} + \left( {1 + \mu } \right)\xi_{d} \omega_{d} } \right]$$
(7)

where, displacement of transfer function square is \(\left| {H\left( \omega \right)} \right|^{2}\). H2 norm is expressed as: \(\left\| H \right\|_{2} = \left( {\mathop \smallint \limits_{ - \infty }^{\infty } \left| {H\left( \omega \right)} \right|^{2} d\omega } \right)^{\frac{1}{2}}\). Minimizing integral is the main criterion for the optimal design process. The primary structural system is under ground acceleration excitation.

The residue theorem [66] is used to investigate the integral of the H2 norm. However, this method is complex for obtaining the optimum parameters with accuracy. In a dynamic equation of motion of a state variable, formulating and arriving at the equation directly is more tedious [67]. The first-order differential equation is expressed from Eq. (3) by considering the state matrix as A and the excitation vector as B, as shown below.

$$\dot{z} = Az + B\ddot{x}_{g}$$
(8)

where the state vector is z. The following equation [67] satisfies the response of the covariance variance matrix V as given below:

$$\dot{V} = AV^{T} + VA^{T} + P$$
(9)

where the transpose matrix of V is represented as \({V}^{T}\). The elements of V and P are shown below as

$$V = z_{i} z_{j} \& P = B_{i} B_{j}$$
(10)

where, \(\left(.\right)\) is the operator of the expectation operator, and the ith element of vectors z and B are zi and Bi, respectively. The Gaussian zero-mean white noise excitation is considered the input earthquake excitation with a random process consisting of constant PSDF as So. The matrix P comprises components representing random variables utilized for Gaussian zero-mean white noise excitation. Based on this condition, the matrix P is shown as:

$$P = 2\pi S_{0} BB^{T}$$
(11)

Equation (9) shows the need for the mean square displacement value of response \(\left( {\sigma_{x}^{2} } \right)\) and acceleration value of response \(\left( {\sigma_{{\ddot{x}_{g} }}^{2} } \right)\), which are the inputs of earthquake excitation of acceleration. The minimization of mean square response and integral values are defined in Eq. (4), which is the main objective of optimization. The normalized mean square displacement is expressed as the ratio of the square response of displacement to the uncontrolled mean square response of displacement \(\left( {\sigma_{x,o}^{2} } \right)\), as shown below:

$$\tilde{\sigma }_{x}^{2} = \frac{{\sigma_{x}^{2} }}{{\sigma_{x,0}^{2} }}$$
(12)

The effective response reduction using supplementary dampers based on values of \(\tilde{\sigma }_{x}^{2}\) is less than unity.

3.1 Optimal Parameters of TMDI

As shown in Fig. 2a, the schematic representation of TMDI is presented. In a SDOF system with an inerter connected parallel to its mass, the main configuration of a geometry results in the generation of damping force that is expressed as:

$$f_{d} = k_{t} y + c_{d} \dot{y} = k_{t} \left( {x - y} \right)$$
(13)

where the relative displacement through terminals 3–2 of TMDI is y. The state variable vector is expressed as \(z = \left\{ {\begin{array}{*{20}c} {\dot{x}} \\ x \\ {f_{d} } \\ \end{array} } \right\}\). The displacement with respect to mass is represented as x, and a state space model of the SDOF with TMDI is formed. To obtain the solution of the covariance matrix (V) for Eq. (8), a MATLAB script written by the authors was used. The numerical minimizing technique by mean square displacement values \(\tilde{\sigma }_{x}^{2}\) of displacement response for exact TMDI positive stiffness ratio \(\beta\) and inherent damping of primary structural system \(\xi\) was used to obtain the optimum parameters of TMDI, including \(\alpha\) and \(\xi_{d}\). The following conditions were considered: (i) TMDI is under damping, (ii) TMDI damping is nonnegative, (iii) TMDI negative stiffness ratio is negative, and (iv) constancy of the system was confirmed. Finally, validation of optimization for \(0 \le \xi_{d} \le 1; - 1 \le \xi_{d} \le 0 \quad \& \quad \alpha < - 1/\left( {1 + \beta } \right)\) was carried out.

The primary system consisted of five inherent damping ratios (ξ = 0, 0.02, 0.05, 0.075, and 0.1) that were used to obtain TMDI optimum parameters. The formulation of an optimization problem in compact form is as follows:

$$\begin{aligned} & {\text{Find}}\;\alpha \;{\text{and}}\;\xi_{d} \\ & {\text{To}}\;{\text{minimize}}\;\sigma_{x}^{2} = \left| {\sigma_{x}^{2} \left( {\alpha ,\beta ,\xi_{d} ,S_{0} } \right)} \right| \\ & {\text{Subjected}}\;{\text{to}}\;0 \le \xi_{d} \le 1 \\ & {\text{Subjected}}\;{\text{to}}\; - 1 \le \alpha \le 1 \\ & {\text{Subjected}}\;{\text{to}}\;\alpha > - 1/\left( {1 + \beta } \right) \\ \end{aligned}$$
(14)

Table A1 represents the tabulated values of an optimal parameter of TMDI obtained from the numerical search findings corresponding to the minima of \(\tilde{\sigma }_{x}^{2}\). It is indicated that the \(\beta\) increases and the corresponding \(\alpha_{opt}\) decreases. It is further observed that with an increase in positive stiffness ratio (\(\beta\)), \(\xi_{d,opt}\) also increases. However, the normalized mean square response for displacement \(\tilde{\sigma }_{x}^{2}\) decreases and the corresponding value of \(\beta\) increases.

3.2 Optimal Parameters of NSADI-1

The schematic representation of NSADI-1 is shown in Fig. 2b. The proposed NSADI-1 configuration consists of an inerter parallel to a positive spring. The H2 norm is used to obtain the optimum parameters of NSADI-1. The formulation of SDOF with NSADI-1 is obtained from the state space representation. Equation (3) represents the equation of motion of the SDOF system under seismic excitation and also considers the damping force shown as follows:

$$f_{d} = k_{ns} \left( {x - y} \right) + c_{d} \left( {\dot{x} - \dot{y}} \right) = k_{p} y + b\ddot{y}$$
(15)

where the state variable vector is represented as: \(z = \left\{ {\begin{array}{*{20}c} x \\ y \\ {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right\}\), and the relative displacement from terminals 3–2 is represented as y, and SDOF system with the NSADI-1 state space model is framed. To investigate the mean square displacement response (\(\sigma_{x}^{2}\)) and to solve Eq. (9), a MATLAB code was developed and employed. For NSADI-1, different parameters, \(\xi\) and \(\xi_{d}\) were used to obtain minima of \(\tilde{\sigma }_{x}^{2}\) using numerical search techniques. The output parameters of the numerical search technique of NSADI-1 are: \(\alpha_{opt}\), \(\mu_{opt}\), and \(\beta_{opt}\). The optimization is valid for \(0 \le \mu \le 1; 0 \le \beta \le 1; - 1 \le \alpha < 0 \& \alpha < \frac{1}{1 + \beta }.\) The primary system consisting of five inherent ξ ratios (0, 0.02, 0.05, 0.075, and 0.1) were used to obtain NSADI-1 optimum parameters. The formulation of an optimization problem in compact form is shown as:

$$\begin{aligned} & {\text{Find }}\mu ,\alpha {\text{and }}\beta \\ & {\text{To minimize }}\sigma_{x}^{2} = \left| {\sigma_{x}^{2} \left( {\alpha ,\beta ,\xi_{d} ,\mu ,S_{0} } \right)} \right| \\ & {\text{Subjected to }}0 \le \xi_{d} \le 1 \\ & {\text{Subjected to}} - 1 \le \alpha \le 0 \\ & {\text{Subjected to }}0 \le \mu \le 1 \\ \end{aligned}$$
(16)

The normalized mean square displacement response of NSADI was obtained in this case. Table A2 presents the results obtained from the numerical search method. It is evident that as the damper damping ratio \(\xi_{d}\) increases, \(\beta_{opt}\) rises while the magnitude of \(\alpha_{opt}\) decreases. Moreover, the findings suggest that an elevation in the damper damping ratio \(\xi_{d}\) results in a slight increase in the inertance ratio \(\mu_{opt}\). However, the associated value of the displacement's mean square response, normalized as \(\tilde{\sigma }_{x}^{2}\), diminishes with higher values of \(\xi_{d}\). The ξ demonstrates a noticeable influence on \(\beta_{opt}\) and \(\mu_{opt}\), ut no effect observed on \(\alpha_{opt}\) values. Nevertheless, an increase in the damping ratio \(\xi\) leads to a reduction in both \(\beta_{opt}\) and \(\mu_{opt}\).

3.3 Optimal Parameters of NSADI-2

Figure 2c represents the NSADI-2. In this configuration system, the inerter is reversed with the element of the dashpot system. In view of Eq. (3), the equation of motion of the SDOF system under seismic excitation and considering damping force is shown as:

$$f_{d} = k_{p} y + c_{d} \dot{y} = k_{ns} \left( {x - y} \right) + b\left( {\ddot{x} - \ddot{y}} \right)$$
(17)

where the state variable vector is represented as: \(z = \left\{ {\begin{array}{*{20}c} x \\ y \\ {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right\}\), the relative displacement from terminals 3–2 is represented as y, and the SDOF system with the NSADI-2 state space model is framed. To investigate the mean square displacement response \(\sigma_{x}^{2}\) and to solve Eq. (6), a developed MATLAB code was used. For NSADI-2, different parameters, \(\xi\) and \(\xi_{d}\) were used to obtain the minima of \(\tilde{\sigma }_{x}^{2}\) using the numerical search technique. The output parameters of the numerical search technique of NSADI-3 are: \(\alpha_{opt}\), \(\xi_{d,opt}\), and \(\beta_{opt}\). The optimization is valid for \(0 \le \xi_{d} \le 1;0 \le \beta \le 1; - 1 \le \alpha < 0 \& \alpha < \frac{1}{1 + \beta }.\) The inertance ratio that exists to behave realistically for the system is also considered a constraint. The primary system consisted of five inherent ξ ratios (0, 0.02, 0.05, 0.075 and 0.1) that were used to obtain the NSADI-2 optimum parameters. The optimization problem was formulated in compact form as given below:

$$\begin{aligned} & {\text{Find}}\;\beta ;\;\alpha \;{\text{and}}\;\xi_{d} \\ & {\text{To}}\;{\text{minimize}}\;\sigma_{x}^{2} = \left| {\sigma_{x}^{2} \left( {\alpha ,\beta ,\xi_{d} ,\mu ,S_{0} } \right)} \right| \\ & {\text{Subjected}}\;{\text{to}}\;0 \le \xi_{d} \le 1 \\ & {\text{Subjected}}\;{\text{to}}\; - 1 \le \alpha \le 0 \\ & {\text{Subjected}}\;{\text{to}}\;\alpha > - 1/\left( {1 + \beta } \right) \\ & {\text{Subjected}}\;{\text{to}}\;0 \le \beta \le 1 \\ \end{aligned}$$
(18)

The normalized mean square displacement response of NSADI-2 was determined, and the results derived from the numerical search method are outlined in Table A3. These findings suggest that augmenting the inertance ratio (\(\mu\)) leads to higher values of \(\beta_{opt}\) and \(\xi_{d,opt}\), while diminishing the magnitude of \(\alpha_{opt}\). Consequently, an enhanced response reduction for higher inertance to mass ratios corresponds to a decrease in the value of \(\tilde{\sigma }_{x}^{2}\), coupled with a proportional increase in \(\mu\). Nevertheless, this heightened \(\mu\) value is also linked to a slight decrease in \(\alpha_{opt}\).

3.4 Optimal Parameters of NSADI-3

The schematic representation of NSADI-3 is depicted in Fig. 2d. Using Eq. (3), the damping force is given as:

$$\left\{ {\begin{array}{*{20}l} {f_{d} = k_{ns} y + b\ddot{q} = k_{p} \left( {x - y} \right)} \hfill \\ {b\ddot{q} = c_{d} \left( {\dot{y} - \dot{q}} \right)} \hfill \\ \end{array} } \right\}$$
(19)

where the state variable vector is represented as: \(z = \left\{ {\begin{array}{*{20}c} {\dot{x}} \\ x \\ {\dot{q}} \\ {f_{d} } \\ \end{array} } \right\}\), the relative displacement from terminals 3–2 is represented as y, and the SDOF system with the NSADI-3 state space model was framed. The displacement of NSADI-3 across terminals 4–2 is represented as q. To investigate the mean square displacement response \(\sigma_{x}^{2}\) and to solve Eq. (9), a developed MATLAB code was used. For NSADI-3, different parameters \(\xi\) and \(\xi_{d}\) were used to obtain minima of \(\tilde{\sigma }_{x}^{2}\) using numerical search technique. The output parameters of the numerical search technique of NSADI-3 are: \(\alpha_{opt}\), \(\xi_{d,opt}\) and \(\beta_{opt}\). The optimization is valid for \(0 \le \xi_{d} \le 1;0 \le \beta \le 1; - 1 \le \alpha < 0 \& \alpha < - \frac{1}{1 + \beta }.\) The inertance ratio that exists to behave realistically for the system was considered as one of the limitations. The primary system consisted of five inherent ξ ratios (0, 0.02, 0.05, 0.075, and 0.1) that were used to obtain the NSADI-3 optimum parameters.

Equation (13) was formulated for the optimization problem of NSADI-3. Table A4 presents the normalized mean square values along with the corresponding optimal parameters of NSADI-3. The results of Table A4 show an increase of \(\mu\) yields an increase in \(\beta_{opt}\) and \(\xi_{d,opt}\) but a decrease in the values of \(\alpha_{opt}\). In addition, it is observed that a better response reduction represents in \(\mu\) and corresponding decrease in \(\tilde{\sigma }_{x}^{2}\). The parameters of \(\alpha_{opt}\), \(\xi_{d,opt}\) and \(\beta_{opt}\) have a critical influence on the performance of damping ratio \(\xi\), but a marginal decrease in the trend of \(\beta_{opt}\) is observed.

3.5 Optimal Parameters of CID

The schematic representation of CID is shown in Fig. 2e. From Eq. (3), the expression for damping force is derived as:

$$f_{d} = k_{p} x + c_{d} \dot{x} = b\left( {\ddot{x} - \ddot{y}} \right)$$
(20)

where the state variable vector is represented as: \(z = \left\{ {\begin{array}{*{20}c} x \\ y \\ {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right\}\), the relative displacement from terminals 3–2 is represented as y, and the SDOF system with the CID state space model was framed. For CID, different parameters, \(\xi\) and \(\xi_{d}\) were used to obtain minima of \(\tilde{\sigma }_{x}^{2}\) by numerical search technique. The output parameters of the numerical search technique of CID are: \(\alpha_{opt}\), \(\xi_{d,opt}\) and \(\beta_{opt}\). The optimization is valid for \(0 \le \xi_{d} \le 1 \& 0 \le \beta \le 1.\)

$$\begin{aligned} & {\text{Find}}\;\beta \;{\text{and}}\;\xi_{d} \\ & {\text{To}}\;{\text{minimize}}\;\sigma_{x}^{2} = \left| {\sigma_{x}^{2} \left( {\alpha ,\beta ,\xi_{d} ,\mu ,S_{0} } \right)} \right| \\ & {\text{Subjected}}\;{\text{to}}\;0 \le \xi_{d} \le 1 \\ & {\text{Subjected}}\;{\text{to}}\;0 \le \beta \le 1 \\ \end{aligned}$$
(21)

The normalized mean square displacement response of CID is determined. Table A5 presents the results from the numerical search method. The results observed that an increase of inertance ratio \(\mu\) results in an increase of \(\beta_{opt}\) and \(\xi_{d,opt}\), and the magnitude of \(\alpha_{opt}\) decreases. It is also observed that the performance of the damping ratio of the damper compared to the stiffness ratio is more important than structural damping.

In the present investigation, five different damper configurations were considered for minimizing the H2 norm, as shown in Tables A1, A2, A3, A4 and A5, by considering different inherent \(\xi\) ratios (0–0.2). A closed-form of expressions for TMDI, NSADI-1, NSADI-2, NSADI-3, and CID were obtained through a two-stage process. In the first stage, optimum parameters by H2 norm were obtained using the numerical search technique, while in the second stage, the findings of the numerical search method were utilized. A consecutive curve fitting scheme was used to reach several closed expressions. This concept is verified in the subsequent section.

4 Optimal Parameters Using Closed-Form of Expressions

As the numerical search technique proves complex, tedious, and challenging in achieving optimum parameters for various control devices, this study utilizes mathematical expressions. Deriving closed-form expressions for supplementary dampers simplifies the process of minimizing response. Employing a curve-fitting method through trial and error, optimal closed-form expressions for supplementary dampers were determined. Additionally, results from the numerical search method were validated against those from the closed-form expressions. The outcomes obtained from the numerical search, minimizing mean square error, are presented in Tables A1, A2, A3, A4 and A5, revealing the optimal parameters. Assessing fit goodness through the sum of squared errors and the coefficient of determination (R2), a match is found satisfactory when R2 = 1.

The optimum parameters of TMDI were obtained from a closed-form of expressions for \(\alpha_{opt} , \xi_{d} \& \tilde{\sigma }^{2}\) as a function of \(\beta \& \xi\):

$$\alpha_{opt} = 1.0021*\frac{{\left( {\beta - 2} \right)\left( {1 + \xi } \right)}}{{2\left( {\beta + 1} \right)}} + 1.444\xi$$
(22)
$$\xi_{d} = \frac{{1.988\beta^{2} }}{{2\left( {\beta + 1} \right)\left( {1 - \xi } \right)^{2} }} + \frac{1.025*\xi }{{\left( {2 + \xi } \right)^{2} }}$$
(23)
$$\tilde{\sigma }_{x}^{2} = \frac{1.325\xi }{{\left( {\beta + 1} \right)}} + \frac{1}{{\left( {1 + \xi } \right)^{2} }}$$
(24)

The numerical search method was used to find the optimum parameters \(\beta_{opt}\), \(\alpha_{opt}\) and \(\mu_{opt}\) for NSADI-1 with functions of \(\xi_{{d{ }}} \& \xi\), as shown below:

$$\beta_{opt} = \frac{{2062\sqrt {\xi_{d} } \left( {0.5 + \xi_{d} } \right)}}{{\left( {2 + \xi_{d} } \right)^{ - 0.0999} \left( {4 + \xi } \right)^{5} }}$$
(25)
$$\alpha_{opt} = \frac{{1.586\sqrt {\xi_{d} } }}{{1 + \xi_{d} }} - \frac{2.71}{{\sqrt {\left( {7 + \xi } \right)} }}$$
(26)
$$\mu_{opt} = \frac{{8.566\xi_{d}^{1.3135} }}{{\left( {1 + \xi } \right)^{2} \left( {1 + \xi_{d} } \right)^{{39.8\left( {1 + \xi } \right)}} }}$$
(27)

The numerical search method was used to obtain the optimum parameters f \(\beta_{opt}\), \(\alpha_{opt}\) and \(\xi_{d,opt}\) for NSADI-2 with functions of \(\mu \& \xi\), as shown below:

$$\beta_{opt} = \frac{{0.5732\sqrt {\frac{\mu }{{1 + \mu^{2} }}} }}{1 + \xi } + \frac{0.04947}{{1 + \xi^{2} }}$$
(28)
$$\alpha_{opt} = \frac{{0.4758\left( {\mu - 8} \right)\sqrt \mu }}{\mu + 4} - \frac{3.716}{{4 + \xi }}$$
(29)
$$\xi_{d,opt} = \frac{1.547\mu }{{\left( {1 + \xi } \right)\left( {4 + \mu } \right)}} + \frac{0.006046}{{1 + \xi }}$$
(30)

The numerical search method was used to find optimum parameters \(\beta_{opt}\), \(\alpha_{opt}\) and \(\xi_{d,opt}\) for NSADI-3 with functions of \(\& \xi\), as shown below:

$$\beta_{opt} = \frac{1.082\mu }{{\sqrt {1 + \mu } }} + \frac{0.04564}{{\left( {1 + \xi } \right)^{2} }}$$
(31)
$$\alpha_{opt} = - \frac{{2.646\left( {\mu - 2} \right)\mu }}{\mu + 2} - \frac{3.732}{{\left( {2 + \xi } \right)^{2} }}$$
(32)
$$\xi_{d,opt} = \frac{{0.56465\mu \left( {1 + \xi } \right)}}{{1 - \mu^{2} }} + \frac{0.2126\xi }{{1 + \xi }}$$
(33)

The optimal parameters of CID are functions of \(\mu\) and \(\xi\) and closed-forms of expression are represented below

$$\beta_{opt} = \frac{{0.9821*\mu \left( {1 + 0.5\mu } \right)}}{{\left( {1 + \mu } \right)^{2} }} - 0.06659\xi$$
(34)
$$\xi_{d,opt} = 0.4436\mu \sqrt {\frac{4 + 3\mu }{{\left( {1 + \mu } \right)\left( {2 + \mu } \right)}}} - \frac{{0.1663\mu^{2} }}{1 + \xi }$$
(35)
$$\tilde{\sigma }_{x}^{2} = \left( {1.125\sqrt {\frac{3 + 2\mu }{{1 + \mu }}} } \right)\xi$$
(36)

The numerically produced 3D graphical depiction of the optimum values is obtained by utilizing equations for all dampers, as shown in Figs. 3, 4, 5, 6 and 7. Figure 5 exhibits a notable discontinuity (C1-type), attributable to variations in optimal parameters derived from the curve fitting technique utilized in the current model. This discrepancy is further exacerbated by the influence of damping and stiffness factors inherent in the present model. The optimal parameter values for all dampers are depicted by the blue surface. In the presented formulations and the observed 3D figure for TMDI (Fig. 3), average errors of 12% and 0.58% were noted for damping and negative stiffness ratio, respectively. Similarly, for NSADI-1 (Fig. 4), errors of 3.2%, 1.5%, and 0.1% were identified for inertance, negative, and positive stiffness ratios, respectively. However, in the case of NSADI-2 (Fig. 5), average errors of 1.7%, 3.18%, and 1.14% for positive stiffness, damping, and negative stiffness ratio, respectively, were observed. For NSADI-3 (Fig. 6), average errors of 2.7%, 3.38%, and 7.14% were noted for positive stiffness, damping, and negative stiffness ratio, respectively. The primary system comprises a damping ratio not exceeding 0.1 and remains valid for explicit mathematical expressions, dependent on the damping ratio for both the primary system and supplementary dampers. Figure 8 illustrates optimal parameter variations concerning the inertance ratio under two distinct optimization conditions: maximum displacement response and maximum acceleration response. Furthermore, Fig. 8 represents the frequency domain conditions.

Fig. 3
figure 3

Comparisons of plots of data from numerical search technique and the results obtained from proposed explicit expressions for TMDI: a Optimum damping ratio \({\xi }_{d,opt}\) (R2 = 0.9952); and b Optimum negative stiffness ratio \({\alpha }_{d,opt}\) (R2 = 0.9997)

Full size image
Fig. 4
figure 4

Comparisons of plots of data from numerical search technique and the results obtained from proposed explicit expressions for NSADI-1: a Optimum stiffness ratio \({\beta }_{d,opt}\) (R2 = 0.9920); b Optimum inertance ratio \({\mu }_{d,opt}\) (R2 = 0.9530); and c Optimum negative stiffness ratio \({\alpha }_{d,opt}\) (R2 = 0.9967)

Full size image
Fig. 5
figure 5

Comparisons of plots of data from numerical search technique and the results obtained from proposed explicit expressions for NSADI-2: a Optimum stiffness ratio \({\beta }_{d,opt}\) (R2 = 0.9962); b Optimum damping ratio \({\xi }_{d,opt}\) (R2 = 0.9996); and c Optimum negative stiffness ratio \({\alpha }_{d,opt}\) (R2 = 0.9945)

Full size image
Fig. 6
figure 6

Comparisons of plots of data from numerical search technique and the results obtained from proposed explicit expressions for NSADI-3: a Optimum stiffness ratio \({\beta }_{d,opt}\) (R2 = 0.9976); b Optimum damping ratio \({\xi }_{d,opt}\) (R2 = 0.9951); and c Optimum negative stiffness ratio \({\alpha }_{d,opt}\) (R2 = 0.9940)

Full size image
Fig. 7
figure 7

Comparisons of plots of data from numerical search technique and the results obtained from proposed explicit expressions for CID: a Optimum stiffness ratio \({\beta }_{d,opt}\) (R2 = 0.9994); and b Optimum damping ratio \({\xi }_{d,opt}\) (R2 = 0.9985)

Full size image
Fig. 8
figure 8

Comparisons of optimization results corresponding to displacement and acceleration for: a Optimal frequency ratio; and b Optimal damping ratio

Full size image

5 Modelling of Base-Isolated Shear Buildings with Supplemental Dampers

Figure 9 displays a schematic representation of the base isolation system of a shear frame model. The following are the assumptions made in the present investigation: (i) Each floor diaphragm of the superstructure is thought to be rigid relative to the columns; (ii) The lateral stiffness of the floor is considered to be linear; (iii) The clutched inerter's resisting force is assumed to be proportional to the relative acceleration at the two ends when engaged and zero when disengaged; (iv) Torsional effect is neglected; and (v) Pounding effect of the structure is neglected. The dynamic equation for the base isolation system with supplementary damper under seismic excitation is expressed below [68].

$$\left[ {\begin{array}{*{20}c} {m_{t} } & {r^{T} m} \\ {\left[ m \right]\left\{ r \right\}} & {\left[ m \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{x}_{b} } \\ {\ddot{x}} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {c_{b} } & 0 \\ 0 & {\left[ c \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {x_{b} } \\ {\dot{x}} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {k_{b} } & 0 \\ 0 & {\left[ k \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {x_{b} } \\ x \\ \end{array} } \right\} + \left\{ \lambda \right\}f_{d} = - \left\{ {\begin{array}{*{20}c} {m_{t} } \\ {\left[ m \right]\left\{ r \right\}} \\ \end{array} } \right\}\ddot{x}_{g}$$
(37)

where the total mass including floor and base slab is \(m_{t}\); mass, damping, and stiffness matrix of the 5-DOF of the fixed base shear model are [m], [c] and [k], respectively; displacement of the base isolator is \(x_{b}\); relative displacement with base isolator of vector in 5 × 1 dimensions is x; relative displacement of the floor is \(\left\{ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } & {x_{4} } & {x_{5} } \\ \end{array} } \right\}^{T} ;\) influence coefficient of the vector of 5 × 1 is r; vector of dimension 6 × 1 is expressed as \(\left\{ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right\}^{T}\); and control force derived from Eqs. (10), (12), (14), (16) and (17) is represented as \(f_{d}\).

Fig. 9
figure 9

Schematic representation of benchmark base isolation system with supplementary dampers under both horizontal and vertical ground motion: a Plan; and b Elevation

Full size image

The model's state space representation is presented in Eq. (32), while Table 1 displays the selected ground motion data for the time history analysis. The base isolation structure nomenclature with supplementary damper is denoted as follows: base isolation with TMDI (BITMDI), base isolation with NSADI-1 (BINSADI-1), base isolation with NSADI-2 (BINSADI-2), base isolation with NSADI-3 (BINSADI-3), and base isolation with CID (BICID).

Table 1 Details of ground motion data record selected
Full size table

Figure 10 illustrates the horizontal and vertical ground motion spectra under analysis, while Fig. 11 depicts the ratio of peak ground acceleration in the vertical to horizontal directions for specific ground motion datasets. The primary mode of vibration for a base-isolated (BI) structure is dominant [50, 69]. Utilizing closed-form expressions, the optimal parameters are derived and applied to the base isolation system within a shear model. The analysis incorporates two sets of ground motion data, NF and FF, detailed in Table 1, which is considered in the current study.

Fig. 10
figure 10

The spectra of chosen ground motions and target spectrum: a Vertical ground motions; and b Horizontal ground motions

Full size image
Fig. 11
figure 11

Selected ground motion values of PGAv/PGAh

Full size image

The study investigates the performance of a BI structure equipped with supplementary dampers (TMDI, NSADI-1, NSADI-2, NSADI-3, and CID) under seismic loads. The BI system with various dampers is subjected to specific ground motion data. The investigation adopts properties of a shear model for the BI structure consistent with prior studies [70, 71], with an isolation period of 2 s. Each story maintains uniform stiffness and lumped mass distribution, with stiffness and mass per DOF set at 1.5228 × 107 N/m and 5000 kg, respectively. For the fixed base case, a fundamental period of 0.5 s is assumed, with damping ratios of 0.02 for the first two modes and the Rayleigh damping method applied to the remaining mode. Key properties of the base isolator include a damping ratio of 0.1, isolation period of 2 s, and base mass of 5000 kg. Model frequencies for the base isolation, obtained through free vibration analysis, are 0.4877, 4.0214, 7.6306, 10.6443, 12.8030, and 13.9288 Hz. The study evaluates three response parameters, including base displacement, drift, and peak story acceleration, to assess the isolated base structure's performance with supplementary dampers. Table 2 presents the optimal parameters of the supplementary damper, derived from the equations elaborated in the previous section. Assumptions for the BI system with a shear frame include: (i) linearity of the structural system, (ii) each story possessing one DOF in the lateral direction with disregarded torsional effects and considered impacts [72], (iii) neglect of soil-structure interaction, and (iv) treatment of the viscous damper as part of the isolation system, behaving linearly alongside a linear spring. Figure 12 presents hysteresis loops illustrating the force–deformation characteristics of the supplementary damper to analyze its nonlinear behavior.

Table 2 Optimum parameters of the TMDI, NSADI and CID
Full size table
Fig. 12
figure 12

Hysteresis loops of the force–deformation of the clutched inerter for a five-story structure (Tb = 3 s, \(\mu \hspace{0.17em}\)= 0.05 & \(\beta \hspace{0.17em}\)= 0.4): a RIITO, 2010 FF Earthquake; and b Brawley Airport

Full size image

6 Performance Investigation

Figure 13 illustrates the base displacement in time history plots for both North New Brighton School (2010) and CHY101 (1999), alongside the comparative effectiveness of various dampers. Peak displacement serves as the primary response metric in these plots. Among the dampers, BICID outperforms others while TMDI exhibits poor performance. Base displacements for NF versus FF data were examined in this study due to the consistently higher amplitudes in NF ground motion data. Furthermore, Fig. 14 depicts the time history analysis of peak story acceleration under NF and FF motion influence, highlighting peak acceleration points. Notably, CID demonstrates superior control over peak acceleration compared to NSADI. Conversely, TMDI dampers exhibit poor performance in controlling acceleration response. In Fig. 15, the story drift control of the IB structure with dampers is illustrated, considering ground motion data from Brawley Airport (1979) and RIITO (2010). It is found that the story drift is satisfactorily controlled by using NSADI and TMDI. However, CID displays elevated acceleration response, particularly in the top story. These findings underscore the seismic load control purposes for the IB structure, including peak acceleration, story drift, and base displacement responses.

Fig. 13
figure 13

Base displacement for time history: a North New Brighton School (2010; and) b CHY101 (1999)

Full size image
Fig. 14
figure 14

Top story acceleration for time history: a Kaiapoi North School (2011); and b Christchurch Cashmere High School (2010)

Full size image
Fig. 15
figure 15

First story drift for time history: a Brawley Airport (1979); and b RIITO (2010)

Full size image

Figure 16 depicts the selected ground motion from El Centro Imp. Co.Cent, demonstrating the Fourier transform of its amplitude. It is observed that a peak frequency exceeding 1 Hz appears as the primary frequency within the selected ground motion, a common characteristic across many such ground motion data. The inherent frequencies of the uncontrolled BI model are identified at 0.4977, 4.0315, 7.7378, 10.6589, 13.7890, and 14.2345 Hz. Furthermore, the analysis reveals that the top-story acceleration response aligns with a Fourier transform frequency of 0.4977 Hz. The supplementary dampers play a pivotal role in reducing the amplitudes of uncontrolled BI systems. Moreover, it is evident that the fundamental mode governs the overall controlled response. Application of supplementary dampers, such as TMDI, NSADI, and CID, results in minor shifts in dominant frequencies, thereby reducing the frequencies of uncontrolled BI systems. This concurs with the assumption of a fundamental model. Structural frequencies experience amplification when they fall below 0.5 Hz for the ground motion. Particularly, the performance of TMDI in reducing resonant amplitudes is poor due to the minor reduction occurring. This analysis primarily focuses on the dominant responses of story displacement and drift.

Fig. 16
figure 16

Selected ground motion of peak acceleration amplitudes and corresponding top story peak acceleration response with different supplementary devices: a Ground motion FFT; and b Top Floor acceleration FFT

Full size image

Figure 17 represents the peak story drift of the mean value, considering both NF and FF ground motion data. Table 3 shows the control of the response of the BI structure having a supplementary damper under different sets of ground motion. It is also noted that base displacement is higher in the case of NF motion compared to FF motion. However, the results indicate that both sets of ground motion data are controlled by using supplementary dampers. The performance of BINSADI and BICID is better compared to BITMDI. In the case of an uncontrolled BI system, the mean displacement demand is 88 mm, while it is 62 mm in the case of NF and FF data, respectively. The base displacement is 65, 62, 53, 60, and 59 mm for BITMDI, BINSADI-1, BINSADI-2, BINSADI-3, and BICID under NF, respectively, and also 46, 44, 45, 38, and 33 mm for BITMDI, BINSADI-1, BINSADI-2, BINSADI-3, and BICID under FF, respectively, based on optimal design. These results suggest that BICID performs better than other supplementary dampers, with poor performance in the case of TMDI.

Fig. 17
figure 17

Comparisons of story drift response of BI with supplementary dampers with two different ground motion: a Yae; and b Duzce

Full size image
Table 3 Control of peak mean response of NF and FF motions
Full size table

Figure 18 represents the mean value of peak story acceleration, as also represented in Table 3. It is observed that peak story acceleration is higher in NF compared to FF. The proposed supplementary damper plays a vital role in controlling acceleration. NSADI-1 and CID were found to play a better role in controlling acceleration response than other supplementary dampers. However, poor performance was observed in the case of a TMDI damper for acceleration control.

Fig. 18
figure 18

Comparisons of story acceleration response of BI with supplementary dampers with two different ground motion: a Lamont 1062; and b Shu

Full size image

The recital of a supplementary damper in reducing story shear is represented in Fig. 19, and the values are also shown in Table 3. NSADI-1, NSADI-2, NSADI-3, and CID are the supplementary dampers for controlling the story shear compared to TMDI. TMDI was also found to have poor performance in controlling the story shear.

Fig. 19
figure 19

Comparisons of story shear response of BI with supplementary dampers with two different ground motion: a Takarazuka; and b Bolu

Full size image

From the results presented in the previous sections, it is found that the time history analysis of NSADI and CID performs better by reducing all objective parameters, whereas BITMDI performs poorly in terms of response reduction. The TMDI configuration is similar to NSADI-2. The numerical results show a consequent reduction in response by using the NSADI-2 supplementary damper. Both H2 and H∞ optimization procedures are used for the investigation of the amplification factor for controlling the response of the MDOF system. Figure 20 represents the optimum inertance ratio and corresponding different floor for different damping ratios of clutched inerter damper for a base isolated structure. As the damping ratio increases and the corresponding optimum inertance ratio decreases, this is due to high damping and also to different base periods. Further, a fast Fourier transformer (FFT) amplitude curve was plotted for the base isolation structure with different supplementary dampers under Takarazuka earthquakes (Tb = 3 s, \({\xi }_{d}\hspace{0.17em}\)= 0.25) as shown in Fig. 21. The maximum reduction of amplitude occurs for NSADI-3, and the minimum will be for the TMDI. This is due to the negative stiffness damper, which has more effect due to the stiffness ratio than the inertance ratio for TMDI.

Fig. 20
figure 20

Effects of the number of floors of the superstructure on the optimum inertance of the clutched inerter damper for different damping ratios: a Base period of 2 s, b Base period of 2.5 s; and c Base period of 3 s

Full size image
Fig. 21
figure 21

FFT plots of the highest floor total acceleration of the five-floor base-isolated building with the TMDI, CID, NSADI-1, NSADI-2 and NSADI-3 under the Takarazuka earthquakes (Tb = 3 s, \({\xi }_{d}\)=0.25)

Full size image

7 Numerical Model Verification

The response of a SDOF system equipped with a CID damper under seismic loading using the Wilson theta method is investigated in this section. Figure 22 illustrates the outcomes regarding the optimal parameter ratios for the CID damper, showing the diverse base periods of CID alongside their corresponding damping ratios. As the stiffness ratio and associated damping ratio increase, the maximum damping ratio reaches 0.6. Furthermore, when the stiffness ratio hits 1, the maximum base period extends to 3 s, with a base damping ratio of 0.05. These proposed optimal parameters maintain their relevance for both the current model and previous research investigations. The findings reveal an agreement between the present study and those reported by Li and Liang [73] and Jangid [2]. Moreover, Fig. 23 compares the top floor displacement of an isolated structure with a tuned mass CID from the present study with previous investigations by Wang and Zhang [74]. The results reveal a good correlation between the present study of a structure with a tuned mass CID and the experimental analysis of top floor displacement.

Fig. 22
figure 22

Comparisons of optimization of design results between displacement and acceleration: a Li and Liang [73]; and b Jangid [2]

Full size image
Fig. 23
figure 23

Comparison between the tuned mass CID of analytical results and experimental measurements for the displacement of the top floor by Wang and Zheng [74]

Full size image

Additionally, Tables 4 and 5 present the optimal parameters for the base-isolated structure with TMDI as explored in our study, offering a comparison with previous studies. The optimum damping ratio of TMDI for minimizing acceleration response of the minimum inertance ratio is 0.1, and the corresponding optimum damping ratio is 0.02. Cheng et al. [78] and Islam and Jangid [70] reported values of 0.0255 and 0.0383, respectively. At the maximum inertance ratio of 0.5, the optimum damping ratio is 0.1496, whereas in the literature, it was found to be 0.1682 and 0.163 [70, 78]. The optimum damping ratio of NSDI for minimizing acceleration response of the minimum inertance ratio is 0.1, and the corresponding optimum damping ratio is 0.0512. Kiran et al. [79] and Naqeeb and Jangid [71] found that the corresponding optimum damping ratios were 0.0389 and 0.0285, respectively. At the maximum inertance ratio of 0.5, the corresponding optimum damping ratio is 0.37464, while the previous studies reported 0.2859 and 0.435 [71, 79]. In addition, the base-isolated structure model properties of our model and the previous investigations [75, 76] are compared, as shown in Fig. 24. As the mass ratio increases and the corresponding optimum damping ratio increases, the maximum mass ratio is 0.1 and the corresponding optimum damping ratio is 0.16. This indicated that the results of the present study are in line with the previous research investigations by Jangid [75] Kiran et al. [79].

Table 4 Comparisons of the optimum damping ratio \({\xi }_{d,opt}\) for TMDI parameters for minimization of accelerations with previous studies
Full size table
Table 5 Comparisons of the optimum damping ratio \({\xi }_{d,opt}\) for NSDI parameters for minimization of accelerations with previous studies
Full size table
Fig. 24
figure 24

Comparisons of optimum parameter of damping ratio between this study and literature investigations by Jangid [75] and Kiran et al. [76]

Full size image

It is worth mentioning that the proposed technique is useful and suitable for analyzing benchmark structures subjected to both real and stochastic excitations. However, a notable limitation of this study is the necessity for a benchmark high-rise building to be analyzed specifically for wind effects [77]. This requirement underscores the need for further investigation. Moreover, future research should encompass high-rise structures confronting various hazards, including wind loads, seismic activity, snow, ice, and fire, among others. Additionally, the model should incorporate the parameter of soil-structure interaction to enhance its comprehensiveness. Moreover, the real-time implementation of control strategies, especially in dynamic systems like the damped system with supplementary dampers, poses several challenges. These include the computational complexity associated with real-time control algorithms and sensor and actuator dynamics. Such challenges become more pronounced in scenarios where rapid responses are critical, demanding fast computation. While our proposed control strategies show promise in minimizing system response and enhancing structural performance, their real-time implementation, especially in scenarios where rapid responses are critical, requires further research.

8 Conclusions

The optimum H2 control design was investigated in the present study. The system subjected to stationary random excitation at all frequencies is minimized by H2 and is interpreted as minimizing energy input. An analysis of the frequency domain under stationary white noise excitation was carried out in the first part. In the second part, the closed-forms of expression were derived for the optimum design of different supplementary dampers, including TMDI, NSADI, and CID. The third part of the study consisted of deriving TMDI, NSADI, and CID using the minimum H2 norm of the numerical search technique, and then the corresponding results were correlated with a closed-form of expressions by the sequence curve fitting technique. The different supplementary devices, such as TMDI, CID and NSADI, are used for irregular base isolated structures with different parameters, namely, mass ratio, negative stiffness ratio, positive stiffness ratio, natural frequency and damping ratio are optimized. Lastly, the performance of a base-isolated structure with supplementary dampers (TMDI, NSADI, and CID) was investigated with the proposed optimum parameters. The verdicts of the present study can be outlined as follows:

  • Optimal control achieved with TMDI, NSADI, and CID designs, meeting all objectives and showing promising performance against both NF and FF ground excitations.

  • Optimal design process confirms maximum damping effect with minimal dashpot usage, suggesting SDOF-derived parameters are applicable to MDOF base-isolated structures.

  • Numerical search approach is effective for minimizing constraints, aiding in reaching optimal parameters by objective function minimization. The fitting curve technique aligns well with closed-form expressions, although closed-form results' complexity increases with more constants.

  • Increase in positive stiffness ratio correlates with decrease in negative stiffness ratio, indicating optimal negative stiffness is associated with higher positive stiffness ratio. NSADI with greater inertance ratio yields minimum mean square response, indicating its advantage over lower negative stiffness ratio, simplifying design compared to increasing negative stiffness.

  • Base-isolated structure performance improves with NSADI over TMDI, suggesting addition of inerter to TMDI for enhanced performance.

  • NSADI demonstrates better control response with H2 optimum norm, while TMDI excels in response mitigation with H∞ optimum norm.

The proposed technique is effective for analyzing benchmark structures under real and stochastic excitations, but it requires further investigation of high-rise buildings. In addition, future research should cover various aspects like wind, seismic activity, snow, ice, and fire, with an added focus on soil-structure interaction. While promising for minimizing system response, more research is also needed for real-time implementation, especially in scenarios requiring rapid responses.