1 Introduction

In the face of depleting and environmentally harmful fossil fuels like oil, gas, and coal, there has been a growing emphasis on developing alternative energy resources. These alternatives are crucial to address environmental concerns arising from greenhouse gas emissions during the extraction of these traditional resources. Among the alternatives, renewable energies stand out, offering a cleaner way to generate electricity and reducing dependency on finite resources. However, they do come with the challenge of managing their inherent natural and occasionally unpredictable fluctuations. One promising source of clean energy is the use of variable-speed wind turbine (VSWT) systems to produce electricity, which has become increasingly competitive in terms of production costs [1, 2]. This shift is contributing significantly to reducing greenhouse gas emissions.

A single rotor wind turbine (SRWT), which has one horizontal axis and three blades, has been commonly used to produce electrical energy. However, various other types of wind turbines, such as the DRWT, have been proposed. Among its advantages are suitability for low wind speeds and an increase in the production of electrical energy compared to the SRWT [3,4,5]. The design of the DRWT consists of two turbines (an auxiliary turbine (AT) and a main turbine (MT)).

Currently, the VSWT employing DFIG technology is the most popular choice [6, 7]. Its primary advantage lies in the sizing of its three-phase static converters, namely the grid side converter (GSC) and rotor side converter (RSC), for only a portion of the generator nominal power. This configuration leads to substantial economic benefits compared to other electrical machines, such as permanent magnet synchronous generators (PMSG). The DFIG permits operation within a speed range of ± 30% around the synchronism speed, which enables downsizing of the static converters. These converters are connected between the electrical network and the rotor winding of the generator, making the system more efficient and compact.

The unbalanced grid voltage scenario, resulting from voltage drop in one or more phases, causes numerous problems in the wind turbine system based on DFIG. These problems include significant undulations in electromagnetic torque and stator powers. Additionally, there are high-frequency components in rotor currents that can lead to winding losses and excessive shaft stress [8]. In the literature, several research studies have been presented to address these issues. For instance, injecting sinusoidal currents for grid-side converter with only positive-sequence components at the point of common coupling with the grid [9], using adaptive PI regulators based on neural network (NN) [10], applying the sliding mode control (SMC) algorithm [11], and implementing model predictive control (MPC) [12].

To control the stator powers of the DFIG, a vector control (VC) approach is commonly employed. VC is typically divided into two methods: stator voltage orientation control (SVOC) and SFOC [13, 14]. In both methods, PI controllers are used to regulate the reactive and active powers of the generator by adjusting d-q rotor currents. Despite its widespread use in wind turbine systems, VC has shown some limitations in terms of robustness, mainly attributed to the use of this type of controller.

Backstepping control (BC) is one of the nonlinear control methods, which is proposed to improve the VC strategy [15]. The concept of dividing entire systems into subsystems is advocated by BC, as it facilitates the derivation and computation of the desired control input. This recursive process extends outward to successive subsystems until the final optimal control is achieved. In a study referenced as [16], both classical and integral BC methods based on a decoupled control using an indirect field orientation strategy were employed for speed regulation of a three-phase induction motor (IM). The classical BC methods resulted in fluctuations in the stator current of the IM and a slight steady-state error between the desired and actual rotor speed of the IM. However, the integral BC method improved robustness despite the presence of model uncertainties and ensured the global stability of the system. A basic BC method might not effectively reject disturbances and guarantee better robustness. Various robust BC strategies have been explored in the literature. For instance, in [17], a robust adaptive BC strategy was utilized for mobile robotic manipulators, demonstrating superior robustness and tracking performance compared to a classical proportional integral and derivative (PID) regulator. In spite of employing all these BC methods, complete suppression of external or internal disturbances is not achieved, resulting in uncertain robustness in certain scenarios.

The sliding mode control (SMC) is another nonlinear control method, which is widely used [18]. While this technique has exhibited great efficiency and robustness in the control of electrical drives, its usage has been limited due to the presence of undesirable chattering phenomenon caused by the discontinuous part of the control law. To mitigate the impact of this phenomenon, several solutions have been presented and proposed in the literature. These include the adoption of the boundary layer approach [19], utilization of the second-order sliding mode control (SOSMC) based on STA [20, 21], incorporation of passivity-sliding mode [22, 23], implementation of backstepping first-order sliding mode [24, 25], utilization of H∞ sliding mode [26], and application of sliding mode predictive control [27, 28]. Each of these strategies mentioned above varies in terms of their underlying principles, level of complexity, ease of implementation, susceptibility to changes in system parameters, and cost.

In this research paper, a newly introduced control method called “backstepping super-twisting control” is adopted to enhance robustness and minimize the chattering issue. This approach, introduced in reference [29], has demonstrated promising outcomes, particularly in the speed control of a three-phase squirrel cage IM. Hence, it will be implemented as the chosen control strategy for this study.

The achievements of this study can be outlined as follows:

  • A new controller was designed for the control of active and reactive power in the DFIG-based DRWT system.

  • Formulation of the proposed controller, integrating elements from BC and STA, hereby referred to as the backstepping super-twisting controller (BSTC).

  • A thorough performance evaluation was conducted, comparing SFOC, BC, and the proposed BSTC for the control of reactive and active power in the DFIG-based DRWT system under varying conditions, including extreme parameter variations and grid voltage drop.

  • Improved the robustness and reduced the total harmonic distortion (THD) value of the stator current. Additionally, decreased the steady-state error (SSE) for the reactive and active power control of the generator.

The rest of the paper is organized as follows: in Sects. 2 and 3, the DRWT and DFIG models are presented. In Sect. 4, the SFOC strategy of the DFIG is explained. The proposed BSTC technique is elucidated in Sect. 5. Section 6 presents the results and their discussion. Finally, in Sect. 7, the paper’s conclusions are presented.

2 DRWT model

The DRWT is a type of turbine that has appeared recently and has provided satisfactory results, as it helps to stabilize the generating system and reduce disturbances. Additionally, it increases the value of the mechanical power gained from the wind and is not affected by the wind generated by other turbines in wind farms.

The aerodynamic torques of the MT (TM) and AT (TA) are given in the following equations [30]:

$$T_{M} = \frac{{\rho \cdot \pi \cdot R_{M}^{5} \cdot C_{p} \cdot \omega_{M}^{2} }}{{2 \cdot \lambda_{M}^{3} }}$$
(1)
$$T_{A} = \frac{{\rho \cdot \pi \cdot R_{A}^{5} \cdot C_{p} \cdot \omega_{A}^{2} }}{{2\, \cdot \,\lambda_{A}^{3} }}$$
(2)

where λM and λA are the tip speed ratio of the MT and AT. RM and RA are the blade radius of the MT and AT. ωM and ωA are the mechanical speed of the MT and AT. ρ is the air density.

The power coefficient (Cp) can be calculated as the following equation [31]:

$$\begin{aligned} C_{p} (\lambda ,\beta ) = & 0.0068\,\lambda + 0.517\,(\frac{116}{{\lambda_{\,i} }} - 0.4\,\beta - 5)\, \cdot \,e^{{\frac{ - 21}{{\lambda_{i} }}}} \, \\ \frac{1}{{\lambda_{i} }} = & - \frac{0.035}{{\beta^{3} + 1}} + \frac{1}{\lambda + 0.08\beta } \\ \end{aligned}$$
(3)

where β is pitch angle.

Tip speed ratios for the AT and MT are given by the following equations:

$$\lambda_{A} = \frac{{\omega_{A} \cdot R_{A} }}{{V_{1} }}$$
(4)
$$\lambda_{M} = \frac{{\omega_{M} \cdot R_{M} }}{{V_{M} }}$$
(5)

3 DFIG model

The Park model of DFIG is given by [32,33,34,35]:

$$\left\{ \begin{gathered} V_{qs} = R_{s} I_{qs} + \frac{d}{dt}\phi_{qs} + \omega_{s} \phi_{ds} \hfill \\ V_{ds} = R_{s} I_{ds} + \frac{d}{dt}\phi_{ds} - \omega_{s} \phi_{qs} \hfill \\ V_{qr} = R_{r} I_{qr} + \frac{d}{dt}\phi_{qr} + \omega_{r} \phi_{dr} \hfill \\ V_{dr} = R_{r} I_{dr} + \frac{d}{dt}\phi_{dr} - \omega_{r} \phi_{qr} \hfill \\ \end{gathered} \right. ,\,\,\left\{ \begin{gathered} \phi_{qs} = L_{s} I_{qs} + MI_{qr} \hfill \\ \phi_{ds} = L_{s} I_{ds} + MI_{dr} \hfill \\ \phi_{qr} = L_{r} I_{qr} + MI_{qs} \hfill \\ \phi_{dr} = L_{r} I_{dr} + MI_{ds} \hfill \\ \end{gathered} \right.$$
(6)

where Iqr, Idr, Iqs and Ids are the rotor and stator currents in the d-q reference frame; Vqr, Vdr, Vqs and Vds are the rotor and stator voltages in the d-q reference frame; ϕqr, ϕdr, ϕqs and ϕds are rotor and stator flux in the d-q reference frame; M, Lr and Ls are respectively the mutual inductance, the inductance on the rotor and the inductance on the stator. Rr and Rs are respectively the resistances of the rotor and stator windings; The rotor and stator angular velocities are linked by the following relation ωs = ωm + ωr; ωr is the electrical pulsation of the rotor and ωs is the stator one, while ωm is the mechanical pulsation of the generator.

The expressions of the stator reactive power (Qs) and active power (Ps) delivered from the DFIG are given by:

$$\left\{ \begin{gathered} Q_{s} = I_{ds} V_{qs} - I_{qs} V_{ds} \hfill \\ P_{s} = I_{ds} V_{ds} + I_{qs} V_{qs} \hfill \\ \end{gathered} \right.$$
(7)

The mechanical equation supplements the generator’s electrical model and is given by Eq. (8).

$$T_{e} = T_{r} + J{\kern 1pt} {\kern 1pt} \frac{d\,\Omega }{{dt}} + f{\kern 1pt} {\kern 1pt} \Omega$$
(8)

where Ω is the mechanical rotor speed, Tr is the load torque, f is the viscous friction, and J is the inertia.

Equation (9) shows the electromagnetic torque Te of DFIG.

$$T_{e} = p\frac{M}{{L_{s} }}\left( {I_{dr} \phi_{qs} - I_{qr} \phi_{ds} } \right)$$
(9)

where p is the number of pole pairs.

4 SFOC strategy

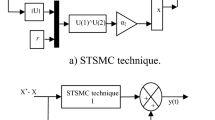
SFOC is a crucial method within the domain of renewable energy systems, specifically applied to DFIGs. SFOC involves aligning the stator flux with the rotor magnetic field, a process that optimizes the generator’s performance, leading to improved efficiency and overall output. This control strategy allows for accurate control of both active and reactive power, ensuring the stable and reliable operation of DFIGs, especially in conditions of variable wind. With the goal of achieving decoupled stator reactive and active power control of the DFIG-based DRWT, the SFOC method will be applied. This control strategy is based on two PI regulators, as illustrated in Fig. 1.

Fig. 1
figure 1

Power control scheme of DRWT system based on SFOC

Full size image

The stator flux vector ϕs will be aligned along the d-axis. We will neglect the stator resistance Rs, and based on the previous Eqs. (6) and (7), we can write:

$$\phi_{qs} = 0\,\,\,\,\,\,{\text{and}}\,\,\,\,\,\phi_{ds} = \phi_{s} \,$$
(10)
$$\left\{ \begin{gathered} V_{qs} = V_{s} = \phi_{s} \omega_{s} \hfill \\ V_{ds} = 0 \hfill \\ \end{gathered} \right.$$
(11)
$$\left\{ \begin{gathered} I_{qs} = - \frac{M}{{L_{s} }}I_{qr} \hfill \\ I_{ds} = \frac{{V_{s} }}{{\omega_{s} L_{s} }} - \frac{M}{{L_{s} }}I_{dr} \hfill \\ \end{gathered} \right.$$
(12)

When using Eqs. (10), (11), and (12), Eqs. (7) and (9) become:

$$\left\{ \begin{gathered} Q_{s} = \frac{{V_{s}^{2} }}{{L_{s} \omega_{s} }} - \frac{{MV_{s} }}{{L{}_{s}}}I_{dr} \hfill \\ P_{s} = - \frac{{MV_{s} }}{{L_{s} }}I_{qr} \hfill \\ \end{gathered} \right.$$
(13)
$$T_{e} = - p\frac{M}{{L_{s} }}\phi_{s} I_{qr}$$
(14)

Posing: \(g = \frac{{\omega_{r} }}{{\omega_{s} }}\) and \(\sigma = 1 - \frac{{M^{2} }}{{L{}_{s}L_{r} }}\,.\)

where g and σ are the slip and the magnetic dispersion coefficient, respectively.

The derivatives of quadrature and direct rotor currents are given by [36]:

$$\left\{ \begin{gathered} \frac{{dI_{qr} }}{dt} = \frac{1}{{\sigma L_{r} }}\left[ {V_{qr} - R_{r} I_{qr} - g\omega {}_{s}\sigma L_{r} I_{dr} - \frac{{gMV_{s} }}{{L_{s} }}} \right] \hfill \\ \frac{{dI_{dr} }}{dt} = \frac{1}{{\sigma L_{r} }}\left[ {V_{dr} - R_{r} I_{dr} + g\omega {}_{s}\sigma L_{r} I_{qr} } \right] \hfill \\ \end{gathered} \right.$$
(15)

The parameters of PI regulators represented in Fig. 1 are given by [37]:

$$K_{i} = \frac{1}{{\tau_{r} }}\,\frac{{L_{s} R_{r} }}{{MV_{s} }}$$
(16)
$$K_{p} = \frac{1}{{\tau_{r} }}\,\frac{{L_{s} L_{r} \,\sigma }}{{MV_{s} }}$$
(17)

where Ki, Kp and τr represent respectively the integral gain, proportional gain and response time.

To simplify the study of the application of the proposed controller, we will consider the following changes of variables:\(f_{1} = - R_{r} I_{qr} - g\omega {}_{s}\sigma L_{r} I_{dr} - \frac{{gMV_{s} }}{{L_{s} }}\) and \(f_{2} = - R_{r} I_{dr} + g\omega {}_{s}\sigma L_{r} I_{qr}\).

Equation (15) becomes:

$$\left\{ \begin{gathered} \frac{{dI_{qr} }}{dt} = \frac{1}{{\sigma L_{r} }}\left[ {V_{qr} + f_{1} } \right] \hfill \\ \frac{{dI_{dr} }}{dt} = \frac{1}{{\sigma L_{r} }}\left[ {V_{dr} + f_{2} } \right] \hfill \\ \end{gathered} \right.$$
(18)

5 Proposed BSTC

The BSTC technique is a control method proposed in this paper to address several challenges, including overcoming stator power ripples, improving stator current quality, and minimizing the impact of grid voltage drop. Additionally, this control is designed to enhance the overall robustness of the system. To implement this suggested control, certain concepts or information must be provided to the conventional BC to facilitate the understanding and application of the proposed control’s working principles.

5.1 Conventional BC

The backstepping approach is implemented utilizing principles from the Lyapunov stability theory, with the control law formulated through the construction of the Lyapunov function. The process of determining the control laws for the conventional controller involves following two fundamental steps:

First step: the tracking error e1 is given by:

$$e_{1} = P_{s}^{*} - P_{s}$$
(19)

The Lyapunov function V1 is given by:

$$V_{1} = \frac{1}{2} \cdot e_{1}^{2}$$
(20)

The derivative of the Lyapunov function V1 is:

$$\dot{V}_{1} = e_{1} \cdot \dot{e}_{1}$$
(21)
$$\dot{e}_{1} = \dot{P}_{s}^{*} - \dot{P}_{s} = \dot{P}_{s}^{*} + \frac{{MV_{s} }}{{L_{s} }} \cdot \,\dot{I}_{qr}$$
(22)

According to Eqs. (18), Eq. (22) becomes, when we replace the derivative of Iqr:

$$\dot{e}_{1} = \dot{P}_{s}^{*} + \frac{{MV_{s} }}{{L_{s} L_{r} \,\sigma }} \cdot \,(V_{qr} + f_{1} )$$
(23)

Posing: \(\psi = \frac{{MV_{s} }}{{L_{s} L_{r} \,\sigma }}\).

Equation (23) becomes:

$$\dot{e}_{1} = \dot{P}_{s}^{*} + \psi \cdot \,(V_{qr} + f_{1} )$$
(24)

Equation (24) is replaced in Eq. (21), we obtained:

$$\dot{V}_{1} = e_{1} \, \cdot \,\dot{e}_{1} = e_{1} \cdot \,(\dot{P}_{s}^{*} + \psi \cdot \,(V_{qr} + f_{1} ))$$
(25)

The first control law of the BC is proposed to be:

$$V_{qr} = - \frac{1}{\psi }(\dot{P}_{s\,}^{*} + k_{1} \, \cdot \,e_{1} )\, - f_{1}$$
(26)

where: k1 is a positive gain.

Equation (26) is replaced in Eq. (25), we obtained:

$$\dot{V}_{1} = - \,k_{1} \, \cdot \,e_{1}^{2} \le 0$$
(27)

Second step: the tracking error e2 is given by:

$$e_{2} = Q_{{s}}^{*} - Q_{s}$$
(28)

The Lyapunov function V2 is given by:

$$V_{2} = V_{1} + \frac{1}{2} \cdot \,e_{2}^{2}$$
(29)

Its derivative is:

$$\dot{V}_{2} = \dot{V}_{1} + e_{2} \, \cdot \,\dot{e}_{2} \,$$
(30)

where:

$$\dot{e}_{2} = \dot{Q}_{s}^{*} + \frac{{MV_{s} }}{{L_{s} }} \cdot \,\dot{I}_{dr}$$
(31)

According to Eqs. (18), Eq. (31) becomes, when we replace the derivative of Idr:

$$\dot{e}_{2} = \dot{Q}_{s}^{*} + \psi \cdot \,(V_{dr} + f_{2} )$$
(32)

Equation (32) is replaced in Eq. (30), we obtained:

$$\dot{V}_{2} = \dot{V}_{1} + e_{2} \, \cdot \,\dot{e}_{2} = \dot{V}_{1} + e_{2} \, \cdot \,(\dot{Q}_{s}^{*} + \psi \cdot \,(V_{dr} + f_{2} ))$$
(33)

The second control law of the BC is proposed to be:

$$V_{dr} = - \frac{1}{\psi }(\dot{Q}_{s}^{*} + k_{2} \, \cdot \,e_{2} ) - f_{2}$$
(34)

where: k2 is a positive gain.

Equation (34) is replaced in Eq. (33), we obtained:

$$\dot{V}_{2} = \dot{V}_{1} - k_{2} \, \cdot \,e_{2}^{2} = - k_{1} \, \cdot \,e_{1}^{2} - k_{2} \, \cdot \,e_{2}^{2} \le 0$$
(35)

Equations (35) and (27) are negative, which guarantee asymptotic stability of the system according to the Lyapunov theorem.

5.2 Conventional STA

In the field of control, STA is one of the simplest types of high-order SMC technique and the easiest to implement, as it can be applied without requiring knowledge of the mathematical form of the system under study. It can be applied directly after identifying the error. Compared with SMC, the STA technique is more robust and significantly reduces the chattering problem. The control laws of the STA are given by the following equations [20]:

$$u = u_{1} + u_{2}$$
(36)
$$u_{1} = - \alpha \cdot \,\left| s \right|^{\frac{1}{2}} \cdot \,sign(s)$$
(37)
$$\dot{u}_{2} = - \beta \cdot \,sign(s)$$
(38)

where s is the sliding surface and β, α are the positive gains.

In order to guarantee the asymptotic stability of the system, the STA control parameters α and β are selected as outlined below [20]:

$$\left\{ \begin{gathered} \beta > \frac{{\delta (5\,\alpha^{2} + 4\delta )}}{2(\alpha - 2\,\delta )} \hfill \\ \alpha > 2\delta \hfill \\ \end{gathered} \right.$$
(39)

where δ is a positive constants.

5.3 BSTC

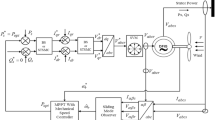
The proposed BSTC technique is a modification of the conventional BC method, where the term representing a STA is added to the control laws. The goal of this technique is to enhance the quality of the energy produced by the DFIG-based DRWT. Figure 2 represents the proposed control scheme for DRWT system based on BSTC technique.

Fig. 2
figure 2

Proposed control scheme for DRWT system based on BSTC

Full size image

The suggested BSTC aims to calculate the reference voltage values according to the following equations:

$$\begin{aligned} V_{qr} = &- \frac{1}{\psi }\left( \dot{P}_{s\,}^{*} + k_{1} \, \cdot \,e_{1} + \alpha_{1} \cdot \left| {e_{1} } \right|^{\frac{1}{2}} \cdot sign(e_{1} )\vphantom{\int\limits_{0}^{t} }\right.\\ &\left. + \int\limits_{0}^{t} {\beta_{1} {\kern 1pt} \cdot {\kern 1pt} {\kern 1pt} sign(} e_{1} ){\kern 1pt} {\kern 1pt} d\tau \right)\, - f_{1}\end{aligned}$$
(40)
$$\begin{aligned} V_{dr} = &\,- \frac{1}{\psi }\left( \dot{Q}_{s}^{*} + k_{2} \, \cdot \,e_{2} + \alpha_{2} \cdot \left| {e_{2} } \right|^{\frac{1}{2}} \cdot sign\left( {e_{2} } \right) \vphantom{\int\limits_{0}^{t} }\right.\\ &\left. + \int\limits_{0}^{t} {\beta_{2} {\kern 1pt} \cdot {\kern 1pt} {\kern 1pt} sign\left( {e_{2} } \right)} {\kern 1pt} {\kern 1pt} d\tau \right) - f_{2} \end{aligned}$$
(41)

where k1, k2, α1, β1, α2 and β2 are the positive gains that satisfy Eq. (39).

5.4 Stability examination of the proposed controller

In this part, our emphasis is on the essential aspect of guaranteeing the stability of control systems. The primary goal of any control system is to ensure stability and achieve optimal performance despite uncertainties and external disruptions. To comprehensively assess the stability of the control methodology presented in this research, we employ Lyapunov theory, a widely recognized mathematical framework known for providing insights into system behavior and confirming stability. This examination aims to demonstrate the effectiveness and reliability of our proposed control strategy in maintaining resilient system stability, ultimately laying the foundation for its successful implementation in practical, real-world scenarios.

The stability of the proposed control system is demonstrated as follow:

We replace the Eq. (40) in Eq. (25), we obtain:

$$\begin{aligned} \dot{V}_{1} = & - k_{1} \cdot e_{1}^{2} - e_{1} \\ &\cdot \left( {\alpha_{1} \cdot \left| {e_{1} } \right|^{\frac{1}{2}} \cdot sign(e_{1} ) + \int\limits_{0}^{t} {\beta_{1} \cdot sign(} e_{1} )d\tau } \right) \\ =& - k_{1} \cdot e_{1}^{2} - \alpha_{1} \cdot \left| {e_{1} } \right|^{\frac{1}{2}} \cdot e_{1} \cdot sign (e_{1}) \\ &- \beta_{1} \cdot e_{1} \cdot sign(e_{1} )\,\int_{0}^{t} {d\tau } \\ = &- k_{1} \cdot e_{1}^{2} - \alpha_{1} \cdot \left| {e_{1} } \right|^{\frac{1}{2}} \cdot e_{1} \cdot sign(e_{1} ) \\ &- \beta_{1} \cdot e_{1} \cdot sign(e_{1} ) \cdot t \\ =& - k_{1} \cdot e_{1}^{2} - \alpha_{1} \cdot \left| {e_{1} } \right|^{\frac{1}{2}} \cdot \left| {e_{1} } \right| - \beta_{1} \cdot \left| {e_{1} } \right| \cdot t \le 0 \\ \end{aligned}$$
(42)

We replace the Eq. (41) in Eq. (33), we obtain:

$$\begin{aligned} \dot{V}_{2} = & \dot{V}_{1} - k_{2} \cdot e_{2}^{2} \\ &- e_{2} \left( {\alpha_{2} \cdot \left| {e_{2} } \right|^{\frac{1}{2}} \cdot sign\,\,\,(e_{2} ) + \int\limits_{0}^{t} {\beta_{2} \cdot sign\,\,\,(} e_{2} ){\kern 1pt} {\kern 1pt} d\tau } \right) \\ = &\dot{V}_{1} - k_{2} \cdot e_{2}^{2} - \alpha_{2} \cdot \left| {e_{2} } \right|^{\frac{1}{2}} \cdot \,e_{2} \, \cdot \,sign\,\,\,(e_{2} ) \\ &- \beta_{2} \,.\,e_{2} \,.\,sign\,\,\,(e_{2} )\,\int_{0}^{t} {d\tau } \\ = &\dot{V}_{1} - k_{2} \cdot e_{2}^{2} - \alpha_{2} \cdot \left| {e_{2} } \right|^{\frac{1}{2}} \cdot \,e_{2} \, \cdot \,sign\,\,\,(e_{2} ) \\ &-\beta_{2} \,.\,e_{2} \,.\,sign\,\,\,(e_{2} )\,\, \cdot \,t \\ =& {\kern 1pt} \dot{V}_{1} - k_{2} \cdot e_{2}^{2} - \alpha_{2} \cdot \left| {e_{2} } \right|^{\frac{1}{2}} \cdot \,\left| {e_{2} } \right|\\ & - \beta_{2} \, \cdot \,\left| {e_{2} } \right|\,\, \cdot \,t \le 0 \\ \end{aligned}$$
(43)

Due to Eqs. (42) and (43), the stability of the proposed controller is guaranteed since the derivatives of the Lyapunov functions are negative.

6 Results and Discussion

The proposed control (BSTC) applied to the DFIG-based DRWT, as explained in Sect. 5, was simulated using MATLAB software, and the obtained results were compared to those of conventional controls.

The mechanical parameters of DRWT are as follows [38]: blade radius of the MT RM = 25.5 m, blade radius of the AT RA = 13.2 m, bevel gear base circle radius of the MT is r1 = 1 m, bevel gear base circle radius of the AT is r2 = 0.5 m, bevel gear base circle radius of the generator is r3 = 0.75 m, MT inertia momentum JM = 1000 kg m2, and AT inertia momentum JA = 500 kg m2.

The parameters of the studied DFIG are as follows [32]: stator voltage Vs = 398 V, Rr = 0.021 Ω, Lr = 0.0136 H, Rs = 0.012 Ω, Ls = 0.0137 H, stator frequency fs = 50 Hz, M = 0.0135 H, p = 2, J = 1000 kg m2, and f = 0.0024 Nm/rad s−1.

In this research, four tests were presented and analyzed: the first one is the reference tracking test (RTT), the second is the robustness test (RT), the third is the grid voltage drop test (GVDT), and the fourth test is the random wind speed test.

In the first, second, and third tests, we studied the performances of SFOC, BC, and BSTC under the wind speed conditions illustrated in Fig. 3.

Fig. 3
figure 3

Wind speed profile

Full size image

6.1 First Test

The obtained simulation results are depicted in Figs. 4, 5, 6, 7 for this first test (RTT). As depicted in Figs. 4 and 5, for the three methods of reactive and active powers control (SFOC, BC, and BSTC), the DFIG stator powers (Ps and Qs) follow their references (Ps* and Qs*) perfectly. We notice that the stator active power reference (Ps*) is obtained using the Maximum Power Point Tracking (MPPT) strategy, which makes the value of the stator active power (Ps) highly related to the rotation speed of the turbine. Nevertheless, we can observe a clear coupling effect between the reactive and active stator powers for SFOC and BC (seen in the active power curve at t = 0.35 s and t = 0.65 s, and in the reactive power curve at t = 0.2 s, t = 0.5 s, and t = 0.8 s). However, we can also notice in these Figures that the decoupling between the stator powers (Ps and Qs) is perfectly ensured for the proposed controller.

Fig. 4
figure 4

Active power

Full size image
Fig. 5
figure 5

Reactive power

Full size image
Fig. 6
figure 6

Stator currents (RTT)

Full size image
Fig. 7
figure 7

THD of stator current (RTT)

Full size image

Figure 6 depicts the simulation results of electric stator currents generated by the DFIG-based DRWT when employing the proposed BSTC. The simulation demonstrates a noticeable relationship between the variation in active power and the electric stator currents. Furthermore, the electric stator currents exhibit a well-defined sinusoidal form for this first test.

Figure 7 shows the THD (Total Harmonic Distortion) of the one-phase electric stator current (ias) of the generator for the three used controls (SFOC, BC, and BSTC) for RTT. These results prove that the value of THD is minimized when we use the proposed BSTC (THD = 0.54%) compared to SFOC (THD = 1.26%) and BC (THD = 0.81%). Hence, it can be asserted that the proposed control resulted in a decrease in THD value by approximately 57.14% compared to SFOC and by 33.33% compared to BC.

The numerical results of steady-state error (SSE) for this test are represented in Table 1. From this table, the proposed control strategy provided better numerical results than the SFOC and BC. Specifically, the BSTC strategy achieved significant reductions in SSE for active power, with percentages estimated at 60%, 28.57%, respectively, compared to the SFOC and BC.

Table 1 Values and ratios of SSE in the first test case
Full size table

In terms of reactive power, the proposed strategy reduced SSE by percentages estimated at 56.25%, 12.5%, respectively, compared to the SFOC and BC.

In conclusion, based on this initial test, it can be stated that BSTC performs significantly better than classical control methods (SFOC and BC).

6.2 Second Test

The robustness test involves varying the parameters of the DFIG model. Specifically, classical regulator calculations rely on transfer functions with assumed fixed parameters. However, in a real system, these parameters undergo variations due to various physical phenomena (such as inductance saturation and resistance heating). Additionally, the identification of these parameters is prone to inaccuracies stemming from the method employed and the measuring devices used.

As part of testing the robustness of the studied controllers (SFOC, BC, and BSTC), we assume that the DFIG parameters are varied under severe conditions as follows:

  • The value of the rotor resistance is doubled starting from 0.5 s;

  • The values of stator inductance (Ls), mutual inductance (M) and rotor inductance (Lr) respectively are decreased up to 50% starting from 0.5 s.

The obtained simulation results are illustrated in Figs. 8, 9, 10, 11, 12, 13. From these results, it can be noticed that the effect of DFIG parameter variations is very clear for SFOC and BC compared to the proposed control method (BSTC), especially when zooming in on the curves of stator active and reactive power (Figs. 10 and 11). Additionally, it is noted that Ps and Q follow the references well for all control methods (Figs. 8 and 9), with a priority given to the proposed control in terms of dynamic response. Moreover, stator power ripples are observed at the level of capacities, and these ripples are greater in the case of SFOC and BC.

Fig. 8
figure 8

Active power

Full size image
Fig. 9
figure 9

Reactive power

Full size image
Fig. 10
figure 10

Zoom (active power)

Full size image
Fig. 11
figure 11

Zoom (reactive power)

Full size image
Fig. 12
figure 12

Stator currents (RT)

Full size image
Fig. 13
figure 13

THD of stator current (RT)

Full size image

Figure 12 shows the outcomes of the simulation conducted on the electric stator currents produced by the DFIG-based DRWT using the proposed BSTC. The simulation clearly illustrates a significant correlation between the variations in the electric stator currents and the stator active power. Additionally, during this second test, the electric stator currents exhibit a good sinusoidal form.

Figure 13 illustrates the THD of ias of the DFIG-based DRWT during the RT. When we compare the THD values of SFOC (1.58%), BC (0.97%), and BSTC (0.58%), we can conclude that the proposed control present the best THD in this second test. Therefore, it can be stated that the implementation of the BSTC technique led to a reduction in the THD value by around 63.29% when compared to SFOC and by 40.20% when compared to BC.

Table 2 displays the quantitative outcomes of SSE in the second test. According to the table, the suggested control approach yielded superior numerical outcomes compared to SFOC and BC. Notably, the BSTC strategy resulted in substantial decreases in SSE for active power, with percentages reaching 62.96% and 52.15% in comparison to SFOC and BC, respectively. Regarding reactive power, the proposed strategy achieved reductions in SSE estimated at 44.73% and 30% compared to SFOC and BC, respectively.

Table 2 Values and ratios of SSE in the second test case
Full size table

In summary, with respect to this second test, it can be asserted that the suggested control method demonstrates greater robustness when compared to traditional control approaches.

6.3 Third Test

When a wind turbine system connected to the grid experiences a drop in grid voltage, various challenges may arise. The immediate consequence is a hindrance to the turbine’s capacity to generate electricity efficiently. A decline in grid voltage can result in diminished power quality, impacting the overall stability and dependability of the entire wind turbine system. This, in turn, can lead to decreased power output and operational efficiency in turbines, potentially resulting in economic losses. Additionally, the occurrence of grid voltage drops may activate protective measures within the turbines, leading to automatic shutdowns or restrictions in power production to prevent harm to the system. Effectively addressing these challenges necessitates the implementation of advanced control systems and grid management strategies to ensure the seamless integration of wind turbines with the grid, even amidst voltage fluctuations.

The objective of this test is to observe the behavior of the proposed control technique in response to a 15% grid voltage drop (GVD) in phase A, assumed to occur between 0.55 and 0.75 s as illustrated in Fig. 14a and b, and compare it to other conventional controls. The simulation results for this test are depicted in Figs. 15–17.

Fig. 14
figure 14

Simulation result of: a Grid voltage, b Zoom of grid voltage

Full size image
Fig. 15
figure 15

Result of the electromagnetic torque

Full size image

Figures 15 and 16 depict the dynamic responses of the electromagnetic torque (Te) of the DFIG-based DRWT during GVDT. As illustrated in these figures, the impact of GVD is evident for all studied control techniques. However, the undulations in Te are noticeably reduced when employing the proposed control compared to other control methods.

Fig. 16
figure 16

Zoom (Electromagnetic torque)

Full size image

Figure 17 illustrates the THD of ias of the DFIG-based DRWT during the GVDT. From these results, it can be noticed that the effect of the grid voltage drop is very clear, resulting in significant THD values for SFOC (THD = 1.47%) and BC (THD = 1.41%), compared to the proposed BSTC (THD = 1.37%). We can infer that, in this test, the proposed control exhibits the lowest THD of stator current value. Consequently, it can be affirmed that employing the BSTC technique resulted in a THD reduction of approximately 6.80% compared to SFOC and 2.83% compared to BC.

Fig. 17
figure 17

THD of stator current (GVDT)

Full size image

6.4 Fourth Test

In this fourth test, a distinct wind speed (WS) is employed, differing from the WS used in prior tests, where the WS applied was random, as depicted in Fig. 18a. Also, Fig. 18b represents the DFIG rotor speed (Ω), through this figure, it can be noticed that Ω follows the WS profile.

Fig. 18
figure 18

Simulation results of: a WS profile b generator speed

Full size image

The objective of this test is to investigate how the behavior of BSTC compares to that of SFOC and BC. The results of this assessment are depicted in Figs. 19 and 20, along with Table 3. Upon reviewing Fig. 19, it is evident that both Ps and Qs closely follow the reference values, with a notable advantage favoring the BSTC method in minimizing ripples. Additionally, active power experiences variations corresponding to changes in WS, while reactive power remains unaffected by these fluctuations, maintaining a constant value of 0 MVAR throughout the simulation period, as depicted in Fig. 19a, b. Furthermore, the proposed BSTC demonstrates fewer ripples in both reactive and active powers, as illustrated in Fig. 20a, b.

Fig. 19
figure 19

Fourth test results

Full size image
Fig. 20
figure 20

Zoom of the fourth test results

Full size image
Table 3 Values and ratios of SSE in the fourth test case
Full size table

Figure 19c depicts the stator current (ias), and its variations are linked to changes in stator active power. Notably, there is a distinct advantage favoring BSTC in terms of ripple reduction when compared to the SFOC and BC techniques, as evident in Fig. 20c. Additionally, when BSTC is employed, the current waveform exhibits a high-quality sinusoidal shape, illustrated in Fig. 19d, e, f. These figures showcase the THD values of the current for SFOC, BC, and BSTC. The recorded THD values are 2.89% for SFOC, 1.85% for BC, and 1.79% for the proposed BSTC. It can be inferred that, in this test, the proposed control demonstrates the lowest THD of stator current. Consequently, employing the BSTC technique resulted in a THD reduction of approximately 38.06% compared to SFOC and 3.24% compared to BC.

Table 3 presents the numerical results of SSE in the fourth test. The table indicates that the recommended control approach produced superior quantitative results compared to SFOC and BC. Specifically, the BSTC strategy led to significant reductions in SSE for active power, with percentages of 75.50% and 56.22% compared to SFOC and BC, respectively. In terms of reactive power, the proposed strategy achieved SSE reductions of 62% and 36.66% compared to SFOC and BC, respectively.

A comparative analysis between the suggested approach (BSTC) and the conventional ones (SFOC and BC) is presented in Table 4. Through this table, it can be noted that very good results are achieved, such as: an improvement in the quality of the current produced, perfect reactive and active stator power tracking, reduction of electromagnetic torque and stator power ripples, high precision, low rise time, negligible overshoot, short settling time, fast dynamic response and excellent robustness with the proposed approach. Moreover, the effect of grid voltage drop scenarios is relatively lower with the proposed approach than with the conventional ones.

Table 4 Comparative study between the proposed technique and conventional ones
Full size table

At the end of this research work, we present a comparison between the suggested BSTC approach and some scientifically published works regarding the percentage of the stator current THD values. The results are illustrated in Table 5. According to this table, it can be observed that the BSTC strategy yielded much lower percentages of the stator current THD than other published control methods, such as direct field-oriented control (DFOC), SMC, Fuzzy SMC, SOSMC based on STA, direct power control (DPC) using an LCL-filter, DPC-PD(1+PI), and direct FOC with third-order sliding mode. Finally, it can be said that the BSTC method proposed in this research work provides a good representation of sinusoidal current.

Table 5 Comparative results between some scientific published articles and the proposed BSTC strategy in terms of the stator current THD
Full size table

7 Conclusion

This research work was presented a robust BSTC strategy for a DFIG-based DRWT under normal operating conditions and grid voltage drop scenarios. The proposed control strategy combines the conventional BC and STA to enhance the quality of electrical energy produced by the DFIG-based DRWT. By employing the Lyapunov function method, the control laws of the BSTC strategy are derived, ensuring the system’s convergence and stability. Extensive simulation tests conducted using MATLAB software, including RTT, RT, GVDT, and random wind speed test, demonstrate the effectiveness of the suggested control.

The results indicate significant improvements compared to conventional control methods such as BC and SFOC. The BSTC strategy effectively mitigates the coupling effect, reduces stator power undulations, and exhibits high robustness. Additionally, the suggested controller achieves a low THD value in stator current when compared to some published controls.

Notably, under grid voltage drop conditions, the proposed BSTC strategy outperforms SFOC and BC by reducing ripples in electromagnetic torque. Consequently, this helps to lower winding losses and alleviate excessive shaft stress. Furthermore, the results indicate that the BSTC led to a 57.14% reduction in THD compared to SFOC and a 33.33% reduction compared to BC in the first test. On the other hand, in the second test, the proposed control minimizes the THD of the stator current by 63.29% compared to SFOC and by 40.20% compared to BC.

Finally, the BSTC strategy proves to be an effective solution for stator power regulation in DFIG-based DRWT systems. Its ability to address various operational conditions and deliver superior performance makes it a promising and practical control approach for enhancing the efficiency and reliability of renewable energy generation from wind turbines.

In future research, we will experimentally validate these findings and compare the results with existing studies. Additionally, we will implement novel strategies to control the studied system and achieve superior quality.