1 Introduction

Majority of the real flows in industrial applications are combinations of shear and extensional deformations. Even the expansion and contraction of channel flows of polymeric liquids contain both deformations, and we do not yet fully understand these complex flows. While the shear flow almost does not affect the distribution of the filaments, the extensional flow manages the alignment of the filaments in the direction of extension. Thus, additional to the rate of shear, the rate of extension also affects the apparent viscosity of the polymeric liquid significantly [1]. The mechanical properties of the polymer, which cools and crystallizes under extensional forces, vary according to the rate of cooling and the morphological orientation. This work explains the morphological and mechanical property changes of PTT fluid under simultaneous effects of non-isothermal bidirectional extension and different processing scenarios. For this purpose, film blowing process is selected as an example flow. Blown film extrusion is a widely used technique for producing various types of plastic sheets for the packaging industry. The film blowing process involves extruding a liquid polymer tube from an annular die and continuously inflating it to a size several times larger than its original dimensions, while crystallization takes place. Generally, semicrystalline polyethylene is employed in this process. The axial extension is maintained by the nip rolls and it is sustained by the blown air where the circumferential extension and cooling occur. The next part of this section is dedicated to literature survey related to the present study. First, the extensional flow studies are summarized. Then, the model papers for crystalline structure development are given.

Since the fundamental studies of Petrie and Pearson [2, 3], the bi-extensional flow of polymeric melts has been studied numerically and experimentally by many researchers [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Majority of the numerical studies in the literature used the thin film approximation where the forces due to gravity, surface tension and air drag are neglected, and a force balance between external forces and viscous forces is satisfied. The bidirectional extension is applied in axial and circumferential directions to a molten polymer melt, and during the flow, the polymer membrane is cooled down both from inner and outer surfaces. Thus, the morphology of the solid polymer constructs.

The thermal and morphological effects are investigated in the study of Muslet and Kamal [4], where a two-zone model is used. For liquid zone before the frost line, the PTT model is adopted, and beyond this line, neo-Hookean solid is employed. The two models used for liquid and solid phases do not match in the vicinity of the frost line. Thus, a smooth transition is not observed.

In a sequence of studies, Hyun et al. investigated the transient behavior of tubular film processes [5,6,7,8,9,10]. They concentrated on the process stability under altering process conditions. The transient [5,6,7,8,9], thermal [5,6,7,8,9,10] and crystallinity effects [9] are included in the linear stability analysis. They emphasized that the inclusion of thermal and morphological effects altered the stability regions of the process significantly. With the inclusion of morphological change, the so-called fictitious secondary stable region in the stability windows for the altering process conditions vanished; and thus, the final version showed better agreement with the experimental observations.

Pirkle Jr. and Braatz [11] performed a comparison study between the readily available models in the literature, the thin shell microstructural model [12,13,14] and the modified quasi-cylindrical model [15,16,17,18] under the same working parameters and tabulated their results. They reported that both models predicted similar results for the trends of important material parameters for altering working conditions. In a following study, Pirkle Jr. and Braatz [19] investigated numerically the thermal effects introducing an empirical heat transfer coefficient (HTC) fit for a known air mass in the bubble. This time, they used a quasi-Newtonian constitutive relation for modeling the polymer blend. They reported that the model failed to predict the experimental observations if the working conditions were closer to values where the film becomes unstable. Therefore, the cooling should be considered in detail, and further experiments are necessary.

In extensional flows, the polymeric liquid is modeled using different viscoelastic constitutive relations, such as, Maxwell model [20,21,22,23], modified Giesekus model [18, 24], the eXtended Pom–Pom (XPP) model [25, 26] and the PTT model [4,5,6,7,8]. In the extensional flow of a Maxwell fluid, the elongational viscosity raises drastically where numerical convergence becomes challenging for higher draw ratio values [23]. The Giesekus model is modified in such a way that it contains the molecular level morphological changes, and thus, it captures the extensional flow physics precisely [24]. The XPP model is generally used for branched polymers like high-density polyethylene (HDPE), where entanglements are significant [26]. In this study, the PTT model is used because it precisely captures viscoelastic liquids physics under extensional forces. The stretching forces are finite in the PTT model which leads an initial rise with a maximum, followed by a plateau under extensional forces. This attribute makes PTT a preferable model for extensional flows because the draw ratio rise does not lead to a dramatic increase in elongational viscosity, which improves numerical stability [23].

In the literature, it is reported that the numerical stability improved with the inclusion of the morphological developments as a result of crystallization of the molten polymer [9]. Typically, the solidification of liquid polymers is influenced by temperature, pressure and flow stresses. However, during the film blowing process, high pressure differentials are not usually present, as is the case with other polymer processes such as extrusion and blow molding. Therefore, the crystallinity of film blown polymers is typically modeled under the influence of only thermal (quiescent) and extensional forces (flow induced). In the literature, a functional relation is used for modeling the crystallization kinetics of blown polymer films [8, 9, 18, 19, 27], where the morphology development is represented by thermal and flow-induced crystallization. The kinetics of flow-induced crystallization (FIC) can be described using either the total stress [8, 9] or the stored free energy of the melt [28], depending on the constitutive model employed. Mubarak et al. [29] studied the logarithmic version of modified non-isothermal Avrami equations and reported an Avrami index of \(n = 3\). Some other well-known versions are Ziabicki [27], Nakamura [30] and Ozawa [31] models. Ziabicki model is valid in a very narrow temperature range where experimental challenges are present. In the formulation, the Nakamura model neglected the induction time effect and considered only isokinetic conditions. The Ozawa model is only applicable for the cases where the rate of cooling is constant, which is very unlikely for real-life polymer processing applications. Different versions of Kolmogorov–Avrami equations are developed to capture realistic behavior of morphology development of polymer melts under quiescent and flow-induced regimes [29, 32,33,34,35,36,37,38], which are used in this study. The use of this sophisticated model to forecast the morphology of semicrystalline materials in commercial software is still limited due to practical and financial considerations. The primary challenge stems from the extensive material characterization is required. A comprehensive rheological analysis of the material is necessary to establish the range of relaxation times. Furthermore, to characterize the quiescent crystallization kinetics, experiments must be conducted where spherulites are counted under an optical microscope for different thermal and pressure histories [38].

The online morphological development of the blown film during the process is studied experimentally by many researchers. Drongelen et al. [39] conducted an experimental study to investigate the morphological changes within a blown film using in situ wide angle X-ray diffraction. In their investigation, the researchers explored three distinct polymer resins with different molecular properties. Their findings revealed that the increase in draw ratio (DR) had a more significant impact on the change of crystallinity over time compared to the rise in blow-up ratio (BUR). However, they encountered challenges in establishing a definitive correlation between the process conditions and the crystalline structure. Zhang et al. [40, 41] conducted a series of experimental study to elucidate the online structure formation using in situ small- and wide-angle X-ray scattering in a custom built film blowing machine. They investigated the film crystallization in the machine direction. They reported crystallization at higher temperature for low DR values and higher orientation factors for high DR values [40]. It is concluded that the longer chained polyethylene resins stabilize the process [41]. The increased relaxation as a consequence of higher DR values does not result in dominant quiescent crystallization; however, flow-induced crystallization is more pronounced. In another in situ small- and wide-angle X-ray diffraction experimental work, Zhao et al. [42] conducted a comparison study for three different polyethylene resins with different comonomers using a custom-made film blowing setup. It is reported that with higher entanglement, the structure formation was affected from both quiescent and flow-induced crystallization; however, with short chain branching the crystallization is dominant in quiescent form. Finally, they reported better mechanical performance with short chain branched polymers and better process stability with the long chain branched polymers [42], but they fail to propose a direct correlation between the morphological structure and the process conditions.

Although the morphological changes of blown films are studied by many researchers, the literature lacks studies of the numerical simulations of morphological investigation of bidirectional extensional flows under different processing conditions and heat transfer scenarios are still incomplete. The main objective of this study is to reveal the combined effect of process conditions and thermal influences on the development of morphological structures under bidirectional extensional flows. To solve the equations related to mass, energy and crystallization, the Adams–Bashforth integration algorithm is employed, alongside the Secant method with proper boundary and initial conditions. Both flow-induced (FIC) and temperature-induced crystallization (TIC) are incorporated into the simulation model, and the steady formulation is used to investigate the mechanical and morphological structure of the system.

In film blowing process, the majority of the morphological changes are finalized at the frost line; thus, the investigated computational domain is limited to the region between the die exit and the frost line. The blown film is modeled as an axisymmetric thin film in tension; where gravity, air drag, surface tension and inertia are neglected [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24].

The semicrystalline polymer is modeled using the PTT constitutive relation. Semicrystalline polymers exhibit highly complex behavior under various loading conditions throughout their lifespan. The advanced crystallization model, present in the literature, enables accurate forecasting of the crystalline structure, commonly known as spherulites and shish kebabs. This study represents a pioneering effort to simulate the alteration of morphological structures (specifically, spherulites and shish kebabs) for a blown film under realistic process conditions.

It has been reported in the literature [4] that the general process parameter ranges for DR is within \(5 \le {\text{DR}} \le 25\) and for BUR is within \(1.5 \le {\text{BUR}} \le 5\). This range ensures that the thickness reduction falls between 20 and 200, which is considered acceptable in practice [17]. In another experimental study by Triosi et al. [43], the chosen process parameter interval is \(8.7 \le {\text{DR}} \le 28.3\) and \(1.4 \le {\text{BUR}} \le 2.5\). In a sequence of related works, Lee et al. [7,8,9,10] conducted a stability analysis for the transient film blowing process and demonstrated that the inclusion of online crystallization expands the stability window for process parameters. To avoid instabilities arising from the process conditions, this study uses a parameter range of \(15 \le {\text{DR}} \le 30\) and \(1 \le {\text{BUR}} \le 2.5\), with a thickness reduction of 20–60. The chosen process conditions are realistic and stable, ensuring reliable results throughout the simulation. Additionally, the heat transfer coefficients from the literature are compared for similar cooling conditions under same process conditions. In the next sections, the detailed mathematical formulation and solution procedure are described, followed by the results and discussion, and the concluding remarks.

2 Mathematical Formulation and Solution Procedure

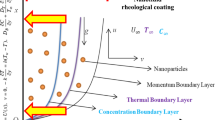
Film blowing process is shown schematically in Fig. 1. The molten polymer extruded from the annular dies with a radius \(r_{0}\) and annular gap \(h_{0}\) at a temperature \(T_{0}\) and an average velocity \(v_{0}\). The film is blown with a pressure difference \(\Delta P\) and it is cooled by the cooling air at a room temperature \(T_{{\text{a}}}\) sent from the rings at the outer sides of the die exit. The TIC and the FICs take place as a combined result of cooling and bi-extensional deformation of the flow. The molten polymer stiffens with development of the microstructures which prevent further bubble growth, leading to an almost constant diameter of the tubular structure starting from the frost line until the nip rolls. Above the die exit where the bubble radius achieves a peak value as a result of blown air, cooling and the onset of crystallization is referred as the frost line height, \(Z_{{\text{F}}}\). The final product is collected at the nip rolls with a velocity \(v_{{{\text{nr}}}}\).

Fig. 1
figure 1

Schematic representation of the film blowing process, the computational domain is between the die exit and the frost line

Full size image

Equation 1 illustrates the relationship between the blow-up ratio (BUR), represented by the ratio of the ultimate bubble radius at the frost line \(\left( {r_{{\text{F}}} } \right)\) to the annular die radius \(\left( {r_{0} } \right)\), and the draw ratio (DR), which is the ratio of the axial velocity at the nip rolls \((v_{{{\text{nr}}}} )\) to the average velocity at the die exit \((v_{0} )\).

$$ {\text{BUR}} = \frac{{ r_{{\text{F}}} }}{{r_{0} }}\quad {\text{DR}} = \frac{{ v_{{{\text{nr}}}} }}{{v_{0} }} $$
(1)

In this study, the calculations are presented between the annular die exit and the frost line, Fig. 1. The present model predicts the flow and morphological parameters of the PTT film starting from the die exit up to the frost line where proper boundary and initial conditions are imposed.

2.1 Mathematical Formulation

The equations that govern the film blowing process of PTT fluids under steady non-isothermal conditions are given below. These equations were developed through the pioneering study by Pearson and Petrie [2, 3], who established the initial modeling equations that have since served as the standard for all further research efforts [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24].

The blown film is considered as a thin shell which is subjected to axial force and blown air which results in a pressure difference between inside and outside of the tubular film. The process is steady state and the geometry of the film is symmetric around the z axis. The film radius is very large compared to its thickness so the film is assumed as a thin shell. Thus, the parameters will be treated as constant values along the thickness [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Additionally, the equations were modified to remove the radii of curvature by including their geometric correlation with the bubble radius and the blowing angle. This adjustment was made to prevent potential instability resulting from the significant axial curvature at the freeze line. This methodology was previously used by many researchers [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. In the following context, all derivatives correspond to the dimensionless variable z. These steady governing equations are inherited from the literature.

The steady mass balance equation [8]

$$ \frac{{\text{d}}}{{{\text{d}}z}}\left( {rhv} \right) = 0 $$
(2)

where

$$ r = \frac{{\overline{r}}}{{r_{0} }},\;h = \frac{{\overline{h}}}{{h_{0} }},\;v = \frac{{\overline{v}}}{{v_{0} }} $$

The steady force balance in the axial direction [8]

$$ F_{z} = \frac{{2rh\left( {\sigma_{11} - \sigma_{22} } \right)}}{{\sqrt {1 + \left( {\frac{{{\text{d}}r}}{{{\text{d}}z}}} \right)^{2} } }} + B\left( {r_{{\text{F}}}^{2} - r^{2} } \right) $$
(3)

Here

$$ F_{Z} = \frac{{\overline{F}_{Z} }}{{2\pi \eta_{0} h_{0} v_{0} }},\;B = \frac{{r_{0}^{2} \Delta P}}{{2\eta_{0} h_{0} v_{0} }},\;\sigma_{ij} = \frac{{\overline{\sigma }_{ij} r_{0} }}{{2\eta_{0} v_{0} }} $$

and the steady force balance in the circumferential direction [8]

$$ B = \frac{{ - h\left( {\sigma_{11} - \sigma_{22} } \right)\left( {\frac{{{\text{d}}^{2} r}}{{{\text{d}}z^{2} }}} \right)}}{{\left[ {1 + \left( {\frac{{d^{2} r}}{{dz^{2} }}} \right)^{2} } \right]^{\frac{3}{2}} }} + \frac{{h\left( {\sigma_{33} - \sigma_{22} } \right)}}{{r\sqrt {1 + \left( {\frac{{{\text{d}}^{2} r}}{{{\text{d}}z^{2} }}} \right)^{2} } }} $$
(4)

where \(r\) is the dimensionless bubble radius; \(h\) is the dimensionless film thickness; \(v\) is the dimensionless fluid velocity; and z is the dimensionless distance in the machine (axial) direction. The subscript 0 denotes the values at the die exit, \(r_{0}\) is the die radius; \(v_{0}\) is the flow velocity at the die exit; and \(h_{0}\) is the annular die gap. \(F_{z}\) is the dimensionless tensile force in axial direction, \(z;\) \(B\) is the non-dimensional pressure difference; \(r_{{\text{F}}}\) is the bubble radius at the frost line; \({\Delta }P\) is the pressure difference between the inner and outer of the film; \(\sigma_{11}\) is the non-dimensional normal stress in the machine direction; \(\sigma_{33}\) is the non-dimensional circumferential (hoop) stress; and \(\eta_{0}\) is the zero shear viscosity. In the simulations, the non-dimensional frost line height is fixed to \(Z_{{\text{F}}} = 5\).

The steady energy balance equation is [9]

$$ \frac{v}{{\sqrt {1 + \left( {\frac{{{\text{d}}r}}{{{\text{d}}z}}} \right)^{2} } }}\frac{{{\text{d}}\theta }}{{{\text{d}}z}} = - \frac{U}{h}\left( {\theta - \theta_{{\text{a}}} } \right) - \frac{{E_{m} }}{h}\left( {\theta^{4} - \theta_{{\text{a}}}^{4} } \right) + {\Delta }H_{{\text{f}}} \left( {\frac{v}{{\sqrt {1 + \left( {\frac{{{\text{d}}r}}{{{\text{d}}z}}} \right)^{2} } }}\frac{{{\text{d}}\chi }}{{{\text{d}}x}}} \right) $$
(5)

where

$$\begin{aligned} \theta = &\frac{T}{{\theta_{0} }},\,\,U =\frac{{\overline{U}r_{0} }}{{\rho C_{p} h_{0} v_{0} }},\\E_{m} =&\frac{{\varepsilon_{m} \sigma_{{{\text{SB}}}} \theta_{0}^{3} r_{0}}}{{\rho C_{p} v_{0} h_{0} }},\,\;\Delta H_{{\text{f}}} =\frac{{\Delta \overline{H}_{{\text{f}}} \chi_{\infty } }}{{C_{p}T_{0} }} \end{aligned}$$

where \(\theta\) is the dimensionless temperature; T is temperature; \(\theta_{{\text{a}}}\) is the non-dimensional ambient temperature, \(U\) is the dimensionless HTC; \(E_{m}\)is the radiation coefficient; \(\varepsilon_{m}\)is the emissivity; \(\sigma_{{{\text{SB}}}}\)is Stefan-Boltzmann constant; \(\rho\)is the density; \(C_{p}\) is the heat capacity; \(\chi_{\infty }\) is the ultimate crystallinity, and \({\Delta }H_{{\text{f}}}\) is the heat fusion.

The PTT model is used to capture both molten and solidified polymer features in the simulations where the Deborah number (De) is defined as a function of the temperature and the space filling. Thus, in this study the non-isothermal and morphological changes due to cooling and deformation are introduced to the flow field [4,5,6,7,8,9].

The constitutive PTT fluid model is [9]

$$ K{\varvec{\tau}} + {\text{De}}\left[ {{\varvec{v}} \cdot \nabla {\varvec{\tau}} - {\varvec{L}} \cdot {\varvec{\tau}} - {\varvec{\tau}} \cdot L^{T} } \right] = \frac{{{\text{De}}}}{{{\text{De}}_{0} }}{\varvec{D}} $$
(6)

where

$$\begin{aligned}K = &\exp \left[ {\frac{{2\varepsilon {\text{Detr}}\tau }}{{\exp \left( {\beta \chi } \right)}}} \right],\;{\varvec{D}} =\frac{1}{2}\left( {\nabla v + \nabla v^{T} } \right),\\{\varvec{L}}= &\nabla v - \xi {\varvec{D}},\;\eta = \eta_{0}{\text{exp}}\left[ {\frac{{E_{{\text{a}}} }}{{RT_{0} }}\left({\frac{1}{T} - 1} \right) + \alpha \chi } \right] \end{aligned}$$
$$ G = G_{0} {\text{exp}}\left[ {\beta \chi } \right] $$
$$ {\text{De}} = \frac{{\lambda_{0} v_{0} }}{{r_{0} }}{\text{exp}}\left[ {\frac{{E_{{\text{a}}} }}{{RT_{0} }}\left( {\frac{1}{T} - 1} \right) + \left( {\alpha - \beta } \right)\chi } \right] $$

where \(\mathrm{De}\) is the Deborah number; \(G\) is the film modulus; \(\mathbf{D}\) is the dimensionless rate of strain tensor; \(\varepsilon \) and \(\xi \) are model parameters of PTT; \(\chi \) is total crystallinity;\( {\lambda }_{0}\) is relaxation time; \(R\) is gas constant; \({E}_{\mathrm{a}}\) is activation energy; \(\alpha \), \(\beta \) are the parameters for the crystalline structure dependence of the material properties polymer viscosity and modulus. The material and process parameters are listed in Table 1.

Table 1 The material and process parameters used in the present work in SI units
Full size table

The boundary conditions are as follows [2, 3]:

$$ \begin{gathered} r = 1,\;h = 1\;{\text{at}}\;z = 0 \hfill \\ r = r_{F} ,\;r\prime = 0\;{\text{at}}\;z = Z_{{\text{F}}} \hfill \\ \end{gathered} $$
(7)

where \(r_{F}\) is the final radius. The bubble radius reaches its maximum at the frost line which results with a zero film angle, \(r{\prime}=0\).

The crystallization model used in this study is adopted from the literature [33,34,35,36,37,38]. This novel crystallization model is successfully used to simulate crystallization of molten polymer in a Poiseuille flow [37], polymer crystallization at elevated pressure [35] and finally the slit flow test [25]. All these previous attempts are mostly rheological flows. To the best of the author’s knowledge, this is the first instance of utilizing this crystallization model for numerical simulation of the film blowing process. The crystallization kinetics is modeled using the Avrami and Schneider rate equations. The quiescent and flow-induced nucleation is represented by nested ordinary differential equations [33,34,35,36,37,38]. While the original equations incorporate the influence of both temperature and pressure changes on the morphological changes, the present study only accounts for temperature effects. This is due to the fact that film blowing involves a bidirectional extensional flow that is predominantly influenced by thermal effects, where the pressure effects being insignificant [37]. The detailed crystallization model given below is taken from literature [35, 37, 38].

The crystal growth for quiescent flow is as follows [33]:

$$ G_{q} = G_{{{\text{max}}}} {\text{exp}}\left( { - c_{g} \left( {T - T_{{g,{\text{ref}}}} } \right)^{2} } \right) $$
(8)
$$ N_{q} = N_{{{\text{max}}}} {\text{exp}}\left( { - c_{n} \left( {T - T_{{n,{\text{ref}}}} } \right)^{2} } \right) $$
(9)

where \(G_{q}\) is the crystal growth, \(N_{q}\) is the number of spherulites per unit volume, \(G_{{{\text{max}}}}\) is the maximum growth rate, and \(N_{{{\text{max}}}}\) is the maximum spherulite number. The values are measured at the reference temperatures \(\left( {T_{{g,{\text{ref}}}} , T_{{n,{\text{ref}}}} } \right)\), and \(c_{g}\) and \(c_{n}\) are constants. The crystalline volume fraction in quiescent condition is evaluated from the following steady equations [33, 37, 38]

$$ \phi_{3} = 8\pi N_{q} $$
(10)
$$ \phi_{2} = G_{q} \phi_{3} $$
(11)
$$ \phi_{1} = G_{q} \phi_{2} $$
(12)
$$ \phi_{0} = G_{q} \phi_{1} $$
(13)

where \(\phi_{0}\) is the total volume, \(\phi_{1}\) is the total surface, \(\phi_{2}\) is the sum of radii, and \(\phi_{3}\) is \(8\pi\) times the number of the spherulites per unit volume.

During the flow-induced crystallization, molecular stretch induces the formation of the oriented lamellar structures. They are typically called shish kebabs [36]. The shish length \(L\) under flow effects is modeled as follows [38]:

$$ L = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\Lambda \le {\Lambda }_{c} } \hfill \\ {g_{l} {\text{J}}_{2} \left( {{\mathbf{B}}_{e,AVG}^{{\text{d}}} } \right),} \hfill & {\Lambda > {\Lambda }_{c} } \hfill \\ \end{array} } \right. $$
(14)

where \({\Lambda }\) is the molecular stretch. Fibrous development occurs when the stretch exceeds the critical threshold of \({\Lambda }_{c}\). The temperature-dependent scaling parameter \(g_{l}\) determines the effect of \({\text{J}}_{2}\) on the fibrous progression [38]. Here, \({\text{J}}_{2} \left( {{\mathbf{B}}_{{{\text{e}},{\text{AVG}}}}^{{\text{d}}} } \right)\) represents the second invariant of the deviatoric elastic finger tensor \({\text{B}}_{{{\text{e}},{\text{AVG}}}}^{{\text{d}}}\) of the viscosity averaged mode, which is a measure of the entire molecular weight distribution in slow mode. The number of nuclei created by flow per unit volume can be expressed as [38].

$$ N_{f} = g_{n} \left( {{\Lambda }^{4} - 1} \right) $$
(15)

where \(g_{n}\) is the temperature-dependent scaling parameter and \({\Lambda }\) is the molecular stretch defined as \({\Lambda } = \sqrt {{\text{tr}}\left( {{\mathbf{B}}_{{\text{e}}} } \right)/3}\) where the elastic finger tensor and its viscosity averaged deviatoric part are \({\mathbf{B}}_{{\text{e}}} = \frac{{{\varvec{\uptau}}}}{{\text{G}}} + {\mathbf{I}}\) and \({\mathbf{B}}_{{{\text{e}},{\text{AVG}}}}^{{\text{d}}} = {\mathbf{B}}_{{\text{e}}} - \frac{1}{3}\left[ {{\text{tr}}\left( {{\mathbf{B}}_{{\text{e}}} } \right){\mathbf{I}}} \right]\), respectively.

The scaling parameters are \(g_{l} = 10^{{c_{L1} T + c_{L2} }}\) and \(g_{n} = 10^{{c_{N1} T + c_{N2} }}\).

Regarding the growth of kebabs on a shish, the equations in flow-induced condition are [37, 38].

$$ \psi_{2} = G_{{\text{f}}} N_{{\text{f}}} L $$
(16)
$$ \psi_{1} = G_{{\text{f}}} \psi_{2} $$
(17)
$$ \psi_{0} = G_{{\text{f}}} \psi_{1} $$
(18)

where \(G_{{\text{f}}}\) represents the crystal growth rate under flow conditions. \(\psi_{2}\) is the shish length per unit volume, \(\psi_{1}\) is the surface area of kebabs, and \(\psi_{0}\) is the volume of kebabs. In the case of isotropic spherulites, it is assumed that the growth rate is equal to that in quiescent conditions (\(G_{q} = G_{{\text{f}}}\)) [37]. Kolmogorov–Avrami model finally reads [38]

$$ \phi_{0} + \psi_{0} = - {\text{ln}}\left( {1 - \chi } \right) $$
(19)

here \(\chi\) is the total crystallinity, which is also called the total space filling [37, 38]. The crystalline volume fractions of spherulites \(\chi_{{{\text{sph}}}}\) and the shish kebabs \(\chi_{{{\text{sk}}}}\) are calculated using [37].

$$ \chi_{{{\text{sph}}}} = \left( {1 - \chi } \right)\phi_{0} $$
(20)
$$ \chi_{{{\text{sk}}}} = \left( {1 - \chi } \right)\psi_{0} $$
(21)

Once the crystallization is finalized \(\chi = \chi_{{{\text{sph}}}} + \chi_{{{\text{sk}}}} = 1\). The corresponding material properties for the morphological Eqs. 8–21 are listed in Table 2 [44].

Table 2 The parameters for the crystal growth in SI units [44]
Full size table

The heat transfer coefficient is assumed to be constant throughout the process by many researchers [18, 45,46,47,48,49]. Some of the constant values of heat transfer coefficients are tabulated in Table 3. However the local heat flux can be significantly affected by both the Coanda effect, which involves the attachment of an air jet to nearby curved surfaces, and the Venturi effect, which involves the design of the air-ring [50,51,52].

Table 3 Constant heat transfer coefficient values from the literature
Full size table

In this study, initially, the effect of the process conditions is investigated under the same cooling conditions. Then, the variation of the heat transfer coefficient in the z-direction has been taken into account and three different heat transfer coefficients from the literature are used and compared, see Table 4. The HTC coefficient presented by Shin et al. [7, 8] exhibits variation along the machine direction radius, and it undergoes exponential changes in response to the local temperature difference between the film and its surrounding environment. The HTC of Doufas [24] is defined as a function of the tubular film axial location with respect to a fixed chosen height. Finally, the HTC of Lee et al. [9] changes with the air velocity along the machine direction. In the presented work, those three different heat transfer coefficient descriptions are compared for equivalent cooling scenarios. The corresponding parameter list for the equivalent U scenarios used in the simulations is tabulated in Table 5.

Table 4 Heat transfer coefficient expressions
Full size table
Table 5 Coefficient list for the equivalent heat transfer coefficients used in the simulations
Full size table

2.2 Numerical Procedure and Validation

In this study, the numerical code has been developed by the author using Fortran Programming Language. Studies of various industrial applications using CFD, including the work by Darbandi et al. [53] on the heat exchangers, require distinct formulations and discretization approaches. As previously explained, the primary objective of this study is to examine the film blowing process. This assessment involves reducing the dimensions of the governing equations, resulting in a set of nested differential equations. This reduction in dimensions is particularly advantageous as it significantly reduces the computer resources required for analysis. For this reason, classical shooting method is used to solve the nonlinear mass balance, force balance and energy equations accompanied with the crystallization kinematics. This technique is used to simulate the bi-extensional steady flow problems by many researchers [4, 54, 55]. The initial value problem is solved using a linear multistep method, Adams–Bashforth 4th order. Secant method is used to ensure the boundary condition at frost line. The schematic representation of the numerical procedure is summarized in Fig. 2. The governing equations from 2 to 21 are discretized using finite difference method where the grid is configured with equally spaced grid points with \(15,000\) elements. Utilizing a range of finer grids for the simulation has yielded remarkably similar results, differing by a maximum of \(0.01\%\) from those attained through the existing grid configuration. At the die exit the initial bubble radius, temperature, velocity, stress, thickness and the crystallization parameters are known. At the frost line, zero blowing angle boundary condition is imposed. Physically it represents that the radius remains constant beyond the frost line. The simulation is performed along the machine direction, starting from the die exit toward the frost line. Initially the material parameters and the crystallinity parameters are calculated. Then at the known temperature, the corresponding stresses, radius and the thickness are calculated. For a fixed axial force and pressure difference, the Secant method is used to satisfy the zero blowing angle condition at the frost line by updating the initial angle at the die exit. The solution is recorded if the desired BUR and DR values are reached at the frost line. If not, a two-variable Secant method is used to find updated force and pressure difference values until the desired BUR and DR values at the frost line are reached. The convergence criterion for the iterations is fixed as \(8 \times 10^{ - 8}\).

Fig. 2
figure 2

Schematic representation of the numerical procedure used in this study. The integration is carried out with Adams Bashforth 4th-order coupled with secant method to update the initial guess

Full size image

In order to validate the numerical solutions of the present study, the results are compared with the experimental and numerical simulation data available in the literature [4, 56,57,58]. The experimental results include those of Butler et al. [56], Ghaneh-Fard et al. [57] and the numerical results are from the work of Muslet [58]. The information for the crystallinity kinetics of the polymer melts are not included in the experimental works of both Butler [56] and Ghaneh-Fard et al. [57]. The morphological material properties of the polymer used for all numerical comparisons and simulations in this study are tabulated in Table 1. These values are taken from experimental studies in the literature which focuses on the structural development of the polymers under pressure and thermal effects [37, 38].

In Fig. 3, comparison of the numerical results and the experimental work of Butler [56] is presented for bubble radius and film thickness in the machine direction where the process conditions are \({\text{BUR}} = 3\), and \({\text{DR}} = 18\). A good agreement is obtained for both radius profile and the thickness reduction.

Fig. 3
figure 3

Comparison of the numerically predicted film dimensionless radius (r) and dimensionless thickness (h) with the experimental measurements of Butler [56] with \(\mathrm{BUR}=3\), \(\mathrm{DR}=18\). Present study is shown with the solid line; the experimental work [56] is shown with \(\times \)

Full size image

The comparison of present work with the experimental work of Ghaneh-Fard et al. [57] and numerical work of Muslet [58] is shown for the change of bubble radius and velocity profile in machine direction with \({\text{BUR}} = 2\) and \({\text{DR}} = 9.5\) in Fig. 4a and b, respectively. The model and material properties for the test cases can be found in detail in the work of Muslet and Kamal [4, 58]. The numerical prediction of the dimensionless radius of the present study is in a better agreement with the experimental study of Ghaneh-Fard et al. [57], compared to the simulation results of Muslet [58]. On the other hand, some discrepancy is observed between the predicted velocity and the experimental work of Ghaneh-Fard et al. [57] as well as Muslet [58] where the velocity distribution of the present study exhibits a greater curvature beyond the die exit. The observed disparity can be attributed to variations in the experimental setups presented in Figs. 3 and 4. In the case of Fig. 3, where cooling occurs from both inner and outer surfaces of the film [56], a close alignment between the heat transfer conditions and the numerical simulation is achieved, resulting in a good agreement between experimental and numerical outcomes. However, in Fig. 4, where cooling is exclusively introduced from the outer surface [57], a departure from real-world cooling conditions for the film blowing process is evident. This divergence can potentially lead to different rates of morphological development, influencing the velocity profile and introducing the variations seen in Fig. 4. The relative error values for dimensionless velocity (Fig. 4b), when normalized with respect to the experimental data, exhibits variations across the dimensionless distance. The errors start relatively low (around 3% for a dimensionless distance of 0.1), increasing gradually until they reach a peak (around 59% for a dimensionless distance of 2), and then decrease again toward the end of the range (around 0.5% at the frost line).

Fig. 4
figure 4

Comparison of the numerically predicted a dimensionless film radius, r and b dimensionless velocity, v profile with experimental measurements of Ghaneh-Fard et al. [57] and of Muslet [58] with \(\mathrm{BUR}=2\), \(\mathrm{DR}=9.5,\) Present study is shown with the solid line; the experimental work [57] is shown with ○, experimental work [58] is shown with + 

Full size image

3 Results and Discussion

3.1 Effect of DR and BUR

This section begins by exploring the impact of process conditions on the bubble radius and velocity under same cooling conditions. The heat transfer coefficient is estimated using the model of Shin et al. [7]. The objective is to highlight predictions related to the thermal and crystallization effects. The bubble shape and the corresponding velocity profile for changing BURs are shown in Fig. 5a, for constant \({\text{DR}} = 20\). The bubble grows for increasing BUR, and stays relatively constant for \({\text{BUR}} = 1\) as seen in Fig. 5a. Present model predicts the extensional kinematics of the bubble, in other words, the expansion or the contraction in the hoop and thickness directions. The experimental results of Han and Park [59] and Gupta et al. [60] as well as the predictions of Doufas et al. [24] support these observations.

Fig. 5
figure 5

Effect of process conditions on dimensionless radius, r and dimensionless velocity, v along the machine direction, z a with constant DR = 20 for changing BUR, b with constant BUR = 2 for changing DR

Full size image

In Fig. 5b, the effect of DR is shown on the radius profiles for constant s\({\text{BUR}} = 2\). When DR increases, there is a competition between stretching in the machine direction and extension in the hoop direction, which leads to an increase in the rate of change of the bubble radius. If all other operating conditions remain constant, a DR of 10 results in an earlier plateau in velocity compared to a DR of 30, where the plateau is not as distinct.

By observing the trend of process parameters such as normal stresses in circumferential and axial directions, it is possible to understand how the process conditions and structure are interrelated. In Tables 6 and 7, the maximum normal stress values are summarized for changing DR and BUR, respectively. Both normal stress components increase with increase in DR and BUR. It is observed that the axial stress (\(\sigma_{1}\)) increases faster than the circumferential stress (\(\sigma_{3}\)) with increase in DR. The trend reverses for the increasing BUR values. This trend can be seen clearly in the third column (\(\sigma_{1} /\sigma_{3}\)) where the ratio increases with increase in DR, and decreases with increase in BUR.

Table 6 Non-dimensional normal stresses in axial and circumferential directions and their ratio, for increasing DR, \(\mathrm{BUR}=1.5\)
Full size table
Table 7 Non-dimensional normal stresses in axial and circumferential directions and their ratio for increasing BUR, \(\mathrm{DR}=20\)
Full size table

Increasing the air pressure which consequently increases BUR and the nip roll velocity which impacts DR, it is anticipated that greater axial and hoop stresses will be attained, as indicated by the numerical results. The stress values and patterns observed are akin to those reported by Lee et al. [9], indicating that the numerical model accurately depicts the expected mechanics of the film blowing process.

The ultimate crystallinity of the molten polyethylene blends depends on the molecular structure and it is independent of the process conditions [41]. Throughout the simulations, die exit temperature and same ultimate crystallinity values are kept the same and constant, see Table 1. Two fundamental crystalline phases are considered in this study. The spherulites are the crystalline structure from the temperature-induced crystallization which is seen in quiescent flow. The shish-kebab crystalline structure is result of the flow-induced crystallization, for the detailed morphology equations, see Eqs. 8–21. The volume fractions of the quiescent crystalline phases, the spherulites, are calculated using Eqs. 10–13 and growth rates of flow-induced crystalline structures, shish kebabs, are calculated using Eqs. 16–18. Total space filling is evaluated with Kolmogorov–Avrami model using Eq. 19.

In Fig. 6a, the temperature distribution along the machine direction is given for increasing DR. As crystallization is an exothermic phenomenon, the onset of morphological changes results in a temperature hump as seen in Fig. 6a. The process time is shortened as a result of increasing DR, the cooling becomes less effective, the onset of the temperature hump gets delayed, and finally, the frost line temperature increases. The resulting temperature distribution causes delay in the morphological development for increasing DR, as shown in Fig. 6b. As a result of the DR increase, both the spherulites (in the quiescent case) and the shish kebab formation (in the flow case) experienced a reduction in their volumetric fraction, as illustrated in Fig. 6c. The volumetric ratio of the spherulites is lower compared to that of the shish kebab, and the peak value was shifted due to the increase in DR. Similar observations are reported by Zhang et al. [41], where in situ experiments were performed for the film blowing process. At fast relaxation case (\({\text{DR}} = 20\)), they reported a less significant TIC and dominating FIC. Similar to the present simulations, for slower flows (\({\text{DR}} = 12\)) the TIC contribution becomes significant and both crystalline structures are present. In the low relaxation mode the FIC is significant.

Fig. 6
figure 6

Comparison of a temperature, b total space filling and c crystal fractions distributions along the machine direction for \(\mathrm{DR}=10\), \(\mathrm{DR}=30\) at constant \(\mathrm{BUR}=2\)

Full size image

The effect of BUR on temperature distribution and the corresponding morphological structure is shown in Fig. 7 at constant \({\text{DR}} = 20\). To illustrate the trends observed as BUR increases, three values were selected for demonstration purposes: 1 for low BUR, 1.5 for medium BUR and 2.5 for high BUR. The temperature curve of \({\text{BUR}} = 1\) does not show a hump caused by the initiation of crystallization. For increasing BUR, the onset of crystallization triggers the temperature increase, and it is clearly seen in \({\text{BUR}} = 2.5\), in Fig. 7a. As more air was blown into the bubble, the total space filling increased with rise in BUR, leading to a corresponding increase in both cooling and stress values (Fig. 7b). Similar findings were reported by Doufas et al. [24] and Pirkle et al. [19]. At BUR = 1.5, the spherulites fraction is higher than the shish-kebab fraction, resulting from the lower stress values. For BUR = 2.5, the spherulites fraction peak value shifts toward the die exit and the stress-enhanced crystallization results in a larger fraction of the shish kebabs (Fig. 7c). In an experimental study, Drongelen et al. [39] investigated the effects of DR and BUR on the transient crystallization of blown film. They reported that increased BUR enhanced the crystallization, which is also shown in the simulation results in the present work. They further highlighted that the increase in DR has a more pronounced effect on crystallinity compared to the rise in BUR. This is attributed to the higher stress rise in the axial direction, as opposed to the stress rise in the circumferential direction. The stress trend obtained in the present study is in line with the observed crystallinity kinematics, as shown in Tables 6, 7.

Fig. 7
figure 7

Comparison of a temperature, b total space filling and c crystal fractions distributions along the machine direction for \(\mathrm{BUR}=1.5\), \(\mathrm{BUR}=2.5\) at constant \(\mathrm{DR}=20\)

Full size image

3.2 Heat Transfer Coefficient

With the present model, a well-calibrated simulation tool is achieved. This section involves a comparison of three HTC that is commonly utilized in the literature to help improve the accuracy of thermal design and analysis of the film blowing processes. The effects of different empirical heat transfer coefficients under the same process conditions are studied. Even though the range of estimated heat transfer factors was chosen based on studies in the literature, a similar comparative study as presented here does not exist in the literature.

It is important to mention that for the empirical heat transfer coefficients, the model of Shin et al. [7] considers the effect of dimensionless blowing angle and the radius of curvature as well as the instantaneous temperature difference between the film and the cooling air. Doufas [24] performs a fitting for the change in film temperature along the bubble, and finally, the heat transfer coefficient of Lee et al. [9] considers the dimensionless distance and the air velocity.

As the first step, the model parameters are calibrated targeting identical cooling rates and the values are tabulated in Table 5 for \({\text{DR}} = 30\) and \({\text{DR}} = 15\). For both \({\text{DR}} = 15\) and \({\text{DR}} = 30\) the distribution of radius, velocity and thickness reduction along the dimensionless distance showed no significant difference for the three HTC models. However, the hoop and machine stresses as well as the temperature and corresponding space filling values altered more significantly for \({\text{DR}} = 15\) compared to \({\text{DR}} = 30\), as seen in Figs. 8 and 9. Among the three models considered in this study, only the one by Doufas [24] provides experimental validation. The results obtained from the model of Doufas provide approximately the average value of the results of the other two models for \({\text{DR}} = 15\), see Fig. 8. This result shows that all three models give acceptable results at \({\text{DR}} = 15\). For higher DR values, the stress, temperature and morphology distributions of all HTC models are close to each other; whereas with the model of Shin et al. [7], the temperature at the frost line is lowest which becomes more sensible in the ultimate space filling, which is mildly larger than the two other estimates. To elucidate the effect of the chosen HTC models on the crystal fraction, the spherulite and shish-kebab ratios are compared in Fig. 10 for \({\text{DR}} = 15\). All three models with a minor discrepancy captured similar quantitative distribution for both crystalline structures. The results obtained using the model of Doufas [24] produce approximately the average of the results using the other two models, as seen in the previous analysis.

Fig. 8
figure 8

Comparison of the bubble mechanics for three different selected cooling models under the same process conditions, \(\mathrm{BUR}=2\), \(\mathrm{DR}=15\)

Full size image
Fig. 9
figure 9

Comparison of the bubble mechanics for three different selected cooling models under same process conditions, BUR = 2, DR = 30

Full size image
Fig. 10
figure 10

Spherulites and shish-kebab fractions along the machine direction for three different selected cooling models at same process conditions, BUR = 2, DR = 15

Full size image

4 Conclusions

In this numerical study, the steady, non-isothermal bi-extensional flow of molten polymer is investigated for different process conditions. The morphological changes are also studied. The simulations are compared with the experimental and numerical results in the literature, and good agreement is achieved. The overall results classified in two categories, namely the effect of process conditions and the effect of the heat transfer model.

The process condition effects can be summarized as follows:

  1. 1.

    The increase in DR and BUR increase stresses in both axial and circumferential directions. Additionally, the ratio of axial stress over circumferential stress increases with increase in DR, and it decreases with increase in BUR.

  2. 2.

    The increase in DR leads to higher frost line temperatures which surpass the morphological development. The increase in BUR leads to lower frost line temperatures resulting in higher space filling percentage.

  3. 3.

    For increasing DR, the quiescent contribution to the crystalline structure does not improve significantly, whereas the flow-induced contribution gets reduced. The spherulites have a lower volumetric ratio compared to the shish kebab, and an increase in DR caused a shift in the peak value of the spherulites. On the other hand, the BUR increase enhances both the quiescent and flow-induced crystallization. Using the present model, a qualitative estimate is calculated using the interrelation of process-structure and material properties. These results combined with the temperature and stress distributions can be used to estimate the mechanical, chemical and optical features of the film once the process conditions are defined.

In the second part of the simulations, three different heat transfer coefficient expressions available in the literature are compared. The results can be summarized as follows:

  1. 1.

    All three expressions lead to similar results for low DR values. The results with that of Shin et al. [7] mildly under predict the stresses and the total space filling, and mildly over predict the temperature. For larger DR values, the results show a better agreement with each other.

  2. 2.

    The crystalline compound distributions evaluated from all three models are similar both qualitatively and quantitatively. For low and moderate DR values, the model choice is not critical. It is important to exercise caution when selecting the appropriate heat transfer coefficient model as needed.

This study provides the systematic validation of a numerical model to predict the bi-extensional flow of PTT fluid under morphological changes, enabling a methodical study of the effects of fundamental process parameters including DR, BUR and empirical heat transfer coefficients. The present study employs a crystallinity model that represents the first endeavor to gain insight into the intricate crystalline structure of a blown film. The validated numerical model presented in this paper allows for the investigation of different crystal structures and morphologies, improving the understanding of the end product properties for the bidirectional extensional processes.

While most studies in the literature have focused on single-layer films, real-world applications are increasingly using multilayer film blowing processes. Developing new constitutive relations to model and capture the physical properties of the composite structure in these multilayer tubular films would be a valuable avenue for research. Currently, numerical studies often restrict the computational domain to the region beyond the die exit, and the changes in flow parameters across the thickness of the film are not considered. Including the annular die region in the computational domain would allow investigating changes in mechanical properties and morphological structure both in the machine direction and across the thickness of the film. Additionally employing a 2-D axis-symmetric formulation would enable direct comparisons of results with in situ experiments. This approach could provide valuable insights into the behavior of the film under various conditions and contribute to a more comprehensive understanding of the film blowing process. Addressing these aspects in future research endeavors could significantly advance the understanding and application of film blowing processes, paving the way for more accurate and efficient production of multilayer films with desirable mechanical properties and morphological structures.