Self-balanced Quadruple-Boost Nine-Level Switched-Capacitor Inverter for Solar PV System

Abstract

Switched capacitor-based multi-level topologies have recently gained attention due to their inherent technical superiority suitable for renewable-based applications. In this work, a single-phase boosting nine-level inverter is proposed, which employs a DC-source ($V_\textrm{dc}$) and three capacitors. It uses 14 switches that require nine independent control signals from the controller, conducts a maximum of 8 switches at any instant and provides a 9-level quadruple-boosted output voltage. The proposed topology is verified for an experimental setup’s steady and transient load conditions. A detailed discussion on the balanced charging of the capacitors is also presented. A novel harmonic elimination-based-nearest level modulation scheme is proposed, wherein the simplified control scheme of the nearest level control is extended to eliminate the undesired low-order harmonics from the output voltage waveform of the 9-level inverter. Moreover, its merits of a simplified control, lower power loss, reduced total voltage stress and enhanced voltage gain are discussed in comparison with various 9-level inverters in detail.

1 Introduction

Power Conversion using power electronic converters is the need of the existing and future power systems fed through renewable energy and energy storage sources (ESS) [1]. Renewable energy systems such as Solar PV have recently been discussed in conjunction with hybrid energy storage systems of various kinds of batteries, supercapacitors, fuel cells, flywheels, pumped hydro energy systems and compressed air energy storage systems (see, e.g. [2,3,4] and references therein). This work also discusses the behaviour of the performance of various ESS in hybrid operations along with solar PV. For this, the researchers have been giving attention to multilevel inverters (MLI) recently because of their better waveform quality, lesser $\textrm{d}v/\textrm{d}t$ ratio, improved electromagnetic performance, low switching frequency, lesser switching losses and reduced common mode voltages [5]. These qualities make it appropriate to be used in integration for renewable energy sources (RES), electric transportation (EV), energy storage systems/sources (ESS) and distributed generation systems [6]. Conventional MLIs like neutral point-clamped inverters (NPC), flying-capacitor inverters (FC), and cascaded H-bridge inverters (CHB) [7, 8] exhibit the issues of a large number of components and capacitor voltage unbalancing [9]. For high-power applications, modular multilevel converters are used for DC-AC and AC-DC conversion. Their application in DC microgrids can be seen in [10]. To incorporate ESS into the solar PV system, the NPC topology is employed in [11].

Photovoltaic (PV) systems are RES that produces low-voltage electrical energy; thus, a boosted AC voltage is desired. One of the traditional methods is to cascade the back-end conventional MLI with a front-end DC-DC boost converter [12, 13]. Alternatively, the switched capacitor multilevel inverter (SCMLI) approach with boost capability and reduced device count is proposed in the literature [14]. For instance, in [15], the presented topology can produce seven levels, but it cannot run an inductive load. In [16], a topology was proposed that integrated a T-type structure with nine-level voltage, where the voltage balance of the switched-capacitor cell was maintained without any sensors. However, two symmetrical DC sources were needed to regulate the DC side clamping capacitor’s voltage. Also, it does not have any boost ability. In [16] presented a nine-level active-neutral-point-clamped (ANPC) based multilevel inverter (MLI) topology for grid-connected applications, which requires only ten switches. Still, it does not have any boost ability. In [17], a quasi-resonant switched-capacitor (QRSC) multilevel inverter (MLI) with self-voltage balancing is proposed for single-phase high-frequency AC microgrids, which also requires ten switches. Again it does not have any boost ability. In [18, 19], two types of single DC source nine-level SCMLIs were proposed. Both circuits require no auxiliary methods for the capacitor’s voltage balance, but both inverters exhibit low boosting capability. A new double-stage asymmetrical MLI based on the level-doubling network is developed for solar PV central inverter application in [20].

Suresh and Parimalasundar in [21] proposed a circuit consisting of three capacitors and eight switches, capable of producing seven-level output, but it can produce only 1.5 times boost factor. Lee in [22] proposed a single-stage switched-capacitor module (S3CM) topology for cascaded multilevel inverter, peak inverse voltage (PIV) for all the switches lie within the DC source voltage, but this topology shows twice boost factor. Sathik and Krishnasamy in [23] proposed a compact switched capacitor multilevel inverter (CSCMLI) topology with a smaller number of switches and self-voltage balancing and boosting ability but again boost factor is only two. In [24], a single-phase hybrid nine-level boost inverter (H9LBI) with single input is proposed reducing the active devices, but the boost factor is twice only. A Voltage source multilevel inverter is proposed in [25] with a step-up nine-level (9 L) inverter comprising nine switches and three capacitors but can produce a double voltage boosting. In [26], a new switched-capacitor-based boost multilevel inverter topology (SCMLI) is proposed using the least number of switches but capable of enhancing the boost factor to twice only. Further authors modify the model for Higher Voltage Gain, which enhances the boost factor to thrice, but the 2 levels are sacrificed, i.e. 7 L operation is achieved. Other 9-level inverters can be seen in [5, 27] In [28], a single-stage 13-level SCMLI is proposed requiring 10 power switches but requires three voltage sources to operate. Another 21-level switched source topology can be seen in [29]. In [30], a switched-capacitor (SC)-based CMI was proposed giving a boost factor four times but requiring 17 switches 5 diodes, and 4 capacitors. The topology proposed in [31] is attaining four times voltage boosting capability but having 15 switches and 3 capacitors. Work is also going on the fault-tolerant operation of the SCMLIs [32].

Fig. 1

a Proposed 9-level quadruple-boost inverter topology, and b possible cascaded structure, and, c possible configuration for solar PV application

Fig. 2

QB9LI’s states for 9-level operation

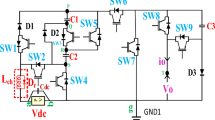
The proposed topology employs a reduced number of active devices. It requires a simple control strategy, having one DC source, three capacitors, one diode, and 14 switches to achieve a quadruple-boosted 9-level output voltage. It is valid for both resistive and inductive loads. Nine independent controller signals are required to switch all 14 IGBTs. The maximum number of conducting switches is not more than eight for any of the levels. Voltages of all three capacitors are maintained at $V_\textrm{dc}$ without any additional auxiliary sensors. The steady and transient performances are verified by experimental validation of the proposed topology.

Additionally, the cost factor (CF) shows the merit of the overall reduction in cost for the design. The proposed inverter’s comparative assessment with nine-level inverters demonstrates its superiority over other inverters. The features and advantages of the proposed topology are discussed as follows:

• i. Reduced active device count: It uses a single DC source and fourteen power switches.

• ii. Reduced control logic: Only 9 control signals driving 12 gate drivers are required.

• iii. Inherent capacitor voltage balancing: Switched capacitor voltages $C_1$, $C_2$ and, $C_3$ are maintained at $V_\textrm{dc}$. It does not require any sensor circuitry or additional control algorithm.

• iv. Boost and multilevel output: Nine-level output and fourfold voltage gain is achieved.

Correct modulation of the inverters plays an important role in the working of the inverters. The modulation strategies can be based on low switching or high switching frequencies and can be implemented on different applications as desired. Nearest Level Modulation (NLC) Scheme [33], selective harmonic elimination [34] and selective harmonic mitigation [35, 36] are the schemes that come under low switching frequency operation. In this work, a novel nth Lower Harmonic Mitigation based-Nearest Level Control (nLHM-NLC) is proposed, which incorporates the advantages of the nearest level control and the selective harmonic mitigation.

The organization of the paper is as follows. Section 2 deals with the operation principles of inverter switching, its possible structure for cascaded operation and the NLC scheme. Section 3 explores the capacitance evaluation and power loss analysis of the topology. Section 4 is dedicated to comparing the inverter with other 9-level topologies. In the next section, the results of the proposed topology are discussed. In Sect. 5 a new selective harmonic elimination-based NLC is proposed, and its benefits are discussed. The results of the proposed topology are shown in Sect. 6. The final section presents a brief conclusion of this paper.

2 The Proposed Topology

The proposed configuration of the nine-level single-phase boost inverter is shown in Fig. 1a. It includes one voltage source, one diode, three capacitors and 14 switches. Figure 1b shows the cascaded operation of the inverter, which can lead to a production of $9^2=81$ levels. The inverter can be utilized as a microinverter for grid-connected or residential loads, as shown in Fig. 1c.

2.1 Operational Principles

Figure 2 presents the different modes of operation in a positive half-cycle and negative half-cycle of the proposed topology. The states of switching for various levels are listed in Table 1. The conduction in different levels for positive and negative half cycles are discussed below.

Table 1 Switching states of the proposed QB9LI

2.1.1 Level $+$4; $V_o=4V_\textrm{dc}$

In this state, the switches $S_1$, $S_3$, $S_7$, $S_9$, $S_{10}$, $S_{11}$ and $S_{13}$ are fired, as shown in Fig. 2a, to connect the load to the series combination of DC source and the switched capacitors $C_1$, $C_2$ and $C_3$. Hence, the output voltage is given by: DC source voltage ($V_\textrm{dc}$) + capacitor $C_1$ voltage ($V_\textrm{dc}$) + capacitor $C_2$ voltage ($V_\textrm{dc}$) + capacitor $C_3$ voltage ($V_\textrm{dc}$) = $4 V_\textrm{dc}$.

2.1.2 Level $+$3; $V_o=3V_\textrm{dc}$

Figure 2b shows that the switches $S_2$, $S_3$ and $S_5$, are fired in this state to connect the switched capacitor $C_1$ in parallel with the DC source and allow it to be charged to $V_\textrm{dc}$. Simultaneously, switches $S_7$, $S_9$, $S_{10}$, $S_{11}$ and $S_{13}$ are also turned on to connect the load to the series combination of DC source and the switched capacitor $C_2$ and $C_3$, which were already charged to $V_\textrm{dc}$ in the previous levels (i.e. level 2 and level 1, respectively) of the same cycle. Hence the output voltage is DC source voltage ($V_\textrm{dc}$) + capacitor $C_2$ voltage ($V_\textrm{dc}$) + capacitor $C_3$ voltage ($V_\textrm{dc}$) = $3V_\textrm{dc}$.

2.1.3 Level $+$2; $V_o=2V_\textrm{dc}$

As exhibited in Fig. 2c, $S_1$, $S_4$ and $S_5$, are fired to connect the switched capacitor $C_2$ parallelly with the DC source and allow it to be charged to the amplitude of $V_\textrm{dc}$. Simultaneously, switches $S_7$, $S_8$, $S_{9}$ and $S_{11}$ are also turned on to connect the load to the series combination of DC source and the switched capacitor C1. Switched capacitor $C_1$ is assumed to be charged to the amplitude of $V_\textrm{dc}$ in level 1 of the previous cycle. Hence the output voltage is DC source voltage ($V_\textrm{dc}$) + capacitor $C_1$ voltage ($V_\textrm{dc}$) = $2V_\textrm{dc}$.

2.1.4 Level $+$1; $V_o=V_\textrm{dc}$

In the first level the switches $S_{2}$, $S_{4}$, $S_{7}$, $S_{8}$, $S_{9}$ and $S_{11}$ are turned on as shown in Fig. 2d. Thus, the load is connected to the DC source, and the output voltage is equal to $V_\textrm{dc}$. The switches $S_{12}$ and $S_{13}$ are also turned on, which causes the switched capacitor $C_3$ to be appeared in parallel with the input supply and charge to the amplitude of $V_\textrm{dc}$.

2.1.5 Level ${0_a}$; $V_o=0$

At level zero, the load terminals are shorted by firing the switches $S_6$, $S_7$, $S_8$ and $S_9$ and thus attaining a zero voltage across the load terminals as shown in Fig. 2e.

2.1.6 Level ${0_b}$ $; V_o=0$

At level zero, the load terminals are shorted by turning on the switches $S_{11}$, $S_{12}$, $S_{13}$ and $S_{14}$ and thus attaining a zero voltage across the load terminals as shown in Fig. 2f.

2.1.7 Level −1; $V_o=-V_\textrm{dc}$

In the negative first level, switches $S_2$, $S_4$, $S_6$, $S_{12}$, $S_{13}$ and $S_14$ are fired as shown in Fig. 2g. Thus, the load is connected to the DC source, and the output voltage is $-V_\textrm{dc}$. The switches $S_7$ and $S_8$ are also turned on, which causes the switched capacitor $C_3$ to appear in parallel with the input supply and charge to an amplitude of $-V_\textrm{dc}$.

2.1.8 Level −2; $V_o=-2V_\textrm{dc}$

Figure 2h shows the switches $S_1$, $S_4$, and $S_5$, firing to connect the switched capacitor $C_2$ in parallel with the DC source and allow it to be charged to the amplitude of $V_\textrm{dc}$. Simultaneously, switches $S_6$, $S_{12}$, $S_{13}$, and $S_{14}$ are also turned on to connect the load to the series combination of DC source and the switched capacitor $C_1$. The switched capacitor $C_1$ is assumed to be charged to the amplitude of $V_\textrm{dc}$ in level +3 of the previous half cycle. Hence the output voltage is DC source voltage ($V_\textrm{dc}$) + capacitor $C_1$ voltage ($V_\textrm{dc}$) = $-2V_\textrm{dc}$.

2.1.9 Level −3; $V_o=-3V_\textrm{dc}$

As shown in Fig.  2i, the switches $S_2$, $S_3$, and $S_5$ are turned on to connect the switched capacitor $C_1$ in parallel with the DC source and allow it to be charged to $V_\textrm{dc}$. Simultaneously switches $S_6$, $S_8$, $S_{10}$, $S_{12}$ and $S_{14}$ are also turned on to connect the load to the series combination of the DC source and the switched capacitor $C_2$ and $C_3$ those were already charged to $V_\textrm{dc}$ in the previous levels (i.e. level $-2$ and level $-1$, respectively). Hence the output voltage is equal to DC source voltage ($V_\textrm{dc}$) + capacitor $C_2$ voltage (Vin) + capacitor C3 voltage ($V_\textrm{dc}$) = $-3V_\textrm{dc}$.

2.1.10 Level −4; $V_o=-4V_\textrm{dc}$

In level -4, the switches $S_1$, $S_3$, $S_6$, $S_8$, $S_{10}$, $S_{12}$ and $S_{14}$ are turned on are as shown in Fig. 2j, to connect the load to the series combination of the DC source and the switched capacitors $C_1$, $C_2$ and $C_3$. Hence, the output voltage is given by: DC source voltage ($V_\textrm{dc}$) + capacitor $C_1$ voltage ($V_\textrm{dc}$) + $C_2$ voltage ($V_\textrm{dc}$) + $C_3$ voltage ($V_\textrm{dc}$) = $-4V_\textrm{dc}$.

2.2 Cascaded Operation of the Proposed Inverter

Two or more units can be connected as shown in Fig. 1b for the possible cascaded operation, which will lead to a higher number of levels of output levels (maximum of $9^2$). Although two sources are required for this operation, the number of levels available at the output will lead to the omission of the output filtration stage. Further, two PV sources can be connected through this configuration to feed the load. The operation of this configuration will be validated in future work.

2.3 Nearest Level Control Algorithm

As shown in Fig. 3, in conventional NLC, a reference sine wave $m\sin (\omega t)$ is compared with constant signals that are generated in the controller as 0.5, 1.5, 2.5, 3.5,..., $(N-1)/2-0.5$ values, where N is the number of levels in the output voltage waveform. The following logic is adopted: When the condition of the reference sine wave lies in the domain explained as $M-0.5<m\sin (\omega t)<M+0.5$, the switching level logic corresponding to M is selected, where M is 1, 2, 3,... $(N-1)/2-0.5$.

Fig. 3

Waveform depicting the nearest level control

3 Capacitance Calculation and Power Loss Analysis

The capacitance calculation and the loss analysis are important discussions to validate the inverters’ efficacy. Firstly, the capacitor values are decided and then the power loss analysis is performed.

3.1 Capacitance Calculation

The proposed SCMLI topology utilizes one DC source and three capacitors $C_1$, $C_2$, and $C_3$ to generate the 9-level output voltage. Voltages of all three capacitors are self-balanced to the desired voltage level by connecting them in parallel to the source at desired levels during the cycle. Voltages of capacitors $C_1$, $C_2$ and $C_3$ maintains at $V_\textrm{dc}$. Figure 4 shows the charging, discharging and idle (neither charging nor discharging) duration for all three capacitors. Here both the half cycles are shown in the upper half just to have an easy and stress-free understanding. To time $t_2$ all three capacitors are at idle state (neither charging nor discharging) except the charging state of capacitor $C_3$ from $t_1$ to $t_2$. Now from $t_2$ to $t_3$ capacitors $C_1$, $C_2$ and $C_3$ are in discharging, charging and idle state, respectively. Furthermore, capacitor $C_1$ changes its state from discharging to charging state between $t_3$ and $t_4$. Afterwards from $t_4$ to the quarter of the cycle (i.e. T/4) it again turns to a discharged state while $C_2$ and $C_3$ enter discharging state after $t_3$ and keep it continued to the quarter of the cycle. The same pattern is followed in a symmetrical way for the remaining quarter of the cycle to complete the first half cycle. As far as the second half cycle is concerned it follows exact same pattern as of first half cycle. For the determination of the optimal value of capacitors, their LDC (largest discharging cycle) and the current capability are considered.

Fig. 4

Charging and discharging patterns of $C_1$, $C_2$ and $C_3$ in one cycle of operation

Hence, during LDC ($\left[ t_4, T/2 - t_4\right]$), the discharge of $C_1$ is given by the expression as follows:

$$\begin{aligned} \Delta Q_{C_1}=\int _{t_{4}}^{T / 2-t_{4}} i_{L}(t) \textrm{d} t \end{aligned}$$

(1)

Capacitors $C_2$ and $C_3$ are having the same LDC. Hence, the expression for the discharge of $C_2$ and $C_3$ during the interval $\left[ {t}_{3}, {T} / 2-{t}_{3}\right]$ is expressed as:

$$\begin{aligned} \Delta Q_{C_{2,3}}=\int _{t_{3}}^{T / 2-t_{3}} i_{L}(t) \textrm{d}t \end{aligned}$$

(2)

So the capacitance $C_1$, $C_2$ and $C_3$ are evaluated using (1) and (2) which is given by,

$$\begin{aligned} C_{1}= & {} \frac{1}{\Delta V_{C_1}} \int _{t_{4}}^{T / 2-t_{4}} i_{L}(t) \textrm{d}t \end{aligned}$$

(3)

$$\begin{aligned} C_{2}= & {} C_{3}=\frac{1}{\Delta V_{C_{2,3}}}=\int _{t_{3}}^{T / 2-t_{3}} i_{L}(t) \textrm{d}t \end{aligned}$$

(4)

Here, $\Delta V_\textrm{C}$ is considered as 10% of the magnitude of the capacitor’s ripple voltage. The following expression is used to fetch the values of $t_1$, $t_2$, $t_3$ and $t_4$:

$$\begin{aligned} V(t)= & {} V_{m} \sin (\omega t) \end{aligned}$$

(5)

$$\begin{aligned} t= & {} \sin ^{-1} \frac{v(t)}{V_{m}} \end{aligned}$$

(6)

Hence, for NLC, $t_1$, $t_2$, $t_3$ and $t_4$ are calculated as 0.804 ms, 1.667 ms, 2.699 ms, and 4.93 ms, respectively. The load current can be expressed by the given equation if 50 $\Omega$ purely resistive load is considered.

$$\begin{aligned} i_{L}(t)=I_{m} \sin (\omega t) \end{aligned}$$

(7)

For the sake of calculation, the output voltage peak is considered as 200 V and load at 50 $\Omega$ which results in the peak value of load current ($I_m$) at 4 A. So the value of capacitor $C_1$ is obtained by solving equation (3) which is given as;

$$\begin{aligned} C_{1}=\frac{2 \times I_{m} \cos \left( \omega t_{4}\right) }{2 \pi f \times \Delta V_{C}} \end{aligned}$$

(8)

The value of capacitors $C_2$ and $C_3$ is obtained by solving (5) which is given as,

$$\begin{aligned} C_{2}=C_{3}=\frac{2 \times I_{m} \cos \left( \omega t_{3}\right) }{2 \pi f \times \Delta V_{C}} \end{aligned}$$

(9)

The value of the capacitance can thus be calculated according to [37], and for a converter design of 4 kVA and 15 A, the size of the capacitor is taken as 2200 $\mu$F.

3.2 Power Loss Analysis

The power loss is generally comprised of switching loss, conduction loss and capacitor ripple loss. The total power losses are given as:

$$\begin{aligned} P_{\text{ Losses } }=P_{sw}+P_{\textrm{c}}+P_{\text{ Ripple } } \end{aligned}$$

(10)

where $P_\textrm{sw}$ are switching losses, $P_\textrm{c}$ conduction loss is and $P_\textrm{ripple}$ are ripple losses, respectively. The conduction losses PC and switching loss $P_\textrm{sw}$ occur because of power semiconductor devices, but ripple loss $P_\textrm{ripple}$ are caused by capacitors.

Fig. 5

Efficiency curve of the proposed inverter

3.2.1 Switching Losses

Switching loss is caused by voltage current overlap during switching state transition because power switches do not have ideal behaviour. The evaluation of $P_\textrm{sw}$ losses in the SCMLI can be obtained using,

$$\begin{aligned} P_\textrm{sw}=\left[ \sum _{\text{ allswitches } } \sum _{\text{ within } \frac{1}{f_\textrm{o}}} \frac{V_\textrm{on} I_\textrm{on} T_\textrm{on}}{6}+\frac{V_\textrm{off} I_\textrm{off} T_\textrm{off}}{6}\right] \times f_\textrm{o} \end{aligned}$$

(11)

where $f_\textrm{o}$ is the frequency of the output voltage. $V_\textrm{on}$ is the voltage, $T_\textrm{on}$ is the time duration, and $I_\textrm{on}$ is the current through a power switch during the ON state. Similarly $V_\textrm{off}$, is the voltage, $T_\textrm{off}$, is the time duration, and $I_\textrm{off}$ is the current of a power switch during the OFF state.

3.2.2 Conduction Losses

The Conduction Losses $P_\textrm{c}$ of the power switch are calculated using:

$$\begin{aligned} P_\textrm{c}=\sum _{\text{ allswitches } } I_{0}^{2}, \text{ switch } R_\textrm{on} \end{aligned}$$

(12)

where $R_\textrm{on}$ is the resistance of the switch in conduction mode and $I_{\textrm{o,switch} }$ is currently flowing in ON-state.

3.2.3 Ripple Losses

The capacitor’s internal resistance (also called equivalent series resistance ESR) causes the voltage drop ($\Delta V_\textrm{C}$) or ripple loss, which appears in the output waveform of SCMLI. These can be calculated using

$$\begin{aligned} P_{\text{ ripple } }=\frac{f_{\text{ sw } }}{2} \times C \times \triangle V_\textrm{c}^{2} \end{aligned}$$

(13)

The power losses are estimated with the help of the PLECS software using the associated component’s thermal modelling for the proposed topology. The efficiency curve is shown in Fig. 5 for the proposed topology. It can be seen that at the output load ranging from 100 W to 500 kW the efficiency of the proposed inverter is around 97%. At the output power of 3 kW, the efficiency of the proposed inverter is approximately 94.5%.

4 Lower Harmonic Mitigation Based-Nearest Level Control (LHM-NLC)

Fig. 6

a Level selection according to LHM-NLC; b control logic implementation; plane of minimum c 3rd, d 5th and e 7th harmonics with respect to m and $\gamma$

The conventional nearest-level modulation reduces the total harmonic distortion considerably. Still, it does not ensure individual harmonic minimization (especially the lower order ones) below the recommended practices of IEEE 519 (2014) practices [38]. But the ease of its implementation has allowed its industrial acceptance in many applications. The selective harmonic elimination (SHE) ensures a lower order harmonic elimination, but real-time implementation is not an easy task [39, 40]. It requires a complex computational algorithm to obtain the firing angles and ensure desired harmonic elimination. Metaheuristic algorithms are used to solve the nonlinear multivariable problem of selective harmonic elimination equations [34]. Convergence to a particular solution, especially at a lower modulation index, is an issue with all types of search-based metaheuristic algorithms [41]. In this work, a novel nth Lower Harmonic Mitigation based-Nearest Level Control (nLHM-NLC) is proposed, which incorporates the advantages of the nearest level control and the selective harmonic mitigation. Three versions of the HM-NLC are presented, namely third harmonic mitigation, fifth harmonic mitigation and seventh harmonic mitigation. The concept of HM-NLC is exhibited in Fig. 6. In the proposed LHM-NLC, the constant signal which was used for comparison in the conventional NLC is replaced by the variable $\gamma$, which can be determined by the following procedure:

The set of angles at the changeover state in the LHM-NLC scheme in a 9-level is given by the following set of equations:

$$\begin{aligned} 4m\sin \left( \alpha _1\right)= & {} \gamma \end{aligned}$$

(14)

$$\begin{aligned} 4m\sin \left( \alpha _2\right)= & {} 1+\gamma \end{aligned}$$

(15)

$$\begin{aligned} 4m\sin \left( \alpha _3\right)= & {} 2+\gamma \end{aligned}$$

(16)

$$\begin{aligned} 4m\sin \left( \alpha _4\right)= & {} 3+\gamma \end{aligned}$$

(17)

The sets of the values of m and $\gamma$ can be found out corresponding to each m by minimizing 3rd, 5th and 7th harmonic magnitude expression given by the following equations:

$$\begin{aligned} H_3= & {} m\left( \cos 3\alpha _1+\cos 3\alpha _2+\cos 3\alpha _3+\cos 3\alpha _4\right) \end{aligned}$$

(18)

$$\begin{aligned} H_5= & {} m\left( \cos 5\alpha _1+\cos 5\alpha _2+\cos 5\alpha _3+\cos 5\alpha _4\right) \end{aligned}$$

(19)

and,

$$\begin{aligned} H_7=m\left( \cos 7\alpha _1+\cos 7\alpha _2+\cos 7\alpha _3+\cos 3\alpha _7\right) \end{aligned}$$

(20)

Consequently, the corresponding values of $\gamma$ are obtained for minimum 3rd, 5th and 7th harmonic magnitude, for all values of m between interval (0,1). the set of (m, $\gamma$) points are used to obtain the relation between m and $\gamma$. The expressions are for the 3rd, 5th and 7th harmonic mitigation (shown pictorially in Fig 6c–e) as follows:

$$\begin{aligned} \gamma= & {} 1.667m-1.224 \quad \left( \text {for }m>\frac{3}{4}\right) \end{aligned}$$

(21)

$$\begin{aligned} \gamma= & {} 3.343m-2.44 \quad \left( \text {for }m>\frac{3}{4}\right) \end{aligned}$$

(22)

$$\begin{aligned} \gamma= & {} 2.725m-2.18 \quad \left( \text {for }m>\frac{3}{4}\right) \end{aligned}$$

(23)

The constraint in (21) has been obtained for 9-level output as follows: From (17), it can be easily expressed that:

$$\begin{aligned} 4m>3+\gamma \end{aligned}$$

as $\sin \alpha _4<1$. Thus,

$$\begin{aligned} m>\frac{3}{4} \end{aligned}$$

(24)

5 Results and Assessment of the Proposed Topology

5.1 Experimental Validation

The experimentation for the proposed topology is carried out in this part to verify its basic performance. The experimental setup is shown in Fig. 7, whose parameters are shown in Table 2. The power switches are controlled through the LAUNCHXL-F28379D controller launchpad development kit. The controller employs a TMS320F28379D microcontroller designed for power electronic and electric drive control. More details on how to use these launchpad pins and programming can be found on [42].

Fig. 7

Experimental prototype of the proposed SCMLI

Table 2 Parameter of experimental setup

Fig. 8

The results of the proposed topology: a with R-load, b with R-load change from 180 $\Omega$ to 90 $\Omega$, c with RL-load of 80 $\Omega$, 190 mH, d change in RL-load from 80 $\Omega$, 190 mH to 160 $\Omega$, 190 mH, e change in modulation index; capacitor voltages and currents for f $C_1$, g $C_2$, and, h $C_3$

Fig. 9

The harmonic profiles of the proposed technique in comparison with conventional NLC

The steady and transient performances of the proposed topology have been recorded and shown in Fig. 8. Figure 8a shows the current and voltage waveform for a resistive load operation, which shows that the magnitude of the output voltage reached 120 V with 30 V input DC sources. Therefore, the nine-level output and fourfold boost ability have been verified. As the resistance decreases, the current increases, as shown in Fig. 8b. Similarly, Fig. 8c, d show the results with the R-L load and RL-load change. Figure 8e exhibits the inverter operation with a change in modulation index. Capacitors $C_1$, $C_2$ and $C_3$ maintain at an average of approximately 30 V, whose voltage and current waveforms are shown in Fig. 8f–h. The results show that the inverter is capable of operation under a variety of conditions.

The proposed topology is used for the elimination of harmonics of different orders. THD and harmonics of third, fifth and seventh order for simulation and experimentation are recorded for varying modulation index and presented in Fig. 9. THDs are found to have almost matching values for simulation and experimentation both. Harmonics with variation in modulation index and g of third, fifth and seventh orders are shown in Fig. 9a–c, respectively. It is shown inFig. 9a that the harmonics of third order those were present on the application of the nearest level control technique (NLC) are found to be mitigated up to a considerable level after application of selective harmonic elimination scheme (LHM-NLC). Here we can see at modulation index 0.88 that the value of the third harmonic for NLC is 1.61, but for LHM-NLC, it is 0.35, which has been considerably reduced. The same fashion is evidenced from the figure for various modulation indices.

Harmonics of the fifth and seventh levels are also found to be minimized up to some extent. Similarly, Fig. 9b evidences that the harmonics of the fifth order are found to be mitigated considerably by using technique selective harmonic elimination scheme (LHM-NLC)those were present when the nearest level control technique (NLC) was used. Other harmonics are also found to be reduced comparatively. It is again experienced for fifth harmonics to be reduced from 2.72 to 0.83 when switching from NLC to LHM-NLC for a modulation index of 0.90.

Similarly, seventh-order harmonics are also mitigated by the application of the selective harmonic elimination scheme (LHM-NLC) technique, those were pictured when the nearest level control technique (NLC) was used. Other harmonics are also reduced comparatively, which is evident by Fig. 9c. Again we can see at modulation index 0.88, the value of the seventh harmonic for NLC is 2.11, but for LHM-NLC, it is 0.09, which has considerably been reduced. The same fashion is evidenced from the figure for various modulation indices.

Harmonics of different orders are found to be minimized by a considerable value after the application of selective harmonic elimination scheme (LHM-NLC) as compared to those found using the nearest level control technique (NLC), which is evident by Fig. 9d–f. It is evident from the results that the LHM-NLC can eliminate the desired harmonics from the output voltage. It is also evident the control methodology employed is simple to implement on the controller platform. The only drawback is to make the operation feasible for other modulation indexes. However, further research on this technique can be performed to tackle this issue.

Table 3 Comparison with recent single-source 9-level inverters

5.2 Comparative Assessment with Recent 9-Level Single-Source Topologies

A fair comparison with recent single-source SCMLIs is presented in this section in terms of the number of switches, number of diodes, number of capacitors, number of gate drivers, boosting factor, total standing voltage (TSV), cost factor (CF) under various operating conditions, and the number of switches involved in switching on each level of operation. The TSV is defined as follows [30]:

$$\begin{aligned} \hbox {TSV}=\sum _{i=1}^{n}V_{\textrm{block}(i)} \end{aligned}$$

(25)

where $V_{\textrm{block}(i)}$ is the transistor’s or diode’s peak voltage stress. TSV is the sum of the voltage amplitude between the levels. In the conventional FC structure, TSV is low as the voltage divides amongst the switches. The TSV of the proposed topology is in the lower range among the topologies shown in Table 3, which shows its advantages on total voltage stress. On the other hand, The CF is defined as [19]:

$$\begin{aligned} \begin{array}{l} \hbox {CF}=N_\textrm{sw}+N_\textrm{d}+N_\textrm{cap}+N_\textrm{cl}+\alpha \hbox {TSV}+\beta \hbox {TCD}_\textrm{av} \end{array} \end{aligned}$$

(26)

where $\hbox {TCD}_\textrm{av}$ (average total conducting devices) is the average of the TCDs at different levels and is equal to 1/4th of the sum of all the TCDs. $\alpha$ and $\beta$ are the coefficients to measure the weightiness of TSV and, $\hbox {TCD}_\textrm{av}$, respectively, and are chosen according to the voltage stress and the component count. Generally, the value of $\alpha$ is taken greater than 1 when the voltage stress is more focused as compared to the component count. On the other hand, if $\alpha$ is selected lower than 1 it means the component count is more focused and the component’s voltage stress is the secondary consideration [43]. The comparison of CF of all the 9-level inverters at different $\alpha$ and $\beta$ is presented in Table 3. The proposed topology exhibits a low CF value when compared with the recent topologies of quadruple boosting. Hence inclusive benefits of the proposed topology in multiple aspects have been described.

In [44], reduction in switches and capacitors is achieved with no boosting capability. 10 switches are employed, respectively, while the number of capacitors is 3. While the inverters shown in [19, 22, 23] possess a number of switches very close to those in [44] with twice the boost factor. In [26], two 9-level topologies are discussed. Their per-level switch conduction is better than the proposed topology, but their boosting capability is limited to 2. The structure presented in [24] uses very few components, but its boosting capability is 2. Further, the requirement of an auxiliary charging circuit is its major drawback. [25] presents a dual boost topology with only 9 switches and 1 diode, but requires 4 capacitors for operation. The boosting capability of the inverter shown in [30] is improved to 4, but the required number of switches is increased to 17 with additional 5 diodes. Another recent quadruple boost topology is presented in [31], which employs 15 switches driven by 13 gate drivers. The reduction in the number of switching devices reduced the CF drastically in comparison to [30]. The proposed topology presents quadruple-boosting with 14 switches and one diode. It requires 12 driver circuits and 3 capacitors and exhibits CF between [30, 31]. In [45], a 9-level quadruple boost inverter with 12 switches and two capacitors is presented which results in the best TSVs and cost factors. However, the capacitor $C_1$ is charged to $V_\textrm{dc}$, while $C_2$ is charged to 2$V_\textrm{dc}$, however, in the presented topology all the capacitors are charged to the equal voltage value of $V_\textrm{dc}$. Hence, the same voltage rating capacitor can be used encouraging its usage for a modular implementation. The number of conducting switches at any instant is comparable to most of the topologies presented in Table 3.

6 Conclusion

This article proposes a quadruple-boost 9-level inverter with a low switch count suitable for solar-PV integration. It employs a single DC source and utilizes 14 switches, a diode and three capacitors. It demonstrates a maximum efficiency of 97.2%. Comparison with recent 9-level inverters reveals that it utilizes fewer components in comparison to recent quadruple boost topologies. It exhibits a per unit TSV of 23, which is equivalent to dual-boost topologies, and a comparable average TCD of 7 which results in low cost-factors of the proposed inverter. This work also proposes a new harmonic elimination-based-nearest level modulation scheme, where the nearest level control is extended to eliminate the undesired low-order harmonics from the output voltage waveform. The lower order harmonics (3rd, 5th and 7th) at various modulation indexes were minimized better than the conventional NLC. The performance of the proposed multilevel inverter is verified for steady and transient load conditions with self-balanced capacitors on a laboratory prototype. In the future, the proposed inverter will be implemented for integration with a solar-PV-based system feeding the grid. Moreover, the proposed modulation strategy can be enhanced to incorporate lower modulation indexes.