1 Introduction

With the increasing demand for interaction between robots and the external environment, contact force control has become a hot topic in the field of robot application. These application scenarios mainly include grinding, grooving, deburring, and supporting, etc. [1]. In these scenarios, the contact force needs to be precisely controlled to avoid adverse consequences that may cause damage to the workpiece or the robot itself [2, 3].

Over decades, many fruits of robot force control have been achieved. These fruits are roughly classified into two categories: (1) Hybrid position/force control and (2) Impedance control. Hybrid position/force control was first presented by Professor Raibert in 1981 [4]. Its basic idea is to divide the task space at the robot end into two orthogonal subspaces through two selection matrices and then carry out position control and force control in the two subspaces, respectively [5, 6]. Since it needs to establish an off-line task and design a special controller, it has a high computational cost and poor versatility, and these are considered to be the main defects limiting its development. Impedance control was first proposed by Professor Hogan in 1984 [7, 8], and its essence is to achieve force control by controlling the equivalent impedance between the robot and the environment [9]. Impedance control greatly simplifies the off-line task in the operation space and does not require the design of a special controller. Therefore, it is more suitable for force control of robots.

Impedance control can obtain perfect force tracking performance when the environmental parameters are known. But for the unknown environment, it is not a good solution to the force tracking problem. To this end, many scholars have done further research based on impedance control. These studies mainly fall into two types: one is the adjustment of reference trajectory [10,11,12], and the other is variable impedance control [13,14,15,16].

To achieve the adjustment of reference trajectory, some studies have been made. Xu et al. [17] proposed a method to adjust the reference trajectory through an iterative learning strategy. Li et al. [18] presented a scheme to adjust the robot reference trajectory by minimizing the cost function, which enabled the robot to maintain the required interaction force under different environmental stiffness. Roveda et al. [19] used an online extended Kalman filter to adjust the reference trajectory. Seraji et al. [20] designed two online force tracking strategies based on impedance control. The first strategy generated directly the reference trajectory online via the force tracking error function. And the second strategy obtained indirectly the reference trajectory via an adaptive control strategy. The two schemes have been verified on a 7-DOF robot and achieved good force tracking results under unknown environments. The above methods are based on the estimation of environmental parameters. Therefore, none of them can guarantee force tracking accuracy.

Variable impedance control is a method of modifying the target impedance parameters according to the error between the actual contact force and ideal force [21]. At present, some studies have been made on variable impedance control. Duan et al. [22] proposed a method to adjust impedance parameters online according to tracking error, which had the capability of compensating the uncertainty of the environment position and obtaining the ideal tracking force. Xu et al. [23] studied the force control method of wheel-legged robots interacting with complex unknown terrain and adopted an adaptive control to adjust the target stiffness. Li et al. [24] presented an impedance learning scheme for robots in unknown environments, which used iterative learning and betterment scheme to obtain the desired impedance model. Mao et al. [25] proposed a method to adjust impedance parameters via fuzzy control strategy and verified the superiority of the method through experiments. Furthermore, neural networks [26,27,28] and reinforcement learning [29, 30] have also been used in variable impedance control. Although the above methods are robust in reducing force tracking error, few studies have considered both response speed and tracking error into force tracking control. Therefore, a new adaptive variable impedance control with Fuzzy-PI compound controller is proposed. It combines the fast response of Fuzzy control with the steady-state error suppression of PI control and can quickly and stably track the ideal force in unknown environments.

The organizational structure of this paper is arranged as follows. The system configuration is presented in Sect. 2. Section 3 introduces the contact model and points out the defects of the classical constant impedance control in unknown environments. In Sect. 4, an adaptive variable impedance control with Fuzzy-PI compound controller is proposed. The stability and convergence of the proposed method in the force tracking process are further analyzed in Sect. 5. Sections 6 and 7 are the simulation and experiment, respectively. Conclusions are listed in Sect. 8.

2 System Configuration

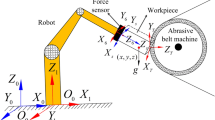
To solve the problems of clamping difficulty and easy deformation of automobile thin-walled parts, a robot trimming system, as shown in Fig. 1, has been designed by our research team. The robot trimming system includes two supporting elements, a base, and a milling robot. The supporting element consists of a robot and an end effector. The workpiece is placed on the base. The supporting element and the milling robot are located on both sides of the workpiece. During machining, the milling robot mills one side of the workpiece, while the other two supporting elements alternately support the opposite side of the workpiece. The detailed machining diagram is shown in Fig. 2.

Fig. 1
figure 1

Robot trimming system

Full size image
Fig. 2
figure 2

Machining schematic diagram of robot trimming system

Full size image

The supporting element supports the workpiece to improve the stiffness of the workpiece. However, the unstable supporting force directly causes vibration and even deformation of the workpiece. Therefore, this paper only studies the force control of the supporting element.

3 Contact Model and Compliant Control

3.1 Contact Model

As in other literature [21, 31], in contact operations, the robot is represented by the second-order mass-spring-damper model with mass m, stiffness k, and damping b, and the environment is represented by a spring model with stiffness ke. The contact model of the system is shown in Fig. 3.

Fig. 3
figure 3

Contact model of the robot and environment: a Schematic diagram of contact model. b Contact force diagram with robot motion

Full size image

Figure 3a shows the two stages during the robot’s contact with the environment. Denote x the actual position of the robot, xe the environmental position. In the first stage, when 0 < x < xe, the robot is getting close to the environment. In the second stage, when xe < x, the robot comes into contact with the environment.

Figure 3b indicates the contact force generated in the process of robot contacting with the environment. When the time is 0–t1, there is no contact at the free-stage, and the contact force is zero. When the time is t1–t3, there is contact at the contact-stage, and the contact force occurs. After the collision of a short period t1–t2, the contact force tends to stabilize. The collision produces undesirable force, which affects the machining quality of the object. Therefore, the purpose of robot force control is to effectively suppress the overshoot and oscillation caused by collision.

3.2 Impedance Control

Based on the difference of realization methods, impedance control is divided into two categories: firstly with force-based impedance control and secondly with position-based impedance control. Force-based impedance control requires knowing the precise dynamic model and actual control torque of the robot, which are considered to be the main drawbacks limiting its application in practical engineering. As an alternative, position-based impedance control avoids exactly these problems.

The block diagram of position-based impedance control is shown in Fig. 4, which consists of an outer impedance control loop and an inner position control loop. The outer impedance control loop receives the force error between the environmental force and desired force to generate the displacement correction, and then transmits the displacement correction to the inner position control loop to modify the position of the robot, thereby obtaining a desired environmental force. In Fig. 4, Xr denotes the reference position trajectory, Xc denotes the commanded position trajectory, and X denotes the measured position trajectory. Suppose that there is no error in the inner position control loop, i.e., X = Xc.

Fig. 4
figure 4

The position-based impedance control schematic

Full size image

The commonly used ideal impedance model is denoted as the form shown in Eq. (1):

$$M_{d} \ddot{E}_{x} (t) + B_{d} \dot{E}_{x} (t) + K_{d} E_{x} (t) = E_{f} (t)$$
(1)

where Ex = Xc—Xr, and Ex denotes the position error. Ef = Fe—Fd, and Ef denotes the force tracking error. Fe denotes the actual contact force. Fd denotes the desired force. Md is the target inertial matrix, Bd is the target damper matrix, and Kd is the target stiffness matrix. The transfer-function of the impedance control is as follows:

$$K(s) = \frac{{E_{x} (s)}}{{E_{f} (s)}} = \frac{1}{{M_{d} s^{2} + B_{d} s + K_{d} }}$$
(2)

Thin-walled part is prone to deform along z direction, so only the force control along z axis is required. Generally, the actual contact force is expressed as:

$$f_{e} = k_{e} (x - x_{e} )$$
(3)

where ke is the environmental stiffness, and xe is the environmental position. The force tracking error satisfies Eq. (4).

$$e_{f} = f_{e} - f_{d} = k_{e} (x - x_{e} ) - f_{d} = k_{e} (x_{r} + e_{x} ) - k_{e} x_{e} - f_{d} = k_{e} (x_{r} + k(s)e_{f} ) - k_{e} x_{e} - f_{d}$$
(4)

Taking k(s) = 1/(mds2 + bds + kd) into Eq. (4), yields

$$\begin{aligned}e_{f} (m_{d} s^{2} + b_{d} s + k_{d} - k_{e} ) =& (m_{d} s^{2} + b_{d} s + k_{d} )(k_{e} x_{r} \\&\quad - k_{e} x_{e} - f_{d} ) \end{aligned}$$
(5)

The steady-state error of the system is then obtained via Eq. (5), i.e.,

$$e_{fss} = \mathop {\lim }\limits_{s \to 0} se_{f} (s) = \frac{{k_{d} }}{{k_{d} - k_{e} }}[k_{e} (x_{r} - x_{e} ) - f_{d} ]$$
(6)

To make \(e_{fss} = 0\), one of the following two conditions requires to be satisfied.

$$x_{r} = x_{e} { + }\frac{{f_{d} }}{{k_{e} }}$$
(7)

Or

$$k_{d} = 0$$
(8)

Equation (7) indicates that xr can be obtained only when xe and ke are known. However, in practical application, it is hard to obtain the values of xe and ke due to the unknown environment. Force tracking error will always exists. Compared with Eq. (7), Eq. (8) is easier to satisfy by setting kd to zero. Therefore, according to Eq. (8), the impedance function in Eq. (1) can be rewritten as Eq. (9).

$$m_{d} (\ddot{x}_{c} - \ddot{x}_{r} ) + b_{d} (\dot{x}_{c} - \dot{x}_{r} ) = e_{f}$$
(9)

3.3 Adaptive Variable Impedance Control

As a result of the environmental uncertainty, it is hard to acquire an accurate reference position trajectory xr. Therefore, replace xr in Eq. (9) with the environmental position xe, and then obtain a new impedance function:

$$m_{d} \ddot{e}_{x} + b_{d} \dot{e}_{x} = e_{f}$$
(10)

where ex = xc—xe.

When the environment is a curved surface, there are \(\dot{x}_{e} \ne 0\) or \(\dot{x}_{e} \ne 0\) and \(\ddot{x}_{e} \ne 0\). So the environmental position xe requires to be estimated. Assuming that the estimation of environmental position is \(\hat{x}_{e} = x_{e} + \delta x_{e}\), and then the estimated position error is denoted as \(\hat{e}_{x} = x_{c} - \hat{x}_{e} = x_{c} - x_{e} - \delta x_{e} = e_{x} - \delta x_{e}\). Substituting \(\hat{e}_{x}\) for \(e_{x}\) in Eq. (10), yields

$$e_{f} = m_{d} \ddot{\hat{e}}_{x} + b_{d} \dot{\hat{e}}_{x} = m_{d} (\ddot{e}_{x} - \delta \ddot{x}_{e} ) + b_{d} (\dot{e}_{x} - \delta \dot{x}_{e} )$$
(11)

where \(e_{f}\), \(\ddot{\hat{e}}_{x}\), and \(\dot{\hat{e}}_{x}\) are time-varying, namely error is inevitable. In addition, the force sensor is susceptible to environmental interference and has time delay effects. Therefore, there will always be steady-state error. To reduce the steady-state error, an adaptive variable impedance control is proposed. Because the change of mass coefficient md is prone to cause system oscillation, this paper only adjusts the damping coefficient bd. The adaptive variable impedance control is as follows

$$m_{d} \ddot{\hat{e}}_{x} (t) + (b_{d} + \Delta b(t))\dot{\hat{e}}_{x} (t) = e_{f} (t)$$
(12)

where ∆b(t) denotes the adjustment value of damping. The steady-state error is eliminated by adjusting the damping value online. To achieve the online adjustment of ∆b(t), a Fuzzy-PI compound controller is introduced. Then a new adaptive variable impedance control with Fuzzy-PI compound controller is proposed in Sect. 4.

4 Adaptive Variable Impedance Control with Fuzzy-PI Compound Controller

4.1 Fuzzy Control

To improve the force tracking performance when the robot interacts with an unknown environment, a fuzzy controller is introduced to update ∆b(t) online. Figure 5 shows the fuzzy controller’s schematic diagram.

Fig. 5
figure 5

The schematic diagram of the fuzzy controller

Full size image

Fuzzification is the beginning of fuzzy controller design, which transforms the clear values of input variables or output variables into the linguistic values of fuzzy linguistic variables.

In the fuzzy controller, input variables are ef and ecf, respectively, and the output variable is ∆b. Each variable is classified into seven linguistic labels, namely positive big (PB), positive medium (PM), positive small (PS), zero (ZO), negative small (NS), negative medium (NM), and negative big (NB). Each linguistic label corresponds to a fuzzy subset. The fuzzy subset adopts the triangular membership function shown in Fig. 6, and the fuzzy subset domain is set to {-3, -2, -1, 0, 1, 2, 3}.

Fig. 6
figure 6

The membership function of the variable

Full size image

Fuzzification uses quantization factors to map clear values to fuzzy domains [32]. Assuming that the basic domains of ef and ecf are, respectively [-Xe, Xe] and [-Xec, Xec], the quantization factors can be represented as:

$$\left\{ {\begin{array}{*{20}c} {K_{e} = \frac{3}{{X_{e} }}} \\ {K_{ec} = \frac{3}{{X_{ec} }}} \\ \end{array} } \right.$$
(13)

where Ke and Kec are the quantification factors of ef and ecf, respectively.

The fuzzy control rule is the heart of the fuzzy reference, which summarizes the relationship between input and output. Fuzzy control rules are generated according to the actual operating experience and knowledge of operators or experts. In this paper, both the force tracking error ef and force tracking error ratio ecf have seven fuzzy subsets. Therefore, 49 fuzzy control rules can be set up (see Table 1).

In Table 1, each control rule gives a fuzzy relationship between input and output, namely:

$$\begin{gathered} R_{1} = {\text{NB(}}e_{f} {)} \cap {\text{NB(}}ec_{f} {)} \cap {\text{NB(}}\Delta b{)} \hfill \\ R_{2} = {\text{NB(}}e_{f} {)} \cap {\text{NB(}}ec_{f} {)} \cap {\text{NB(}}\Delta b{)} \hfill \\ \quad \quad \vdots \hfill \\ R_{49} = {\text{NB(}}e_{f} {)} \cap {\text{NB(}}ec_{f} {)} \cap {\text{NB(}}\Delta b{)} \hfill \\ \end{gathered}$$
(14)
Table 1 Fuzzy control rules
Full size table

The union of 49 fuzzy relations Ri(i = 1, 2,···, 49) constitutes the total fuzzy relation R, namely:

$$R{ = }R_{1} \cup R_{2} \cup \cdots \cup R_{49} = \mathop \cup \limits_{i = 1}^{49} R_{i}$$
(15)

Then, the total output of approximate inference is denoted as:

$$\Delta B^{*} = \left( {e_{f} \times ec_{f} } \right) \circ R$$
(16)

Defuzzification is the process of converting output fuzzy values into clear values. In this paper, the centroid method is adopted to defuzzify the output fuzzy set [33]:

$$\Delta b^{*} = \frac{{\sum\nolimits_{i = 1}^{n} {\mu_{i} (e_{f}, ec_{f} )B_{i}^{*} } }}{{\sum\nolimits_{i = 1}^{n} {\mu_{i} (e_{f}, ec_{f} )} }}$$
(17)

where n is the fuzzy rule number. µi(ef, ecf) is the membership grade of the i-th fuzzy output. \(B_{i}^{ * }\) is the fuzzy output when the value of the output membership grade is 1.

Fuzzy controller uses scale factors to map fuzzy domains to clear values [34]. Assuming that the basic domain of ∆b is [-Yb, Yb], the scale factor of ∆b can be represented as:

$$K_{b} = \frac{{Y_{b} }}{3}$$
(18)

Then, the clear value of ∆b can be expressed as:

$$\Delta b = K_{b} \Delta b^{*}$$
(19)

4.2 Fuzzy-PI Compound Control

The fuzzy controller takes the force tracking error and force tracking error rate as input variables, so it has the function of proportional-differential control [35]. Proportional control can speed up the response speed of the system, and differential control can reduce the overshoot of the system. However, the steady-state error of the system is difficult to eliminate due to the lack of an integral link in fuzzy control. To this end, a PI controller with an integral link is introduced and combined with the fuzzy controller to form a Fuzzy-PI compound controller. Figure 7 shows the basic principle of the Fuzzy-PI compound controller.

Fig. 7
figure 7

The basic principle of the Fuzzy-PI compound controller

Full size image

In the Fuzzy-PI compound controller, when the force tracking error ef is greater than a certain threshold, the control system uses the fuzzy controller to adjust ∆b online to obtain a faster response speed. When the force tracking error ef is less than a certain threshold, the control system uses PI controller to adjust ∆b online to obtain a small steady-state error. The PI control scheme for online adjustment of ∆b is given by:

$$\Delta b = \left( {k_{p} e_{f} + k_{i} \int_{0}^{t} {e_{f} (\tau )d\tau } } \right)\dot{\hat{e}}_{x}^{ - 1}$$
(20)

where kp is the proportional gain, and ki is the integral gain.

Then, the Fuzzy-PI compound controller can be denoted as:

$$\Delta b = \left\{ {\begin{array}{*{20}c} {\{ \Delta b\}_{{{\text{Fuzzy}}}},\quad \quad \left| {e_{f} } \right| > \varepsilon } \\ {\left\{ {\Delta b} \right\}_{{{\text{PI}}}},\quad \quad \;\;\;\left| {e_{f} } \right|\;\; \le \varepsilon } \\ \end{array} } \right.$$
(21)

where ε is the threshold. The selection of the threshold directly affects the performance of the system. When the threshold is set too high, the system switches to PI control prematurely, which affects the system's response speed. When the threshold value is set too small, the system switches to PI control later, which affects the system's steady-state error. Therefore, the threshold needs to be selected via many trials.

The principle block diagram of the entire controller is shown in Fig. 8. An adaptive variable impedance control with Fuzzy-PI compound controller is proposed to compensate for the force tracking error caused by the environmental uncertainty. The control system combines the advantages of fuzzy control and PI control, with faster response speed and small steady-state error.

Fig. 8
figure 8

The principle block diagram of adaptive variable impedance control with Fuzzy-PI compound controller

Full size image

5 Stability and Convergence Analysis

To test the force tracking performance of the proposed control method, the stability and convergence analysis are conducted. Substituting Eq. (20) into Eq. (12), yields:

$$e_{f} (t) = m_{d} \ddot{\hat{e}}_{x} (t) + [b_{0} + (k_{p} e_{f} (t) + k_{i} \int_{0}^{t} {e_{f} (\tau )} d\tau )\dot{\hat{e}}_{x}^{ - 1} ]\dot{\hat{e}}_{x} (t)$$
(22)

Submitting \(\hat{e}_{x} (t) = e_{x} (t) - \delta x_{e} (t)\) into Eq. (22), yields:

$$e_{f} (t) = m_{d} [\ddot{e}_{x} (t) - \delta \ddot{x}_{e} (t)] + b_{0} [\dot{e}_{x} (t) - \delta \dot{x}_{e} (t)] + k_{p} e_{f} (t) + k_{i} \int_{0}^{t} {e_{f} (\tau )} d\tau$$
(23)

Reorganizing Eq. (23), yields:

$$m_{d} \ddot{e}_{x} (t){ + }b_{0} \dot{e}_{x} (t){ + (}k_{p} - 1{)}e_{f} (t) + k_{i} \int_{0}^{t} {e_{f} (\tau )} d\tau = m_{d} \delta \ddot{x}_{e} (t){ + }b_{0} \delta \dot{x}_{e} (t)$$
(24)

According to fe(t) = ke(x-xe) = keex, Eq. (25) can be obtained.

$$\dot{e}_{x} (t) = \frac{{\dot{f}_{e} (t)}}{{k_{e} }},\quad \ddot{e}_{x} (t) = \frac{{\ddot{f}_{e} (t)}}{{k_{e} }}$$
(25)

Combining Eq. (24) and Eq. (25), yields:

$$m_{d} \ddot{f}_{e} (t) + b_{0} \dot{f}_{e} (t) + (k_{p} - 1)k_{e} e_{f} (t) + k_{i} k_{e} \int_{0}^{t} {e_{f} (\tau )} d\tau = m_{d} k_{e} \delta \ddot{x}_{e} (t) + b_{0} k_{e} \delta \dot{x}_{e} (t)$$
(26)

Defining \(\hat{f}_{e} = k_{e} \delta x_{e}\), and then Eq. (26) is denoted as:

$$\begin{gathered} m_{d} \ddot{f}_{e} (t) - m_{d} \ddot{f}_{d} (t) + b_{0} \dot{f}_{e} (t) - b_{0} \dot{f}_{d} (t) + (k_{p} - 1)k_{e} e_{f} (t)\hfill \\ \quad + k_{i} k_{e} \int_{0}^{t} {e_{f} (\tau )} d\tau \hfill \\ \;\;\;\quad = m_{d} \ddot{\hat{f}}_{e} (t) - m_{d} \ddot{f}_{d} (t) + b_{0} \dot{\hat{f}}_{e} (t) - b_{0} \dot{f}_{d} (t) \hfill \\ \end{gathered}$$
(27)

Let \(g(t) = \hat{f}_{e} (t) - f_{d} (t)\), Eq. (27) can be written as:

$$m_{d} \ddot{e}_{f} (t) + b_{0} \dot{e}_{f} (t) + (k_{p} - 1)k_{e} e_{f} (t) + k_{i} k_{e} \int_{0}^{t} {e_{f} (\tau )} d\tau = m_{d} \ddot{g}(t) + b_{0} \dot{g}(t)$$
(28)

By Laplace transformation of Eq. (28), the steady-state transfer function is obtained as follows:

$$\frac{{e_{f} (s)}}{g(s)} = \frac{{m_{d} s^{3} + b_{0} s^{2} }}{{m_{d} s^{3} + b_{0} s^{2} + (k_{p} - 1)k_{e} s + k_{i} k_{e} }}$$
(29)

To ensure the stability of Eq. (29), the following condition requires to be satisfied:

$$m_{d} s^{3} + b_{0} s^{2} + (k_{p} - 1)k_{e} s + k_{i} k_{e} = 0$$
(30)

In the light of the Routh criterion, the Routh array of Eq. (30) can be denoted as:

$$\begin{gathered} s^{3} \quad m_{d} \quad \quad \quad \quad \quad \quad \quad \quad \;\;\;\;(k_{p} - 1)k_{e} \hfill \\ s^{2} \quad b_{0} \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;k_{i} k_{e} \hfill \\ s^{1} \quad \frac{{b_{0} {\kern 1pt} (k_{p} - 1)k_{e} - m_{d} k_{i} k_{e} }}{{b_{0} }}\quad \quad 0 \hfill \\ s^{0} \quad k_{i} k_{e} \quad \quad \quad \quad \quad \quad \quad \quad \;\;\;0 \hfill \\ \end{gathered}$$
(31)

The system is stable only when the coefficient of the Routh array is positive:

$$\left\{ {\begin{array}{*{20}c} {\;(k_{p} - 1)k_{e} > 0\quad \quad \quad \quad \quad } \\ {\frac{{b_{0} {\kern 1pt} (k_{p} - 1)k_{e} - m_{d} k_{i} k_{e} }}{{b_{0} }} > 0} \\ \end{array} } \right.$$
(32)

Typically, the steady-state error efss is denoted as:

$$e_{{fss}} = \mathop {\lim }\limits_{{s \to 0}} s(e_{f} (s) - g(s)){\mkern 1mu} = \mathop {\lim }\limits_{{s \to 0}} s\left[ {\frac{{m_{d} s^{3} + b_{0} s^{2} }}{{m_{d} s^{3} + b_{0} s^{2} + (k_{p} - 1)k_{e} s + k_{i} k_{e} }}g(s) - g(s)} \right]$$
(33)

Assuming that the input is a step function, i.e., g(s) = 1/s, and then Eq. (33) yields:

$$e_{fss} = \mathop {\lim }\limits_{s \to 0} s(e_{f} (s) - g(s)) = - 1$$
(34)

According to Eq. (34), Eq. (35) can be obtain:

$$\mathop {\lim }\limits_{s \to 0} se_{f} (s) = 0\quad \mathop {\lim }\limits_{t \to 0} e_{f} (t) = 0$$
(35)

Which means that when t → ∞, fe → fd, i.e., the actual contact force fe converges to the desired force fd.

6 Simulation Study

In this section, the traditional constant impedance control given by Eq. (9) and the adaptive variable impedance control with Fuzzy-PI compound controller given by Eq. (12) and (20) are tested and compared in different environments. The simulation program is carried out in Matlab/Simulink. The simulation block diagram of the entire controller is shown in Fig. 9.

Fig. 9
figure 9

The simulation block diagram of adaptive variable impedance control with Fuzzy-PI compound controller

Full size image

For facilitate expression, in the following, IC is used to denote the traditional constant impedance control, and AVIC is used to denote the adaptive variable impedance control with Fuzzy-PI compound controller.

6.1 Force Tracking Under Constant Environmental Stiffness

The force tracking performance of the two methods is compared by supporting a point on the plane. Set md = 1 Ns2/m, bd = 400 Ns/m, kd = 0 N/m, and fd = 5 N. The gains of PI controller are set as kp = 20 and ki = 2, which satisfy the stability requirements of Eq. (32). The threshold ε, determined through many experiments, is 0.8 N. To test force tracking performance of the two control methods under constant environmental stiffness, the stiffness ke of the support point is set to 500 N/m.

The force tracking results of two force control methods under constant environmental stiffness are shown in Fig. 10. When the time is 0-1 s, it can be seen that the response time of AVIC is shortened by 0.1 s (versus 0.19 s in the IC). When the time is 1-3 s, the steady-state error of AVIC, compared with the IC, is reduced, but it is not eliminated. This is attributed to the fact that the variation of the damping coefficient bd affects force tracking error. Figure 11 shows the variation of damping increment Δb with time under AVIC. It can be observed that Δb is relatively small when the force tracking error is large, and then gradually increases with the decrease in force tracking error until it tends to stabilize.

Fig. 10
figure 10

Force tracking under constant environment stiffness. a Force tracking (0–1 s). b Force tracking (1–3 s)

Full size image
Fig. 11
figure 11

The change of damping increment Δb with time under AVIC (constant environment stiffness)

Full size image

The simulation results show that AVIC is superior in terms of increasing response speed and suppressing steady-state error than IC under constant environmental stiffness.

6.2 Force Tracking Under Variable Environment Stiffness

Considering that the stiffness of different positions on the thin-walled part may be different, the robustness of the proposed force control algorithm requires to be tested under variable environment stiffness. Suppose that the environmental stiffness of the support point is:

$$k_{e} = \left\{ {\begin{array}{*{20}c} {500{\kern 1pt} {\kern 1pt} ({\text{N/m}}),\quad 0 \le t \le 2} \\ {1000{\kern 1pt} {\kern 1pt} ({\text{N/m}}),\;\;2 < t \le 4} \\ \end{array} } \right.$$
(36)

Other parameter settings are consistent with Sect. 6.1. The force tracking results after simulation are shown in Fig. 12. It can be observed that the force tracking performance of AVIC is superior to that of IC when the environmental stiffness ke changes at t = 2 s. The overshoot is reduced by 81.8% (compared with 11 N overshoot of IC), and the response speed is increased by 51% (compared with 0.05 s response time of IC). Figure 13 shows the variation of damping increment Δb with time under AVIC. When the environmental stiffness ke changes, Δb decreases and then gradually tends to be stable after a short time.

Fig. 12
figure 12

Force tracking under variable environment stiffness

Full size image
Fig. 13
figure 13

The change of damping increment Δb with time under AVIC (variable environment stiffness)

Full size image

It can be seen from the simulation results that AVIC can track to the ideal value with faster response speed and smaller overshoot under variable environment stiffness.

6.3 Dynamic Force Tracking Under Variable Environment Stiffness

To test whether the proposed force control algorithm is also suitable for dynamic force tracking, the ideal supporting force fd is set as step force. Let fd to be:

$$f_{d} = \left\{ {\begin{array}{*{20}c} {5{\text{N,}}\;\;{0} \le t \le 2} \\ {10{\text{N,}}\;\;2{ < }t \le 4} \\ \end{array} } \right.$$
(37)

Other parameter settings are consistent with Sect. 6.2. Figure 14 shows the dynamic force tracking results. When the ideal force fd and environment stiffness ke change suddenly, AVIC, compared with IC, has a relatively small overshoot force and can achieve the ideal force from 5 to 10 N in a shorter time.

Fig. 14
figure 14

Dynamic force tracking under variable environment stiffness

Full size image

The simulation results clearly shown that AVIC has better dynamic force tracking than IC.

6.4 Force Tracking Under Different Thresholds

To test the influence of different thresholds on the force tracking performance of the proposed method, three thresholds, which are a high threshold 2 N, a desired threshold 0.8 N, and a low threshold 0.25 N, respectively, are using in this simulation. The desired threshold is obtained by the following method. We start with a higher threshold (ε = 2 N) and gradually reduce the threshold until a satisfactory force tracking result is obtained. The desired threshold is finally determined to be ε = 0.8 N. Other parameter settings are consistent with Sect. 6.1.

Figure 15 shows the simulation results under different thresholds. It can be observed that as the threshold ε increases, the steady-state accuracy of the system increases, but the response speed of the system decreases. This is because the system switches from fuzzy control to PI control prematurely at a larger threshold, resulting in a shorter time for fuzzy control and a longer time for PI control. A shorter time for fuzzy control reduces the response speed of the system. Conversely, a longer time for PI control improves the steady-state accuracy of the system. Hence, the force tracking performance of the system can be improved by selecting a desired threshold.

Fig. 15
figure 15

Force tracking under different thresholds

Full size image

7 Experiment Study

To further validate the proposed force control method in practical application, experiments are carried out on a simplified supporting device as shown in Fig. 16. The hardware structure of the supporting device is shown in Fig. 17, which mainly includes SR20A Industrial robot, Serve drives, SNRC-6C-A10 Motion controller, Piezoelectricity force sensor, HANDYSCOPE HS6D Data acquisition card (DAQ), Charge amplifier, and Computer. The sampling frequency of DAQ is set to 1 kHz. The computer obtains the supporting force data from the force sensor to generate the displacement correction, and then transmits the displacement correction to the robot controller to drive the robot end to make a certain position adjustment, thereby maintain a stable supporting force.

Fig. 16
figure 16

Experimental device

Full size image
Fig. 17
figure 17

The hardware structure of the experimental device

Full size image

The impedance parameters are selected as md = 1 Ns2/m, bd = 400 Ns/m, and kd = 0 N/m. The gain of PI controller is set as kp = 20 and ki = 2. The workpiece is a part cut from the car dashboard, with outline dimensions of 380 mm × 260 mm and a thickness variation range of 2–3 mm. To validate the efficiency of the proposed method under unknown environments, two support points with different stiffness on the workpiece are selected for testing. The stiffness of the support points is unknown. The support time of the robot at each support point is 5 s, and the desired supporting force is set to 15 N.

The first experiment is based on IC, and the second experiment is based on AVIC. To further understand the influence of threshold on AVIC, a third experiment is conducted. Figure 18 shows the experimental results based on IC. From 0–2 s, the robot moves from the work origin to the first support point. Once the robot contacts the first support point, a large overshoot occurs, and the force gradually stabilizes after about 3 s. At 7 s the robot leaves the first support point and then reaches the second support point at 10 s. The robot exhibits similar force tracking performance at the second support point to that of the first support point. Figure 19 shows the experimental results based on AVIC. It can be observed that the robot produces a relatively small overshoot when in contact with the first support point compared to IC. Meanwhile, the force is stable at 15 N after a short time adjustment of about 2 s, and the steady-state error of the force is reduced. When the robot is at the second support point (i.e., the environmental stiffness changes), the robot also shows superior force tracking performance. The experimental results under different thresholds is shown in Fig. 20. When the threshold is too high, the response speed of the system reduces. When the threshold is too low, the steady-state error increases. Therefore, it is significant to select a desired threshold to improve the force tracking performance.

Fig. 18
figure 18

Experimental results of constant impedance control

Full size image
Fig. 19
figure 19

Experimental results of adaptive variable impedance control (ε = 2.4 N)

Full size image
Fig. 20
figure 20

Experimental results of adaptive variable impedance control under different thresholds. a Force tracking (0–18 s). b Force tracking (2–5 s)

Full size image

8 Conclusion

To solve the force tracking problem of the supporting element, an adaptive variable impedance control with Fuzzy-PI compound controller is proposed. The control method, which combines the fast response of Fuzzy control and the steady-state error suppression of PI control, can track the ideal force quickly and stably.

A control method for online adjustment of target impedance by the Fuzzy-PI compound controller is expounded, and the convergence and stability of the control system during force tracking are further analyzed in this paper. To verify the superiority of this method, simulations and experiments are conducted. And the results show that, compared with the traditional constant impedance control, the proposed force control method has faster response speed and smaller steady-state error in unknown environments. In addition, the proposed control method is also suitable for other force tracking scenarios.