1 Introduction

Space debris has been steadily increasing in recent years as a result of the ongoing deployment of numerous orbiting satellites, which is cause for great concern. As a result of a task failure triggered by a collision through another spacecraft, such debris could become an impediment to the launch of a satellite [1]. Handling a floating body by a space manipulator with complexity in controlling its dynamics, on the other hand, is extremely difficult. The response of the robot arms changes the position and orientation of the space robot during docking operation [2, 3]. As a result, effective synchronization amid the robot base and manipulator dynamics may be able to overwhelm the system's pose disturbance. The gripping force should be adequate to keep the object from slipping while also establishing a maximum force limit to prevent rotation of the free-floating body [4]. To meet the above challenges, cooperative manipulation can be better choice for the debris removal.

Another challenge in the space robot is capturing a free-floating object effectively followed by desired trajectory. The deviation in end-effector trajectory due to floating object from the expected one results disturbance in the robot base. The tracking error is caused by the space robot system's unintegrated angular momentum constraints [5]. These unintegrated constraints can be expressed mathematically as equations in values of generalized velocities. Furthermore, issues develop as a result of redundancy and the capture of a floating body of considerable mass and shape. Because of the manipulator non-holonomic characteristics, the control methodology necessitates advanced controllers such as Amnesia controller to neutralize trajectory deviation.

Space robot performs several tasks like servicing the spacecraft, deploying satellites, capturing the object with accurate positioning. The positioning of the object in an unknown environment is effectively and accurately achieved through the collaboration of the robots. The stability of the object at a certain height (altitude) is the main aspect of docking operation [6]. Many researchers investigated the control of space robots, but only a few have examined the control of multi-space robots with advanced control methodology. Some of relevant works are described as; She and Li [7] used an active force controller (AFC) and a proportional-derivative (PD) controller to control the attitude of 2DOF manipulator. Patolia et al. [8] exhibited force modulation in a dual armed space robot having two arms for cooperative manipulation. Moghaddam and Chhabra [9] created a two-arm space robot system, with one arm (mission arm) performing the capture mission and the second arm (balancing arm) mitigating base disturbance. Dongming et al. [10] investigated the dynamics of a multi-arm coordinated free-flying space robot with an external force operating on it. Yan et al. [11] investigated dynamic balance control for target capturing and manipulating objects. The notion of passive degree of freedom (DOF) was described by Pathak et al. [12] as a virtual foundation for controlling the contact force between the space robot tip and the environment. Wen-Fu et al. [13] demonstrated the cooperative trajectory planning of dual-arm space robots keeping the base stabilized. Bera et al. [14] used a heuristic equation incorporating actual and limiting forces to modulate virtual compensation gain.

Attitude control of two degrees of freedom manipulator by integrating the PID controller with conventional PD controller was conducted by Varatharajoo et al. [15]. The obstacles in the path, failure in joints, restricted workspace and constrained configuration create difficulties during task completion. These conditions necessitate a robot to be flexible and dextrous, which is evident through the extra degrees of freedom (DOF) given to the robot. At the same time, for each extra degree of freedom, its inverse kinematics increases complexity. It is desirable for a robot to predict the uncertainty in the path and navigate accordingly to reach the goal [16]. Trajectory planning is the problem of finding the path between the initial and the terminal position of the tip considering time constraints. Further, the optimized trajectory planning by using multiple objective functions and stochastic trajectory planning technique is reported by Gasparetto et al. [17]. Trajectory planning with the obstacles in the path has also been elaborately overviewed in the studies by [18, 19]. Moreover, path planning by using intermediate waypoints with collision probability was conducted by Lin and Saripalli [20]. Ata [21] investigated the direct variational approach, which includes path integral for smooth joint movement and confined control over the trajectory. When the robot performs the docking operation, the control over trajectory tracking becomes even more important. The trajectory description has an impact on the robot joint parameters and overall configuration. Patolia et al. [22] designed an overwhelming controller composed of linear time-invariant controllers for robust trajectory. All trajectory planning methods mentioned above was unaware of the payload on the tip of the manipulator. According to the nature of the gripped object, i.e., rigid or flexible, the dynamics can vary significantly. Henshaw et al. [23] conducted a study on dynamic control of shuttle remote manipulator system (SRMS) with flexible appendages for smooth capturing of satellite payloads. The module architecture for a ground robot and the kinematic relationship between the two modules had been conducted as per the study of Alattas et al. [24]. However, in the space robot, it is not possible to consider all links as one system, as the force applied by every link creates a disturbance in the position of the base.

The control of the redundant robot joints is critical for reaching the tip of the robot to absolute points in sequence and achieving its position in a specific time. As a result, each point in the trajectory affects the joint parameters. Rybus et al. [25] investigate the accelerometer's location information for each point in a trajectory. Jia et al. [26] proposed that the point-to-point tracking of the trajectory by a three-link redundant space manipulator can be optimized using GA, which is implemented to optimize the required control parameters or the trajectory path of the space manipulator. The genetic algorithm focuses on the vibration amplitude and total execution time required for an end-effector without any payload on it. Owing to the force and impedance applied by the interacted floating object, the vibrations created are not dampened by the manipulator base as is evident in the case of the field robot. Hence, the dynamics of the robot due to external body force changes significantly [27]. The methodology for reducing the disturbances and vibrations by using dual-manipulators has been designed by the study of Samewoi et al. [28]. Furthermore, Sahu et al. [29] implemented the control methodology for optimum jerk trajectory without considering the impact of any external body force upon the system. Dynamics control, modeling, and planning of free-flying space manipulator is overviewed by Moosavian and Papadopoulos [30]. According to them, the motion equations of manipulators consist of nonlinear equations because of uncertain dynamics. For control over uncertain behavior of kinematics, dynamics, and actuators, the adaptive Jacobian controller has been used by Ahmadi and Fateh [31].

Papadopoulos [32] investigated the path planning of non-holonomic motion of a 6DOF space robot employing a unidirectional method, such that, pose and joint control through controlling the joint variables through using Kernel function. Although the technique was effective, the control law was unable to accomplish various space vehicle orientations. To address non-holonomic constraints, the multispectral feedback imaging technique was used to create a dynamic model of a space robot. This feedback approach uses multiple images to produce 3D geometric information about the floating body [33]. This image may be used to calculate the free-floating object's position and orientation. However, the authentic trajectory tracking and base attitude disturbance was not investigated in this study using simulation results. Except for closed-loop structures, Smith et al. [33] developed a proficient numerical method for a generalized Jacobian matrix of a multi-arm manipulator that is applicable to every tree-structured multi arm space robot having rotary and prismatic joints. There is no theoretical or experimental verification for their suggested method.

This work presents the trajectory control strategies of redundant planar robots that dealt with a floating object. The docking operation of rectangular floating object and dynamics control methodology is considered to control the position and orientation of the tip of the robot. The control methodology consists of PID controller and Amnesia controller. As a result, in the suggested technique, a tip trajectory with reduced error may be seen if only a typical PID controller is used. Furthermore, any remaining errors may be totally eliminated utilizing amnesia recovery control that addresses space robot non-holonomic property. On behalf of this, the controller, kinematics equations of the redundant two planar robots and model of the rectangular floating object are structured using the BGT. In BGT, the generated dynamic equations can be used to obtain the trajectory of manipulator joints that ensures realization of the reference trajectory of the tip [34,35,36].

1.1 PID Algorithm

PID algorithm consists of three basic coefficients; proportional, integral and derivative which are varied to get an optimal response. The PID algorithm regulates the output to the control point to attain a setpoint. The setpoint can be specified as a static variable or a dynamic variable derived from a mathematical model [37].

1.2 Program of PID Controller

The flowchart of the PID algorithm is illustrated in Fig. 1. Initially, desired value of Xtip and Ytip of end-effector are entered, then joint angles of each manipulator are evaluated. After reaching the desired pose of end-effector, the algorithm is terminated. Otherwise, tuning of gain value (Kp, Ki and Kd) is carried out till nth iteration.

Fig. 1
figure 1

Flowchart of PID control algorithm

Full size image

1.3 Use of PID Controller

PID controllers are the most precise and reliable controllers because they employ a control loop feedback mechanism to control process variables. PID controllers are common in industrial control systems and other applications that require constantly modulated control (to control the amount of flow in a system). PID controller anticipates the error signal between the previous input signal and the desired output signal, and then generates the corrected signal to decrease positional error. Actual tip movements that differ from reference flow inputs (velocity) cause tip trajectory errors. PID controllers address these errors by transmitting Jacobian corrections to every joint of the relevant space robot. The PID controller converts the corrected signals to joint torque (\(\tau\)) signals, which are then supplied to the actuator of the manipulator joints.

1.4 Disadvantages of PID Controller

Limitation of PID controllers is its poor control performance when used to regulate an integrating process with a large time delay. Furthermore, it is unable to accommodate ramp-type set-point change. A smooth control law, such as a PID controller, cannot produce an accurate trajectory for non-holonomic mechanical structures. In PID-controlled space robotic systems, a noteworthy revolution of a floating body may also be witnessed. This might cause the robot systems to have additional trajectory errors. In 2RPR, this error is effectively handled employing an Amnesia controller in count to the PID controller, resulting in zero rotation in floating body.

1.5 Output of PID Controller

A proportional controller's output is proportionate to the current error e(t). It compares the current value or the value of the feedback process to the desired set point. By multiplying the resultant error by a proportional constant, the output is produced. If indeed the error value is zero, this controller output is 0. The output of proportional controller is represented as \(P_{out} = K_{p} e(t)\). The magnitude of the error as well as the duration of the error is directly proportional to the integral term. The integral term is used to determine the sum of instantaneous errors in terms of time. After that, the reading is multiplied by the integral gain and added to the output of the system. The output of Integral controller is represented as \(I_{out} = K_{i} \int {e(t)} dt\). The derivative term is in charge of computing the error's derivative and determining the error slope over time, as well as multiplying this derivative by the derivative gain Kd. The output of Derivative controller is represented as \(D_{out} = K_{d} {{de} \mathord{\left/ {\vphantom {{de} {dt}}} \right. \kern-\nulldelimiterspace} {dt}}\).

1.6 Transfer Function of Sensor

Sensor gives feedback of robot behavior to the controller. Every sensor has an ideal output–stimulus relationship. The output of such a sensor would always represent the real value of the stimulus if it is perfectly designed and built using ideal materials by ideal workers using ideal tools. The transfer function describes an ideal output–stimulus relationship. This function creates a relationship between the sensor's electrical signal S and the stimulus s as \(S = f(s)\). The equation represents a one-dimensional linear relationship as \(S = a + bs\).Where, the intercept (the output signal at zero input signal) is referred as a, and the slope (also known as sensitivity) is denoted by b. S is one of the parameters of the output electric signal employed as the sensor's output by data acquisition devices.

The term “K” is referred as the transfer function gain parameter that links the transfer function to its steady-state conditions and provides stability. Under steady-state conditions, it is the ratio of what you receive as output from the system to what you put into it.

Based on literature, following research questions are specified as: a) Can this proposed control strategy will achieve the desired trajectory by controlling and switching over various joints with greater accuracy? b) Is error between the reference and the actual trajectory reduced to the negligible extent, and the rotation of a floating rectangular body is reduced to the minimum extent because of PID and amnesia controller? c) Is docking operation of rectangular floating object and dynamics control methodology considered in this research controlled the position and orientation of the tip of the robot?

Further, this paper is structured in the following manner:

  1. 1

    Section 2–Modeling of two redundant planar robots (RPR) docking a floating body

  2. 2

    Mathematical model of 2RPR to generate kinematic equations

  3. 3

    Mathematical modeling of the free-floating object for kinematic equation formulation

  4. 4

    Section 3 Control strategy for dynamic control of two redundant planar robots (RPR)

  5. 5

    Section 4 Optimal tuning of gain parameters using genetic algorithm (GA)

  6. 6

    Section 5 Comparison of the present work with existing works

  7. 7

    Section 6 Conclusion and discussion

2 Modeling of Two Redundant Planar Robots (RPR) Docking a Floating Body

The modeling of space robot having extra DOFs consists of the dynamic model created by bond graph technique (BGT) shown in Appendix 1. The kinematic analytical model is developed which results in the Jacobian form. The velocities from joint coordinates can be traversed to the tip co-ordinates by using Jacobian. PID and Amnesia controllers, kinematic relations and Jacobian are used for the advancement of BGM. The detailing of the above-mentioned models is discussed below:

2.1 Mathematical Model of 2RPR to Generate Kinematic Equations

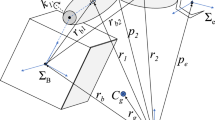
Kinematic relations consisting of robot end tip velocities are required for deriving system BGM. The BGT has been used to generate dynamic equations based on kinematic inputs and graphical representation. The RPR model consists of linear and rotational dynamic links. The base and eight links of each robot are assumed to be rigid. In addition, robots are considered as a single arm that consists of spherical joints which comprises of unfastened kinematic chain. The pictorial representation of the robot system is depicted in Fig. 2, in which the absolute frame \(\{ A\}\) and two movable frames {M}, \(\{ M^{\prime}\}\) are placed at the manipulator base CM. \(X_{m}\) and \(Y_{m}\) are X-axis and Y-axis of the movable frame {M}, respectively. \(X_{{m^{\prime}}}\) which is similar for each frame. On this basis, frames \(\{ 0\}\) and {\(0^{^{\prime}}\)} are located at their roots. It is depicted that Frames {1} and {\(1^{^{\prime}}\)} are positioned at the first joint of the space robot. At the starting point of 2nd to 8th and 10th to 16th links frames {2},{3}….,{8} and {10}, {11},….,{16} are located, respectively. Frame {9} and frame {17} are located at the tip of the manipulator. The base frame {0} is considered to be at the distance of ‘r’ from movable frame {M}.

Fig. 2
figure 2

Geometric model of 2RPR docking the floating object

Full size image

The derivation of the expressions given by Eqs. (1) through (13) are made through geometrical approach. Let, \(l_{1}\) to \(l_{16}\) represents the length of 1st to 16th active links of the space robot, respectively. It is assumed that ϕ represents movable frame {M} rotation with frame {A}. Let \(\theta_{1}\) to \(\theta_{16}\) be the joint angles of manipulators 1st to 16th, respectively. (\(X_{{cm_{\,1} }} ,Y_{{cm_{\,1} }}\)) and (\(X_{{cm_{\,2} }} ,Y_{{cm_{\,2} }}\)) have been assumed as the coordinates of the center of mass (CM) of manipulator base 1 and 2, correspondingly with respect to absolute frame {A}. The base frame {0} is considered to be at the distance of ‘r’ from movable frame {M}. (\(X_{{tip_{\,1} }} ,Y_{{tip_{\,1} }}\)) and (\(X_{{tip_{\,2} }} ,Y_{{tip_{\,2} }}\)) representing position of manipulator tips of RPR 1 and 2, respectively with respect to absolute frame {A} is expressed as

$$ X_{tip1} = X_{cm1} + r{\text{c}}_{\phi } + l_{1} {\text{c}}_{\phi 1} + l_{2} {\text{c}}_{\phi 12} + \cdots + l_{8} {\text{c}}_{\phi 1...8} $$
(1)
$$ Y_{tip1} = Y_{cm1} + \, rs_{\phi } + \, l_{1} s_{\phi 1} + \, l_{2} s_{\phi 12} + \cdots .. + \, l_{8} s_{\phi 1 \cdots 8} $$
(2)
$$ X_{tip2} = X_{cm2} + \, rc_{{\phi_{2} }} + \, l_{9} c_{{\phi_{2} 9}} + \, l_{2} c_{{\phi_{2} 910}} + \cdots .. + \, l_{16} c_{{\phi_{2} 910.....16}} $$
(3)
$$ Y_{tip2} = Y_{cm2} + \, rs_{{\phi_{2} }} + \, l_{9} s_{{\phi_{2} 9}} + \, l_{10} s_{{\phi_{2} 910}} + \cdots .. + \, l_{16} s_{{\phi_{2} 910.....16}} $$
(4)

where, c and s denote cosine and sine, respectively

$$ c_{\phi } = \cos (\phi ),\,\,\,c_{\phi 1} = \, \cos (\phi + \theta_{1} ), \cdots \cdots ..,c_{\phi 1.....8} = \, \cos (\phi + \theta_{1} + \theta_{2} + ....... + \theta_{8} ) $$
$$ c_{{\phi_{2} }} = \cos (\phi_{2} ),\,\,\,\,c_{{\phi_{2} 2}} = \, \cos (\phi_{2} + \theta_{9} ), \cdots \cdots ..,c_{{\phi_{2} 9...16}} = \, \cos (\phi_{2} + \theta_{9} + \theta_{10} + \cdots \cdots + \theta_{16} ) $$
$$ s_{{\phi_{2} }} = \sin (\phi_{2} ),\,\,\,\,s_{{\phi_{2} 9}} = \, \sin (\phi_{2} + \theta_{9} ), \cdots \cdots ..,s_{{\phi_{2} 9...16}} = \, \sin (\phi_{2} + \theta_{9} + \theta_{10} + \cdots \cdots + \theta_{16} ) $$

The orientation (\(\theta_{tip1}\),\(\theta_{tip2}\)) of manipulator tips of RPR 1 and 2, respectively with respect to absolute frame {A}is formulated as

$$ \theta_{tip1} = \phi + \theta_{1} + \theta_{2} + ............ + \theta_{8} $$
(5)
$$ \theta_{tip2} = \phi_{2} + \theta_{9} + \theta_{10} + ............ + \theta_{16} $$
(6)

By differentiating Eqs. (1)–(4), we have obtained robot tip velocities that can be written as

$$ \dot{X}_{tip1} = \dot{X}_{cm1} - r\dot{\phi }{\text{s}}_{\phi } - l_{1} (\dot{\phi } + \dot{\theta }_{1} ){\text{s}}_{\phi 1} - ........... - l_{8} (\dot{\phi } + \dot{\theta }_{1} + \dot{\theta }_{2} + ..... + \dot{\theta }){\text{s}}_{\phi 12....8} $$
(7)
$$ \dot{Y}_{tip1} = \dot{Y}_{cm1} + r\dot{\phi }c_{\phi } + l_{1} (\dot{\phi } + \dot{\theta }_{1} )c_{\phi 1} + ........... + l_{8} (\dot{\phi } + \dot{\theta }_{1} + \dot{\theta }_{2} + ..... + \dot{\theta }_{8} )c_{\phi 12...8} $$
(8)
$$ \dot{X}_{tip2} = \dot{X}_{cm2} - r\dot{\phi }_{2} {\text{s}}_{{\phi_{2} }} - l_{9} (\dot{\phi }_{2} + \dot{\theta }_{9} ){\text{s}}_{{\phi_{2} 9}} - ........... - l_{16} (\dot{\phi }_{2} + \dot{\theta }_{9} + \dot{\theta }_{10} + ..... + \dot{\theta }_{16} ){\text{s}}_{{\phi_{2} 910....16}} $$
(9)
$$ \dot{Y}_{tip2} = \dot{Y}_{cm2} + r\dot{\phi }_{2} c_{{\phi_{2} }} + l_{9} (\dot{\phi }_{2} + \dot{\theta }_{9} )c_{{\phi_{2} 9}} + ........... + l_{16} (\dot{\phi }_{2} + \dot{\theta }_{9} + \dot{\theta }_{10} + ..... + \dot{\theta }_{16} )c_{{\phi_{2} 910...16}} $$
(10)
$$ \dot{\theta }_{tip1} = \dot{\phi } + \dot{\theta }_{1} + \dot{\theta }_{2} + ............. + \dot{\theta }_{8} ; $$
(11)
$$ \dot{\theta }_{tip2} = \dot{\phi }_{2} + \dot{\theta }_{9} + \dot{\theta }_{10} + ............ + \dot{\theta }_{16} $$
(12)

Equations (7) and (8) can be simplified to obtain results in the Jacobian formulation as

$$ \left[ \begin{gathered} \dot{X}_{tip1} \hfill \\ \dot{Y}_{tip1} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \dot{X}_{cm1} - r\dot{\phi }{\text{s}}_{\phi } \hfill \\ \dot{Y}_{cm1} + r\dot{\phi }c_{\phi } \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} \beta_{1n} \, \,\beta_{2n} ..... \, \beta_{8n} \, \hfill \\ \beta_{1m} \,\,\,\beta_{2m} .....\,\,\beta_{8m} \hfill \\ \end{gathered} \right]\left[ {\dot{\theta }} \right]^{T} + \left[ \begin{gathered} \beta_{1n} \hfill \\ \beta_{1m} \hfill \\ \end{gathered} \right]\left[ {\dot{\phi }} \right] $$
(13)

where,

\(\left[ \begin{gathered} \beta_{1n} \, \,\beta_{2n} ..... \, \beta_{8n} \, \hfill \\ \beta_{1m} \,\,\,\beta_{1m} .....\,\,\beta_{8m} \hfill \\ \end{gathered} \right]\) = \(\left[ J \right]\), \(\left[ J \right]\) represents the Jacobian matrix and \(\beta_{1n}\),\(\beta_{2n}\),…,\(\beta_{8n}\),\(\beta_{1m}\),\(\beta_{2m}\),…,\(\beta_{8m}\) are the velocity influence coefficients for robot 1. Gains are required to model the Jacobian and expressed as

$$ \begin{aligned} & \beta_{1n} = - \,l_{1} s_{\phi 1} - \,l_{2} s_{\phi 12} - \cdots .. - \, l_{8} s_{\phi 1......8} , \hfill \\ & \beta_{2n} = - \,l_{2} s_{\phi 12} - \cdots .. - \, l_{8} s_{\phi 1......8} ,.......,\beta_{8n} = - \, l_{8} s_{\phi 1......8} \,; \hfill \\ & \beta_{1m} = l_{1} {\text{c}}_{\phi 1} + l_{2} {\text{c}}_{\phi 12} + ...... + l_{8} {\text{c}}_{\phi 1...8} , \hfill \\ & \beta_{2m} = l_{2} {\text{c}}_{\phi 12} + ...... + l_{8} {\text{c}}_{\phi 1...8} ,......,\beta_{8m} = l_{8} {\text{c}}_{\phi 1...8} \hfill \\ \end{aligned} $$

An electrical transformer or lever is treated as a transformer in the proposed bond graph model. It has characteristic of not providing or diminishing the energy while it can only give power and provide it with a scaling factor called transformer modulus, denoted as μ. The relation between efforts and flows within themselves is balanced by the transformer. To understand for a general reader, the word bond graph model is developed depicting all the major components. The BGM is developed by using Eqs. (7)–(10) and shown in appendix section, Fig. 11a. It also includes Jacobian and controller designs.

Actuator (as a part of Fig. 3), gives sufficient torque to joint of each link which enables reaching the end-effector to the desired points. As space robot is non-holonomic, the tip of space robot cannot achieve the reference path with PID controller only. The actual trajectory differs from the reference trajectory and is called amnesia. To remove Amnesia, an additional controller named by Amnesia controller is used with the PID controller. Jacobian converts the joint velocities into tip velocities.

Fig. 3
figure 3

Representation of word BGM of the two RPR handling a floating body

Full size image

2.2 Mathematical Model of the Free-Floating Object for Kinematic Equation Formulation

The rectangular object is considered as a free-floating body. According to the geometry of the surface, the location of mating points of tip and floating body is determined. The pictorial illustration of a floating rectangular object is revealed in Fig. 4. There are chances of the floating body to rotate about the \(Z\)-axis (perpendicular to the plane of the paper). It has been assumed that the rectangular object has ‘\(2d\)’ diagonal and ‘\(\gamma\)’ angular rotation about \(Z\)-axis. Points to be mated on the free-floating body will have displacements in the X direction and Y direction. Let, \(O_{x} \,{\text{and}}\,O_{y}\) be the X and Y coordinates of the origin \(O\) of the local frame {L} (fixed to the floating body), calculated from the absolute frame {A}, respectively. Let the initial positions of mating points be \(P_{1} ,P_{2}\) and after rotations \(P_{1}^{^{\prime}} ,P_{2}^{^{\prime}}\) be the positions of mating points of tip and floating object. The location of mating points on the floating body of robots 1 and 2 are expressed as:

$$ X_{{p_{1} }} = - dc(\alpha ) = - dc(30) = - d(\sqrt 3 /2);\quad Y_{{p_{1} }} = 0 $$
(14)
$$ X_{{p_{2} }} = dc(\alpha ) = dc(30) = d(\sqrt 3 /2);\quad Y_{{p_{2} }} = 0 $$
(15)
Fig. 4
figure 4

Geometric model of the floating object

Full size image

After rotation of the floating body by an angle \(\gamma\) about the \(Z\)-axis, a new position of mating points (\(P_{1}^{^{\prime}} ,P_{2}^{^{\prime}}\)) are expressed in Eqs. (16) and (17). Equations (22)–(25) express velocities of the floating object.

$$ \left[ \begin{gathered} X_{{p_{1}^{^{\prime}} }} \\ Y_{{p_{1}^{^{\prime}} }} \\ 1 \\ \end{gathered} \right] = \left[ \begin{gathered} c\gamma \quad - s\gamma \hfill \\ s\gamma \quad \;\;c\gamma \hfill \\ \,0\quad \quad 0 \hfill \\ \end{gathered} \right.\left. \begin{gathered} 0 \hfill \\ 0 \hfill \\ 1 \hfill \\ \end{gathered} \right]\,\left[ \begin{gathered} - \sqrt 3 d/2 \\ 0 \\ 1 \\ \end{gathered} \right] = \left[ \begin{gathered} - (\sqrt 3 d/2)c\gamma \\ - (\sqrt 3 d/2)s\gamma \\ 1 \\ \end{gathered} \right] $$
(16)
$$ \left[ \begin{gathered} X_{{p_{2}^{^{\prime}} }} \\ Y_{{p_{2}^{^{\prime}} }} \\ 1 \\ \end{gathered} \right] = \left[ \begin{gathered} c\gamma \quad - \quad s\gamma \hfill \\ s\gamma \quad \quad \;c\gamma \hfill \\ \,0\quad \quad \quad 0 \hfill \\ \end{gathered} \right.\left. \begin{gathered} 0 \hfill \\ 0 \hfill \\ 1 \hfill \\ \end{gathered} \right]\,\left[ \begin{gathered} \sqrt 3 d/2 \\ 0 \\ 1 \\ \end{gathered} \right] = \left[ \begin{gathered} (\sqrt 3 d/2)c\gamma \\ (\sqrt 3 d/2)s\gamma \\ 1 \\ \end{gathered} \right] $$
(17)

The resultant positions of the mating points can be obtained by subtracting initial position from the new position of the floating body for robots 1 and 2, respectively. The translation movement of mating points in X and Y directions is derived as

$$ X_{1} = \Delta X_{p1} = X_{{p^{\prime}_{1} }} - X_{{p_{1} }} = - d\cos \alpha \cos \gamma + d\cos \alpha = d\cos \alpha (1 - cos\gamma ) $$
(18)
$$ Y_{1} = \Delta Y_{p1} = Y_{{p_{1}^{^{\prime}} }} - Y_{{p_{1} }} = - d\cos \alpha \sin \gamma - 0 = - d\cos \alpha \sin \gamma \, $$
(19)
$$ X_{2} = \Delta X_{p2} = X_{{p_{2}^{^{\prime}} }} - X_{{p_{2} }} = d\cos \alpha \cos \gamma - dcos\alpha = dcos\alpha (\cos \gamma - 1) $$
(20)
$$ Y_{2} = \Delta Y_{p2} = Y_{{p_{2}^{^{\prime}} }} - Y_{{p_{2} }} = d\cos \alpha sin\gamma - 0 = d\cos \alpha sin\gamma $$
(21)

The mating point velocities can be obtained from the displacement equations that are expressed as

$$ \dot{X}_{1} = d\cos \alpha (\sin \gamma )\dot{\gamma } = \mu_{1} \dot{\gamma } $$
(22)
$$ \dot{Y}_{1} = - d\cos \alpha (\cos \gamma )\dot{\gamma }\, = \mu_{2} \dot{\gamma } $$
(23)
$$ \dot{X}_{2} = - dcos\alpha (\sin \gamma )\dot{\gamma } = \mu_{3} \dot{\gamma } $$
(24)
$$ \dot{Y}_{2} = d\cos \alpha (\cos \gamma )\dot{\gamma } = \mu_{4} \dot{\gamma } $$
(25)

where, \(\mu_{1}\),\(\mu_{2}\), \(\mu_{3}\), and \(\mu_{4}\) are the moduli of the transformer which are used to create the BGM of the proposed system. These transformer moduli are depicted in Fig. 3 as modulated transformer (MTF). By implementing this technique, the dynamic equations are automatically derived for given kinematic inputs. Here, \(\alpha\) is not restricted to 300 only, the proposed control design allows different values of \(\alpha\).

3 Control Strategy for Dynamic Control of Two Redundant Planar Space Robots (RPSR)

In this section control strategy for dynamic control of two redundant planar robots (RPR) for docking operation using amnesia and PID controller is discussed (shown in Appendix 1). Simulation and animation results are also performed to emphasize the cogency of the proposed control strategy.

3.1 Implementation PID Controller and its Mechanism

The PID controller [38,39,40] is well known and commonly used to enhance the dynamic response and minimize the steady state error. The derivative controller adds a finite zero to the transfer function of the open loop plant and enhances the transient response. A pole at the origin is added by the integral controller, thereby reducing the steady state error to zero due to a phase function. The PID controller composed of three control types: proportional, integral and derivative controller.

3.1.1 Proportional Controller

To regulate the system, the proportional controller output makes use of a 'proportion' of the system error.

$$ P_{{term^{\prime}}} = K_{p} \times Error $$
(26)

3.1.2 Integral Control

The integral controller's output is proportional to the amount of time that an error occurs in the system. The integral action removes the offset imposed by the proportional control, but it inserts a phase lag into the system.

$$ I_{{term^{\prime}}} = K_{i} \times \int {Error} \,dt $$
(27)

3.1.3 Derivative Control

The output of the derivative controller is proportional to the rate at which an error change. To decrease overshoot, derivative control is used and adds a phase lead action that eliminates the phase lag introduced by the integral action.

$$ D_{{term^{\prime}}} = K_{d} \times \frac{d(Error)}{{dt}} $$
(28)

PID controllers, as seen in Fig. 11a, are used to regulate robot tip motion by comparing real velocity signal with reference velocity signal and rectifying it in case of an error. The Jacobian is then used to convey the rectified signals to every actuating joint. As a consequence, the task is completed with accurate trajectory tracking. In Fig. 11a, the PID controllers are shown as signal block diagrams. The terms Kp, Ki and Kd within those block diagrams denote proportional gain, integral gain, and derivative gain, correspondingly.

The control law of PID scheme is expressed as

$$ \tau = K_{p} \hat{\theta } + K_{i} \int {\hat{\theta }dt + K_{d} } \dot{\hat{\theta }} $$
(29)

where, \(\hat{\theta }\) denotes divergence from preferred angle (\(\hat{\theta }_{d}\)).

The PID control law integral Eq. (29) creates a new state variable, denoted by \(\gamma\) whose time derivative is \(\dot{\gamma } = \hat{\theta }\).

The PID control law Eq. (29) is now changed to Eq. (30) as

$$ \tau = K_{p} \hat{\theta } + K_{i} \gamma + K_{d} \dot{\hat{\theta }} $$
(30)

where,\(\,\tau\) represents actuator torque vector.

The PID close-loop equation is referred as

$$ D(\theta^{\prime})\ddot{\theta }^{\prime}\, + \,C^{\prime}_{L} (\theta^{\prime},\dot{\theta }^{\prime})\dot{\theta }^{\prime}\, + g(\theta^{\prime})\, = \,K_{p} \hat{\theta } + K_{i} \gamma + K_{d} \dot{\hat{\theta }}\, $$
(31)

where, \(C^{\prime}_{L} (\theta^{\prime},\dot{\theta }^{\prime})\) depicts Coriolis term for space manipulator and \(g(\theta^{\prime})\) denotes gravity force vector.

Equation (31) is expressed in the state form as

$$ \frac{d}{dt}\left[ \begin{gathered} \tau \hfill \\ {\hat{\theta }} \hfill \\ {\dot{\hat{\theta }}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {\hat{\theta }} \hfill \\ {\dot{\hat{\theta }}} \hfill \\ \ddot{\theta }^{\prime}_{d} - D(\theta^{\prime})^{ - 1} [K_{p} \hat{\theta } + K_{i} \tau + K_{d} \dot{\hat{\theta }}\, - C^{\prime}_{L} (\theta^{\prime},\dot{\theta }^{\prime})\dot{\theta }^{\prime}\, - g(\theta^{\prime}) \hfill \\ \end{gathered} \right] $$
(32)

where, \(\gamma\) is an additional state variable, whose time derivative is \(\dot{\gamma } = \hat{\theta }\).

It is observed that at equilibrium condition i.e., \(\hat{\theta } = 0\) and \(\dot{\hat{\theta }} = 0\), we get \(\theta^{\prime} = \theta^{\prime}_{d}\).

Hence, Eq. (32) yields Eq. (33) as

$$ \left[ {\gamma^{T} \,\hat{\theta }^{T} \,\dot{\hat{\theta }}^{T} } \right] = \left[ {\lambda^{ * } \,0\,\,0} \right] $$
(33)

PID controller [41, 42] is installed at every joint of links to control the joint angular displacements shown in Fig. 11a. Equation for control of actuator is generalized as

$$ \tau_{i} = K_{pi} (\theta_{di} - \theta_{ai} ) - K_{di} \dot{\theta }_{ai} $$
(34)

where, \(\tau_{i}\) is the joint ith torque; where, i = 1,…,8. The terms \(\theta_{ai}\) and \(\theta_{di}\) are the actual and desired position of ith joint. \(\dot{\theta }_{ai}\) represents real angular velocity of ith joint. \(K_{pi}\) and \(K_{di}\) resembles proportional and derivative gain parameters, correspondingly, of the ith joint.

The PID controller predicts the error signal between the previous input signal and the desired output signal and the corrected signal is generated to reduce the positional error. The error signals are derived as \(e_{x} = \dot{X}_{ref} - \dot{X}_{tip}\) and \(e_{y} = \dot{Y}_{ref} - \dot{Y}_{tip}\) where \(\dot{X}_{ref}\) and \(\dot{Y}_{ref}\) are the reference input signals regarding velocity of end-effector in the X and Y directions, correspondingly. \(\dot{X}_{tip}\) and \(\dot{Y}_{tip}\) are the actual signals for velocity of robot end tip in X and Y direction, correspondingly. The corrected signals by the PID controller are converted to joint torque (\(\tau\)) signals through the Jacobian and these signals are transmitted toward the actuator of joint of manipulator.

The time domain output of a PID controller, which is equivalent to the control input to the plant, is computed from the feedback error as

$$ v(t) = K_{p} e(t) + K_{i} \int {e(t)} dt + K_{d} \frac{de}{{dt}} $$
(35)

where, variable (e) denotes trajectory error.

The proportional gain (\(K_{p}\)) times the magnitude of the error plus the integral gain (\(K_{i}\)) times the integral of the error plus the derivative gain (\(K_{d}\)) times the derivative of the error equals the control signal (\(v\)) to the plant.

Hence, transfer function of a PID controller is computed by integrating Eq. (36) as

$$ K_{p} + \frac{{K_{i} }}{s} + K_{d} s = \frac{{K_{p} s + K_{d} s^{2} + K_{i} }}{s} $$
(36)

3.2 Control Strategy Using Amnesia Removal

Because of the non-holonomic characteristics of RPR, the displacement of robot tips varies from the reference command given to them [43, 44]. Hence, control over the positioning of tips is more significant in the trajectory planning of the redundant robots. The generation of errors obtained from the non-holonomic nature of the robot is known as Amnesia. The positioning errors obtained are recorded by the Amnesia controller and forwarded to the tip of the robots. These errors in X and Y directions are calculated as

$$ X_{ta} = e^{{ - t_{a} t}} \int\limits_{{t_{i} }}^{t} {e^{{ - t_{a} \delta }} (X_{refn} - X_{tipn} )} d\delta \, $$
(37)
$$ Y_{ta} = e^{{ - t_{a} t}} \int\limits_{{t_{i} }}^{t} {e^{{ - t_{a} \delta }} (Y_{refn} - Y_{tipn} )} d\delta $$
(38)

where, (\(X_{refn}\),\(Y_{refn}\)) and (\(X_{tipn}\),\(Y_{tipn}\)) are coordinates of reference and real tip of the robot (n = 1; for robot 1 and n = 2; for robot 2) in X and Y directions, correspondingly. \(t_{a}\) represents time constant and tiindicates initial time of docking maneuver and t is arbitrary time taken during the docking maneuver.

3.3 Simulation and Animation Results

The proposed control strategy is used to restrict the movement of the floating body from the initial position to the required position in a specific time with minimum dislocation of the base. Due to control on movement of base, disturbances proceeding to the tip of robot reduces significantly. SYMBOLS Shakti software was used for bond graph technique (modeling, simulation, and animation).

The circular reference trajectory is employed during the docking process, and its parametric form is described in Eq. (39). This equation gives the reference path to the robot tips.

$$ (X_{ref} - X_{0} )^{2} + (Y_{ref} - Y_{0} )^{2} = R^{2} $$
(39)

where, Xref and Yref are the reference given to tips in X and Y direction, respectively. These are expressed as

$$ X_{ref} = Rc(\delta (t)) + X_{0} $$
(40)
$$ Y_{ref} = Rs(\delta (t)) + Y_{0} \,\, $$
(41)

where, R represents the radius of spherical trajectory, \(X_{0}\) and \(Y_{0} \,\) represents coordinates of the center of the rounded disk and \(\delta (t)\) denotes 3rd degree multinomial blend of t and it is denoted as

$$ \delta (t) = \delta_{0} + 3(\delta_{f} - \delta_{0} )(t/t_{f} )^{2} - 2(\delta_{f} - \delta_{0} )(t/t_{f} )^{3} $$
(42)

where, \(\delta_{0}\) and \(\delta_{f}\) represents the preliminary and concluding angles, correspondingly, of the smooth-edged input trajectory and the maximum time needed to influence \(\delta_{f}\) is \(t_{f}\). The reference velocity can be obtained by differentiation of Eqs. (40) and (41), which derive as

$$ \dot{X}_{ref} = - R\left[ {\frac{{6(\delta_{f} - \delta_{0} )t}}{{t_{f}^{2} }} - \frac{{6(\delta_{f} - \delta_{0} )t^{2} }}{{t_{f}^{3} }}} \right]s(\delta (t)) $$
(43)
$$ \dot{Y}_{ref} = - R\left[ {\frac{{6(\delta_{f} - \delta_{0} )t}}{{t_{f}^{2} }} - \frac{{6(\delta_{f} - \delta_{0} )t^{2} }}{{t_{f}^{3} }}} \right]c(\delta (t)) $$
(44)

Equations (43) and (44) ensure the starting and ending of simulation, i.e., \(\dot{X}_{ref}\) = \(\dot{Y}_{ref} = 0 \cdot\).

Simulation is run for 10 s to generate the desired trajectory of the two RPR composed of PID and Amnesia control. At the start of docking, the end-effectors are linked with the floating body. The circular trajectory is achieved with the help of both the RPR and initial configuration as shown in Fig. 4.

Initial base angles for robot 1, i.e., \(\phi_{{_{1} }}\) is taken as \(0^{ \circ }\) and for robot 2, i.e., \(\phi_{2}\) is taken as \(180^{0}\). The joint angles for robot 1 are considered as \(\theta_{1} = \theta_{2} = \theta_{3} = \theta_{4} = 40^{ \circ }\), \(\theta_{5} = \theta_{6} = \theta_{7} = \theta_{8} = - \,40^{ \circ }\) and for robot 2, the joint angles are \(\theta_{9} = \theta_{10} = \theta_{11} = \theta_{12} = - \,40^{ \circ }\), \(\theta_{13} = \theta_{14} = \theta_{15} = \theta_{16} = 40^{ \circ }\). Other input parameter values used for simulation is mentioned in Table 1.

Table 1 Amnesia and PID controller: components and their properties used for simulation
Full size table

The results of simulation and animation of the suggested control strategy are discussed later. The amnesia control and PID control parameters are initially selected manually. As a space robot, its base is not fixed hence the values of mass (\(m = 200\) kg) and inertia (\(I = 40\) kgm2) of the robot base is taken as low as possible.

The radius of the circle is taken as 0.15 m. For the proposed work, workspace of the robot is limited to this value, beyond this value the robot cannot reach to the desired location. For one complete revolution of circular trajectory, the initial angle is considered as 0°and the final angle is considered as 360°. Now, the results of simulation and animation have been discussed. Figure 5(a) and Fig. 5(b) shows the reference and the actual trajectory obtained by the PID controller for robots 1 and 2, respectively. The reference and the actual trajectory obtained after Amnesia control for RPR 1 and 2 are shown in Fig. 5(c) and Fig. 5(d). Figure 5(a) and (b) shows the deviations in the actual and the reference, and demonstrate the huge difference when there is only PID controller. This unacceptable error is as a result of non-holonomic feature of the space manipulator and additional mobility owing to excess DOF. Therefore, the achievement of the desired trajectory becomes very difficult. Hence, the Amnesia controller is used along with the PID controller to neutralize the deviations between the reference and actual trajectory. Because of Amnesia controller, the results obtained are very close to reference trajectory which is shown in Fig. 5(c) and (d).

Fig. 5
figure 5

Reference and actual tip displacement

Full size image

During the docking operation, every change in position of the floating body has greater significance on force and torque applied on links and joints, respectively. The proposed control methodology is robust for any shape and movement of the floating object. It has been considered that there may be some rotation and translation of free-floating body during the docking operation. Figure 6(a) and Fig. 6(b) demonstrates the rotation and translation of the rectangular floating body, respectively.

Fig. 6
figure 6

Rotation and translation of the free-floating body of PID-controlled 2RPR systems having amnesia recovery control

Full size image

In Fig. 7(a), Xtip1 error deviates from -1.18 × 10–3 to 1.1 × 10−3 m, while Ytip1 error deviates from -1.19 × 10–3 to 2.0 × 10−3 m. In Fig. 7(b), Xtip2 error deviates from -1.17 × 10–3 to 1.5 × 10−3 m, while Ytip2 error deviates from −2.0 × 10–3 to 1.99 × 10−3 m. From the tip trajectory (Fig. 5) and tip error (Fig. 7), it is detected that error in PID controller 2RPR is owing to non-holonomic characteristic of space manipulator. However, with Amnesia controller the errors between the reference and the actual trajectory are reduced to 0.002 m as shown in Fig. 7(a) and Fig. 7(b).

Fig. 7
figure 7

Error amid the reference and the actual tip displacement of the 2RPR systems with PID and amnesia controller

Full size image

After the simulation, the animation is obtained by using SYMBOLS SHAKTI software’s animator tool. By creating frames at different times lag, during the animation, the total docking operation is observed. Animation of the two redundant planar robots (RPR) docking a rectangular floating body is depicted in Fig. 8.

Fig. 8
figure 8

Animation outcomes of the two RPR, handling a floating object

Full size image

4 Optimum Tuning of Gain Parameters using Genetic Algorithm (GA)

The noticeable trajectory error is observed in Fig. 7, even with the integration PID and amnesia controller. Hence, it is desired to minimize error further for enhancing dynamic stability of robot. For this purpose, optimum tuning of gain parameters using genetic algorithm (GA) is implemented in this section.

4.1 Overview of Genetic Algorithm (GA)

J. P. Holland first suggested the fundamental concepts of GA [45]. The technique was inspired by the natural selection mechanism, a biological phenomenon in which the winners in a competitive system are likely to be stronger individuals. In order to solve extremely complex problems, GA uses a simple comparison of such natural evolution to global optimization. It suggests that an entity may be described by a collection of parameters and is a potential solution to a problem. These parameters are known as chromosomal genes and can be organized by a string of concatenated values. The encoding scheme determines the type of representation of variables. The variables may be represented, depending on the application data, by binary, real numbers or other types. The problem typically defines the scope, or search space. Genetic Algorithms (GAs) are a stochastic global search approach that replicates the process of natural evolution [46]. To arrive at the best solution, evolution operators such as mutation, reproduction, and crossover are used.

GA starts with a single chromosome and evaluates its fitness value. The best chromosomes are chosen as parents, and they are repeated, crossed over, and mutated. Each repeat of this method is referred to as an iteration. GA is often iterated from 0 to 500 iterations or more. A run refers to the entire set of iterations. The flowchart functioning of genetic algorithm (GA) based PID controller is depicted in Fig. 9.

Fig. 9
figure 9

Implementation of GA algorithm

Full size image

4.2 Genetic Algorithm as an Intelligent Agent

Some of the characteristics of GA as an intelligent agent are as follows:

  1. i.

    The GA's strength is the continuous approach of searching for optimum parameters.

  2. ii.

    GA necessitates recombination because it consents for the expansion of original solutions that are advanced from their parent’s success.

  3. iii.

    Crossover seeks to improve offspring solutions by eliminating undesired components, however the unpredictable nature of mutation is much more capable of damaging rather than strengthen a robust offspring solution.

  4. iv.

    By restricting the reproduction of weak offspring, GA removes not just that solution, but all of its descendants as well. As a result, after a few iterations, the GA meets to superior solutions.

Unlike traditional gradient techniques, GA allows you to minimize functions by employing a group of search agents. The agents explore with two major operators: crossover and mutation. GA, like all other random-search oriented optimization algorithms (Simulated Annealing, Cross-Entropy, and so on), does not need any knowledge of the structure of the function to be improved and treats it as a Black Box. In contrast to the particle swarm optimization (PSO) algorithm, GA can optimize the values of the related run parameters, notably the PID gain parameters ( Kp, Ki and Kd), PD gain parameters (\(K_{p2}\; \rm{and}\;K_{d2}\)) in nth iteration. Hence, after performing these tasks GA then minimizes trajectory tracking error between reference and actual trajectory.

4.3 Optimization of End-effector Trajectory

The error between reference and actual trajectory is minimized to enhance the positional accuracy of end-effector in X and Y direction. The objective function is formulated and implemented in MATLAB environment based on GA approach.

The formulation of objective function is shown as

$$ \,e(t) = e^{{ - t_{a} t}} \int\limits_{{t_{i} }}^{t} {e^{{ - t_{a} \delta }} \left[ {(X_{refn} - X_{tipn} ) + (Y_{refn} - Y_{tipn} )} \right]} $$
(45)

In the X and Y directions, (\(X_{refn}\),\(Y_{refn}\)) and (\(X_{tipn}\),\(Y_{tipn}\)) denote the robot reference and actual tip (n = 1 for robot 1 and n = 2 for robot 2), respectively. \(t_{a}\) stands for time constant, ti for the docking operation initial time, t is arbitrary time taken throughout the docking operation and e(t) denotes trajectory error.

The required parameters for executing genetic algorithm are given in Table 2. Table 2 shows the presence of five parameters to be optimized.

Table 2 Inputs to the GA
Full size table

Table 2 shows the results of sensitivity analysis on factors such as population size, crossover probability, and mutation probability. The parameters of GA would depend on the formulation of specific problem. So, in general, the best way to determine the probability is to perform a sensitivity analysis, which entails running multiple runs of the algorithms with different probabilities, such as 0.1, 0.2,.., 0.9 and different population sizes, and comparing the results. For more complicated search spaces, a higher crossover probability (> 0.5) will aid in the initial search. However, as time goes on, it should be reduced to a value close to 0.1 or 0.2. Normally, mutation probabilities should be kept as low as possible (0.01–0.1), or else convergence could be unnecessarily delayed. To achieve the convergence criterion, 150 iterations are used. The upper and lower bounds are given for the optimization of the optimized PID and PD controls are determined by trial-and-error method.

Taking into consideration the subsequent parameters shown in Table 2 in the GA, the numerical values of gain parameters are evaluated by manual tuning as shown in Table 3.

Table 3 Gain parameters
Full size table

The procedure of calculating these parameters are as follows,

  1. i.

    Set Ki and Kd to zero, then increase kp until the system converges to the setpoint rapidly and with little overshoot. There is no need to set Ki or Kd if the system acts well enough.

  2. ii.

    Set Kp to half the value of Kp at which the system oscillates if the proportional controller was not good enough, then raise Ki until the process increases rapidly enough and oscillates around the setpoint. There is no need to set Kd if the oscillations fade down quickly enough.

  3. iii.

    Increase Kd until the oscillations are no longer visible.

We acquire the numerical values of Kp, Ki and Kd over 150 generation from Table 2. Table 3 represents the value of gain parameters calculated from generations (0–150).

Table 4 shows the outcomes of the GA. The total number of runs is considered to be six. The convergence reached in 65 iterations. The least error i.e., 0.0012 m is obtained at 3rd runs. As a result, the values of associated run parameters, such as PID and PD gain parameters, are optimized.

Table 4 Results of GA
Full size table

In Fig. 10(a), Xtip1 error differs from -1.1 × 10–3 to 1.12 × 10−3 m, while Ytip1 error differs from -0. 89 × 10–3 to 1.10 × 10−3 m. In Fig. 10(b), Xtip 2 error differs from -1.19 × 10–3 to 1.12 × 10−3 m, while Ytip2 error differs from -1.8 × 10–3 to 1.02 × 10−3 m. It is observed that with Amnesia recovery control the errors between the reference and the actual trajectory are reduced to 0.0012 m as shown in Fig. 10(a) and Fig. 10(b).

Fig. 10
figure 10

Error amid the reference and the actual tip displacement of the 2RPR systems with PID and Amnesia controller (using GA)

Full size image

It is observed that convergence reached in 65 generations. The least error i.e., 0.0012 m is obtained at 3rd runs which stipulates that our research work is competent in following ways:

  1. i.

    The least error i.e., 0.0012 m at 3rd run indicates that there is less deviation between reference and actual trajectory. The end-effector achieves the desired pose with minimum error from reference path with controlled position and orientation tip of the robot.

  2. ii.

    Fig. 5(a) and (b) illustrates the deviations between the actual and reference values, demonstrating the significant difference when simply a PID controller is used. This undesirable inaccuracy is caused by the space manipulator non-holonomic characteristic and increased mobility due to excess DOF. As a result, achieving the required trajectory becomes extremely challenging. As a result, the Amnesia controller is utilized in conjunction with the PID controller to compensate for deviations between the reference and actual trajectories. Because of the Amnesia controller, the acquired results are quite near to the reference trajectory, as illustrated in Fig. 5(c) and (d).

  3. iii.

    Prior to optimization, the error between the reference and actual tip displacement of the two RPR systems with PID and Amnesia controller was 0.002 m (Fig. 7), but it was reduced to 0.0012 m after optimization (Fig. 10). As a result of Table 4 and (Fig. 7 and Fig. 10), a 40.00% reduction in error was observed with optimal trajectories and control parameters. The reduced error is 0.0012 m, whereas the non-optimized error is 0.002 m. As a result, the error percentage equals (0.002–0.0012/0.002) *100 = 40%.

Hence, the suggested control approach tends to limit the movement of the floating body from its initial position to the desired position in a certain period while causing the base to dislocate as little as possible. Error propagating to the tip of the robot is greatly reduced as a result of control over base movement.

5 Comparison of the Present Work with Existing Works

According to a review of the literature, the authors [41, 47, 48] appear to have focused on trajectory tracking and made utilization of the non-holonomy of space robots. Several of them also utilized dual-arm with 3 or 4DOF, with one arm dealing with a floating body and the other eradicating trajectory tracking error [49, 50]. To overcome non-holonomic restraints, a dynamic model of a space manipulator was created using the binocular stereo vision feedback approach [51, 52]. This feedback method generates 3D geometric information about the floating body by combining multiple images. However, the real trajectory tracking and base disturbance are not investigated in this work using simulation data. Huang et al. [53] examined the cooperative manipulation of an inflexible passive body in orbit by a space robot utilizing a unique controller designed on back-stepping and Lyapunov stabilization. They also emphasized its dependability, durability, and strength. A 3D system's motion, on the other hand, is substantially more intricate. Zong et al. [54] proposed an optimal trajectory planning strategy for regulating the coupled system, i.e., the spacecraft and floating object, with the least magnitude of attitude disturbance. The coupled system's mass properties and overall momentum change when the target is captured. It destabilizes the system. Meng et al. [55] developed a position and force control approach for a dual-arm space manipulator with minimal internal force. The advantage of zero internal force control is that it saves fuel when in use. Nevertheless, because their method relies on coordinated dynamic control, no specific controller was used to solve the system's nonholonomy. As a result of this, the simulation results reveal a considerable trajectory error (0.007 m).

We intended to propose the strategy for cooperative manipulation of redundant planar robot to address all these issues mentioned above as.

  1. i.

    In our proposed approach, 2RPR robots would interact with a floating body and provide steady grasping. As a result, the suggested approach may be even more stable than dual-arm space manipulator because the disturbances induced by a floating body and manipulator arm motion are balanced among both robots.

  2. ii.

    Tip trajectory error is caused by disturbances in the manipulator base. As a result, in the suggested technique, a tip trajectory with reduced error (0.005 m) may be seen if only a typical PID controller is used. Furthermore, any remaining errors (0.002 m) may be totally eliminated utilizing Amnesia recovery control, which controls the space robot non-holonomy. As a consequence, simulation and animation results satisfactorily verify the suggested control approach.

  3. iii.

    During the docking operation, any change in position of the floating body has a greater impact on the force and torque imparted to the links and joints, respectively. The suggested control methodology is resilient for any shape and movement of the floating object.

  4. iv.

    In contrast to prior work based on cooperative manipulation of redundant space robots, our technique relied on GA to find optimal parameters. In the nth iteration, the values of the related run parameters, notably the PID gain parameters ( Kp, Ki and Kd), PD gain parameters (\(K_{p2}\; \rm{and}\;K_{d2}\)), may be optimized using GA. As a consequence, once these tasks are completed, GA lowers the difference of trajectory tracking error between the reference and actual trajectories. Hence, 40.00% reduction in error with optimum trajectories is detected. Mathematically, the optimized error is 0.0012 m, whereas the non-optimized error is 0.002 m. As a result, the error percentage is calculated as (0.002–0.0012/0.002) *100 = 40%.

6 Conclusion and Discussion

A controller strategy for dynamic control of two redundant planar manipulators (RPR) has been developed for docking operation. The eight-links 2RPR are modeled and simulated for docking the rectangular floating body. The result of computer simulation shows that the docking operation of only PID controlled 2RPR is not the accurate trajectory but after the introduction of PID and Amnesia removal, it is achieved with minimized error in consideration to the concern with complexity of dynamics of this RPR. Furthermore, GA is applied as an intellectual agent for choosing the optimum probable values of parameters that reduces 40% error between the reference and the actual tip displacement of the 2RPR systems. The rotation of a floating rectangular body is reduced to the minimum extent because of PID and Amnesia control. The proposed control strategy is compared with the existing works. Furthermore, the proposed control approach will be expanded to accomplish the required trajectory by more precisely managing and switching over various joints. The structure constrained flexibility to the robot will be rendered by the proposed model of 2RPR. Collision avoidance while docking operation will be achieved through the proposed control methodology.