1 Introduction

Ground settlement due to tunnel construction requires a reliable analysis technique, in which several factors are involved, such as geological conditions, the geometry of the tunnel, construction method, and depth of the tunnel. The tunnel construction results in transverse and longitudinal ground surface settlements, which can be analysed using several analytical, empirical, and numerical methods [1,2,3,4,5,6,7,8,9,10,11,12].

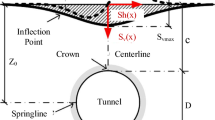
The empirical assessment based on the normal distribution curve under green-field conditions proposed by Peck [1] and Schmidt [2] is an effective assessment technique adequately modelling the transverse settlement trough as verified by numerous centrifugal tests along with field observations [13]. Peck's [1] empirical method to analyse the ground deformation and to assess the settlement profile is presented in Eq. 1, and the normal distribution curve is illustrated in Fig. 1.

$${S_{v\left( y \right)}} = \;{S_{\max }}{e^{\left( { - \frac{{x^2}}{{2{i^2}}}} \right)}}$$
(1)

where \({S}_{v(y)}\) is the vertical settlement corresponding to horizontal distance from tunnel centreline, \(x\); \({S}_{max}\) is the maximum settlement at the tunnel centreline, and \(i\) corresponds to the inflection point of the settlement curve. The \({S}_{max}\) is described as directly proportional to volume loss \(\left({V}_{L}\right)\) and tunnel radius \((R)\) and inversely proportional to the inflection point \(\left(i\right)\) as provided in Eq. 2.

$${S_{{\text{max}}}} = \;1.252\;\frac{{{V_L}\;{R^2}}}{i}$$
(2)
Fig. 1
figure 1

Gaussian settlement curve [1]

Full size image

The precise estimation of \(i\) and \({V}_{L}\) is required to predict the settlements, which are a function of geological conditions and tunnelling methods. The surface settlement occurs due to the convergence of the ground into the tunnel as stresses are released due to excavation. Such convergence of tunnel is referred to as ground or volume loss. The volume loss usually occurs due to soil movement into the gap between the shield and surrounding soil due to overcutting and is significant in soft grounds [14]. However, volume loss can be controlled with the use of the tunnel boring machine (TBM) or other support measures ensuring the stability of the ground [15]. Based on the tunnelling methods such as open-face tunnelling in soft clays, Mair [16] suggests that \({V}_{L}\) varies between 1 and 3%, while, using Earth Pressure Balance Machine (EPBM), the \({V}_{L}\) is indicated to be relatively low, whereas the suggested values for sand are 0.5%. However, in shield tunnelling, the \({V}_{L}\) prediction difficulties still arise due to ground disturbance, face loss, over-excavation, pitching, and tail void closure [17]. Therefore, in shield tunnelling, to avoid differences between predicted and actual volume loss (actual volume loss due to internal deformation of the tunnel during tunnelling), three main aspects such as face loss, shield loss, and tail loss are considered [18]. Based on all the factors combined, in Table 1, the standard practice in ground loss estimation is summarized [17]. The estimation of volume loss in the tunnelling process is presented in Eq. 3 [14].

$${V_L} = {V_{L,f}} + {V_{L,s}} + {V_{L,t}} + {V_{L,c}}$$
(3)

where \({V}_{L,f}\) corresponds to tunnel face volume loss, \({V}_{L,s}\) is the volume loss occurring along the shield, \({V}_{L,t}\) is representing volume loss at the tail, and \({V}_{L,c}\) is volume loss due to consolidation. \({V}_{L,f}\) can be obtained as proposed by Macklin [18] given in Eq. 4. In this equation, \(LF\) is the load factor that can be obtained as suggested by O’Reilly [19] as given in Eq. 5.

$${V_{L,f}}\left( \% \right) = 0.23\;{e^{\;4.4\;LF}}$$
(4)
$${\text{LF}} = \;\frac{N}{{N_C}}$$
(5)
Table 1 Closed face machines volume loss factors [17]
Full size table

In Eq. 5, \(N\) is the stability number for cohesive soils obtained based on the work by Broms and Bennermark [20] for open excavations, which is defined by Mair and Taylor [21], as presented in Eq. 6. The collapse stability number \(({N}_{C})\) as presented in Eqs. 7 and 8 is defined by Mair and Taylor [21].

$$N = \;\frac{{Z\;{\gamma_n} + {\sigma_s} - {\sigma_T}}}{{c_u}}$$
(6)
$${N_C} = 2 + 2{\text{ln}}\left( {\frac{2C}{D} + 1} \right)\;\;\;\left( {{\text{For}}\;\;0\; \leqslant \frac{C}{D} \leqslant 1} \right)$$
(7)
$${N_C} = 4{\text{ln}}\left( {\frac{2C}{D} + 1} \right)\;\;\;\left( {{\text{For}}\;\;1\; \leqslant \frac{C}{D} \leqslant 1.8} \right)$$
(8)

where \(Z\) is the depth to tunnel centreline, \({\gamma}_n\) is the soil natural unit weight, \({\sigma_s}\) represents soil surcharge, \({\sigma_T}\) corresponds to TBM face pressure, \(c_u\) is the undrained cohesion, and \(C\) is the depth to tunnel crown. In addition, another parameter critical stability ratio (tunnel cover depth to diameter ratio, \(C/D\)) is also required to be taken into consideration [22, 23]. The \(N\) factor indicates the tunnel face stability, while \(C/D\) represents stability state due to the depth effect (i.e. if \(C/D < 2\) requires detailed stability investigation).

On the other hand, volume loss along the shield \(({V}_{L,s})\) is related to the cutting wheel (in front of TBM), and it might lead to overcut during tunnelling as the cutting wheel is often larger than the diameter of the shield. The estimation of \({V}_{L,s}\) is presented in Eq. 9 [23].

$${V_{L,s}}\left( \% \right) = \frac{4\delta }{D}{\;\times}\;100$$
(9)

where \(\delta\) corresponds to an average thickness of the overcut. For volume loss estimation at the tail \(({V}_{L,t})\), the \({V}_{L,t}\) occurs due to the surface settlement because of grouting pressure \(({V}_{s,t})\) as illustrated in Eq. 10 [14].

$${V_{L,t}} = \frac{{{V_{s,t}}}}{{\pi {{\left( \frac{D}{2} \right)}^2}}}$$
(10)

Similarly, the consolidation settlement \({(V}_{L,c})\) is estimated as described in Eq. 11 [14].

$${V_{L,c}} = \frac{{{V_{{\text{cons}}}}}}{{\pi {{\left( \frac{D}{2} \right)}^2}}}$$
(11)

where \({V}_{cons}\) corresponds to the volume of consolidation settlement and is calculated as shown in Eq. 12.

$$V_{{\text{cons}}} = \mathop \sum \limits_{{j = 1}}^{n} u_{c}^{j} \Delta x$$
(12)

where \({u}_{c}^{j}\) is the consolidation settlement, which is estimated using Terzaghi’s one-dimensional consolidation theory.

For cohesionless soils, theoretically, the tunnel face is not stable. The factors influencing the instability of the tunnel face are difficult to evaluate as limited data are available [24]. The tunnel face stability in cohesionless soils, as described by Lee and Rowe [25], is also affected by changes in geology and anisotropy in elastic parameters of the ground. On the other hand, in saturated sand, a slight cohesion can be generated due to capillary tension (or temporarily in a partially saturated state), which might contribute to the stability factor [24]. For stability in cohesionless soils, studies related to centrifuge experiments and physical modelling are available, and relationships are established to evaluate the possible face instabilities [26,27,28]. In Table 2, based on the experimental, field, and theoretical data, the conditions related to the tunnel face instability for cohesive and cohesionless soils are summarized [24, 26].

Table 2 Tunnel face instability conditions and requirements
Full size table

Similarly, several relationships are available in the literature based on field observations and laboratory testing to estimate the inflection point, such as the one given in Eq. 13 [1, 29].

$$i = K\;Z$$
(13)

where \(K\) corresponds to the trough width parameter, and \(Z\) is the depth to the tunnel centreline. Equation 13 is developed for homogenous strata and is a function of tunnel depth. The \(K\) value is independent of the tunnelling method and diameter; however, it is dependent on the soil type, as stated by Mair and Taylor [21], who provide that \(K\) varies in the range of 0.4–0.6 for clayey soils. Similarly, for sandy soils, \(K\) is stated to vary in the range of 0.25–0.45. Various other researchers have also reported inflection point equations as listed in Table 3.

Table 3 Inflection point estimation equations
Full size table

Nowadays, the prediction of tunnelling-induced settlements by closed-form empirical relationships under green-field conditions is still considered an effective method, especially during planning or preliminary design stages. Green-field predictions are effective in terms of obtaining a quick estimation of the impact of tunnelling, which can be improved with field monitoring or further analysis using more sophisticated tools such as continuum methods (finite element method, FEM; finite difference method, FDM; and boundary element method, BEM), discontinuum methods (discrete element method, DEM; discontinuous deformation analysis, DDA; and particle flow method, PFC), or hybrid continuum/discontinuum methods. Depending on the construction technique of a particular tunnel, it is necessary to understand the concept of ground behaviour, especially in terms of geological assessment. Two terminologies are widely adopted in this case, such as soft and hard ground [11, 16, 31, 34, 38,39,40,41]. As the names imply, the stiff ground is referred to ground conditions that are stiff enough to carry out the construction of the tunnel without any additional supports and vice versa for soft grounds [42, 43].

The primary aim of this research is to provide a generalized assessment technique for the prediction of maximum ground surface settlement and a preliminary analysis of ground settlement profile due to tunnelling in various soil types.

2 Research Methodology

The surface settlement in different soil types were modelled in Plaxis 2D finite element program. The research strategy for FEM modelling steps and the analysis approach to establish the settlement prediction equation are illustrated in Fig. 2. A total of 1672 models (418 models for each soil type) were established and analysed. The modelling procedure of every numerical model was based on the steps described in the following subsections.

Fig. 2
figure 2

Research strategy and FEM simulation analysis flowchart

Full size image

2.1 Model Geometry

The FEM simulation in Plaxis 2D was carried out by modelling the tunnel in homogenous and isotropic strata. The boundary conditions were considered by taking into account that there will be no boundary effect on the influence zone developed due to tunnel modelling. The horizontal boundary condition was considered as a maximum of approximately 3 times the tunnel diameter with full fixity conditions (\({u}_{x}={u}_{y}=0)\). The vertical boundary condition was considered as 5 times the tunnel diameter for every analysis with horizontal fixity \(({u}_{x}=0)\). In Fig. 3, the model geometry of tunnel diameter of 6.3 m at a depth of 19 m is illustrated as an example.

Fig. 3
figure 3

Plaxis 2D FEM simulation model

Full size image

2.2 Material Properties

The soil parameters for different soil types obtained from parametric studies are tabulated in Table 4 [42, 44,45,46,47,48]. In all soil models, the Mohr–Coulomb (MC) model was considered with drained analysis for cohesionless soil and undrained analysis (using effective stress parameters) for cohesive soils. The MC model is a first-order linear-elastic-perfectly plastic model to express the stress–strain behaviour, and thus, no hardening or softening occurs (Fig. 4). The elastic part of the MC model is based on Hooke’s law (isotropic elasticity), and the failure criterion represents the plastic part. The MC model requires 5 input parameters, two of which are stiffness parameters, i.e. Young’s modulus (\(E\)) and Poisson’s ratio (\({\upnu }\)), and three strength parameters, i.e. friction angle (\(\phi\)), cohesion (\(c\)), and dilatancy angle (\(\psi\)). The boundary between elastic and plastic behaviour is the yield criteria which is a stress–strain function. Another aspect of the MC model is that the irreversible strains are developed in plastic behaviour, and these strains are reversed when the unloading of stress occurs [42]. Since the selection of constitutive model in numerical simulation greatly influences the deformation characteristics of soil, advanced constitutive models are also available in Plaxis software (e.g. hardening soil, HS model), which provides in-depth details of soil deformation. The selection of the MC model was considered due to the absence of HS input soil parameters in two selected soil types from the literature, i.e. soft clay and loose sand [44, 48]. Due to this aspect, the Mohr–Coulomb model was implemented for all soil types for comparison purposes so that the primary working principle of MC model analysis can be compared based on the soil input parameters.

Table 4 Plaxis 2D input soil material properties data set
Full size table
Fig. 4
figure 4

Modified from Möller [42])

Mohr–Coulomb model basic ideas for a linear elastic-perfectly plastic materials and b principal stress space yield surface for \({c}^{^{\prime}}=0, {\phi }^{^{\prime}}={30}^{0}\) (

Full size image

The post-soil modelling involved the modelling of tunnel lining at varying depths by taking into consideration the boundary conditions as discussed earlier. In all soil types models, 3 different tunnel diameters 6.13, 6.3, and 8.3 m were considered with varying depths of 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, and 31 m. The tunnel lining was represented by the elastic plate element and was simulated as a bored tunnel. The details of the tunnel lining parameters obtained from parametric studies are tabulated in Table 5 [42, 44, 46, 47].

Table 5 Plaxis 2D input tunnel lining properties data set
Full size table

2.3 Mesh Generation

The post-modelling of soil and tunnel lining involved generation and optimization of the mesh size. In Fig. 3, the mesh was generated throughout the model, and all models consist of 15-node elements. The mesh was refined at the tunnel lining and inside the tunnel cluster due to stress concentration in the tunnelling area. After mesh generation, initial conditions involved the generation of water pressure and initial stresses. The water pressure was generated based on the general phreatic level at the ground surface (\(Z=0\)) with a unit weight of water as 10 \(kN/{m}^{3}\). Note that the effect of the groundwater table variation was not taken into consideration in this study; therefore, the groundwater table was set at \(Z=0\) in all models.

2.4 Initial Conditions

In numerical modelling, especially in underground tunnelling, the geostatic initial stresses are evaluated before modelling the tunnel as a starting point since the ground is not in stress-free conditions [42]. The initial effective stresses were generated based on the \({K}_{o}\) procedure, and before the generation of initial stresses, the tunnel lining was deactivated. The \({K}_{o}\) value for each soil type was considered based on Jáky’s formulation [49] as given in Eq. 14.

$${K_o} = 1 - {\text{sin}}\left( {\phi ^{\prime}} \right)$$
(14)

where \({K}_{o}\) is the coefficient of lateral earth pressure at rest and \({\phi }^{^{\prime}}\) is the angle of internal friction of soil.

2.5 Simulation Procedure

The post-finite element modelling steps included the execution of finite element calculations. The tunnelling-induced surface settlement was analysed by activation of tunnel lining, and then, contraction was applied at the centre of the tunnel with varying \({V}_{L}\) percentages. The \({V}_{L}\) percentages were set as 0.1, 0.25, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 4.0, 5.0, and 6.0 for varying tunnel diameters and depths. The \({V}_{L}\) values were considered as theoretical total volume loss and considered in correspondence with the cases mentioned in Table 1 as if these cases will occur. The contraction method is applied to simulate the soil volume loss due to shield tunnel construction. The contraction method involves the reduction of tunnel cross section area and is expressed in terms of ratio as provided in Eq. 15. In addition, the pre-assigned total contraction is achieved through stepwise uniform contraction of tunnel lining.

$${\text{Total\,contraction}} = \,\frac{{{\text{Tunnel\,original\,area}} - {\text{Tunnel\,area\,at\,current\,step}}}}{{{\text{Tunnel\,original\,area}}}}$$
(15)

Before contraction, the tunnel excavation was simulated by removal of soil inside the tunnel lining through soil element deactivation and activation of the tunnel lining afterwards. The excavation procedure was based on a full-face excavation sequence (bored tunnels), and the staged excavation sequence, which is generally considered for the New Austrian Tunnelling Method (NATM), is not applied. In terms of pore pressure distribution, the cluster dry condition was selected in water pressure mode after the deactivation of the soil element inside the tunnel. The negative interface was activated around the tunnel as a standard approach available in Plaxis software. After obtaining the settlement profile, the maximum settlement and the inflection point values were selected for prediction charts, and the equations were developed for different soil types. In addition, in Table 6, the type of element and integration for soil, plate (tunnel lining) and the interface are summarized.

Table 6 Summary of numerical modelling type of element and integration
Full size table

3 Results and Discussion

The FEM simulation results to analyse the parameters affecting maximum settlement \(\left({S}_{max}\right)\) are presented in Figs. 5 and 6 relating to \({V}_{L}\) and diameter-to-depth ratio \(\left(D/Z\right),\) respectively. It is observed from Fig. 5 that the maximum settlement can be related to the \({V}_{L}\) linearly and a nonlinear relationship was observed for depth \(D/Z\) (Fig. 6). Combining both aspects, it was observed that the intensity of settlement in all soil types is beyond \({V}_{L}\) > 3% and \(D/Z\) > 0.35. This indicates that for tunnels which exceed these conditions, detailed analyses shall be carried out regarding stability and support conditions. Therefore, by combining the observed behaviours in terms of \({V}_{L}\) and \(D/Z\), in Fig. 7, a multivariable plot was established. Another aspect observed in Fig. 7 is that tunnels modelled at lower depths (\(D/Z\) = 0.82–0.92) resulted in much greater settlements as expected due to the absence of sufficient ground cover. Combining the observed relationships, a nonlinear power function can be established, as illustrated in Eq. 16.

$$\frac{{{S_{{\text{max}}}}}}{Z} = \;\alpha \;{V_L}\;{\left( \frac{D}{Z} \right)^\kappa }$$
(16)

where \(\alpha\) and \(\kappa\) are fitting coefficients and \({V}_{L}\) is in terms of ratio. Based on the modelled soil parameters, in Table 7, the values of \(\alpha\) and \(\kappa\) are listed for different conditions analysed. Note that the validity of Eq. 16 was developed ranging between \(D/Z\) of 0.198 – 0.922 and for \({V}_{L}\) as described in the methodology section. The nonlinear relationship obtained in Eq. 16 is only dependent on the volume loss, and the inflection point parameter is replaced with fitting coefficients. The proposed relationship was further used to produce a settlement prediction chart, as presented in Fig. 8.

Fig. 5
figure 5

Volume loss effect on the settlement of a soft clay, b stiff clay, c loose sand, and d dense sand with respect to depth

Full size image
Fig. 6
figure 6

Variation of settlement with respect to D/Z for a soft clay, b stiff clay, c loose sand, and d dense sand

Full size image
Fig. 7
figure 7

Normalized multivariable variations for settlement versus volume loss and depth a soft clay, b stiff clays, c loose sand, and d dense sand

Full size image
Table 7 Fitting coefficients based on the analysis performed
Full size table
Fig. 8
figure 8

Settlement prediction chart

Full size image

The advantage of the proposed relationship and prediction chart (Fig. 8) is that the maximum settlement can be estimated by reducing the preliminary analysis time required; therefore, a quick estimation of \({S}_{max}\) can be carried out before proceeding with advanced FEM modelling and detailed monitoring aspects in projects. In addition, since volume loss is dependent on ground conditions and tunnelling method, if any changes during construction occur, \({S}_{max}\) can be directly estimated. Considering the total volume loss (Eq. 3), since all the components of volume loss are time-dependent (such as face stability, applied grouting pressure, post grouting pressure stress relief, installation time of tunnel linings, or stoppage time of the machine), if they are prolonged, the volume change will also be highly influenced. Thus, a trend can be observed from Fig. 8 that how the maximum settlement will occur based on the changes in \({V}_{L}\). Although in Eq. 2, the inflection point parameter can also be established based on the equations provided in Table 3, therefore a detailed comparison is held in Sect. 5 considering the maximum settlement obtained with Eq. 16.

Since the excavation of the tunnel causes a redistribution of stresses, in Fig. 9, the redistribution of effective vertical stress \(\left({\sigma }_{v}^{^{\prime}}\right)\) in soft clay at the tunnel crown is illustrated. Given that a total of 1672 numerical models were established for different soil types, therefore, in Fig. 9, the variation of \({\sigma }_{v}^{^{\prime}}\) at selected depths (7 m, 13 m, 17 m, and 25 m) for 6.13 m tunnel diameter in soft clay is presented. As observed, the redistribution of \({\sigma }_{v}^{^{\prime}}\) at tunnel crown \(\left(C\right)\) at shallow depths is quite significant and with an increase in \({V}_{L}\), the \({\sigma }_{v}^{^{\prime}}\) is condensing, resulting in greater surface settlement (Fig. 9-a). Such an aspect indicates that in order to ensure the stability of the tunnel, stiffer tunnel linings or additional tunnel support must be considered. In addition, with an increase in tunnelling depth, the \({\sigma }_{v}^{^{\prime}}\) is primarily affected near the tunnel crown (Fig. 9, b-d). Therefore, in Fig. 10, the normalized vertical effective stress \(\left({\sigma }_{v}^{^{\prime}}/{\sigma }_{v,o}^{^{\prime}}\right)\) with respect to \({V}_{L}\) is presented. From Fig. 10, the rate of stress redistribution in clay and sand differs significantly, and the reduction in stresses in the sand is higher as compared to clay, especially at lower \({V}_{L}\). Such phenomenon also directs to the explanation of higher surface settlement occurrence in sand, as observed in Figs. 5 and 8. In addition, in Fig. 10, it is observed that the \({V}_{L}\) is directly associated with the change in stresses at the tunnel crown and thus the settlement values as observed in Figs. 5 and 8. Since the proposed Eq. 16 is based on 3 input parameters, the \({V}_{L}\) can be interpreted based on the combined observations. Therefore, it is recommended that redistribution of stresses in relation with \({V}_{L}\) must be checked at tunnel crown upon utilizing the proposed Eq. 16. Although the \({V}_{L}\) does correspond to the redistribution of stresses, in Fig. 11, the \({S}_{max}\) values of the selected tunnel dimension and depths show approximately similar behaviour in correspondence with redistribution of \({\sigma }_{v}^{^{\prime}}\) at the tunnel crown.

Fig. 9
figure 9

Variation of effective vertical stress with depth in soft clay a Z = 7 m, b Z = 13 m, (c) Z = 17 m, and (d) Z = 25 m

Full size image
Fig. 10
figure 10

Redistribution of normalized vertical effective stress in a clay and b sand with respect to \({V}_{L}\)

Full size image
Fig. 11
figure 11

Redistribution of normalized vertical effective with respect to \({S}_{max}\) in a clay and b sand

Full size image

4 Depth Effect on the Infection Point

Figure 12 illustrates the effect of depth variation on the location of the inflection point. The illustration in Fig. 12 is provided for the volume loss of 1% and the tunnel diameter of 8.3 m for soft and stiff clays along with loose and dense sands. It was observed that the tunnels analysed in sandy soil resulted in a steeper hogging region regardless of the state as compared to clayey soil at lower depths, and on the contrary, the influence zone at the ground surface in sands due to tunnelling was also lesser in comparison with clays under same volume loss and diameter. Similar behaviour was observed for other volume loss and diameters. In addition, in Fig. 12, the inflection point obtained from Eq. 13 [1, 29] is plotted by taking into consideration \({K}_{\mathrm{mean}}\) = 0.5 for cohesive soils and \({K}_{\mathrm{mean}}\) = 0.35 for cohesionless soils [21, 29, 42]. For soft clays (Fig. 12-a), the inflection points obtained in FEM simulation are quite similar to the \(i\) values obtained by Eq. 13 with a slight difference at lower depths, whereas, in the case of stiff clays (Fig. 12-b), the \(i\) values are similar to FEM values at greater depths (\(Z\) > 23 m) and are closer towards the tunnel centreline. For loose sand, the difference becomes prominent with the increase in depths as the location of \(i\) shifts away from the tunnel centreline (Fig. 12-c). Similar to the stiff clays, the \(i\) values obtained from Eq. 13 for dense sand are plotting closer to the tunnel centreline, and the difference decreases with an increase in depth in context with the FEM \(i\) values (Fig. 12-d).

Fig. 12
figure 12

Tunnelling depth effect on \({S}_{v\left(y\right)}\) and inflection points for a soft clay, b stiff clay, c loose sand, and d dense sand

Full size image

In order to analyse the factors affecting the inflection point, in Figs. 13 and 14, the effect of \({V}_{L}\) and the tunnel diameter is illustrated. As observed from Fig. 13, the \({V}_{L}\) has no relation with the inflection point, and only the tunnel depth is influencing. An interesting point noted in the case of stiff clay (Fig. 13-a) is that, at greater depths (\(Z\) > 23 m), the inflection points are shifting towards the tunnel in comparison with soft clays. Such aspects indicate that tunnel construction in stiff clays might create a lower influence zone compared to soft clays at greater depths, whereas, in terms of the tunnel diameter (Fig. 14), a positive trend was observed as the tunnel diameter also influences the location of \(i\). However, the influence of the tunnel diameter is only prominent at lower depths on the location of \(i\), whereas, at greater depths, the tunnelling depth is more dominant. From the aforementioned observations, the parameters influencing the inflection points for different soil types are illustrated in Fig. 15 as a multivariable plot, and the linear relationship was observed as described in Eq. 17.

$$\frac{i}{Z}\; = \;\beta \;\left( \frac{D}{Z} \right)\; + \;\zeta$$
(17)

where β and ζ are the constants and are tabulated in Table 8 in correspondence with different soils types. Settlement curves obtained for stiff clays yielded a relatively steeper hogging region as compared to other soil types, as presented in Fig. 16. For other soil types, similar curvature was observed in the hogging region. From the aforementioned discussions, it was observed that the diameter and depth primarily affect the inflection point's location; however, the inflection point is also greatly influenced by the magnitude of secondary stress developed due to tunnel excavation. In this aspect, the stress vector plays a significant role in the inflection point location, which defines the geometric characteristics of the surface settlement curve by determining the hogging and sagging regions. In this regard, a detailed investigation is required for the influence of the development of secondary stresses on inflection point location. Therefore, in this research, the tunnel geometries are only considered for comparison purposes with the available inflection point equations (Table 3).

Fig. 13
figure 13

Effect of volume loss on the inflection point a stiff clay, b soft clay, c dense sand, and d loose sand

Full size image
Fig. 14
figure 14

Effect of diameter on the inflection point a stiff clay, b soft clay, c dense sand, and d loose sand

Full size image
Fig. 15
figure 15

Multivariable plot for inflection point a stiff clay, b soft clay, c dense sand, and d loose sand

Full size image
Table 8 Inflection point fitting coefficients for different soils
Full size table
Fig. 16
figure 16

Variation of inflection point with respect to soil types

Full size image

5 Comparison and Validation of Proposed Relationships

The validation of the proposed maximum settlement equation was performed in accordance with different soil types, as illustrated in Fig. 17. The validation assessment showed a good congruence with maximum field settlement \({(S}_{\mathrm{max},\mathrm{ field}})\) data although a slight overestimation was observed in some cases. The accuracy of the proposed equation ranges is illustrated in Table 9. Note that the \({V}_{L}\) values substituted in Eq. 16 were obtained from corresponding references provided in Table 10. From Table 9, the proposed equation accuracy in all cases on average is approximately 18% compared to field data. On the other hand, due to limited data available for tunnels in loose sands, the proposed equation for \({S}_{max}\) can be validated by future studies. Therefore, care should be taken while utilizing the coefficients of loose sand. The selected field settlements and corresponding proposed equation settlement values are tabulated in Table 10, along with the tunnelling details. Considering the 1:1 ratio line, the stiff clays trendline behaviour is plotting in closest proximity of the line with an average difference of 2.3 mm, whereas for soft clays and dense sands, the trendline behaviour is approximately on 1:1 ratio line with an average difference of 5.0 mm and 2.0 mm, respectively.

Fig. 17
figure 17

\({S}_{\mathrm{max}}\) values comparative validation with \({S}_{max, field}\)

Full size image
Table 9 Accuracy range of proposed \({S}_{\mathrm{max}}\) equation
Full size table
Table 10 Field and calculated maximum settlement values
Full size table

In addition, the \({S}_{max}\) values obtained from Eq. 2 are plotted with respect to \({S}_{max, field}\) which is illustrated in Fig. 18 by substituting \(i\) values from equations tabulated in Table 3. For dense sand (Fig. 18-a), Peck’s equation [1] with \(n\) = 0.8, Cording and Hansmire [31], Arioglu [33]b, and Atkinson and Potts [38] are resulted in correspondence with each other and slightly lower in comparison with \({S}_{max, field}\) values, whereas, with the increase in \(n\) value in Peck’s equation [1], the values are quite lower in comparison and are similar in correspondence with Attewell and Farmer [30], Herzog [32], Glossop [34], Kimura and Mair [22] and Rankin [35]. Whereas Arioglu [33]a equation values yielded very low values, O'Reilly and New [29] resulted in quite high values and Sugiyama et al. [37] slightly higher. For stiff clays (Fig. 18-b), in general, Attewell and Farmer [30], Herzog [32] Arioglu [33]a, Glossop [34], Kimura and Mair [22], O'Reilly and New [29] and Rankin [35] equations yielded similar values to each other and are closer to field values, whereas, with the \(n\) value increment in Peck’s equation [1], values are becoming closer to field values, and Peck’s equation [1] with \(n\) = 0.8, Cording and Hansmire [31], Arioglu [33]b, c, Clough and Schmidt [36], and Sugiyama et al. [37] are overestimating the \({S}_{max}\). For soft clays (Fig. 18-c), with the \(n\) value increment in Peck’s equation [1], the values are becoming closer to field values along with Attewell and Farmer [30] and Arioglu [33]c equations, whereas a scatter trend is observed in Glossop [34], Kimura and Mair [22], and Rankin [35] equations and overestimation is observed for Peck with \(n\) = 0.8 [1], Cording and Hansmire [31], Arioglu [33]b and Clough and Schmidt [36]. For Herzog [32], O'Reilly and New [29], Arioglu [33]a, and Sugiyama et al. [37] equations.

Fig. 18
figure 18

\({S}_{\mathrm{max}}\) values comparison with \({S}_{max, field}\) in accordance with Table 3 equations for a dense sand, b stiff clay, and c soft clay

Full size image

To observe the differences and reasons behind over and underestimation, in Figs. 19 and 20, a comparative analysis is done for cohesive soils based on the inflection point as described in Eq. 17 and the equations provided in Table 3 for cohesive soil and all soil types. For stiff clays (Figs. 19-a and 20-a), it is observed that the inflection points from FEM simulations are obtained in context with Arioglu [33]a equation. On the other hand, Peck’s \(n=1\) [1], Attewell and Farmer [30], Glossop [34], Kimura and Mair [22], Rankin [35], and Sugiyama et al. [37] \(i\) values generated the closest results with FEM values at greater depths \((Z>20 m),\) and the difference becomes more prominent as the tunnelling depths reduces, whereas, at lower depths, the location of \(i\) is closer to the tunnel. For Herzog [32] and O'Reilly and New [29], the \(i\) values are more comparable to FEM values and are parallel. The rest of the equations for cohesive soils and all soil types showed a wide range of differences. In contrast to soft clays (Figs. 19-b and 20-b), quite similar \(i\) values in comparison with FEM results are observed for Herzog [32], whereas, in Peck’s \(n\) = 1 [1], Glossop [34], Kimura and Mair [22], O'Reilly and New [29], Rankin [35], and Sugiyama et al. [37], an increasing trend is observed after \(Z\) > 13 m.

Fig. 19
figure 19

Comparison between FEM and Table 3 inflection points for a stiff and b soft clays

Full size image
Fig. 20
figure 20

Comparison between FEM and Table 3 inflection points with respect to depth for a stiff and b soft clays

Full size image

In terms of cohesionless soil, the comparison is illustrated in Figs. 21 and 22. For dense sand (Figs. 21-a and 22-a), Peck (1969) \(n = 0.8\) [1], Cording and Hansmire [31], and FEM \(i\) values are in close proximity up to \(Z=13 m,\) and beyond that, a slightly increasing trend is observed in FEM values. By substituting \(n=0.9\) in Peck (1969) equation [1], Atkinson and Potts [38], Sugiyama et al. [37], and Arioglu [33]b, a minimal difference is observed with FEM values, and the results are quite similar in both cases and are parallel. Peck (1969) \(n =1.0\) [1], Attewell and Farmer [30], Glossop [34], Kimura and Mair [22], and Rankin [35] yielded higher values, and the difference becomes more prominent as the depth increases. Herzog [32] and Arioglu [33]a are plotting higher and parallel in context with FEM values. A significant difference in O'Reilly and New's [29] equation is observed, resulting in very low values. For loose sand (Figs. 21-b and 22-b), the FEM \(i\) values are in good agreement with O'Reilly and New [29] and Atkinson and Potts [38] equations, whereas the other proposed equations are resulting in higher \(i\) values.

Fig. 21
figure 21

Comparison between FEM and Table 3 inflection points for a dense and b loose sand

Full size image
Fig. 22
figure 22

Comparison between FEM and Table 3 inflection points with respect to depth for a dense and b loose sand

Full size image

Therefore, in the aforementioned comparison discussion, the volume change required to match field settlement values is illustrated in Fig. 23. In Fig. 23, the basis of the analysis was based on back analysing the \({V}_{L}\) required to match \({S}_{\mathrm{max},\mathrm{field}}\). The primary reason for this analysis was to evaluate the underestimation or overestimation of \({S}_{\mathrm{max},\mathrm{field}}\) and Eq. 16. The equations generated the \({S}_{\mathrm{max},\mathrm{field}}\) values in closest proximity were based on equivalent or more than 90% accuracy. The colour coding was based on selecting the mentioned volume loss \({(V}_{L-refs})\) from Table 10 references as the corresponding parameter (mid-value, ≈), the underestimated settlement values that require higher \({V}_{L}\) to reflect the \({S}_{max,field}\) value as highest value (green colour coded, ↑), and for overestimated values to match the \({S}_{max,field}\) value as lowest \({V}_{L}\) value (red colour coded, ↓). Equation 16, in general, resulted in approximately similar \({S}_{\mathrm{max},\mathrm{field}}\) in all soil types by substituting \({V}_{L-\mathrm{refs}}\); therefore, based on the ground conditions, the calculated or estimated \({V}_{L}\) value can be utilized to estimate the potential \({S}_{\mathrm{max}}\) value for preliminary screening provided that detailed investigation should also be taken into account. For dense sand, by substituting \(i\) values obtained from Peck’s equation with \(n\) = 0.8 [1], Cording and Hansmire [31], Arioglu [33]b, and Atkinson and Potts [38] equations, with accurate \({V}_{L}\), the potential \({S}_{\mathrm{max}}\) can be estimated. For Peck’s equation with \(n\) = 0.9 and 1.0 [1], Attewell and Farmer [30], Herzog [32], Glossop [34], Kimura and Mair [22], Rankin [35], and Arioglu [33]a equations, higher \({V}_{L}\) is required, whereas for O'Reilly and New [29] and Sugiyama et al. [37], lower \({V}_{L}\) is required. In terms of stiff clays, Peck’s equation with \(n\) = 1.0 [1], Attewell and Farmer [30], Herzog [32], Arioglu [33]a, Glossop [34], Kimura and Mair [22], O'Reilly and New [29], and Rankin [35] equations, the potential \({S}_{\mathrm{max}}\) can be estimated with accurate \({V}_{L}\), whereas, for the rest of the equations, lower \({V}_{L}\) is required. For soft clays, by substituting \(n\) = 0.9 and 1.0 in Peck’s equation [1], Attewell and Farmer [30], and Arioglu [33]c equations, \({S}_{max}\) can be evaluated with accurate \({V}_{L}\), whereas for Glossop [34], Kimura and Mair [22], and Rankin [35] equation, special care must be taken for \({V}_{L}\) as generally, a scatter trend is observed. For overestimation case, the lower \({V}_{L}\) values are required for Peck \(n\) = 0.8 [1], Cording and Hansmire [31], Arioglu [33]b, Clough and Schmidt [36]. Lastly, Herzog [32], Arioglu [33]a, O'Reilly and New [29], and Sugiyama et al. [37] equations require higher \({V}_{L}\) percentages.

Fig. 23
figure 23

Back analysis for volume loss required to match \({S}_{\mathrm{max},\mathrm{ field}}\)

Full size image

6 Proposed Equations Advantages, Comparison, and Limitations

Considering the discussion as mentioned earlier, the validation and comparison of the proposed \({S}_{\mathrm{max}}\) equation developed through numerical modelling with the field data showed satisfactory performance. However, the estimation of the \({S}_{\mathrm{max}}\) from Eq. 2 can also be obtained. The main aspect in Eq. 2 is the inflection point estimation, and as observed in the previous section, the \({S}_{\mathrm{max}}\) values yielded different results for different inflection point equations in Fig. 18 compared to the field data as presented in Table 10. Such an aspect prompted the question of which equation can be utilized to yield the closest value to \({S}_{\mathrm{max},\mathrm{field}}\). Therefore, in this context, the replacement of the inflection point parameter with the coefficients with respect to soil type in Eq. 16 is done in order to estimate \({S}_{\mathrm{max}}\) so that the uncertainty can be addressed, and the settlement curve can be established afterwards by applying inflection point either by Eq. 17 or approximately similar equation from Table 3. Although the ground settlement can be analysed from the proposed equations, detailed FEM modelling and field monitoring importance still exist since the ground behaviour changes frequently and the application of the proposed equations is for the certain \(D/Z\) ratios of 0.198 – 0.922.

7 Conclusions

Based on the analyses performed in FEM simulations, modelling the single tunnel with varying depth, diameters, and volume loss in soft and stiff grounds was carried out to establish a relationship for quick assessment of maximum field settlement values. Therefore, the following aspects of the research are concluded:

  • The proposed maximum settlement equation was developed based on the FEM simulation by selecting parametric studies' material and tunnel lining properties. The accuracy of the proposed maximum settlement prediction equation was validated using data from the literature on tunnelling in different soil types.

  • On the other hand, due to the lack of sufficient data for loose sand, the proposed equation coefficients for loose sand should be employed with caution. Therefore, based on the performance of the proposed equation compared to the existing literature for dense sand, soft clay, and stiff clay, it can be concluded that the maximum settlement prediction is performed successfully with the help of FEM analysis. For successful predictions in practice, analyses should be supported with field measurements.

  • The prediction chart provided for maximum settlement can be helpful in terms of varying depth, diameter, and volume loss to analyse the changes in ground surface conditions due to time-dependent parameters such as volume loss.

  • In terms of ground behaviour, the influence zone of tunnelling in cohesive soils is greater as compared to cohesionless soils, whereas a steeper hogging zone was observed in cohesionless soils, which are interpreted to be in line with the previous research published on this topic [21, 29, 37, 38]

  • The inflection point analysis based on the diameter, depth, and volume change highlights the significance of the tunnelling depth as a more dominant parameter affecting the location of the inflection point. The tunnel diameter was observed to be effective only at shallow depths, and the volume loss indicated no significant correlation with the location of the inflection point.