1 Introduction

Sun is the most prognosticating renewable energy source and also the ultimate alternative to fossil fuels. The sun light can be converted to electricity by photoelectric effect and to heat through photothermal conversion. Both the photoelectric effect and photothermal conversion processes are being applied to generate electricity using photovoltaic panels and concentrated solar thermal plants. The efficiency of photovoltaic cells and concentrated solar thermal plants can be improved appreciably by increasing the solar absorption. The solar energy efficient absorption and conversion into thermal energy are required to reliably use as renewable source and to reduce the dependence on fossil fuels. However, the absorption of sunlight by collecting panels and heat collector tubes is quite inefficient that causes significant loss of energy. Therefore, water dispersed nanoparticles are being investigated quite extensively to improve the absorption of sunlight. Different research groups have proposed and tested different nanomaterials for increase in absorption efficiency.

Photoactive nanomaterials are proposed to enhance the light absorption capability of polymeric photovoltaic devices. The current polymer photovoltaic devices have active region (bandgap) of around 2-ev to absorb photons. The wider solar energy band absorption above specified bangap can be achieved by adding nanomaterials. Kim et al. fabricated solar cells by employing organic substances as two hemicyanine photosensitizer, and electronic intercessor for n-type titanium dioxide (TiO2) nanotube arrays of varying π-coupling lengths that have wider solar absorption spectrum from visible to near-infrared region [1]. Wild et al. utilized increased light sensitivity of silane (Si–H4) to form a solar up-converter for sub-bandgap light by exciting it with wide spectrum light [2]. Hua et al. examined the possibility of large-size heterojunction solar cells by converting horizontally oriented single-crystalline silicon (c–Si) core/shell into half-coaxial nanowires arrays [3]. Pakhuruddin et al. proposed liquid-phase crystallization of Si films on textured glass with large light quality grain of 27.8 mA/cm2 in solar cells or 36.3% enhancement compared with a planar reference film without light-trapping features [4]. Ishizaki et al. investigated the direct surface etched microcrystalline silicon (μc–Si) photovoltaic cells, where intrinsic microcrystalline layer intensified through raising the coupling of resonant modes of incident light. They reported 11% increase in efficiency for microcrystalline photovoltaic cell composed of intrinsic Si [5]. Chen et al. proposed that a two-dimensional perovskite solar cell (PSC) with absorption efficiency reaches 65.7% over the visible range for a 100-nm-thick perovskite layer [6]. Mehmood et al. reported 7.9% absorption improvement by applying lead xanthate spray on titanium dioxide outer boundary to implant lead sulfide (PbS) nanocrystals in dye-sensitized solar cells [7]. Liang et al. proposed that a light intensity detector with density sensitivity reaches 1.5291 dB/(mW-mm) embellished by microstructured optical fiber (MOF) with two air holes in the innermost layer instilled with ionic liquid between two segments [8]. Satoshi Ishii et al. numerically proved the increase in solar energy absorption by immersing the transition metal nitrides and carbides in water, which they later also verified through experimental results [9]. Raffaelle et al. demonstrated the synthesis of indium antimonide (InSb) quantum dots for better absorption efficiency in long infrared region of the solar spectrum. They discovered that nanoparticles doped with rare earth oxides can raise photons to energies above the bandgap energy of polymers [10]. Gondal et al. showed that absorption can be enhanced for visible range by spraying anatase phase semispherical titanium dioxide (TiO2) nanoparticles along with 3–4-nm gold particles on TiO2 surface compared to absorption of copper-doped TiO2 or pure TiO2 [11]. Hogan et al. adjudged that the steam could be produced in aqueous solutions containing light-absorbing nanoparticles when exposed to sun light at the bulk fluid temperature much lower than its boiling point [12]. Ishii et al. demonstrated experimentally that sprinkling of silicon nanoparticles in water has acted as splendid solar heat transducers to utilize solar energy for quick vaporization of water [13]. Hameed et al. reported an increase in efficiency of one-meter optical energy receiver with glass-to-copper tube size ratio of (1/4), (1/2) and (3/4) of flow rate up to 51.8%, 61% and 47%, respectively, through numerical model for inclined receiver tube with flowing water under thermo-siphon effect and nanofluid annular region [14]. Wang et al. demonstrated that heat deposit ability and light-to-heat conversion of the plasmonic nanocomposites could be improved by altering nanocomposites ratios [15]. Mushtaq et al. studied Rosseland approximation for thermal radiation and simplified the governing equations by transforming boundary layer into dimensionless form through Runge–Kutta method (RKM) transformations by exploiting appropriate shooting technique [16]. Ghasemi et al. conducted a numerical study to understand the effect of light radiation on the magneto-hydrodynamic (MHD) nanofluid flow by applying Rosseland approximation through Keller–Box numerical method [17]. Besides these, there are many reported studies in which the dynamics of nanofluidic problems are investigated in diversified fields; see [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34] and references cited therein.

In the current study, the analysis of the nanofludics system is carried out numerically with following highlights in terms of salient features as:

  • Novel application of numerical solvers is presented to study the effects of the nonlinear radiative heat transfer due to solar radiation in MHD fluid flow mixed with nanomaterial using the competency of Adams and explicit backward finite difference approaches.

  • Similarity transformation is exploited for reduction of partial differential equations (PDEs) to system of ordinary differential equations (ODEs).

  • The dynamics of the system by mean of velocity, temperature and nanoparticle concentration profiles are presented to study the effects of radiation parameter for, thermophoresis, Brownian motion, magnetic field, Lewis, Prandtl, Eckert and Biot numbers.

  • The comparative study through graphical and numerical illustrations established the worth of the solvers in terms of accuracy, robustness and stability for analysis of the model.

Rest of the paper organized as follows: The system model of nanofluidic problem is given in Sect. 2, the overview of the proposed numerical solvers is presented in Sect. 3, results of numerical experimentation are provided in Sect. 4, conclusions are listed in Sect. 5 while convergence and complexity analysis is provided in Sect. 6.

2 System model

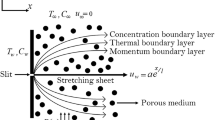
Let us assume the nanomaterial mixed flow over a stretched wall with convectively heated at y = 0. The stretching velocity along horizontal axis is \( u_{w} = ax \), whereas the free stream velocity is \( u_{\infty } (x) = bx \). Magnetic field having strength \( H_{0} \) is introduced perpendicularly to the flow. The analysis of heat transfer is considered in the presence of Joule heating, thermal radiation and impact of viscous dissipation. The combined influence of Brownian motion and thermophoresis is also considered. The governing relations for the flow model are given as follows: [16, 17]

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$
(1)
$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = u_{\infty } \frac{{du_{\infty } }}{\partial x} + v_{f} \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\sigma_{e} H^{2}_{0} }}{{\rho_{f} }}\left( {u - u_{\infty } } \right) $$
(2)
$$ \begin{aligned} & u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\nu_{f} }}{{C_{f} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} - \frac{1}{{\left( {\rho C} \right)_{f} }}\frac{{\partial q_{r} }}{\partial z} + \frac{{\sigma_{e} H_{0}^{2} }}{{\left( {\rho C} \right)_{f} }}\left( {u_{\infty } - u} \right) \\ & + \tau D_{B} \left( {\left( {\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}} \right) + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right), \\ \end{aligned} $$
(3)
$$ u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{B} \left( {\frac{{\partial^{2} C}}{{\partial y^{2} }}} \right) + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right). $$
(4)

In Eqs. (1–4), u and v are velocity components in the direction of x-axis and y-axis, respectively, \( \upsilon = {\raise0.5ex\hbox{$\scriptstyle \mu $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\rho_{f} }$}} \) stands for the dynamic viscosity, \( \rho_{\text{f}} \) denotes the density of the base fluid, \( \alpha = {\raise0.5ex\hbox{$\scriptstyle k$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\left( {\rho C} \right)_{\text{f}} }$}} \) is the based fluid thermal diffusivity, \( \left( {\rho C} \right)_{\text{f}} \) and \( \left( {\rho C} \right)_{p} \) represent the heat capacities, C is nanoparticle concentration, \( q_{\text{r}} \) is the radiative heat flux parameter, \( D_{\text{B}} \) and \( D_{\text{t}} \) are coefficients for the Brownian and thermophoretic diffusion parameter, respectively. The radiative heat flux relations are given mathematically as follows:

$$ q_{\text{r}} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial y} = - \frac{{4\sigma^{*} }}{{3k^{*} }}T^{3} \frac{\partial T}{\partial y} $$
(5)

where \( \sigma^{*} \) is the Stefan–Boltzmann constant while \( k^{*} \) is the mean absorption coefficient. The set of differential equations (Eqs. 2–4) are transformed into ODEs given by

$$ \frac{{d^{3} f}}{{d\eta^{3} }} + f\frac{{d^{2} f}}{{d\eta^{2} }} - \left( {\frac{df}{d\eta }} \right)^{2} + M\left( {\lambda - \frac{df}{d\eta }} \right) = 0, $$
(6)
$$ \begin{aligned} & \left[ {1 + R_{d} \left( {1 + \left( {\theta_{w} - 1} \right)\theta^{3} } \right)\frac{d\theta }{d\eta }} \right]^{\prime } + \Pr f\frac{d\theta }{d\eta } + \Pr N_{b} \frac{d\theta }{d\eta }\frac{d\phi }{d\eta } + \Pr N_{t} \left( {\frac{d\theta }{d\eta }} \right)^{2} + \Pr E_{c} \left( {\frac{{d^{2} f}}{{d\eta^{2} }}} \right)^{2} \\ & + \Pr ME_{c} \left( {\lambda - \frac{df}{d\eta }} \right)^{2} = 0, \\ \end{aligned} $$
(7)
$$ \frac{{d^{2} \varphi }}{{d\eta^{2} }} + Le \, f\frac{d\varphi }{d\eta } + \frac{{N_{t} }}{{N_{b} }}\frac{{d^{2} \theta }}{{d\eta^{2} }} = 0 $$
(8)

Along with wall properties

$$ \begin{aligned} & f\left( 0 \right) = 0{ , }f^{\prime}\left( 0 \right) = 1{ , }f^{\prime}\left( \infty \right) \to \lambda \\ & \theta^{\prime}\left( 0 \right) = - \gamma \left[ {1 - \theta \left( 0 \right)} \right]{ , }\varPhi ( 0 ) { = 1, } \, \theta (\infty )\to 0 , { }\varPhi (\infty )\to 0\\ \end{aligned} $$
(9)

The surface heat and mass fluxes in dimensionless form are given by

$$ \begin{aligned} & \frac{{Nu_{x} }}{{\sqrt {\text{Re}_{x} } }} = - \left[ {1 + R_{d} \theta_{w}^{3} } \right]\theta^{\prime}\left( 0 \right) = Nur, \\ & \frac{Sh}{{\sqrt {\text{Re}_{x} } }} = - \phi^{\prime}\left( 0 \right) = Shr. \\ \end{aligned} $$
(10)

3 Numerical Procedure

In the current study, we have exploited the strength of Adams predictor–corrector method along with backward difference method (BDF) [18,19,20,21,22] to solve the system of Eqs. (6–8) by using boundary conditions as given in Eq. (9). The generic workflow graph of the proposed study is presented in Fig. 1.

Fig. 1
figure 1

Workflow graph of proposed study for analysis of heat transfer in MHD nanofluid flow

Full size image

3.1 Numerical Solver: Adams Method

To solve the ODEs, the Adam numerical method is used. In this method, predictor solution is predicted firstly; then, corrector is used to find the accurate solution by using already calculated solution. Considering Eqs. (7–8) in case of velocity, temperature and concentration profile as:

$$ \frac{df}{d\eta } = v(\eta ,f),\quad f(\eta_{0} ) = f_{0} , $$
(11)
$$ \frac{d\theta }{d\eta } = v(\eta ,\theta ),\quad \theta (\eta_{0} ) = \theta_{0} , $$
(12)
$$ \frac{d\varphi }{d\eta } = v(\eta ,\varphi ),\quad \varphi (\eta_{0} ) = \varphi_{0} , $$
(13)

Adams–Moulton two-step predictor relations in case of profiles for temperature and concentration are given as:

$$ f_{k + 1} = f_{k} + \frac{h}{2}\left( {3v(\eta_{k} ,f_{k} ) - v(\eta_{k - 1} ,f_{k - 1} )} \right), $$
(14)
$$ \theta_{k + 1} = \theta_{k} + \frac{h}{2}\left( {3v(\eta_{k} ,\theta_{k} ) - v(\eta_{k - 1} ,\theta_{k - 1} )} \right), $$
(15)
$$ \varphi_{k + 1} = \varphi_{k} + \frac{h}{2}\left( {3v(\eta_{k} ,\varphi_{k} ) - v(\eta_{k - 1} ,\varphi_{k - 1} )} \right), $$
(16)

while the two-step corrector formulas for Adams–Moulton are given by

$$ f_{k + 1} = f_{k} + \frac{h}{2}\left( {v(\eta_{k + 1} ,f_{k + 1} ) - v\left( {\eta_{k} ,f_{k} } \right)} \right), $$
(17)
$$ \theta_{k + 1} = \theta_{k} + \frac{h}{2}\left( {v(\eta_{k + 1} ,\theta_{k + 1} ) - v\left( {\eta_{k} ,\theta_{k} } \right)} \right), $$
(18)
$$ \varphi_{k + 1} = \varphi_{k} + \frac{h}{2}\left( {v(\eta_{k + 1} ,\varphi_{k + 1} ) - v\left( {\eta_{k} ,\varphi_{k} } \right)} \right), $$
(19)

Accordingly, the four-step Adam-Moulton predictor corrector expressions can be seen in literature [18].

4 Implicit Backward Difference Method

Backward difference method (BDF) uses method of numerical integration to solve system of ODEs Eqs. (6–8) by using boundary conditions as given in Eq. (9). The general expression for the method is given by

$$ \sum\limits_{k = 0}^{s} {d_{k} } v_{n + k} = dwf(t_{n + s} ,u_{n + s} ), $$
(20)

In the above equation, d represents the step size. For the maximum convergence coefficient d and W are incorporated as follows

$$ v_{n + 1} - v_{n} = df(t_{n + 1} ,u_{n + 1} ), $$
(21)

thus,

$$ \begin{aligned} & v_{n + 6} - \tfrac{360}{147}v_{n + 5} + \tfrac{450}{147}v_{n + 4} - \tfrac{400}{147}v_{n + 3} + \tfrac{225}{147}v_{n + 2} - \tfrac{72}{147}v_{n + 1} + \tfrac{10}{147}v_{n} \\ & - \tfrac{60}{147}df(t_{n + 6} ,v_{n + 6} ) = 0. \\ \end{aligned} $$
(22)

5 Numerical Results with Interpretations

The analysis on the effect of solar radiation in the presence of magnetic field over stretched plate on a nanofluid boundary layer by using Adams and BDF methods is presented here. We have described the influence of radiation parameter \( R_{d} \) along with thermophoresis parameter \( N_{t} \), Brownian motion parameter \( N_{\text{b}} \), magnetic field parameter \( M \), Lewis number \( Le \), Prandtl number \( \Pr \), Eckert number \( E_{c} \) and Biot number \( \gamma \) on temperature profile \( \theta (\eta ) \), nanoparticle concentration profile \( \phi (\eta ) \), local Nusselt and local Sherwood numbers graphically and numerically. The effect of error analysis is also described graphically for above-mentioned parameters. Numerical illustration of the results for local Nusselt number and local Sherwood number against different physical quantities is also provided, respectively, in Tables 1 and 2.

Table 1 Local Nusslet and local Sherwood numbers for parameters \( \gamma \) = 0.5, \( \Pr \) = 7 and \( E_{c} \) = 0.1, \( L_{e} \) = 1
Full size table
Table 2 Local Nusslet and local Sherwood numbers for \( N_{t} \) = \( N_{b} \) = 0.1 and \( M \) = 0.5
Full size table

Figure 2 describes the effect of \( N_{t} \) along with \( R_{d} \) on \( \theta \) profile, and results show that \( \theta \) increases with increment in both \( N_{t} \) and \( R_{d} \). The \( \theta \) profile has highest value at \( N_{t} \) = 0.5 with \( R_{d} \) = 3 and then decreases with decrease in value of \( R_{d} \). Also \( R_{d} \) values increase with increment in \( N_{t} \). The larger values of thermophoretic parameter \( N_{t} \) depict large difference in temperature \( \theta \) and shear gradient. It is also observed from Fig. 1 that as the thermophoretic effect strengthens, then decreasing behavior is observed in the temperature gradient at the sheet. Thus increment in \( N_{t} \) will result large temperature inside boundary layer. Figure 3 describes error analysis between Adam’s and BDF numerical methods. It is quite clear from figure that error in temperature profile \( \phi (\eta ) \) for various values of \( R_{d} \) and \( N_{t} \) is quite negligible and it exists in the range of 10−07–10−10. Figure 4 depicts the influence of \( N_{t} \) along with \( R_{d} \) on nanoparticle concentration profile. It can be observed from Fig. 4 that nanoparticle concentration profile increases with an increment in \( N_{t} \) but decreases with \( R_{d} \). Figure 6 describes that local Nusselt number increases with increment in \( N_{t} \) but decreases with \( R_{d} \), whereas decreasing trend is observed for local Sherwood number with an increment in \( N_{t} \) and \( R_{d} \) values as shown in Fig. 8. Figures 5 and 7 describe the error analysis by using two numerical approaches for nanoparticle concentration profile and local Nusselt number, respectively, and it exists in the range of 10−07 to 10−10 which is quite negligible, whereas the gauges of the error validate computational accuracy of the level around 10−7

Fig. 2
figure 2

Influence of \( N_{t} \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 3
figure 3

Absolute error of \( N_{t} \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 4
figure 4

Variation of \( N_{t} \) and \( R_{d} \) on \( \phi (\eta ) \)

Full size image
Fig. 5
figure 5

Absolute error of \( N_{t} \) and \( R_{d} \) on \( \phi (\eta ) \)

Full size image
Fig. 6
figure 6

Variation of \( N_{t} \) and \( R_{d} \) on local Nusselt number

Full size image
Fig. 7
figure 7

Absolute error of \( N_{t} \) and \( R_{d} \) with local Nusselt number

Full size image

(Figs. 6, 7).

The influence of \( N_{\text{b}} \) on \( \theta \) profile along with \( R_{d} \) is shown in Fig. 8, which elucidates that \( \theta \) profile increase with the increment in \( N_{b} \) while decreases with the increment in \( R_{d} \). In nanofluids, the Brownian motion takes place because of nanoparticles size having nanometer scale, and as a result, the effect of particles motion on nanofluid has a vital role in transfer of heat. According to Brownian motion definition, as values of \( N_{\text{b}} \) are increased, the nanoparticles kinetic energy also increases due to chaotic motion intensity, and as a result, temperature of nanofluid also increases. Figure 10 depicts that as the values of \( N_{\text{b}} \) are increased along with an increment in \( R_{d} \), the values of nanoparticle concentration profile decreases. The local Nusselt number values increase with an increment in \( N_{\text{b}} \) and decrease in \( R_{d} \) values as shown in Fig. 10. Figures 9 and 11 elucidate the analysis of error with radiation parameter and local Nusselt number for Brownian motion parameter (\( N_{\text{b}} \)), respectively. It is quite clear from error analysis graphs that error lies in the range of 10−06 –10−10 which is quite negligible and proves the validity (Figs. 10, 11).

Fig. 8
figure 8

Influence of \( N_{b} \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 9
figure 9

Absolute error of \( N_{b} \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 10
figure 10

Variation of \( N_{b} \) and \( R_{d} \) on local Nusselt number

Full size image
Fig. 11
figure 11

Absolute error of \( N_{b} \) and \( R_{d} \) on local Nusselt number

Full size image

The effect of \( M \) along with \( R_{d} \) on temperature profiles can be easily noticed in Fig. 12. It is quite clear from Fig. 12 that increasing trend is found for \( \theta \) profile with an increment in \( M \) and \( R_{d} \). One may also depict from Fig. 12 that the layer of thermal boundary increases as the strength of \( M \) is increased. The variation of \( M \) and \( R_{d} \) with local Nusselt number and local Sherwood number is depicted in Figs. 14 and 16. Figures 13, 15, 17 describe the error analysis of radiation parameter with temperature profile, local Nusselt number and local Sherwood number for \( M \), respectively. It is observed from error analysis graphs that error lies in the range of 10−06 –10−10 which is quite negligible and proves the validity obtained results (Figs. 14, 15, 16, 17).

Fig. 12
figure 12

Influence of \( M \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 13
figure 13

Absolute error of \( M \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 14
figure 14

Variation of \( M \) and \( R_{d} \) on local Nusselt number

Full size image
Fig. 15
figure 15

Absolute error of \( M \) and \( R_{d} \) on local Nusselt number

Full size image
Fig. 16
figure 16

Influence of \( M \) and \( R_{d} \) on local Sherwood number

Full size image
Fig. 17
figure 17

Absolute error of \( M \) and \( R_{d} \) on local Sherwood number

Full size image

The variation in \( Le \) on \( \theta (\eta ) \) and radiation parameter is shown in Fig. 18. It is observed from Fig. 18 that increasing behavior is found for \( \theta (\eta ) \) with an increment in \( Le \) and \( R_{d} \), whereas the influence of \( Le \) on concentration profile \( \phi (\eta ) \) and \( R_{d} \) is shown in Fig. 20. Figures 18 and 20 describe that with the gradually increase in \( Le \) will result in larger difference in temperature and a thinner concentration boundary layer due to weaker molecular diffusivity. The effect of local Nusselt number on \( Le \) and \( R_{d} \) is depicted in Figs. 22, and it is noticed that local Nusselt number initially increases with increment in \( Le \) and \( R_{d} \), but later it decreases with an increase in \( Le \) and \( R_{d} \). While from Figs. 19, 21, 23, it is quite clear that error lies in the range of 10−06 to 10−10 for both temperature and concentration profiles as well as local Nusselt numbers (Figs. 20, 21, 22, 23) .

Fig. 18
figure 18

Influence of \( Le \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 19
figure 19

Absolute error of \( Le \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 20
figure 20

Effect of \( Le \) and \( R_{d} \) on \( \phi (\eta ) \)

Full size image
Fig. 21
figure 21

Absolute error of \( Le \) and \( R_{d} \) on \( \phi (\eta ) \)

Full size image
Fig. 22
figure 22

Effect of \( Le \) and \( R_{d} \) on local Nusselt number

Full size image
Fig. 23
figure 23

Absolute error of \( Le \) and \( R_{d} \) on local Nusselt number

Full size image

The effect of temperature profile \( \theta (\eta ) \) on \( \Pr \) and \( R_{d} \) is presented in Fig. 24, and it is found from that \( \theta (\eta ) \) increases with decrease in \( \Pr \) values and increases with an increment in \( R_{d} \) and depicts that an increment in \( \Pr \) will result in decrease in thermal diffusivity, and as a result, the fluid temperature and thickness of thermal boundary layer decrease. The effect of local Nusselt number on \( \Pr \) and \( R_{d} \) is shown in Fig. 26. Figures 25 and 27 describe the error analysis with \( \Pr \) and \( R_{d} \), for both temperature and Nusselt numbers. It is observed from error analysis graphs that error lies in the range of 10−07 to 10−10 which is quite negligible (Figs. 26, 27).

Fig. 24
figure 24

Effect of \( \Pr \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 25
figure 25

Absolute error of \( \Pr \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 26
figure 26

Influence of \( \Pr \) and \( R_{d} \) on local Nusselt number

Full size image
Fig. 27
figure 27

Absolute error of \( \Pr \) and \( R_{d} \) on local Nusselt number

Full size image

The effect of \( \theta \) on \( E_{c} \) and \( R_{d} \) is presented in Fig. 28, and results show that increasing trend is observed in temperature profile \( \theta (\eta ) \) with increase in \( E_{c} \) and decrease in \( R_{d} \), while \( E_{c} \) has inverse influence on \( \theta \) as compared to \( \Pr \). From Fig. 30, it is noticed that local Nusselt number increases with increment in \( E_{c} \), but with \( R_{d} \), initially it increases but later it decreases with an increase in \( R_{d} \). Figures 29 and 31 describe the error analysis graphs of \( E_{c} \) for temperature profiles as well as Nusselt numbers. It is noted that quite negligible error lies in the range of 10−07 to 10−10 (Figs. 30, 31).

Fig. 28
figure 28

Influence of \( E_{c} \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 29
figure 29

Absolute error of \( E_{c} \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 30
figure 30

Influence of \( E_{c} \) and \( R_{d} \) on local Nusselt number

Full size image
Fig. 31
figure 31

Absolute error of \( E_{c} \) and \( R_{d} \) on local Nusselt number

Full size image

The effect of Biot number \( \gamma \) on \( \theta (\eta ) \) and concentration \( \phi (\eta ) \) with radiation parameter is shown in Figs. 32 and 34, and it is found that value of both \( \theta (\eta ) \) and \( \phi (\eta ) \) increases with increment in both \( \gamma \) and \( R_{d} \). The influence of local Nusselt number for \( \gamma \) and \( R_{d} \) is shown in Fig. 36. From Fig. 36, it is observed that the values of local Nusselt number increase with increment in \( \gamma \) and decrease in \( R_{d} \). Error analysis graph for \( \gamma \) for both temperature and concentration profiles, as well as, Nusselt numbers, is shown in Figs. (33, 35 and 37). From these figures, it is quite clear that error lies in the range of 10−07 –10−10 which is quite negligible and shows the validity of computation (Figs. 34, 35, 36, 37).

Fig. 32
figure 32

Effect of \( \gamma \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 33
figure 33

Absolute error of \( \gamma \) and \( R_{d} \) on \( \theta (\eta ) \)

Full size image
Fig. 34
figure 34

Influence of \( \gamma \) and \( R_{d} \) on \( \phi (\eta ) \)

Full size image
Fig. 35
figure 35

Absolute error of \( \gamma \) and \( R_{d} \) on \( \phi (\eta ) \)

Full size image
Fig. 36
figure 36

Influence of \( \gamma \) and \( R_{d} \) on local Nusselt number

Full size image
Fig. 37
figure 37

Absolute error of \( \gamma \) and \( R_{d} \) on local Nusselt number

Full size image

Numerical illustrations for the results are presented in Tables 1 and 2 by variation of local Nusselt and Sherwood numbers for different physical quantities. The tabulated results established the convergence of the solutions on the basis of both Sherwood and Nusselt numbers. Additionally, the numerical values for skin friction coefficient with different parameters, i.e., M and \( \lambda \), are listed in Table 3.

Table 3 Numerical values for skin friction coefficient with parameters \( N_{t} \) = \( N_{b} \) = 0.1, \( \gamma \) = 0.5, \( \Pr \) = Le = 1 and \( E_{c} \) = 0.1
Full size table

6 Convergence and Complexity Analysis

In this section, stability analysis is presented on the basis of different levels of accuracy goal for numerical computing algorithms. Additionally, the comparison of the complexity indices for Adams method (AM), backward difference method (BDF), explicit Runge–Kutta (ERK), implicit Runge–Kutta method (IRK) and extrapolation technique (ET) is presented.

Result of stability analysis and complexity operators on the basis of stiff and nonstiff accuracy goals, i.e., 10−05, 10−10, 10−15 and 10−20, is calculated for AM, BDF, ERK, IRK and ET and are provided in Tables 4, 5, 6 and 7 for variation of Ec, M, Pr and Rd of fluidic model, respectively.

Table 4 Convergence and complexity measures of the system in case of \( E_{c} = 0.1 \)
Full size table
Table 5 Convergence and complexity measures of the system in case of \( M = 1.0 \)
Full size table
Table 6 Convergence and complexity indices for the model in case of \( \Pr = 4 \)
Full size table
Table 7 Convergence and complexity measure of the system in case of \( R_{d} = 2 \)
Full size table

It can be seen that all five numerical methods are applicable for both nonstiff, i.e., 10−05 and 10−10, and stiff, i.e., 10−15 and 10−20, accuracy goals for all four variation of the fluidic model, which established the stability and convergence of the numerical procedures, whereas comparison of the complexity indices based on time, step and function evaluations shows that for better accuracy goals, the complexity of the all five numerical computing algorithm increases. However, it is found that on average the Adams numerical procedure is the most efficient from the rest of computing methodologies.

7 Conclusions and Future Recommendations

In this work, strength of numerical solvers has been exploited to analyze the dynamics of the system model based on laminar two-dimensional nanofluid flow over stretching sheet. We have investigated the effect of radiation parameter along with thermophoresis parameter, Brownian motion parameter, magnetic field parameter, Lewis Number, Prandtl Number, Eckert number, Biot number on temperature profile \( \theta (\eta ) \), nanoparticle concentration profile \( \phi (\eta ) \), local Nusselt and local Sherwood number through sufficient number of graphically and numerical illustration. Following are the main outcomes.

  • Temperature profile \( \theta (\eta ) \) increases with increment in thermophoresis parameter, Brownian motion parameter, magnetic field parameter, Lewis number, Eckert number and Biot number while temperature profile \( \theta (\eta ) \) decreases with the increment in Prandtl number.

  • Increasing trend is observed for nanoparticle concentration profile \( \phi (\eta ) \) with an increment in thermophoresis parameter, magnetic field parameter, Lewis Number, Prandtl Number and Biot number while concentration profile decreases with an increment in Brownian motion parameter.

  • Local Nusselt number enhances with an increment in thermophoresis parameter, Brownian motion parameter, magnetic field parameter, Lewis number, Eckert number and Biot number

  • Local Sherwood number increases with an increment in Brownian motion parameter and Lewis number, while its value decreases with an increment in thermophoresis parameter, magnetic field parameter, Eckert number and Biot number.

  • Error analysis lies in the range of 10−07–10−10 which is quite negligible and shows the validity of computation.

In future, one may explore/exploit the strength of intelligent computing paradigm for solving fluid dynamics problems arising in diversified field of applied science and technology [35,36,37,38,39,40].