Transfer Coordination-Based Train Organization for Small-Size Metro Networks

Abstract

This paper addresses the train organization problem of a small-size metro network during the peak hour, with a special consideration of transfer coordination. The problem is formulated as a multi-objective programming (MOP) model, where the economic cost, capacity utilization, and transfer coordination are considered together based on the routing selection analysis. Train marshaling number and headway on different routes are key decision variables in the model. The economic cost consists of generalized trip cost, operation cost, and external benefits, and the capacity utilization describes the remaining section capacity expressed by a difference quadratic sum. The proposed model highlights the transfer coordination, which targets at minimizing the number of left-behind passengers on platforms, considering the time-varying arrival rate and the remaining train capacity. Based on the sequencing method, an integration of genetic algorithm and ant colony optimization is devised to solve the MOP model. Finally, a real-world case study of Xi’an metro network has been conducted. Results show that the number of left-behind passengers in the network decreased 55.3$\%$, the total remaining capacity decreased 15.3$\%$ and the number of trains decreased 8.5$\%$, while the total time cost increased 1.6$\%$. To further check the passenger distribution density on the platform, a simulation of Beidajie transfer station has been elaborately designed via Viswalk 7.0. Both theoretical results and simulation data have validated the feasibility and reliability of presented method.

1 Introduction

Transfer stations are essential nodes to realize passengers exchange among lines in the metro network. Metro lines usually operate independently because of the spatial separation, rolling stock, signal control and particular management. Compared to a single metro line, passengers exchange and resource allocation in a metro network are more complicated. The scheme of network transport highlights the global optimization, considering the connection among lines under limits like infrastructure layout and signal control. Recent studies on this topic involve the transfer coordination and the train organization.

The transfer coordination is an important indicator when analyzing the train organization of urban rail network [1]. Ji et al.[2] and Wang et al.[3] demonstrated the transfer effectiveness in a metro network. Pedestrian characteristics have been frequently studied before and during the optimization of transfer performance. Tang and Liu [4] calibrated the velocity-density model of passenger flow as a basic support for the improvement in a transfer station. Zhou et al. [5] further identified the crowding degree to evaluate the performance in a transfer station. To better evaluate the transfer efficiency, a microsimulation based on potential field theory [6] was designed to analyze the key affecting factors of transfer behaviors and find the relationship among transfer efficiency, passenger behavior and train schedule. Wang et al. [7] applied an event-driven model where transfer behaviors like walking and dwelling were taken into account. Meanwhile, it was revealed that passengers psychological perception would affect the walking speed and transfer path decision [8, 9], and the psychological analysis could be applied in the emergency evacuation and streamlines design [10]. When considering the interaction between transfer passengers and arrival trains, Li et al. [11] proposed a multi-line cooperation model for passenger flow disposal at a transfer station. Nowadays, with the help of multi-source data, the relationship between delay and transfer capacity could be fully analyzed, upon which an interline transfer capacity coordination model was formulated to adjust the operation strategy [12].

In order to formulate an optimization model for train organization, it is necessary to determine the decision variables, objectives and fundamental constraints. Train organization problem is usually formulated by the multi-objective programming (MOP). The often used decision variables include the train routing, train headway and train marshaling number [13, 14]. The constraints are associated with passenger demands, infrastructure conditions and signal control [15, 16]. Xu et al. [17] applied the computer simulation to discuss train organization schemes under different circumstances like separate operation and joint operation. Stoilova and Stoev [18] also conducted a simulation model to decide the departure frequency and number of trains depending on the passenger flow. As to the optimization objectives, different objectives have been established in different research aspects. Traditional objectives include the transportation efficiency, operation cost and passengers travel time [19], while recent studies focus on the level of service [20, 21] and energy consumption [22, 23]. Guo et al. [24] maximized the transfer synchronization for a better service quality considering passenger demand during the transition period. Zhao et al. [25] developed an integrated method to optimize the metro operation aiming to save energy.

As previously discussed, we can see that researches about transfer coordination focus on modeling passenger behaviors in a disaggregate way, and related scheduling methods are applicable to improve the transfer performance. For train organization, kinds of effective models have been formulated to optimize the global scheme with mentioned objectives. While the transfer coordination and organization optimization have been explored extensively, few research has considered their combination in a metro network. However, it should be noticed that the metro network is a complex system with kinds of demands and objectives, and we intend to formulate a simplified but comprehensive model to unify the transfer coordination and global organization.

The remainder of this paper is structured as follows. Section 2 analyzes factors affecting train routing and proposes a suitability model to select turn-back stations. Section 3 explains the modeling of transfer coordination-based optimization and the solution method, where objectives of economic cost, capacity utilization and transfer coordination are established, respectively, based on reasonable assumptions. Section 4 presents the case analysis of Xi’an metro network, followed by a comprehensive evaluation to the model performance both in theory and in simulation. Finally, the study is concluded by highlighting major contributions and future research aspects in Sect. 5.

2 Train Routing Analysis

Train routing modes usually include single routing, connected routing and nested routing, as shown in Fig. 1. Each mode has its applicability when considering the passenger distribution, line capacity, and service quality.

Fig. 1

Three common train routing modes of metro lines

2.1 The Selection of Routing Mode

The spatial distribution of passenger volume is always the basis in train route design. The selection of routing mode usually depends on the section volume drop and the non-equilibrium coefficient of passengers spatial distribution.

Besides the spatial distribution, the train routing mode should also consider the transportation efficiency, the time consumption and the trains turnover conditions. Generally, the connected routing will generate extra transfer time at the joint station for those passengers with cross-routing demands, while the nested routing will cost more waiting time for passengers with destination outside the overlapped route section. To guarantee the equilibrium between different routing sections, the headway on the long route (H$_{1}$) should be an integral multiple of headway on the short route (H$_{2}$). Otherwise the wasted time (t$_\mathrm{waste}$) will extend the turn-back time of trains on the short route (t$_{\mathrm{turn}2}$); see Fig. 2.

Fig. 2

Time waste caused by uneven headway

2.2 Train Routing Selection

In a small-size metro network, nested routing is usually applied to enhance the section capacity utilization and resource allocation, where trains running on the short route have to turn back at switchback stations. The switchback stations could be determined by the degree of suitability [26], calculated by a modified model as:

$$\begin{aligned} {F_i} = \frac{{\Delta {p_{i1}}}}{{\Delta {p_{1\max }}}} \cdot \theta + \frac{{\Delta {p_{i2}}}}{{\Delta {p_{2\max }}}} \cdot \left( {1 - \theta } \right) , \theta {\mathrm{= }}\frac{{\Delta {p_{1\max }}}}{{\Delta {p_{1\max }}{\mathrm{+ }}\Delta {p_{2\max }}}} \end{aligned}$$

(1)

In Eq. 1, ${{F}_{i}}$ denotes the suitability degree of the ith middle station; $\Delta {{p}_{i1}}$ is the absolute value of the passengers volume drop between adjacent segments at the ith middle station in the upward direction, passengers/h; $\Delta {p_{i2}}$ is the absolute value in the downward direction, passengers/h; $\Delta {p_{1\max }}$ and $\Delta {p_{2\max }}$ are the maximum absolute value of the upward and downward direction, respectively, passengers/h; $\theta$ is the weighting coefficient to erase the non-equilibrium between the values of upward and downward passenger volume.

3 Model Formulation

3.1 Problem Setting

Given a small-size metro network and the corresponding passenger O-D distribution, the hybrid model aims to find out an optimal scheme of train routing, departure interval and train marshaling number for different lines, with a special consideration of transfer coordination. Besides the transfer coordination, basic objectives include the economics and capacity usage. The following assumptions and constraints are necessary for an effective modeling:

• Trains stop at every station during peak hours.

• Passengers prefer to take trains on the long route (LR) when their destination is outside the range of short route (SR).

• The boarding and alighting passengers are in an equilibrium spatial distribution along the platform edge.

• To guarantee the equilibrium of departure frequency, the ratio of the number of trains on SR to the number of trains on LR should be an integer (Sect. 2.1). The empirical value of this ratio is 1 or 2.

• The tolerable waiting time during the peak hour is 7 min upon a pilot investigation, and the extreme headway under the communication-based train control (CBTC) system is 1.5 min [27] .

• 6-car trains run on the full-length train route to guarantee the global performance, while the number of cars in a train running on short route should be at least 4.

The following symbols of key variables and major parameters are used in the modeling.

• ${I_L}$ the train headway of line L, min.

• ${\alpha _L}$ the marshaling number of trains running on the long route of line L.

• ${\beta _L}$ the marshaling number of trains running on the short route of line L.

• ${r_L}$ the ratio of the number of trains on SR to the number of trains on LR.

• n the total number of stations in network.

• N the total number of metro lines.

• K the total number of transfer stations.

• ${p_L}$ and ${q_L}$ the serial numbers of two turn-back stations on the short route of line L.

• ${m_L}$ the total number of stations on line L.

• ${\eta _L}$ the overloading coefficient of line L.

• ${c_L^\alpha }$ the rated carriage capacity of trains running on the long route of line L.

• ${c_L^\beta }$ the rated carriage capacity of trains running on the short route of line L.

3.2 Economic Objective

The economic objective consists of generalized trip cost, operation cost, and external benefit.

3.2.1 Generalized Trip Cost

The generalized trip cost is usually a combination of ticket cost and time cost.

Ticket Cost Ticket cost is the ticket expenses of passengers, and it can be calculated in a simplified expression:

$$\begin{aligned} {M_p} = \sum \limits _{x = 1}^n {\sum \limits _{y = 1}^n {{a_{xy}} \cdot {c_{xy}} \cdot {\mathrm{1}}{{\mathrm{0}}^{{\mathrm{- 3}}}}} } \end{aligned}$$

(2)

where ${a_{xy}}$ is the passenger flow volume from station x to station y ($x \ne y$), and ${c_{xy}}$ is the ticket price based on official pricing standards, Yuan.

Time Cost Given passengers O-D distribution, the total travel time is usually a constant under a fixed traveling speed. Therefore, only the waiting time and transfer time affected by the organization scheme are taken into account when formulating the time cost. Before formulation, a hypothesis that the average waiting time is half the headway is first verified. Under the high-frequency transit services during the peak hour, passengers arrive in batches with a time-varying rate. Therefore, the arrival rate during each headway can be seen as a constant.

Fig. 3

Trains operating diagram at a station

According to a simplified train diagram at a station (see Fig. 3), the total waiting time during the ith train headway is calculated as:

$$\begin{aligned} T_w^i = \int _{(i - 1) \cdot I}^{i \cdot I} {{o^i} \cdot \left( {i \cdot I - t} \right) {d_t}} = \frac{1}{2}{o^i}{I^2} \end{aligned}$$

(3)

where $o^i$ is the arrival rate during the ith train headway, passengers/min. Then the average waiting time during the ith headway is:

$$\begin{aligned} t_w^i = {{T_w^i}/{P_a^i}} = {{\frac{1}{2}{o^i}{I^2}} / {{o^i}I}} = \frac{1}{2}I \end{aligned}$$

(4)

Therefore, when a station s only lies in the long routing section of line L, the total passengers waiting time of these stations is:

$$\begin{aligned} T_L^1{\mathrm{= }}\sum \limits _{s \notin [{p_L},{q_L}]} {\sum \limits _{i = 1,i \ne s}^{{m_L}} {{a_{si}} \cdot \frac{{{I_L}}}{2}} } \end{aligned}$$

(5)

where $T_L^1$ is the total waiting time for stations only belong to the long route, min; ${a_{si}}$ is the passenger volume from station s to station i.

Meanwhile, when a station s lies in the overlapped section of long route and short route, the total waiting time of these stations is:

$$\begin{aligned} \begin{array}{l} T_L^2 = \\ \sum \limits _{s = {p_L}}^{{q_L}}{\displaystyle \frac{1}{2}}{\left[ {\left( {\sum \limits _{i = 1,i\ne s}^{{m_L}} {{a_{si}}} - \sum \limits _{i\notin [{p_L},{q_L}]} {{a_{si}}} }\right) \cdot \displaystyle \frac{{{I_L}}}{{1 + {r_L}}} + \sum \limits _{i \notin [{p_L},{q_L}]} {{a_{si}}{{I_L}}}}\right] } \end{array} \end{aligned}$$

(6)

Then the total waiting time at normal stations is:

$$\begin{aligned} T_{\mathrm{normal}}^{\mathrm{wait}} = \sum \limits _{L = 1}^N {{{\left( {T_L^1 + T_L^2} \right) }/{{\mathrm{60}}}}} \end{aligned}$$

(7)

The phenomenon of passengers crowding is inevitable during the peak hour, thus making the average waiting time longer. Since passengers at transfer stations can be split into entering passengers and transferring passengers, the total waiting time at a platform of one track direction can be calculated by:

$$\begin{aligned} {T_{d(i)}} = \left( {P_{i - 1}^{le} - {A_{i - 1}}} \right) \cdot I + \int _{(i - 1) \cdot I}^{i \cdot I} {\left( {o_E^i + o_T^i} \right) \cdot \left( {i \cdot I - t} \right) {d_t}} \end{aligned}$$

(8)

where ${T_{d(i)}}$ is the total waiting time of dth direction during the ith headway, min; $P_{i - 1}^{le}$ represents the number of left-behind passengers after the i-1th headway, and ${A_{i - 1}}$ is the number of alighting passengers; ${o_E^i}$ and ${o_T^i}$ are the arrival rate of station entering passengers and transferring passengers during the ith headway, respectively, passengers/min.

As illustrated in Fig. 4, a transfer station of two crossed lines usually has 2 platforms, 4 tracks, and 8 transfer paths. Therefore, the total waiting time at all transfer stations is calculated as:

$$\begin{aligned} T_{\mathrm{transfer}}^{\mathrm{wait}} = \sum \limits _{k = 1}^K {\sum \limits _{d = 1}^4 {\sum \limits _{i = 1}^{\left\lceil {{{60} /{{I_d}}}} \right\rceil } {{{T{{_d^k}_{(i)}}}/{{\mathrm{60}}}}}}} \end{aligned}$$

(9)

where d is the running direction of each rail track; ${I_d}$ denotes the headway of the dth track direction during the peak hour, min; $T_{d(i)}^{k}$ is calculated from Eq. 8.

Fig. 4

Transfer paths and directions at a crossed transfer station

Passengers transferring from platform P$_{1}$ to platform P$_{2}$ have 4 paths, and the average walking distances on different paths are nearly the same under the third assumption; see Sect. 3.1. It should be noted that passengers walking speeds are different in different areas [28]. The walking time on each path is:

$$\begin{aligned} \begin{array}{l} T_{\mathrm{transfer}}^{\mathrm{walk}} = \\ \sum \limits _{k = 1}^K {\sum \limits _{i = 1}^8 {{{P_{{f_i}}^k \cdot \left( {\displaystyle \frac{{L_{ki}^{{P_1}}}}{{v_{{P_1}}^k}} +\displaystyle \frac{{L_{ki}^{{P_2}}}}{{v_{{P_2}}^k}} +\displaystyle \frac{{L_{ki}^c}}{{v_{ki}^c}} +\displaystyle \frac{{L_{ki}^e}}{{{v^e}}}} \right) } / {3600}}} } \end{array} \end{aligned}$$

(10)

where $P_{{f_i}}^k$ is the transfer volume on the ith path at transfer station k, passengers/h; $L_{ki}^{{P_1}}$ and $L_{ki}^{{P_2}}$ are the average walking distance on platform P$_{1}$ and platform P$_{2}$, m; $v_{{P_1}}^k$ and $v_{{P_2}}^k$ denotes the average walking speed on platform P$_{1}$ and platform P$_{2}$, respectively, m/s; $L_{ki}^c$ and $L_{ki}^e$ are the total length of corridors and elevators on the ith path, m; $v_{ki}^c$ is the average walking speed on corridors, and ${v^e}$ is the speed of escalators, m/s.

According to Eqs. 2, 7, 9, and 10, the total generalized trip cost can be obtained by:

$$\begin{aligned} C_p^{\mathrm{net}} = {M_p} + \left( {T_{\mathrm{normal}}^{\mathrm{wait}} + T_{\mathrm{transfer}}^{\mathrm{wait}} + T_{\mathrm{transfer}}^{\mathrm{walk}}} \right) \cdot \mathrm{Vot} \cdot {\mathrm{1}}{{\mathrm{0}}^{{\mathrm{- 3}}}} \end{aligned}$$

(11)

where Vot is the value of time, Yuan/h.

3.2.2 Operation Cost

Different from the fixed cost like civil construction investment, the operation cost changes with the organization scheme, and it is additive since the train dispatching of each line is independent.

The operation cost of line L can be calculated by:

$$\begin{aligned} \begin{array}{l} C_t^L = \\ \left( {{\alpha _L} \cdot \frac{{60}}{{{I_L}}} \cdot 2\sum \limits _{i = 1}^{{m_L} - 1} {l_L^{i,i + 1}} + {\beta _L} \cdot {r_L}\frac{{60}}{{{I_L}}} \cdot 2\sum \limits _{i = {p_L}}^{{q_L} - 1} {l_L^{i,i + 1}} } \right) \cdot {\phi _L} \end{array} \end{aligned}$$

(12)

where $C_t^L$ is the operation cost of line L during the peak hour, 10${^3}$ Yuan; and ${\phi _L}$ is the average unit carriage cost, 10${^3}$ Yuan/km.

Thus we have the total train operation cost of metro network as:

$$\begin{aligned} C_t^{\mathrm{net}} = \sum \limits _{L = 1}^N {C_t^L \cdot \gamma _t^L} \end{aligned}$$

(13)

where $\gamma _t^L$ is the reduction coefficient, to erase the imbalance between ticket revenue and operation cost.

3.2.3 External Benefit

As a mass public transit, the metro transportation will generate external benefits. Direct benefits of rail transportation including time-saving benefit and energy-saving benefit should be considered.

Time-Saving Benefit Compared to bus transit and non-motorized transportation, metro serves for trips of medium-long distance rapidly. To calculate the time saved by metro, original share rates of public transportation need adjustment (see Eq. 14) under the circumstance without metro.

$$\begin{aligned} {\lambda _i}^\prime = {{{\lambda _i}} /{\left( {{\lambda _{\mathrm{1}}} + {\lambda _{\mathrm{2}}}} \right) }}, i = 1, 2 \end{aligned}$$

(14)

where ${\lambda _i}^\prime$ is the modified share rate of the ith public transportation mode; ${\lambda _i}$ is the original rate, i = 1 represents bus transit and i = 2 represents the non-motorized transportation.

After introducing the coefficient Vot of metro passengers, the time-saving benefit of passengers in peak hour is calculated by:

$$\begin{aligned} {C_{\mathrm{ts}}}{\mathrm{= }}{T_{\mathrm{trip}}} \cdot \left( {\sum \limits _{i = 1}^2 {{\lambda _i}^\prime \frac{{{{\bar{v}}_s}}}{{{{\bar{v}}_i}}} - 1} } \right) \cdot \mathrm{Vot} \cdot \gamma \times {\mathrm{1}}{{\mathrm{0}}^{ - {\mathrm{3}}}} \end{aligned}$$

(15)

where ${\bar{v}_s}$ is the average traveling speed of metro, and ${\bar{v}_i}$ is the traveling speed of the ith public transportation mode, km/h; $\gamma$ is the ratio between average ticket prices with and without metro transit.

Energy-Saving Benefit As to the energy consumption, power sources like fuel and electricity are considered. Special consideration is also given to the occupancy of different public transportation modes. Therefore, the energy-saving benefit is obtained by:

$$\begin{aligned} {C_{\mathrm{es}}} = \sum \limits _{i = 1}^2 {{P_s} \cdot \frac{{{\lambda _i}^\prime }}{{{\rho _i}}} \cdot {\chi _i}{\varphi _i}} - {E_s} \cdot {\varphi _s} \end{aligned}$$

(16)

where ${P_s}$ is the total passenger-kilometers of metro network during the peak hour; ${\chi _i}$ is the average unit energy consumption of the ith public transportation, the fuel-powered is L/km and the electricity-powered is Kwh/km; ${\varphi _i}$ is the average cost of the ith transportation mode, where the unit of fuel-powered is 10${^3}$ Yuan/L, the unit of electricity-powered is 10${^3}$ Yuan/Kwh; ${\rho _i}$ is the average occupancy, passenger/vehicle; ${E_s}$ is the total energy consumption of trains running in the peak hour, with a calculation similar to Eq. 12.

Combining Eqs. 15 and 16, the external benefits $B_s^{\mathrm{net}}$ of metro during the peak hour is:

$$\begin{aligned} B_s^{\mathrm{net}} = {C_{\mathrm{ts}}}{\mathrm{+ }}{C_{\mathrm{es}}} \end{aligned}$$

(17)

From the foregoing modeling and analysis, the economic objective of the whole network is formulated as:

$$\begin{aligned} \min {Z_1} = C_p^{\mathrm{net}}{\mathrm{+ }}C_t^{\mathrm{net}} - B_s^{\mathrm{net}} \end{aligned}$$

(18)

3.3 Line Capacity Usage Objective

An ideal scheme should maximize the section capacity usage and reach the best balance, where the section capacity usage is defined as the ratio of maximum segment volume to current transportation capacity, namely:

$$\begin{aligned} {\sigma _s} = {{\max \left( {Q_s^u,Q_s^d} \right) } /{\left( {{C_s} \cdot {\mathrm{60}}/{I_s}} \right) }} \end{aligned}$$

(19)

where ${\sigma _s}$ is the capacity usage rate of the sth segment; $Q_s^u$ and $Q_s^d$ are the segment volume in up direction and down direction, respectively, passengers/h; ${C_s}$ is the average train capacity in the routing section including segment s, passengers/train; I$_{s}$ is the relevant train headway, min.

As we know, a higher section capacity usage is equivalent to a fewer line capacity remaining. The capacity of overlapped section is train capacity of both long route and short route, while capacity outside the overlapped section is the basic capacity of the long route (see Fig. 5).

Fig. 5

Line capacity under different routing sections

Therefore, the average transportation capacity of line L is:

$$\begin{aligned} {\bar{A}_L} = \left\{ {\begin{array}{cc} {\alpha {c_\alpha } \cdot \frac{{{\mathrm{60}}}}{{{I_\alpha }}}\left( {1 + {\eta _L}} \right) }&{}{{\mathrm{LR}}}\\ {\alpha {c_\alpha } \cdot \frac{{{\mathrm{60}}}}{{{I_\alpha }}}\left( {1 + {\eta _L}} \right) {\mathrm{+ }}r\beta {c_\beta }\frac{{{\mathrm{60}}}}{{{I_\alpha }}}\left( {1 + {\eta _L}} \right) \cdot \frac{{q - p - 1}}{{m - 1}}}&{}{{\mathrm{SR}}} \end{array}} \right. \end{aligned}$$

(20)

where ${\bar{A}_L}$ is the average section capacity of line L during the peak hour.

To guarantee the nonnegativity, the remaining of section capacity usage is constructed via the method of difference quadratic sum (DQS):

$$\begin{aligned} \begin{array}{l} {\Gamma _L}{\mathrm{= }}{\sum \limits _{i \notin \left[ {{p_L},{q_L} - 1} \right] } {\left( {1 -\displaystyle \frac{{\max \left\{ {Q_{i,i + 1}^u,Q_{i,i + 1}^d} \right\} }}{{{\alpha _L}c_L^\alpha \cdot \frac{{60}}{{{I_L}}}\left( {1 + {\eta _L}} \right) }}} \right) } ^2} +\\ \qquad {\sum \limits _{i \in \left[ {{p_L},{q_L} - 1} \right] } {\left( {1 -\displaystyle \frac{{\max \left\{ {Q_{i,i + 1}^u,Q_{i,i + 1}^d} \right\} }}{{\left( {{\alpha _L}c_L^\alpha + {r_L}{\beta _L}c_L^\beta } \right) \cdot \frac{{60}}{{{I_L}}}\left( {1 + {\eta _L}} \right) }}} \right) } ^2} \end{array} \end{aligned}$$

(21)

where ${\Gamma _L}$ is the DQS of capacity usage remaining in line L; $Q_{i,i + 1}^u$ is the segment volume between the ith and i+1th station in the up direction, and $Q_{i,i + 1}^d$ is the volume in the down direction, passengers/h.

In order to define the objective of network transportation efficiency, the section capacity remaining is combined with line capacity by linear weighting as:

$$\begin{aligned} \min {Z_2} = \sum \limits _{L = 1}^N {\left( {{{{{\bar{A}}_L}} /{\sum \limits _{L = 1}^N {{{\bar{A}}_L}} }}} \right) {\Gamma _L}} \end{aligned}$$

(22)

3.4 Transfer Coordination Objective

Three major goals should be considered for transfer coordination during the peak hour as follows:

• The capacity of adjacent segments should satisfy the passenger demand in every possible direction.

• The number of left-behind passengers with secondary queuing should be as lower as possible.

• The waiting time of passengers should be minimized, which has been considered in the time cost

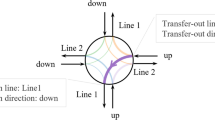
Due to the disequilibrium of passenger O-D distribution under urban land-use composition, different transfer directions have different passenger flow volumes. However, the less busier directions will naturally get satisfied when the busiest direction of each line gets optimized. Typical busy directions at a crossed transfer station are shown in Fig. 6

Fig. 6

Direction analysis of a crossed transfer station

Segment Volume Constraints Based on the capacity usage analysis in Sect. 3.3, we can get the segment capacity constraint for line L$_{i}$ as Eq. 23, by introducing $Q_{{L_i}k}^{\max }$, the maximum adjacent segment volume of Line L$_{i}$ at transfer station k, passengers/h.

$$\begin{aligned} \left\{ {\begin{array}{cc} {\left( {{\alpha _{{L_i}}}c_\alpha ^{{L_i}} + {r_{{L_i}}}{\beta _{{L_i}}}c_\beta ^{{L_i}}} \right) \cdot \frac{{{\mathrm{60}}}}{{{I_{{L_i}}}}}\left( {1 + {\eta _{_{{L_i}}}}} \right) \ge Q_{{L_i}k}^{\max }}&{}{{\mathrm{Nested}}}\\ {{\alpha _{{L_i}}}c_\alpha ^{{L_i}} \cdot \frac{{{\mathrm{60}}}}{{{I_{{L_i}}}}}\left( {1 + {\eta _{_{{L_i}}}}} \right) \ge Q_{{L_i}k}^{\max }}&{}{{\mathrm{Single}}} \end{array}} \right. \end{aligned}$$

(23)

Left-Behind Passengers The disequilibrium in passengers arrival rate leads to the discontinuity of secondary queuing during the peak hour. Therefore, the cumulative number of left-behind passengers in the ultra-peak period is taken into account.

When L applies the single routing, we have:

$$\begin{aligned} \begin{array}{l} N_L^{pk} = \\ P_{L({t_a})}^{de} + \int _{{t_a}}^{{t_b}} {\left( {\alpha _{(t)}^{LE} + \sum \limits _j {\alpha _{j(t)}^{LT}} - \displaystyle \frac{{({\eta _{\max }} - \eta ){\alpha _L}c_\alpha ^L}}{{{I_L}}}} \right) } dt. \end{array} \end{aligned}$$

(24)

When L applies the nested routing mode, we have:

$$\begin{aligned} \begin{array}{l} N_L^{pk} = P_{L({t_a})}^{de} + \\ \displaystyle \int \limits _{{t_a}}^{{t_a}} {\left( {\alpha _{(t)}^{LE} + \sum \limits _j {\alpha _{j(t)}^{LT}} - \frac{{({\eta _{\max }} - \eta )\left( {{\alpha _L}c_\alpha ^L + {r_L}{\beta _L}c_\beta ^L} \right) }}{{{{{I_L}} / {\left( {1{\mathrm{+ }}{r_L}} \right) }}}}} \right) } dt. \end{array} \end{aligned}$$

(25)

Here $N_L^{pk}$ is the cumulative number of left-behind passengers in the busiest transfer direction of line L during the ultra-peak period;${t_a}$ and ${t_b}$ represent the beginning time and ending time, min; $P_{L({t_a})}^{de}$ is the number of left-behind passengers before ${t_a}$; $\alpha _{(t)}^{LE}$ is the arrival rate of entering passengers in the busiest direction, while $\alpha _{j(t)}^{LT}$ is the arrival rate of transfer-in passengers from the other jth direction , passengers/min; $\eta$ is the average occupancy rate of related section in view of arrival trains, section volume and the peak hour factor (PHF) $\kappa$.

Therefore, the network transfer coordination objective is formulated as:

$$\begin{aligned} \min {Z_{\mathrm{3}}} = \sum \limits _{i = 1}^N {\sum \limits _{k = 1}^K {N_{{L_i}}^{pk}}}. \end{aligned}$$

(26)

3.5 Hybrid Solution Algorithm

The optimization model is formulated as an MOP (see Eq. 27), with decision variables ${\alpha _L}$, ${\beta _L}$, ${r_L}$ and ${I_L}$.

$$\begin{aligned} \begin{array}{l} \min \left\{ \begin{array}{l} {Z_1} = {f_1} ({\alpha _L}, {\beta _L},{r_L},{I_L}) , {Z_{\mathrm{2}}} = {f_{\mathrm{2}}} ( {\alpha _L}, {\beta _L},{r_L},{I_L}) ,\\ {Z_3} = {f_3}({\alpha _L},{\beta _L},{r_L},{I_L} ) \end{array} \right\} \\ s.t.\left\{ {\begin{array}{l} {1.5(1 + {r_L}) \le {I_L} \le 7,{r_L} \in \left\{ {1,2} \right\} }\\ {{\beta _L} \in \left\{ {4,5,6} \right\} }\\ {\left( {{\alpha _L}c_\alpha ^L + {r_L}{\beta _L}c_\beta ^{{L_i}}} \right) \cdot \frac{{{\mathrm{60}}}}{{{I_L}}}\left( {1 + {\eta _{_L}}} \right) \ge Q_{Lk}^{\max },{\mathrm{Nested}}}\\ {{\alpha _L}c_\alpha ^L \cdot \frac{{{\mathrm{60}}}}{{{I_L}}}\left( {1 + {\eta _{_L}}} \right) \ge Q_{Lk}^{\max },{\mathrm{Single}}}. \end{array}} \right. \end{array} \end{aligned}$$

(27)

MOPs are usually solved by methods like linear weighting, distance function, and stratified sequencing. After analysis, the forbearing stratified sequencing method (FSSM) is applied, with the advantage in expanding the optimal solution space by introducing a forbearance threshold at each sequence [29]. The feasible solution of the ith objective is defined as:

$$\begin{aligned} {F_i}{\mathrm{= }}{F_{i - {\mathrm{1}}}} \cap \left\{ {\left. {\tilde{x}} \right| {{Z'}_{i - 1}}(\tilde{x}) \le {{Z'}_{i - 1}}^ * + {\varepsilon _{i - 1}}} \right\} \begin{array}{cc} ,&{i \ge 2}, \end{array} \end{aligned}$$

(28)

where ${F_{i - {\mathrm{1}}}}$ denotes the feasible solution of the i-1th sub-objective; $\tilde{x}$ is the vector of decision variables; ${Z'_{i - 1}}^ *$ is the optimal value of the i-1th objective; ${\varepsilon _{i - 1}}$ is the forbearance threshold.

Fig. 7

Algorithm process of GA–ACO

Fig. 8

Segment volume distribution of line 2 (peak hour)

Table 1 Basic parameters used in the model

The ant colony optimization (ACO) can merge heuristic information into the evolution because of the positive feedback mechanism, but it is apt to plunge into local optimum. While the genetic algorithm (GA) can perform a global parallel searching with a faster convergence, but it lacks the feedback mechanism[30, 31]. So we nest a GA inside the ACO to weaken the dependence on pheromones, shown in Fig. 7.

4 Case Analysis

Taking the metro network of Xi’an as an example, which is a small-size transit network consist of 3 lines, with a volume over 130,000 passengers during the peak hour. The optimization of current train scheme in the peak hour is performed in this section, followed by a comprehensive evaluation.

4.1 Data Collection

The O-D data of passenger flow distribution during the peak hour (December 8, 2016) provides as the basis of routing mode selection and parameters calibration. Table 1 shows the value of major parameters used in the MOP.

Routing Mode Selection According to the passengers O-D data and shortest path assignment, the spatial distribution of segment volume of each line can be obtained. Taking line 2 as an example, the volume distribution along the line is shown in Fig. 8.

Upon routing analysis, a nested mode is necessary for line 2 during the peak hour. To determine the turn-back stations, the degree of suitability is calculated using Eq. 1, and results are listed in Table 2.

As indicated in Table 2, the suitability of middle stations like FCWL, STSG, HZZX, and SY are relatively high. In a deep analysis, the segment volumes outside the line section STSG–HZZX are below the basic line capacity, and station HZZX has been reserved as a transfer station. Therefore the reasonable section for short routing is from STSG to SY.

Transfer Analysis There are 3 transfer stations in this small-size metro network, basic data are listed in Table 3.

Table 2 Station suitability analysis of line 2

Table 3 Basic data of transfer stations (peak hour)

Table 4 Passengers flow distribution at Beidajie station

According to Fig. 6, only the two busiest directions require analysis for a crossed transfer station. Therefore, the passengers flow distribution at each transfer station should be specified before modeling. Taking the Beidajie station as an example, the passenger flow distribution is shown in Table 4. It is obvious that the up direction of Line 1 and down direction of Line 2 are the busiest transfer directions at Beidajie station.

4.2 Model Solution

Since the model is oriented at transfer coordination, when using the FSSM, the sequence of sub-objectives is transfer coordination, economic cost and capacity utilization accordingly in view of the priority. Transfer Coordination Objective The objectives at this level are:

$$\begin{aligned} \left\{ \begin{array}{l} \min {Z_{{\mathrm{13}}}} = {\mathrm{7043}} - {{{\mathrm{26280}}} /{{I_1}}}\\ \min {Z_{{\mathrm{23}}}} = {\mathrm{22306}} - 30\left( {\displaystyle \frac{{{\mathrm{1460}} + {r_2}{\beta _{{L_2}}}c_\beta ^{{L_2}}}}{{{{{I_2}} / {(1 + {r_{\mathrm{2}}})}}}}} \right) \\ \min {Z_{{\mathrm{33}}}} = {\mathrm{5620}} - {{{\mathrm{24090}}} /{{I_{\mathrm{3}}}}} \end{array} \right. \end{aligned}$$

(29)

Considering Eq. 27,the variable constraints are updated as:

$$\begin{aligned} s.t.\left\{ {\begin{array}{c} {{\mathrm{3}}{\mathrm{.73}} \le {I_{\mathrm{1}}} \le {\mathrm{7}}{\mathrm{4}} \le {I_{\mathrm{2}}} \le {\mathrm{6}}{\mathrm{.82}}{\mathrm{4}}{\mathrm{.28}} \le {I_{\mathrm{3}}} \le {\mathrm{6}}{\mathrm{.3}}}\\ {{r_{\mathrm{2}}} = 1,{\beta _{\mathrm{2}}} \in \left\{ {4,5,6} \right\} } \end{array}} \right. \end{aligned}$$

(30)

Economic Objective The economic objective of each line can be calibrated as:

$$\begin{aligned} \left\{ \begin{array}{l} \min {Z_{{\mathrm{11}}}} = {\mathrm{5}}{\mathrm{.06}}{I_1} + {{{\mathrm{103}}{\mathrm{.76}}} /{{I_1}}} + C_1^1\\ \min {Z_{{\mathrm{21}}}} = {\mathrm{6}}{\mathrm{.55}}{I_{\mathrm{2}}} + {{\left( {{\mathrm{109}}{\mathrm{.7 + 10}}{\mathrm{.48}}{\beta _{{L_{\mathrm{2}}}}}} \right) } /{{I_{\mathrm{2}}}}} - \\ {\mathrm{3}}{\mathrm{.12}}{\beta _{{L_{\mathrm{2}}}}} + C_2^1\\ \min {Z_{{\mathrm{31}}}} = {\mathrm{4}}{\mathrm{.15}}{I_{\mathrm{3}}} + {{{\mathrm{106}}{\mathrm{.76}}} /{{I_{\mathrm{3}}}}} + C_3^1 \end{array} \right. \end{aligned}$$

(31)

where the $C_1^1$, $C_2^1$, and $C_3^1$ are fixed items arising from ticket cost and some external benefits.

The economic objective of Line 2 is a function of LR headway and SR marshaling number, and the variable economic cost will achieve the minimum when the SR marshaling number is 6, as shown in Fig. 9. Equation 32 is the objective function when ${\beta _{{L_{\mathrm{2}}}}}$ is 6, and Fig. 10 shows the corresponding curve.

$$\begin{aligned} \min {Z_{{\mathrm{21}}}} = {\mathrm{6}}{\mathrm{.55}}{I_{\mathrm{2}}} + {{{\mathrm{172}}{\mathrm{.58}}} / {{I_{\mathrm{2}}}}} - 18.72 + C_2^1 \end{aligned}$$

(32)

Fig. 9

Relationship surface of economic objective (line 2)

Fig. 10

Minimum curve of economic objective (line 2)

According to Eq. 32, the economic cost of line 2 achieves the minimum when the LR headway I$_{2}$ is 5.13 min under a 6-car SR marshaling. Given the forbearance value $0.4 \times {10^3}$ Yuan, the constraint of headway I$_{2}$ is replaced by ${\mathrm{4}}{\mathrm{.60}} \le {I_{\mathrm{2}}} \le {\mathrm{5}}{\mathrm{.72}}$. Headway constraints of other lines are updated in a similar way. Capacity Utilization According to Eq. 22, the network capacity objective is a linear weighting of line transportation capacity:

$$\begin{aligned} \begin{array}{l} {\min {Z_{\mathrm{3}}}{\mathrm{= }}\displaystyle \frac{{{\mathrm{0}}{\mathrm{.284}}{I_1}{I_2}{I_3}^2 + \Omega \cdot {I_3} + 55{I_1}{I_2}}}{{(3.3{I_1} + 2.4{I_2}) \cdot {I_3} + 2.2{I_1}{I_2}}}}\\ {\Omega = {\mathrm{0}}{\mathrm{.547}}{I_1}^2{I_2} + {\mathrm{0}}{\mathrm{.828}}{I_1}{I_2}^2 - 29.29{I_1}{I_2}}\\ \qquad + 66{I_1} + 43.2{I_2} \end{array} \end{aligned}$$

(33)

The GA–ACO algorithm is then applied to solve this problem because of its complexity and nonlinearity. The number of ants is set as 40, while the generation gap, crossover probability and mutation probability are 0.9, 0.7 and 0.001, respectively. Before achieving the maximum iteration, the optimal solution is found as I$_{1}$=4.9400, I$_{2}$=5.7198, I$_{3}$=5.5899, and the objective value is 6.7704. The convergence becomes stable at 120th iteration, shown in Fig. 11.

Fig. 11

Algorithm iteration process

4.3 Model Evaluation

Global Evaluation Table 5 lists the train organization schemes before and after the optimization. Table 6 shows the evaluation of major indicators. Obviously, the optimized scheme has a fewer left-behind passengers, a higher capacity utilization, a lower consumption and a fewer rolling stocks. However, the total trip time cost is higher than the original scheme due to a longer headway of line 3. In general, the optimized scheme is better than the original one in the network transfer performance and transport efficiency.

Table 5 Key variables of original and optimized scheme

Table 6 Theoretical value of major indicators (peak hour)

Microevaluation Since the model gives a specific consideration to transfer coordination, it is necessary to evaluate the performance at transfer stations at a microlevel. The simulation module Viswalk (PTV VISSIM 7.0) is applied to perform a simulation of interaction among passengers, trains and platform infrastructure at a transfer station. Taking the Beidajie station as an example, which is a transfer station of line 1 and line 2. Figure 12 shows the 3D simulation.

Fig. 12

The 3D simulation of Beidajie station

The microsimulation has been performed before and after the optimization, respectively, by adjusting parameters like the passengers alighting proportion, the train marshaling number and the operation schedule. According to Table 3, the platform of line 2 attracts more passengers than the platform of line 1, therefore we focus on the platform’s passenger density of line 2. The number of passengers gathered on platform [32] and distribution density [33] are key indicators of transfer coordination among metro lines. Figure 13a shows the maximum passenger density distribution on the platform of line 2 under the original organization scheme, while Fig. 13b reflects the density distribution under the optimized scheme. For the original scheme, the maximum number of platform passengers is 1670, and the average distribution density is 1.86 passengers/m$^{2}$. While under the optimized scheme, the maximum number of platform passengers is 1490, and the distribution density has decreased to 1.66 passengers/m$^{2}$.

Fig. 13

Platform’s passenger density distribution of line 2 at Beidajie station (passengers/m$^{2}$)

Discussion As compared to the original scheme, under the optimized train organization, the network left-behind passengers in busy directions decreased 55.3$\%$, the capacity remaining decreased 15.3$\%$, the number of rolling stocks decreased 8.5$\%$, while the total time cost increased 1.6$\%$. From the perspective of transfer simulation, it is obvious that the average passenger density on the platform of line 2 reduced to 1.66 passengers/m$^{2}$ from 1.86 passengers/m$^{2}$ at Beidajie station. The results of theoretical solution and microsimulation have validated the feasibility of our proposed model.

5 Conclusions

This study developed the modeling method for train operation considering transfer coordination in a small-size network. It is formulated as a multi-objective programming, solved by a sequencing method together with GA–ACO, where data of passengers O-D flow and network infrastructures are used in model formulation and parameter calibration.

The biggest contribution is the problem formulation. The MOP model targets the generalized cost, the capacity utilization and the transfer coordination, by setting the train headway and the marshaling number as decision variables based on preliminary routing analysis. The economic objective gives an extra consideration of external benefits brought by metro transit. The capacity usage objective minimizes the section capacity remaining considering a basic transport efficiency. The transfer coordination objective is highly considered with an emphasis on the left-behind passengers and train capacity remaining. Furthermore, a case analysis to the metro network in Xi’an has verified the feasibility of proposed model, and the theoretical results have been validated via a microsimulation. As a result, the presented MOP model is useful in optimizing train operation for the alleviation of passengers crowding at transfer stations.

More specifically, the proposed method has several advantages. Firstly, the model can greatly reduce the number of left-behind passengers on busy platforms, at a small sacrifice of trip time on other lines. Secondly, the basic routing mode and transport efficiency are guaranteed by necessary analysis and constraints. Thirdly, the hybrid algorithm of GA–ACO is applied to solve the model accurately and efficiently.

The major limitation of this paper lies in the analysis of passengers transfer behaviors and network route choice. On the one hand, the transfer behaviors usually consist of walking behavior, queuing behavior and target choice behavior [34,35,36]. These behaviors are usually affected by the factors from station infrastructure, operation scheme and individual characteristics, while the model only targets at the relation between the left-behind passengers and operation scheme. On the other hand, when the left-behind passengers continues increasing at a transfer station, the phenomenon of crowding effect [37] will lead to some changes in passengers’ route choice [38]. Therefore, some parameters like the segment volume and arrival rate calibrated in the model will get affected accordingly. However, applications of the proposed method can provide basic implications in the evaluation of train operation schemes for transfer stations.

Our future research will be focused on the following aspects. First, it is important to further consider other train routing modes [39] (Y-type routing, circular routing and etc.) and their applicability, so that a more optimal organization scheme can be figured out for a metro network with higher complexity. Second, supplementary study of multi-station coordinated passenger route choice and control [40] are necessary to maintain the transfer equilibrium in the metro network. Last but not least, self-mediated algorithms like Pareto-based PSO [41] and NSGA-II are worth applying to improve the solution, considering the conditionality and relevance between sub-objectives.