1 Introduction

As one of the main environmental loads of the bridge, the temperature load has always been the key monitoring object of the health monitoring system [1, 2]. Due to the constant thermal interaction between the structure and the external environment, the temperature load and temperature field distribution in the concrete structure is always changing [3, 4]. The significant variability of the temperature effect and the complexity of the temperature field distribution cause interference with the accuracy of structure evaluation [5]. For example, the high-order frequency of the structure is sensitive to damage, but the temperature change will also cause a change in the structure frequency [6]. Besides, the strain, deflection, and other output responses of the bridge structure health monitoring usually contain temperature components, and a sudden drop in temperature may conceal the change in response caused by structural damage [7]. To obtain more accurate structural condition assessment and damage identification based on temperature effects, many scholars have done lots of work on the laws and characteristics of temperature load and temperature response. Specifically, Brownjohn et al. and Hedegaard et al. carried out the long-term observation of temperature load and bridge temperature response and provided the strain response characteristics under multiple cyclic temperature loads [2, 8]. Tayşi et al. proposed the temperature distribution characteristic parameters of the box-girder bridges by combining field section tests and numerical simulation methods [9]. Xia et al. revealed the temporal and spatial patterns of the structural response of a large-span suspension bridge by 1 year`s measured data [10]. These research works provide valuable insight into the study of the bridge temperature effect.

The output response of a bridge structure in service generally contains the combined effect of environmental and vehicle loads [11,12,13]. The two are superimposed in the time domain. Achieving the separation of the environmental and vehicle load components in the response signal is a prerequisite for further study of each load and a fundamental task for accurate structural assessment [14, 15]. There are two main methods for the separation of temperature effects: signal feature separation methods and temperature compensation methods. The first one is based on the difference in signal characteristics between the temperature response and the vehicle response in the time and frequency domains to achieve the purpose of separation [16, 17]. Zhao et al. adopted wavelet transform to identify temperature-induced/train-induced deflections of the bridge girder from deflection data [18]. Ding et al. implemented an adaptive finite impulse response (FIR) filter to obtain the different components of the strain influence line of the Dashengguan Yangtze River Bridge [19]. This is a common and effective approach, but its applicability in the sudden cooling condition is still lacking studied, besides it is only a rough implementation of signal processing without theoretical support of mechanical mechanisms. The second method is based on the theory that the temperature response of the structure is linearly dependent on the temperature, to separate different components by mathematical methods such as regression or fitting [6, 20]. Although all the above studies have yielded good results, they lack sufficient consideration of the complexity of temperature field effects and the temporal characteristics of temperature transformation. However, the accurate separation of temperature-induced effects and the identification of bridge structural damage based on temperature effects are based on a clearer understanding of the temperature-temperature response relationship [21,22,23].

The most important feature of the temperature response and temperature is the presence of the time-lag effect. The time-lag effect of the temperature response refers to the phenomenon that the change of the temperature response of the structure lags behind the temperature itself in the time domain [24, 25]. The time-lag effect has attracted widespread attention from scholars [26]. Yang et al. made a preliminary discussion on its law and proposed an elimination method adopting the Fourier series [25]. Jiang et al. eliminated the time-lag effect using the nonlinear phase-shifting method [27]. However, it is far from enough to summarize its characteristic laws, theoretical analysis of its generation mechanism, and further exclude the effect of this effect in damage identification and assessment to improve assessment accuracy.

To address the above problems, this paper attempts to explore the inner mechanism of the time-lag effect in small box girder bridges by combining measured data mining and numerical simulation methods, as shown in Fig. 1. On this basis, a method to reduce the effect is proposed. Specifically, firstly, relying on the long-term observation of a large amount of measured data of a real bridge, the law and time characteristics of the time-lag effect are summarized. Then, the finite element simulation of the temperature–time-lag effect is realized, and the temperature–time-lag effect is studied with the help of various temperature load model inputs. Consequently, the time and spatial characteristics of this effect can be revealed. Subsequently, the laws of measured data and the results of numerical simulations are combined to reveal the mechanism. A key indicator that affects the time-lag effect is put forward, and based on this indicator, a method to eliminate the temperature–time-lag effect is proposed, which is applied to the measured data to verify the practicability of the method. Finally, based on the damage simulation experiment, the sensitivity of the time-delay feature to structural damage is verified (Fig. 1).

Fig. 1
figure 1

Framework of this paper

Full size image
Fig. 2
figure 2

Lieshihe bridge: (a) photo of the Lieshihe bridge; (b) schematic diagram of measuring point location

Full size image

2 Study on the mechanism of temperature time-lag effect

2.1 The time-lag effect

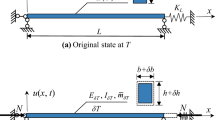
Taking the Lieshihe bridge in a province of China as an example, we excavated the temperature-induced strain and the time-lag effect of temperature in the measured data and performed numerical simulations to try to reveal the generation mechanism, influencing factors, and elimination methods of the time-lag effect. The Lieshihe bridge is a multi-span simply supported box girder bridge. With a span of 25 m the bridge is composed of 5 small box beams with a beam height of 1.5 m, as shown in Fig. 2a. This type of bridge is very common on expressways and arterial roads, and the study of its temperature effect is of more general significance for concrete bridges. The bridge is equipped with 4 temperature measuring points and 10 strain measuring points. The temperature measuring points are displaced transversely to the positions of the bottom and top plates of the two outermost box girders. The strain measuring points are evenly distributed on the bottom plate of each box girder. The specific positions are as shown in Fig. 2b.

The effect of temperature includes the heat exchange between the structure and the environment such as solar radiation and air heat convection. Typically, the temperature load has significant variability over days. However, there are significant time characteristics in different time dimensions such as seasons and days, which are manifested in the large temperature difference between spring and autumn, and the significant effect of winter and summer temperatures. A typical temperature load, during the day, usually starts to fall slowly from 24:00 in the morning and then rises rapidly after the sun rises at 7:00 in the morning. It reaches the highest temperature of the day at about 3:00 in the afternoon, and then slowly decreases until the next day begins in the early morning. In addition, as shown in Fig. 3a, temperature measurement point 1 heats up faster in the morning hours compared to temperature measurement point 3. This is due to the fact that measurement point T1 is located on the east baseplate of the north–south oriented bridge, which is exposed to sunlight directly in the morning and therefore heats up faster and reaches its peak temperature before measurement point T3. However, if the weather drops suddenly, the temperature will drop significantly in a short period. As shown in Fig. 3a, b respectively.

Fig. 3
figure 3

Temperature time history: (a) typical daily temperature load; (b)sudden cooling temperature load

Full size image

The measured data of long-term monitoring found that there is a certain degree of hysteresis between the temperature-temperature response. The temperature lag phenomenon refers to the phenomenon that the temperature-induced structural response, such as temperature-induced strain or temperature-induced deflection lags behind the temperature itself in time. It turns out that the peak of the temperature response lags behind the peak of the temperature on the time scale. If the temperature-temperature response is plotted in one graph, it appears as a non-linear ring-shaped feature as shown in Fig. 4. For a typical daily temperature effect, there is a process in which the temperature first rises and then falls. In the rising process, the strain response of the structure has a lag, and its value at the characteristic moment is less than the representative temperature at that moment, so it turns into a concave curve. In the same way, when the temperature drops, the actual measured value of the structure is higher than the representative temperature of the current moment, and the graph shows a convex curve. Therefore, during the whole day's temperature rise and fall, the image characteristic of temperature-temperature-induced strain appears as a spindle curve. For the measured data, we adopt the time lag curves corresponding to T1-S2 as the benchmark. It`s clear that the temperature and strain measurement points at these two points are the closest, and their time lag curves are also the least significant, which satisfies the conditions for the benchmark.

Fig. 4
figure 4

The time-lag effect of temperature response

Full size image

2.2 Strain of simply supported beam under nonlinear temperature gradient

Regardless of temperature change, for a certain moment, under a specific temperature, for a simply supported beam bridge, the free longitudinal strain of the box-section beam under the load of the nonlinear vertical temperature gradient \(T(y)\) is:

$$\varepsilon_{T} (y) = \alpha T(y)$$
(1)

where, \(\alpha\) is the concrete expansion coefficient.

Since the actual beam section conforms to the assumption of a flat section, the strain at height y is:

$$\varepsilon (y) = \varepsilon_{0} + \psi y$$
(2)

where, \(\varepsilon_{0}\) Is the strain at the bottom edge of the beam; \(\psi\) is the curvature after deformation.

The temperature self-strain is the difference between the constraint strain expressed by the above two formulas, namely:

$$\varepsilon_{t} (y) = \alpha T(y) - (\varepsilon_{0} + \psi y)$$
(3)

The generation of temperature self-stress does not affect the internal force balance of the section. And according to the internal force balance equation \(\sum {N_{x} = 0}\) and \(\sum {M = 0}\), it can be obtained that:

$$E\int\limits_{0}^{h} {\varepsilon_{t} b(y)dy} = 0$$
(4)
$$E\int\limits_{0}^{h} {\varepsilon_{t} b(y)(y - y_{c} )dy} = 0$$
(5)

where, \(b_{(y)}\) Indicates the width at the height y of the section.

Incorporating Eq. (3) into Eq. (4) and Eq. (5) in parallel, we can get:

$$\varphi = \frac{\alpha }{I}\int\limits_{0}^{h} {T(y)b(y)(y - y_{c} )dy}$$
(6)
$$\varepsilon_{0} = \frac{\alpha }{A}\int\limits_{0}^{h} {T(y)b(y)dy - \varphi } y_{c}$$
(7)

The constraint strain can be obtained by substituting Eq. (6) and Eq. (7) into Eq. (3):

$$\varepsilon_{t} (y) = \alpha T(y) - \frac{\alpha }{A}\int\limits_{0}^{h} {T(y)b(y)dy - \frac{\alpha }{I}} (y_{c} - y)\int\limits_{0}^{h} {T(y)b(y)} (y_{c} - y)dy$$
(8)

It can be seen from Eq. (8) that the structural strain caused by the uneven temperature gradient of a simply supported statically determinate single beam that does not consider the boundary effect is not only related to the material elastic modulus, cross-sectional area, the moment of inertia, etc. but also related to the temperature gradient mode.

In reality, the temperature strain of a beam bridge composed of multiple small box beams is more complicated under the action of time-varying temperature. First, the temperature is unevenly distributed among multiple beams, resulting in different vertical temperature gradients in different beams, causing uneven distribution of temperature strain in the horizontal direction. Secondly, the non-linear change of temperature in time causes uneven temperature differences in the lateral direction at different moments, which causes the strain difference at multiple points in the lateral direction at different moments to be different.

In general, the temperature response exhibits complex nonlinear characteristics due to the non-uniformity of temperature distribution and the nonlinearity of temperature time-varying. The temperature effect will be more complicated if the changes in materials, geometry, and boundary conditions caused by components and connection damage are considered. However, the above derivation clearly shows that the temperature-induced strain of a specific beam is closely related to the vertical temperature gradient. Therefore, it can be reasonably inferred that when the actual temperature gradient effect of the beam body lags behind the characterizing temperature, the temperature response and characterizing temperature naturally have hysteresis-related characteristics.

2.3 The characteristics and laws of temperature time-lag effect

Figure 5 shows the seasonal characteristics of the time-lag effect. It can be noticed that the degree of the time-lag effect of the same sensor is more significant in summer compared to winter in the measured data. This feature may be related to the more prominent structural temperature gradient due to the more intense solar radiation in summer. And this reflects the long-period time characteristics of the time-lag effect.

Fig. 5
figure 5

Seasonal characteristics of temperature lag effect: (a) summer; (b) winter

Full size image

The time-lag characteristics of temperature-induced strain at different locations on the same day are shown in Fig. 6. It can be found that the degree of the time-lag effect of different strain sensors corresponding to the same temperature sensor varies with the position of the strain sensor. This characteristic may be related to the inhomogeneous distribution of the lateral temperature gradient of the structure. This reflects the spatial distribution characteristics of the time-lag effect.

Fig. 6
figure 6

The time-lag effect of different strain measuring points

Full size image

To analyze the specific correspondence between the temperature sensor and the strain sensor in the same day measured data in detail, the temperature-induced strain of the same temperature sensor and the strain sensor at different positions are plotted on a graph, as in Fig. 7. It is found that the time-lag curves of different strain sensors vary with the sensor positions, reflecting the differences in the lateral distribution of the structural response, i.e. the inhomogeneity of the temperature-induced strain field in the lateral direction. Similarly, the time-lag curves of different temperature sensors at the same location are plotted in Fig. 8, and it is easy to find that the time-lag curves of the same strain sensor for different temperature sensors vary with the location of the sensor, reflecting the inhomogeneity of the horizontal and vertical temperature gradients of the structure. Combining Figs. 7 and 8, it can be found that the complexity of the time-lag curve is influenced by both the inhomogeneity of the temperature distribution and the inhomogeneity of the corresponding field of the structure, which together create the complexity and diverse variability of the time-lag curve.

Fig. 7
figure 7

The characteristics of time-lag corresponding to different strain measuring points

Full size image
Fig. 8
figure 8

The characteristics of time-lag corresponding to different temperature measurement points

Full size image

The temperature-strain time-lag curves for more than 90 days were classified according to the morphological characteristics of the curves and plotted in Fig. 9. The most common one is the fusiform shape, followed by the hat shape, and the less common ones are the clover shape and the 'X' shape. As for the various types, it can be found that the daily temperature variation corresponding to the shuttle shape is most typical in the form of a relatively slow-varying sinusoidal-like curve. The hatched rows correspond to daily temperature curves with significant abrupt cooling or warming. The daily temperature curves corresponding to cloverleaf and 'X'-shaped curves usually have significant temperature crossover variations. The above correspondence between time-lag curves and temperature curves illustrates that the time-lag characteristics are closely related to the trend and rapidity of temperature curves. And the fusiform and clover shapes in Fig. 9a, c, can be interpreted in terms of bridge position and sunlight exposure. For the fusiform shape, the strain measurement point S4 is close to the temperature measurement point T1. Because the temperature gradient near S4 follows the temperature gradient of T1 closely during the warming and cooling process from morning to evening, it only shows a lag in the trend, so the fusiform shape appears. For the clover shape, since the strain measurement point, S9 is located on the west side of the bridge, the actual sunlight radiation process it receives is exactly opposite to that on the east side of S1, showing an inverse slope. In addition, after entering the night, the slopes of temperature and strain return to normal without being affected by the effect of sunlight from east to west, so the time-lag graph shows a clover shape with both positive and negative slopes.

Fig. 9
figure 9

Basic characteristics of time-delay graphs: (a) fusiform; (b) hat shape; (c) clover shape; (d) the ‘X’ shape

Full size image

2.4 Generation mechanism of temperature time-lag effect

The finite element simulation explores the corresponding relationship between the time-lag effect and the temperature load and temperature field distribution from the time and space characteristics. Combined with the specific analog temperature input and the corresponding time-lag shape characteristics, it is fed back to the measured data to verify the correctness of the mechanism conclusion. The finite element model uses solid elements, the thermal expansion coefficient of concrete material is 8.9/℃ × 10–6, and the grid division accuracy is 0.1 m. The temperature load of one day is simulated as a load step every 10 min, and a total of 144 temperature load time steps are taken in a day.

2.4.1 The influence of temperature time rate of change

Considering the significant variability of the temperature load over time within a day and the complexity of the temperature distribution, only the effect of temperature change rate on the time-lag effect is considered first. To exclude the influence of the temperature field, a uniform temperature field is used, as shown in Fig. 10. Guo et al. reveal that the displacement response of a suspension bridge lags the temperature change by 45 min [28], so it is reasonable to assume that the temperature response of concrete bridges lags the temperature by one hour. In this paper, the temperature-induced strain is assumed a lag of 1 h to simulate the heat conduction process with uniform temperature diffusion. Linear, fold line, and sinusoidal temperature loading patterns are used to simulate different rates of temperature change, respectively. Then the strains at each point location under the corresponding temperature loading modes were calculated by ANSYS finite element software, subsequently, the temperature-strain correlation curves were made.

Fig. 10
figure 10

Uniform temperature field loading pattern

Full size image

As shown in Fig. 11, the temperature and strain diagrams show different shapes when different temperature loading patterns are used. The temperature-strain curve is linear for the linear growth temperature loading pattern. The temperature-strain curves for linear temperature loading with dash lines are multiple dash lines, all of which differ significantly from the characteristics of the time-lag loop in practice. It indicates that the linearly varying temperature is not capable of producing the typical time-lag effect. The third sinusoidal temperature loading pattern appears to have the standard elliptical shape feature closest to the characteristics of the time-lag loop. It can be inferred that the variation of temperature with time affects the generation of the time-lag phenomenon or not. The effect of time is essentially related to the rate of change in temperature over time. When a linearly increasing temperature loading pattern is adopted, there is no hysteresis loop; when a folding form of temperature loading pattern is used, there is a reciprocal alternation of temperature and temperature response with the same slope, but there is still no typical hysteresis loop; when a sinusoidal form of temperature load time course is used, the rate of change of temperature with time keeps changing alternately, so a significant hysteresis loop finally appears. For the simulated data, the temperature load condition with a liner uniform temperature field was adopted as the benchmark model and it was found that there is no time lag in the ideal simulation results (as seen in Fig. 11(b) blue line). Consequently, the correlation between the time-lag phenomenon and time is verified, i.e., the time effect is the essential cause.

Fig. 11
figure 11

Temperature time change mode: (a) Time history data of temperature load; (b) Simulated temperature-acting time-delay effects

Full size image

2.4.2 Spatial action, temperature gradient

Then, the temperature load model is further refined to explore the influence of temperature gradient distribution on the time-lag effect. Four temperature gradient models: uniform temperature field, transverse temperature field, vertical temperature field, and horizontal and vertical temperature field were applied to the finite element model to investigate the law of the time-lag effect. The three-temperature time-history data shown in Fig. 12 correspond to the structural temperature inputs at the three temperature measurement points of the finite element model. The temperature inputs at other locations of the model are obtained by linear interpolation of the three temperatures, to realize the dynamic temperature field load. As for Fig. 13a, the uniform temperature field will cause the linear change of the structure with the temperature change. And the changes of strain are completely consistent with the change of the temperature itself. While the regularity changes from Fig. 12b, the lateral temperature gradient causes the difference of the temperature time-lag effect with different characteristics along the lateral direction and affects the slope at different points. However, the difference in time-lag characteristics in the lateral direction is smaller relative to that in Fig. 13c, mainly due to the smaller horizontal temperature gradient relative to the vertical temperature gradient. As for Fig. 13c, the vertical temperature gradient causes significant hysteresis characteristics, and the hysteresis loop is the fullest, which is the main source of the time-lag effect. At last, the hysteresis characteristics under the horizontal and vertical temperature gradients in Fig. 13d are closest to those in reality. The slope magnitude of the hysteresis loops at different points is different while including the characteristics of the horizontal and vertical simulations mentioned above. The reduction of the hysteresis loop area at the distal strain measurement point is due to the neutralization compensation of the horizontal and vertical temperature gradients. Thus, it is convinced that the time-lag contains the combined effect of the overall temperature field lift, lateral and vertical temperature difference, although each part has its characteristics and different degrees of effect, together they determine the final shape of the time-lag.

Fig. 12
figure 12

Simulated temperature load time history

Full size image

The coupling of temporal and spatial effects can be explained by the concept of a generalized temperature field [27]. The temperature at any point inside a concrete box girder bridge can be expressed as T = T(x,y,t), which includes not only the relationship between temperature T and time t but also the relationship between temperature T as a function of spatial position x and y. In essence, the time-varying temperature field affects whether the time-lag effect of the concrete box girder bridge is generated and its image characteristics. After multiple simulation studies and analyses, it can be found that the time-lag effect occurs when the images of the temperature–time history curves at the ends of the main girders of concrete box girder bridges have specific patterns. Firstly, the precondition for the appearance of the time-lag phenomenon is that there must be a fallback in the temperature time-history curve, i.e., the temperature rises and then falls, or falls and then rises so that there will be multiple moments with the same temperature and the time-lag curve produces a closure and forms a loop. Secondly, no time-lag effect can be introduced in the case that the temperature difference ΔT at the two ends of the main beam must be different, i.e., there is an inhomogeneous temperature gradient with dynamic changes. If the temperature difference ΔT is the same, i.e., for a uniform temperature gradient, no time-lag is introduced. Only when the temperature–time profile image has both of these characteristics does the time-lag phenomenon arise. From this, it can be presumed that there are both temporal and spatial influence mechanisms for the time-lag effect, but among them, the nonlinear rate of change of temperature is the root cause, and the temperature gradient affects the degree and morphological characteristics of the time-lag effect.

3 Elimination method of temperature time-lag effect

3.1 The method principle

The above simulation experiments have proved that the time-lag characteristics of the temperature effect are related to the temperature nonlinear change rate and the temperature gradient distribution, so a reasonable idea to eliminate the time-lag effect should consider the temperature change rate with time and the temperature gradient. Owing to that the temperature response of the statically determinate structure is linearly related to the temperature, it is reasonable to assume that the temperature-strain relationship should be linear after the time-lag effect of the temperature effect is eliminated. The detailed characteristics of the time-lag curve have two levels of error in slope and intercept compared to the linear relationship, from the perspective of image features. The next focus of error elimination lies in exploring the relationship between slope and intercept and temperature. To investigate the influence of the temperature change rate and the size of the temperature difference on the time-lag curve, the sinusoidal temperature input is used to study the relationship between the temperature change rate with time and the local slope and intercept of the hysteresis curve (Fig. 14).

Fig. 13
figure 13

The time-lag characteristics in various temperature field models

Full size image

As shown in Fig. 14, the temperature-strain relationship at the 6th measurement with uniform temperature field (at the leftmost top plate of the box beam) is linear at the ideal sinusoidal temperature load pattern, while the structure is linear intrinsically conditioned, i.e., there is no time-lag effect. The expression of the line Z is \({\text{Y}} = px + q\)(the blue line in Fig. 14). There are two points on the temperature-strain hysteresis curve (the red line in Fig. 14): A \((T_{1} ,\varepsilon_{1} )\) and B \((T_{2} ,\varepsilon_{2} )\). The two points are connected by line AB and the expression of line AB is obtained as \({\text{y}} = kx + b\), the slope difference between line AB and line Z is ΔK and the intercepts distance difference is ΔB, \(\Delta {\text{k}} = k - p\), \(\Delta {\text{b}} = b - q\). Consequently, the angle between line AB and the X-axis is \(\theta = \arctan (k)\), the angle between line Z and the X-axis is \(\beta = \arctan (p)\). Obviously, the key to recovering each small segment of the time-lag curve is to find the appropriate slope difference and intercept difference, and then rotate and translate to obtain a correction curve that coincides with the linear relationship.

Fig. 14
figure 14

Time-lag curve slope characteristics

Full size image

To investigate the relationship between slope difference ΔK and intercept distance difference ΔB with the temperature change rate, i.e., \(\left(\frac{dT}{dt}\right)\), taking \(T=20\times \mathrm{sin}\left(\frac{\pi }{72}t\right)\) as the temperature–time history, t = 1:144, represents 144 time-steps, each representing 10 min in practice. Then the temperature change rate and the slope and intercept of the time-lag curve at each time step are calculated. By extensive calculations, it is found that the slope difference ΔK and the intercept difference ΔB are normally distributed with the square of the first-order derivative of the temperature time history i.e., \({(\frac{dT}{dt})}^{2}\). Let the variable \(i=\frac{1}{\sqrt{2\pi }}\times {e}^{-\frac{{\left(\Delta K\right)}^{2}}{2}}\), and \(j=\frac{1}{\sqrt{2\pi }\times 0.131}\times {e}^{-\frac{{\left(\frac{\Delta B}{10A}\right)}^{2}}{2\times 0.131}}\), then \({(\frac{dT}{dt})}^{2}\) is scatter plotted against ΔK, ΔB, i, and j as showen in Fig. 15 and Fig. 16, respectively.

Fig. 15
figure 15

Relationship between the temperature change rate and the slope of the time-lag curve

Full size image
Fig. 16
figure 16

Relationship between the temperature change rate and the intercept of time-lag curve

Full size image

The relationship between the standard normal distribution function of slope difference ΔK and intercept ΔB and the \({(\frac{dT}{dt})}^{2}\) can be obtained by linear regression analysis as:

$$\left( {\frac{{{\text{d}}T}}{dt}} \right)^{2} = {1}{\text{.6925}} \times \frac{{1}}{{\sqrt {{2}\pi } }} \times {\text{e}}^{{ - \frac{{(\Delta K)^{2} }}{2}}} + 0.098{2}$$
(9)
$$\left( {\frac{{{\text{d}}T}}{dt}} \right)^{2} = {0}{\text{.36096}} \times \frac{{1}}{{0.131 \times \sqrt {{2}\pi } }} \times {\text{e}}^{{ - \frac{{(\Delta B)^{2} }}{0.262}}} + 0.06152$$
(10)

The \({R}^{2}\) coefficient of determination of linear fit between i and \({(\frac{dT}{dt})}^{2}\) is 0.93276. To simplify Eq. (9), E is used to represent the slope and F represents the intercept so we can get:

$$\left( {\frac{{{\text{d}}T}}{dt}} \right)^{2} = {\text{E}} \times \frac{{1}}{{\sqrt {{2}\pi } }} \times {\text{e}}^{{ - \frac{{(\Delta K)^{2} }}{2}}} + F$$
(11)

In further studies, we found that the amplitude of the temperature load affects the parameters E and F of the above equation. Then, the relationship between the standard normal distribution function of the slope difference ΔK and the squared \({(\frac{dT}{dt})}^{2}\) was fitted utilizing a linear fit to vary the amplitude A of the temperature time history, and the parameters of the linear fit results for both at each amplitude A were obtained as shown in the following Table 1.

Table 1 Relationship between amplitude and each fitted parameter
Full size table

The linear fitting results under different temperature range functions show that the \({R}^{2}\) discriminant coefficient is basically around 0.935, and the fitting results are relatively ideal. The parameters E and F under variable amplitude A present a certain pattern. The mathematical expression of the relationship between parameter E and \({A}^{2}\) is: \(y=0.00422x-1.04505\times {10}^{-4}\), where the discriminant coefficient \({R}^{2}=0.9998\). And the mathematical expression of the relationship between parameter F and the square \({A}^{2}\) of amplitude A is: \(y=2.4897\times {10}^{-4}x+0.00111\), where the discriminant coefficient \({R}^{2}=0.9993\). The \({R}^{2}\) discrimination coefficient in both linear fitting results is close to 1, which can be considered as highly linearly correlated. Finally, we can obtain the fitted expressions of E, F for \({A}^{2}\) as:

$$\left( {\frac{{{\text{d}}T}}{dt}} \right)^{2} = {(0}{\text{.00422A}}^{2} { - 1}{\text{.04505}} \times {10}^{ - 4} {)} \quad \times \frac{{1}}{{\sqrt {{2}\pi } }} \times {\text{e}}^{{ - \frac{{(\Delta K)^{2} }}{2}}} + (2.4897 \times {10}^{ - 4} {\text{A}}^{2} + 0.00111)$$
(12)

Similarly, the relationship between the intercept and the temperature amplitude is studied below. To make the data processing more accurate, the intercept difference ∆B was reduced by a factor of 10A, and a linear regression analysis was performed by squared \({(\frac{dT}{dt})}^{2}\) of the normal distribution function of the temperature–time range function \(\frac{\Delta B}{10A}\). The \({R}^{2}\) coefficient of determination of the linear fit is 0.9202 in Eq. (12). Then, G is used to represent the slope and H represents the intercept. Then, we can get:

$$\left( {\frac{{{\text{d}}T}}{dt}} \right)^{2} = G \times \frac{{{\text{e}}^{{ - \frac{{(\frac{\Delta B}{{10A}})}}{2 \times 0.131}^{2} }} }}{{\sqrt {{2}\pi } \times {0}{\text{.1310}}}} + H$$
(13)

The relationship between the normal distribution function of the intercept difference \(\frac{\Delta B}{10A}\) and \({(\frac{dT}{dt})}^{2}\) was fitted by means of a linear fit for varying the amplitude A in the temperature–time function, and the parameters of the linear fit results for the two at each amplitude A were obtained as shown in the following Table 2.

Table 2 Relationship between amplitude and each fitted parameter for intercept distance
Full size table

Through the linear fitting results for different temperature–time range functions, the \({R}^{2}\) coefficient of determination is basically around 0.925, and the fitting results are relatively satisfactory.

After the above data processing, the mathematical expression of the relationship between parameter G and the square of amplitude \({A}^{2}\) is: \(y=9.05515\times {10}^{-4}x+0.00103\), where the discriminant coefficient \({R}^{2}=0.9999\); the mathematical expression of the relationship between parameter G and the square of amplitude \({A}^{2}\) is: \(y=1.55954\times {10}^{-4}x-0.00152\), where the coefficient of discrimination \({R}^{2}=0.99997\). The \({R}^{2}\) coefficient of determination in both linear fitting results is close to 1, which can be considered as highly linearly correlated. The relationship between the normal distribution function of the intercept difference \(\frac{\Delta B}{10A}\) and \({(\frac{dT}{dt})}^{2}\) is shown in Eq. (14).

$$\left( {\frac{{{\text{d}}T}}{dt}} \right)^{2} = (9.0552 \times 10^{ - 4} A^{2} + {0}{\text{.0010}}) \quad \times \frac{{{\text{e}}^{{ - (\frac{\Delta B}{{10A}})^{2} }} }}{{\sqrt {{2}\pi } \times {0}{\text{.1310}}}} + (1.5596 \times 10^{ - 4} A^{2} - 0.0015)$$
(14)

Finally, the correction slope ∆k and intercept correction ∆B corresponding to any temperature load amplitude can be obtained with the help of Eqs. (12) and (14). Afterward, the time-lag effect can be eliminated by correcting the slope and intercept of each time step of the time-lag curve. It is crucial to note that the parameters fitted by the above method are only applicable to the Lieshihe bridge due to the difference in the bridge type and the difference in temperature load effects caused by the difference in climatic conditions at the location of the bridge. However, the ideas and processes of the above method are applicable to similar bridges.

3.2 The time-lag elimination method

The above study shows that the relationship between the slope difference ΔK as well as the intercept difference ΔB and the square of the first-order derivative of temperature \({(\frac{dT}{dt})}^{2}\) reveals the relationship between the time-lag curve and temperature. In practical applications, first, the temperature time-lag curve is fitted to obtain the temperature amplitude A, and then the time-lag plot and temperature-strain relationship plot for the day are made. Then, by taking the temperature and strain data at two adjacent points of the time-lag curve at each time step in turn, the slope k and intercept b of the line connecting the two points are obtained, and the difference between the slope ∆K and the intercept ∆B is back-calculated by Eqs. (12) and (14) in the previous section. This eliminates the time-lag effect and reveals the essential characteristics of the temperature response. The list of time-lag elimination algorithms based on the amplitude and time rate of change of temperature, the specific algorithm steps are as shown in Table 3.

Table 3 Time-ag effect elimination algorithm list
Full size table

3.3 Result and discussion

3.3.1 Method effect demonstration

The above method was applied to remove the time-lag effect from the measured strain and temperature data, and the results are shown in Fig. 17. This method has a good elimination effect on the time-lag effect at different dates and different measurement points. Obviously, the area of the hysteresis loop after elimination is significantly reduced, and the linear characteristic is more obvious. The biggest advantage of this method is that it captures the non-linear change characteristics of the temperature load is the fundamental factor that causes the time-lag and uses this as the basic index to calculate the accurate slope and intercept offset at each time in a refined manner. This completes the accurate elimination of the time-lag effect. Compared with the aforementioned research directly shifting the response output and temperature-independent variables in a specific period in a day, the principle of this method is more reasonable and the effect is more significant.

Fig. 17
figure 17

Comparison chart before and after time-lag elimination: (a) April 26; (b) November 17

Full size image

To quantify the effect of the time delay elimination method, we use the correlation coefficient and the area of the hysteresis loop proposed by Yang et al. [25] as indexes, as shown in Table 4. Considering that the T1-S2 measurement point is the closest, the time delay effect is the weakest, so it is used as the benchmark to verify the effect of the method. When the time delay effect is eliminated, the area of the hysteresis loop is significantly reduced, which is close to the T1-S2 hysteresis area of the benchmark, and the data correlation is significantly enhanced, which shows that the effect of the method is good. It is worth mentioning that T1-S2 is the benchmark, but its hysteresis area is not zero. It is speculated that although the location of T1-S2 is the closest, the structural response at this location is not only affected by the temperature load at this location. The overall response of the beam is affected by the constraints of other parts of the structure. That is, the strain response at S2 is not caused by the temperature load only there, so there will still be an insignificant time-delay effect (Fig. 18).

Table 4 Time-ag effect elimination result
Full size table
Fig. 18
figure 18

Comparison of time-lag effect elimination methods

Full size image

3.4 Comparison of methods

Bai et al. proposed a hysteresis elimination method based on multivariate fitting of the temperature difference for the nonlinear hysteresis effect of temperature-induced strain and temperature [29]. To verify the effectiveness of this paper's method, the same measured data were applied to test this paper's time-lag elimination method and Bai's method, and the results are shown in Fig. 19. Compared with the former research this paper's method is significantly better than Bai's method in terms of elimination effect, and the time-lag loop is significantly reduced. The superiority of this paper's method is based on the profound grasp of the rate of change of temperature, which is the fundamental index affecting the time-lag, so that it can consider the change of time-lag curve caused by the change of local rate of change of temperature, and can make detailed corrections.

Fig. 19
figure 19

Slope of temperature and temperature-induced strain after time-ag elimination by different methods: (a) scatter chart of 90 days in different seasons; (b) slope distribution box plot

Full size image

Finally, the methods of this paper and Bai's regression method [29] were adopted to eliminate the time-lag effect in the spring, summer, and winter seasons, and the overall slope of the curve after time-lag elimination is fitted as shown in Fig. 19. From Fig. 19a, the multi-day slope distribution obtained by the time-lag elimination method based on the rate of temperature change in this paper is more concentrated and the error fluctuation is significantly smaller, which further verify the stability of the method of this paper. As shown in Fig. 19b, the 1/4 and 3/4 quartiles of the fitted slopes of 90 days` time-lag curve by this paper`s method are 0.3594 and 0.3726, respectively, with a difference of only 3.7%, which further demonstrates the stability of the slope index after the time-lag elimination of the measured data. Owing to that the development of structural damage and deterioration inevitably leads to the decrease of structural stiffness, the failure of inter-component connections, and the change of boundary conditions, which brings the relationship change of temperature and strain. Thus, the short-term stability of the slope index can provide an important basis and pave the way for long-term structural damage warning and condition assessment based on the change of temperature response after time-lag elimination.

4 Conclusions

  1. 1.

    It is a common phenomenon that the relationship between temperature load and temperature-induced strain response has different degrees of hysteresis correlation at different moments and measurements. The temperature–time-lag effect has significant seasonal and time characteristics, representing that the time-delay effect has the characteristics of space–time distribution.

  2. 2.

    The generation mechanism of the time-lag effect is closely related to the non-linear change rate of temperature. The non-linear change rate of temperature external load causes the temperature field distribution of the structure to be different at different times, thus leading to the difference in response and temperature correspondence.

  3. 3.

    The structural horizontal and vertical temperature gradients are closely related to the characteristics and extent of the time-lag effect. The overall temperature rise and fall affect the shape characteristics of the time-lag loop; the lateral temperature gradient affects the slope, but to a small degree; the vertical temperature gradient is the main factor of the effect. The three work together to cause structural temperature self-strain, resulting in nonlinearity and complexity of temperature response characteristics.

  4. 4.

    Based on the relationship between the temperature change rate and the local slope and intercept of the curve, the time-lag effect elimination method can be constructed. Compared with the traditional translation lag time method, this method pays attention to the difference in the local details of the time-lag curve caused by the temperature change rate. It is a more refined method of elimination.

In summary, the time-lag effect of temperature response is an inconsistent change relationship feature between structural temperature input and response output time correspondences. The root causes of the time-lag effect are the non-linear rate of temperature change. On this basis, the temperature gradient affects the hysteresis and hysteresis characteristics of the response. By adopting an appropriate method to eliminate the time-lag, a more stable temperature-strain mapping relationship can be obtained, the stable slope index, providing a solid basis for further structural evaluation based on temperature effects. The work to make the in-depth exploration of the time-lag effect by combining measured data and finite element simulation provides a new perspective on the temperature response which is instructive.