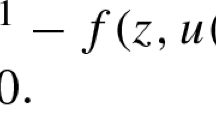1 Introduction

We consider the following semilinear elliptic equation with Dirichlet boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{1}{2}\Delta u -F\left( \, \cdot \,, u\right) =0 \ \text{ in } D, \\[2mm] \hspace{-1.5mm}\displaystyle \lim _{D\ni x\rightarrow y} u(x)= \phi (y) \ \text{ for } y\in \partial D, \end{array} \right. \end{aligned}$$
(1.1)

where D is a bounded regular domain in \(\mathbb {R}^{d},\) \(d\ge 3,\) the boundary condition \(\phi \) is a non-negative, bounded and Borel measurable real-valued function defined on the boundary \(\partial D\) of D, and F is a real-valued Borel measurable function on \(D\times \left( 0,b\right) \) for some \(b\in (0,\infty ]\) such that \(F\left( x,\cdot \right) \) is continuous on (0, b) for every \(x\in D\) and \(0\le F\left( x,u\right) \le U\left( x\right) u\) for every \(\left( x,u\right) \in D\times \left( 0,b\right) ,\) where U is a positive Green-tight function on D. We refer to assertions (iii.2) and (iii.3) of Remark 3.3 for specific examples of functions F satisfying the above conditions. Here the regularity of D is in the sense of the linear Dirichlet problem; see Sect. 2.1 below where we also present the precise definition and some properties of the Green-tight functions, following [6].

A continuous function u on D solving (1.1) is called classical weak solution to the nonlinear Dirichlet problem ( 1.1) with boundary data \(\phi ,\) associated with the operator \(u\longmapsto \frac{1}{2}\Delta u-F\left( \cdot ,u\right) \); in (1.1) the equation is understood in the weak sense. A positive solution means a solution that is strictly positive on D.

If \(\phi \) is a non-negative and continuous real-valued function on \( \partial D,\) then (1.1) is a special case of the problem studied by Chen, Williams, and Zhao in [6]. Under additional restrictions on \(\phi \), they proved the existence of positive continuous solutions to the problem (1.1) in the weak sense (Theorem 1.1 from [6]), using an implicit probabilistic representation together with Schauder’s fixed point theorem and compactness criteria on spaces of continuous functions. The existence of positive solutions of singular nonlinear elliptic equations (of the type (1.1)) with Dirichlet boundary conditions was also studied in [12].

If \(\phi \) is discontinuous on \(\partial D\) then the problem (1.1) has no classical weak solution (see Proposition 2.2 below), therefore we need a more general kind of solution for the above nonlinear Dirichlet problem if the boundary data \(\phi \) is not continuous.

The purpose of this paper is to present a method of solving Eq. (1.1) for discontinuous boundary data. Instead of the pointwise convergence we use A. Cornea’s controlled convergence to the boundary data (cf. [9] and [10]). It turns out that this type of convergence provides a way to describe the boundary behaviour of the solution to the boundary value problems for general (not necessarily continuous) boundary data and it was already used in the linear case for the Dirichlet problem on an Euclidean domain (cf. [2]) but also for the Dirichlet problem associated with the Gross-Laplace operator on an abstract Wiener space (in [3]), and for the Neumann problem on an Euclidean ball (see [5]); see also the Remark 2.1 below.

Our strategy is to modify the procedure of [6] for solving (1.1), since we have to work with spaces of discontinuous functions, in particular, the above mentioned compactness criteria are not more suitable. However, the imposed additional hypothesis on the nonlinear term F permits us to use Banach fixed point theorem. As a byproduct we prove an uniqueness result and a probabilistic representation of the solution to (1.1), an approximation with stochastic terms, which might be considered an analogue of the stochastic solution to the linear Dirichlet problem. Note that in [1] the authors mention an "implicit" probabilistic representation of the solution, in the case when \(F(\cdot ,u)=u^{p}\), and \(\phi \) a non-negative continuous function on the boundary.

The structure of the paper is the following. The controlled convergence is introduced at the beginning of Sect. 2. We expose then the linear Dirichlet problem with general boundary data (Theorem 2.5), based on the controlled convergence, improving essentially the result from [2] which shows that that the stochastic solution solves the problem in this case; we put its proof in the “Appendix” of the paper. In Theorem 2.7 we show the uniqueness of the solution to the Dirichlet problem associated with the operator \(\frac{1}{2} \Delta +q\), it is a generalization to discontinuous boundary data of a result from [8] (Theorem 3.21). The main result of the paper (Theorem 3.1), the existence of the solution to Eq. (1.1), and its proof are presented in Sect. 3. The probabilistic representation of the solution is stated in Remark 3.3. We complete the section by proving (in Theorem 3.4) the uniqueness of the solution to Eq. (1.1).

Finally, we thank the anonymous referee for the valuable remarks and questions which lead to improvements in the paper at various places. In addition, the authors acknowledge enlightening discussions with Gheorghe Bucur and Iulian Cîmpean during the preparation of this paper.

2 Solutions to the Dirichlet problem based on controlled convergence

Controlled convergence. Let \(f:\partial D\longrightarrow \overline{\mathbb {R}}\) and \( h,k:D\longrightarrow {\mathbb {R}},\) \(k\ge 0.\) We say that h converges to f controlled by k (we write \(h\overset{k}{\longrightarrow }f\)) provided that for every \(A\subset D\) and \(y\in \partial D\cap \overline{A}\) the following conditions hold:

\(\left( *\right) \):

If \(\underset{A\ni x\rightarrow y}{\lim \sup }\) \(k\left( x\right) <\infty \) then \(f\left( y\right) \in \mathbb {R}\) and \(f\left( y\right) =\underset{A\ni x\rightarrow y}{\lim }h\left( x\right) \)

\(\left( **\right) \):

If \(\underset{A\ni x\rightarrow y}{\lim }\) \(k\left( x\right) =\infty \) then \(\underset{A\ni x\rightarrow y}{\lim }\frac{ h\left( x\right) }{1+k\left( x\right) }=0.\)

The function k is called control function.

Remark 2.1

  1. (i)

    This type of convergence was introduced by A. Cornea in [9] and [10]. A first motivation was to solve the (linear) Dirichlet problem with general (discontinuous) boundary data. The monograph [13] presents the controlled convergence with application to the Perron-Wiener-Brelot solution of a Dirichlet problem in the frame of a harmonic space.

  2. (ii)

    In [3] the controlled convergence was used to state and solve the Dirichlet problem for the Gross-Laplace operator on an abstract Wiener space, for general (not necessarily continuous) boundary data. Note that a main difficulty in proving the existence of the solution is the construction of a convenient control function.

  3. (iii)

    In [4] and [5] the controlled convergence was used to solve the Neumann problem on a ball with discontinuous boundary data.

  4. (iv)

    One can see that if \(h_i\) converges controlled by \(k_i\) to the real-valued function \(f_i\), \(i=1,2,\) and \(\alpha \in \mathbb {R}\), then \(h_1+ \alpha h_2\) converges controlled by \(k_1+k_2\) to \(f_1+ \alpha f_2\).

We denote by \(b\mathcal {B}_+(A) \) the set of all bounded, positive and Borel measurable functions on a set A, by C(A) the set of all continuous functions on A, by \(C_{b}(A)\) the set of all bounded and continuous functions on A, and by \(\left| \left| \cdot \right| \right| _{\infty }\) the supremum norm of a real-valued function over its domain of definition, in particular \( \left| \left| \phi \right| \right| _{\infty }=\underset{x\in \partial D}{\sup }\left| \phi (x) \right| ,\) provided that \(\phi \) is defined on the boundary \(\partial D\) of D. Let \(\mathcal {B}_+(\partial D)\) denote the set of all positive, numerical, Borel measurable functions on \(\partial D\).

Proposition 2.2

If the nonlinear Dirichlet problem (1.1) has a classical weak solution \(u\in C\left( D\right) \) then the boundary data \(\phi \) is continuous on \(\partial D\).

Proof

See the proof of Remark 1.1 from [2]. \(\square \)

According to Proposition 2.2 if the boundary data \(\phi \) is discontinuous then the problem (1.1) has no classical weak solution. Below we introduce a more general solution to our problem (1.1).

A function \(u\in C\left( D\right) \) is called a weak solution to the nonlinear Dirichlet problem with boundary data \(\phi \in b\mathcal {B}_+\left( \partial D\right) \) associated with the operator \(\frac{1}{2} \Delta u-F\left( \cdot ,u\right) ,\) provided that there exists a control function k which is superharmonic in D such that

$$\begin{aligned} \left\{ \begin{array}{l} \frac{1}{2}\Delta u-F\left( \cdot ,u\right) =0\text { in }D \text { in the weak sense,} \\[2mm] u\text { converges to }\phi \text { controlled by }k. \end{array} \right. \end{aligned}$$

2.1 The linear case

A solution to the classical Dirichlet problem on D with boundary data \(f: \partial D \longrightarrow \mathbb {R}\) is a harmonic function \(h: D \longrightarrow \mathbb {R}\) such that \(\displaystyle \lim _{D\ni x \rightarrow y} h(x) = f(y)\) for all \(y \in \partial D.\)

For \(x\in \mathbb {R}^d \) let \( \left( X\left( t\right) ,t\ge 0\right) \) under the probability \(\mathbb {P}^x\) be the d-dimensional Brownian motion starting from x, denote by \(\mathbb {E}^{x}\) the expectation under \(\mathbb {P}^{x}\), and let \(\tau _{D}=\inf \{t>0:\) \(X\left( t\right) \notin D\}\) be the exit time from D. Recall that a point \(x\in \partial D\) is said to be regular boundary point of D provided that \(\mathbb {P}^{x}(\tau _{D}=0)=1 \); see e.g. [7], page 97, or [8], page 23. The domain D is called regular provided that every point of \(\partial D\) is a regular boundary point of D.

If \( f: \partial D \longrightarrow \overline{\mathbb {R}}\) is a bounded below Borel measurable function and \(x\in D\) define

$$ H_D f(x) := \mathbb {E}^x f (X({\tau _{D})}) . $$

By Theorem 3.7 from [15], page 106, it follows that \(H_D f\) is a (real-valued) harmonic function on D provided that \(H_D f\) is not equal \(+\infty \) everywhere on D. According to [7], Theorem 2, page 163 (or Theorem 2.2 from [15]) we have that D is regular if and only if \(H_{D}f\) is the solution to the linear Dirichlet problem with boundary data f for every \(f \in C(\partial D)\). Therefore \(H_D f\) is called the stochastic solution to the Dirichlet problem. Recall that we already assumed in the Introduction that D is a bounded and regular domain in \(\mathbb {R}^d,\) \(d\ge 3\).

The Dirichlet problem based on controlled convergence. A function \(f: \partial D \longrightarrow \overline{\mathbb {R}}\) is called resolutive provided that there exists a harmonic function h on D which converges to f controlled by a real-valued, non-negative superharmonic function k. If f is resolutive, then the unique function h (see Corollary 2.4 below) is called the solution on D to the Dirichlet problem with boundary data f.

Remark 2.3

  1. (i)

    According to [9] and [10], and as mentioned in the Introduction, the controlled convergence offers a method for setting and solving the Dirichlet problem for general open sets and general boundary data. The above function f should be interpreted as being the boundary data of the harmonic function h.

  2. (ii)

    A harmonic function h on D is the solution to the classical Dirichlet problem with boundary data f if and only if h converges to f controlled by a bounded function k; see [9], and Remark 5.2 (ii) from [3].

The next corollary is a version of Corollary 4.3 from [2].

Corollary 2.4

If the Dirichlet problem has a solution then it is unique. In particular, if u is a harmonic function on D which converges controlled by k to zero then \(u=0\) on D.

Proof

We can argue as in the proof of Corollary 4.3 from [2], where it was assumed that the superharmonic control function k is continuous. The only additional argument we need is the fact that in our case here we may suppose that the control function is continuous, according to Proposition 2.2 from [10]. \(\square \)

The next result shows that the stochastic solution solves the Dirichlet problem with general boundary data. It is an improvement of the main result from [2], Theorem 4.8; for the relation with the resolutivity for the method of Perron-Wiener-Brelot see Corollary 2.13 from [10]. Some arguments in the proof are like in the proofs of Theorem 4.8 from [2] and Theorem 5.3 from [3]. For the reader convenience we present in the “Appendix” the proof of the next theorem.

Theorem 2.5

Let \(D \subset \mathbb {R}^d\) be a bounded domain. Let \( f: \partial D \longrightarrow \mathbb {R}\) be a bounded below Borel measurable function and assume that \(H_D f\) is not equal \(+\infty \) everywhere on D. Then \(H_D f\) is the unique solution to the Dirichlet problem with boundary data f. More precisely, there exists \(g \in \mathcal {B}_+(\partial D)\) such that the function \(k:= H_D g\) is real-valued and \(H_D f\) converges to f controlled by k.

The Kato class. Let \(g:\mathbb {R}^d \longrightarrow \mathbb {R}\cup \{\infty \}\) be the Green function on \(\mathbb {R}^d\) without the constant factor (cf. [8], page 62), \(g(u)= \left| u\right| ^{2-d} \), \(d\ge 3\). Following [8], page 62, we define the Kato class J of the function g: the set of all real-valued Borel measurable functions q defined on \(\mathbb {R}^{d}\) such that

$$ \ \lim _{\alpha \searrow 0}\left[ \sup _{x\in \mathbb {R}^{d}}\int _{\left| y-x\right| \le \alpha }\left| g\left( y-x\right) q\left( y\right) \right| dy\right] =0. $$

If the function q is only defined on the domain D, then we extend it to \(\mathbb {R}^{d}\) by setting it to vanish on the complement of D.

Green-tight functions. A function \(w:D\longrightarrow \mathbb {R}\) is said to be Green-tight on a bounded domain D of \(\mathbb {R}^{d}\) (cf. [6], page 547) provided that it is Borel measurable and such that

$$\begin{aligned} \lim _{\begin{array}{c} \lambda \left( A\right) \rightarrow 0, \\ A\subset D \end{array}}\{\sup _{x\in D}\int _{A}\frac{|w\left( y\right) |}{|x-y|^{d-2}}dy\}=0, \end{aligned}$$

where \(\lambda \) denotes the Lebesgue measure on \(\mathbb {R}^{d}\). If w is Green-tight on D then it satisfies

$$\begin{aligned} \left| \left| w\right| \right| _{D}:=\sup _{x\in D}\int _{D} \frac{\left| w\left( y\right) \right| }{\left| x-y\right| ^{d-2}}dy<\infty . \end{aligned}$$

Let G be the Green function of the operator \(\frac{1}{2}\Delta \) on D. Since D is regular we have by Theorem 2.6 in [8] that \( \lim _{x \rightarrow z}G(x,y)=0\) for every \(z \in \partial D\) and \(y\in D\). We have also \(G(x,y)=0\) for \(x\in \partial D\) and \(y\in D\) and

$$\begin{aligned} 0\le & {} G\left( x,y\right) \le c\, g(x-y) \text { for all }x,y\in D, \end{aligned}$$

with \(c:=\) \(\Gamma \left( \frac{d}{2}-1\right) /2\pi ^{d/2};\) see e.g. (1.5) and (1.6) from [6] (cf. [7], page 181) and also Theorem 2.6 (ii) from [8].

As in (1.9) from [6] and Theorem 3.2 of [8] for any Green-tight function q on D, 

$$\begin{aligned} Gq ( x ):=\int _{D}G\left( x,y\right) q(y) dy,\text { }x\in \overline{D}, \end{aligned}$$

defines a bounded and continuous function on \(\overline{D}\) which vanishes on the boundary of D. Furthermore, by Proposition 2.10 from [8] Gq satisfies the equation

$$\begin{aligned} \frac{1}{2}\Delta \left( Gq\right) =-q\text { on }D \end{aligned}$$
(2.1)

in the weak sense, that is for every test function \(\psi \in C_{c}^{\infty }\left( D\right) :=\{f\in C^{\infty }\left( D\right) :\) f has compact support in \(D\} \) Gq satisfies the equation

$$\begin{aligned} \frac{1}{2}\int _{D}Gq(x)\Delta \psi \left( x\right) dx=-\int _{D}q\left( x\right) \psi \left( x\right) dx. \end{aligned}$$

Remark 2.6

According to [6], because D is bounded, a real-valued Borel measurable function w on D is Green-tight if and only if \(1_{D}w\in J\).

2.2 Uniqueness of the solution for the operator \(\frac{1}{2} \Delta +q\)

For \(q\in J\) let \(\{T_{t}\}_{t}\) be the Feynman-Kac semigroup on D associated with the multiplicative functional \( \left( e^{ \int _{0}^{t} q ( X( s) ) ds } \right) _{t\ge 0}\),

$$ T_{t}f\left( x\right) =\mathbb {E}^{x} ( e^{\int _{0}^{t}q( X( s) ) ds } f ( X( t) ); t<\tau _{D}), \ x \in D. $$

Consider further the potential operator of the semigroup \(\{T_{t}\}_{t}\),

$$ Vf\left( x\right) =\int _{0}^{\infty }T_{t}f\left( x\right) dt= \mathbb {E}^{x} \int _{0}^{\tau _{D}} e^{\int _{0}^{t}q( X( s) ) ds} f( X(t) )dt \ \text { for } f\in \mathcal {B}_{+} (D) . $$

Let \(q\in J\) and \(\phi \in b{\mathcal {B}}_+ ( \partial D)\). A function \(u\in C\left( D\right) \) is called weak solution to the Dirichlet problem associated with the operator \(\frac{1}{2} \Delta +q\), with boundary data \(\phi \), provided that there exists a superharmonic control function \(k:D\longrightarrow \mathbb {R}_{+}\) such that

$$ \left\{ \begin{array}{c} \frac{1}{2}\Delta u+qu=0\text { in }D\text { in the weak sense,} \\[2mm] \hspace{-8mm} u~\text {converges to }\phi \text { controlled by }k. \end{array} \right. $$

Theorem 2.7

Let \(q\in J\) and \(\phi \in b{\mathcal {B}}_+( \partial D )\). If the linear Dirichlet problem associated with the operator \(\frac{1}{2} \Delta +q\), with boundary data \(\phi \), has a weak solution in \(C_{b}\left( D\right) \) then it is unique.

Proof

Let \(u_{1},\) \(u_{2}\in C_{b}\left( D\right) \) be two weak solutions to the linear Dirichlet problem associated with the operator \(\frac{1}{2} \Delta +q\), with \(k_{1}\) and, respectively, \(k_{2},\) their control functions, that is, \(u_{1}\overset{k_{1}}{\longrightarrow }\phi \) and \(u_{2}\overset{k_{2}}{\longrightarrow }\phi ,\) where \( k_{1},k_{2}:D\rightarrow \mathbb {R}_{+}\) are two positive superharmonic functions. Let \(v:=u_{1}-u_{2}\). By assertion (iv) of Remark 2.1 we have \( \frac{1}{2}\Delta v+qv = 0\) in the weak sense on D and \(v\overset{k}{\longrightarrow }0,\) with \(k=k_{1}+k_{2}.\) We use now some arguments from the proof of Theorem 3.21 from [8]. Let \(f:=v-G\left( qv\right) \). Then v is bounded and since \(q\in J\) we have that \(1_{D}qv\in J\cap L^1(D)\), using also Proposition 3.1 from [8]. By Theorem 3.2 from [8] we conclude that \(G\left( \left| qv\right| \right) \) is bounded in D and so it belongs to \(L^{1}\left( D\right) \). Therefore, by Proposition 2.10 from [8] we have

$$ \frac{1}{2}\Delta G\left( qv\right) =-qv\text { on }D\text { in the weak sense,} $$

hence \(\Delta f=\Delta v-\Delta G\left( qv\right) =-2qv+2qv=0\text { on }D\) in the weak sense. Again by Theorem 3.2 from [8] we get that \(G\left( qv\right) \in C \left( D\right) \), therefore \(f\in C \left( D\right) \). Thus by Weyl’s lemma (see e.g. [11], page 118) f is harmonic on D. We have also \(\lim _{x\rightarrow z}G\left( qv\right) \left( x\right) =0\text { for all } z\in \partial D,\) and since \(v=u_{1}-u_{2}\overset{k_{1}+k_{2}}{\longrightarrow }0,\) we get that \(f\overset{k_{1}+k_{2}}{\longrightarrow }0.\) Thus f is a solution to the Dirichlet problem

$$ \left\{ \begin{array}{l} \Delta w=0\text { in }D, \\[3mm] w\text { converges to }0\text { controlled by } k_1+k_2. \end{array} \right. $$

From Corollary 2.4 it follows that \(f=0\) on D, hence \(v=G\left( qv\right) \) on D. Further, we argue as in the last part of the proof of Theorem 3.21 from [8]. By Theorem 3.2 from [8] we have that G|q| is bounded in D, hence \(G\left| qv\right| \le \left| \left| v\right| \right| _{\infty }\left| \left| G|q|\right| \right| _{\infty }<\infty \) and therefore \(V\left( \left| q\right| G\left| qv\right| \right) <\infty \) by Theorem 3.18 from [8]. Note that V is a bounded kernel because \(V1(x)\le \mathbb {E}^x [\tau _B]\le \frac{R^2}{d}\), where 1 stands for the constant function 1 on D, and B is a ball of radius R centered at the origin, containing D; see (3.6) below for more details on the proof of the last inequality. Thus, by (45) from [8] we obtain \(V\left( qv\right) =G\left( qv\right) +V\left( qG\left( qv\right) \right) \), hence \(V\left( qv\right) =v+V\left( qv\right) \) on D. Since \(V\left( qv\right) <\infty ,\) we get \(v=0\) on D,  therefore \( u_{1}=u_{2}\) on D. \(\square \)

3 The nonlinear Dirichlet problem

Let \(b\in (0,\infty ]\) such that \(\Vert \phi \Vert _{\infty }< b\). As in [6], (3.8)-(3.10), we fix a positive Green-tight function U on D such that

$$\begin{aligned} 0\le F\left( x,u\right) \le U\left( x\right) u \end{aligned}$$
(3.1)

for all \( (x,u)\in D\times \left( 0,b\right) \). Let

$$\begin{aligned} \gamma _{0}:=\inf \{\phi \left( x\right) :x\in \partial D\},\text { }\beta :=c\left| \left| U\right| \right| _{D}, \end{aligned}$$

and

$$ \Lambda :=\{u\in b\mathcal {B}_+ ( D) : m:=e^{-\beta }\gamma _{0}\le u\le \left| \left| \phi \right| \right| _{\infty }=: \widetilde{m}\text { on }D\}. $$

Assume that \(\gamma _{0}>0\), so \(m=e^{-\beta }\gamma _{0}>0\). We endow \(\Lambda \) with the metric induced by the supremum norm and clearly we obtain a complete metric space.

We can state now the main result of this paper. Consider a ball B of radius R centered at the origin, containing D.

Theorem 3.1

Let \(\phi \) be a bounded, Borel measurable function on \( \partial D\) such that \(\gamma _{0}>0\). Assume that F is a real-valued Borel measurable function on \(D\times \left( 0,b\right) \) satisfying condition (3.1) and suppose that for every \(x\in D\) the function \(H_{x}:[m,\widetilde{m}]\longrightarrow [0,\infty )\) defined as \(H_{x}\left( y\right) :=\frac{F\left( x,y\right) }{y}\) is Lipschitz continuous on \([m,\widetilde{m}]\) with the constant C that does not depend on x. Suppose that \(\phi \) is such that

$$\begin{aligned} \left| \left| \phi \right| \right| _{\infty }<\frac{d}{R^{2}C }. \end{aligned}$$
(3.2)

Then the nonlinear Dirichlet problem with boundary data \(\phi \) associated with the operator \(u\longmapsto \frac{1}{2}\Delta u-F\left( \cdot ,u\right) \) has a weak solution \(u\in C\left( D\right) \), that is,

$$\begin{aligned} \left\{ \begin{array}{l} \frac{1}{2}\Delta u-F\left( \cdot ,u\right) =0\text { in }D \text { in the weak sense,} \\[3mm] u\text { converges to }\phi \text { controlled by }k, \end{array} \right. \end{aligned}$$
(3.3)

where the control function is \(k:= H_D g\) for some function \(g\in \) \(\mathcal {B}_+ ( \partial D) \).

Proof

We use some arguments from the proof of Theorem 1.1 in [6]. For any real-valued Borel measurable function w defined on D such that \(\left| \left| w\right| \right| _{D}<\infty \) and for every \(x\in D,\) \( \mathbb {P}^{x}\)-a.s., we consider the following stopped Feynman-Kac functional which is well defined, positive and finite for all \(t\ge 0\)

$$\begin{aligned} e_{w}\left( t\right) :=\exp (\int _{0}^{t\wedge \tau _{D}}w\left( X\left( s\right) \right) ds)\text {.} \end{aligned}$$

For any \(u\in \Lambda \) and \(x\in D\) the function

$$\begin{aligned} q_{u}\left( x\right) :=\frac{-F\left( x,u\left( x\right) \right) }{u\left( x\right) }\text { } \end{aligned}$$

is well defined and

$$\begin{aligned} -U\left( x\right) \le q_{u}\left( x\right) \le 0\text { and }\left| q_{u}\left( x\right) \right| \le U\left( x\right) . \end{aligned}$$

Thus \(\left| \left| q_{u}\right| \right| _{D}\le \left| \left| U\right| \right| _{D}<\infty \) and \(q_u\) is Green-tight on D or equivalently (cf. Remark 2.6), \(1_Dq_u\) belongs to J.

As in (3.15) and (3.16) from [6]

$$\begin{aligned} \mathbb {E}^{x} \int _{0}^{\tau _{D}}U\left( X\left( t\right) \right) dt \le c\left| \left| U\right| \right| _{D}=\beta \end{aligned}$$

and

$$\begin{aligned} e^{-\beta }\le \mathbb {E}^{x}\left[ e_{-U}\left( \tau _{D}\right) \right] \le \mathbb {E}^{x}\left[ e_{q_{u}}\left( \tau _{D}\right) \right] \le 1 \text { for each }x\in D. \end{aligned}$$
(3.4)

We define the operator T on \(\Lambda \) as in (3.18) from [6],

$$\begin{aligned} Tu\left( x\right) :=\mathbb {E}^{x}\left[ e_{q_{u}}\left( \tau _{D}\right) \phi \left( X\left( \tau _{D}\right) \right) \right] \text { for all } u\in \Lambda \text{ and } x\in D. \end{aligned}$$

By (3.4), we have that

$$\begin{aligned} e^{-\beta }\gamma _{0}\le \mathbb {E}^{x}\left[ e_{-U}\left( \tau _{D}\right) \phi \left( X\left( \tau _{D}\right) \right) \right] \le Tu\left( x\right) \le \left| \left| \phi \right| \right| _{\infty }\mathbb {E}^{x}\left[ e_{q_{u}}\left( \tau _{D}\right) \right] \le \left| \left| \phi \right| \right| _{\infty }, \end{aligned}$$

thus Tu is well defined, finite and bounded on D and in particular \(T\Lambda \subset \Lambda .\)

We show that T is a contraction map on \(\Lambda \) with respect to the supremum norm. For any \(x\in D\) and u,  \(v\in \Lambda \) we have that

$$\begin{aligned} \left| Tu\left( x\right) -Tv\left( x\right) \right|= & {} \left| \mathbb {E}^{x}\left[ e_{q_{u}}\left( \tau _{D}\right) \phi \left( X\left( \tau _{D}\right) \right) \right] -\mathbb {E}^{x}\left[ e_{q_{v}}\left( \tau _{D}\right) \phi \left( X\left( \tau _{D}\right) \right) \right] \right| \\\le & {} \left| \left| \phi \right| \right| _{\infty }\mathbb {E }^{x}\left[ \left| e_{q_{u}}\left( \tau _{D}\right) -e_{q_{v}}\left( \tau _{D}\right) \right| \right] \\= & {} \left| \left| \phi \right| \right| _{\infty }\mathbb {E} ^{x}[|e^{-\underset{0}{\overset{\tau _{D}}{\int }}\frac{F\left( X(s),u\left( X(s)\right) \right) }{u\left( X(s)\right) }ds}-e^{-\underset{ 0}{\overset{\tau _{D}}{\int }}\frac{F\left( X(s),v\left( X(s)\right) \right) }{v\left( X(s)\right) }ds}|]. \end{aligned}$$

From \(\left| e^{-x}-e^{-y}\right| \le \left| x-y\right| \) for all x,  \(y\ge 0,\) we get

$$\begin{aligned} \left| Tu\left( x\right) -Tv\left( x\right) \right|\le & {} \left| \left| \phi \right| \right| _{\infty }\mathbb {E} ^{x} \left| \underset{0}{\overset{\tau _{D}}{\int }}\frac{F\left( X(s),u\left( X(s)\right) \right) }{u\left( X(s)\right) }ds-\underset{0}{ \overset{\tau _{D}}{\int }}\frac{F\left( X(s),v\left( X(s)\right) \right) }{v\left( X(s)\right) }ds\right| \\= & {} \left| \left| \phi \right| \right| _{\infty }\mathbb {E} ^{x}\underset{0}{\overset{\tau _{D}}{\int }} |H_{x}(u(X(s)))-H_{x}(v(X(s)))|ds. \end{aligned}$$

Since, by hypothesis, \(H_{x}\) is Lipshitz continuous with the constant C for every \(x\in D,\) we have that

$$\begin{aligned} \left| Tu\left( x\right) -Tv\left( x\right) \right| \le \left| \left| \phi \right| \right| _{\infty } \mathbb {E}^{x} \underset{0}{\overset{\tau _{D}}{\int }}C|u(X(s))-v(X(s))|ds\le \end{aligned}$$
(3.5)
$$ \left| \left| \phi \right| \right| _{\infty }C\left| \left| u-v\right| \right| _{\infty } \mathbb {E}^{x} \int _{0}^{\tau _{D}}ds =\left| \left| \phi \right| \right| _{\infty }C\left| \left| u-v\right| \right| _{\infty }\mathbb {E}^{x}[\tau _{D}] . $$

Let \(\tau _{B}=\inf \{t>0\)  :  \(X(t) \notin B\}\) be the exit time of B,  then \(\mathbb {E}^{x}[\tau _{D}]\le \mathbb {E}^{x}[\tau _{B}]\) and by (7.4.2) from [14], we have that

$$\begin{aligned} \mathbb {E}^{x}[\tau _{B}]=\frac{1}{d}\left( R^{2}-\left| x\right| ^{2}\right) \le \frac{R^{2}}{d}. \end{aligned}$$
(3.6)

Then by (3.5) we have \(\left| Tu\left( x\right) -Tv\left( x\right) \right| \le \left| \left| \phi \right| \right| _{\infty }C\frac{R^{2}}{d}\left| \left| u-v\right| \right| _{\infty }\) and applying the supremum we get \(\left| \left| Tu-Tv\right| \right| _{\infty }\le \left| \left| \phi \right| \right| _{\infty }C\frac{R^{2}}{d}\left| \left| u-v\right| \right| _{\infty }.\) From (3.2) we have that \(0\le \left| \left| \phi \right| \right| _{\infty }C\frac{R^{2}}{d} <1\) and thus the operator T is a contraction map over the complete metric space \(\Lambda \) (with respect to metric induced by the supremum norm). Applying the Banach fixed-point theorem, there exists a unique fixed-point \(u_{0}\in \Lambda \) such that \(Tu_{0}=u_{0}.\) We need now the following lemma. \(\square \)

Lemma 3.2

Let \(u\in \Lambda \). Then Tu is a continuous weak solution to the problem

$$\begin{aligned} \left\{ \begin{array}{c} \frac{1}{2}\Delta v-\frac{F\left( \cdot ,u\right) }{u}v=0\text { in }D \text { in the weak sense,} \\[2mm] \hspace{-15mm} v\text { converges to }\phi \text { controlled by }k,\end{array} \right. \end{aligned}$$
(3.7)

where the control function is \(k:= H_D g\) for some function \(g\in \) \(\mathcal {B}_+ ( \partial D) \).

Proof of Lemma 3.2

We consider the linear Dirichlet problem on D with boundary data \(\phi \in b\mathcal {B}_{+}\left( \partial D\right) \). Let h be the stochastic solution to this problem, \(h=H_D \phi \). We already noted that h is a bounded harmonic function on D. By Theorem 2.5 there exists a function \(g\in \) \(\mathcal {B}_+ (\partial D) \) such that h converges to \(\phi \) controlled by k, where \(k:= H_D g\) is a real-valued, positive superharmonic control function, so

$$\begin{aligned} h\overset{k}{\longrightarrow }\phi . \end{aligned}$$
(3.8)

As in (3.26) from [6], by a straightforward calculation, Fubini’s theorem (in which the required absolute integrability is implied by \( \left| \left| q_{u}\right| \right| _{D}<\infty ),\) the strong Markov property, and the regularity of D, we have that for each \( x\in D\)

$$\begin{aligned} Tu\left( x\right) -h\left( x\right) =G\left( q_{u}Tu\right) \left( x\right) . \end{aligned}$$
(3.9)

From the boundedness of Tu and the fact that U is Green-tight on D and \(\left| q_{u}\left( \cdot \right) \right| \le U\left( \cdot \right) \) we have that \(q_{u}Tu\) is Green-tight on D, thus \(G(q_{u}Tu)\) is continuous and bounded on \(\overline{D}\), it vanishes on the boundary of D and satisfies the Eq. (2.1) with \(q_{u}Tu\) instead of q,  that is

$$\begin{aligned} \frac{1}{2}\Delta G(q_{u}Tu)=-q_{u}Tu \ \text { on }D \text{ in } \text{ the } \text{ weak } \text{ sense }. \end{aligned}$$
(3.10)

Furthermore, we have that \(\Delta h=0\) on D, thus by (3.10) Tu satisfies the equation

$$\begin{aligned} \frac{1}{2}\Delta v+q_{u}v=0~\text { on }D \text{ in } \text{ the } \text{ weak } \text{ sense. } \end{aligned}$$

Hence by (3.8), (3.9), and since \(\lim _{D\ni x\rightarrow y}G(q_{u}Tu)\left( x\right) =0 \) when \( y\in \partial D\), we conclude that Tu converges to \(\phi \) controlled by k. Therefore Tu is continuous and bounded on D and it is a weak solution to the problem (3.7), so, the proof of Lemma 3.2 is complete.

We return now to the proof of Theorem 3.1. By Lemma 3.2 it follows that the fixed point \(u_{0}=Tu_{0}\) satisfies the equation \(\frac{1}{2}\Delta u_{0}+q_{u_{0}}u_{0}=0~\) on D and \(u_{0}\) converges thus to \(\phi \) controlled by k, therefore \( u_{0}\) is a weak solution to the problem (3.3). \(\square \)

Remark 3.3

  1. (i)

    The proof of Theorem 3.1 allows to emphasize the following probabilistic representation of the solution to the nonlinear Dirichlet problem (1.1). Let \(v_0\in \Lambda \) and define recurrently

    $$ v_{n+1}:=\mathbb {E}^\mathbf{\cdot } [ e_{q_{v_n}}\left( \tau _{D}\right) \phi \left( X\left( \tau _{D}\right) \right) ] \ \text{ for } \ n\ge 0. $$

    Then the sequence \((v_n)_{n\ge 0}\) from \(\Lambda \) converges uniformly to the solution to the problem (1.1).

  2. (ii)

    Condition (3.2) over the "size" of \(\phi \) is similar to condition (b) from Theorem 1.1 in [6].

  3. (iii)

    Examples of functions F satisfying the hypothesis from Theorem 3.1, that is, F fulfills condition (3.1) and the Lipschitz constant of \(y \longmapsto H_x(y) =\frac{F(x,y) }{y}\), \(y \in [m,\widetilde{m}]\), does not depend on x, i.e., \(C:=\sup _{x\in D} \sup _{y\ne z}\frac{\left| H_{x}\left( y\right) -H_{x}\left( z\right) \right| }{\left| y-z\right| } <\infty \). The following assertions hold. (iii.1) If for every \(x\in D,\) the function \(H_{x}\) is continuous on \( [m,\widetilde{m}]\) and differentiable on \((m,\widetilde{m}),\) such that \(C=\sup _{x\in D} \sup _{y\in (m,M)}|H_{x}^{\prime }\left( y\right) | <\infty \), then clearly, for every \(x\in D,\) \(H_{x}\) is Lipschitz continuous on \([m,\widetilde{m}]\) with the constant \(C<\infty .\) If F has an extension of class \(C^1\) to \(\overline{D}\times [m,\widetilde{m}]\), then \(H_x\) is Lipschitz continuous with the constant \(C<\infty \). (iii.2) We can take \(F(x,u):=\frac{f(x)}{|x|}u\) in the case \(d=3, 0 \notin \overline{D}\), where \(f:D\longrightarrow \mathbb {R}_+\) is a bounded function, thus \(U(x):=\frac{f(x)}{|x|}=f(x)g(x)\) is a Green-tight function on D (see Example 3 in [8], page 66) and consequently F satisfies (3.1). For each \(x\in D\) we have that \(H_x\) is the constant function U(x). Clearly, it is a Lipschitz function and its Lipschitz constant does not depend on x. So, F satisfies the hypothesis from Theorem 3.1. (iii.3) More general, let \(F(x,u):=U(x)u\), where U is understood as the restriction to D of a positive function \(U \in C^1(\mathbb {R}^d)\) such that \(\sup _{x}\int _{|y-x|\le 1} U(y)^pdy < \infty \) and \(p>d/2\). According to Example 2 from [8], page 66, U is a Green-tight function on D, therefore F satisfies (3.1). By the above assertion (iii.1) it follows that in this case \(H_x\) is Lipschitz continuous with the constant \(C<\infty \). We conclude that in this case too F satisfies the hypothesis from Theorem 3.1.

We close this section with a result of uniqueness of the solution to Eq. (1.1).

Theorem 3.4

If the nonlinear Dirichlet problem associated with the operator \(v\longmapsto \frac{1}{2}\Delta v -F\left( \cdot ,v\right) \), with boundary data \(\phi \in b\mathcal {B}_+\left( \partial D\right) \), has a weak solution in \( \Lambda \) then it is unique.

Proof

Let \(u_{1}, u_{2}\in \Lambda \) be two weak solutions to the nonlinear Dirichlet problem associated with the operator \(v \longmapsto \frac{1}{2}\Delta v-F\left( \cdot ,v \right) \), with boundary data \(\phi \). Therefore \(u_{1}\) and \(u_{2}\) are also weak solutions to the linear Dirichlet problems associated with the operator \(v\longmapsto \frac{1}{2}\Delta v-\frac{ F\left( \cdot ,u_{1}\right) }{u_1}v\) and respectively \(v\longmapsto \frac{1}{2}\Delta v-\frac{ F\left( \cdot ,u_{2}\right) }{u_2}v\). Then \(q_{u_{1}}=-\frac{F\left( \cdot ,u_{1}\right) }{u_{1}}\) and \(q_{u_{2}}=-\frac{F\left( \cdot ,u_{2}\right) }{u_{2}}\) are Green-tight functions on D and by Theorem 2.7 we have that \(u_{1}\) and \(u_{2}\) are the unique weak solutions to the linear Dirichlet problems associated with the operator \(\frac{1}{2} \Delta +q_{u_{1}}\) and respectively \(\frac{1}{2} \Delta +q_{u_{2}}\). By Lemma 3.2 we have that \(u_{1}=Tu_{1}\) and \(u_{2}=Tu_{2}\), thus \(u_{1}\) and \(u_{2}\) are two fixed-points of the contraction operator T on \(\Lambda \) (cf. the proof of Theorem 3.1) and we conclude that \(u_{1}= u_{2}\). \(\square \)