Two-dimensional solitary waves and periodic waves on coupled nonlinear electrical transmission lines

Abstract

By using the dynamical system approach, the exact travelling wave solutions for a system of coupled nonlinear electrical transmission lines are studied. Based on this method, the bifurcations of phase portraits of a dynamical system are given. The two-dimensional solitary wave solutions and periodic wave solutions on coupled nonlinear transmission lines are obtained. With the aid of Maple, the numerical simulations are conducted for solitary wave solutions and periodic wave solutions to the model equation. The results presented in this paper improve upon previous studies.

1 Introduction

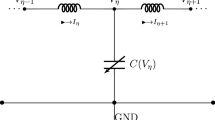
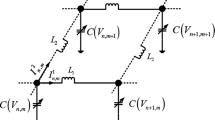
In this paper, we consider a system of coupled nonlinear electrical transmission lines [1]

$$\begin{aligned} u_{t}+u^pu_{x}+u_{xxx}+u_{xyy}=0, \end{aligned}$$

(1.1)

where p is an arbitrary constant, u is a real function, x and y are the transverse and longitudinal coordinates, respectively, and t is the temporal variable. Equation (1.1) is an important kind of coupled nonlinear wave equation. When $p=1$, it is the known Zakharov–Kuznetsov equation. When $p=2$, it is the known modified Zakharov–Kuznetsov equation.

In Duan et al. [1], studied the nonlinear solitary wave solutions of Eq. (1.1). In the continuum limit and suitably scaled coordinates, the voltage on the system is described by a modified Zakharov–Kuznetsov equation. The cut-off frequency of the growth rate for the solitary waves under transverse perturbations is obtained analytically. However, we note that the dynamic characteristics of Eq. (1.1) have not been studied. It is meaningful and necessary to consider the dynamical behavior of Eq. (1.1) and to find some possible new exact travelling wave solutions of Eq. (1.1). In the present paper, we shall use the dynamical system approach to investigate the travelling wave solutions of the coupled nonlinear electrical transmission lines.

To find travelling wave solutions of (1.1), we assume that

$$\begin{aligned} u(x,y,t)=P(\xi ),\xi =kx+wy-ct, \end{aligned}$$

(1.2)

where k, w and c are travelling wave parameters. Substituting (1.2) into (1.1), integrating once for (1.1) (taking the integral constant as zero), we have

$$\begin{aligned} (k^3+kw^2)P''+\frac{k}{p+1}P^{p+1}-cP=0, \end{aligned}$$

(1.3)

which corresponds to the two-dimensional Hamiltonian system

$$\begin{aligned} \frac{dP}{d\xi }=y, \frac{dy}{d\xi }=\frac{c}{k^3+kw^2}P-\frac{k}{(p+1)(k^3+kw^2)}P^{p+1}. \end{aligned}$$

(1.4)

Suppose that $k^3+kw^2\ne 0$ and write that

$$\begin{aligned} a=\frac{c}{k^3+kw^2},b=-\frac{1}{k^2+w^2}. \end{aligned}$$

(1.5)

Thus, we have the following dynamical system

$$\begin{aligned} \frac{dP}{d\xi }=y, \frac{dy}{d\xi }=aP+\frac{1}{p+1}bP^{p+1}, \end{aligned}$$

(1.6)

with the Hamiltonian

$$\begin{aligned} H(P,y)=\frac{1}{2}y^2-\frac{1}{2}aP^2-\frac{1}{(p+1)(p+2)}bP^{p+2}=h. \end{aligned}$$

(1.7)

To study uniformly the dynamical behaviors of travelling wave solutions of Eq. (1.3) for $p \ge 3$, making the transformation $P=\phi ^{\frac{1}{p}}$, we have

$$\begin{aligned} \ p\phi \phi ''+(1-p)(\phi ')^2-p^2\left[ a\phi ^2+\frac{1}{p+1}b\phi ^3\right] =0, \end{aligned}$$

(1.8)

which corresponds to the two-dimensional Hamiltonian system

$$\begin{aligned} \frac{d\phi }{d\xi }=y, \frac{dy}{d\xi }=\frac{(p-1)y^2+p^2\left[ a\phi ^2+\frac{1}{p+1}b\phi ^3\right] }{p\phi }, \end{aligned}$$

(1.9)

system (1.9) is a singular system, making the transformation $d\xi =p\phi \, d\zeta$, we have

$$\begin{aligned} \frac{d\phi }{d\zeta }=p\phi y, \frac{dy}{d\zeta }=(p-1)y^2+p^2\left[ a\phi ^2+\frac{1}{p+1}b\phi ^3\right] . \end{aligned}$$

(1.10)

Both systems (1.9) and (1.10) have the same invariant curve solutions, when $\phi \ne 0$ and $d\xi =p\phi \, d\zeta$, we have the first integral of (1.9) and (1.10)

$$\begin{aligned} H(\phi ,y)_p=\phi ^\frac{2-2p}{p}y^2-p^2\phi ^\frac{2}{p}\left( a+\frac{2b}{(p+1)(p+2)}\phi \right) =h. \end{aligned}$$

(1.11)

According to the first integral (1.7) and (1.11), we can obtain all kinds of phase portraits of systems (1.6) and (1.10) in the parametric space. Because the phase orbits defined by the vector fields of systems (1.6) and (1.10) determine the exact travelling wave solutions of Eq. (1.1) when $p=1$, $p=2$, and $p \ge 3$, we can investigate the bifurcations of phase portraits of systems (1.6) and (1.10) to look for the travelling wave solutions of Eq. (1.1) when $p=1$, $p=2$, and $p \ge 3$ (see [2,3,4,5,6,7,8,9,10,11]). The detailed calculation procedure regarding the dynamical system approach is given in the “Appendix”.

The rest of this paper is structured as follows. In Sect. 2, we give all phase portraits of system (1.6) for $p=1,2$ and system (1.10) for $p\ge 3$, and discuss the bifurcations of phase portraits of systems (1.6) and (1.10). In Sect. 3, according to the dynamics of the phase orbits of systems (1.6) and (1.10) given in Sect. 2, we solve Eq. (1.1) and numerical simulations are conducted for the solitary wave solutions and the periodic travelling wave solutions to Eq. (1.1) with the aid of Maple software. Finally, a short conclusion is given in Sect. 4.

2 The bifurcations of phase portraits of systems (1.6) and (1.10)

In this section, we consider the bifurcations of the phase orbits of (1.6) when $p=1,2$ and (1.10) when $p\ge 3$. Because $b=-\frac{1}{k^2+w^2}<0$, we only consider the phase orbits of systems (1.6) and (1.10) in its parameter space when $b<0$. With the aid of Maple software, we can obtain the phase portraits of systems (1.6) and (1.10).

By the qualitative theory of planar dynamical system [12], we know that for an equilibrium point of a planar integrable system, if the determinant of the coefficient matrix of the planar dynamical system is less than zero, then the equilibrium point is a saddle point; if the determinant of the coefficient matrix of the planar dynamical system is greater than zero and the trace is equal to zero, then it is a center point; if the determinant is equal to zero and the index of the equilibrium point is also equal to zero, then it is a cusp; if the determinant is equal to zero and the index of the equilibrium point is not equal to zero, then it is a high-order equilibrium point. After we know the type of the equilibrium point of the system, we can study the dynamics of the phase portraits of the system.

2.1 The case $p=1$

When $p=1$, there are two equilibrium points of (1.6) $S(-\frac{2a}{b},0)$ and O(0, 0). For the Hamiltonian $H(P,y)=\frac{1}{2}y^2-\frac{1}{2}aP^2-\frac{1}{6}bP^{3}=h$, we have $h_0=H(0,0)=0$, $h_1=H(-\frac{2a}{b},0)=-\frac{2a^3}{3b^2}$. With the aid of Maple software, the phase portraits of (1.6) are shown in Fig. 1.

Fig. 1

The bifurcations of phase portraits of (1.6) when $p=1. (1-1)a<0, b<0. (1-2)a>0, b<0. (1-3)a=0, b<0$

From Fig. 1, we summarize the crucial conclusions as follows when $p=1$ and $b<0$.

• (1) When $a>0 \ (<0)$, O is a saddle point (center) and S is a center (saddle point). When $a=0$, O is a cusp.

• (2) The system (1.6) has a unique homoclinic orbit $\Gamma$ which is asymptotic to the saddle and enclosing the center. There is a family of periodic orbits which are enclosing the center and filling up the interior of the homoclinic orbit $\Gamma$.

2.2 The case $p=2$

When $p=2$, there exist three equilibrium points $S_{\pm }(\sqrt{-\frac{3a}{b}},0)$ and O(0, 0) if $ab<0$. For the Hamiltonian $H(P,y)=\frac{1}{2}y^2-\frac{1}{2}aP^2-\frac{1}{12}bP^{4}=h$, we have $h_0=H(0,0)=0$, $h_1=H(\sqrt{-\frac{3a}{b}},0)=\frac{3a^2}{4b}$. If $ab>0$, there exists only an equilibrium point O(0, 0). With the aid of Maple software, with the change of parameter (a, b), the bifurcations of phase portraits of (1.6) when $p=2$ are shown in Fig. 2.

Fig. 2

The bifurcations of phase portraits of (1.6) when $p=2. (2-1)a<0, b<0. (2-2)a>0, b<0. (2-3)a=0, b<0$

From Fig. 2, we summarize the crucial conclusions as follows when $p=2$ and $b<0$.

• (1) When $a\le 0$, $b<0$, there are a unique equilibrium point O(0, 0) which is a center. There is a family of periodic orbits that contains the origin.

• (2) When $a>0$, $b<0$, there are three equilibrium points $S_{\pm }(\sqrt{-\frac{3a}{b}},0)$ and O(0, 0). Here O is a saddle point and $S_{\pm }$ are center points. There are two families of periodic periodic orbits and two homoclinic orbits which is asymptotic to the origin.

2.3 The case $p\ge 3$

When $p\ge 3$ and $a\ne 0$, there are two equilibrium points $S(\phi _1,0)$ and O(0, 0) for the system (1.10), where $\phi _1=-\frac{(p+1)a}{b}$. With the change of parameter (a, b), the bifurcations of phase portraits of (1.10) are shown in Fig. 3. In addition, when $p\ge 4$ and p is an even number, as $P=\phi ^{\frac{1}{p}}$, we can only discuss the case $\phi \ge 0$ and study the right-half of the phase plane for the phase portraits of (1.10).

From Fig. 3, we arrive at the following conclusions when $p\ge 3$ and $a\ne 0$.

• (1) The origin O is a two-order equilibrium of (1.10). When $a>0(<$0), S is a center (saddle point).

• (2) The system (1.10) have many homoclinic orbits $\Gamma ^{h}$ which are asymptotic to the origin.

Fig. 3

The bifurcations of phase portraits of (1.10) when $p\ge 3. (3-1)a<0, b<0. (3-2)a>0, b<0. (3-3)a=0, b<0$

3 The exact travelling wave solutions of Eq. (1.1)

In this section, corresponding to all phase orbits given by Sect. 2, through bifurcation theories and the Jacobian elliptic functions [13], we discuss the exact travelling wave solutions of Eq. (1.1). Because the bounded travelling waves are only meaningful to a physical model, we just pay attention to the bounded travelling wave solutions of Eq. (1.1).

Fig. 4

The three-dimensional graphics of $u_1$ ($k=1, w=1, c=1, t=0.2, -5\le x\le 5, -5\le y\le 5$)

3.1 The case $p=1$

• (1) When $a>0$, $b<0$, and $h=h_{0}=0$, there exists a smooth solitary solution which corresponds to a smooth homoclinic orbit $\Gamma$ of (1.6) defined by $H(P,y)=h_{0}=0$. By using the first equation of (1.6), we have the parametric representation $P(\xi )=\frac{-3a+3a\tanh ^2(\frac{\sqrt{a}}{2}\xi )}{B}.$ Thus, we obtain the solitary wave solution of Eq. (1.1) as follows:

  $$\begin{aligned} u_1(x,y,t)=\frac{-3a+3a\tanh ^2\left( \frac{\sqrt{a}}{2}(kx+wy-ct)\right) }{b}. \end{aligned}$$

  (3.1)

• (2) When $a<0,b<0$ and $h=h_{1}$, there exists a smooth solitary solution which corresponds to a smooth homoclinic orbit $\Gamma$ of (1.6) defined by $H(P,y)=h_{1}$. By using the first equation of (1.6), we have the parametric representation $P(\xi )=\frac{2|a|}{b}(1-\frac{3}{2}sech^2(\frac{\sqrt{|a|}}{2}(\xi ))).$ Thus, we obtain the solitary wave solution of Eq. (1.1) as follows:

  $$\begin{aligned} u_2(x,y,t)=\frac{2|a|}{b}\left( 1-\frac{3}{2}sech^2\left( \frac{\sqrt{|a|}}{2}\left( kx+wy-ct\right) \right) \right) . \end{aligned}$$

  (3.2)

• (3) When $a>0 \ (a<0)$, $b<0$, there exist periodic travelling wave solutions corresponding to the family of periodic orbits $\Gamma ^h$ of (1.6) defined by $H(P,y)=h,h\in (h_1,0)(h\in (0,h_1))$, we have following parametric representation $P(\xi )=z_1-(z_1-z_2)sn^2(\frac{\sqrt{3|b|(z_1-z_3)}}{6}\xi ,\sqrt{\frac{z_1-z_2}{z_1-z_3}})$, where the parameters $z_1$, $z_2$, $z_3$, and $z_1>z_2>z_3$ are defined by $y^2=2h+aP^2+\frac{1}{3}bP^3=\frac{1}{3}|b|(z_1-P)(P-z_2)(P-z_3)$.

Thus, we obtain a family of periodic wave solutions of Eq. (1.1) as follows:

$$\begin{aligned} u_3(x,y,t)=z_1-(z_1-z_2)sn^2\left( \frac{\sqrt{3|b|(z_1-z_3)}}{6}(kx+wy-ct),\sqrt{\frac{z_1-z_2}{z_1-z_3}}\right) . \end{aligned}$$

(3.3)

Fig. 5

The three-dimensional graphics of $u_2$ ($k=1, w=1, c=-1, t=0.2, -5\le x\le 5, -5\le y\le 5$)

Fig. 6

The three-dimensional graphics of $u_3$ ($k=\frac{1}{2}, w=\frac{1}{2}, c=\frac{1}{2}, t=0.2, h=-\frac{2}{3}, -10\le x\le 10, -10\le y\le 10$)

3.2 The case $p=2$

• (1) When $a<0$, $b<0$, there exists a unique equilibrium point of (1.6) O(0, 0). Here O is a center. There exists a family of periodic orbits enclosing the origin. We see from (1.7) that $y^2=-\frac{b}{6}[-\frac{12h}{b}-\frac{6a}{b}P^2-P^4]=-\frac{b}{6}[(r_1^2+P^2)(r_1^2-P^2)]$, where $r_1^2=-\frac{3}{b}[-a+\sqrt{a^2-\frac{4hb}{3}}],r_2^2=-\frac{3}{b}[a+\sqrt{a^2-\frac{4hb}{3}}]$. The family of periodic orbits defined by $H(P,y)=h$, $h\in (0,\infty )$ of (1.7) has the results $P(\xi )=\pm \tfrac{sn(\frac{1}{2}\sqrt{\tfrac{2b}{3}}r_2\xi ,\sqrt{-\frac{r_1^2}{r_2^2}})}{\sqrt{-\frac{1}{r_1^2}}}$. Thus, we obtain a family of periodic wave solutions of Eq. (1.1) as follows:

  $$\begin{aligned} u_4(x,y,t)=\pm \frac{sn\left( \frac{1}{2}\sqrt{\frac{2b}{3}}r_2(kx+wy-ct),\sqrt{-\frac{r_1^2}{r_2^2}}\right) }{\sqrt{-\frac{1}{r_1^2}}}. \end{aligned}$$

  (3.4)

• (2) When $a=0$, $b<0$, there exists a unique equilibrium point of (1.6) O(0, 0). Here O is a center. There exists a family of periodic orbits enclosing the origin. We see from (1.7) that $y^2=-\frac{b}{6}[-\frac{12h}{b}-P^4]=\frac{|b|}{6}[(\sqrt{\frac{12h}{|b|}}-P^2)(P^2+\sqrt{\frac{12h}{|b|}})]$. The family of periodic orbits defined by $H(P,y)=h$, $h\in (0,\infty )$ of (1.7) has the results $P(\xi )=\pm \frac{6h}{|b|}cn((\frac{2h|b|}{3})^{\frac{1}{4}}\xi ,\frac{1}{\sqrt{2}})$. Thus, we obtain a family of periodic wave solutions of Eq. (1.1) as follows:

  $$\begin{aligned} u_5(x,y,t)=\pm \frac{6h}{|b|}cn\left( \left( \frac{2h|b|}{3}\right) ^{\frac{1}{4}}(kx+wy-ct),\frac{1}{\sqrt{2}}\right) . \end{aligned}$$

  (3.5)

• (3) When $a>0$, $b<0$, there exist three equilibrium points of (1.6) $A_{\pm }({\pm }\frac{(-3a)}{b},0)$, O(0, 0). Here O is a saddle point and $A_{\pm }$ are saddle center points. For $h\in (\frac{3a^2}{4b},0)$, it can be written as $y^2=\frac{-b}{6}[\frac{12h}{(-b)}+\frac{6a}{-b}P^2-P^4]=\frac{(-b)}{6}[(r_1^2-P^2)(r_2^2+P^2)]$, where $r_1^2=\frac{3}{-b}[(-a)+\sqrt{a^2-\frac{4hb}{3}}], r_2^2=\frac{3}{-b}[a+\sqrt{a^2-\frac{4hb}{3}}]$. Thus, the two families of periodic orbits defined by $H(\phi ,y)=h$ have the parametric representations $P(\xi )={\pm }r_2 dn(\sqrt{\frac{(-b)}{6}}r_2\xi ,\sqrt{\frac{r_1^2+r_2^2}{r_2}})$. Two homoclinic orbits defined by $H(\phi ,y)=0$ have the results $P(\xi )={\pm }\sqrt{\frac{6a}{-b}}sech(\sqrt{\frac{a(-b)}{6}}\xi )$.

Fig. 7

The three-dimensional graphics of $u_4$($k=1, w=1, c=-1, t=0.2, h=0.005, -10\le x\le 10, -10\le y\le 10$)

Fig. 8

The three-dimensional graphics of $u_5$ ($k=1, w=1, c=0, t=0.2, h=0.005, -40\le x\le 40, -40\le y\le 40$)

Fig. 9

The three-dimensional graphics of $u_6$($k=0.152, w=4.12, c=2, h=-2, t=0.2, -20\le x\le 20, -20\le y\le 20$)

Fig. 10

The three-dimensional graphics of $u_7$ ($k=0.152, w=4.12, c=2, t=0.2, -10\le x\le 10, -10\le y\le 10$)

Fig. 11

The three-dimensional graphics of $u_8$($k=1, w=1, c=1, p=3, t=0.2, -5\le x\le 5, -5\le y\le 5$)

Thus, we obtain the periodic wave solution and the solitary wave solution of Eq. (1.1) as follows:

$$\begin{aligned} u_6(x,y,t)= & {} {\pm }r_2dn\left( \sqrt{\frac{(-b)}{6}}r_2(kx+wy-ct),\sqrt{\frac{r_1^2+r_2^2}{r_2}}\right) \end{aligned}$$

(3.6)

$$\begin{aligned} u_7(x,y,t)= & {} {\pm }\sqrt{\frac{6a}{-b}}sech\left( \sqrt{\frac{a(-b)}{6}}(kx+wy-ct)\right) . \end{aligned}$$

(3.7)

3.3 The case $p\ge 3$

When $p\ge 3$ and $b<0$, if and only if $h\equiv 0$, through $H(\phi ,y)_p=h\equiv 0$, it will be meaningful for the integral of the first equation of (1.10). When $h=0$, then we have $y^2=-p^2\phi ^2(a+\frac{2b}{(p+1)(p+2)})$. There exists a smooth solitary solution which corresponds to a smooth homoclinic orbit $\Gamma$ of (1.10) defined by $H(\phi ,y)=0$. By using the first equation of (1.10), we have the parametric representation $\phi _(\xi )=\frac{a(p+1)(p+2)(1+\tanh ^2(\frac{p\sqrt{a}\xi }{2}))}{2b}.$ Therefore, we have $P(\xi )=(\frac{a(p+1)(p+2)(1+\tanh ^2(\frac{p\sqrt{a}\xi }{2}))}{2b})^\frac{1}{p}.$

Thus, we obtain the solitary wave solution of Eq. (1.1) as follows:

$$\begin{aligned} u_8(x,y,t)=\left( \frac{a(p+1)(p+2)\left( 1+\tanh ^2\left( \frac{p\sqrt{a}(kx+wy-ct)}{2}\right) \right) }{2b}\right) ^\frac{1}{p}. \end{aligned}$$

(3.8)

By using the numerical simulation method, with the aid of Maple software, the three-dimensional graphics of the bounded solutions of Eq. (1.1) are shown in Figs 4, 5, 6, 7, 8, 9, 10 and 11.

Usually, a solitary wave solution of a travelling wave equation corresponds to a homoclinic orbit of a dynamical system. A periodic wave solution of a travelling wave equation corresponds to a periodic orbit of a dynamical system. From Figs 4, 5, 6, 7, 8, 9, 10 and 11, it is easy to see that (3.1), (3.2), (3.7), and (3.8) are solitary wave solutions and (3.3), (3.4), (3.5), and (3.6) are periodic wave solutions. Obviously, the computer simulations can show the correctness of our results.

4 Conclusion

In summary, by using the dynamical system method, we obtained eight exact explicit traveling wave solutions of Eq. (1.1). Among them, (3.1), (3.2), (3.7), and (3.8) are solitary wave solutions, which are expressed by the hyperbolic function, and (3.3), (3.4), (3.5), and (3.6) are periodic wave solutions, which are expressed by Jacobian elliptic function. Thus, we conclude that Eq. (1.1) has both solitary wave solutions and periodic wave solutions.

From the above discussions, we obtain the two-dimensional solitary waves and periodic waves of Eq. (1.1). Obviously, the dynamical system method with the aid of Maple software is a very powerful method to seek exact travelling wave solutions for nonlinear travelling wave equations. This method is based on the bifurcation theory of planar dynamical systems, and then the analytical solutions of the nonlinear wave equations are solved by qualitative analysis and the Jacobian elliptic functions. The dynamical system method can also be widely used for other nonlinear travelling wave equations in mathematical physics and engineering.

Appendix

Here we describe the dynamical system method for finding traveling wave solutions of nonlinear wave equations. A $(n+1)$-dimensional nonlinear partial differential equation is given as follows:

$$\begin{aligned} P(t, x_{i}, u_{t}, u_{x_{i}}, u_{x_{i}x_{i}}, u_{x_{i}x_{j}}, u_{tt}, \ldots )=0,\quad i,j=1,2,\ldots ,n. \end{aligned}$$

(A.1)

The main steps of the dynamical system method are as follows.

Step 1 Reduction of Eq. (A.1).

Making a transformation $u(t,x_{1},x_{2},\ldots ,x_{n})=\phi (\xi )$, $\xi = \sum _{i=1}^{n}k_{i}x_{i}-ct$, Eq. (A.1) can be reduced to a nonlinear ordinary differential equation

$$\begin{aligned} \ D(\xi , \phi , \phi _{\xi }, \phi _{\xi \xi }, \phi _{\xi \xi \xi }, \ldots )=0, \end{aligned}$$

(A.2)

where $k_{i}$ are non-zero constants and c is the wave speed. Integrating several times for Eq. (A.2), if it can be reduced to the following second-order nonlinear ordinary differential equation

$$\begin{aligned} E(\phi , \phi _{\xi }, \phi _{\xi \xi })=0, \end{aligned}$$

(A.3)

then let $\phi _{\xi }=d\phi /d\xi =y$, Eq. (A.3) can be reduced to a two-dimensional dynamical system

$$\begin{aligned} \frac{d\phi }{d\xi }=y,\quad \frac{dy}{d\xi }=f(\phi ,y), \end{aligned}$$

(A.4)

where $f(\phi ,y)$ is an integral expression or a fraction. If $f(\phi ,y)$ is a fraction such as $f(\phi ,y)= F(\phi ,y)/g(\phi )$ and $g(\phi _{s})=0$, $\frac{dy}{d\xi }$ does not exist when $\phi =\phi _{s}$. Then we shall make a transformation $d\xi =g(\phi )d\zeta$, thus system (A.4) can be rewritten as

$$\begin{aligned} \frac{d\phi }{d\zeta }=g(\phi )y,\quad \frac{dy}{d\zeta }=F(\phi ,y), \end{aligned}$$

(A.5)

where $\zeta$ is a parameter. If Eq. (A.1) can be reduced to the above system (A.4) or (A.5), then we can go on to the next step.

Step 2 Discussion of bifurcations of phase portraits of system (A.4).

If system (A.4) is an integral system, systems (A.4) and (A.5) can be reduced to the differential equation

$$\begin{aligned} \frac{dy}{d\phi }=\frac{f(\phi ,y)}{y},\quad \frac{dy}{d\phi }=\frac{F(\phi ,y)}{g(\phi )y}=\frac{f(\phi ,y)}{y}, \end{aligned}$$

(A.6)

then systems (A.4) and (A.5) have the same first integral (that is, Hamiltonian) as follows

$$\begin{aligned} H(\phi ,y)=h, \end{aligned}$$

(A.7)

where h is an integral constant. According to the first integral, we can obtain all kinds of phase portraits in the parametric space. Because the phase orbits defined the vector fields of system (A.4) [or system (A.5)] determine the travelling wave solutions of Eq. (A.1), we can investigate the bifurcations of phase portraits of system (A.4) [or system (A.5)] to seek the travelling wave solutions of Eq. (A.1). A periodic orbit always corresponds to a periodic wave solution; a homoclinic orbit always corresponds to a solitary wave solution; a heteroclinic orbit (or so-called connecting orbit) always corresponds to a kink (or anti-kink) wave solution. When we find all phase orbits, we can obtain the value of h or its range.

Step 3 Calculation of the first equation of system (A.4).

After h is determined, we can obtain the following relationship from Eq. (A.7)

$$\begin{aligned} y=y(\phi ,h), \end{aligned}$$

(A.8)

that is, $d\phi /d\xi =y(\phi ,h)$. If the expression (A.8) is an integral expression, then substituting it into the first term of Eq. (A.4) and integrating it, we obtain

$$\begin{aligned} \int _{\phi _{0}}^{\phi }\frac{d\varphi }{y(\varphi ,h)}=\int _{0}^{\xi } \, d\tau . \end{aligned}$$

(A.9)

where $\phi (0)$ and 0 are initial constants. Usually, the initial constants can be taken by a root of Eq. (A.8) or inflection points of the travelling waves. Taking proper initial constants and integrating Eq. (A.9), through the Jacobian elliptic functions, we can obtain the exact travelling wave solutions of Eq. (A.1).

This is the whole process of the dynamical system method. The different nonlinear wave equations correspond to different dynamical systems. The different dynamical systems correspond to different travelling wave solutions.