1 Introduction

Because of the rapid growth of railway transportation, the likelihood of an earthquake occurring when a train is crossing a bridge has increased. Seismic dynamic analysis for this kind of vehicle–bridge interaction (VBI) system under seismic ground motions becomes critical for safety of both the vehicle and its occupants. As a result, various seismic analyses of the VBI system have been conducted. Yang et al. (2016) proposed an analysis of a coupled train and bridge system excited by an artificial seismic wave and analyzed the running safety; Zeng and Dimitrakopoulos (2016) investigated seismic responses for a couple of trains and a horizontally curved railway bridge subjected to frequent earthquakes; and Hong et al. (2020) presented a framework for the seismic analysis of the coupled train and bridge system isolated by the friction pendulum bearing. According to the findings of the previous studies, seismic excitations significantly affect the VBI system. Uniform seismic excitations were used in these studies.

For long, multi-span bridges, the arrival times of traveling seismic ground motions at different bridge support points are different. The wave passage effect is used to represent this kind of spatial variation (Oliveira et al., 1991). When the bridge is not a one-span bridge, the spatial variation of the seismic excitations should be incorporated in the seismic analysis of the VBI system. Many scientists and engineers have performed seismic analyses of bridges considering the wave passage effect. Jia et al. (2013) adopted a multi-span continuous bridge to investigate the effect of the seismic spatial variation; Wang et al. (2015) studied the impact of seismic propagation wave velocities on the response of a multi-span suspension bridge; Adanur et al. (2017) investigated the stochastic analysis of a three-span suspension bridge subjected to traveling seismic ground motions by employing various seismic wave velocities; Ateş et al. (2018) determined the effect of multiple support seismic excitations on the dynamic vibration performances of cable-stayed bridges; and Ramadan et al. (2020) studied the mutual impact of the wave passage effect on the seismic performance of multi-span continuous box girder concrete bridges. Unfortunately, these studies have not considered interactions of the vehicle with the multi-span bridge. There has been relatively little research on the VBI system that has taken into account spatial variations. Even though some studies performed dynamic analyses of the train-bridge coupled system subjected to spatially varying seismic excitations (Xia et al., 2006), they employed the numerical history integral approach, i.e., the traditional Monte-Carlo method (MCM). Compared to the frequency-domain pseudo-excitation method (PEM) (Lin, 1992), this method is inefficient, especially for complex systems or problems. Zhang et al. (2011), Zhu et al. (2014), and Zeng et al. (2015) adopted the PEM to study the seismic vibrations of a train-bridge coupled system when it is excited by traveling seismic ground motions. However, they did not derive the random running safety of the vehicle or discuss the impact of the wave passage effect on it. In short, the wave passage effect is important for the coupled system of a train and multi-span bridge. Because of the low efficiency of the MCM, the stochastic responses of this kind of system are better analyzed in the frequency domain by PEM. Until now, no one has presented a running safety assessment of this kind of system in the stochastic seismic analysis in the frequency domain by PEM.

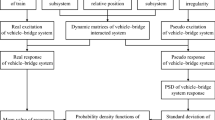
To fill the gap, the random dynamic responses of the VBI system and the vehicle running safety under traveling seismic ground motions are investigated in this paper. A three-dimensional VBI model is constructed in this study. The equation of motion (EOM) of the VBI system is derived through the wheel-rail contact relationship. The wave passage effect is included in the seismic simulation. The random excitations due to track irregularities and traveling seismic ground motions are replaced by corresponding pseudo-excitations according to PEM. The standard deviation (SD) of the responses and vehicle running safety are efficiently calculated by computing the pseudo-responses under the corresponding pseudo-excitations.

The MCM is used to validate the accuracy of the proposed PEM by investigating the bridge's random responses. Then taking a multi-span simply supported bridge and a Chinese-made electric multiple unit (EMU) train under traveling seismic ground motions as an example, random responses and the safety factor of the system are presented to elucidate the effects of train speeds, seismic intensities, and seismic wave propagation velocities.

2 EOM for VBI Systems Under Traveling Seismic Ground Motions

The random excitations applied to the VBI system in this paper are seismic ground motions imposed on the bridge piers and the track irregularities between the wheel and the rail.

2.1 Seismic Ground Motions Model

The seismic ground motion is assumed to be a nonstationary random process described by the uniformly modulated evolutionary process model as \(\ddot{u}_{sj} \left( t \right) = g\left( t \right)\ddot{u}_{e} \left( t \right)\) for the jth support of the bridge (To, 1986). \(\ddot{u}_{e} \left( t \right)\) is a stationary ground acceleration process with a 0 mean value. The auto-power spectral density (PSD) of this process is \(S_{{\ddot{u}_{e} \ddot{u}_{e} }}\), which is characterized by the Clough-Penzien spectrum model in this paper (Clough & Penzien, 2010)

$$S_{{\ddot{u}_{e} \ddot{u}_{e} }} \left( \omega \right) = \frac{{1 + 4\zeta_{g}^{2} \left( {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{g} }}} \right. \kern-\nulldelimiterspace} {\omega_{g} }}} \right)^{2} }}{{\left[ {1 - \left( {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{g} }}} \right. \kern-\nulldelimiterspace} {\omega_{g} }}} \right)^{2} } \right]^{2} + 4\zeta_{g}^{2} \left( {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{g} }}} \right. \kern-\nulldelimiterspace} {\omega_{g} }}} \right)^{2} }} \cdot \frac{{\left( {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{f} }}} \right. \kern-\nulldelimiterspace} {\omega_{f} }}} \right)^{4} }}{{\left[ {1 - \left( {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{f} }}} \right. \kern-\nulldelimiterspace} {\omega_{f} }}} \right)^{2} } \right]^{2} + 4\zeta_{f}^{2} \left( {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{f} }}} \right. \kern-\nulldelimiterspace} {\omega_{f} }}} \right)^{2} }} \cdot S_{0}$$
(1)

Here: \(\omega_{g}\) is the dominant frequency, while \(\zeta_{g}\) is the damping ratio of the soil on a specific site; \(\omega_{f}\) and \(\zeta_{f}\) are the parameters of the second filter that primarily control the low-frequency component of the seismic ground motion, generally \(\omega_{f} = 0.1\omega_{g} \sim 0.2\omega_{g}\), \(\zeta_{f} = \zeta_{g}\); and \(S_{0}\) is the spectral scale factor, which can be calculated by

$$S_{0} = \frac{{\overline{a}_{\max }^{2} }}{{\gamma^{2} \pi \omega_{g} \left( {2\zeta_{g} + {1 \mathord{\left/ {\vphantom {1 {2\zeta_{g} }}} \right. \kern-\nulldelimiterspace} {2\zeta_{g} }}} \right)}}$$
(2)

where \(\overline{a}_{\max }\) is a parameter relevant to the seismic peak ground acceleration (PGA); and \(\gamma\) is the peak value factor (Chen et al., 2017; Xu & Zhai, 2017). The parameters of the Clough-Penzien spectrum model for different seismic intensities (GB50111-2006, 2009) are listed in Table 1.

Table 1 Parameters of seismic ground motions
Full size table

The uniform modulation function of the seismic excitation has an exponential form (Jennings et al., 1968)

$$g(t)=\begin{cases}(t/t_{b})^{2} & 0\leq t\leq t_{b}\\1 & t_{b}\leq t\leq t_{c}\\\exp[-c(t-t_{c})] & t\geq t_{c}\end{cases}$$
(3)

where \(c\) is the attenuation constant, \(t_{b}\) and \(t_{c}\) define the ramp duration and the decay starting time. These parameters are listed in Table 1.

In this paper, a bridge with a total of \(N_{b}\) supports is considered. It is assumed that seismic ground motions propagate from the first bridge support on the left to the final bridge support on the right. Therefore, the arrival times of the seismic ground motions for each bridge support are different. The phase lags that exist between the jth bridge support and the left end bridge support are denoted as \(\tau_{bj} \;\left( {j = 1,\,2,\, \ldots ,\,N_{b} } \right)\). The seismic ground motion vector for all \(N_{b}\) bridge supports can be established as

$$\begin{gathered} {\mathbf{\ddot{u}}}_{s} \left( t \right) = \left[ {\begin{array}{*{20}c} {\ddot{u}_{s1} \left( t \right)} & {\ddot{u}_{s2} \left( t \right)} & \cdots & {\ddot{u}_{{sN_{b} }} \left( t \right)} \\ \end{array} } \right]^{{\text{T}}} \hfill \\ = \left[ {\begin{array}{*{20}c} {g\left( {t - \tau_{b1} } \right)\ddot{u}_{e} \left( {t - \tau_{b1} } \right)} & {g\left( {t - \tau_{b2} } \right)\ddot{u}_{e} \left( {t - \tau_{b2} } \right)} & \cdots & {g\left( {t - \tau_{{bN_{b} }} } \right)\ddot{u}_{e} \left( {t - \tau_{{bN_{b} }} } \right)} \\ \end{array} } \right]^{{\text{T}}} \hfill \\ = {\mathbf{G}}\left( t \right){\mathbf{\ddot{u}}}_{e} \left( t \right) \hfill \\ \end{gathered}$$
(4)

where the superscript ‘T’ means the transposition of the matrix, and

$${\mathbf{G}}\left( t \right) = diag\left[ {\begin{array}{*{20}c} {g\left( {t - \tau_{b1} } \right)} & {g\left( {t - \tau_{b2} } \right)} & \cdots & {g\left( {t - \tau_{{bN_{b} }} } \right)} \\ \end{array} } \right]$$
(5)
$${\mathbf{\ddot{u}}}_{e} \left( t \right) = \left[ {\begin{array}{*{20}c} {\ddot{u}_{e} \left( {t - \tau_{b1} } \right)} & {\ddot{u}_{e} \left( {t - \tau_{b2} } \right)} & \cdots & {\ddot{u}_{e} \left( {t - \tau_{{bN_{b} }} } \right)} \\ \end{array} } \right]^{{\text{T}}}$$
(6)

Spatial variation of the traveling seismic ground motions is represented by the coherency function in the frequency domain (Yang, 1986). The coherency function for seismic ground motions of the jth and kth supports is defined as (Arman, 1996)

$$\gamma_{jk} \left( \omega \right) = \frac{{S_{jk} \left( \omega \right)}}{{\sqrt {S_{jj} \left( \omega \right)S_{kk} \left( \omega \right)} }}$$
(7)

where \(S_{jj} \left( \omega \right)\) and \(S_{kk} \left( \omega \right)\) indicate the auto-PSD of the seismic ground accelerations at the jth support and kth support; and \(S_{jk} \left( \omega \right)\) indicates their cross-PSD. The coherency function is usually adopted to represent the spatial variability between seismic excitations at two sites. It can be written numerically as (Li & Chen, 2009)

$$\gamma_{jk} \left( \omega \right) = \exp \left[ {i\theta_{jk} \left( \omega \right)} \right]$$
(8)

where \(\gamma_{jk} \left( \omega \right)\) is also called the traveling wave effect factor. The phase angle \(\theta_{jk} \left( \omega \right)\) is relevant to the propagation speed of the seismic ground motions and the distance length between the jth and kth bridge supports along the wave propagation direction which is represented as \(d_{jk}\) (Oliveira et al., 1991). The phase angle can be written as

$$\theta_{jk} \left( \omega \right) = - \frac{{\omega d_{jk} }}{{V_{app} }} = \omega \left( {\tau_{bj} - \tau_{bk} } \right)$$
(9)

where \(V_{app}\) is the seismic apparent wave velocity (O'Rourke et al., 1982).

Thus, the PSD matrix of the vector \({\mathbf{\ddot{u}}}_{e} \left( t \right)\) for \(N_{b}\) bridge supports is:

$${\mathbf{S}}_{{{\mathbf{\ddot{u}}}_{e} {\mathbf{\ddot{u}}}_{e} }} \left( \omega \right) = \left[ {\begin{array}{*{20}c} {\gamma_{11} S_{11} } & {\gamma_{12} \sqrt {S_{11} \left( \omega \right)S_{22} \left( \omega \right)} } & \cdots & {\gamma_{{1N_{b} }} \sqrt {S_{11} \left( \omega \right)S_{{N_{b} N_{b} }} \left( \omega \right)} } \\ {\gamma_{21} \sqrt {S_{11} \left( \omega \right)S_{22} \left( \omega \right)} } & {\gamma_{22} S_{22} } & \cdots & {\gamma_{{2N_{b} }} \sqrt {S_{22} \left( \omega \right)S_{{N_{b} N_{b} }} \left( \omega \right)} } \\ \vdots & \vdots & \ddots & \vdots \\ {\gamma_{{N_{b} 1}} \sqrt {S_{11} \left( \omega \right)S_{{N_{b} N_{b} }} \left( \omega \right)} } & {\gamma_{{N_{b} 2}} \sqrt {S_{22} \left( \omega \right)S_{{N_{b} N_{b} }} \left( \omega \right)} } & \cdots & {\gamma_{{N_{b} N_{b} }} S_{{N_{b} N_{b} }} } \\ \end{array} } \right]$$
(10)

The PSD matrix \({\mathbf{S}}_{{{\mathbf{\ddot{u}}}_{e} {\mathbf{\ddot{u}}}_{e} }} \left( \omega \right)\) can be decomposed as follows:

$${\mathbf{S}}_{{{\mathbf{\ddot{u}}}_{e} {\mathbf{\ddot{u}}}_{e} }} \left( \omega \right) = {\mathbf{B}}^{*} \left( \omega \right){\mathbf{D}}\left( \omega \right){\mathbf{\Gamma D}}\left( \omega \right){\mathbf{B}}\left( \omega \right)$$
(11)

in which the asterisk * represents the complex conjugate, and

$${\mathbf{B}}\left( \omega \right) = {\text{diag}}\left[ {\begin{array}{*{20}c} {e^{{ - {\text{i}}\omega \tau_{b1} }} } & {e^{{ - {\text{i}}\omega \tau_{b2} }} } & \cdots & {e^{{ - {\text{i}}\tau_{{bN_{b} }} }} } \\ \end{array} } \right]$$
(12)
$${\mathbf{D}}\left( \omega \right) = {\text{diag}}\left[ {\begin{array}{*{20}c} {\sqrt {S_{11} \left( \omega \right)} } & {\sqrt {S_{22} \left( \omega \right)} } & \cdots & {\sqrt {S_{{N_{b} N_{b} }} \left( \omega \right)} } \\ \end{array} } \right]$$
(13)

\({{\varvec{\Gamma}}}\) is a square matrix of order \(N_{b}\), all elements of it are 1. It can be decomposed into

$${{\varvec{\Gamma}}} = \left\{ {\begin{array}{*{20}c} 1 \\ 1 \\ \vdots \\ 1 \\ \end{array} } \right\}\left\{ {\begin{array}{*{20}c} 1 & 1 & \cdots & 1 \\ \end{array} } \right\} = {\mathbf{QQ}}^{{\text{T}}}$$
(14)

Therefore, the PSD matrix \({\mathbf{S}}_{{{\mathbf{\ddot{u}}}_{e} {\mathbf{\ddot{u}}}_{e} }} \left( \omega \right)\) also can be written as:

$${\mathbf{S}}_{{{\mathbf{\ddot{u}}}_{e} {\mathbf{\ddot{u}}}_{e} }} \left( \omega \right) = {\mathbf{P}}^{*} \left( \omega \right){\mathbf{P}}^{{\text{T}}} \left( \omega \right)$$
(15)

in which

$${\mathbf{P}}\left( \omega \right) = {\mathbf{B}}\left( \omega \right){\mathbf{D}}\left( \omega \right){\mathbf{Q}}$$
(16)

2.2 Track Irregularities Model

Three kinds of track irregularities are investigated in this paper: alignment track irregularity \(r_{a} \left( x \right)\), vertical track irregularity \(r_{v} \left( x \right)\), and cross-level track irregularity \(r_{c} \left( x \right)\). They can be considered as a stationary random process with a 0 mean value. Their auto-PSD is given as \(S_{ra} \left( \Omega \right)\), \(S_{rv} \left( \Omega \right)\), and \(S_{rc} \left( \Omega \right)\); where \(\Omega\) is the spatial frequency (rad m−1). The relationship of the track distance \(x\) and the vehicle velocity \(V_{t}\) can be expressed as \(t = {x \mathord{\left/ {\vphantom {x {V_{t} }}} \right. \kern-\nulldelimiterspace} {V_{t} }}\). Therefore, the space domain of the track irregularities can be transformed into the time domain as

$$r_{a} \left( t \right) = \frac{{r_{a} \left( x \right)}}{{V_{t} }};\quad r_{v} \left( t \right) = \frac{{r_{v} \left( x \right)}}{{V_{t} }};\quad r_{c} \left( t \right) = \frac{{r_{c} \left( x \right)}}{{V_{t} }}$$
(17)

In matrix form

$${\mathbf{r}}\left( t \right) = \left\{ {\begin{array}{*{20}c} {r_{a} \left( t \right)} & {r_{v} \left( t \right)} & {r_{c} \left( t \right)} \\ \end{array} } \right\}$$
(18)

Their corresponding auto-PSD can be transformed similarly as

$$S_{ra} \left( \omega \right) = \frac{{S_{ra} \left( \Omega \right)}}{{V_{t} }};\quad S_{rv} \left( \omega \right) = \frac{{S_{rv} \left( \Omega \right)}}{{V_{t} }};\quad S_{rc} \left( \omega \right) = \frac{{S_{rc} \left( \Omega \right)}}{{V_{t} }}$$
(19)

The Federal Railroad Administration (FRA) track irregularity spectrum (Xia et al., 2018) is adopted in the present paper, i.e.,

Alignment track irregularity

$$S_{ra} \left( \omega \right) = {{S_{ra} \left( \Omega \right)} \mathord{\left/ {\vphantom {{S_{ra} \left( \Omega \right)} {V_{t} }}} \right. \kern-\nulldelimiterspace} {V_{t} }} = \frac{{kA_{v} \Omega_{c}^{2} }}{{V_{t} \Omega^{{2}} \left( {\Omega^{{2}} + \Omega_{c}^{2} } \right)}}$$
(20)

Vertical track irregularity

$$S_{rv} \left( \omega \right) = {{S_{rv} \left( \Omega \right)} \mathord{\left/ {\vphantom {{S_{rv} \left( \Omega \right)} {V_{t} }}} \right. \kern-\nulldelimiterspace} {V_{t} }} = \frac{{kA_{a} \Omega_{c}^{2} }}{{V_{t} \Omega^{{2}} \left( {\Omega^{{2}} + \Omega_{c}^{2} } \right)}}$$
(21)

Cross-level track irregularity

$$S_{rc} \left( \omega \right) = {{S_{rc} \left( \Omega \right)} \mathord{\left/ {\vphantom {{S_{rc} \left( \Omega \right)} {V_{t} }}} \right. \kern-\nulldelimiterspace} {V_{t} }} = \frac{{4kA_{v} \Omega_{c}^{2} }}{{V_{t} \left( {\Omega^{{2}} + \Omega_{c}^{2} } \right)\left( {\Omega^{{2}} + \Omega_{s}^{2} } \right)}}$$
(22)

where \(A_{v}\) and \(A_{a}\) are the roughness constants, \(k\) is the safety factor, and \(\Omega_{c}\) and \(\Omega_{s}\) are the cutoff frequencies. The track spectrum is divided into six grades, and the above parameters for different grades can be found in Xia et al. (2018).

The track irregularity spectrum matrices are expressed as

$${\mathbf{S}}_{{\mathbf{r}}} \left( \omega \right) = \left\{ {\begin{array}{*{20}c} {S_{ra} \left( \omega \right)} & {S_{rv} \left( \omega \right)} & {S_{rc} \left( \omega \right)} \\ \end{array} } \right\}$$
(23)

2.3 VBI System Model

The vehicles of the train model in this paper consist of motor-cars and trailer-cars. As shown in Fig. 1, these vehicles are modeled as an independent spring-damper-mass system with 27 degrees of freedom (DOFs) (Xia et al., 2018). Both car bodies and bogies have five DOFs. Only three DOFs are considered in each wheel-set. The symbols of the vehicle model in Fig. 1 are defined in Table 2, and they can also be found in Xia et al. (2018).

Fig. 1
figure 1

Three-dimensional model of the vehicle

Full size image
Table 2 Parameters of the Chinese-made EMU train
Full size table

The EOM of the train can be constructed as:

$$\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{v} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{w} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{\ddot{u}}}_{v} } \\ {{\mathbf{\ddot{u}}}_{w} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{v} } & {{\mathbf{C}}_{vw} } \\ {{\mathbf{C}}_{wv} } & {{\mathbf{C}}_{w} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{u}}}_{v} } \\ {{\dot{\mathbf{u}}}_{w} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{v} } & {{\mathbf{K}}_{vw} } \\ {{\mathbf{K}}_{wv} } & {{\mathbf{K}}_{w} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{v} } \\ {{\mathbf{u}}_{w} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\mathbf{F}}_{d} } \\ \end{array} } \right\}$$
(24)

where \({\mathbf{M}}_{v}\) is the mass matrix, \({\mathbf{C}}_{v}\) is the damping matrix, and \({\mathbf{K}}_{v}\) is the stiffness matrix of bodies and bogies of the vehicles; while \({\mathbf{M}}_{w}\) is the mass matrix, \({\mathbf{C}}_{w}\) is the damping matrix, and \({\mathbf{K}}_{w}\) is the stiffness matrix of the wheel-sets; \({\mathbf{u}}_{v}\) and \({\mathbf{u}}_{w}\) are the corresponding displacement vectors of the vehicles and the wheel-sets, respectively; and \({\mathbf{F}}_{d}\) is the vector of the dynamic wheel-rail contact force at the center of wheel-sets. The expansion of the above vectors and matrices are given in Xia et al. (2018).

As shown in Fig. 2, the rail, bridge deck and bridge pier are modeled as three-dimensional Euler beam elements. The Rayleigh damping is considered for the beam elements (Chopra, 1995). Discrete, massless dampers and springs are used to represent the fasteners supporting layers’ damping properties and elasticity. The EOM of the coupled track structure and bridge structure can be written in the following form:

$$\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{r} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{b} } & {{\mathbf{M}}_{bs} } \\ {\mathbf{0}} & {{\mathbf{M}}_{sb} } & {{\mathbf{M}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{\ddot{u}}}_{r} } \\ {{\mathbf{\ddot{u}}}_{b} } \\ {{\mathbf{\ddot{u}}}_{s} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{r} } & {{\mathbf{C}}_{rb} } & {\mathbf{0}} \\ {{\mathbf{C}}_{br} } & {{\mathbf{C}}_{b} } & {{\mathbf{C}}_{bs} } \\ {\mathbf{0}} & {{\mathbf{C}}_{sb} } & {{\mathbf{C}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{u}}}_{r} } \\ {{\dot{\mathbf{u}}}_{b} } \\ {{\dot{\mathbf{u}}}_{s} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{r} } & {{\mathbf{K}}_{rr} } & {\mathbf{0}} \\ {{\mathbf{K}}_{br} } & {{\mathbf{K}}_{b} } & {{\mathbf{K}}_{bs} } \\ {\mathbf{0}} & {{\mathbf{K}}_{sb} } & {{\mathbf{K}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{r} } \\ {{\mathbf{u}}_{b} } \\ {{\mathbf{u}}_{s} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {{\mathbf{F}}_{b} } \\ {\mathbf{0}} \\ {{\mathbf{P}}_{s} } \\ \end{array} } \right\}$$
(25)
Fig. 2
figure 2

FEM models for the bridge and the track

Full size image

where \({\mathbf{u}}_{s}\) is the ground displacement vectors; \({\mathbf{u}}_{r}\) and \({\mathbf{u}}_{b}\) are the displacement vectors of the rail and the non-supporting part of the bridge; \({\mathbf{M}}_{r}\) is the mass matrix, \({\mathbf{C}}_{r}\) is the damping matrix, and \({\mathbf{K}}_{r}\) is the stiffness matrix of the rail; while \({\mathbf{M}}_{b}\) is the mass matrix, \({\mathbf{C}}_{b}\) is the damping matrix, and \({\mathbf{K}}_{b}\) is the stiffness matrix of the non-supporting part of the bridge; and \({\mathbf{M}}_{s}\) is the mass matrix, \({\mathbf{C}}_{s}\) is the damping matrix, and \({\mathbf{K}}_{s}\) is the stiffness matrix of the supporting part of the bridge. \({\mathbf{P}}_{s}\) is the reaction force vector of the bridge supporting part due to the seismic ground motions; \({\mathbf{F}}_{b}\) is the force vector which can be expressed as

$${\mathbf{F}}_{b} = - {\mathbf{N}}^{{\text{T}}} {{\varvec{\Gamma}}}^{ - 1} {\mathbf{F}}_{c} = - {\mathbf{N}}^{{\text{T}}} {{\varvec{\Gamma}}}^{ - 1} \left( {{\mathbf{F}}_{d} + {\mathbf{F}}_{w} } \right)$$
(26)

in which \({\mathbf{F}}_{w}\) is the train self-weight vector; \({\mathbf{N}}\) is the cubic Hermite interpolation matrix between rails and wheel-sets (Yang et al., 2004); and \({{\varvec{\Gamma}}}\) is the displacement transformation matrix. Details of these matrices can be found in Yang et al. (2004).

If the mode superposition method is adopted, the responses of the rail can be expressed as

$${\mathbf{u}}_{r} = {{\varvec{\Phi}}}_{r} {\mathbf{q}}_{r} {,}\quad {\dot{\mathbf{u}}}_{r} = {{\varvec{\Phi}}}_{r} {\dot{\mathbf{q}}}_{r} {,}\quad {\mathbf{\ddot{u}}}_{r} = {{\varvec{\Phi}}}_{r} {\mathbf{\ddot{q}}}_{r}$$
(27)

The responses of the non-supporting part of the bridge can be expressed as

$${\mathbf{u}}_{b} = {{\varvec{\Phi}}}_{b} {\mathbf{q}}_{b} {,}\quad {\dot{\mathbf{u}}}_{b} = {{\varvec{\Phi}}}_{b} {\dot{\mathbf{q}}}_{b} {,}\quad {\mathbf{\ddot{u}}}_{b} = {{\varvec{\Phi}}}_{b} {\mathbf{\ddot{q}}}_{b}$$
(28)

where \({{\varvec{\Phi}}}_{r}\) and \({{\varvec{\Phi}}}_{b}\) are the mode shape matrixes for the rail and the non-supporting bridge; \({\mathbf{q}}_{r}\) and \({\mathbf{q}}_{b}\) are the corresponding modal coordinate displacement vectors. Substituting Eqs. (27) and (28) into Eq. (25) and pre-multiplying by \({{\varvec{\Phi}}}_{r}^{{\text{T}}}\) and \({{\varvec{\Phi}}}_{b}^{{\text{T}}}\) for the first and second rows, respectively, gives the EOM of the track and bridge coupled system as

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {{{\varvec{\Phi}}}_{r}^{{\text{T}}} {\mathbf{M}}_{r} {{\varvec{\Phi}}}_{r} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{{\varvec{\Phi}}}_{b}^{{\text{T}}} {\mathbf{M}}_{b} {{\varvec{\Phi}}}_{b} } & {{{\varvec{\Phi}}}_{b}^{{\text{T}}} {\mathbf{M}}_{bs} } \\ {\mathbf{0}} & {{\mathbf{M}}_{sb} {{\varvec{\Phi}}}_{b} } & {{\mathbf{M}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{\ddot{q}}}_{r} } \\ {{\mathbf{\ddot{q}}}_{b} } \\ {{\mathbf{\ddot{u}}}_{s} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{{\varvec{\Phi}}}_{r}^{{\text{T}}} {\mathbf{C}}_{r} {{\varvec{\Phi}}}_{r} } & {{{\varvec{\Phi}}}_{r}^{{\text{T}}} {\mathbf{C}}_{rb} {{\varvec{\Phi}}}_{b} } & {\mathbf{0}} \\ {{{\varvec{\Phi}}}_{b}^{{\text{T}}} {\mathbf{C}}_{br} {{\varvec{\Phi}}}_{r} } & {{{\varvec{\Phi}}}_{b}^{{\text{T}}} {\mathbf{C}}_{b} {{\varvec{\Phi}}}_{b} } & {{{\varvec{\Phi}}}_{b}^{{\text{T}}} {\mathbf{C}}_{bs} } \\ {\mathbf{0}} & {{\mathbf{C}}_{sb} {{\varvec{\Phi}}}_{b} } & {{\mathbf{C}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{q}}}_{r} } \\ {{\dot{\mathbf{q}}}_{b} } \\ {{\dot{\mathbf{u}}}_{s} } \\ \end{array} } \right\} \hfill \\ + \left[ {\begin{array}{*{20}c} {{{\varvec{\Phi}}}_{r}^{{\text{T}}} {\mathbf{K}}_{r} {{\varvec{\Phi}}}_{r} } & {{{\varvec{\Phi}}}_{r}^{{\text{T}}} {\mathbf{K}}_{rb} {{\varvec{\Phi}}}_{b} } & {\mathbf{0}} \\ {{{\varvec{\Phi}}}_{b}^{{\text{T}}} {\mathbf{K}}_{br} {{\varvec{\Phi}}}_{r} } & {{{\varvec{\Phi}}}_{b}^{{\text{T}}} {\mathbf{K}}_{b} {{\varvec{\Phi}}}_{b} } & {{{\varvec{\Phi}}}_{b}^{{\text{T}}} {\mathbf{K}}_{bs} } \\ {\mathbf{0}} & {{\mathbf{K}}_{sb} {{\varvec{\Phi}}}_{b} } & {{\mathbf{K}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{q}}_{r} } \\ {{\mathbf{q}}_{b} } \\ {{\mathbf{u}}_{s} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {{{\varvec{\Phi}}}_{r}^{{\text{T}}} {\mathbf{F}}_{b} } \\ {\mathbf{0}} \\ {{\mathbf{P}}_{s} } \\ \end{array} } \right\} \hfill \\ \end{gathered}$$
(29)

In this study, it is assumed that the wheel-sets and the rail keep in touch with each other; namely, perfect contact between wheels and rails is assumed in this paper. Motions of the wheel-set are dependent on the movements of the rails \({\mathbf{u}}_{r}\) and the track irregularity vector \({\mathbf{r}}\) can be calculated using the cubic Hermite interpolation matrix \({\mathbf{N}}\) and displacement transformation matrix \({{\varvec{\Gamma}}}\), where they can be written as follows

$$\left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{w} } \\ {{\dot{\mathbf{u}}}_{w} } \\ {{\mathbf{\ddot{u}}}_{w} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {{\mathbf{\Gamma Nu}}_{r} + {\mathbf{r}}} \\ {V_{t} {\mathbf{\Gamma N}}_{,x} {\mathbf{u}}_{r} + {\mathbf{\Gamma N\dot{u}}}_{r} + {\dot{\mathbf{r}}}} \\ {V_{t}^{2} {\mathbf{\Gamma N}}_{,xx} {\mathbf{u}}_{r} + 2V_{t} {\mathbf{\Gamma N}}_{,x} {\dot{\mathbf{u}}}_{r} + {\mathbf{\Gamma N\ddot{u}}}_{r} + {\mathbf{\ddot{r}}}} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {{\mathbf{\Gamma N}}} & {\mathbf{0}} & {\mathbf{0}} \\ {V_{t} {\mathbf{\Gamma N}}_{,x} } & {{\mathbf{\Gamma N}}} & {\mathbf{0}} \\ {V_{t}^{2} {\mathbf{\Gamma N}}_{,xx} } & {2V_{t} {\mathbf{\Gamma N}}_{,x} } & {{\mathbf{\Gamma N}}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{r} } \\ {{\dot{\mathbf{u}}}_{r} } \\ {{\mathbf{\ddot{u}}}_{r} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\mathbf{r}} \\ {{\dot{\mathbf{r}}}} \\ {{\mathbf{\ddot{r}}}} \\ \end{array} } \right\}$$
(30)

where the subscript ‘,x’ represents the derivative with respect to the longitudinal distance along the bridge. Substituting Eqs. (27), (28), and (30) into the second row of Eq. (24), \({\mathbf{F}}_{d}\) can be obtained as

$$\begin{gathered} {\mathbf{F}}_{d} = {\mathbf{M}}_{w} {\mathbf{\ddot{u}}}_{w} + {\mathbf{C}}_{wv} {\dot{\mathbf{u}}}_{v} + {\mathbf{C}}_{w} {\dot{\mathbf{u}}}_{w} + {\mathbf{K}}_{wv} {\mathbf{u}}_{v} + {\mathbf{K}}_{w} {\mathbf{u}}_{w} \hfill \\ \quad \, = {\mathbf{M}}_{w} {\mathbf{\Gamma N\Phi }}_{r} {\mathbf{\ddot{q}}}_{r} + \left( {2V_{t} {\mathbf{M}}_{w} {\mathbf{\Gamma N}}_{,x} + {\mathbf{C}}_{w} {\mathbf{\Gamma N}}} \right){{\varvec{\Phi}}}_{r} {\dot{\mathbf{q}}}_{r} + {\mathbf{C}}_{wv} {\dot{\mathbf{u}}}_{v} + {\mathbf{K}}_{wv} {\mathbf{u}}_{v} \hfill \\ \quad \; + \left( {V_{t}^{2} {\mathbf{M}}_{w} {\mathbf{\Gamma N}}_{,xx} + V_{t} {\mathbf{C}}_{w} {\mathbf{\Gamma N}}_{,x} + {\mathbf{K}}_{w} {\mathbf{\Gamma N}}} \right){{\varvec{\Phi}}}_{r} {\mathbf{q}}_{r} + {\mathbf{M}}_{w} {\mathbf{\ddot{r}}} + {\mathbf{C}}_{w} {\dot{\mathbf{r}}} + {\mathbf{K}}_{w} {\mathbf{r}}\quad \; \hfill \\ \end{gathered}$$
(31)

The coupled EOM of the VBI system under the traveling seismic ground motions can be obtained by combining Eqs. (24) and (29) through Eq. (31), which can be expressed as

$$\left[ {\begin{array}{*{20}c} {{\mathbf{M^{\prime}}}_{vb} } & {{\mathbf{M}}_{vbs} } \\ {{\mathbf{M}}_{svb} } & {{\mathbf{M}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{\ddot{X}}}_{vb} } \\ {{\mathbf{\ddot{u}}}_{s} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{C^{\prime}}}_{vb} } & {{\mathbf{C}}_{vbs} } \\ {{\mathbf{C}}_{svb} } & {{\mathbf{C}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{X}}}_{vb} } \\ {{\dot{\mathbf{u}}}_{s} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{K^{\prime}}}_{vb} } & {{\mathbf{K}}_{vbs} } \\ {{\mathbf{K}}_{svb} } & {{\mathbf{K}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{X}}_{vb} } \\ {{\mathbf{u}}_{s} } \\ \end{array} } \right\} = - {\mathbf{TR}}\left\{ {\begin{array}{*{20}c} {{\mathbf{F}}_{r} } \\ {\mathbf{0}} \\ \end{array} } \right\} - {\mathbf{T}}\left\{ {\begin{array}{*{20}c} {{\mathbf{F}}_{sw} } \\ {\mathbf{0}} \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\mathbf{P}}_{s} } \\ \end{array} } \right\}$$
(32)

where the superscripts ‘v’, ‘b’, and ‘s’ refer to the vehicle body, non-supporting bridge part, and supporting bridge part, respectively; the vector \({\mathbf{X}}\) is the displacement vector; \({\mathbf{F}}_{sw}\) and \({\mathbf{F}}_{r}\) are vectors related to the train self-weight load and track irregularities, respectively. The components in the above equation are given in the appendix.

3 Random Dynamic Vibration Analysis of the VBI System Using PEM

The PEM, which was proposed by Lin (1992), was applied in this study to investigate the random responses of the VBI system under the traveling seismic ground motions and track irregularities.

3.1 Random Responses of the VBI System

The EOM of the VBI system can be solved separately for the seismic excitation and track irregularities based on the superposition principle of linear systems. The EOM for the VBI system under traveling seismic ground motions can be extracted from Eq. (32) as

$$\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{vb} } & {{\mathbf{M}}_{vbs} } \\ {{\mathbf{M}}_{sbv} } & {{\mathbf{M}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{\ddot{X}}}_{vb}^{s} } \\ {{\mathbf{\ddot{u}}}_{s} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{vb} } & {{\mathbf{C}}_{vbs} } \\ {{\mathbf{C}}_{sbv} } & {{\mathbf{C}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{X}}}_{vb}^{s} } \\ {{\dot{\mathbf{u}}}_{s} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{vb} } & {{\mathbf{K}}_{vbs} } \\ {{\mathbf{K}}_{sbv} } & {{\mathbf{K}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{X}}_{vb}^{s} } \\ {{\mathbf{u}}_{s} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\mathbf{P}}_{s} } \\ \end{array} } \right\}$$
(33)

where the superscript ‘s’ denotes the responses caused by the seismic excitations. The absolute displacement of the system can be divided into two parts: the quasi-static displacement and the relative dynamic displacement, under the multi-support seismic ground motions through the quasi-static decomposition method (Chen et al., 1997)

$${\mathbf{X}}_{vb}^{s} = {\mathbf{X}}_{vb}^{sq} + {\mathbf{X}}_{vb}^{sd}$$
(34)

in which the superscripts ‘sq’ and ‘sd’ denote the quasi-static motions and dynamic motions that are induced by the static and dynamic effects of the support movements, respectively; the static equilibrium relationship is

$$\left[ {\begin{array}{*{20}c} {{\mathbf{K^{\prime}}}_{vb} } & {{\mathbf{K}}_{vbs} } \\ {{\mathbf{K}}_{sbv} } & {{\mathbf{K}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{X}}_{vb}^{sq} } \\ {{\mathbf{u}}_{s} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\mathbf{P}}_{s}^{sq} } \\ \end{array} } \right\}$$
(35)

Expanding the first row of Eq. (35) gives

$${\mathbf{X}}_{vb}^{sq} = - \left( {{\mathbf{K^{\prime}}}_{vb} } \right)^{ - 1} {\mathbf{K}}_{vbs} {\mathbf{u}}_{s} = {\mathbf{R}}_{sq} {\mathbf{u}}_{s}$$
(36)

where \({\mathbf{R}}_{sq}\) is the quasi-static influence matrix. Taking the derivative of Eq. (36) with respect to the time t gives quasi-static velocity

$${\dot{\mathbf{X}}}_{vb}^{sq} = {\mathbf{R}}_{sq} {\dot{\mathbf{u}}}_{s}$$
(37)

Similarly, the quasi-static acceleration of the system can be calculated as

$${\mathbf{\ddot{X}}}_{vb}^{sq} = {\mathbf{R}}_{sq} {\mathbf{\ddot{u}}}_{s}$$
(38)

By substituting Eqs. (36), (37), and (38) into the first row of Eq. (33), the dynamic vibrations satisfy the following equation

$${\mathbf{M^{\prime}}}_{vb} {\mathbf{\ddot{X}}}_{vb}^{sd} + {\mathbf{C^{\prime}}}_{vb} {\dot{\mathbf{X}}}_{vb}^{sd} + {\mathbf{K^{\prime}}}_{vb} {\mathbf{X}}_{vb}^{sd} = - \left[ {{\mathbf{M^{\prime}}}_{vb} {\mathbf{R}}_{sq} + {\mathbf{M}}_{vbs} } \right]{\mathbf{\ddot{u}}}_{s} - \left[ {{\mathbf{C^{\prime}}}_{vb} {\mathbf{R}}_{sq} + {\mathbf{C}}_{vbs} } \right]{\dot{\mathbf{u}}}_{s}$$
(39)

The effect of the damping part is minimal and can be omitted in the above equation (Clough & Penzien, 2010). By omitting the velocity part, Eq. (39) can be simplified as

$${\mathbf{M^{\prime}}}_{vb} {\mathbf{\ddot{X}}}_{vb}^{sd} + {\mathbf{C^{\prime}}}_{vb} {\dot{\mathbf{X}}}_{vb}^{sd} + {\mathbf{K^{\prime}}}_{vb} {\mathbf{X}}_{vb}^{sd} { = } - \left[ {{\mathbf{M^{\prime}}}_{vb} {\mathbf{R}}_{sq} + {\mathbf{M}}_{vbs} } \right]{\mathbf{\ddot{u}}}_{s}$$
(40)

Based on the PEM, pseudo-deterministic harmonic excitations can be contructed, replacing the right-hand-side loads in Eqs. (36), (37), and (38) with these pseudo-excitations; then pseudo-quasi-static responses can be calculated by solving the following equations

$${\tilde{\mathbf{X}}}_{vb}^{sq} = {\mathbf{R}}_{sq} {\tilde{\mathbf{u}}}_{s} ;\quad {\mathbf{\dot{\tilde{X}}}}_{vb}^{sq} = {\mathbf{R}}_{sq} {\mathbf{\dot{\tilde{u}}}}_{s} ;\quad {\mathbf{\ddot{\tilde{X}}}}_{vb}^{sq} = {\mathbf{R}}_{sq} {\mathbf{\ddot{\tilde{u}}}}_{s}$$
(41)

where \({\tilde{\mathbf{u}}}_{s}\), \({\mathbf{\dot{\tilde{u}}}}_{s}\) and \({\mathbf{\ddot{\tilde{u}}}}_{s}\) are pseudo-excitation vectors due to the seismic ground displacement, velocity, and acceleration.

The pseudo-excitation of the seismic ground acceleration \({\mathbf{\ddot{\tilde{u}}}}_{s}\) can be constructed as the following equations according to the PEM

$${\mathbf{\ddot{\tilde{u}}}}_{s} = {\mathbf{G}}\left( t \right){\mathbf{\ddot{\tilde{u}}}}_{e} \left( t \right) = {\mathbf{G}}\left( t \right)\sqrt {{\mathbf{S}}_{{{\mathbf{\ddot{u}}}_{e} {\mathbf{\ddot{u}}}_{e} }} \left( \omega \right)} e^{{{\text{i}}\omega \,t}} = {\mathbf{G}}\left( t \right)\sqrt {{\mathbf{P}}^{*} \left( \omega \right){\mathbf{P}}^{{\text{T}}} \left( \omega \right)} e^{{{\text{i}}\omega \,t}} = {\mathbf{G}}\left( t \right){\mathbf{P}}\left( \omega \right)e^{{{\text{i}}\omega t}}$$
(42)

thus, the pseudo-excitation of the seismic ground velocity \({\mathbf{\dot{\tilde{u}}}}_{s}\) and the pseudo-excitation of the seismic ground displacement \({\tilde{\mathbf{u}}}_{s}\) can be written as

$${\mathbf{\dot{\tilde{u}}}}_{s} = \frac{{{\mathbf{\ddot{\tilde{u}}}}_{s} }}{i\omega }{ = }\frac{{{\mathbf{G}}\left( t \right){\mathbf{P}}\left( \omega \right)e^{{{\text{i}}\omega t}} }}{i\omega }$$
(43)
$${\tilde{\mathbf{u}}}_{s} = - \frac{{{\mathbf{\ddot{\tilde{u}}}}_{s} }}{{\omega^{2} }} = - \frac{{{\mathbf{G}}\left( t \right){\mathbf{P}}\left( \omega \right)e^{{{\text{i}}\omega t}} }}{{\omega^{2} }}$$
(44)

Similarly, the pseudo-dynamic responses can be computed using a numerical integration scheme by solving the following equation, which is transformed from Eq. (40)

$${\mathbf{M^{\prime}}}_{vb} {\mathbf{\ddot{\tilde{X}}}}_{vb}^{sd} + {\mathbf{C^{\prime}}}_{vb} {\mathbf{\dot{\tilde{X}}}}_{vb}^{sd} + {\mathbf{K^{\prime}}}_{vb} {\tilde{\mathbf{X}}}_{vb}^{sd} = - \left[ {{\mathbf{M^{\prime}}}_{vb} {\mathbf{R}}_{sq} + {\mathbf{M}}_{vbs} } \right]{\mathbf{\ddot{\tilde{u}}}}_{s} = - \left[ {{\mathbf{M^{\prime}}}_{vb} {\mathbf{R}}_{sq} + {\mathbf{M}}_{vbs} } \right]{\mathbf{G}}\left( t \right){\mathbf{P}}\left( \omega \right)e^{{{\text{i}}\omega t}}$$
(45)

Then, the vector of the pseudo-absolute displacement can be expressed as

$${\tilde{\mathbf{X}}}_{vb}^{s} \left( {\omega ,t} \right) = {\tilde{\mathbf{X}}}_{vb}^{sd} \left( {\omega ,t} \right) + {\tilde{\mathbf{X}}}_{vb}^{sq} \left( {\omega ,t} \right)$$
(46)

Based on the PEM, the PSD vector of the response \({\mathbf{X}}_{vb}^{s}\) is

$${\mathbf{S}}_{{{\mathbf{X}}_{vb}^{s} {\mathbf{X}}_{vb}^{s} }} \left( {\omega ,t} \right) = {\tilde{\mathbf{X}}}_{vb}^{s*} \left( {\omega ,t} \right){\tilde{\mathbf{X}}}_{vb}^{s} \left( {\omega ,t} \right)$$
(47)

First, only consider the track irregularities in Eq. (32) and calculate the system's random responses under these excitations. That means there will be no seismic ground motions. Thus, according to the first row of Eq. (32), the equation of the random vibrations of the VBI system under the track irregularities can be written as

$${\mathbf{M^{\prime}}}_{vb} {\mathbf{\ddot{X}}}_{vb}^{r} + {\mathbf{C^{\prime}}}_{vb} {\dot{\mathbf{X}}}_{vb}^{r} + {\mathbf{K^{\prime}}}_{vb} {\mathbf{X}}_{vb}^{r} { = } - {\mathbf{TRF}}_{r} = - {\mathbf{TR}}\left[ {\begin{array}{*{20}c} {{\mathbf{\ddot{r}}}\left( t \right)} & {{\dot{\mathbf{r}}}\left( t \right)} & {{\mathbf{r}}\left( t \right)} \\ \end{array} } \right]^{{\text{T}}}$$
(48)

where the superscript ‘r’ represents the vibrations under track irregularities, and

$${\mathbf{r}}\left( t \right) = \left[ {\begin{array}{*{20}c} {{\mathbf{r}}\left( {t - \tau_{w1} } \right)} & {{\mathbf{r}}\left( {t - \tau_{w2} } \right)} & \cdots & {{\mathbf{r}}\left( {t - \tau_{{wN_{w} }} } \right)} \\ \end{array} } \right]^{{\text{T}}}$$
(49)

in which \(N_{w}\) is the wheel-sets number, and \(\tau_{wl} \;\left( {l = 1,\;2,\;...,\;N_{w} } \right)\) is the time lag between the lth wheel-set and the first one as they pass the same point on the track. \({\mathbf{r}}\left( t \right)\) is a stationary process with a 0 mean value, generated from the track irregularity spectrum \({\mathbf{S}}_{{\mathbf{r}}} \left( \omega \right)\).

Based on the PEM, Eq. (48) can be rewritten by replacing the right-hand-side term with the pseudo-excitation of the track irregularities

$${\mathbf{M^{\prime}}}_{vb} {\mathbf{\ddot{\tilde{X}}}}_{vb}^{r} + {\mathbf{C^{\prime}}}_{vb} {\mathbf{\dot{\tilde{X}}}}_{vb}^{r} + {\mathbf{K^{\prime}}}_{vb} {\tilde{\mathbf{X}}}_{vb}^{r} { = } - {\mathbf{TR}}\left[ {\begin{array}{*{20}c} {{\mathbf{\ddot{\tilde{r}}}}\left( t \right)} & {{\mathbf{\dot{\tilde{r}}}}\left( t \right)} & {{\tilde{\mathbf{r}}}\left( t \right)} \\ \end{array} } \right]^{{\text{T}}} = - {\mathbf{TR}}\left[ {\begin{array}{*{20}c} { - \omega^{2} } & {{\text{i}}\omega } & 1 \\ \end{array} } \right]^{{\text{T}}} \sqrt {{\mathbf{S}}_{{\mathbf{r}}} \left( \omega \right)} e^{{{\text{i}}\omega t}} {\mathbf{V}}\left( t \right)$$
(50)

in which

$${\mathbf{V}}\left( t \right) = \left[ {\begin{array}{*{20}c} {e^{{{\text{ - i}}\omega \tau_{w1} }} } & {e^{{{\text{ - i}}\omega \tau_{w2} }} } & \cdots & {e^{{{\text{ - i}}\omega \tau_{{wN_{w} }} }} } \\ \end{array} } \right]^{{\text{T}}}$$
(51)

The pseudo-displacement response \({\tilde{\mathbf{X}}}_{vb}^{r}\) under the pseudo-excitation of track irregularities can be computed using the numerical integration scheme. Then, the PSD of \({\mathbf{X}}_{vb}^{r}\) is

$${\mathbf{S}}_{{{\mathbf{X}}_{vb}^{r} {\mathbf{X}}_{vb}^{r} }} \left( {\omega ,t} \right) = {\tilde{\mathbf{X}}}_{vb}^{r*} \left( {\omega ,t} \right){\tilde{\mathbf{X}}}_{vb}^{r} \left( {\omega ,t} \right)$$
(52)

The PSD of responses \({\mathbf{X}}_{vb}^{s}\) and \({\mathbf{X}}_{vb}^{r}\) under the seismic excitations and track irregularities are \({\mathbf{S}}_{{{\mathbf{X}}_{vb}^{s} {\mathbf{X}}_{vb}^{s} }} \left( {\omega ,t} \right)\) and \({\mathbf{S}}_{{{\mathbf{X}}_{vb}^{r} {\mathbf{X}}_{vb}^{r} }} \left( {\omega ,t} \right)\) in Eqs. (47) and (52). As there is no correlation between the seismic excitations and track irregularities, the PSD matrix for the total response of the system under both seismic excitations and track irregularities is

$${\mathbf{S}}_{{{\mathbf{X}}_{vb} {\mathbf{X}}_{vb} }} \left( {\omega ,t} \right) = {\mathbf{S}}_{{{\mathbf{X}}_{vb}^{s} {\mathbf{X}}_{vb}^{s} }} \left( {\omega ,t} \right) + {\mathbf{S}}_{{{\mathbf{X}}_{vb}^{r} {\mathbf{X}}_{vb}^{r} }} \left( {\omega ,t} \right)$$
(53)

The time-dependent SD of the total response is given by (Li & Chen, 2009)

$$\sigma_{{{\mathbf{X}}_{vb} {\mathbf{X}}_{vb} }} \left( t \right) = \sqrt {\int_{ - \infty }^{ + \infty } {{\mathbf{S}}_{{{\mathbf{X}}_{vb} {\mathbf{X}}_{vb} }} \left( {\omega ,t} \right)d\omega } }$$
(54)

3.2 The Offload Factor

The offload factor is used to evaluate the running safety of the vehicle given by the Interim PR Code, HSR code, Interim PFR Code, and Vehicle Code (Xia et al., 2018). The offload factor is defined as

$${\text{Offload}}\;{\text{factor}} = \frac{{\overline{P} - {\mathbf{F}}_{d}^{V} }}{{\overline{P}}}$$
(55)

where \(\overline{P}\) is the average static load of two wheels; the vertical wheel-rail dynamic contact force \({\mathbf{F}}_{d}^{V}\) can be extracted from the wheel-rail dynamic contact force \({\mathbf{F}}_{d}\).

After the pseudo-responses of the rails and vehicles are obtained, which are \({\mathbf{\ddot{\tilde{u}}}}_{w}\), \({\mathbf{\dot{\tilde{u}}}}_{v}\), \({\mathbf{\dot{\tilde{u}}}}_{w}\), \({\tilde{\mathbf{u}}}_{v}\) and \({\tilde{\mathbf{u}}}_{w}\), substituting them into Eq. (31) gives the pseudo dynamic contact force \({\tilde{\mathbf{F}}}_{d} \left( {\omega ,t} \right)\) as

$${\tilde{\mathbf{F}}}_{d} = {\mathbf{M}}_{w} {\mathbf{\ddot{\tilde{u}}}}_{w} + {\mathbf{C}}_{wv} {\mathbf{\dot{\tilde{u}}}}_{v} + {\mathbf{C}}_{w} {\mathbf{\dot{\tilde{u}}}}_{w} + {\mathbf{K}}_{wv} {\tilde{\mathbf{u}}}_{v} + {\mathbf{K}}_{w} {\tilde{\mathbf{u}}}_{w} \;$$
(56)

As the pseudo dynamic contact force is obtained, the corresponding PSD of the random lateral and vertical dynamic contact forces can be computed by

$${\mathbf{S}}_{{{\mathbf{F}}_{d}^{L} {\mathbf{F}}_{d}^{L} }} \left( {\omega ,t} \right) = {\tilde{\mathbf{F}}}_{d}^{L*} \left( {\omega ,t} \right){\tilde{\mathbf{F}}}_{d}^{L} \left( {\omega ,t} \right)$$
(57)
$${\mathbf{S}}_{{{\mathbf{F}}_{d}^{V} {\mathbf{F}}_{d}^{V} }} \left( {\omega ,t} \right) = {\tilde{\mathbf{F}}}_{d}^{V*} \left( {\omega ,t} \right){\tilde{\mathbf{F}}}_{d}^{V} \left( {\omega ,t} \right)$$
(58)

and the SD of the random lateral and vertical dynamic contact forces can be calculated according to Eq. (54) as

$$\sigma _{{{\mathbf{F}}_{d}^{L} }} \left( t \right)\, = \,\sqrt {\int_{{ - \infty }}^{{ + \infty }} {{\mathbf{S}}_{{{\mathbf{F}}_{d}^{L} {\mathbf{F}}_{d}^{L} }} \left( {\omega ,t} \right)d\omega } }$$
(59)
$$\sigma_{{{\mathbf{F}}_{d}^{V} }} \left( t \right)\, = \,\sqrt {\int_{ - \infty }^{ + \infty } {{\mathbf{S}}_{{{\mathbf{F}}_{d}^{V} {\mathbf{F}}_{d}^{V} }} \left( {\omega ,t} \right)d\omega } }$$
(60)

Thus, the SD of the offload factor \(\sigma_{offload} \left( t \right)\) is

$$\sigma_{offload} \left( t \right) = \frac{{\sigma_{{{\mathbf{F}}_{d}^{V} }} \left( t \right)}}{{\overline{P}}}$$
(61)

4 Numerical Examples

A three-dimensional multi-span simply supported bridge is adopted for random seismic dynamic analysis in this section. The bridge supports the central section of the railway track, while the left and right sections are supported on subgrades adjacent to two bridge end supports. The Chinese-made EMU train running on the tracks consists of two trailer-cars (the 2nd and 5th vehicles) and four motor-cars (the 1st, 3rd, 4th, and 6th vehicles). The main parameters of each vehicle can be found in Table 2 or Xia et al. (2018). The track properties are listed in Table 3 or can be found in Zeng et al. (2015). This 10-span bridge has a total length of 240 m. The parameters of the bridge model for each span are listed in Table 3. The bridge is assumed to have a Rayleigh damping matrix. Assumed damping ratios of the first two modes are \(\zeta_{1}\) = \(\zeta_{2}\) = 0.02. The Poisson’s ratio is 0.25. The first 500 vibration modes of the structure are considered.

Table 3 Parameters of the track and bridge
Full size table

The PSD of the lateral seismic ground motions has the Clough–Penzien model form in Eq. (1) with the frequency integral interval \(\omega \in \left[ {0.2\pi ,\;\;100\pi } \right]\) rad s−1. The uniform modulation function of the seismic excitation with the exponential form in Eq. (3) is applied. The parameters for different seismic intensities (GB50111-2006, 2009) are listed in Table 1.

The FRA spectrum was taken as track irregularities PSD in the study, calculated using Eqs. (20), (21), and (22). Grade 6 of the FRA spectrum is adopted, with parameters \(A_{v} = A_{a} = 0.0339\) cm2 rad m−1, \(\Omega _{c} = 0.8245\) rad m−1, \(\Omega _{s} = 0.4380\) rad m−1, and k = 0.25. The spatial wavelength of the PSD lies in the range from 1.11 m to 120 m.

4.1 Verification by the MCM

To assess the accuracy of the PEM, a nonstationary random vibration analysis was performed by comparing the vibrations using PEM with those using the MCM (Li et al., 2016). That is, the random responses of the bridge are investigated by the PEM in the frequency domain and by the MCM in the time domain with 50 and 1,000 samples of artificial seismic processes separately. A lateral seismic excitation with intensity VI is considered in this example. The samples of artificial seismic processes are generated using the Clough–Penzien model spectrum by the trigonometric series method (Preumont, 1980), which is

$$\ddot{u}_{ej} \left( t \right) = \sum\limits_{j = 1}^{{N_{\omega } }} {\sqrt {2S_{{\ddot{u}_{e} \ddot{u}_{e} }} \left( {\omega_{j} } \right)\Delta \omega } \cos \left( {\omega_{j} t + \phi_{j} } \right)}$$
(62)

where \(\ddot{u}_{ej} \left( t \right)\) is the sequence of the artificial seismic process at the jth bridge support; \(\Delta \omega = {{\left( {\omega_{\,u} - \omega_{\,l} } \right)} \mathord{\left/ {\vphantom {{\left( {\omega_{\,u} - \omega_{\,l} } \right)} {N_{\omega } }}} \right. \kern-\nulldelimiterspace} {N_{\omega } }}\), where \(\omega_{\,u}\) is the upper limit of the seismic frequency and \(\omega_{\,l}\) is the lower limit of the seismic frequency, and \(\phi_{j}\) is the random phase angle of the jth frequency component.

The SD curves of the acceleration and displacement at the midpoint of the 6th bridge span in the lateral direction are shown in Fig. 3. It can be seen that as the sample size grows, the MCM result approaches the PEM result. When only 50 samples are applied, the maximum differences between the MCM and the PEM are 28.04% and 36.95% for the acceleration and displacement, respectively, while with 1,000 samples, the differences are reduced to 6.64% and 7.50%, respectively. The excellent accuracy of the proposed PEM for the nonstationary random vibration analysis is demonstrated.

Fig. 3
figure 3

Comparison of the SD curves of the bridge midpoint obtained by the PEM and MCM: a lateral acceleration; b lateral displacement

Full size image

4.2 Influence of the Train Speed

The effect of the train speed on the random responses of the system is now taken into account by varying the train speed from 110 to 420 km h−1 with a 10 km h−1 increment. A seismic excitation with intensity VI is considered in this study. The maximum SD of the random acceleration responses of all bridge span midpoints and all vehicle car bodies, random lateral wheel-rail contact forces, and offload factors of all wheel-sets for different train speeds are shown in Fig. 4.

Fig. 4
figure 4

Maximum SD for different train speeds: a bridge span midpoint lateral acceleration; b bridge span midpoint vertical acceleration; c vehicle lateral acceleration; d vehicle vertical acceleration; e lateral wheel-rail contact force; f offload factor

Full size image

Referring to Fig. 4a, b, it can be seen that the maximum SD of the random accelerations of bridge midpoints varies significantly with the train speeds. The random responses of bridge midpoints grow with increasing train speeds, even though this growth is not monotonic. In this example, the effect of the train speed on the random bridge responses becomes more significant when the train speed is higher than 200 km h−1.

For the random vehicle responses shown in Fig. 4c, d, the maximum SD of vehicle accelerations varies significantly with the train speeds. In the vertical direction, the random vehicle responses do not always increase with the train speeds; indeed, its values decrease slightly with the train speeds between 340 and 380 km h−1 for the motor-cars, and between 310 and 340 km h−1 for the trailer-cars. This is because of the changes in track irregularities and time-lags. The random lateral wheel-rail contact forces increase almost monotonically with the train speeds, except for the trailer-cars when train speeds increase from 230 to 250 km h−1, and from 340 to 370 km h−1, which can be seen in Fig. 4e. Similarly to the above, the random offload factor is shown in Fig. 4f, which becomes higher with the increasing train speeds.

The growth rates for the random vehicle responses and random wheel-rail contact forces are higher than those rates for the random responses of bridge midpoints. These results indicate that compared to the random responses of bridge midpoints, the train speed affects the random vehicle responses and random wheel-rail contact forces more significantly because the effect of different track irregularity spectrums and different time-lags due to the changing train speeds directly affect the wheel-sets and rails, but do not directly affect the bridge. The train speed should not be ignored when analyzing the random responses of the VBI system because the maximum speed of trains has continued to increase in the recent past.

4.3 Influence of the Seismic Intensity

The effect of the seismic intensity on the random vibrations of the VBI system is investigated in this section for a train crossing the bridge at a constant speed of 210 km h−1.

The maximum SD of the random acceleration responses of all bridge span midpoints and all vehicle car bodies, random lateral wheel-rail contact forces, and offload factors of all wheel-sets for different seismic intensities (intensities 0, VI, VII, VIII, and IX) are shown in Fig. 5. The intensity of 0 means there is no seismic excitation applied to the system. The maximum SD of the lateral bridge accelerations is higher in the mid-spans and smaller in the side-spans, as shown in Fig. 5a, due to the fundamental modes. Figure 5c, d show that the random responses of the 1st, 3rd, 4th, and 6th vehicles, which are motor-cars, are comparatively higher than those of the 2nd and 5th vehicles, which are trailer-cars. Figure 5e, f show that the random lateral wheel-rail forces and offload factors of wheel-sets belonging to the motor-cars (Wheel-set No. 1-4, 9-16, 21-24) are comparatively higher than those belonging to the trailer-cars (Wheel-set No. 5-8, 17-20).

Fig. 5
figure 5

Maximum SD for different seismic intensities: a bridge span midpoint lateral acceleration; b bridge span midpoint vertical acceleration; c vehicle lateral acceleration; d vehicle vertical acceleration; e lateral wheel-rail contact force; f offload factor

Full size image

From all figures in this section, it is seen that the greater the intensity is, the more significant the random responses and offload factors are. Additionally, the random responses of the coupled system under track irregularities and the seismic excitations simultaneously are greater than those under only track irregularities. That means the random responses of the VBI system are dominated by the seismic excitations when it is subjected to track irregularities and the seismic excitations simultaneously. The intensity of the seismic excitation significantly affects the random vibrations of the VBI system, and it should not be ignored when investigating the random vibrations of the VBI system and assessing the running safety of the vehicle.

4.4 Influence of the Apparent Wave Velocity

The seismic apparent wave velocities \(V_{app}\) are employed in this section to study the influence of the wave passage effect on the system’s random vibration. The \(V_{app}\) is the apparent velocity of seismic waves along the surface (De, 2005). It is affected by many factors, usually taken as a constant in the interval \(\left( {{0,}\,{ + }\infty } \right)\) in practical computations (Zhang et al., 2009). The variations of apparent wave velocity are adopted in this section to study the wave passage effect on stochastic structural responses, and to investigate whether the wave passage effect plays a significant role in stochastic structural responses. The values of \(V_{app}\) are assumed to be 100, 500, 1500, 5000, \(+ \infty\) m s−1 in this study. Here, \(V_{app} { = + }\infty\) denotes the uniform seismic excitation, which means no phase lag between bridge supports. Intensity VI of the seismic excitation is assumed. The train crosses the bridge with a constant speed of 210 km h−1. The random acceleration SD curves of the 10th bridge span midpoint and the 5th vehicle body under the traveling seismic ground motions are shown in Fig. 6. They are chosen because they offer relatively more significant differences. It is observed that the acceleration SD varies with the seismic apparent wave velocities \(V_{app}\). When considering the wave passage effect, the random accelerations of bridges and vehicles may be greater than or less than those under uniform seismic excitations, which means the wave passage effect of the seismic excitation may increase or decrease the random responses of the VBI system. From Fig. 6a, it can be seen that the acceleration SD of midpoints of all bridge spans are different from those under uniform seismic excitations when considering the seismic apparent wave velocities \(V_{app}\) no matter what value it is. The random acceleration SD of the 10th bridge span increases about 70% with considering 1500 m s−1 seismic apparent wave velocity compared to the response under the uniform seismic excitation. Therefore, the wave passage effect should be taken into account, especially in seismic analyses of long, multi-span bridges, or random responses will be underestimated. The effect of the seismic apparent wave velocities on vehicles is smaller than that on bridges, as shown in Fig. 6b. That is because when seismic apparent wave velocities change, a corresponding change will occur in phase lags between different bridge support points, and this change acts directly on the bridge but not on the vehicle. The most significant difference appears in the 5th vehicle. It can be seen that the random acceleration SD of the 5th vehicle increases about 30% with consideration of the 100 m s−1 seismic apparent wave velocity compared to the vibration under uniform seismic excitation.

Fig. 6
figure 6

SD curves for different seismic apparent wave velocities: a the 10th bridge span midpoint lateral acceleration; b the 5th vehicle lateral acceleration; c the 18th wheel-set lateral wheel-rail contact force; d the 18th wheel-set offload factor

Full size image

The time-dependent SD of lateral wheel-rail contact forces and offload factors of the 18th wheel-set are shown in Fig. 6c, d. There are too many results for a total of 24 wheel-sets. For brevity, only the time-dependent SD curves of the 18th wheel-set are shown in this paper. The 18th wheel-set is chosen because it shows more significant differences. From Fig. 6c, d, compared to those under the uniform seismic excitation, the maximum SD increases by about 20% for the lateral wheel-rail contact forces and the offload factors considering \(V_{app} = 500\) m s−1. The wave passage effect also affects the random lateral wheel-rail contact forces and offload factors significantly. That is why it should be included in the dynamic vehicle analysis. If not, the random vehicle accelerations, wheel-rail contact forces, and offload factors will be underestimated when the train is crossing a long, multi-span bridge.

5 Conclusions

In this study, the random dynamic vibrations of a Chinese-made EMU train crossing a 10-span simply supported railway bridge under traveling seismic ground motions are studied using the PEM. The method is validated against traditional MCM and demonstrated to be accurate and efficient, especially for the analysis of nonstationary random excitation problems. The following conclusions can be drawn based on the results of the numerical examples:

  1. (1)

    The random responses of bridge midpoints and vehicles, and the random lateral wheel-rail contact forces grow with increasing train speeds, but these increases are not monotonic. The random offload factors increase monotonically with train speeds. The differences in the random responses with different train speeds are caused by the different PSDs of track irregularities and different time-lags due to the changing train speeds. Compared to the random responses of bridge midpoints, the train speed affects the random vehicle responses, random wheel-rail contact forces, and random offload factors more significantly.

  2. (2)

    The random responses of bridge midpoints are dominated by the seismic excitations when the whole system is subjected to track irregularities and seismic excitations simultaneously. The seismic intensity significantly affects the random vibrations of the VBI system and the random offload factors. Hence it could be an essential parameter in estimating the random vibrations of the VBI system and assessing the running safety of the vehicle under seismic excitations.

  3. (3)

    The apparent wave velocity significantly affects the random bridge responses, particularly for long, multi-span bridges. The apparent wave velocity may increase or decrease the random responses of the VBI system.

  4. (4)

    The effect of seismic apparent wave velocities on the random vehicle responses is less significant compared than the effect on the random bridge responses. That is because when seismic apparent wave velocities change, a corresponding change will occur in phase lags between different bridge support points, and this change acts directly on the bridge but not on the vehicle. However, the wave passage effect still cannot be ignored in the vehicle analysis because it has a slignt impact on the random vehicle accelerations, wheel-rail contact forces, and offload factors.

In short, for a VBI system in this study, the wave passage effect must be considered when analyzing the random dynamic vibrations subjected to the seismic ground motions; otherwise, the results will be underestimated or overestimated.

It should be noted that the conclusions presented above are based on several case studies in the present paper. Therefore, more numerical computations are required to support those conclusions. The random dynamic vibration analysis of the VBI system under track irregularities and traveling seismic ground motions is a very complex problem. The algorithm presented in the paper, as well as the conclusions drawn from numerical examples, can be regarded as reference materials for the dynamic design of a multi-span railway bridge and to evaluate the running safety of the vehicle.