Study on Residual Stress Distributions in Press-Braked Stainless Steel Sections

Abstract

The distribution of residual stresses is one of the substantial issues in determining mechanical behaviors of stainless steel structural members. Proper residual stress distribution models are necessary to include the residual stress influence in the analysis and design. Currently, the existing residual stress distribution model for press-braked stainless steel sections is either relatively complicated for the application, or only focuses on the longitudinal residual stress. In this study, a simplified residual stress distribution model was proposed based on the analysis of the key mechanisms in the press-braking process that was assumed as two-stage (bending and rebounding) plane strain pure bending process. The stress–strain relationship was represented as a simplified three–stage material model, and all the minor effects like the coiling and uncoiling, the material anisotropy, and the shift of neutral axis, etc. were neglected. Compared with test data, the predicted results by the proposed simplified model indicate good agreement for specimens within the commonly used ratio of internal corner radius over the thickness (r_i/t). Finite element models for the press-braking process were then developed in ABAQUS and validated using the available data from literature. A series of models with varied ratios of r_i/t were analyzed. Simulation results indicate that the center of the corner region in the press-braked sections has the largest equivalent plastic strain and residual stresses. From the center to the edge, the equivalent plastic strain and residual stresses declined significantly. As the ratios of r_i/t become smaller and smaller, the neutral axis moves towards to the compression side and the proposed simplified model gradually loses its prediction accuracy. Based on the theoretical and finite element analysis, the proposed simplified model is applicable for press-braked stainless steel sections with r_i/t ratios higher than 2.0.

1 Introduction

Stainless steel structures have a wide-range of civil applications, particularly for those under extremely corrosive environment. Currently, cold-formed stainless steel structure is the dominated type in applications due to its load bearing efficiency and attractive architectural appearance. Traditional cold-forming processes include the press-braking and cold-rolling. Compared with cold-rolling, press-braking has the potential in producing large cross-sections and thin to medium thick walled sections.

For press-braked sections, cold-forming effects (including the residual stresses and material enhancement), have a considerable influence on the mechanical behaviors of members and joints, which have received considerable investigation efforts. Ingvarsson (1975), Dat (1980), and Weng and Pekoz (1990) quantified longitudinal residual stresses in steel channel sections using the sectioning method, and demonstrated that the longitudinal residual stresses in corner regions were higher than those in flat regions. Weng and White (1990) measured residual stresses along the circumferential direction and presented the residual stresses through plate thickness as a zigzag distribution for press-braked thick walled steel corner sections. Weng and Pekoz (1990) proposed a longitudinal bending residual stress distribution model, in which the whole inside and outside surfaces of a channel section had 0.5f_y compression stress and 0.5f_y tension stress, respectively (f_y is the nominal yield stress). Schafer and Pekoz (1998) collected and analyzed residual stress data in press-braked steel channel sections, and provided different residual stress magnitude values for corner regions and flat regions. For stainless steel cross-sections, systematic experimental studies have been done for welded (Yuan et al. 2014) and cold-rolled (Huang and Young 2012; Jandera et al. 2008; Cruise and Gardner 2008) sections, while rare experimental studies have been reported on press-braked sections. Cruise and Gardner (2008) and Gardner and Cruise (2009) proposed a longitudinal residual stress distribution model for press-braked stainless steel angle sections based on experimental results measured using the sectioning method, in which the residual stress was assumed by a linear or rectangular stress block distribution along the thickness direction due to measurement difficulty for the longitudinal residual stress through thickness direction.

Residual stress measurement is time and labor consuming, and only the residual stresses on the plate surfaces could be obtained. Thus, many researchers made efforts in predicting residual stresses from theoretical aspect. Ingvarsson (1975) developed a program to calculate longitudinal and circumferential residual stresses in press-braked sections using incremental theory of plasticity. The whole manufacturing process was separated into a plastic loading step and an elastic unloading step. Rondal (1987) proposed a program which was similar to that by Ingvarsson (1975), but without considering the effect of the internal pressure on the distribution of residual stresses. Dat (1980) developed the method reported in Ingvarsson (1975), evaluated the purely elastic unloading assumption and proposed a close-formed solution for steel channels base on a full plastic loading assumption. Moen et al. (2008) proposed a mechanics-based prediction method for the determination of initial residual stresses and effective plastic strain in cold-rolled steel members, in which, some of factors that had minor effects on the final residual stresses were neglected, and derived a simple close-formed solution. Quach et al. (2004, 2006, 2009a, b), carried out systematically theoretical studies on residual stresses in press-braked steel and stainless steel sections, and proposed a series of formulas for accurate prediction of residual stresses, where relevant aspects on the residual stress distribution (e.g. the whole manufacturing process, the material anisotropy, the shift of the neutral axis, the full range stress–strain curve…) were all considered in derivations.

For press-braked steel sections, explicit expressions for the residual stress distribution through the thickness direction are available in Dat (1980) and Moen et al. (2008). Thus, researchers and engineers can directly incorporate residual stresses into numerical modeling. For press-braked stainless steel sections, the explicit expression for residual stresses through the thickness direction is unavailable due to the complex stress–strain curves of stainless steel. Although Quach’s method (Quach et al. 2009a, b) can provide accurate predictions for stainless steel sections, numerical integrations and finite element modeling in spring-back process were necessary in the obtaining final results, which would be time-consuming and inconvenient for applications.

The objective of this paper is to develop a simplified, approximate, close-formed expression to characterize the residual stress distribution in press-braked stainless steel sections. The proposed solution would have the advantages of simplicity and satisfactory accuracy. To that end, Sect. 2 presented the deduction of a simplified residual stress distribution model for press-braked stainless steel sections. In Sect. 3, finite element model of the press-braking process was developed and validated, and then used to discuss the residual stress distribution across the whole section. The feasible range of the proposed simplified distribution model was discussed through comparisons with test and numerical results.

2 Analytical Solution of the Residual Stress Distribution in Press-Braked Sections

In this section, a brief introduction of the press-braking process were given firstly, and the theoretical model to deduce residual stress distributions were then developed based on the mechanism and some assumptions on the press-braking process.

2.1 Press-Braking Process

Press-braking process is a commonly used cold-forming process in producing small quantities of open sections such as channel sections and angle sections. It is applicable for the production of medium to large scale pipe and box sections combined with welding process.

For stainless steel plates with the thickness less than 5 mm, plates are usually supplied in the form of the steel coil which must be reformed to sheets before the press-braking process. The whole reforming process includes uncoiling and flattening usually by a flattening machine. For stainless steel plates with the thickness larger than 5 mm, plates are often supplied in sheets that can be used directly in press-braking process.

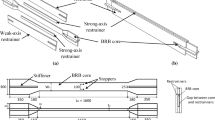
The basic mechanism of press-braking process is shown in Fig. 1. At the beginning of the press-braking process, the stainless steel sheet is installed between the upper and lower dies. The upper die controlled by a hydraulic actuator slowly moves towards to the lower die, leading to an inward bending of the stainless steel sheet. The radius of curvature of the inner surface of the stainless steel sheet is equal to that of the upper die in the end. After the stainless steel sheet reaches the surface of the lower die (a small clearance is necessary), the upper die quickly reverses its movement direction, to be away from the lower die. At this stage, the stainless steel sheet rebounds from the surface of the lower die. This process may repeat until the pre-specified dimension of the production is obtained.

Fig. 1

Basic steps of press-braking process (‘SS sheet’ denotes stainless steel sheet)

2.2 Derivation of the Simplified Residual Stress Distribution Model

2.2.1 Assumptions

As the actual press-braking manufacturing process is a complex elastic–plastic loading and unloading process, assumptions are necessary in deriving the residual stress distribution with simple expressions. It is also necessary to keep a clear physical meaning and a proper accuracy when simplifying the process. In this study, the following assumptions were adopted:

• (1) The effects of coiling, uncoiling and flattening on the residual stress distributions are neglected. For stainless steel plates with the thickness equal or larger than 5 mm, the virgin material is stored in the form of sheets instead of coils. What is more, for stainless steel plates with the thickness less than 5 mm, the plastic strain during the coiling, uncoiling and flattening is negligible compared to that during the press-braking process.

• (2) The whole press-braking process is simplified as two stages, i.e. the bending stage and the rebounding stage. Although, the bending–rebounding process may repeat for several times, the first trail of the bending–rebounding process generates the primary deformation and stress–strain field.

• (3) Plane pure bending is assumed during the bending and rebounding stages. Since the length of the products is much longer than the maximum dimensions of cross-section, and the loading and supporting conditions are applied evenly along the longitudinal direction, strain along the longitudinal direction could be considered as zero.

• (4) The shift of neutral axis and the change in the thickness of sheet are neglected. According to Hill theory (Hill 1998) on the plane pure bending status of elastic–perfect plastic material, the neutral axis would move towards to the inner surface of corner, and the radius of neutral surface is (r_i^2+r_i*t)^0.5, where r_i is the internal corner radius, and t is the thickness. For typical press-braked sections, the radius r_i of corners varies from 2t to 6t (SFIA 2012; AISI 1996), and the corresponding shift of the neutral axis is less than 6.5% of the thickness. In terms of the thickness changes, the reduction of thickness for the case when r_i/t is equal to 1.0 is less than 5% (Zhang and Yu 1988).

• (5) The rebounding is an elastic unloading process. Dat (1980) discussed the unloading process in detail, and confirmed this assumption.

• (6) The radial residual stresses along the thickness direction are small and neglected in the derivation process (Ingvarsson 1975; Dat 1980; Alexander 1959).

• (7) The material anisotropy is neglected and a simplified material model is adopted to reduce the deduction difficulty. Based on material test results reported in Becque and Rasmussen (2009) and Yuan et al. (2014), the material anisotropy of stainless steel is relatively low, and has a negligible influence on member behaviors (Lecce 2005). As press-braking is a complex elastic–plastic loading–unloading process, the expression of the material stress–strain curve dominates the deduction difficulty of the residual stress distribution model. Several popular two-stage material models (Rasmussen 2003; Gardner and Nethercot 2004; Arrayago et al. 2015) and three-stage material models (Quach et al. 2008), have been developed based on the assumption that the stress–strain curve in the range of (σ_0.2 to σ_u) is of the similar shape as the initial curve in the range below σ_0.2 (Mirambell and Real 2000), and thus have relatively complex expressions as the stress beyond the proof stress. To reduce the deduction difficulty, a simplified three-stage material model (Zheng et al. 2019) was used with the expressions shown in Eqs. (1) and (2), which was developed based on the concept of a piecewise equation and the method proposed by Macdonald et al. (2000) (i.e. by keeping the strain hardening exponent n in Ramberg–Osgood model varied to fit the full-range stress–strain curve). It should be mentioned that discontinuities in slope are existed at the intersection points of the three stages in the simplified material model, which need more attentions in numerical modeling but have a minor influence on the residual stress distribution.

$$\varepsilon = \left\{ {\begin{array}{*{20}l} {\frac{\sigma }{{E_{0} }} + 0.002\left( {\frac{\sigma }{{\sigma_{0.2} }}} \right)^{n} } \hfill & {0 \le \sigma \le \sigma_{0.2} } \hfill \\ {\frac{\sigma }{{E_{0} }} + 0.002\left( {\frac{\sigma }{{\sigma_{0.2} }}} \right)^{{n_{2} }} } \hfill & {\sigma_{0.2} < \sigma \le \sigma_{1.0} } \hfill \\ {\left( {\frac{\sigma }{p}} \right)^{q} } \hfill & {\sigma_{1.0} < \sigma \le \sigma_{u} } \hfill \\ \end{array} } \right.$$

(1)

$$\left\{ {\begin{array}{*{20}l} {n = \frac{{\ln \left( {20} \right)}}{{\ln \left( {{{\sigma_{0.2} } \mathord{\left/ {\vphantom {{\sigma_{0.2} } {\sigma_{0.01} }}} \right. \kern-0pt} {\sigma_{0.01} }}} \right)}},} \hfill & {n_{1} = \frac{\ln \left( 5 \right)}{{\ln \left( {{{\sigma_{1.0} } \mathord{\left/ {\vphantom {{\sigma_{1.0} } {\sigma_{0.2} }}} \right. \kern-0pt} {\sigma_{0.2} }}} \right)}}} \hfill \\ {n_{2} = n + \left( {\frac{{\sigma - \sigma_{0.2} }}{{\sigma_{1.0} - \sigma_{0.2} }}} \right)\left( {n_{1} - n} \right)} \hfill & {} \hfill \\ {q = \frac{{\ln \left( {{{\varepsilon_{u} } \mathord{\left/ {\vphantom {{\varepsilon_{u} } {\varepsilon_{1.0} }}} \right. \kern-0pt} {\varepsilon_{1.0} }}} \right)}}{{\ln \left( {{{\sigma_{u} } \mathord{\left/ {\vphantom {{\sigma_{u} } {\sigma_{1.0} }}} \right. \kern-0pt} {\sigma_{1.0} }}} \right)}},} \hfill & {p = \frac{{\sigma_{1.0} }}{{\sqrt[q]{{\varepsilon_{1.0} }}}}} \hfill \\ \end{array} } \right.$$

(2)

where ε is the engineering strain; σ is the engineering stress; E₀ is the Young’s modulus; σ_0.2 is the 0.2% proof stress; n and n₂ are strain hardening exponents for the first and the second stages, respectively; σ_1.0 is the 1.0% proof stress; σ_u is the ultimate tensile stress; ε_u is the ultimate strain (i.e. the total strain corresponding to the ultimate tensile stress); n₁, p and q are material parameters.

2.2.2 Coordinate System

Test results have indicated that residual stresses in the corner region are higher than those in the flat region (Dat 1980; Cruise and Gardner 2008). Therefore, this section mainly focuses on the residual stresses in the corner region of press-braked sections.

The coordinate system and the geometric notations used in the following derivation are defined in Fig. 2. The x, y, and z axes are referred as the transverse, longitudinal, and thickness directions, respectively.

Fig. 2

Coordinate system definition

2.2.3 Equivalent Plastic Strain

Suppose the curvature at the mid-thickness of the corner specimen after press-braking is r. According to assumptions (3) and (4), the plastic strain in the transverse direction $\varepsilon_{x}^{p}$ at the point with the coordinate z in the thickness direction, is approximate equal to z/r. Based on the plane strain condition, the plastic strain in the longitudinal direction $\varepsilon_{y}^{p}$ is zero. Since the material is incompressible during the plastic deformation process, the plastic strain $\varepsilon_{z}^{p}$ in the thickness direction is –z/r. Then the equivalent plastic strain can be calculated using Eq. (3).

$$\varepsilon_{p} = \sqrt {\frac{2}{3}\left( {\left( {\varepsilon_{x}^{p} } \right)^{2} + \left( {\varepsilon_{y}^{p} } \right)^{2} + \left( {\varepsilon_{z}^{p} } \right)^{2} } \right)} = \frac{2}{\sqrt 3 }\varepsilon_{x}^{p} = \frac{2}{\sqrt 3 }\frac{z}{r}$$

(3)

where $\varepsilon_{x}^{p}$, $\varepsilon_{y}^{p}$, and $\varepsilon_{z}^{p}$ are the plastic strains in the transverse, longitudinal and thickness directions respectively; and $\varepsilon_{p}$ is the equivalent plastic strain. It can be seen that the equivalent plastic strain is linear with the coordinate z, which is shown in Fig. 3.

Fig. 3

Equivalent plastic strain in press-braked corners

2.2.4 Bending Process

The bending process of press-braking is a plastic loading process. Following the Von Mises yield rule, the yield function in term of the stress components can be expressed in Eq. (4), where the equivalent stress σ_e can be calculated using Eq. (5).

$$f\left( {\sigma_{ij} } \right) = J_{2} - k^{2} \left( {\varepsilon_{p} } \right) = \left( {\sigma_{x}^{2} + \sigma_{y}^{2} - \sigma_{x} \sigma_{y} } \right) - \sigma_{e}^{2} = 0$$

(4)

$$\sigma_{e} = f\left( {\varepsilon_{p} } \right) = p\left( {\varepsilon_{p} } \right)^{{\frac{1}{q}}} = p\left( {\frac{2}{\sqrt 3 }\frac{z}{r}} \right)^{{\frac{1}{q}}}$$

(5)

For typical press-braked sections, the equivalent plastic strain at most of points away from the mid-thickness surface is much higher than the strain corresponding to the proof stress σ_1.0. Thus, the equivalent stress–strain relationship follows the third stage in Eq. (1). For example, for the case when the ratio of the radius of curvature at mid-thickness over the thickness is equal to 6, the equivalent plastic strain at the outer surface is about 0.096 according to Eq. (3), which is over 7 times higher than ε_1.0 (approximately 0.013).

According to the assumptions (3), (6) and (7), the generalized stress–strain incremental relationship could be expressed in Eq. (6) base on the isotropic hardening law and the Prandtl–Reuss flow rule.

$$\left\{ {\begin{array}{*{20}l} {d\varepsilon_{x} = \frac{1}{{E_{0} }}\left( {d\sigma_{x} - vd\sigma_{y} } \right) + \frac{{3s_{x} }}{{4H_{p} }} \cdot \frac{{dJ_{2} }}{{J_{2} }}} \hfill \\ {d\varepsilon_{y} = \frac{1}{{E_{0} }}\left( {d\sigma_{y} - vd\sigma_{x} } \right) + \frac{{3s_{y} }}{{4H_{p} }} \cdot \frac{{dJ_{2} }}{{J_{2} }}} \hfill \\ {d\varepsilon_{z} = \frac{1}{{E_{0} }}\left( { - vd\sigma_{x} - vd\sigma_{y} } \right) + \frac{{3s_{z} }}{{4H_{p} }} \cdot \frac{{dJ_{2} }}{{J_{2} }}} \hfill \\ {s_{x} = \frac{{2\sigma_{x} - \sigma_{y} }}{3},\,s_{y} = \frac{{2\sigma_{y} - \sigma_{x} }}{3},\,s_{z} = \frac{{ - \sigma_{x} - \sigma_{y} }}{3}} \hfill \\ \end{array} } \right.$$

(6)

where E₀ is the initial elastic Young’s modulus; v is the Poisson ratio; dε_x, dε_y, and dε_z are the strain increments in the transverse, longitudinal, and thickness directions, respectively; dσ_x and dσ_y are the stress increments in the transverse, longitudinal directions, respectively; s_x, s_y, and s_z are the stress deviators in the transverse, longitudinal, and thickness directions, respectively; H_p is the tangent elastic modulus; and J₂ is the invariants of the stress deviator.

According to the plane strain assumption, the strain increment in the longitudinal direction dε_y is zero. In the expression of dε_y in Eq. (6), the first and the second parts correspond to the elastic and plastic strain increments, respectively. The ratio of two stress increments dσ_y/dσ_x can be approximately determined according to the expression of dε_y. In the elastic stage or the initial stage of plastic loading, the ratio dσ_y/dσ_x is dominated by the elastic part. The ratio dσ_y/dσ_x is approximate equal to the Poisson ratio v (0.3). During the development of plasticity, the ratio dσ_y/dσ_x is gradually controlled by the plastic component [i.e. the second part of the expression dε_y in Eq. (6)]. Thus, the ratio dσ_y/dσ_x gradually approaches to 0.5 (i.e. s_y = 0).

Since corners in the press-braked sections experience very large plastic deformation, the ratio dσ_y/dσ_x is assumed as 0.5 in this bending process. Then, the expressions of σ_y and σ_x can be deduced based on Eqs. (4) and (5) and the ratio of σ_y/σ_x, shown in Eqs. (7) and (8). In these equations, the subscript ‘b’ denotes the result at the end of the bending stage.

$$\sigma_{x,b} = \frac{\sqrt 3 }{2}\sigma_{e} = \frac{\sqrt 3 }{2}p\left( {\frac{2}{\sqrt 3 }\frac{z}{r}} \right)^{{\frac{1}{q}}}$$

(7)

$$\sigma_{y,b} = 0.5 \cdot \sigma_{x,b} = \frac{\sqrt 3 }{4}p\left( {\frac{2}{\sqrt 3 }\frac{z}{r}} \right)^{{\frac{1}{q}}}$$

(8)

2.2.5 Rebounding Process

According to the assumption (5), the rebounding is an elastic unloading process, when the bending moment accumulated in the bending stage is released. The bending moment My accumulated in the bending process can be derived by the integration of the transverse stress multiplied by the distance away from the neutral axis with the expression shown in Eq. (9).

$$M_{y} = \int\limits_{ - t/2}^{t/2} {\sigma_{x,b} zdz} = 2\int\limits_{0}^{t/2} {\frac{\sqrt 3 }{2}p\left( {\frac{2}{\sqrt 3 }\frac{z}{r}} \right)^{{\frac{1}{q}}} zdz } =\; \frac{{t^{2} }}{2}\frac{q}{2q + 1}\frac{\sqrt 3 }{2}p\left( {\frac{2}{\sqrt 3 }\frac{t}{2r}} \right)^{{\frac{1}{q}}} = \frac{{t^{2} }}{2}\frac{q}{2q + 1}\left. {\sigma_{x,b} } \right|_{t/2}$$

(9)

In the elastic rebounding process, the increments of strain and stress are all linearly distributed along the thickness direction. And the ratio of dσ_y,rb/dσ_x,rb is 0.3, where dσ_y,rb and dσ_x,rb are the stress increments in the longitudinal and transverse directions respectively. Thus, the increments of stress in the transverse and longitudinal directions can be determined shown in Eqs. (10) and (11), respectively.

$$\sigma_{x,rb} = - \frac{{M_{y} }}{I}z = - \frac{{t^{2} }}{2}\frac{q}{2q + 1}\left. {\sigma_{x,b} } \right|_{t/2} \cdot \frac{12z}{{t^{3} }} = - \frac{z}{t} \cdot \frac{6q}{2q + 1}\left. {\sigma_{x,b} } \right|_{t/2}$$

(10)

$$\sigma_{y,rb} = - 0.3 \cdot \sigma_{x,rb} = - \frac{z}{t} \cdot \frac{1.8q}{2q + 1}\left. {\sigma_{x,b} } \right|_{t/2}$$

(11)

where I is the moment inertia of the sheet with unit width.

2.2.6 Final Residual Stress Distribution

The final residual stress distribution can be obtained by combining the stresses in bending and rebounding processes. Typical stress distributions though the thickness direction at the bending and rebounding stages are shown in Figs. 4 and 5, respectably, where the parameter q is taken 5.24, i.e. the averaged value of austenitic stainless steel obtained in (Zheng et al. 2019). The final residual stress distributions for the transverse and longitudinal directions are shown in the Figs. 4c and 5c as solid lines, respectively.

Fig. 4

Residual stress distribution in transverse direction

Fig. 5

Residual stress distribution in longitudinal direction

Observations from Fig. 4c indicate that: (1) the residual stress shows a zigzag type distribution, i.e. anti-symmetric distribution to the mid-thickness surface; (2) the outer surface of the corner is in compression, while the inner surface is in tension; (3) as the calculation point moves from the outer surface to the mid-thickness surface, the value of compression stress decreases linearly, and then shifts to tension stress; and (4) the residual stress reaches the maximum at the point about 0.05t away from the mid-surface, and rapidly decreases to zero when moving towards the mid-thickness.

Observations from Fig. 5c show that: (1) the residual stress has an anti-symmetric distribution to the mid thickness surface; (2) the outer half thickness of the corner is in tension, while the inner part is in compression; (3) as the calculation point moving from the outer surface to the mid-thickness surface, the value of tension stress increases linearly; and (4) at the calculation point about 0.05t away from the mid-surface, the residual stress reaches the maximum, while that at the mid-thickness is zero.

The residual stress results described above have a nonlinear expression in both the half thicknesses, and a complex distribution around the mid-thickness, which are inconvenient for structural analyses and design applications. A simplified residual stress model was then proposed following two assumptions: (1) residual stress varies linearly through half thickness (both the inner half and outer half). The reason for this assumption is that in the rebounding process, stress is linearly distributed through the thickness direction, and in the bending process, the stress–strain relationship lies in the third stage of material model [Eq. (1)] where the strain hardening is not obvious. (2) the residual stress distribution around mid-thickness is simplified to instantaneous change at the mid-thickness. Due to the shift of the neutral axis, the actual residual stress distribution around the mid thickness is much more complex, and cannot be expressed accurately. Here, a reasonable simplification is acceptable.

Following the above two additional assumptions, the residual stresses at key points (i.e. the mid-thickness, the inner surface and the outer surface) were deduced.

The residual stress at the outer surface, was derived by combining the residual stresses in the bending and rebounding process with the expression shown in Eqs. (12) and (13) for the transverse and longitudinal directions, respectively.

The residual stress at the inner surface could be obtained easily according to the symmetry of the residual stress distribution.

$$\left. {\sigma_{x} } \right|_{t/2} = \left. {\sigma_{x,b} } \right|_{t/2} + \left. {d\sigma_{x,rb} } \right|_{t/2} = \left. {\sigma_{x,b} } \right|_{t/2} - \frac{t}{2t} \cdot \frac{6q}{2q + 1}\left. {\sigma_{x,b} } \right|_{t/2} = - \frac{q - 1}{2q + 1}\left. {\sigma_{x,b} } \right|_{t/2}$$

(12)

$$\left. {\sigma_{y} } \right|_{t/2} = \left. {\sigma_{y,b} } \right|_{t/2} + \left. {d\sigma_{y,rb} } \right|_{t/2} = 0.5 \cdot \left. {\sigma_{x,b} } \right|_{t/2} - \frac{t}{2t} \cdot \frac{1.8q}{2q + 1}\left. {\sigma_{x,b} } \right|_{t/2} = \frac{0.1q + 0.5}{2q + 1}\left. {\sigma_{x,b} } \right|_{t/2}$$

(13)

The transverse residual stress at the mid thickness was derived based on the bending moment equilibrium in the transverse direction.

$$\left. {\sigma_{x} } \right|_{0} = - 2 \cdot \left. {\sigma_{x} } \right|_{t/2} = \frac{{2\left( {q - 1} \right)}}{2q + 1}\left. {\sigma_{x} } \right|_{t/2}$$

(14)

The longitudinal residual stress at the mid thickness was approximately taken as 0.5 times of the transverse residual stress, shown in Eq. (15).

$$\left. {\sigma_{y} } \right|_{0} = \left. {0.5 \cdot \sigma_{x} } \right|_{0} = \frac{q - 1}{2q + 1}\left. {\sigma_{x} } \right|_{t/2}$$

(15)

The final simplified distribution models are shown as the dot lines in Figs. 4c and 5c. Comparison of the initially derived distribution and the final simplified distribution indicates that the difference is only in the region close to the mid-thickness surface.

2.3 Validation

Cruise and Gardner (2008) and Cruise (2007) reported tests on the longitudinal residual stresses in press-braked austenitic stainless steel corner sections. In their studies, the longitudinal bending residual stresses were measured and calculated based on an assumption of the rectangular stress block distribution in the thickness direction.

In this section, the proposed simplified model was validated through comparing prediction results with experimental measurements in Cruise and Gardner (2008) and Cruise (2007). It should be mentioned that for each specimen, the average material properties of the flat region were used in the proposed simplified model. The results are shown in Table 1, where t and r_i are the thickness and the internal corner radius of the press-braked corners; σ_b,test is the tested longitudinal bending residual stress; p and q are the material parameters used in Eq. (1); σ_b,s and σ_b,m are the predicted residual stresses at the surface and mid-thickness, respectively; and σ_b,pred is the predicted longitudinal bending residual stresses calculated according to the rectangular stress block distribution assumption, i.e. σ_b,s + (σ_b,m − σ_b,s)/3.

Table 1 Comparison between the predictions of the proposed model and test data in Cruise and Gardner (2008) and Cruise (2007)

On average, the proposed model provides good predictions for the residual stresses with the average ratio of test data over the predictions at 1.17. However, the scatter of the predictions is very large at 0.45. This is probably due to two reasons. The first one is the nature of residual stresses. Except the manufacturing process, lots of other factors, such as the material properties, the transportation of specimens, etc. have effects on the residual stress distributions. Take PB50×50×2-3.2 and PB50×50×2-3.5 for an example, these two specimens have very similar material and geometric parameters, while the measured residual stress in PB50×50×2-3.2 is about 1.5 times of that in PB50×50×2-3.5. The second reason lies in small values of the ratio of r_i/t. For the last three specimens, r_i/t is less than 1.0, which means the corners experienced extensive plastic strain during the press-braking process, and the proposed simplified distribution model may be not applicable in case due to the considered assumptions used in the model development.

3 Finite Element Modeling for the Press-Braking Process

In this section, finite element models were developed to understand the distribution of residual stresses in press-baked sections, and to determine the applicable range of the deduced simplified residual stress distribution model.

3.1 Finite Element Model

ABAQUS/Standard module (2012) was employed to develop the finite element models. The following aspects were considered in the modeling.

Material Model

Stainless steel was assumed to be an isotropic material. Von Mises yield rule, Isotropic hardening law, and the Prandtl–Reuss flow rule were adopted. The stress–strain data input in ABAQUS was generated from Eq. (1) based on material parameters. Since the material would experience large plastic strain in the press-braking process, the engineering stress and strain, were converted to the true stress and strain data, respectively.

Element and Mesh

In the press-braking machine, the upper and lower dies are much stronger than the thin sheet. Therefore, the upper and lower dies were considered as rigid in the modeling. Analytical Rigid Surface, which needs the surface geometry data only, was selected to model the dies. The stainless steel sheet was modeled using a plane strain element CPE4R, and meshed into 12 elements along the thickness direction. The length of the element in the width direction of the sheet was no more than 2 times the width of the element (along the thickness direction). Typical mesh of the finite element model is shown in Fig. 6.

Fig. 6

Typical finite element model for press-braking

Interaction

Surface-to-Surface interaction was used to model the contact behavior between the dies and the stainless steel sheet. In the tangent direction, the friction coefficient was taken as 0.02, while “hard contact” was used in the normal direction.

Boundary Conditions

Reference nodes were generated for the upper and lower dies, respectively. All the degrees of freedom of the lower and upper dies were tied to the corresponding reference point. For the reference point of the lower die, all the degrees of freedom were restrained. For the reference point of upper die, the horizontal translation and rotation degrees of freedom were restrained. Thus the upper die could move vertically.

Analysis Method

The whole analysis was separated into two steps: the bending step and the rebounding step. In both of these two steps, the displacement load was applied to the reference point of the upper die. Both the material and geometric nonlinearity were considered in the analysis.

Typical Von Mises stress distributions at the end of bending stage and the rebounding stage are shown in Fig. 7.

Fig. 7

Von Mises stress distributions in the press-braking process (thickness = 3.0 mm, internal corner radius = 5.0 mm)

3.2 Validation

Although residual stress distributions through the thickness direction have been measured in press-braked steel sections (Weng and White 1990), cold-rolled steel sections (Li et al. 2009; Tong et al. 2012; Chen and Ross 1978) and cold-rolled stainless steel sections (Jandera et al. 2008), relevant test data in press-braked stainless steel sections is not available yet. Thus, results from the residual stress distribution model proposed by Quach et al. (2009a, b) were used to validate the finite element model.

Quach et al. (2009a, b) reported modeling and theoretical residual stresses results in press-braked stainless steel channel sections, where the internal corner radius and the thickness of the corner were 3.96 mm and 1.8 mm, respectively. The material properties used came from the longitudinal compression tests of stainless steel S31803 in Rasmussen et al. (2003).

According to the material properties of S31803, the material parameters used in the proposed model of this paper can be obtained through curve fitting. The nominal yield stress σ_0.2, the parameters p and q were 527 MPa, 4.5, and 1605 MPa, respectively. The residual stresses were calculated with the results shown in Figs. 8, 9 and 10 for the transverse residual stresses, the longitudinal residual stresses, and the equivalent plastic strain, respectively. In these figures, the dash and solid red lines are the calculation results according to the finite element model and the theoretical analysis proposed by Quach et al. (2009a, b), respectively. The dash and solid black lines are the calculation result according to the finite element model and the theoretical analysis proposed in this study, respectively.

Fig. 8

Comparison of the calculation results of transverse residual stresses by the methods in Quach et al. (2009a, b) and this paper

Fig. 9

Comparison of the calculation results of longitudinal residual stresses by the methods in Quach et al. (2009a, b) and this paper

Fig. 10

Comparison of the calculation results of the equivalent plastic strains by the methods in Quach et al. (2009a, b) and this paper

From Fig. 8, it can be seen that all the four curves show a similar trend, i.e. a zigzag type distribution in the thickness direction. The biggest difference among these results lies around the mid-thickness. The finite element model (both the Quach’s model and the simulation model in this study) can presents the shift of neutral axis towards the inner surface, while the neutral axis in the theoretical models remains around the original position. In terms of the proposed simplified model, the magnitude of the predicted residual stresses around the mid-thickness agrees well with that from the finite element model. On the outer surface, the magnitude of the predicted stress is a little higher than that by others models, while on the inner surface, the magnitude of the predicted stress is slightly lower.

In terms of the longitudinal bending residual stresses shown in Fig. 9, the four curves also show a similar trend. However, the predictions by the proposed simplified model and the finite element model are smaller than those from the theory and modeling in Quach et al. (2009a, b). It should be mentioned that coiling and uncoiling processes were considered in Quach et al. (2009a, b), which affect the distribution of residual stresses, especially in the longitudinal direction since the plastic loading and unloading mainly occurred along the longitudinal direction during the coiling and uncoiling processes.

With respect to the equivalent plastic strain shown in Fig. 10, the predictions of the proposed simplified model agree well with those by the theoretical model proposed by Quach et al. (2009a, b) The finite element model developed by this study and by Quach et al. (2009a, b) provide almost the same results. The magnitude of the proposed model in this study also fits well with that from the finite element model. However, the shift of the neutral axis is not reflected by the proposed model.

Based on the above comparison results, the finite element model and the theoretical model proposed in this study provide similar predictions with the models proposed by Quach et al. (2009a, b), and can be used in future analysis.

3.3 Further Analysis on Press-Braking Process

A series of finite element models were built to provide more knowledge about the press-braked sections. The material and geometric informations used in modeling are shown in Table 2. The material properties used are the average values of austenitic stainless steel in (Zheng et al. 2019). The upper and lower dies were designed by a local factory shown in Fig. 11. The width of the stainless steel sheets was taken as 50 mm.

Table 2 Geometric and material information of press-braked specimens for modeling

Fig. 11

Upper and lower dies of press-braking for modeling

Typical equivalent plastic strain distribution on the surfaces along the width direction of the cross-section is shown in Fig. 12.

Fig. 12

Equivalent plastic strain distribution in press-braked section R5T3

From Fig. 12, it can be seen that: (1) the equivalent plastic strain on the bottom (tension) and the top (compression) surface have a similar distribution; and (2) the equivalent plastic strain is equal to zero at the edge and most of flat region. For the corner region and the adjacent flat region, the equivalent plastic strain markedly increases as the measuring point moves towards the center of the sheet. It also means that the equivalent plastic strain in the corner region is not evenly distributed.

Longitudinal residual stresses were obtained from finite element models, and then converted to the equivalent residual stresses based on rectangular stress block assumption. The results are shown in Fig. 13.

Fig. 13

Equivalent longitudinal residual stress in press-braked section R5T3

From Fig. 13, it can be seen that: (1) generally, the equivalent residual stress σ_y,eq gradually increases from the edge to the center of the sheet. However at the intersection point of the corner region and the flat region, the equivalent residual stress is lower than that in the adjacent region; at this point, the curvature of the sheet is not continuous, and the residual stresses through the thickness direction are very complex; and (2) in the corner region, the equivalent residual stress is not evenly distributed which indicates the measured values in the available tests are an averaged value.

Typical results of residual stresses and equivalent plastic strain distribution along the thickness direction are shown in Figs. 14 and 15, respectively. In these figures, the predictions of the proposed simplified residual stress distribution model were also provided. The meanings of the symbols in these figures are listed below: ‘FEM-Long’ and ‘FEM-Trans’ are the calculated longitudinal and transverse residual stresses using finite element models, respectively; ‘Theo-Long’ and ‘Theo-Tran’ are the predicted longitudinal and transverse residual stresses using the proposed simplified residual stress distribution model, respectively; ‘FEM-1 mm’, ‘FEM-3 mm’ and ‘FEM-5 mm’ are the calculated equivalent plastic strains using finite element method for the specimens R5T1, R5T3, and R5T5, respectively; ‘Theo-1 mm’, ‘Theo-3 mm’ and ‘Theo-5 mm’ are the predicted equivalent plastic strains using the proposed simplified residual stress distribution model for the specimens R5T1, R5T3, and R5T5, respectively.

Fig. 14

Comparisons of residual stress distributions by the proposed simplified model and the finite element method

Fig. 15

Comparison of equivalent plastic strain by the proposed simplified model and the finite element method

Observations from Figs. 14 and 15 show that: (1) for the specimen R5T1, both the predicted residual stresses and the equivalent plastic strain fit well with the corresponding finite element results; (2) for the specimen R5T5 with the ratio of r_i/t at 1.0, the predicted residual stress distribution is apparently different from the finite element results; the predicted longitudinal residual stress is obviously lower than the finite element simulation result; the equivalent longitudinal residual stress according to rectangular stress block assumption is 95 MPa for the predicted model, while the calculation result by the finite element model reaches to 185 MPa; the neutral axis moves by 20% of the thickness to the inner surface (compression side), which leads to apparent difference between the proposed equivalent plastic strain model and the finite element model; and (3) for the specimen R5T3 with r_i/t equals to 1.67, the error of the proposed simplified model lies between that for R5T1 and R5T5. The proposed model is still applicable for this specimen in general. For commonly used press-braked sections, the internal radius r_i of corners varies from 2t to 6t (SFIA 2012; AISI 1996), the proposed simplified residual stress distribution model has appropriate accuracy in the predictions of residual stresses.

4 Conclusions

This paper conducted theoretical and finite element studies on the residual stresses in press-braked stainless steel sections. A simplified residual stress distribution model for corners of press-braked sections was deduced. Finite element models were also developed to study the residual stress distribution of the whole sections and to validate the applicable range of the proposed simplified model. The following conclusions can be drawn:

• (1) A simplified residual stress distribution model for press-braked stainless steel sections was proposed. Comparison results with test data and finite element simulation results show that the proposed model is applicable to commonly used press-braked sections, with the ratio of internal corner radius to the thickness r_i/t varying from 2 to 6.

• (2) For press-braked sections with the r_i/t ratio less than 1.0, the predicted longitudinal residual stress by the proposed simplified model is lower than test data and the finite element result due to the extensive plastic deformation in press-braking process. The shift of the neutral axis reaches 20% of the thickness, which causes obvious differences between the prediction results by the proposed simplified model and finite element simulation.

• (3) In press-braked sections, the residual stress and plastic strain are concentrated in the corner and the adjacent flat region. The distributions of the residual stress and plastic strain are not evenly distributed in the corner region, and the maximum values occur in the center of the corner.