1 Introduction

Complex networks have become a natural representation of entities and their interactions in systems of all domains. They can be used to describe social networks, genetic and protein interaction networks, airline and road traffic networks, brain connectivity networks, web graphs as well as any other system composed of entities, represented as graph nodes, interacting with each other thereby forming the edges of the graph. In many applications, the same set of nodes may participate in multiple different types of interactions each forming a different and independent layer of the network. Then, the system is represented as a multiplex graph, and the term monoplex can be used for single layer networks. Alternative terminology has been used over the years for such complex networks, with examples including multidimensional networks, multinetworks, multirelational networks, or multislice networks. More general representations are used in cases where layers are ordered or otherwise correlated, or in cases where the nodes across layers are not aligned, or even represent entities of different types with inter-layer connections. The resulting networks are frequently called multilayer networks, but other terms such as multilevel, multitype, or networks of networks are used, as discussed in detail in Kivelä et al. (2014).

A variety of network theoretic tools are used for the analysis of these complex systems (Bunke et al. 2007), and the question of graph distinguishability or graph similarity is often a central aspect of study. Examples include analysis of networks for classification purposes, such as comparison of networks created by brain fMRI images of patients, but also analysis of networks for clustering or outlier detection purposes, such as comparisons of daily traffic networks to facilitate the detection of abnormal change in traffic patterns. In all these settings, the similarity between two graphs with overlapping sets of nodes is assessed and the detection of changes in the connectivity patterns is essential. This problem is different from the problem of inexact graph matching, the graph isomorphism or the maximum common subgraph problem, where the node correspondence is unknown (Bunke 2000).

Several approaches have been proposed to solve different variations of the problem of calculating graph similarity. The most straightforward approach would be the calculation of a variety of the graphs’ structural properties (diameter, edges distribution, degree and eigenvalues) and their subsequent comparison, but this approach is not able to capture every aspect of the graphs. More commonly, methods that estimate the graph edit distance (GED) are used. GED measures the dissimilarity between two graphs as the minimal cost of a sequence of elementary operations transforming one graph into another. The exact computation of GED is NP-hard, and typically, approximate or tangent solutions are implemented. Other solutions have been proposed, such as the usage of the graph spectra (Bunke et al. 2007; Wilson and Zhu 2008), or measures inspired by document similarity (Papadimitriou et al. 2010), and other intuitive approaches (Koutra et al. 2013; Monnig and Meyer 2018). More recently, spectral distances, as well as distances based on node affinities, have been studied in more depth (Wills et al. 2020); the usage of Quantum Jensen Divergence (QJSDiv) as a measure of graph distinguishability has been proposed (Domenico and Biamonte 2016); and recently a series of measures that have been effectively used in quantum mechanics and quantum information theory were proposed (Polychronopoulou et al. 2021).

Quantum mechanics has proven to be a valuable resource for the investigation of the behavior of complex networks (Biamonte et al. 2019). A variety of quantum systems have been seen as metaphors for natural systems described by complex networks. Quantum gases have been used to describe network evolution, and the emergence of different structures in complex networks has been represented in terms of a quantum-classical transition for quantum gases (Javarone et al. 2013). Quantum transport probability and state fidelity have been implemented as a closeness function and used for community detection (Mauro et al. 2014), while quantum random walks have been shown to offer significant performance improvements on traditional computer science algorithms with respect to the classical random walks (Kempe 2003), and have been implemented for a quantum-inspired ranking algorithm (Sánchez-Burillo et al. 2018). Quantum distances are used to reduce the complexity of calculating Euclidean distances between multidimensional points and improve the performance of algorithms such as k-means (Trávníşek et al. 2019). Given this interconnection between quantum mechanics and complex networks, quantum network theory is a natural place to look for similarity measures.

In the work of Polychronopoulou et al. (2021), four measures that have been broadly used in quantum information theory for the comparison of quantum states (Michael and Chuang 2002), systems, and processes (Jerzy et al. 2011; Gilchrist et al. 2005) were proposed for use with monoplex networks. These quantum-inspired methods offer a mathematical method of graph comparison, they satisfy the mathematical properties of a metric, offer intelligible results with high interpretability, and were shown in Polychronopoulou et al. (2021) to satisfy intuitive graph similarity properties for monoplex networks. In this work, the techniques are further extended for use with multiplex networks. An analysis of the intuitive requirements of multiplex graph comparison is presented, and we elucidate the properties of the four distance measures on both monoplex and multiplex networks. A series of artificial data is utilized to characterize their effectiveness, and showcase their behaviour. We then report results on real-world applications, answering different data mining problems from a variety of domains. The quantum-inspired measures are compared to a series of state-of-the-art and well established methods, adding in this work new baseline techniques based on the most recent publications in the domain. The code is available on GitHub (https://github.com/NancyPol/Quantum_Graph_Distances).

2 Methods

Mathematically, the structure of an undirected single layer network, or monoplex, \(G = \{V, E\}\), on a set of N vertices \(V = \{1,2,\ldots ,n\}\) and a set of edges \(E\subseteq V \times V\), is represented by a binary matrix A, known as adjacency matrix, whose element \(A_{u,v} = 1\) if \({u,v} \in V\) and \(A_{u,v} = 0\) otherwise. In order to extend distance measures that were initially developed for quantum states, to be used with graphs, we utilise the definition of a density matrix.

In quantum mechanics, a density matrix is a matrix that describes the statistical state of a quantum mechanical system. Mathematically, it is a hermitian matrix that is positive semidefinite with trace equal to 1. In graph theory, the density matrix \(\rho\) of a graph can be defined through the combinatorial Laplacian of the graph (Braunstein et al. 2006), as \(\rho _G=\frac{\Delta -A}{Tr(\Delta )}\). In this equation A is the adjacency matrix, \(\Delta\) is the degree matrix, which is a diagonal matrix with elements equal to the degree d(u) of each node u. The normalization using the trace of \(\Delta\) guarantees that the density matrix will have a trace of 1. For a weighted graph \(G = (V, E, W)\) each edge is associated with an edge weight and in this case the density matrix becomes \(\rho _G=\frac{\Delta -W}{Tr(\Delta )}\), where W is the weights matrix with \(W_{u,v}=w_{uv}\) and \(W_{u,v}=0\) if the nodes u and v are not connected. The degree matrix \(\Delta\) is again a diagonal matrix holding for each node u the value \(d_u = \sum _{v=1}^{n} w_{uv}\).

Using this formulation we can then compare networks the same way we would compare states in quantum mechanical systems. In the following sections we present and evaluate measures of quantum states comparison that are particularly important in Quantum Information Science (Michael and Chuang 2002; Jerzy et al. 2011; Gilchrist et al. 2005). They have been shown to be metrics, are mathematically well established and have high interpretability; thereby satisfying the mathematical requirements of distance measures for graphs. The metric character of a distance for the comparison of two complex networks \(G_{\sigma }\) and \(G_{\rho }\), guarantees three fundamental properties: \(D(G_{\sigma }\), \(G_{\rho }) \ge 0\), with the equality to zero occurring if and only if \(G_{\sigma } = G_{\rho }\), \(D(G_{\sigma }\), \(G_{\rho }) = D(G_{\rho }\), \(G_{\sigma })\) i.e. the distance measure is symmetric and finally the triangle inequality is satisfied and \(D(G_{\sigma }\), \(G_{\rho }) \le D(G_{\sigma }\), \(G_{\tau }) + D(G_{\tau }\), \(G_{\rho })\).

2.1 Trace distance

The trace distance between two quantum states, or two networks, with density matrices \(\sigma\) and \(\rho\) is given by:

$$\begin{aligned} d_{trace}(G_\sigma , G\rho ) = \frac{1}{2} [\text{trace} \, (\sqrt{(\sigma - \rho )^2})] \end{aligned}$$
(1)

It is a metric and is bounded to be \(0 \le D_{\text{trace}} \le 1\) with the equality to 0 holding if and only if \(\rho = \sigma\) and the equality to 1 holding if and only if \(\rho\) and \(\sigma\) have orthogonal supports. The trace distance is the quantum generalization of the Kolmogorov distance for classical probability distributions and, as it’s classical counterpart, the trace distance can be interpreted to represent the maximum probability of distinguishing between two quantum systems, or in our case two networks.

2.2 Hilbert–Schmidt distance

The Hilbert-Schmidt distance

$$\begin{aligned} d_{HS}(G_\sigma , G\rho ) = \sqrt{trace(\sigma - \rho )^2} \end{aligned}$$
(2)

is a Riemannian metric that is bounded to be \(0 \le D_{HS} \le 2D_{trace}\). As it is defined on the space of operators it is unclear how to impose an operational interpretation, however, in Jinhyoung and Brukner (2003) the authors suggest that it can be seen as an information distance between two quantum states. It has been recently used in Trávníşek et al. (2019) to reduce the complexity of calculating Euclidean distances between multidimensional points and thereby reduce the complexity of classification algorithms such as k-means but it has not been studied so far as a measure for the distinguishability of graphs.

2.3 Hellinger distance

The Hellinger distance is given by:

$$\begin{aligned} d_{H}(G_\sigma , G\rho ) = \sqrt{2[1 - A(\sigma ,\rho ) ] } \end{aligned}$$
(3)

with

$$\begin{aligned} A(\sigma ,\rho ) = trace(\sqrt{\sigma }\sqrt{\rho }) \end{aligned}$$
(4)

representing the quantum affinity, a measure that characterizes the closeness of two quantum states and whose classical analog is the Bhattacharya coefficient between two classical probability distribution. The Hellinger distance is a metric, bounded to be \(0 \le D_{H} \le \sqrt{2}\) (Muthuganesan et al. 2020).

2.4 Bures distance

The Bures distance is expressed through quantum Fidelity (Jozsa 1994), which is a measures of overlap between two quantum states:

$$\begin{aligned} F(\sigma ,\rho ) = [trace(\sqrt{\sqrt{\rho } \sigma \sqrt{\rho }})]^2 \end{aligned}$$
(5)

It can be shown that the fidelity is symmetric and is bounded to be \(0 \le F(\sigma ,\rho ) \le 1\), with \(F(\sigma ,\rho ) = 1\) if and only if \(\sigma =\rho\). Although not a metric, the fidelity can easily be turned into a metric and the most common approach is the Bures metric:

$$\begin{aligned} d_B(G_\sigma , G\rho ) = \sqrt{2[1 - \sqrt{F(\sigma ,\rho )}]} \end{aligned}$$
(6)

2.5 Quantum JSDiv

The Von Neumann entropy of a network, similarly to the Von Neumann entropy of a quantum system, can be interpreted as a measure of regularity and is given by the expression:

$$\begin{aligned} S(\rho ) = - Tr(\rho \log _2\rho ) \end{aligned}$$
(7)

Then, the distinguishability of two quantum states or two networks with density matrices \(\sigma\) and \(\rho\) can be measured using the von Neumann relative entropy (or quantum relative entropy) defined as:

$$\begin{aligned} S_N(\sigma ,\rho ) = Tr\sigma (ln\sigma - ln\rho ) \end{aligned}$$
(8)

where \(ln\sigma\) is the matrix base 2 logarithm of \(\sigma\). Notice that the quantum relative entropy is the quantum mechanical analog of relative entropy, otherwise called Kullback–Leibler divergence, commonly used in statistics as a measure of comparison for probability distributions. Relative entropy is not symmetric, does not satisfy the triangle equality and it is well defined only if the support of \(\sigma\) is a subset of the support of \(\rho\) (the support being the subspace spanned by the eigenvectors of the density matrix with non-zero eigenvalues). However, it can be extended to provide the Quantum Jensen-Shannon divergence (QJSDiv) (Majtey et al. 2005), given by:

$$\begin{aligned} QJSDiv \, (G_\sigma , G\rho ) = \frac{1}{2} [S_N(\sigma , \frac{\sigma + \rho }{2}) + S_N(\rho , \frac{\sigma + \rho }{2})] \end{aligned}$$
(9)

where \(S_N\) is the quantum relative entropy of equation 8. Quantum Jensen–Shannon divergence was introduced as a measure of distinguishability between mixed quantum states (Majtey et al. 2005; Lamberti 2008). It is bounded to be \(0 \le QJSDiv \le 1\), with the equality to 0 holding if and only if \(\rho = \sigma\), and it is always well-defined, with the restriction previously imposed on the supports of \(\rho\) and \(\sigma\) now lifted. The authors of Domenico and Biamonte (2016) have shown that Quantum Jensen-Shannon divergence can be used to quantify the distance between pairs of networks, and they have applied it to successfully cluster the layers of a multilayer system. In this work, we use Quantum Jensen-Shannon as a quantum-inspired baseline and aim to compare it’s performance with the rest of the measures presented here.

2.6 Comparison of multiplex networks

Mathematically, a Multiplex Network G with L layers can be seen as a collection of L single-layer networks: \(G = \{G_l\mid l \in \{1,\ldots ,L\}\}\). Each of these networks has a set of edges, that can either be weighted or not, and they all share the same set of N nodes V, while some nodes may not have connections in all layers. Each of the layers is represented by a weighted or non-weighted adjacency matrix \(A_l\). A natural representation of the entire multiplex uses the supra-adjacency matrix \({\mathcal {A}}\) of the network (Kivelä et al. 2014; Stefano et al. 2014; Domenico et al. 2013). \({\mathcal {A}}\) is obtained from the intra-layer adjacency matrices \(A_l\) and a coupling matrix K, whose elements \(K_{lm}\) represent the inter-layer connections between layers l and m. Then the supra-adjacency matrix becomes \({\mathcal {A}} = \bigoplus _{l} A_l + K \otimes I_{N}\), with a term representing the direct sum of \(A_l\) and \(I_N\) the \(N \times N\) identity matrix. Notice that, in multiplex networks, the only possible type of inter-layer connection is the one in which a given node is connected to its counterpart node in the remaining layers, resulting in a coupling matrix K whose non-diagonal elements are typically equal to 1.

This formulation allows multiplex networks to be compared using the distance measures introduced for single layer graphs, with the supra-adjacency matrix substituting the monoplex adjacency. However, as the size of the networks under study grow, either in terms of nodes or in terms of layers, so does the size of the supra-adjacency, rendering the use of complex algorithms computationally expensive and infeasible. In addition, the complexity of the representation is not necessarily increasing the informative power. As the addition of layers increases the effective dimension of the model, the intrinsic information becomes more sparse, and may remain hidden within the noise of the representation (Tiago 2015).

Therefore, alternative representations have been proposed for multiplex networks, typically constructing a monoplex network by aggregating the various layers. An example of such an aggregation is the average network (Albert et al. 2013), where the aggregated monoplex is a simple average of the layers. Similarly, weighted or non-weighted overlapping networks (Battiston et al. 2014) have been constructed by summarising the various layers. The authors of Domenico et al. (2013) have used the projected monoplex, and the overlay monoplex networks. Both are obtained from a multiplex network by summing the edges over all layers, but the overlay network ignores the interlayer connections of nodes. Finally, the authors of Sánchez-García et al. (2014) introduced the notion of graph quotients and an aggregate network that summarizes the connections of nodes among the different layers, normalised by the multiplexity degrees of the nodes.

In this work we introduce an alternative representation, that can be seen as a very intuitive approach to layer aggregation, the noisy-OR function. In this case, the weight of the edge between nodes u and v of the aggregate monoplex is calculated as: \(1-\prod _{l=1}^L (1-w^l_{u,v})\). This function has been used in many domains and real-world applications for approximating relationships in which there is a set of two or more sources of information that can potentially explain a single variable (Sampath 1993). If the monoplex aggregate is seen as the network describing the absolute connection between nodes, and the layers are seen as evidence of this connection, then the extension for use with multiplex networks is natural. Alternatively, the aggregate monoplex describes the reliability of connections between nodes, as affected by multiple sources of information, the layers of the multiplex network. In the case of non-weighted networks, this function acts as a projection to a flattened network, but in the case of weighted networks, the final weight of an edge between two nodes is affected by the weights of the various layers.

The monoplex aggregations presented above can be used as adjacency matrices for the representation of the multiplex, and networks can be compared using the corresponding density matrices. In the case of Projected and Quotient monoplex, that take into account interlayer connections of nodes, the degree matrix should also include those, so that the trace of the density matrix will remain equal to 1. In the following sections, we utilize a series of experiments on artificial multiplex data to quantify the ability of these multiplex representations and similarity measures to distinguish between graphs, and capture intuitive similarity aspects. Then we use real-world complex applications to evaluate the performance of alternative methods of graph comparison.

3 Evaluation on artificial data

3.1 Monoplex networks

A similarity measure needs to satisfy several requirements in order to be considered as a means of single layer network comparison. First, the measure should satisfy mathematical requirements (be a metric), and have high interpretability. But some more important challenges are graph-specific and are associated with the ability of the measure to capture changes in important structural characteristics such different kinds of centrality measures. Examples include the fact that a modification of a graph is more important in smaller graphs than larger ones, also that targeted modifications should be given higher importance, and that edge weights should be considered.

The performance of the proposed measures is evaluated on artificial data, created as Erdős-Rényi random graphs with given number of nodes (100) and edges (1000). These artificial networks are then continuously modified using a discrete-time process in which one elementary graph edit operation is applied at every step. The distance between the modified and original network is calculated for every step and the results are summarised in Fig. 1. More detailed results, accommodating all possible elementary graph edit operations, and different graphical structures are included in Polychronopoulou et al. (2021).

Fig. 1
figure 1

The progression of each of the distance measures between the original graph and the graph after applying a series of elementary graph edit operations. For edge removals, two operations are compared: random vs targeted edge removals, targeting the popular nodes (middle) or edges of higher weight (right)

Full size image

In the simple case of repeated node removals, the monotonically increasing behavior of the distance measures is evident and confirms that they all act as measures of graph distinguishability. Several other intuitive aspects are evident on this figure. First, with the exception of Bures distance, the measures have identified that the removal of one node is more crucial for smaller networks, as is evident by the slope of the curves. Interestingly, Hellinger distance is equally sensitive to modifications of large and small networks. Furthermore, all distances are sensitive to distinguishing targeted from random operations, both for the case of continuous edge removals targeting popular nodes, and continuous edge removals targeting edges of higher weights. The sensitivity of the methods differs, although they all exhibit distance values that are lower for random modification, compared to targeted ones. The behavior of trace distance is notable, with a lower sensitivity when the compared graphs are either very similar or very dissimilar.

3.2 Multiplex networks

A similar analysis is applied to the case of multiplex networks. Different network generation techniques are used to create multiplex networks with two or three layers following Poisson multidegree distribution and scale-free multidegree distribution (Bianconi 2013), as well as duplex networks with linear (Vincenzo et al. 2013) and nonlinear kernels (Vincenzo et al. 2014). Each network is then continuously modified, applying at each step one elementary graph edit operation, and the distance between the modified and original network is calculated. The process is repeated for all multiplex representations.

Fig. 2
figure 2

The progression of the distance measures between the original graph and the graph after applying a series of elementary graph edit operations for: Left: supra-adjacency representation, 3-layer poisson multidegree distribution network, and various distance measures. Middle: hellinger distance, 3-layer poisson multidegree distribution network, and various multiplex representations. Right: hellinger distance, supra-adjacency representation, and various multiplex artificial networks of L number of layers and different generation techniques

Full size image

The first results are created by applying continuous random node removals and are presented in Fig. 2. In each part of the plot, two of the three variables of study (distance, multiplex representation, multiplex generation technique) remain constant, while the third one varies. Similarly to the case of monoplex networks, quantum distances satisfy intuitive similarity aspects: they continuously increase as the networks are further modified and this applies to most multiplex representations and all types of data. As observed in the middle plot of Fig. 2, in the case of Quotient and Projected monoplex networks that incorporate inter layer connections of nodes, this is not always the case. The inter layer connections become prevalent at very small size networks affecting the expected continuous increase of distance in the plots of Fig. 2.

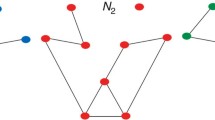
In the case of multiplex networks the measures used for their comparison should be able to capture some additional intuitive aspects. For example, removal of nodes with higher centrality should create graphs more distinguishable from the original one. Even more so, when the nodes that are removed act as a bridge between layers (Albert et al. 2014), such as node \(n_3\) in Fig. 3. Similarly, the effect of an edge removal should depend on whether the adjacent nodes have a connection in other layers or not, such as the case with edge \(e_2\) in Fig. 3.

Fig. 3
figure 3

Examples of multiplex networks, where each layer is represented by a different color of edges. The removal of each of the nodes \(n_1, n_2\) or \(n_3\) should create graphs with different distances from the original one. The same applies to the removal of each of single layer edges \(e_1\) and \(e_2\)

Full size image

In this small scale example, we can calculate the distances of some possible modifications using the supra-adjacency representation of the multiplex, and directly compare the results of Table 1. In the cases of node removals from graph \(G^A\), when node \(n_1\) is removed all distance measures calculate a distance that is smaller than when nodes \(n_2\) and \(n_3\) are removed. Then, comparing the effect of removing nodes \(n_2\) and \(n_3\), we can see that GED is the same in both cases, as expected since it only incorporates structural changes, while Hellinger, Trace and QJSDiv, report that the removal of the bridge node is more substantial. In the cases of edge removals, all quantum measures, except Hilbert-Schmidt, agree that the removal of edge \(e_1\) increases the distinguishability of the graph more than the removal of edge \(e_2\) , since in that second case the two adjacent nodes maintain their connection over the other layer.

Table 1 Distances between different sample multiplex networks G and \(G'\)
Full size table

Similar conclusions can be reached using alternative representations for the multiplex. Table 2 shows the values of Hellinger Distance for the same modifications and different aggregated monoplex representations. All representation identify the removal of node \(n_1\) as less substantial. However, with the exception of the projected and quotient monoplex, they are not able to differentiate between the removals of nodes \(n_2\) and \(n_3\). In the case of edge removals most aggregate representations agree that the distance of graphs G and \(G'\) is larger when edge \(e_1\) is removed, while since this is a non-weighted network, the noisy-OR function does not distinguish between G and \(G'\) when \(e_2\) is removed.

Table 2 Hellinger distance between sample multiplex networks G and \(G'\), for different aggregate monoplex representations
Full size table

We can generalise these findings, using larger scale artificial networks, generated as two and three layer artificial multiplex networks, with the multiplex generation techniques reported above. Then, at every node removal step, the distance of the new graph with the previous, and the MultiRank centrality of the removed node are calculated. For this centrality, an algorithm by Christoph et al. (2018) is used, as it considers the multiplex structure and assigns higher centrality values to nodes that are linked to central nodes in highly influential layers. There is a clear correlation between these values, as evident by the Pearson correlation of the distances and node centralities, reported for the supra-adjacency representation and each of the distance measures, in Table 3. Other multiplex representations produce similar results, and an example for the correlations of Hellinger distance is presented in the same table for all other multiplex representations.

We can generalise the findings of the edge removal examples, using again larger scale artificial networks, while for every removal of an edge \(e^{l}_{u,v}\) from a layer l, we monitor the number of layers in which an edge between the adjacent nodes u and v exists. The resulting distributions of distance values, across all types of networks and for the case of the supra-adjacency representation and Hellinger distance is reported in Fig. 4. The three plots, when normalised to the same integral, present distributions of distances that can be fitted with functions holding different exponential parameters, shown on the plots. These values have 95% Confidence Intervals given in this example by: \(CI_b^{1\,L} = (-0.1573, -0.1303)\), \(CI_b^{2\,L} = (-0.3306, -0.2752)\), \(CI_b^{3\,L} = (-0.6758, -0.4288)\), indicating that the removal of an edge is creating less distinguishable graphs, when the adjacent nodes are also connected in different layers. It is also evident that the larger the number of layers in which the adjacent nodes u and v were originally connected, the more narrow the distribution is, or the smaller the expected distance value will be. Similar trends are observed on the plots of all other quantum distances, as well as the majority of multiplex representations, with the exception of overlap and Noisy-OR representations similar to the results of the small scale example.

Fig. 4
figure 4

Distribution of the values of Hellinger distance between G and \(G'\) when an edge \(e^{l}_{u,v}\) from layer l is removed, while the adjacent nodes u and v are connected in 1, 2 or 3 layers

Full size image
Table 3 Pearson Correlation of node centrality and Distance between G and \(G'\)
Full size table

4 Applications on real data

In this section, we evaluate the effectiveness of the proposed distance measures on real world applications. For each application we utilise data from different domains and we compare our results with several well-established and state of the art baseline methods.

4.1 Baselines

The first of our baselines is based on the Normalized Laplacian spectral distance of two graphs \(G_{\sigma } = (V_{\sigma }, E_{\sigma })\) and \(G_{\rho } = (V_{\rho }, E_{\rho })\), as calculated by:

$$\begin{aligned} d_{{\mathcal {L}}} \, (G_{\sigma }, G_{\rho }) = \sqrt{\sum _{i=1}^N{(\lambda _i^{\sigma } - \lambda _i^{\rho })^2}} \end{aligned}$$
(10)

with \(\lambda _i^{\sigma }\) and \(\lambda _i^{\rho }\) the \(i^{th}\) eigevalue of the Normalised Laplacian of graphs \(G_{\sigma }\) and \(G_{\rho }\) correspondingly. The spectral distances of graphs have been studied (Wilson and Zhu 2008; Wills et al. 2020) and proven to be effective means of graph comparison, although they are not true metrics, since two graphs may exist that are co-spectral but not isomorphic.

We also compare our results with the resistance-perturbation distance, introduced in Monnig and Meyer (2018). In this work the authors represent each graph G by it’s effective graph resistance R, with elements: \(R_{ij} = L^\dag _{ii} + L^\dag _{jj} - 2\,L^\dag _{ij}\), where \(L^\dag\) denotes the Moore-Penrose pseudoinverse of the combinatorial Laplacian matrix L. Then the resistance-perturbation distance between two graphs \(G_{\sigma } = (V_{\sigma }, E_{\sigma })\) and \(G_{\rho } = (V_{\rho }, E_{\rho })\) is defined as the element-wise p-norm of the difference between their effective resistance matrices:

$$\begin{aligned} d_{PR} \, (G_{\sigma }, G_{\rho }) = \Vert R_{\sigma } - R_{\rho } \Vert _p \end{aligned}$$
(11)

The last of our state-of-the-art baselines is DELTACON, an intuitive algorithm proposed by Koutra et al. (2013), that uses fast belief propagation to model the diffusion of information throughout the graph and represent each graph by an affinity matrix \({\varvec{S}}\), defined as: \({\varvec{S}} = [{\varvec{I}} +\epsilon ^2{\varvec{D}} + {\varvec{A}}]^{-1}\). Then the two graphs \(G_{\sigma } = (V_{\sigma }, E_{\sigma })\) and \(G_{\rho } = (V_{\rho }, E_{\rho })\) are compared via the Matusita difference of their reprsentations:

$$\begin{aligned} d_{DELT}(G_{\sigma }, G_{\rho }) = \sqrt{\sum _{i,j}{( \sqrt{S_{ij}^\sigma } - \sqrt{S_{ij}^\rho } )^2}} \end{aligned}$$
(12)

We also compare with two well-established measures of graphs similarity, the graph edit distance (GED) and the edge-weight distance (DEW), studied in detail in Bunke et al. (2007). Mathematically, the graph edit distance (GED) between two graphs \(G_{\sigma } = (V_{\sigma }, E_{\sigma })\) and \(G_{\rho } = (V_{\rho }, E_{\rho })\) is given by:

$$\begin{aligned} d_{GED}(G_{\sigma }, G_{\rho })= \frac{\mid V_{\sigma }\mid + \mid V_{\rho }\mid - 2\mid V_{\sigma } \cap V_{\rho } \mid + \mid E_{\sigma } \mid + \mid E_{\rho } \mid - 2\mid E_{\sigma } \cap E_{\rho } \mid }{\mid V_{\sigma } \mid + \mid V_{\rho } \mid + \mid E_{\sigma } \mid + \mid E_{\rho } \mid } \end{aligned}$$
(13)

while the edge-weight distance for the two graphs, on the simplified case of \(V_{\rho } = V_{\sigma } = V\) is defined in Bunke et al. (2007) as:

$$\begin{aligned} d_{DEW}(G_{\sigma }, G_{\rho }) = \sum _{u,v \in V}^{} \frac{ \mid w_{uv}^{\sigma } - w_{uv}^{\rho } \mid } {max \, (w_{uv}^{\sigma }, w_{uv}^{\rho })} \end{aligned}$$
(14)

with \(w_{uv}^{i}\) the weight of the edge between nodes u and v of graph \(G_{i}\).

4.2 Single layer graph classification

As a first application, we evaluate the effectiveness of the distance measures on classification problems with real world single layer networks. The data sets used, are available online, under (SNAP datasets), or (Austin datasets) and the results are reported in terms of the F1 score in Table 4.

Table 4 F1 scores for each of the classification tasks and distinguishability methods
Full size table

For each data set, we construct labeled graphs using the ego-networks of each node. For the classification task, the dissimilarities between all possible combinations of graphs are calculated, a leave-one-out approach is implemented and each ego-network is assigned to the label that is on average most similar. The classification is based on the assumptions that researcher who belong in the same department will have similar email ego-networks (Leskovec et al. 2007), butterflies who belong in the same class will have similar visual similarities ego-networks (Bo et al. 2018), individuals from the same class have similar interaction ego-networks (Mastrandrea et al. 2015; Juliette et al. 2011; Philip et al. 2021), US Counties with a majority vote of the same party in the U.S. presidential elections will have similar Facebook social connectedness ego-networks, or physical proximity ego-networks (Jia and Benson 2022), and that Congresspersons with the same political party affiliation have similar bill co-sponsoring egonetworks (James 2006; Philip et al. 2021).

The results indicate that the quantum-inspired distance measures in most cases outperform the more traditionally used baselines, with Hellinger achieving the highest classification accuracy most often.

4.3 Multiplex layer clustering

As described earlier, in multiplex networks entities are connected to each other via multiple types of connections. The increased complexity of such systems has motivated the study of layer aggregation (Manlio et al. 2015) or layer clustering. Through this process it is possible to minimize the total number of layers in a system, resulting in a network that can be analysed more efficiently, but not without some loss of information content. Although the benefit of aggregating layers with structural similarities is not always clear, it typically depends on the system under study (Tiago 2015), and remains an open research problem.

Following this motivation, we evaluate the effectiveness of the quantum-inspired graph distance measures in the problem of computing pairwise similarities between layers, and then performing hierarchical clustering of structurally similar layers in multiplex networks. We utilise real-world data from various domains (Manlio Datasets), and the result are presented in Table 5. The same table includes the number of nodes N for each data set, the original number of layers L, and the number of layers after their hierarchical grouping \(L_G.\)

Table 5 Evaluation of layer hierarchical clustering in terms silhouette scores
Full size table

For the evaluation of the clusters created based on each of the dissimilarities of layers, the silhouette is utilized, which calculates how similar the data are within the cluster, as compared to other clusters. More specifically, for each layer, we calculate a silhouette score given by: \(S_l = (Dist_{out}-Dist_{in})/(max(Dist_{out}, Dist_{in}))\), where \(Dist_{out}\) is the distance of layer l with layers that are clustered in the closest cluster of layer l but not the same, and \(A_{in}\) is the intra cluster distance defined as the average distance to all other layers in the same cluster as l. For this distance we used GED, accounting for the structural changes. The results of Table 5 indicate that in most cases the quantum-inspired distance methods are forming clusters of higher silhouette values, thereby clustering the layers in more concise clusters.

4.4 Multiplex graph classification

In this section we utilize data collected by the Food and Agriculture Organization of the United Nations (FAO), that describe trade relationships among countries for 2010, available under (Manlio Datasets). This is a multiplex network consisting of 214 nodes, each representing a country, and 364 layers, each holding import/export relationships of a specific food product. For each node, the trade ego-network is extracted, and the classification problem is the prediction of the country’s development status, according to the composition of economies available from United Nations Conference on Trade and Development (UNCTADStat (as of June 2021)), using only the information of the ego-networks. The classification task is completed using all possible multiplex representations and distance measures listed above, while the F1 score is used as a measure of the performance of each classifier. In order to evaluate the ability of each representation to incorporate information from multiple layers, we repeat the classifications each time including a different number of layers, in decreasing size order. The results are reported in Figs. 5 and 6.

Fig. 5
figure 5

Bar plots, for different multiplex representations, of the change in F1 scores as more layers are included in the classification, and for different graph distance methods. The plots for the natural representation of Supra-adjacency, the most common representation of Average and the newly-introduced Noisy-OR are included, while for all other representations the plots are very similar

Full size image

The results of Fig. 5 focus on presenting how the F1 score changes as more layers are used for the classification, for different multiplex representations and distance measures. The plot indicates that most of the distances are able to achieve an accurate classification when two or more layers are used, with an F1 score that is increasing with the addition of more layers. The results are similar for all possible multiplex representations.

Fig. 6
figure 6

Comparison of F1 scores, for each of the distance measures, when different multiplex representations are used, and as more layers are incorporated in the calculation. Some distances are omitted for space but their results are discussed in the main text. The inserts focus on the use of only 1, to 5 layers

Full size image

As the number of the layers increases even more, the use of the supra-adjacency becomes impractical, however the monoplex aggregation techniques, with a smaller computational complexity, are able to achieve comparable accuracy scores, that continuously increases with the addition of more layers. Figure 6 illustrates the change of F1 score as even more layers are used for the classification. What is evident is that traditional methods, and the baselines, such as DELTACON, as well as quantum distances are increasing their accuracy with the addition of more layers. Out of the traditional methods, for this weighted dataset the edge-weight distance outperforms GED, while DELTACON outperforms the normalized Laplacian spectral distance and the resistance-perturbation distance. For the quantum measures, trace and Bures distances present the highest F1-scores, with Quantum JSDiv and Hellinger distances following closely. For many of the multiplex representations the accuracy is starting to drop after the addition of a given number of layers, defining a point at which the complexity of the problem increases, more evidently for the edge-weight and trace distances. The same behavior is observed for the Hellinger distance, while the Hilbert-Schmidt distance presents the lowest F1-score overall and the added complexity affects it the most.

The previously reported findings are specific to the FAO dataset and cannot be generalised for all possible applications. In general, the increased complexity of multiplex systems does not always guarantee an increase in the informative power of these structures. Layers are informative only if their incorporation into the network yields a more detailed description of the data and if they unveil structural patterns not otherwise present (Tiago 2015). If this is not the case, additional layers increase the complexity of the system, and as dictated by Occam’s razor, eventually obscure useful structural information. Such examples are seen in the classification results of Table 6, for two datasets available under (Manlio Datasets), the Krackhardt High-Tech company and the Lazega law firm.

Table 6 Average classification accuracy, using Supra-Adjacency representation in terms of F1 scores, when using one, combinations of two, or three layer
Full size table

In the Lazega law firm data set the three layers represent “advice”, “friendship”, and “co-work”. For the prediction of Practice, all 3 layers independently perform well, with “co-work” outperforming the other two, while use of combinations of these layers reduces the resulting accuracy. In the same data set, the prediction of node status behaves differently. In this case, as is intuitively expected, layers “advice”, and “friendship” appear to perform better than “co-work”, while their combination outperforms all other options. Notice that the monoplex aggregate representations provide similar results with F1 scores for the prediction of Practice (when using the Hellinger distance) ranging between 0.902, and 0.928.

It becomes evident that the benefit of utilization of additional layers depends on the system under study, and is beneficial only when the layers are informative, meaning that for classification purposes the layers need to be well correlated with the label and contain structural information not otherwise present. In most cases the quantum-inspired methods perform better than the baselines, and all multiplex representations are able to capture the underlying structure.

5 Discussion

In this work, measures for graph similarity inspired by information physics were introduced. These measures are well-established mathematical methods that incorporate the intrinsic structure of the entire network and have high interpretability. They can be used with both weighted and unweighted networks, are shown to effectively distinguish monoplex and multiplex networks, and capture graph intuitive aspects of structural changes, such as node centrality. In the case of multiplex networks, the noisy-OR aggregate monoplex is introduced and contrasted with aggregates previously proposed in the bibliography. We utilized artificial data to characterise the methods and real-world data sets to showcase that they can be effectively used on a variety of applications outperforming previously well-established and state-of-the-art methods.

Quantum and information physics undoubtedly compose a rich resource of mathematically established and interpretable measures, used for the evaluation or comparison of natural systems. Many of these measures have been translated into meaningful complex network tools, in this work and previous ones (Biamonte et al. 2019). For many other measures their graph-interpretation remains to be seen. For example, quantum error correction methods, typically used to remove environmental interactions and other forms of noise from quantum states, could inspire methods eliminating different forms of noise from complex systems and highlighting the information they carry. Another possible example would be measures of quantum entanglement such as the entropy of entanglement, quantum concurrency, or quantum negativity, which are typically used to measure how entangled two quantum states are, or how far these states are from achieving separability. For complex networks the quantum separability can be translated into network distinguishability. In addition, in the case of multiplex networks, quantum states separability can be seen as layer separability, a possible measure of the layers’ informative power.