Flight and engine control laws integration based on robust control and energy principles

Abstract

Integration aspects of flight and engine control laws in the context of the longitudinal motion control of commercial aircraft are the concern in this paper. The application of the entailing concepts in the scope of an energy-based multivariable control design is developed along with a case study using dedicated aircraft and engine models. It consists of an enhancement of the Total Energy Control System (TECS), which is modified with respect to the following aspects: (a) the inclusion of engine feedback variables to its core control loop, which is extended and improved with respect to the command interface from the throttle control channel, and (b) the use of a two degree of freedom linear control law based on independent multivariable gain scheduled feed-forward and feedback controllers. Additionally, a systematic design framework is proposed to account for the robustness of stability and performance of the control law in face of plant uncertainties, as well as to allow the evaluation and integration of engine restrictions already in the early design stages.

1 Introduction

This work presents the development of an integrated flight and engine control law architecture directed to the longitudinal motion control of a commercial aircraft. In conventional designs, the flight control system (FCS) uses the elevator to control variables such as load factor, flight path angle, angle of attack and attitude. It may also control airspeed, using the engine throttles or the elevators, depending on the task to be performed [1, 2]. Engine control is provided by the engine control system (ECS), which converts external demands into suitable engine demands. Usually, these control laws are initially designed as separate SISO systems and then integrated during several design stages. By the nature of this approach, either the FCS or the ECS are to face limitations imposed by this strategy, e.g., particular engine regimes can affect the control of the longitudinal motion or unreasonable FCS demands can affect the engine control. In such context, this paper proposes a control law architecture which allows for additional layers of integration between the FCS and the ECS. The underlying idea is to promote an integrated design of the core FCS and ECS control laws, encompassing also restrictions associated with engine limitations (surge, stall, etc). The proposal is to develop a systematic design framework which allows to account for these various trade-offs since early design stages and to facilitate the integration between these systems.

This approach is used to improve the Total energy control system (TECS), a well-known control law architecture, based on energy management principles, which was developed in the 1980’s as a joint effort between The Boeing Co. and NASA [1, 3]. This choice provides a suitable starting point for the development of this proposal because this architecture is already tailored with integrated features within the Automatic Flight Control System (AFCS), which provides not only coordinated control of the longitudinal motion (airspeed and attitude) but also eliminates functionality overlap of different operational modes as well as the need of a dedicated system to control airspeed, such as the Auto Throttle (AT). The TECS architecture advances the conventional approach providing a framework for the design of an integrated control law for the longitudinal motion and airspeed, adopting as control variables the elevators and thrust. Subsequent integration aspects of the TECS architecture are briefly discussed in the literature [4], but aspects related to the integration of FCS and ECS control laws are not approached. Other references in the literature [5,6,7,8,9] explore such aspects in the context of different architectures and focus on the computation of high order feedback controllers, which are reduced and partitioned among different subsystems.

This development explores an alternative to these works with an extension of the original TECS control law, denominated More Integrated TECS (MI-TECS), supported by three main pillars. In the first one, the original architecture is modified, its degree of integration is increased, and additional methods of analysis are developed. Explicit interactions of the FCS and the ECS can be incorporated in the design process and quantified. Examples of these are the integrated computation of the FCS and ECS control loop, accounting for aircraft level requirements and methods for control activity evaluation. The second one is the enhancement of the original approach based on a multivariable two degree of freedom control law. It retains the core aspects of coordinated control of airspeed and attitude, while it offers the possibility to treat performance and robustness aspects independently. Finally, the third one is the control law design and analysis methods, based on robust multivariable linear control law principles. This enhanced methodology allows the fulfillment of performance and stability requirements in the context of multivariable systems, in the presence of uncertainties and non-minimal phase MIMO systems.

1.1 Total energy control system review

Fig. 1

TECS control architecture, adapted from [10]

The TECS was successfully developed and tested in a joint effort of Boeing and NASA using a Boeing 737 test bed [11]. The TECS control law has also been applied to several fields, from military applications such as the Condor High Altitude Long Endurance autonomous UAV program [12], to general aviation [13, 14] and more recently in novel vehicle configurations related to urban air mobility initiatives [15, 16].

The TECS control law employs a multivariable approach based on an energy controller to provide longitudinal motion decoupling in terms of flight path angle and airspeed. The control variables correspond to the engine’s thrust setting and the elevator surfaces: the former is used to regulate the aircraft total energy and the latter is used to redistribute this energy between flight path and airspeed. Control coordination is achieved by regulating the error associated with the rate of the aircraft specific total energy ($\dot{E}$) and the rate of the aircraft specific total energy distribution ($\dot{L}$). The controller provides satisfactory decoupling when both variables have a similar error dynamic. These quantities are estimates obtained directly from the aircraft flight path angle and longitudinal acceleration, according to Eqs. 1 and 2.

$$\begin{aligned} \dot{E}= & {} \gamma + \frac{\dot{V}}{g} \end{aligned}$$

(1)

$$\begin{aligned} \dot{L}= & {} \gamma - \frac{\dot{V}}{g} \end{aligned}$$

(2)

Figure 1 shows an overview of the basic core TECS controllers. Basically, there are two PI controllers, one for each controlled variable ($\dot{E}$ and $\dot{L}$). The elevator control path is equipped with a stability augmentation system for short period motion improvement, based on inertial attitude feedback variables ($\theta$ and q). The engine control channel produces normalized thrust demands, as a function of the aircraft weight, which are transmitted to the engine control system. Automatic Flight Controls outer loops are defined in terms of the speed and path modes, such that normalized errors in terms of longitudinal acceleration and flight path angle are produced using proportional factors. These errors are subsequently transformed into energy variables using the relations provided by Eqs. 1 and 2. Improvements in the performance of the control law are obtained through dedicated feed-forward terms, which are not represented in the diagram.

1.2 Engine control system review

Fig. 2

Engine control system schematics

The Engine Control System architecture and design is extensively discussed in [17,18,19,20,21]. Despite the fact that the aircraft engine has an intrinsic complexity in terms of physical phenomena involved, assembly and operational constraints, for the purposes of control law design, a two spool turbofan engine behavior can be fairly approximated by a linear varying parameter second order system, in terms of $N_1$ and $N_2$, which correspond to the shaft speeds of the low and high pressure assembly, respectively. As a matter of fact, much of the complexity of the controller architecture comes from the need to add a protection layer to preserve the engine integrity in a vast range of operational conditions. In general, the engine control system is composed by two main components: the setpoint and the transient and protection limit controllers. This is exemplified in Fig. 2.

Usually, thrust is not directly measured by the Engine Control System. This limitation is overcome by providing indirect control either through regulation of the engine pressure ratio (EPR) or $N_1$. The setpoint controller has a built-in static schedule, which is a function of the flight condition and converts a given throttle demand to an adequate EPR or $N_1$ reference, that feeds an inner loop based on $N_1$ and $N_2$. This produces a fuel flow rate demand transmitted to the fuel flow valve actuator. The transient and protection limit controller is composed by a large set of SISO controllers and a nonlinear logic which constantly monitors the current fuel flow rate demand. The set of SISO controllers constantly updates the saturation limits of the fuel flow rate based on the current engine state and operating constraints (temperature, pressure, engine limits, etc). It has the authority not only to limit, but also to select the most suitable fuel flow rate demand among the setpoint and the various SISO controllers. This strategy employs a nonlinear min–max algorithm.

1.3 Flight and engine control laws integration

In a conventional development, the flight and engine control laws are designed independently. The 1980s and 1990s had some research effort regarding the integration of those systems, which led to a series of studies that vary from full state feedback techniques to robust control theory application of high order centralized feedback controllers, accounting for aircraft and engine dynamics [18]. Partitioning and model order reduction techniques have also been studied as a result. One of the main efforts on this behalf was the Integrated Flight Propulsion Control, developed by the Air Force Wright Aeronautical Laboratory, described at [5,6,7]. As a continuation of their works, NASA Lewis Research Center also developed a related program, denominated Integrated Methodology for Propulsion and Airframe Control, referenced by [8, 9]. Figure 3 provides the schematic used in the context of these works, in which high order feedback controllers are computed and then distributed in separate partitions allocated in each subsystem. This requires a decentralization scheme to compute equivalent distributed controllers.

Fig. 3

Integrated Methodology for Propulsion and Airframe Control Schematics, adapted from [8]

The approach used herein provides an alternative to these strategies. It differs from previous studies in the sense that it eliminates the need of a high order feedback controller and does not require a decentralization scheme, which facilitates the controller design, scheduling and parametrization. It also explores the harmonization of system interfaces, so that indirect thrust command is achieved along with the flight control laws. Additionally, the mutual effects of the airframe and engine dynamics are considered since early design stages, so that the engine transient and protection limit controller remains effective.

2 More integrated TECS architecture (MI-TECS)

The main aspect of the MI-TECS architecture is to replace the demand based on the fuel flow rate ($\dot{W_f}$) from the setpoint controller of the ECS, by a demand computed in the TECS controller, which results mostly from the energy balancing characteristics inherent from the TECS control law. In practice, the feedback loops from the setpoint controller ($N_1$, $N_2$ and $W_f$) are integrated with the existent feedback loops in the TECS algorithm ($\dot{E}$, $\dot{L}$, q and $\theta$), providing indirect thrust control, in the same fashion as in the set point controller, and eliminating the need to convert normalized thrust commands to $N_1$ or EPR references.

The original TECS is extended to account also for setpoint controller characteristics. The throttle control channel becomes responsible for determining the fuel flow rate demand required to balance the aircraft in terms of thrust and to provide decoupled and coordinated longitudinal motion. This extension follows the same principles from the original TECS proposal, with the advantage that the fuel flow rate demand can be readily combined with the transient and protection logics algorithm and there is no need for using a built-in static schedule for command conversion.

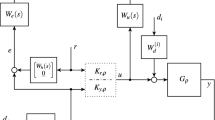
The general view of the MI-TECS architecture is summarized in Fig. 4. Besides the account for the engine open loop dynamics and the addition of feedback loops to the basic TECS core controller schematics, it adopts a two degree of freedom approach such that the feed-forward and feedback controllers are computed separately. This feature allows for better allocation of the design requirements. The feedback controller is used mainly to provide robustness to uncertainty, considered here in terms of multivariable systems, along with some command decoupling to a certain extent. The feed-forward controller is used mainly to allocate controller performance and to better shape the desired behavior of the integrated system in the time domain.

Fig. 4

More integrated TECS architecture

This schematic is referenced in the remainder of this work as the Kreisselmeier architecture, following [22]. It consists of a MIMO generalization of its original SISO proposal, which is motivated in [23]. This approach is preferred because, as stated in [24], in most cases a single degree of freedom might be insufficient to attain performance and robustness specifications, especially in the domain of multivariable control and highly integrated control systems. In that sense, this approach simplifies the allocation of robustness and performance requirements to the feedback and feed-forward controllers. This fact corroborates this choice, as better designs can be explored systematically.

In terms of design strategy, the control law gains are computed by systematic methods, using linear quadratic minimization techniques oriented towards linear multivariable robust control principles. An additional checkpoint is included in the design process to evaluate the TECS controller activity in terms of sensitivity of the engine variables against the set of controllers that compose the transient and protection logic algorithm. This is used to refine the gain computation in the linear domain and to identify possible weaknesses at early design stages as well as to validate a particular gain set.

2.1 MI-TECS design within a robust linear control framework

A variety of methods have been used to address the controller design in the TECS framework. Early references suggest possible enhancements to the original procedures, which were oriented by simple physics-based principles. The authors of [25] proposed the adoption of an eigenstructure assignment method to derive the control law gains systematically. An alternative approach is used by [10], which makes use of constrained parameter optimization. Alternatives that propose the use of robust control methods are suggested at [26] and [27]. Herein, yet an alternative design method is suggested, in which the I/O behavior associated with flight path and airspeed is governed by the ensemble of feed-forward controller and the target dynamics, and the robustness properties are governed by the feedback controller. This follows directly from the Kreisselmeier architecture, depicted in Fig. 4 for the MI-TECS controller.

2.1.1 Methodology for feed-forward controller computation

From Fig. 4, the transfer function matrix F(s) designates the feed-forward controller, D(s) designates the reference model associated with the target dynamics and G(s) designates the plant. The basic principles for the determination of F(s) and D(s) are derived from [22, 23]. Their main idea is that there exists F(s) such that it approximates the response of the closed loop system to D(s), without interfering in the properties of the feedback controller, making their computation independent to some extent. In the case of multivariable systems, this concept is valid as long as F(s) verifies the following identity: $F(s) = G^{+}(s)D(s)$, where $G^{+}(s) = G^T(GG^T)^{-1}$ is the pseudo-inverse of G(s) or simply its inverse in the case of square systems. Another requirement, which provides information of the stability properties of F(s), states that for F(s) to be stable, the desired dynamics must contain the multivariable zeros of G(s), respecting its magnitudes and directions. Herein, the system response is considered in terms of (V and $\gamma$), which results in a non-minimum phase system. These references provide little insight on practical means to treat non-minimum phase systems in the MIMO case and an extension of these methods is proposed using [28].

The task of shaping D(s) so that it contains multivariable zeros is not straightforward, because in the MIMO domain the concept of zeros from a transfer function matrix has different implications in comparison with the SISO scenario. These zeros impose immediate restrictions on the achievable D(s), so that it would be desirable to devise a method to minimize the impact of these restrictions. The work of [28] does not deal directly with this question, but its methodology, when combined with other methods from linear robust control theory, provides useful insights on how to handle the problem of determining a suitable D(s) in the context of the Kreisselmeier method. First, G(s) is decomposed according to a co-prime factorization [29], such that $G(s) = N(s)M(s)^{-1}$. The factor N(s) contains all RHP zeros of G(s). Let F(s) be rewritten according to this decomposition, assuming the system as square, as in $F(s) = M(s)N(s)^{-1}D(s)$. The transfer matrix $\tilde{D}(s)$ represents an additional transfer to be determined in the design process. By defining the relation $D(s) = N(s)\tilde{D}(s)$, F(s) can be computed as $F(s) = M(s)\tilde{D}(s)$.

The problem becomes the determination of the most suitable $\tilde{D}(s)$ to shape $N(s)\tilde{D}(s)$, so that D(s) yields the desired I/O behavior with good approximation, even in the face of the limitations imposed by N(s). In this framework, D(s), the reference model, is determined by design requirements, N(s) results from the co-prime factorization of the augmented plant and $\tilde{D}(s)$ is computed using linear quadratic techniques. Applying the method described in [28], let N(s) have a state space realization represented by $(A_1,B_1,C_1)$ and D(s) have the realization $(A_2,B_2,C_2)$; the system $(A_D,B_D,C_D)$ outlines a version of an augmented linear system composed by D(s) and N(s), augmented with integrators added to its outputs. The parameter $\varGamma$ is an arbitrary weighting matrix and $I_2$ is the identity matrix of second order. This formulation is described in Eq. 3.

$$\begin{aligned} \begin{array}{ccc} A_D = \left[ \begin{array}{lll} A_1 &{} 0 &{} 0 \\ 0 &{} A_2 &{} 0 \\ C_1 &{} C_2 &{} 0 \\ \end{array} \right] , &{} B_D = \left[ \begin{array}{c} B_1\\ 0 \\ 0 \\ \end{array} \right] , &{} C_D = \left[ \begin{array}{ccc} 0 &{} 0 &{} I_2\\ \end{array} \right] \\ \varGamma = \left[ \begin{array}{c} 0\\ B_2 \\ 0 \\ \end{array} \right]&\,&\end{array} \end{aligned}$$

(3)

The transfer $\tilde{D}(s)$ is computed as the solution of a stochastic linear quadratic regulator problem. The algebraic Riccati equation given in Eq. 4 is solved for $P_c$. Then, $K_c$ and $\tilde{D}(s)$ are computed according to Eqs. 5 and 6. The parameter $\rho$ controls the approximation quality of $N(s)\tilde{D}(s)$ with respect to D(s). Making $\rho$ too small leads to good approximations, but also might introduce higher control activity at higher frequency ranges, what could lead to poor interactions of the MI-TECS controller and the transient and protection limit controller. Therefore, this parameter is used to establish an adequate trade-off within the design strategy.

$$\begin{aligned}&A_D^TP_c + P_cA_D + C_D^TC_D - \frac{1}{\rho }P_cB_DB_D^TP_c = 0 \end{aligned}$$

(4)

$$\begin{aligned}&K_c = \frac{1}{\rho }B_D^TP_c \end{aligned}$$

(5)

$$\begin{aligned}&\tilde{D}(s) = K_c(sI-A_D+B_DK_c)^{-1}\varGamma \end{aligned}$$

(6)

2.1.2 Methodology for feedback controller computation

The feedback controller is computed according to a full state feedback methodology, adapted from [30] and [31]. Especially for the case of multivariable systems, this methodology allows for frequency domain shaping and simplifies the design in terms of choices related to stability margins, input control activity and disturbance rejection, without the need of high order feedback controllers. The general procedure for determining the controller involves the definition of a linear design model, which consists of an open loop model of the plant, augmented with actuators and integrators, with output weighting in the frequency domain. This model is used for solving a linear quadratic optimization problem and the matrices Q and R are used as additional parameters for balancing control activity and shaping the closed loop frequency response. The controller is computed according to the minimization of the cost function detailed in Eq. 7, where u is the input vector of the design model and z is the weighted output vector.

$$\begin{aligned} J = \int _{0}^{\infty } \left( z^T Q z + u^T R u\right) dt \end{aligned}$$

(7)

In the case of the MI-TECS design, the inputs are the control variables ($\dot{W_f}$ and $\delta _{elev}$) and the outputs are the weighted signals associated to the specific energy variables ($\dot{E}$ and $\dot{L}$), whose weights are shaping transfers, and engine variables ($T_{45}$ and $P_{s3}$), whose weights are scalars. These relations are depicted in Eq. 8.

$$\begin{aligned} z_i = \left\{ \begin{array}{cc} a_i\left( \dot{y_i}+2\zeta \omega _ny_i+\omega _n^2\int y_i dt\right) ,&{} \quad i \in [1,2] \\ a_i y_i, &{}\quad i \in [3,4] \end{array} \right. \end{aligned}$$

(8)

where $y_{1,2} = \left[ \dot{E}, \; \dot{L}\right]$ and $y_{3,4} = \left[ T_{45}, \; P_{s3}\right]$.

All the signals required for the computation of z are obtained from the linear design model, which is composed by the linear aircraft model, augmented with the engine linear model, elevator actuator and integrators associated with ($\dot{E}$ and $\dot{L}$). A linear similarity transformation is used to obtain the state space equations in terms of the variables used by the full state feedback controller. Then, the computed controller will match the desired configuration. Figure 5 provides the linear design model schematics.

Fig. 5

Linear design model

The framework used to shape the frequency domain response of the linear design model consists in the choice of the shaping transfers and the scalar parameters. By transforming the functions associated with $y_{1,2}$ to the frequency domain, these weights allow for setting target zeros at the complex plane located at $-\zeta \omega _n\pm j\omega _n\sqrt{1-\zeta ^2}$, so that they become attractors of the closed loop poles in the linear quadratic method [30]. The role of scalar parameters is to scale the frequency response of the design model in the presence of the engine variables. They introduce additional degrees of freedom used to balance the control activity relative to the engine.

2.1.3 Methodology for outer loop modes computation

In the original TECS formulation, a proportional controller is used to close the outer loop relative to the airspeed control, according to Fig. 1. Herein, the outer loop controller acts as an outer loop to the Kreisselmeier architecture. This controller provides a command in terms of airspeed that feeds F(s) and D(s), according to Fig. 4. The output commands ($V^{cmd}_{D}$ and $\gamma ^{cmd}_{D}$), computed from the target dynamics D(s), are converted into energy commands ($\dot{E}_{cmd}$ and $\dot{L}_{cmd}$), and fed to the feedback controller. This conversion uses Eqs. 1 and 2, where the acceleration command ($\dot{V}^{cmd}_{D}$) is computed using the washout filter described in Eq. 9.

$$\begin{aligned} \frac{\dot{V}^{cmd}_{D}}{V^{cmd}_{D}} = \frac{s}{10^{-2}s+1} \end{aligned}$$

(9)

The outer loop controller should have minimal interference with the prescribed reference model D(s). This arrangement makes the use of a simple proportional controller unfeasible, to preserve robustness and performance characteristics obtained through the design process. Therefore, a PI controller was used in this channel instead. This approach provided more consistent results in terms of steady state error rejection, albeit the additional complexity. It was designed such that the proportional and integral gains, $K_{VP}$ and $K_{VI}$, provide adequate disturbance rejection and tracking as well as it preserves the frequency domain response in comparison to D(s). This was accomplished by simple search methods. Besides that, the integral action serves to the purpose of removing small steady state tracking errors, as the tracking performance is already greatly improved by the two degree of freedom strategy. Also, as different flight conditions will attain the behavior prescribed by D(s) through gain scheduling of the core controller, there is no need to also schedule the outer loop mode controller. It was not necessary to add any loop closures to the path error mode, as an adequate performance and robustness was obtained with the proposed architecture.

2.2 Integrated analysis with engine transient and limit protection controllers

Fig. 6

Design flowchart for integrated analysis of MI-TECS and engine limit controllers

The general background theory related to the integrated analysis of engine limit controllers is covered in [17]. This analysis consists in the determination of possible switchings among the main setpoint controller and the limit controllers. The application of linear methods is very restricted, since this analysis constitutes a problem in the nonlinear domain, with multiple controller switchings, based on saturation logics with variable limits computed by dynamic controllers, and subject to the limit reference of each one. It is demonstrated that it is possible to apply frequency response-based methods using the initial and final value theorems to infer which controllers are active at initial and final times. The analysis becomes more complex when detection of intermediate switchings is sought. This work adapts and applies parts of these methods, proposing a specific strategy to address integration aspects. The purpose is to evaluate how far the MI-TECS controller is from switching to an engine limit controller.

The general idea is to use the engine limit variables explicitly in the MI-TECS controller design and to further evaluate their maximum allowable variation in the linear domain with respect to demands at the aircraft level, i.e., to the target speed and flight path. The main goal of this approach is to capture the impact of input demands at the aircraft level and translate them to engine limit levels. This allows to check the overall performance of the MI-TECS controller not only with respect to flight dynamics, but also regarding engine dynamics. Since this is an integrated control system, reinforced by the fact that the main engine control loop is integrated with the flight control algorithm, it is crucial to determine its capabilities and preserve engine operating aspects.

Given a main MI-TECS controller and individual engine limit controllers, they are confronted using integrated linear simulations. First, using fixed speed and flight path demands as inputs, the maximum steady state value for each limit variable is determined with the main controller always active. These are used as a first guess reference settings for each limit controller and a transient analysis of the fuel flow rate derivative is conducted. A heuristic search algorithm is used to re-adjust the reference values such that no switching occurs, i.e., $\dot{W_f}^{TECS} \le \dot{W_{f_i}}^{Lim}$, where each i designates a limit controller. The further the computed limits are from steady state values, the more aggressive the control action from the main controller is in terms of its transient response.

This procedure is intended to check the controller performance against transient fuel flow rate demands. It contributes to establish grounds for comparison of different linear designs with respect to its proneness to activating the limit controllers. If all previous design requirements are satisfied, it is reasonable to trade off input control activity for a more balanced design with respect to engine limits. This is performed by adjustment of the scalar weights of engine variables during linear control design. The integrated design is also verified using nonlinear simulations including representative models of the aircraft and engine. The flowchart in Fig. 6 summarizes the proposed methodology.

In this modified strategy, engine limit controller restrictions are part of the design process so that high level requirements, related with the controller performance and robustness at the aircraft level, are also considered. This extends the original purpose of the TECS control law, so that it can be used to assess the influence of the main controller with regard to the engine limits and vice-versa, within a unified framework.

3 Case study

This section exemplifies the application of the MI-TECS architecture and methodology for a model representative of a commercial aircraft. It is assumed that both aircraft and engine can be treated as systems with smooth dynamics such that the linearization over several flight conditions is an adequate strategy to deal with the nonlinearities related to the aerodynamic and engine modeling. In that sense, the core feedback and feed-forward controllers are gain scheduled as a function of the flight condition, constituting linear parameter varying controllers.

The results presented comprise simulations in the linear and nonlinear domain. The models are derived from a dedicated nonlinear model of the aircraft and another for the engine dynamics, which were integrated, along with the MI-TECS controller, to perform the nonlinear simulations. This section covers a brief description of these models and the formulation used for each in the context of the control design framework. Also, it covers details of requirements used for controller synthesis and analysis, with practical examples of its applications.

3.1 Aircraft, engine and elevator models

The model used for the aircraft corresponds to a six degree of freedom, nonlinear and non proprietary Boeing 747 Simulink^® simulation package, described in [32, 33]. Detailed information and modeling data is presented in [34, 35]. The formulation of the state space models of the longitudinal dynamics is written on the aircraft stability axis. Recalling Eqs. 1 and 2 for the definition of energy variables, combined with the fact that the equation for $\dot{V}$ is provided from the state space formulation, the output vector can be transformed to represent energy outputs. The system state, input and output vectors are defined as in Eqs. 10, 11 and 12.

$$\begin{aligned} x= & {} \left[ V \quad \alpha \quad q \quad \theta \right] ^T \end{aligned}$$

(10)

$$\begin{aligned} u= & {} \left[ T \quad \delta _{elev} \right] ^T \end{aligned}$$

(11)

$$\begin{aligned} y= & {} \left[ \dot{E} \quad \dot{L} \right] ^T \end{aligned}$$

(12)

The engine model corresponds to a non proprietary model of a Pratt & Whitney JT9D two spool turbofan engine available in the Simulink^® package provided by the Toolbox for the Modeling and Analysis of Thermodynamic Systems (T-MATS) [36]. In particular, the engine input command is modeled in terms of the fuel to air ratio. For this case study, $W_f$ designates this quantity, which is directly related to the fuel flow rate through a factor of proportionality. Therefore, previous assumptions are retained.

Due to the fact the engine linear models are not strictly proper and that it is desirable to compute commands in terms of $\dot{W_f}$, a fuel metering valve actuator (FMV) model and an input integrator are added to the engine linear dynamics. The actuator is modelled as a second order low-pass filter with unitary damping and natural frequency equal to $18.7\,rad/s$, as in [17]. The augmented engine linear model is represented by five states variables: one from the appended integrator, two of them related to the engine dynamics and the remainder, to the actuation valve, according to Eqs. 13, 14 and 15.

$$\begin{aligned} x_{eng}= & {} \left[ W_f \quad N_1 \quad N_2 \quad x_{1fmv} \quad x_{2fmv}\right] ^T \end{aligned}$$

(13)

$$\begin{aligned} u_{eng}= & {} \left[ \dot{W_f} \right] \end{aligned}$$

(14)

$$\begin{aligned} y_{eng}= & {} \left[ T \quad T_{45} \quad P_{s3}\right] ^T \end{aligned}$$

(15)

The elevator actuator model consists of a simple low-pass first order filter, with cutoff frequency of $20\,rad/s$.

3.2 Design envelope

The choice of linearization conditions is based on FAA statistical operational report for the Boeing 747 [37], considering the practical maximum operating Mach number for a given altitude. The conditions for this case study vary in the range of 10,000–25,000 ft and 0.4 to 0.7 Mach number, with flaps retracted. Figure 7 depicts all conditions for which the linear models were generated. As for the choice of weight and balance points, most of the linear models used for design are generated in the range of 200,000–250,000 kg, at mid to aft CGs. This is driven by the fact that, in general, the gain set obtained for this region proved to be adequate for heavier weights and forward CGs, eliminating the need to provide any schedule with these variables. Figure 8a and 8b shows the open loop pole-zero map for aircraft and engine linear models obtained in each design condition. Actuator dynamics (elevator and fuel metering valve) are not considered for being much faster than engine and aircraft dynamics.

Fig. 7

Design envelope

Fig. 8

Design envelope and open loop pole-zero map for aircraft and engine models

3.3 Design requirements

The design requirements are given in time and frequency domains. The requirements in the time domain specify the aircraft closed loop response in terms of airspeed and flight path angle tracking performances, whereas the requirements in the frequency domain are more general and specify properties related not only to the controller performance, such as steady state error and disturbance rejection, but also address stability and robustness to model uncertainty.

3.3.1 Time domain requirements

In terms of time domain requirements, the closed loop step response is used as a measure of tracking performance. The requirements for speed and flight path angle responses are derived from [38], which establishes a benchmark for robust control design in the context of an automatic landing system of a civil aircraft model. It is proposed a maximum rise time of $12$ s and a settling time smaller than $45$ s, with no overshoots. In particular, the closed loop response of the aircraft shall also provide a decoupled and coordinated response, as in the original TECS formulation.

3.3.2 Frequency domain requirements

The frequency domain requirements are regarded from the perspective of two main aspects, stability and performance, each of them considered for nominal and uncertain conditions, in the context of MIMO controller design. The uncertain conditions are modeled as a lumped uncertainty appended to the plant, which increases the uncertainty level of the model according to the frequency range, as suggested in [24]. This is represented by the transfer whose general form is given in Eq. 16. The rationale is that there is less uncertainty in the low frequency range, i.e., between $10$ to $20\%$, adding up to $200\%$ beyond a certain cutoff frequency defined by $\tau ^{-1}$, in higher frequencies. This uncertainty modeling is used as a basis for the robustness analysis, either for performance or stability.

$$\begin{aligned} W_{I}(s) = \frac{\tau s + r_0}{(\tau /r_{\infty })s+1} \end{aligned}$$

(16)

Following the Kreisselmeier architecture, stability and robustness properties are ensured by the feedback controller. Stability in nominal conditions is verified by simply mapping the poles of the closed loop system. As for uncertain conditions, it is required that $\mu (T)< W_I^{-1}$, where $\mu$ is the structured singular value of the complementary sensitivity transfer function T(s). This criterion is adopted for the complementary sensitivity transfer function obtained at system inputs $T_i(s)$ and feedback sensors $T_s(s)$, combining the approaches adopted by [24] and [30]. The lumped uncertainty parameters adopted in each case of the analysis regarding $\mu _{T_i}$ and $\mu _{T_s}$ are described according to Table 1.

Table 1 Uncertainty model parametrization

Performance requirements in the frequency domain are established based in a boundary applied to the singular values of the sensitivity transfer S(s) of the closed loop system, considering both the feedback and feed-forward controllers. Primarily, this boundary is used to assess performance under nominal conditions. This boundary has the shape described by Eq. 17. Each parameter is associated with a specific property: $\omega _{B}$ ensures adequate bandwidth, M is related to limiting the peak values of S(s) and A is associated with the steady state tracking error. For adequate disturbance rejection, a cutoff frequency in the range of $0.1\,rad/s$ to $1\,rad/s$ is considered an adequate target, therefore $\omega _{B} = 0.1rad/s$. Peak values are limited to $M = 2$ and $A = 10^{-6}$, where A is kept sufficiently small to improve numerical conditioning.

$$\begin{aligned} W_{P}(s) = \frac{M^{-1}s + \omega _{B}}{s+\omega _{B}A} = \frac{0.5s + 0.1}{s + 10^{-7}} \end{aligned}$$

(17)

Fig. 9

Generalized closed loop plant

In multivariable systems, nominal performance and robust stability do not ensure robust performance, motivating a dedicated analysis. The robust performance is considered with the goal of determining the tightest uncertainty boundary in the form of Eq. 16, such that S(s) verifies the performance boundary from Eq. 17. This criterion recurs to the closed loop generalized plant H(s), ensuring that $\mu (H) < 1$. The generalized plant is illustrated in Fig. 9; signals w and z correspond to exogenous inputs (command references) and outputs (weighted error with respect to input command) and $\varDelta$ represents structured uncertainty. An uncertainty boundary of the form given by Eq. 16 is considered at input level, i.e., between the controller block and the plant, with its parametrization provided in Table 1.

3.4 Feedback controller synthesis

The linear design model accounts for the linear aircraft, engine, elevator actuation and, through a similarity transformation, all variables used in the feedback control loop are represented as state variables. Integrators are also appended to the state space formulation. The output vector is appended with engine variables $T_{45}$ and $P_{s3}$, to account for components from the engine transient and limit protection algorithm in the design model. The state, inputs and outputs variables are given in Eqs. 18 to 20. Although included in the formulation, some of the feedback paths associated with actuator states are neglected without undermining the design. In particular, the paths $\delta _{elev}$, $x_{1fmv}$ and $x_{2fmv}$ are disregarded, since these are associated with faster actuator dynamics. The feedback paths related to $N_1$, $N_2$ and $W_f$ are retained and act as the engine setpoint controller in the MI-TECS architecture.

$$\begin{aligned} x_{dsn}= \;& {} \left[ \dot{E} \ \dot{L} \ q \ \theta \ W_f \ N_1 \ N_2 \ x_{1fmv} \ x_{2fmv} \ \ldots \right. \end{aligned}$$

(18)

$$\begin{aligned}&\left. \ldots \ x_{elev} \ \int \dot{E} \ \int \dot{L} \right] ^T \nonumber \\ u_{dsn}= & {} \left[ \dot{W}_f \ \delta ^{cmd}_{elev}\right] ^T \end{aligned}$$

(19)

$$\begin{aligned} y_{dsn}= \;& {} \left[ \dot{E} \ \dot{L} \ T_{45} \ P_{s3}\right] ^T \end{aligned}$$

(20)

Recalling Fig. 5, the selection of target zeros has an influence on the I/O transfer relations of the design model and in the cost function. The role of the frequency domain weight is to shape the open loop linear design model, so to facilitate the choice of Q and R. Energy variables are shaped by a frequency domain weight and variables $T_{45}$ and $P_{s3}$ are associated with scalar weights. Variables $N_1$, $N_2$ and $W_f$ are engine variables already accounted in the feedback loop. The frequency domain weight is selected equally on both control channels, represented by a transfer function with $\omega _n = 1\,rad/s$ and $\zeta = 0.8$, which adds two complex target zeros located at $-0.8 \pm 0.6j$. An important remark is that the selection is not influenced by the addition of scalar weighted engine variables. Due to the multivariable nature of the problem, the resulting matrix transfer function of the design model becomes non-square, in such a way that zeros from the original dynamics are eliminated and only the target zeros remain. This results from the definition of zeros in multivariable systems: by changing its dimensions with the addition of new elements to the transfer function matrix, it is possible to influence zero locations, especially when dealing with non-square systems. Figure 10 a shows the frequency response of the open loop scaled aircraft model with engine, actuators and integrators and the linear design model augmented with the frequency domain weighting function. Figure 10b shows the pole-zero map of the same models before and after the addition of target zeros. This considers a specific design condition at 20,000 ft and Mach 0.6 and illustrates the possible trade-offs involved in this parametrization.

Fig. 10

Open loop frequency domain response considering the design point at 20,000 ft and Mach 0.6

The weighting matrices Q and R are selected as $Q = diag(1,\;1,\;0.01,\;0.01)$ and $R = diag(1,\;1)$. The main trade-off for this choice is to provide an adequate behavior on the frequency domain as well as preserving I/O activity. Given the uncertainty model, a robustness barrier is defined for the loop transfer function L(s) as Eq. 16 is simplified on the low frequency spectrum, where $W_{I}^{-1}(\omega )>> 1$. The reference design criterion for robustness is provided by Eq. 21:

$$\begin{aligned} L(s) < \frac{1}{W_{I}^{Input}}, \;W_{I}^{Input}(s) \approx \frac{0.5s}{0.25s + 1} \end{aligned}$$

(21)

The resulting loop transfer for this design is depicted on Fig. 11a, together with the target robustness barrier. The closed loop poles in the feedback portion are presented in Fig. 11b, showing adequate damping, close to 0.7 for all poles. The closed loop system is stable and the RHP zeros remain unchanged, as expected.

Fig. 11

Closed loop frequency domain response considering all design conditions

3.5 Feed-forward and outer loop speed mode controller synthesis

The target dynamics is selected according to Eq. 22, where the cross-terms are set to zero to comply with the decoupling requirement, and the diagonal terms corresponds to a second order transfer function with $\zeta = 1$ and $\omega _n = 0.4\,rad/s$, such that each channel is capable of providing a maximum rise time $t_r$ from $10\%$ to $90\%$ of around 9s, with no overshoots.

$$\begin{aligned} D_T(s) = diag\left( \begin{array}{ccc} \frac{0.16}{s^2 + 0.8s +0.16}&,&\frac{0.16}{s^2 + 0.8s +0.16} \end{array} \right) \end{aligned}$$

(22)

For the feed-forward controller synthesis, the plant model must be rewritten in terms of the outputs of the target function, (V and $\gamma$). It shall account for the presence of the inner feedback loops, except for the appended integrators, which are not part of the plant. From $D_T(s)$ requirement, proceeding with the computation of the co-prime factorization, and adopting $\rho = 10^{-2}$, the achieved target model D(s) is plotted against the desired target $D_T(s)$ on Fig. 12a, for all design conditions, confirming that to a certain degree limitations are imposed to the feed-forward design in terms of cross-coupling between command channels.

Fig. 12

Linear simulations time history responses for desired and achieved target dynamics

The last step consists in computing the airspeed outer loop PI controller to match the system response with respect to D(s). Figure 12b shows the system output response in the linear domain in either situations, to demonstrate that the outer loop speed mode has a minimal influence to the transitory response of the system. Furthermore, as the inner loop already accounts for gain scheduling as a function of the flight envelope, adjustments in this portion of the design are minimized and the same gain set is used throughout the envelope. Since in the linear domain the basic controller scheme is capable of providing speed errors near zero, its action becomes more noticeable in the nonlinear simulations for removing small steady state errors.

3.6 Interaction with limit controllers

The limit controllers are computed separately from the MI-TECS design using the method suggested by [17]. It employs a simple linear quadratic technique, such that each limit controller maintains the controlled variable within a fixed reference limit, with little overshoot and rise time of approximately $4\,s$. Then, using the heuristic procedure proposed in Fig. 6, lower boundaries for each limit variable can be determined for a given controller configuration. Table 2 compares three gain sets computed for the same design point, changing only weights of the matrices Q and R. The first design corresponds to the one adopted and previously demonstrated. The second one, has the weight values relative to outputs $T_{45}$ and $P_{s3}$ increased by one order of magnitude, yielding a controller with less feedback activity at the engine control channel. Finally, the third design augments the same weights by two orders of magnitude, yielding even less feedback activity at this control channel.

Table 2 Engine limits comparison for linear design

Thus, the method allows a relative comparison of the impact that the choice of the gain set of the MI-TECS controller has on engine limit variables, even without strict requirements on these limits. It provides the designer with a quantitative insight into how engine transient and protection limiting might be influenced, helping to balance controller activity and allowing the identification of potential limitations and issues in early design stages.

Fig. 13

Multivariable robust stability criteria

Fig. 14

Multivariable robust performance criteria

Fig. 15

Time history of speed and flight path angle for nonlinear simulations

Fig. 16

Time history of energy variables for nonlinear simulations

3.7 Simulation results

The frequency domain analysis related to the two degree of freedom controller is presented. This analysis was conducted using a total of 190 conditions. From the basic design points depicted in Fig. 7, additional conditions were added by varying weight and balance within the operational range for retracted flaps. The center of gravity (CG) variation was $15\%MAC$ to $30\%MAC$ and the weight variation was $200,000\;kg$ to $320,000\;kg$. Overall, the design requirements are verified, with adequate robustness and performance properties, as illustrated in Figs. 13 and 14. It is emphasized that the controller is gain scheduled as a function of the atmospheric condition, but not with weight and CG.

Fig. 17

Time history of fuel to air ratio and elevator deflection for nonlinear simulations

Fig. 18

Time history of engine shaft speeds $N_1$ and $N_2$ for nonlinear simulations

Fig. 19

Time history of engine pressure and temperature for nonlinear simulations

Time histories of nonlinear simulations are presented in Figs. 15, 16, 17,18, 19, obtained with the implementation of the MI-TECS controller and evaluated for a condition trimmed at 20, 000 ft and Mach number equal to 0.6. Figures to the left side are related to an input demand on speed and the figures to the right, to an input demand on flight path angle. Figure 15 demonstrates that the resulting two degree of freedom controller is capable of tracking the input demands according to the reference model and also there is adequate decoupling between speed and flight path angle responses.

Adequate tracking is also achieved for the energy variables $\dot{E}$ and $\dot{L}$, demonstrating that the adopted two degree of freedom strategy is indeed effective, as presented in Fig. 16. Figure 17 shows that the engine and elevator commands have adequate excursions, attaining new steady state values compatible with the input demands. Finally, the engine variables excursion is checked against its operating limits. All of them remain within its boundaries, as presented in Fig. 18 for the shaft speeds, and in Fig. 19 for pressure and temperature.

4 Conclusion

This paper proposed an integrated architecture and a design framework for flight and engine control laws. Energy and linear robust control principles were applied to the development of the MI-TECS architecture. The features from the original TECS control law are extended to support indirect thrust control, besides coordinated and decoupled longitudinal motion as in the original concept. This is accomplished by changing the original controller interface to use the fuel flow rate instead of thrust commands and adding feedback loops typical from the setpoint controller of the ECS into the core TECS control law. The controller architecture is also modified to use a two degree of freedom approach with independent feedback and feed-forward controllers, following the principles from Kreisselmeier’s work, considered herein in the context of a multivariable control system.

A systematic methodology is proposed for the controller design, which covers from stability and performance requirements, for nominal design conditions or in the presence of uncertainty, to integration aspects particular of engine control system designs, considering engine operation restrictions. This methodology results from the combination of several operations from linear robust control system theory, some of them extended or modified, with special attention to the procedure used for the computation of the feed-forward controller for multivariable non-minimum phases systems and to the heuristic approach to evaluate the MI-TECS control activity against the engine limit and transient controllers. In a comprehensive case study, each step of the design is presented in detail, along with a set of simulations in the frequency and time domains, using linear and nonlinear models, respectively, representative of a commercial aircraft with a two spool turbofan engine.