1 Introduction

The structures are exposed to the dynamic type of loading during their service, which may lead to severe vibrations. Laminated plates with cut-outs are extensively used in automobiles, aircraft, and space vehicles. Holes of different shapes—circular, square, rectangular, elliptical are used in plates. They serve the purpose of weight reduction, altering resonant frequency, inspection, maintenance, venting, and attachment to other units, for the cables to pass through and so on. It is needed at the bottom plate for passage of liquid in liquid-retaining structures. These structures are subjected to undesirable vibration, deflection, and rotation during their service life. The presence of cut-outs adds to the complexity of the analysis and design of such structures. The present study deals with the free vibration of isotropic and laminated composite plates with a central cut-out. The exact solutions to free vibration problems of plates are mathematically involved and in many complicated cases not available. A great need exists for an elaborate study on the free vibration of laminated plates with central cut-outs and the present work is one attempt in this direction.

The earlier studies on free vibration characteristics of plates are those of Rajamani et al. [1, 2] investigated the effects of central circular holes and square cut-outs on the natural frequencies of the plate under two end conditions—simply supported and clamped–clamped were investigated. The large amplitude vibration of anisotropic rectangular laminated composite plates with cut-outs by varying side-to-thickness ratio, aspect ratio, and plate side to cut-out side ratio and observed the variation in nature of vibration, Reddy [3]. The effect of cut-outs and double square cut-outs on simply supported orthotropic rectangular composite plates was investigated using Rayleigh principle by Lee et al. [4] to predict the natural frequencies, fundamental modes and higher modes of the composite plates. The finite element method was adopted by Bicos et al. [5] to describe the free damped vibrations of plates and shells. The studies were extended to study the natural frequencies, mode shapes and damping factors of rectangular plates, cylinders and cylindrical panels under different boundary with cut-outs and without cut-outs. The natural frequencies of vibration of the laminated composite plate with a central circular hole using hybrid-stress finite element were determined by Ramakrishna et al. [6]. The effects of fiber orientation, width-to-thickness ratio, aspect ratio and hole size on the first four natural frequencies were studied and reported. Chai Gin Boay [7] used finite element method to study free vibration of laminated composite plates containing a central circular hole considering the aspect ratio and hole size as variables and material properties and stacking sequence were kept constant. Sivakumar et al. [8] investigated the free vibration of laminated composite plates with cut-outs undergoing large oscillations using Ritz finite element model and obtained results for plates with cut-outs of various geometries—circle, square, rectangular and ellipse in the large amplitude range.

Liew et al. [9] developed a Ritz procedure to extract the frequencies and mode shapes of plates with discontinuities in cross-section. Myung Jo Jhung et al. [10] developed an analytical method, based on finite Fourier–Bessel series expansion and Rayleigh–Ritz method to analyze the free vibration of the circular plate with an eccentric hole. The effects of hole size on the vibration characteristics of the plate were studied and results are reported. Ovesy and Fazilati [11] employed the third-order shear deformation theory for buckling and free vibration finite strip analysis of composite plates with cut-out based on two different modeling approaches (semi-analytical and spline method). Sivakumar et al. [12] investigated the free vibration responses of composite plates with an elliptical cut-out based on FSDT and using a genetic algorithm. Kumar and Shrivastava [13] employed a finite element formulation based on HSDT and Hamilton’s principle to study the free vibration responses of thick square composite plates having a central rectangular cut-out, with and without the presence of a delamination around the cut-out. Sahu and Datta [14] studied the dynamic stability of curved panels with cut-outs in the framework of FSDT and used the Bolotin’s method. Ju et al. [15] employed a finite element approach to analyze the free vibration behavior of square and circular composite plates with delaminations around internal cut-outs. Liew et al. [16] analyzed the free vibration of rectangular plates with internal discontinuities due to central cut-outs using the discrete Ritz method.

Dhanunjaya Rao and Sivaji Babu [17] studied the modal analysis of thin FRP skew-symmetric angle-ply laminate with circular cut-out in the framework of CLT. Krishna Reddy and Palaninathan [18] analyzed the free vibration responses of laminated skew plates using a general high-precision triangular plate bending finite element. Free vibration analysis using a nine-noded isoparametric plate element in conjunction with first-order shear deformation theory was carried out on both thick and thin rectangular plates with central cut-out [19], composite laminated plates with central cut-out [20] and a special focus was given on effect of rotary inertia on the natural frequencies of rectangular plates was investigated [21].

Srinivasa, Suresh and Prema Kumar [22,23,24,25,26,27] studied the free vibration response of skew plates and cylindrical skew panels using experimental methods and finite element method. The effects of the skew angle and aspect ratio on the natural frequencies of isotropic skew plates were studied. The effects of the skew angle, aspect ratio, fiber orientation angle and laminate sequence (keeping the number of layers constant) on the natural frequencies of anti-symmetric composite laminates have been presented.

Most of the literature dealt with either the analytical or numerical method for the free vibration analysis of isotropic and laminated composite plates with cut-out. There were very few publications on experimental approach. The present paper is an attempt to address this aspect at least in a partial manner. The present paper adopts the experimental method to aid to fill the gap in the literature and uses the analytical and finite element results for the validation for both the isotropic and laminated composite plates with cut-out for various parameters.

2 Materials and methods

2.1 Test specimens used in experimental studies

In this study, isotropic plates made of Aluminum 7075-T6 were used. The material was supplied by the Rio Tinto Alcan Inc. The material properties of the Aluminum 7075-T6 are: E = 71.7 GPa, µ = 0.33 and ρ = 2800 kg/m3 and these data were supplied by the manufacturer. The values provided by the manufacturer were verified by conducting experiments as per ASTM standards. The experimental values obtained were quite close to those supplied by the manufacturer and hence the values given by the manufacturer were adopted. The isotropic assumption was verified by conducting experiments.

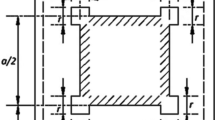
The laminated composite plate specimens were fabricated by hand lay-up technique using unidirectional Glass fibers, Epoxy-556 Resin and the Hardener (HY951) supplied by Ciba-Geigy India Ltd. The laminated composites were prepared according to ASTM standards ASTM D 5687/D5687M-95 [28]. A flat, rigid plywood platform is selected. A plastic sheet (mold releasing) was kept on plywood platform is selected and cleaned thoroughly using acetone to remove any dust or dirt. Then a thin film of polyvinyl alcohol is applied as a releasing agent. After fabrication, the entire surface was covered with a thin layer of releasing film, whose main purpose was to provide a smooth external surface and to protect the fibers from direct exposure to the environment. At a time one flat plate of 500 × 500 mm was cast and it was later cut into the required specimen dimensions. Figure 1 shows a laminated composite plate after preparation with the details of laminate stacking sequences used in the present study.

Fig. 1
figure 1

Fabrication and laminate stacking sequence

Full size image

For laminated glass/epoxy composite plates the material constants E1 and E2 were evaluated experimentally using INSTRON 1195 universal testing machine at Central Institute of Plastics Engineering and Technology (CIPET), Mysore, as per ASTM Standard D 3039/D 3039M [29]. The density of the composite is evaluated as per ASTM D 3171 [30].

The average of three experimental determinations was adopted. For the determination of Poisson’s ratio υ12, two strain gauges were bonded to the specimen, one in the direction of the loading and the other at right angles to it. The strains were measured in longitudinal and transverse directions using the strain indicator as per ASTM Standard ASTM E132–04 [31].

The ratio of transverse-to-longitudinal strain gives the Poisson’s ratio within the elastic range. The average of three experimental determinations was adopted. The shear modulus G12 was computed using the expression available in Jones [32].

The composite material properties used in the present study are:

$${E_1}=38.07\;{\text{GPa}},\;\;{E_2}=8.1\;{\text{GPa}},\;\;{G_{12}}=3.05\;{\text{GPa}},\;\;{\upsilon _{12}}=0.22,\;\;{\rho _1}=2200\;{\text{kg}}/{{\text{m}}^3}.$$

2.2 Methods

2.2.1 Experimental method

The experimental set-ups are shown in Fig. 2. First, the test specimen was placed in the fixture with two opposite edges fully clamped and the remaining two edges completely free. The piezoelectric accelerometer was directly mounted on the test specimen at the geometric center using an adhesive. The accelerometer was then connected to a signal conditioning unit (fast Fourier transform analyzer), where the signal goes through the charge amplifier and an analog-to-digital converter (ADC). The specimen was excited at a selected point by means of an impact hammer. Five trials were made and the average value of the frequency response function (FRF) was input to the computer through a USB port. Sufficient precautions were taken for ensuring that the strike of the impact hammer was normal to the surface of the specimen. The pulse lab software accompanying the equipment was used for recording the signals directly in the memory of the computer. The signal was then read and processed to extract different features including frequencies. The frequencies were measured by moving the cursor to the peaks of the FRF. Five separate experimental determinations were done for the natural frequency of each specimen and then the average value was adopted.

Fig. 2
figure 2

Experimental setup

Full size image

2.2.2 Finite element analysis

Finite element method was employed to obtain the natural frequencies using MSC/NASTRAN software.

In normal modal analysis, there is no applied load and the structure has no damping properties. The equation of motion is of the form:

$$\left[ K \right]\{ \delta \} + [M]\{ \delta \} =0,$$
(1)

where [K] and [M] are the stiffness and mass matrices representing the elastic and inertial properties of the structure, respectively. These system matrices are generated automatically by MSC/NASTRAN, based on the geometry and properties of the FE model.

Assuming a harmonic solution, Eq. (1) reduces to an eigenvalue problem. The governing differential equation for linear free vibration analysis is given by,

$$\left[ {\left[ K \right] - {\lambda _i}\left[ M \right]} \right]\{ {\phi _I}\} =0,$$
(2)

where {\(\phi\)} is the eigenvector (or mode shape) corresponding to the eigenvalue \(\lambda\) (the natural or characteristic frequency). For each eigenvalue, which is proportional to a natural frequency, there is a corresponding eigenvector or mode shape. The eigenvalues are related to the natural frequencies as follows:

$${f_i}=\sqrt {\lambda {}_{i}/2\pi .}$$
(3)

Eigenanalysis is carried out to evaluate the eigenvalue \(\lambda\) and associated mode shapes. Lanczos method was used in the present study as it combines the best features of the other methods and computes accurate eigenvalues and eigenvectors (MSC/NASTRAN Software, User Reference Manual [33]).

3 Convergence studies and validation

3.1 Convergence studies

The analyses of isotropic and laminated composite plates were performed using CQUAD4 and CQUAD8 elements. The CQUAD4 element is a four-node plate element having 6 degrees of freedom/node,

$${\text{translational }}(u,v,w)\;\;{\text{and}}\;\;{\text{rotational }}({\theta _x},{\theta _y},{\theta _z}).$$

The CQUAD8 element is an eight-node isoparametric shell element having 6 degrees of freedom/node [\({\text{translational}}(u,v,w)\;\;{\text{and}}\;\;{\text{rotational}}({\theta _x},{\theta _y},{\theta _z})\)]. The formulation of the CQUAD4 and CQUAD8 elements are based on the Mindlin–Reissner shell theory and both the elements take into account the shear deformations. Figures 3 and 4 show the CQUAD4 and CQUAD8 element geometry and coordinate system. Figure 5 shows the finite element meshes of plate without cut-out and with cut-outs.

Fig. 3
figure 3

CQUAD4 element geometry and coordinate system

Full size image
Fig. 4
figure 4

CQUAD8 element geometry and coordinate system

Full size image
Fig. 5
figure 5

Finite element models

Full size image

The convergence study has been performed on clamped-free–clamped-free (C-F–C-F) plates having an aspect ratio (a/b) of 1.0 and length-to-thickness ratio (a/t) of 50 considering with and without cut-outs for isotropic plates using CQUAD4 (four-node plate element) and CQUAD8 (eight-node isoparametric curved shell element) elements of MSC/NASTRAN. The convergence details are furnished in Table 1.

Table 1 Convergence study details for natural frequency of C-F–C-F isotropic plates (a/b = 1 and a/t = 50)
Full size table

3.2 Validation

Non-dimensional frequency coefficients for simply supported square plate with a square cut-out at the center (E = 200 GPa, µ = 0.3, ρ = 8000 kg/m3a/b = 1 d/a = 0.1 and a/t = 100) are presented Table 2. The non-dimensional frequency solutions are checked by comparing the results with that of Haung et al. [34]; Ali et al. [35]. In a similar manner the validation study has been extended to composite materials by considering the free vibration response of a simply supported three-layered carbon/epoxy square laminate with a central elliptical hole. The principal material properties of the layers are:

Table 2 Non-dimensional fundamental frequencies of simply supported square plate with a square hole at the center (a/b = 1, a/t = 100)
Full size table
$${E_1}=172\;{\text{GPa}},\;\;{E_2}=7.0\;{\text{GPa}},\;\;{G_{12}}=3.5\;{\text{GPa}}\;\;{\text{and}}\;\;{\nu _{12}}=0.25\;\;{\text{and}}\;\;\rho =1600\;{\text{kg}}/{{\text{m}}^3}.$$

The non-dimensional frequency coefficients obtained from the present elements are compared with the results that of (Ramakrishna et al. [36]; Noor [37]; Putcha et al. [38]) are presented Table 3.

Table 3 Non-dimensional fundamental frequency (Kf) of three-layered cross-ply square plate with a central elliptical hole
Full size table

The Kf values obtained here are in good agreement with those available in the literature. It was found that CQUAD8 element yielded better results compared to the CQUAD4 element. Hence CQUAD8 element was preferred for the further analysis of isotropic and laminated composite plates.

4 Results and discussion

The results of the present work are presented in tables in terms of non-dimensional frequency coefficient (Kf) defined by \({K_{\text{f}}}=\frac{{\omega {a^2}}}{{{\pi ^2}}}\sqrt {\frac{{\rho t}}{D}}\) for isotropic plates and by \({K_{\text{f}}}=\omega {a^2}\sqrt {\frac{{{\rho _1}}}{{{E_2}{\text{ }}{t^3}}}}\) for laminated composite plates.

The thickness of the plates was taken as 2.0 mm. The aspect ratio varied from 1.0 to 2.5, cut-out shapes were considered are circular and square with d/a ratio varied from 0.1 to 0.3. The effects of aspect ratio, cut-out size, and cut-out shape on the fundamental frequencies of isotropic plates are presented. The effects aspect ratio, cut-out size and cut-out shape on the natural frequencies of isotropic and laminated anti-symmetric cross-ply composite [keeping the total thickness constant at 2.0 mm and number of layers (NL) = 20] were studied.

4.1 Isotropic plates

Table 4 shows the variation of non-dimensional frequency coefficient Kf with aspect ratio, cut-out shapes and cut-out sizes for isotropic plates.

Table 4 Non-dimensional frequency coefficients (Kf) for isotropic plates
Full size table

  • In case of plates without cut-out The first non-dimensional frequency coefficient decreases as the aspect ratio increases, whereas second natural frequency increases with an increase in the aspect. The third natural frequencies are initially increased and later decreases.

  • In case of plate cut-outs The first, natural frequencies decreases and second natural frequencies are increases monotonically with an increase in the aspect ratio irrespective of d/a ratios and cut-out shapes. The frequencies are increased monotonically as the d/a ratio increases irrespective of cut-out shapes.

  • The natural frequencies are found to increase as the mode number increases, the number of curvatures in flexure increases resulting in the increase in stiffness of the structure which in turn increases the frequency.

The experimental values of the non-dimensional frequency coefficient Kf are in very good agreement with those of the finite element solution. The maximum non-dimensional frequency coefficient Kf is observed for the plate with the square hole of side-to-length (d/a) ratio of 0.3. The first three mode shapes obtained by finite element analysis are shown in Fig. 6 for the aspect ratio = 1.0 without and with circular and square cut-out having d/a ratio of 0.1.

Fig. 6
figure 6

Mode shapes for isotropic plates

Full size image

4.2 Laminated anti-symmetric cross-ply plates

Table 5 shows the variation of non-dimensional frequency coefficient Kf with aspect ratio, cut-out shapes and cut-out sizes (d/a ratio).

Table 5 Non-dimensional frequency coefficients (Kf) for laminated anti-symmetric cross-ply laminated composite plates (0°/90°)
Full size table

  • In case of plates without cut-out The non-dimensional frequency coefficient Kf increases monotonically with an increase in the aspect ratio irrespective of hole size and shapes for all the three modes of vibration.

  • In case of the plate with cut-outs The non-dimensional frequency coefficient Kf increases as the d/a ratio increases as well as aspect ratio increases irrespective of cut-out shape.

The natural frequency depends on the stiffness of the cross-section of the laminate among other factors such as boundary conditions, etc. The stiffness of the cross-section depends upon the contribution made by extensional stiffness, coupling stiffness and bending stiffness terms Jones [39].

The experimental values of the non-dimensional frequency coefficient Kf are in very good agreement with those of the finite element solution. The maximum non-dimensional frequency coefficient Kf is observed for the plate with without cut-outs and the maximum frequencies being observed for the plate having an aspect ratio of 2.5.

The first three mode shapes obtained by finite element analysis are shown in Fig. 7 for the aspect ratio = 1.0 without and with circular and square cut-out having d/a ratio of 0.1.

Fig. 7
figure 7

Mode shapes for laminated antisymmetric cross-ply plates

Full size image

5 Conclusion

The following conclusions are made in respect of free vibration of isotropic and laminated anti-symmetric cross-ply composite plates with and without central cut-out:

  • The experimental values of the first, second and third natural frequencies are in good agreement with those of the finite element solution in the case of both isotropic and laminated composite plates with and without cut-outs.

  • The non-dimensional frequency coefficient Kf increases with increase in length–to-cut-out size ratio (d/a) irrespective of the cut-out shape.

  • In case of the laminated composite plates, the non-dimensional frequency coefficient Kf increases monotonically with an increase in the aspect ratio irrespective of hole size and shapes for all the three modes of vibration.

  • In case of laminated composite, the natural frequency depends on the stiffness of the cross-section of the laminate among other factors such as boundary conditions, etc. The stiffness of the cross-section depends upon the contribution made by extensional stiffness, coupling stiffness and bending stiffness terms (Jones [36]).