Numerical investigation of blade-tip-vortex dynamics

Abstract

Numerical computations on a finite wing are carried out using DLR’s finite-volume solver TAU. The tip-vortex characteristics during static stall and deep dynamic stall are analyzed and compared to particle image velocimetry (PIV) measurements carried out in the side wind facility Göttingen. Computational fluid dynamics (CFD) and experiment are in good agreement, especially for sections close to the blade tip. Too large dissipation within the numerical computations leads to larger vortex size than in the experiment. The dissipation effect increases with larger distances from the wing. The analysis shows that the numerical method is able to capture the complex vortex structures shed from the wing and helps understanding the source of these structures.

1 Introduction

The ability to accurately predict the blade loading of a helicopter in forward flight is still a challenging task for the aerodynamicists. Different flow features, like dynamic stall and blade vortices, are formed simultaneously at the rotor blades. These features can influence each other and the cause and effect is often indistinguishable. Negative effects of dynamic stall, such as intense vibration and heavy loads, considerably limit the flight velocity and agility of helicopters. Dynamic stall can be triggered by the blade-tip vortex of a previous rotor blade striking the blade surface and causing flow separation [1]. The blade-tip vortex is also known for its effect on the noise footprint of a helicopter including blade–vortex interaction (BVI) [2, 3].

Research into dynamic stall is usually carried out on pitching airfoils [4, 5] to isolate the dynamic stall evolution and propagation from other influence factors. Inherently, three-dimensional phenomena such as spanwise flow or blade-tip effects are neglected in these test cases. In contrast to this, a pitching blade tip offers the opportunity to investigate the tip vortex under simplified conditions with respect to a full helicopter configuration. Thus, the investigation of a pitching finite wing can be considered as an intermediate approach between two-dimensional state-of-the-art configurations and investigations in the rotating frame. In addition, the complex lift characteristic of dynamic stall can also be found in the circulation of the tip vortex. Therefore, investigations on tip models are a promising resource for validating numerical computations, since, contrary to two-dimensional airfoil sections, flow information can be obtained both at the wing and the blade tip. For a pitching finite wing experiment, it is much simpler to gather flow information over a whole pitching cycle compared to experiments with rotation. For this reason, the pitching finite wing is particularly suitable to validate CFD computations.

However, only a few pitching finite wing investigations on tip-vortex behavior can be found in the literature. One of the first investigations was carried out on a NACA 0015 wing with an aspect ratio of 2 and a Reynolds number of $Re=1.8\times 10^5$ by Ramaprian and Zheng [6]. In this light stall case, slight changes in the position of the tip vortex are visible between the up- and downstroke of the blade. The differences between the static and the dynamic case are rather small. Chang and Park [7] presented a tip-vortex analysis of a NACA 0012 wing at $Re=3.4\times 10^4$ during deep dynamic stall. Their results show that during downstroke, the flow is heavily separated resulting in a weaker and less organized vortex with respect to the upstroke. Birch and Lee [8, 9] performed tip-vortex investigations on a NACA 0015 wing with an aspect ratio of 2.5 and $Re=1.86\times 10^5$. In their study, the investigated pitching frequencies and amplitudes result in test cases ranging from attached flow up to deep dynamic stall. Hot-wire measurements provided flow information up to 3 chords downstream of the wing tip. The observations with fully attached flow confirmed the findings of Ramaprian and Zheng [6], as only small differences are noticeable between up- and downstroke. During deep stall however, strong hysteresis effects are present between up- and downstroke. During the downstroke, the vortex is weaker, larger, and less symmetric. With increasing frequencies, the hysteresis effects become stronger. In addition, the flow inside the vortex changes from jet-like to wake-like during the upstroke. Numerical computations from Mohamed et al. [10] compared wind tunnel data from Birch and Lee in terms of velocity profiles, vortex strength, and trajectory. The detached eddy simulations (DES) were found to be superior to the Reynolds-averaged Navier–Stokes (RANS) approach, as the comparison was in better agreement with the experimental data during fully separated flow. Within the long-term DLR-ONERA cooperation, numerical simulations were carried out on the ONERA finite wing configuration to investigate three-dimensional stall effects. Richez et al. [11] performed DES at constant angle of attack, whereas Costes et al. [12] and Kaufmann et al. [13] investigated the three-dimensional dynamic-stall effects of the pitching wing using unsteady RANS (URANS) computations.

Fig. 1

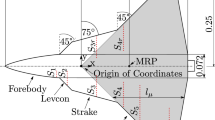
DSA-9A airfoil, wing planform, and coordinate system, dimensions in millimeters from Wolf et al. [16]

Fig. 2

Sketch of the experimental setup and applied measurement techniques from Wolf et al. [16]

In this work, extensive three-dimensional URANS computations using DLR’s finite-volume solver TAU are conducted to study the blade-tip-vortex dynamics during dynamic stall on a pitching blade-tip model. The simulations are validated with experimental data from Wolf et al. [16], who conducted a wind tunnel test campaign at DLR’s side wind facility. This experiment is particularly suited for tip-vortex investigations under dynamic stall conditions as it combines highly resolved PIV measurements of the tip vortex and unsteady pressure measurements of the entire dynamic stall cycle. This study focuses on a single pitching motion with an angle of attack at the wing’s root of $\alpha _{\text{r}}=11^\circ \pm 6^\circ$ and a reduced frequency of $k=\pi fc/U_{\infty }=0.076$. The inflow conditions are kept constant at a Mach number and a Reynolds number of $M=0.16$ and $Re=9\times 10^5$, respectively. The aim of this work is the analysis of the blade-tip-vortex dynamics under dynamic-stall conditions as well as the comparison of the numerical and experimental data of a full dynamic-stall cycle. Special emphasis is placed on the hysteresis effects of tip vortex between static and dynamic cases as well as between up- and downstroke during the dynamic-stall cycle. In addition, the relationship between tip-vortex circulation and lift distribution is used to gain further insight into the dynamic-stall behavior.

2 Experimental setup

Details of the wind tunnel test campaign are described in Refs. [14,15,16] and will, therefore, only be briefly summarized here. The experiments were carried out in the closed test section of a closed-circuit wind tunnel in accordance to the freestream conditions stated above. The DLR blade-tip model, see Fig. 1, has a chord length of 0.27 m and a span of 1.62 m, as well as a parabolic shaped tip similar to those used in current helicopter configurations. The industry relevant helicopter profile DSA-9A is used along the span and is positively twisted to shift the onset of stall towards the blade tip, minimizing side wall effects. The blade-tip model was attached to a test rig that enables sinusoidal pitch motions about the airfoil’s quarter chord.

The aerodynamic coefficients of the model can be integrated at three sections of constant span using unsteady pressure data. The PIV measurement planes are perpendicular to the freestream direction. They are located at distances of 0.25, 1.50, and 3.00 chord lengths downstream of the model’s trailing edge, see Fig. 2, and cover the area of the blade-tip vortex within the relevant angle of attack range. The high-speed PIV system has a data acquisition rate of 1 kHz and consists of a double-pulse laser system and a stereoscopic camera system, providing instantaneous distributions of the velocity components ($u,\,v,\,w$). For static test points, 150 samples of the flow field were acquired. For dynamic pitch motions, ten pitch cycles were taken into account. The start of each PIV sequence was synchronized to the minimum pitch angle, which for a reduced frequency of $k=0.076$ results in the acquisition of 195 phase-locked samples per cycle. Wolf et al. [16] describe additional experimental considerations such as spatial resolution and measurement uncertainty of the PIV system. The velocity fields were transformed from the wind tunnel coordinate system into the moving coordinate system of the blade-tip model for a better comparison to the CFD results. This approach required an accurate monitoring of the blade-tip’s position through a stereo pattern recognition system (SPR, e.g., see Ref. [17]) with a second set of cameras, also see Fig. 2.

3 Numerical setup

The computations were run using the finite-volume solver DLR-TAU.

Fig. 3

Hemispherical grid domain, surface grid, as well as sections of the grid at $y/c=0.00$ and $x/c=0.25$ (from left to right). For the latter, side and front views of the wing are shown in addition as a reference for orientation

The settings are based on the simulations shown in Kaufmann et al. [18]. The discretization in time was performed using a dual-time stepping approach with 3000 time steps per period and up to 600 iterations for each pseudo-time step. The usage of the Cauchy convergence control helps to reduce the amount of inner iterations, especially when the flow is attached. For the dynamic-stall computations, a pseudo-time step is considered as converged, as soon as the relative change of selected flow parameters during the last 50 iterations is below a threshold of $10^{-7}$. As critical flow parameters, the aerodynamic coefficients ($C_{\text{L}}$, $C_{\text{D}}$, $C_{\text{M}}$) as well as the maximum eddy viscosity and the total kinetic energy are chosen. The density residuum of a physical time step is thereby reduced by at least one order of magnitude during the entire cycle. The RANS equations are closed using Menter’s Shear Stress Transport (SST) model [19]. A central method with artificial matrix dissipation is used for the viscous and inviscid fluxes. The computations were run for two cycles on 960 cores of the SuperMUC Petascale System consuming approximately 10$^5$ CPUh per pitching cycle.

For the generation of the grid, the same settings as in Kaufmann et al. [18] were used, beside an additional refinement of the tip-vortex region. The computations are run on a semi-hemispherical computational domain with a radius of 500 chord lengths, see Fig. 3. The hybrid grid has 30 prisms in the direction normal to the wing’s surface. The first cell height is set to obtain $y_+<1$, and a stretching factor of 1.22 is used to resolve the wing’s boundary layer. The prisms in the middle of the wing are stretched in spanwise direction to reduce computational costs, but no stretching is applied at the root and the tip. A minimum cell size of $0.033\%\,c$ is used at the nose and the trailing edge of the wing, while the maximum cell size at the wing’s surface is set to $1\%\,c$. In the remaining computational domain, tetrahedrons are used. A refined trapezoidal area with a length of $6\,c$ and a height of $5\,c$ in the x–z-plane is used, similar to the two-dimensional computations of Richter et al. [20]. This area is stretched from the wing’s root up to $1\,c$ beyond the blade tip and the maximum tetrahedron size of 3.3% is set to resolve the wake as well as the vortices shed from the wing. The tetrahedron size in the tip-vortex region is reduced from 3.3 to $0.75\%\,c$ for a better resolution of the blade-tip vortex. Results from [18] were taken as an a priori estimate of the vortex positions and the area to be refined. The refined hexahedral area has a constant width in the spanwise direction starting from the beginning of the parabolic blade tip up to $10\%\,c$ beyond the blade tip. In the streamwise direction, the area starts from the leading edge up to 4 chord downstream of the trailing edge. This way, an upstream effect of a possible vortex bursting due to the grid coarsening is prevented. At the leading edge, the area is refined between $-0.25\, < \, z/c\, <\, 0.25$ and at $x/c=4.0$ between $0\, <\, z/c\, < \,1$. Figure 3, right, shows a section through the grid in the x–z-plane at the blade tip and in the y–z-plane at $x/c=0.25$, where also the first PIV plane is located. During the entire pitching motion, the tip vortex is located inside of the refined area. Compared to the grid used in [18], the grid has an additional 7.6 million nodes in the tip-vortex region and a total size of 28.8 million nodes.

4 Results

4.1 Constant angle of attack

For the comparison of the flow fields, the

Fig. 4

Tip-vortex behavior at constant angle of attack and $x/c=0.25$. Left: instantaneous PIV. Middle: time-averaged PIV. Right: CFD

numerical data are interpolated on a symmetric grid to fit the PIV evaluation windows. The streamwise velocity is normalized by the inflow velocity to compensate for small fluctuations inside the wind tunnel. The trailing edge of the blade tip is set as the origin of the coordinate system. The wind tunnel measurements at constant angle of attack are compared to RANS computations. Figure 4 shows the nondimensional streamwise velocity components at $x/c=0.25$ and vectors of the in-plane velocity components at three angles of attack. Instantaneous (left) and time-averaged (middle) PIV data are shown to illustrate the averaging effect. The CFD flow fields are shown in the right column. When the flow is fully attached (Fig. 4, upper row), a concentrated vortex is located close to the blade tip. The position of the vortex center, $y/c=-0.04$ and $z/c=0.07$, was determined in analogy to [16] using the swirling strength criterion. The vortex positions of the numerical data match the experimental positions, but the velocities in the vortex center are lower in the experiment ($u/U_{\infty }=0.42$) than in CFD ($u/U_{\infty }=0.49$). In addition, the vortex size is larger in CFD. The wake is gradually entrained into the tip vortex, an effect which is still very low at the $x/c=0.25$ plane. The flow in between the tip vortex and the wing’s shear layer is accelerated because of the displacement effect. The velocity deficit inside the shear layer and the tip-vortex block and, therefore, deflect the flow in these regions leading to an acceleration of the flow in between the two flow structures. This effect is more pronounced in the PIV data. The vortices shed from the wing are illustrated in Fig. 5. The tip vortex evolves directly at the blade tip and expands afterwards almost conically in the downstream direction (Fig. 5, $\alpha _{\text{r}}=8^\circ$).

Between $12^\circ\, <\, \alpha _{\text{r}}\, <\, 14^\circ$, the flow separates in the blade-tip area, which first takes place in the numerical simulations. As discussed by Wolf et al. [16], the tip-vortex size increases and the vortex is deflected towards the blade root after separation sets in. At $14^\circ$, a strongly increased area of decelerated flow is visible in the experiment as well as in CFD. In contrast to $8^\circ$, the flow in the isosurface image at $14^\circ$ (Fig. 5b) is strongly influenced by the separation occurring further inboard as well as by the separation starting at the leading edge of the parabolic blade tip. The vortex shape is complex and arises partly from the separation occurring at the leading edge as well as from the vortex evolution directly at the blade tip. The vortex at $x/c=0.25$ is still strongly affected by the separation and takes on a nearly symmetrical shape only after several chords downstream of the tip. In Fig. 4f, the vortex radius is increased and takes on an elliptic shape. The core center ($y/c=-0.100$, $z/c=0.138$) is located further inboard and higher with respect to the fully attached case. At the outer edge of the vortex, a bulge is visible, which is a result of the vortex evolution directly at the tip, see Fig. 5b. In Fig. 4, lower row, the flow is fully separated with the exception of a small region at the beginning of the parabolic blade tip (Fig. 5c). The vortex structure is smaller than for $\alpha _{\text{r}}=14^\circ$ and still has an elliptic shape. The inclination is slightly different between the experimental and the numerical data, and the height of the wake as well as the size of the vortex is larger in the numerical data compared to the PIV measurements.

Fig. 5

Static separation behavior of the DLR blade-tip model. Vortices visualized by means of the $\lambda _{2}$ criterion [22] and color-coded with $C_\text{p}$

Fig. 6

Time-averaged swirl velocity distributions (left) and circulation (right) over the core radius for two angles of attack

Fig. 7

Static behavior of the vortex core radius at $x/c=0.25$ (left) and circulation of the tip vortex at $x/c=0.25$ and $r/c=0.2$ (right) over angle of attack

Figure 6 depicts the time-averaged swirl velocity (left) and the time-averaged circulation (right) of the tip vortex over the radius. The swirl velocity (or tangential velocity, $u_\theta$) and the corresponding circulation $\Gamma$ were calculated with respect to the identified vortex center. The values with a given radial distance to this center were averaged over the entire azimuth, assuming rotational symmetry. Even though this is a strong simplification of the actual flow field, it still provides valid insight to the structure of the tip-vortex.

Two angles of attack are considered, where for $\alpha _{\text{r}}=8.0^{\circ }$, the flow is fully attached; and for $\alpha _{\text{r}}=16.0^{\circ }$, it is fully separated. The analysis is carried out at $x/c=0.25$, $x/c=1.50$, and $x/c=3.00$. For $\alpha _{\text{r}}=8.0^{\circ }$, the maximum swirl velocity of the experimental data is between $0.8<u_\theta /U_\infty <\, 0.9$ and the core radius, i.e., the radius of the maximum of $u_\theta /U_\infty$ is at $r/c=0.035$ for all three PIV planes. In contrast to this, the maximum swirl velocity is lower in the numerical data and also the streamwise decay of the velocity is more pronounced (from $u_\theta /U_\infty =0.67$ at $x/c=0.25$ up to $u_\theta /U_\infty =0.38$ at $x/c=3.00$). Another difference is that the radial distance of the maximum velocity increases in the numerical data with increasing distance from the wing’s tip. This indicates that the dissipation inside the numerical simulations is too high. Nevertheless, the experimental and numerical curves approach each other with increasing radial distance, and for radial position $r/c\, \ge\, 0.2$, the numerical data match the experiments. The same trends can also be seen in the circulation, where differences between the PIV planes up to $r/c=0.1$ are low. As shown by Wolf et al. [16], the circulation distribution can directly be linked to the lift distribution at sections close to the blade tip and a comparison between the circulation and the lift distribution is presented for the dynamic-stall case in Sect. 4.2. For larger radii, the circulation increases in the streamwise direction and also slightly in radial distance, due to the successive entrainment of the wing’s shear layer. In the numerical data, a local maximum in the circulation is visible for $x/c=1.50$ between $0.10\, <\, r/c\, <\, 0.15$ and for $x/c=3.00$ between $0.13\, <r/c\, <\, 0.20$. The reason for the subsequent drop in circulation is a secondary, counter-rotating vortex and this effect is discussed in Sect. 4.2. At larger radii, the numerical data fit the experimental data at all three investigated planes, and for this angle of attack, a linear increase in the circulation is visible up to the highest evaluated radial position.

At $\alpha _{\text{r}}=16^\circ$, the maximum swirl velocity is reduced and shifted to higher radial positions compared to the fully attached case. Now, for both numerical and experimental data, a decay of the maximum swirl velocity from $x/c=0.25$ to 3.0 is obtained. This mirrors the large and turbulent tip vortex already seen in Fig. 4, bottom row. Nevertheless, the decay is still stronger in CFD. In addition, both approaches show a shift of the radial distance of the maximum velocity with increasing distance from the trailing edge. Due to the larger turbulent mixing, the tip vortex grows faster when the flow is fully separated as in the attached case. At outer radial positions, the values seem to approach each other again, but due to the limited optical access within the PIV measurements, this cannot be confirmed. At $\alpha _{\text{r}}=16^\circ$, the circulation of the tip vortex is larger than for the fully attached case. In the numerical data, again, an overshoot in circulation can be observed at the locations at $x/c=1.50$ and 3.00, which is shifted to higher radial positions compared to $\alpha _{\text{r}}=8.0^{\circ }$. For both the numerical and experimental data, the circulation is stagnating after a certain radial position. The circulation values of experiment and CFD are in good agreement.

In Fig. 7, the tip-vortex core radius at $x/c=0.25$ (left) as well as the circulation at $x/c=0.25$ and $r/c=0.2$ over the angle of attack are compared between experimental and numerical data. As discussed by [16], the circulation at this fixed radius $\Gamma _{0.2}=\Gamma (r/c=0.2)$ is taken as a substitute for the total circulation $\Gamma (r\rightarrow \infty )$, limited by the fields of view of the PIV system. $\Gamma _{0.2}$ neglects a small part of the total circulation, particularly vorticity shed into the wing’s wake left outside of the field of view. Nevertheless, it provides a useful approximation of the strength of the tip vortex.

As already shown for $\alpha _{\text{r}}=8^\circ$ and $\alpha _{\text{r}}=16^\circ$, the data show that the CFD core radii are larger than in the PIV data for the entire angle of attack range. For both experiment and CFD, the core radius gradually increases with the angle of attack, except for the numerical data at $\alpha _{\text{r}}=12^\circ$, where the numerical data exhibit a peak in the core radius. The circulation increases almost linearly with the angle of attack, until at $\alpha _{\text{r}}=10^\circ$, the numerical data show strong fluctuations, probably because of the vortex structure which differs significantly from a circle when the flow is separated. This analysis indicates that the numerical simulations are able to reproduce the flow situation found in the PIV measurements. Nevertheless, the comparability decreases with increasing distance from the trailing edge, due to a too strong dissipation. Therefore, only the measurement plane at $x/c=0.25$ is considered for further investigations. Eddy viscosity models like Menter SST are known to produce too high viscosities in longitudinal vortices. In addition, with finer grids, the Menter SST turbulence model will not essentially improve the dissipation of the blade-tip vortex, as shown by Goerttler et al. [21] in the rotating frame.

4.2 Dynamic-stall case

In Fig. 8, the local lift coefficient of the

Fig. 8

Comparison of the lift coefficients for the dynamic case at $y=1400$ mm from the wing’s root

deep dynamic-stall case is shown for the most outboard section, as shown in Fig. 1. The cycle-to-cycle variations are very low, and therefore, only the numerical lift distributions of the second cycle is depicted in Fig. 8. The numerical and the experimental data are in good agreement during the upstroke. The separation position between experiment and CFD matches well at this section. After stall and during the first part of the downstroke, the lift coefficients of the numerical simulation are lower compared to the experimental data indicating a too strong separation in CFD.

Fig. 9

Tip-vortex behavior during the dynamic-stall case at different time instants and $x/c=0.25$. Left: instantaneous PIV. Middle: phase-averaged PIV. Right: CFD

Fig. 10

Global tip-vortex behavior during dynamic stall at the model. Vortices visualized by means of the $\lambda _{2}$ criterion [22] and color-coded with $C_\text{p}$

Fig. 11

Isosurfaces of streamwise vorticity $\omega _{\text{x}}=-500$/s (blue) and $\omega _{\text{x}}=1500$ /s (red) to show the emerging vortex system at the blade tip

In Fig. 9, the dynamic behavior of the tip vortex during the dynamic-stall cycle with $\alpha _{\text{r}}=11^\circ \pm 6^\circ$, $M=0.16$, $Re=9\times 10^5$ and $k=\pi fc/U_{\infty }=0.076$ is shown. The flow is visualized by the dimensionless velocity component in the streamwise direction and the in-plane vector field at $x/c=0.25$ behind the trailing edge for selected angles of attack. The flow fields of the instantaneous and phase-averaged data of the experiment as well as the numerical simulations are shown from left to right. At $\alpha _{\text{r}}=8.0^{\circ }$ on the upstroke $(\uparrow )$, the flow is fully attached in both experiment and CFD. In the instantaneous snap-shots, small turbulent flow structures and shear layer instabilities are visible which disappear in the phase-averaged data. The vortex center is shifted slightly inboard and upward with respect to the trailing edge. The vortex position of the experimental and the numerical data matches with a deviation of $0.007\,c$. Nevertheless, a jet with a maximum velocity of $u/U_{\infty }=1.23$ inside the vortex core can be seen in the experiment, which is not captured by the numerical simulations. In CFD, the core velocity shows a velocity deficit of $52\%\,U_{\infty }$. At the same angle of attack, no jet is visible for the static case. This change from jet to wake during a pitching motion with fully attached flow was already reported by Birch and Lee [9]. Similar to the static case, flow acceleration can be noticed between the wake and the vortex core, due to displacement effects. The position of the wing’s wake is captured well by CFD and fits the PIV data. Like for the static case, the core radius of the numerical simulations is larger than in the experiment.

At $\alpha _{\text{r}}=14^\circ \uparrow$ (Fig. 9, second row), the tip vortex is stronger and larger compared to $\alpha _{\text{r}}=8.0^{\circ }$ because of extra lift produced by the wing, compared to Fig. 8. At higher angles of attack the tip vortex evolves not only directly at the blade tip, but at the leading edge of the parabolic tip. Therefore, the vortex moves upward and inboard compared to lower angles of attack. In Fig. 10, isosurfaces of the $\lambda _{2}$ criterion are shown to illustrate the evolution of the blade-tip vortex during the dynamic-stall case. The tip vortex moves up the leading edge of the parabolic tip with increasing angle of attack, see Fig. 10a–c. Thereby, the vortex moves inboard and the shape of the vortex at $x/c=0.25$ is influenced by this effect. The large hysteresis effects of the deep dynamic-stall case can also be observed in the tip-vortex behavior. For the static case with $\alpha _{\text{r}}=14^\circ$, the tip vortex is already strongly enlarged and has lost its circular shape due to the flow separation. In contrast, the vortex is still circular and has its origin directly at the tip for the same angle of attack during the upstroke of the pitching motion. This is a result of the difference in separation behavior between the static and the dynamic case. For the static case, separation first takes place directly at the parabolic blade tip and is then pushed back by the separation further inboard of the model. In the dynamic case, the separations at the blade tip and at the middle of the model occur simultaneously. This effect seems to be driven by the reduced frequency, as the flow separation with a reduced frequency of $k=0.025$ starts from the blade tip and then spreads inboard, while for the higher frequencies, the dynamic-stall vortex evolves in the middle of the model, see Kaufmann et al. [18], Fig. 10. In addition, separation takes place at higher angles of attack when the pitching frequency is increased. The flow behavior inside the vortex changes from jet-like to wake-like and the phase-averaged data is in good agreement with the CFD prediction (Fig. 9e, f).

In Fig. 11 isosurfaces of the streamwise vorticity are shown to identify the source and propagation of the blade-tip vortex and the emerging flow structures at the section at $x/c=0.25$. At $\alpha _{\text{r}}=8.0^{\circ }$, a concentrated vortex, which rotates in positive x direction (red), is formed directly at the blade tip. At $\alpha _{\text{r}}=14.0^{\circ }(\uparrow )$, the tip vortex moves further inboard and vorticity is generated directly at the parabolic blade tip. In addition, a secondary vortex is formed directly at the trailing edge, which rotates in counter-rotating direction (blue). At $\alpha _{\text{r}}=17.0^{\circ }$, the flow is completely separated and vorticity is produced along the entire parabolic blade tip. The secondary, counter-rotating vortex is located further inboard and more powerful at this angle of attack. This vortex is responsible for the drop in circulation with increasing radial distance, seen for the static case in Fig. 7, right. This effect also occurs at a few angles of attack in the experimental data (not shown here), but is more pronounced in CFD compared to the experiment.

Fig. 12

CFD lift distribution over span for the static and the dynamic cases

Figure 12 depicts the sectional lift coefficient over the spanwise position along the wing. Three angles of attack during the static and the dynamic case are shown to compare the separation behavior along the span. For the static case at $\alpha _{\text{r}}=10^\circ$, the flow is still attached along the wing and two local maxima are visible close to the blade tip and at $y/S=0.6$. This lift distribution is a result of the positive geometric twist of $\Delta \alpha =5.5^\circ$ over the wing’s span. At $\alpha _{\text{r}}=12^\circ$, the flow is separated along large parts of the parabolic blade tip leading to a loss in lift at the outer wing region. Due to this separation, the blade-tip vortex and the separated flow at the tip merge into a large region of decelerated flow. This region is larger than the integration area of $r/c=0.2$ and results in the very large core radius as well as a loss in circulation seen in Fig. 7. As stall occurs almost along the entire span of the wing ($\alpha _{\text{r}}=14^\circ$), the lift coefficient recovers at the blade tip. This lift recovery comes along with a decrease of the blade-tip core radius, as shown in Fig. 7 (left).

For the dynamic case, the lift coefficient during attached flow ($\alpha _{\text{r}}=15.7^\circ \uparrow$) is qualitatively similar to the static flow case ($\alpha _{\text{r}}=10^\circ$). Nevertheless, the dynamic lift coefficient is approximately $30\%$ larger than for the static case. As dynamic separation starts to occur ($\alpha _{\text{r}}=16.4^\circ \uparrow$), the lift coefficient begins to drop simultaneously at the blade tip as well as at $y/S=0.6$. During the evolution of the $\Omega$-shaped dynamic-stall vortex ($\alpha _{\text{r}}=16.8^\circ \uparrow$), additional lift is produced at $y/S\approx 0.5$ and $y/S\approx 0.7$ as the two base points of the vortex move over these sections. In contrast to the static case, the strong loss in lift and the accompanying increase in blade-tip-vortex size does not occur within the dynamic case.

As dynamic-stall occurs, a complex blade-tip-vortex structure can be observed (Fig. 9, third row). The agreement between experiment and CFD remains very good for the shape of the vortex as well as the velocities of the flow. The tip vortex moves further inboard and upward, and the shape of the vortex changes significantly. Both the bent trajectory and the elliptical vortex shape can be seen in the isosurfaces of Fig. 10c. The averaging effect is more pronounced within the PIV images with fully separated flow (Fig. 9g, h, j, k). In Fig. 9g, small-scale, turbulent structures are visible, which indicate the unsteadiness of the flow. The strong fluctuations of the velocities, caused by small-scale turbulent structures, disappear in the phase-averaged images and the averaging results in a larger wake area compared to the instantaneous snap-shots, also because of the vortex meandering seen in the instantaneous images.

During the downstroke and fully separated flow (Fig. 9 j–l), a large separated region downstream of the blade tip is visible and the size of the “vortex” is overpredicted by the numerical computations. The averaging effect becomes even clearer resulting in a significantly enlarged area of decelerated flow. Note again, the large differences between up- and downstroke of the dynamic case (Fig. 9, second and last row) as well as between the dynamic and the static case (Fig. 4, second row), which are all captured well by the numerical computations. Nevertheless, the area of flow separation is overpredicted by CFD both in the static case and the dynamic case.

Fig. 13

Circulation of the tip vortex at $r/c=0.2$ during dynamic stall

In Fig. 13, the numerically and experimentally circulations of the tip vortex at $r/c=0.20$ ($\Gamma _{0.2}$) are compared. In addition, a compensation curve using the gradient of the static experimental data is shown to highlight the dynamic effects. During the first part of the upstroke, the circulation of the dynamic case is lower than for the static case. At $\alpha _{\text{r}}=12.5^\circ$, the circulation of the dynamic case exceeds the static case followed by a non-linear increase of the circulation. This increase is stronger in the numerical data and the maximum circulation of $\Gamma _{0.2}/c\,U_\infty =0.68$ at $\alpha _{\text{r}}=16.15\uparrow$ is reached earlier than in the PIV measurements ($\Gamma _{0.2}/c\,U_\infty =0.72$ at $\alpha _{\text{r}}=16.88\uparrow$). Afterwards, a drop in circulation is visible and the values during the downstroke are lower than for the static case. Again, stronger separation at the blade tip is visible in the numerical data than in the PIV measurements.

Fig. 14

Swirl velocity distributions (left) and corresponding circulation (right) over the core radius during dynamic stall

The swirl velocity distributions and the corresponding circulation of the dynamic-stall case for the same angles of attack as in Fig. 10 are depicted in Fig. 14. At $\alpha _{\text{r}}=8^\circ \uparrow$, large differences between the experimental and numerical maximum swirl velocity occur in the vortex core, which are also shown in the flow fields of Fig. 9. Like for the static case, the maximum swirl velocity within CFD is lower and shifted to an outer radial position compared to the PIV data. For a core radius $r/c>0.07$, the swirl velocities match each other. Differences between the experiment and CFD also occur within the circulation up to a core radius $r/c=0.07$. In the PIV data, the circulation increases faster than in CFD. For core radii $r/c>0.07$, the circulation increases linearly and the CFD data match the experiment. At $\alpha _{\text{r}}=14^\circ \uparrow$, the maximum velocity deficit of the numerical method is still visible, but much smaller compared to $8^\circ$. Again, for larger radii, the velocity and circulation profiles of CFD and experiment are very similar. A local maximum at $r/c\approx 0.1$ is visible for the experimental as well as the numerical data. The reason for the subsequent drop is the secondary vortex, which can be seen in Fig. 11 (blue). This vortex evolves at the tip’s trailing edge and rotates in negative x-direction. For the maximum angle of attack, the radial position of the maximum swirl velocity is close to each other. Nevertheless, for this angle of attack, the circulation at outboard position is higher in the PIV data indicating a stronger separation within CFD. This becomes even clearer at $\alpha _{\text{r}}=14^\circ \downarrow$, where large differences between the numerical and experimental data can be observed for all radial positions. The reason for the large differences between experiment and numerical data in axial and swirl velocity close to the vortex core, especially during the first part of the upstroke, is unclear. Nevertheless, the remaining flow field seems not to be essentially affected. On one hand, the velocity profiles and the related circulation of the experimental and numerical data approach each other with increasing distance to the core center, and on the other hand, these differences decrease during the subsequent upstroke of the wing. In addition, the complex flow fields during static and dynamic stall are predicted well by CFD. Nevertheless, the differences between experiment and CFD as well as the reason for the accelerated axial velocity remain a field of research.

5 Conclusions

Numerical computations using the DLR-TAU code are compared to PIV measurements of the tip vortex of a finite wing. The investigations at $M=0.16$ and $Re=9\times 10^5$ are carried out at constant angles of attack as well as for a deep dynamic-stall case with $\alpha _{\text{r}}=11^\circ \pm 6^\circ$ and $k=\pi fc/U_{\infty }=0.076$. The tip-vortex investigations show that the applied numerical methods are able to capture the evolution of the complex flow structures evolving at the blade-tip model. Especially, the strong hysteresis effects between up- and downstroke as well as between static and dynamic stall are visible in both experiment and CFD. Even though the comparability between CFD and experiment decreases with increasing distance to the blade-tip model, because of the too strong dissipation of the numerical simulations, the numerical simulations help to identify the origin of the complex flow structures formed at the blade-tip model. Further investigations will address the grid sensitivity in the blade-tip region and the deployment of low-dissipation methods like underresolved DES. Appropriately resolved DES seem to be limited to investigations at constant angles of attack, see, e.g., Richez et al. [11] (computation with 150 million grid points and $2.6\times 10^6$ CPU hours). Other approaches for better vortex preservation are the application of Reynolds stress models and low-dissipation low-dispersion schemes [23].