A Patient-Specific Computational Fluid Dynamic Model for Hemodynamic Analysis of Left Ventricle Diastolic Dysfunctions

Abstract

This work presents a computational fluid dynamic (CFD) model to simulate blood flows through the human heart’s left ventricles (LV), providing patient-specific time-dependent hemodynamic characteristics from reconstructed MRI scans of LV. These types of blood flow visualization can be of great asset to the medical field helping medical practitioners better predict the existence of any abnormalities in the patient, hence offer an appropriate treatment. The methodology employed in this work processed geometries obtained from MRI scans of patient-specific LV throughout a cardiac cycle using computer-aided design tool. It then used unstructured mesh generation techniques to generate surface and volume meshes for flow simulations; thus provided flow visualization and characteristics in patient-specific LV. The resulting CFD model provides three dimensional velocity streamlines on the geometries at specific times in a cardiac cycle, and they are compared with existing literature findings, such as data from echocardiography particle image velocimetry. As an important flow characteristic, vortex formation of the blood flow of healthy as well as diseased subjects having a LV dysfunction condition are also obtained from simulations and further investigated for potential diagnosis. The current work established a pipeline for a non-invasive diagnostic tool for diastolic dysfunction by generating patient-specific LV models and CFD models in the spatiotemporal dimensions. The proposed framework was applied for analysis of a group of normal subjects and patients with cardiac diseases. Results obtained using the numerical tool showed distinct differences in flow characteristics in the LV between patient with diastolic dysfunction and healthy subjects. In particular, vortex structures do not develop during cardiac cycles for patients while it was clearly seen in the normal subjects. The current LV CFD model has proven to be a promising technology to aid in the diagnosis of LV conditions leading to heart failures.

Introduction

Left ventricular diastolic dysfunction carries a considerable risk of heart failure and thus reduced survival of a person. It is found that up to 40% of heart failure patients are diagnosed with diastolic dysfunction.12 Cardiac or heart failure accounts for a significant portion of money spent in treatments for heart disease, for example, in United States alone, 33 billion US Dollars had been spent in fighting for this disease.19 Therefore, it is evident that the prevalence of heart failure is staggering. The mortality rate of systolic heart failure is similar to that of diastolic heart failure, at 15% per year in patients older than 65 years old.6 However, diagnostic means of systolic heart failure receives more focus in development than diastolic heart failure diagnosis, and the result is that the survival of patients suffering from systolic heart failure improves over the last 20 years, but the number does not change for diastolic heart failure patients.6

A heart beat comprises of systole and diastole. Systole is a period of a heart beat where the ventricles pump blood into the body, while diastole corresponds to the remaining of a heart beat where the atria fills the ventricles with blood, and it also corresponds to the relaxing of the ventricle muscles. There are many factors affecting the LV filling during diastolic phase including LV and atrial geometry, performance of LV relaxation and atrial contraction, pericardial restrain, heart rate, valve function and even systolic function.12,24,26 Causes to diastolic dysfunction can be conceptually classified into two main categories of a decrease in myocardial diastolic compliance and an impairment relaxation of LV. The clinical syndrome of diastolic heart failure is normally characterized by an isolated diastolic dysfunction with normal LV ejection fraction (EF). This work concerns with the development of diagnostic tools for diastolic heart failures, specifically to the condition of isolated diastolic dysfunction of restrictive filling due to impaired relaxation. Impairment of LV relaxation is caused by the stiffening of the heart muscles of the ventricle walls as well as other factors, such as errors in the chemical processes that happen within the cells of the heart muscle.21 Diastolic dysfunction in the LV is usually related to hypertension and ischemic heart disease.9

Using CFD to generate flow pattern visualization in patient-specific LV can be useful to assist medical doctors to analyze and predict the various functions of the heart chamber muscles in relation to effectively pump blood into the circulation.13 This type of visualization can be a great asset in the medical field that allows doctors to prescribe appropriate treatments to patients. Research on this topic has proven that this methodology to visualize flow pattern in the LV has a promising diagnostic capabilities.14,18 CFD, while having a massive advantage in the medical field, presents a hurdle of challenges that need to be looked into, for example, the fact that blood flow dynamics in the heart is a coupled motion, with the force of the wall muscles defining the movement of blood and in turn the pressure of the fluid exerted on the heart wall defines its movement. Nevertheless, we can have the assumption that the effect of force exerted by the heart muscles into the blood is much larger than the effect of force exerted by the blood into the heart muscles.18 Other than that, boundary conditions have to be correctly prescribed and ventricular wall quality and structure to be considered in the remodeling of the heart chambers for a fluid-structure interaction (FSI) computation.23

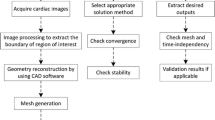
Much of development on LV CFD models over the past decades has been centered around quantitative improvement of numerical techniques in order to better approximate physiological data with more accuracy and robustness. The quality and accuracy of CFD models have been improved tremendously in those applications; however, there remain many challenges in practices to generate patient-specific CFD models for assisting medical practitioners in clinical usages. The CFD process is normally tedious and labour intensive for usage in practice; even more cumbersome for most of surgeons or medical practitioners. This is evidently due to the fact that the process is heavily relied on operator dependent steps such as image segmentation, mesh generation and CFD simulations. Despite much of advancement in computational methods and power, this process of simulating flows in patient specific LV is still time consuming and resource intensive. In our earlier work,16 a semi-automated process for CFD LV model was proposed to conduct numerical simulations of flow in patient specific MRI scans with minimal operator involvement in the process. The approach is a step closer to automated CFD process. The results were also validated with other LV models and shown a good prospect for clinical usage.

A natural extension of the earlier work is presented in the present study where the automated process is further enhanced with more robust techniques in handling geometrical reconstructed geometries from MRI scans as well as improved solver performance and efficiency for a large sample of data. The objective of the current work is to further develop the methodology to successfully model patient-specific LV and simulate the flow dynamics of blood using CFD techniques. The CFD process involves many steps to achieve a patient-specific LV CFD modeling, beginning from the generation of surface mesh, and then a reconstruction of the LV mesh geometry being a crucial step in the process. The automation step will also focus on a three-dimensional geometry reconstruction until a numerical simulation is completed. The current process takes in segmented patient specific LV geometries acquired from MRI scans and the associated post-processing module. Using subdivision techniques, the proposed approach enables us to accept low resolution surface mesh data and convert it into a smoother and higher resolution geometry. The reconstructed geometry serves as input surface meshes to the volume mesh generation process based on Delauney triangulation.16 Motion of the LV walls during a cardiac cycles was captured in MRI scans and incorporated into the unsteady computational model as a dynamic moving boundary problem. A fast radial basis function (RBF) interpolation technique is implemented to translate the pumping motion of LV walls into boundary mesh motions in simulations. The blood flow dynamics in LV are realized by using an unsteady incompressible Navier-Stokes solver in arbitrary Lagrangian Eulerian (ALE) framework. With the improvement in the dynamic mesh motion solver, the current approach is able to handle large deformation of LV walls for various subjects while maintaining the mesh quality for stable and accurate simulations. This whole process from surface smoothing to grid generation and flow simulations are streamlined and made automated with no user intervention.

The proposed approach is employed in a trial for a set of human data including healthy subjects and patients with diastolic dysfunction conditions. Results from the computational model are then used to evaluate some of the heart conditions including vortex formation and other flow characteristics in healthy and diseased subjects. Optimal vortex formation in the blood flow to the LV during diastole is crucial for an ideal transfer of momentum and energy during the following systolic period from the ventricle to the aorta. However, in a left ventricular diastolic dysfunction, the flow pattern of the blood does not create the optimum vortex to transfer momentum and energy into the aorta.7,26 The present study extends the usage of the proposed numerical framework and aims at aiding professional medical practitioners to analyse flow patterns and vortices formation in patient-specific remodeled heart obtained from Magnetic Resonance Imaging (MRI) images in a spatiotemporal dimension, in order to better assess the existence of a diastolic dysfunction.

Data Acquisition

MRI scanning was performed in a set of 4 healthy volunteers and 2 patients using 1.5T Siemens scanner (Avanto, Siemens Medical Solutions, Erlangen). Ventricular 2-chamber, 4-chamber and short-axis planes with 12–14 equidistant slices covering both ventricle, atrium and aorta were acquired. The field of view was typically 320 mm with in-plane spatial resolution of less than 1.5 mm. Images were acquired in a single breath hold, with approximately about 25 temporal phases per heart cycle. The short- and long-axes views from the MRI were used to reconstruct 3D LV geometry in conjunction with dynamic left atrium (LA) and ascending aorta using CMRtools suits (CVIS, Imperial College, UK) as well as customized algorithm and used in other studies.14 This method allows the representation of the dynamic morphology of anatomical features in the LV, LA and aorta. The smooth surfaces was generated from a set of arbitrarily control points with an interpolation scheme by using polar Catmull Rohm spines. Temporal spline interpolation was used to generate a complete time series of models. The processing methods of MRI data for LV were also used in our previous study.16 Table 1 summarizes some key clinical data of the six subjects in this study including two healthy subjects and four patients with diastolic dysfunction (DD). They are denoted as H1-H4, P1-P2 correspondingly in the subsequent discussion.

Table 1 Mean and standard deviation of some key clinical data of 6 subjects in the current study.

Figure 1

Volume data and rate of volume change obtained from MRI scan during one cardiac cycle for various subjects in the present study.

As a product from patient specific MRI scans and segmentation, a discrete surface of the left ventricular geometry is constructed at different time during one cardiac cycle. In the current work, raw data of LV discrete surfaces was obtained from a set of 4 healthy volunteers and patients during a typical cardiac cycle. The data comprises a series of approximately 22–25 frames recorded during the cardiac cycle and each frame consists of a relatively coarse resolution of about three thousand vertices representing the LV. Left ventricle volumes can be measured from the segmented images as shown in Fig. 1 for variation of LV volumes during one cardiac cycle for all the subjects in the current study. The rate of volume change can be determined from this data and it subsequently enables us to derive the volume flow rate as well as velocity profile through LV in a cardiac cycle.

In order to perform CFD simulations of intra-ventricular flows, this raw data of LV discrete surfaces needs to be smoothed and computational grids are generated to conform with the motion of LV’s wall. We proposed a process of smoothing surfaces using subdivision surface together with an unstructured grid generation algorithm for producing computational grids and an effective mesh moving scheme to conform the computational grids to motions of LV wall. The process of smoothing surfaces and volume mesh generation are only applied to an arbitrarily chosen frame, considered as a seed frame. The information on LV wall motion will then be interpolated and translated into other frames subsequently. In the subsequent subsections these processes will be elaborated further from smoothing surfaces using subdivision to volume mesh generation; and interpolation of MRI captured surface motions into computational mesh movement. Finally a brief description of the in-house CFD solver coupled with the dynamic patient specific LV mesh motion module for simulations of blood flows is presented.

Patient Specific Left Ventricle CFD Model

In this work, blood flows are modeled as incompressible viscous fluids and governed by incompressible Navier-Stokes equations. The solution of the incompressible Navier–Stokes equations can be achieved using either a pressure based method, such as the fractional step method, or a density based method, such as the artificial compressibility approach. In the present work, the artificial compressibility method is employed. In the arbitrary Lagrangian Eulerian (ALE) framework, the three dimensional Navier–Stokes equations can be written in the non-dimensional form as

$$\begin{aligned} \bar{{\varvec{I}}}\frac{{\mathrm {d}}}{{\mathrm {d}}t}\int \limits _{\Omega (t)} {\varvec{U}} {\mathrm {d}}\Omega +\int \limits _{\partial \Omega _t}({\varvec{F}}_j-\hat{{\varvec{F}}}_j)n_j{\mathrm {d}}S -\int \limits _{\partial \Omega _t}{{\varvec{G}}_j}n_j{\mathrm {d}}S= {\mathbf {0}}, \end{aligned}$$

(1)

where $n_j$ is the component, in direction $x_j$, of the outward unit normal vector to $\partial \Omega _t$. ${\varvec{U}}=(p,u_{1},u_{2},u_{3})^{\text{T}}$ is the non-dimensional unknown variable, $\bar{{\varvec{I}}} = \text {diag}(0,1,1,1)$ is the modified unit matrix. In the above description, the inviscid fluxes ${\varvec{F}}_j$, the ALE fluxes $\hat{{\varvec{F}}}_j$ and the viscous fluxes ${\varvec{G}}_j$ are defined by

$$\begin{aligned} {\varvec{F}}_j= \left[ \begin{array}{c} u_{j} \\ u_{1}u_{j} + p\delta _{1j} \\ u_{2}u_{j} + p\delta _{2j} \\ u_{3}u_{j} + p\delta _{3j} \\ \end{array} \right] \quad \hat{{\varvec{F}}}_j= \left[ \begin{array}{c} 0 \\ u_{1}\hat{v}_j \\ u_{2}\hat{v}_j \\ u_{3}\hat{v}_j \\ \end{array} \right] \quad {\varvec{G}}_j= \left[ \begin{array}{c} 0 \\ \tau _{1j} \\ \tau _{2j} \\ \tau _{3j} \\ \end{array} \right] \end{aligned}$$

(2)

respectively, where $u_j$ is the velocity components of the fluid, $\delta _{ij}$ is the Kronecker delta and

$$\begin{aligned} \tau _{ij}=\frac{1}{Re}\left( \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}\right) \end{aligned}$$

(3)

denotes the deviatoric components of the stress tensor. In these equations, velocity vector is denoted by $\varvec{u}$, $\rho$ is the density, p is the pressure and $\mu$ is the dynamic viscosity of the fluid. In the ALE flux term, $\hat{\varvec{v}}$ is the mesh moving velocity derived from LV wall motions. The blood is considered as Newtonian fluid of density $\rho =1025$ kg m³ and kinematic viscosity of $\nu =3.81 \times 10^{-5}$ m² s⁻¹. The equations are closed with boundary conditions imposed on the boundary of the domain $\Gamma = \delta \Omega$ as

$$\begin{aligned} \varvec{u} = \bar{\varvec{u}} \quad \text {in } \Gamma_{\text{D}},\end{aligned}$$

(4)

$$\begin{aligned} \varvec{\sigma }\cdot \varvec{n} = \bar{\varvec{\tau }} \quad \text {in } \Gamma_{\text{N}}, \end{aligned}$$

(5)

where $\Gamma = \Gamma_{\text{N}} \cup \Gamma_{\text{D}}$. $\Gamma_{\text{N}}$ denotes a boundary where Neumann conditions are applied in the form of prescribed tractions ($\bar{\varvec{\tau }}$) and $\Gamma_{\text{D}}$ corresponds to a Dirichlet boundary on which the velocity is imposed.

In the present work, we first presented an approach for reconstruction of LV volume from segmented MRI scans and triangulation of the reconstructed domain for computations into unstructured three dimensional grids. The governing Eq. (1) were then discretized using the finite volume method where a finite set of discrete equations were constructed on unstructured grids to approximate the NS equations. The construction was performed by a edge-based cell-centered FV approach where the FV discretization was based on the integral form of the governing equation over a polyhedral control volume. To handle movement of LV walls, the arbitrary Lagrangian Eulerian (ALE) formulation was used to discretize the system. A dynamic moving mesh approach was adopted to deform and regenerate the mesh following moving boundaries. The main features of these approaches was discussed in details in Ref. 16. In the following section, a summary of the proposed approach is described.

Dynamic Mesh for 4D Left Ventricle Model

The above section described a patient specific MRI scan and segmentation protocol in which a discrete surface of the left ventricular geometry is constructed at different time during one cardiac cycle. Raw data of LV discrete surfaces was obtained from subjects during their cardiac cycle. As an output from the present protocol, the data normally comprises a series of 25 frames recorded during the cardiac cycle and each frame consists of a relatively coarse resolution of LV surfaces. Figure 2 shows snapshots of LV discrete surfaces at different instances. The segmented raw LV surfaces maintain the same number of nodes across all the frames thus ensuring one-to-one connectivity with consistent mesh topology. While the raw surfaces provide good rendering of the LV dynamic motions, the surface mesh resolution and quality are inadequate for numerical simulations of intra-ventricular flows. In order to perform CFD simulations, it requires further smoothing, refinement of those raw surfaces and volume mesh construction of LV volumes. We proposed a process of smoothing surfaces using subdivision surface together with an unstructured grid generation algorithm for producing computational grids and an effective mesh moving scheme to conform the computational grids to motions of LV wall. The process of smoothing surfaces and volume mesh generation are only applied to an arbitrarily chosen frame, considered as a seed frame. The information on LV wall motion will then be interpolated and translated into other frames subsequently. In Ref. 16, the processes was described in details from smoothing surfaces using subdivision to volume mesh generation; and finally interpolation of MRI captured surface motions into computational mesh movement.

Figure 2

Snapshots of LV discrete surfaces obtained from MRI scan and segmentation at different time in a cardiac cycle for one of the subjects in this present study.

Raw surfaces obtained from MRI scans were firstly refined and smoothened using subdivision schemes which construct smooth surfaces through a recursive limiting procedure of refinement from the initial mesh, also known as control mesh of the surface. In this approach, a frame is chosen as seed frame to smooth and refine; the chosen frame is normally taken as the end diastole or end systole corresponding the maximum or minimum volume respectively. Once the surface mesh of LV are sufficiently refined to desirable resolution, the Delaunay triangulation is employed to generate the volume unstructured grid from the refined smooth surface mesh of the seed frame. During one cardiac cycle, the movement of LV wall were captured and segmented to a series of frames in the form of raw surface triangular meshes containing the positions of points. As the raw surfaces were refined by subdivision surfaces and tetrahedral volume meshes were generated from the refined smooth surfaces, it is necessary to derive the motion of the volumes mesh from the raw data in order to account for the dynamics of the LV walls in CFD simulations. Due to consistent mesh topology of segmented raw surfaces and given their nodal positions at different frames, the nodal displacement is calculated as

$$\begin{aligned} \varvec{d}^n_r(\varvec{x}^n_r) = \varvec{x}^n_r - \varvec{x}^{n-1}_r \end{aligned}$$

(6)

where the superscript n denotes the time frame number and $\varvec{x}_r$ is the coordinates of raw surface nodes. The motion of volume mesh can then be interpolated from the nodal displacement derived from segmented raw surfaces by first spreading the motion of raw surfaces to smooth surfaces, then nodal positions of volume meshes are constructed from the movement of smooth surfaces as the boundaries of volume meshes. Radial basis function interpolation is employed to spread the nodal displacements from raw surfaces to smooth surfaces.16 The interpolation function, $\varvec{s}(\varvec{x})$, describing the displacement of nodes on refined meshes can be approximated by a sum of basis functions

$$\begin{aligned} \varvec{s}(\varvec{x}) = \sum ^{N_r}_{j=1}{\lambda _j \phi (||\varvec{x} - \varvec{x}_{bj}||)} + \sum ^{M}_{k=1}{c_k p_k(\varvec{x})}, \end{aligned}$$

(7)

where $\varvec{x}_{rj}=[x_{rj},y_{rj},z_{rj}]$ are the nodal positions on raw surfaces. $N_r$ is number of nodes on the raw surfaces, $p_k(\varvec{x})$ is the basis for polynomial of total degree at most M and $\phi$ is a given basis function. The interpolating coefficients $\lambda _j$ and polynomial coefficients $c_k$ are determined by the condition that interpolation function must return the exact displacement at the nodes on the raw surface, $\varvec{d}_{rj}$

$$\begin{aligned} \varvec{s}(\varvec{x}_{rj}) = \varvec{d}_{rj}. \end{aligned}$$

(8)

Further conditions are imposed on coefficient vector $\varvec{\lambda }$ that

$$\begin{aligned} \sum _{j=1}^{N_r}{\lambda _j} p_k(\varvec{x}_{rj}) = 0, \quad \forall k=1,2,\ldots,M. \end{aligned}$$

(9)

The augmented RBF interpolation guarantees uniquely solvable conditions and dynamic mesh motion of refined surfaces can be then constructed from the known nodal displacement on the raw surfaces. As the boundary surfaces motion is computed from the RBF interpolation procedure, the internal mesh nodes position is adjusted using mesh smoothing technique based on spring analogy. In many cases, under large deformations of LV wall motions mesh smoothing technique alone is not sufficient to maintain good mesh quality; mesh modification using the edge and face swapping technique is used to adjust the mesh while preserving good mesh quality. Figure 3 summarizes the process of constructing dynamic mesh motion of patient specific LV from segmented MRI images with a typical case of volume mesh for one of the subjects in this study depicted in Fig. 4. Using mesh smoothing combined with swapping procedure, it is possible to maintain good mesh quality during simulation of a whole cardiac cycle. Moreover, maintaining number of nodes in the computational grids eliminates interpolation and its associated error while updating solutions between meshes during transient simulations.

Figure 3

Dynamic mesh process of a subject in this study including (1) segmentation of raw surface from MRI scan, (2) smoothen and refine a seed frame’s surface using subdivision technique, (3) generation of volume mesh from refined, smooth surface and (4) interpolate surface movement to dynamic mesh motion during one cardiac cycle.

Figure 4

Images of volume mesh at two stages in a cardiac cycle for one of the subjects in this study. Using edge and face swapping technique, number of nodes in those grids are kept constant while adapting to the motion of LV walls and ensuring good mesh quality. As the number of nodes are maintained across all the frames during cardiac cycles, there is no error introduced in interpolation between different meshes in normal remeshing approach.

Second Order Finite Volume Solver for Simulations of Blood Flows in Left Ventricles

In this work, a second order cell based vertex centered finite volume procedure16 was employed to discretize the Navier-Stokes equations in the arbitrary Eulerian Lagrangian (ALE) framework for simulations of blood flows in deformable LV. To enable the implementation of a cell vertex finite volume solution approach, a median dual mesh is constructed by connecting edge midpoints, element centroids and face centroids such that only one node is present in each control volume. The finite volume discretization transforms surface and volume integrals of governing Eq. (1) into a sum of face and control volume integrals and approximates them to second order accuracy.

The computational domain $\Omega$ is subdivided into a set of non-overlapping $N_e$ tetrahedral elements from $N_p$ nodes $\Omega = \mathcal {T}_h(N_e,N_p) = \{\kappa _i, i=1,N_e\}$ using a Delaunay mesh generation process as described in the above section . To enable the implementation of a cell vertex finite volume solution approach, a median dual mesh $\mathcal {D}_h$ is constructed by connecting edge midpoints, element centroids and face centroids such that only one node is present in each control volume, $\mathcal {D}_h=\{\chi ^I,I=1,N_p\}$. The contribution of the inviscid flux over the control volume surface for node I ($\partial \chi ^I$) is then computed as

$$\begin{aligned} \int \limits _{\partial \chi ^I} F_{ij} n_j {\mathrm {d}}{\varvec{x}} \approx \sum \limits _{J \in \Lambda _I} \frac{C^{IJ}_j}{2} \left( F_{ij}^I + F_{ij}^J\right) + \sum \limits _{J \in \Lambda ^B_I} D^{IJ}_j F_{ij}^I \end{aligned}$$

(10)

where $\Lambda _I$ denotes the set of nodes connected to node I by an edge and $\Lambda _I^B$ denotes the set of nodes connected to node I by an edge on the computational boundary. In the above formulation, $C^{IJ}_j$ and $D^{IJ}_j$ are the value of edge coefficients for internal and boundary edges, respectively. Similarly, the viscous terms are approximated by

$$\begin{aligned} \int \limits _{\partial \chi ^I} G_{ij} n_j {\mathrm {d}}{\varvec{x}} \approx \sum \limits _{J \in \Lambda _I} C^{IJ}_j G_{ij}^{IJ} + \sum \limits _{J \in \Lambda ^B_I} D^{IJ}_j G_{ij}^I \end{aligned}$$

(11)

where

$$\begin{aligned} {\varvec{G}}_{j}^{IJ} = \left[ \begin{array}{c} 0 \\ \tau _{1j}^{IJ} \\ \tau _{2j}^{IJ} \\ \tau _{3j}^{IJ} \\ u_k^{IJ} \tau _{kj}^{IJ} - q_j^{IJ} \end{array} \right] \mathrm {;} \quad {\varvec{G}}_{j}^{I} = \left[ \begin{array}{c} 0 \\ \tau _{1j}^{I} \\ \tau _{2j}^{I} \\ \tau _{3j}^{I} \\ u_k^{I} \tau _{kj}^{I} - q_j^{I} \end{array} \right] . \end{aligned}$$

These discretization coefficients are calculated for each edge using the dual mesh segment associated with the edge as follows,

$$\begin{aligned}&C^{IJ}_j \equiv {n}^{IJ}_j = \sum _{K\in \Gamma _{IJ}} A_{\Gamma _I^K} n_j^{\Gamma _I^K} \\&D^{IJ}_j = \sum _{K\in \Gamma ^B_{IJ}} A_{\Gamma _I^K} n_j^{\Gamma _I^K}. \end{aligned}$$

In the above expression, $A_{\Gamma _I^K}$ is the area of facet ${\Gamma _I^K}$ and $n_j^{\Gamma _I^K}$ is the outward unit normal vector of the facet from the viewpoint of node I. And $\Gamma ^B_{IJ}$ is the set of dual mesh facets on the computational boundary touching the edge between nodes I and J. One can refer to Ref. 16 for more details on the discretization scheme.

The discrete ALE term for node I at time $t=t^n$ can be computed as

$$\begin{aligned} \int \limits _{\partial \chi ^I} \hat{F}_{ij} n_j {\mathrm {d}}{\varvec{x}} \approx \sum \limits _{J \in \Lambda _I} \frac{S^{IJ}_j}{2} \left( \hat{F}_{ij}^I + \hat{F}_{ij}^J\right) + \sum \limits _{J \in \Lambda ^B_I} T^{IJ}_j \hat{F}_{ij}^I \end{aligned}$$

(12)

where $S_{IJ}^n$ and $T_{I}^n$ are the ALE coefficients such that the geometric conservation law is satisfied. Here the approach for computing ALE coefficients in Ref. 16 is followed,

$$\begin{aligned} \Delta t S_{IJ}^{n+1} = \sum _{K\in \Gamma _{IJ}}\delta V_{\Gamma _I^K}^{n+1,n}, \quad \Delta t T_{IJ}^{n+1} = \sum _{K\in \Gamma ^B_{IJ}} \delta V_{\Gamma _I^K}^{n+1,n}. \end{aligned}$$

In the above expression, $\delta V_{\Gamma _I^K}^{n+1,n}$ is the volume swept over by triangular facet $\Gamma _I^K$ from time level n to $n+1$.

At a general node I, the physical time derivative term in Eq. (1) is approximated, using a three level second order accurate finite difference scheme, as

$$\begin{aligned} \begin{array}{ll} &{} \frac{{\mathrm {d}}}{{\mathrm {d}}t} \left. \int \limits _{\chi ^I(t)}{\varvec{U}} {\mathrm {d}}{\varvec{x}} \right| ^{t=t_n} \approx \partial ^{t_n}_h(V_I{\varvec{U}}^n) \\ &\quad= \frac{1}{\Delta t} \left( \frac{3}{2} V_I^n {\varvec{U}}^{n} -2 V_I^{n-1}{\varvec{U}}^{n-1} + \frac{1}{2} V_I^{n-2}{\varvec{U}}^{n-2} \right) \end{array} \end{aligned}$$

(13)

Here, the superscript n refers to an evaluation at time level $t=t_n$, the time levels are taken to be equally spaced with a time step $\Delta t$ and $V_I$ is the volume of $\Omega _I$. To stabilize computations, biharmonic form of artificial viscosity term constructed as in the JST11 fashion were added to the discretization.

When all the terms in Eq. (1) are approximated in the above described fashion, the final form of the discrete equation at a node I is then written as

$$\begin{aligned} {{\varvec{R}}}^n_I({\varvec{U}}) = {\varvec{0}}, \qquad \forall I \in [0,N_p], n\in [1,N_T] \end{aligned}$$

(14)

where ${{\varvec{R}}}^n_I$ represents the discretisation at time $t=t_n$ of the time derivative (13), the inviscid fluxes (10), the ALE fluxes (12), the viscous fluxes (11) and the biharmonic artificial dissipation. The discrete equation system is then solved directly in each time step with multigrid procedure to drive convergence of the non-linear system. In this work a non-linear full approximation storare scheme was employed as the solution procedure. In using this approach, the discrete non-linear system of equations (14) are solved in each step by integrating in pseudo–time to steady-state:

$$\begin{aligned} V_I\frac{{\mathrm {d}}{{\varvec{U}}}^n}{{\mathrm {d}}\tau } ={{\varvec{R}}}^n({\varvec{U^n}}),\qquad \forall n\in [1,N_T]. \end{aligned}$$

(15)

For direct explicit scheme, solution can be found by relaxing (15) until convergence using different time stepping schemes such as multi-stage Runge–Kutta schemes. It would require large number of iterations to converge due to nature of explicit method in eliminating low error frequencies. Multigrid approach provides an effective way to dampen errors of all frequencies while retaining the fast computation per iteration and low memory usage of the explicit schemes by solving the system in cascades of successively coarser meshes. In this work, multigrid meshes are generated from the finest dual mesh level using automatic agglomeration procedure.15 The semi-discrete system of equations (15) is first relaxed on the fine mesh using 3-stage Runge–Kutta scheme to obtain an approximate solution ${\varvec{U}}_n^s$ at cycle s such that

$$\begin{aligned} {{\varvec{R}}}^{n}_f\Big({\varvec{U}}^{n,s}_f\Big) = {\varvec{S}}^{n,s}_f, \end{aligned}$$

(16)

where ${\varvec{S}}^n_f$ depicts error of solution approximation at current cycle on fine mesh. On the next coarser mesh level, an approximation of solution can be found by solving the system of equations

$$\begin{aligned} {{\varvec{R}}}^{n}_c\Big({\varvec{U}}^{n,s}_c\Big) = {\varvec{S}}^{n,s}_c, \end{aligned}$$

(17)

where ${\varvec{S}}^{n,s}_c$ is defined as error term projected on the coarser mesh as:

$$\begin{aligned} {\varvec{S}}^{n,s}_c = {\varvec{R}}^{n}_s\Big({\varvec{I}}_c^f\Big(U_{n,s}^f\Big)\Big) - {\varvec{I}}_c^f\Big({\varvec{R}}^n_f\Big({\varvec{U}}^{n,s}_f\Big)\Big). \end{aligned}$$

(18)

Here ${\varvec{I}}_c^f$ is a mapping of vector from fine to coarse level, also known as restriction operator. The system of equations (17) is now can be relaxed by using the same multistage Runge-Kutta scheme; or a similar multigrid step involving a coarser mesh level 2. By solving the system of equations on successive coarser level meshes, each mesh level eliminates errors that appears locally as high frequency and the result is an approximation of solution at cycle s on coarse level mesh ${\varvec{U}}^{n,s}_c$. The coarser mesh approximation can then be used to update solution on the finer mesh as a new initial guess at the next cycle:

$$\begin{aligned} {\varvec{U}}^{n,s+1}_f = {\varvec{U}}^{n,s}_f + {\varvec{I}}^c_f\Big({\varvec{U}}^{n,s}_c - {\varvec{I}}^f_c\Big({\varvec{U}}^{n,s}_f\Big)\Big). \end{aligned}$$

(19)

Here ${\varvec{I}}^c_f$ is a mapping of vector from coarse mesh to fine mesh, also known as prolongation operator. The procedure is repeated until convergence. The multigrid procedure is efficient at $\mathcal {O}(N)$ for viscous incompressible flows with an optimal convergence rate of 0.75.15

Boundary Conditions

For any computational fluid dynamics model, flow solutions are very sensitive to the types of boundary conditions specified at the computational domain boundaries. It is essential to determine appropriate boundary conditions for generation of an efficacious CFD model of LV. It is more important for the case of patient specific LV model in this work as information at the boundaries are often hard to get from the onset or it may require a separate protocol to obtain those flow conditions. In the present patient specific model, the wall boundary condition is applied at the LV wall while inflow and outflow conditions are applied at the mitral and aortic inlets as follows.

Wall Boundary Condition

For a viscous flow, the boundary conditions on the wall are the no-slip and no-penetration conditions, namely

$$\begin{aligned} \big ( ({\varvec{u}}-{\varvec{w}}) \cdot {\varvec{t}} \big )_\mathrm {wall}= 0,\;&\text {(no-slip)}\end{aligned}$$

(20)

$$\begin{aligned} \big ( ({\varvec{u}}-{\varvec{w}}) \cdot {\varvec{n}} \big )_\text {wall} = 0&\text \; {(no-penetration)} \end{aligned}$$

(21)

where ${\varvec{w}}$ is the velocity of the wall, ${\varvec{t}}$ and ${\varvec{n}}$ are the tangential and the normal unit vectors to the wall respectively. The fluid velocity at the LV wall will effectively be taken the same as the wall velocity derived from MRI scan as described in the earlier section.

Inflow Outflow Boundary Condition

Both outflow and especially inflow into the LV have been found to have significant impact on intra-ventricular flow patterns.2 For example, locations of vortices have been known to form at different locations in the ventricle when slightly different boundary conditions are applied. The challenge in applying this type of boundary condition has inspired many works in literature, including the type of baffle boundary condition18 and hybrid boundary condition.14 Despite unique strengths of the aforementioned boundary conditions, it is to date unclear which boundary condition type is best suited for simulating patient-specific intra-ventricular flow. In light of this we hence propose a relatively simplified boundary condition for our method namely an image-based definition of inflow and outflow conditions. This method is similar to the one used in Refs. 10,14 and essentially allows us to estimate the flow rate into and out of the ventricle using a formula which only requires ventricular volume information. A key advantage of this method is that it does not require patient-specific ventricular pressure data of which acquisition is likely invasive and hence undesirable. Given the volume data obtained from MRI data, the volume flow rate can be derived as the change of volume in time as shown in Fig. 1. Assuming that the total mass are conserved during one cardiac cycle, with the information on the area of mitral and aortic inlets, the flow velocity can be calculated. Figure 5 showed the derived velocity profile for all subjects in the present study during one cardiac cycle.

Figure 5

Velocity profile derived from LV volume change rate that is obtained from MRI data as shown in Fig. 1. This velocity profile will be set at the aortic and mitral inlet depending on phases in one cardiac cycle. In systole velocity is set at aortic inlet while velocity is specified at mitral inlet in diastole phase.

For the inflow boundary condition, velocity is prescribed and pressure is computed from the solution. The inflow boundary condition can be written as

$$\begin{aligned} {\varvec{u}}={\varvec{u}}_\mathrm {in}; \qquad ( {\varvec{u}} \cdot {\varvec{n}})_\text {inflow} < 0 \end{aligned}$$

(22)

where ${\varvec{u}}_\mathrm {in}$ denotes the prescribed inflow velocity. Given the velocity profile determined from MRI images, a mixed type of boundary condition with a switch between inflow and slip wall boundary condition is applied at mitral and aortic boundaries during a cardiac cycle. In systole, inflow boundary condition is applied at the aortic inlet and no-slip boundary condition applied at mitral inlet to take into account the closure of mitral valve. The boundary conditions are then changed in diastole in which velocity is prescribed at mitral inlet and no-slip wall at the aortic inlet. The pressure is set to zero reference pressure at the aortic inlet from the beginning of systole.

Results and Discussion

Using the presented approach for simulations of blood flows in patient specific LV models, numerical results obtained from current study on a small sample of six subjects are presented in this section. Key flow features during cardiac cycles are highlighted and compared with available literature data. The current work also presents some diagnostic findings derived from CFD simulations and verify with existing tools for understanding characteristics of LV diastolic dysfunction in patients.

Blood Flow Analysis from Patient-Specific CFD Simulations

Figure 6 shows blood vector streamlines during one cardiac cycle of a subject (H4) starting from early systole to end diastole. For all the subjects in this work, the cardiac cycle is started from systole and simulations was run for 3–4 full cycles to get the flow solution converged. A total run time for a typical case with 4 full cycles takes about 11.2–13.8 h on 4 CPUs of a 8-core Intel Xeon(R) workstation with 32 GB RAM dependant on the mesh size. From all the cases in this study, it can be observed that LV wall experiences a large motion during a cardiac cycle; this dynamic wall motion could potentially affect numerical stability and convergence. Here the dynamic meshing process developed in this work ensures high quality computational mesh through out the cycle. In Fig. 7, mesh quality in all the frames during cardiac cycle are shown using minimum dihedral angle of tetrahedral element as a mesh quality metric. It can be seen that throughout cardiac cycle, the majority of the elements in the mesh are kept within the acceptable range of minimum dihedral angle of $30^{\circ}\le \theta _d\le 60$; thus producing good mesh for numerical simulations.

In Fig. 8, the flow patterns clearly demonstrate a typical blood flow dynamics in cardiac cycle of human LV from systole to diastole in a healthy subject. In systole under contraction of LV blood is pumped out into the aorta and flows are shown to be regular, laminar towards aorta as viewed in the anterior–posterior (A–P) plane. In diastole, the blood starts to fill in the LV via mitral valve. It can be observed that vortex structures start to form from early E-filling (frame 11–13) as shown in Fig. 8(d–e). Counter rotating pair of vortices is clearly shown in this stage and the vortices continue to grow during diastasis (frame 16–19). Those vortices merge into a single vortex at the late diastole period and maintains its momentum until the fluid is pumped out into the aorta. The formation and development of vortices in LV are consistent with earlier CFD results14,17,18 and 4D MRI observation.3,20 Figure 9 shows snapshots of blood flow streamlines of all subject in the present study at various phases in cardiac cycle. Difference can be found between presented subjects during diastole. In early filling a jet of blood flow straight down from mitral valve can be observed from all of the cases shown in Fig. 9 and LV volume changes quickly from early to mid diastole. In mid diastole, large vortices are formed in some of the cases and grow bigger subsequently. In particular, the vortex structures grows from mid to late diastole in several subjects (H2, H3, H4) but still maintains to be small in other subjects (H1, P1, P2) including two subjects with diagnosed diastolic dysfunction. The vortex structures for all the cases merged into a big vortex at the late diastole period. The vortex that was formed at the late diastole often maintains its momentum until the fluid is pumped out into the aorta. Figure 10 shows a comparison between blood streamlines derived from present CFD simulations for two healthy subjects and echocardiography particle imaging velocimetry.20 Formation and growth of vortices are clearly shown in both ECG-PIV and present numerical results during mid and late diastole. It can be seen that the basic flow dynamics are well captured in CFD simulations as compared with ECG-PIV of healthy subjects. Though there is no direct comparison can be similarly made in the present study due to limitation of the imaging protocol; the above analysis and comparison can provide some confidence to the proposed numerical model.

Figure 6

Flow vector streamlines on one of the subjects (H4) in this study during one cardiac cycle, starting from early diastole.

Figure 7

Mesh quality statitics as percentage of elements with specified dihedral angle for all of the frame during one cardiac cycle. It is noted that most of the elements with good dihedral angle showing consistent mesh quality during the whole cycle.

Figure 8

Details of flow streamlines shown in anterior–posterior (A–P) viewing plane during a cardiac cycle of a healthy subject (H3). The streamlines are colored with velocity magnitude showing blood flow in ejection and filling phases during systole and diastole. In particular vortex formation is apparent in diastolic phase from peak E-filling to A-filling.

Figure 9

Snapshots of blood flow streamlines in one cardiac cycle for all the subject in this study, from top to bottom: H1, H2, H3, H4, P1, P2 shown in anterior–posterior view plane. In each row, streamlines are shown for each subject from early systole to end diastole. The results show typical flow patterns in one cardiac cycle including clear ejection phase in systole as well as vortices formed in diastole phase.

Figure 10

Comparison of flow streamlines between CFD results with echocardiography PIV data in three phases of cardiac cycle (from left to right): mid-diastole, late diastole and early systole. In the middle row, the streamlines colour encoded with kinetic energy derived from echocardiography particle imaging velocimetry (echo-PIV) are shown with velocity obtained from healthy volunteer with reprint permission from Elseivier for the images. Top and bottom are the streamlines derived from CFD simulations for healthy subjects in the present study.

CFD Based Diagnosis from Patient-Specific Study

The velocity streamlines and observations above suggest that there is a significant difference in the time of vortex formation during the diastole stage between studied subjects, especially between the present healthy subjects with patients with diastolic dysfunction (DD). The momentum is easily lost in DD subjects, because the formation was late, thus compromising the efficacy of energy transfer during the systole. As shown in the above Fig. 5, the velocity profiles for the healthy subjects show the presence of generally two distinct features during the diastole period except for the case of H1, and these are the E-wave filling and the A-wave filling. However, for the DD subjects, the E- and A-wave filling phases are not distinct, that is, a late development of E-wave filling phase is observed. As a result, the volume contributed by the E-wave filling phase was not considerably bigger than that contributed by the A-wave filling. In a normal functioning heart, the E-wave filling phase contributes about 80% of the stroke volume.7 The results presented here are consistent with literature findings, where, at the presence of a diastolic dysfunction, a greater portion of the end-diastolic volume is the result of the late filling phase rather than the early filling phase. Consequently, the E/A ratio is reduced in the DD subjects.3 Impaired relaxation affects the early filling phase, thus the E-wave component of the diastolic period is reduced. This effect can be seen clearly in the comparison of flow characteristics between healthy volunteers and DD subjects during diastole shown in Fig. 11 . For the healthy subjects (H3, H4) it is observed that vortices were quickly formed on both sides of the chamber in early filling and grow larger in mid-diastole; however the vortices were formed later and does not grow much in the patients as compared to the healthy subject. In the healthy subjects, those vortices further agglomerates till late diastole to form a strong vortices in the same directions generating momentum for ejection; whereas it remains small vortices in the chamber for the patients as seen in the Fig. 11.

Figure 11

Flow patterns in three different subjects (from top to bottom: H3, H4, P1) at various stages of diastole phase during a cardiac cycle. The streamlines are shown in A–P plane with clear vortices formed during diastole as observed from the present subjects. It is noted that the formation of vortices in the patient P1 is much less apparent as compared to healthy subject H3 and H4.

From the existing data and numerical results, another observation is carried out to validate the current method, by calculating the vortex formation time (VFT) of each subject. VFT is a dimensionless numerical index characterising vortex rings formation in a fluid ejection7 calculated as follows

$$\begin{aligned} T_{VFT} = \frac{4(1-\beta )}{\pi } \times \alpha ^3 \times EF \end{aligned}$$

(23)

In this expression, $\alpha = \frac{EDV^{1/3}}{\bar{D}}$ with $\bar{D}$ is the time-averaged mitral valve diameter; $\beta =\frac{V_A}{SV}$ is the fraction of stroke volume (SV) contributed from LV A-wave filling ($V_A$) and $EF=\frac{SV}{EDV}$ is the ejection fraction measured as a ratio of stroke volume and end diastolic volume (EDV). The vortex formation time Eq. (23) takes in subject-specific variables, such as diameter and volume of the LV, and is in effect the measure of the length to diameter ratio of an ejected fluid column. It measures the optimum ratio needed for an efficient fluid transport through the formation of a vortex structure. The study7 has shown that the optimal vortex formation time is 4, however, there is a discrepancy with the current results, which will be shown in this section. Table 2 shows the estimated vortex formation time of all the subjects in this study. We can observe from the results of vortex formation time calculated for each subject that there is significantly different range of values for the healthy heart and the diseased heart. The values of T for the four healthy cases are larger than 2, while that for the DD cases are less than 2, except for the case H1, whose geometry is possibly faulty. While a study has shown that the range of optimal vortex formation time is between 3.5 and 5.5, the calculated values in this project are, however, generally lower than the values suggested by the earlier work.7 This may be due to several factors, such as geometrical variation in patient-specific study. A cylindrical nozzle was used in the study to generate the vortex ring instead of a physiological mitral annulus that has varying diameter according to the orientation of the diameter orientation.8 Some other geometrical differences may contribute to the discrepancy as well, for example, the time variation of exit diameter ($\bar{D}$) in this study does not take into account opening and closing of the mitral valve; thus resulting in larger average value and smaller VFT. From the results of vortex formation time in Table 2, the two cases that have diastolic dysfunction are observed to have a lower vortex formation time value as seen in the calculation results above. This may be verified from the fact that impaired relaxation, or impaired lusitropy, reduces the volume of fluid contributed by the E-wave filling phase that results in a lower calculated vortex formation time. Therefore, it can be safely concluded that the current results have a plausible agreement with literature findings.

Table 2 Vortex formation time of all subjects in the present study.

As blood flows through LV in a cardiac cycle, it experiences different phases from early filling to late ejection. Changes in LV volumes are proportional to the blood inflow and outflow volumes. Normally blood will not be fully ejected out of the LV in one cardiac cycle as it enters the chamber; part of it will be retained for next ejection as well as being circulated in the LV for many cycles. In Ref. 1, the authors suggested to divide the inflow and outflow blood volumes into four different components including direct flow, retained flow, delayed ejection flow and residual flow. Direct flow is defined as blood flow that enters the LV from diastole and leaves the LV from systole during one cardiac cycle; the amount of direct flow volume contributes to both inflow and outflow volume. Retained flow is the blood flow entering the LV in diastole but not exiting in systole during one heart beat. The blood flow ejected from the LV in systole without entering in diastole is defined as delayed ejection flow. And the blood flow residing within the LV within at least two cardiac cycles is classified as residual flow. Figure 12 shows blood pathlines in one heart beat for two subjects in the present study; the pathlines are coloured by the four blood flow components. It is noted that pathlines are easily constructed from CFD solutions given velocity vector everywhere inside the LV during a cardiac cycle. Starting from isovolumetric contraction frame, the pathlines are computed forward and backward in time using velocity data in each time frame. Tracing the pathlines during a cardiac cycle helps to determine the blood flow components as shown in Fig. 13. Here volumes of four flow components are averaged from all the existing subjects as well as from the unhealthy subjects. It can be seen from Fig. 13 that the two main flow components are direct flow and residual volumes. For healthy subjects, the direct and residual flow components are in the range of previous results reported in Ref. 5. Compared with the average, unhealthy subjects have higher volume of residual flow and lower direct flow volume. The difference are not significant and the standard deviation from the two averages are large indicating a small sample of subjects in the present study. However the present estimation and comparison are consistent with earlier studies using 4D MRI images.4 The present CFD analysis nevertheless shows potential in assisting diagnosis using this component volume information.

Figure 12

Particle pathlines showing blood flows in two subjects in this present study colour coded by four different flow volume components: direct flow (blue), retained flow (green), residual flow (yellow) and delayed ejection flow (red).

Figure 13

Percentage of four blood flow volume component shown as ensemble averages for all the subjects and comparison with average volume percentage of unhealthy subjects. It is noted a small difference in the percentage of direct and residual volume components; however the results may not be reflecting the trend with a small sample as in the present study.

Limitations

The present approach has shown some encouraging results towards patient-specific CFD analysis for heart dysfunctional diagnosis; there are certainly some limitations with the current proposed framework. First, there is absence of patient-specific valve inside the geometry, for both the aortic and mitral annulus. The current CFD modeling methodology makes an approximation that there is instantaneous closing and opening of the mitral and aortic orifice at the top of the geometry. This could be present an inaccuracy of the CFD simulation results, because physiological valves do not open and close instantaneously, rather they are driven by the pressure exerted by fluid that pass through the orifices. However due to coarse time resolution of MRI scans; the above assumption is still reasonable as time step interval in the present protocol is larger than typical time for opening and closing valves. A finer time resolution of scanning procedure potentially poses challenges to the current approach and requires some explicit representation of valves in simulations. Not only the time factor of the heart valve system, but there is also baffle structures on the wall of the ventricle near the valve, and this could affect the development of the vortex during fluid inflow in the diastole stage. Moreover, there is an absence of patient specific pressure data applied at the inlet and outlet boundaries in the current study that can affect the resulting flow characteristics. For the Robin-type of boundary conditions, the reference pressures were currently taken as typical pressure values for normal healthy subjects. It is understood that obtaining patient-specific pressure information is very invasive and quite challenging in imaging procedures; a simplified model of predicting patient-specific pressure can be employed for this purpose such as Windkessel model of the whole blood circulation system.22,25

Conclusions

A computational fluid dynamic framework has been developed in this work and demonstrated successfully a semi-automated procedure for blood flow simulations in patient-specific LV. Using the presented framework, it was able to simulate the blood flow characteristics in patient-specific LV from segmented CMR images to post-processing. Using advanced meshing techniques, reconstruction of smooth geometrical surfaces as well generation of volume meshes for normal and unhealthy subjects’ LV were carried out from coarse surfaces obtained from MRI scans. Dynamic motion of LV walls was translated into mesh motions for CFD simulations using second order ALE finite volume approach. Results from CFD simulations were adeptly analysed by comparing the flow characteristics seen in the LV models of healthy subjects and those with heart dysfunction, as well as with existing literature studies. The CFD results were also post-processed for further analysis of blood flow characteristic and LV functions including vortex formation time, flow component volume. This completes a pipeline allowing development of in-silica techniques that can aid medical professionals to correctly assess the clinical problems. Although with several limitations, the proposed computational framework has shown encouraging results and features. The most promising feature of the patient-specific CFD modeling is the use of the semi-automated method that is efficient and robust enough to take in various LV geometries for further analysis. The semi-automated method is also flexible enough to be modified and further improved, if desired, to suit certain requirements for a potential diagnostic tool.