Evolution of Aggression in Consumer-Resource Models

Abstract

The Hawk–Dove model has been used to explain how aggression evolves in animal species. However, testing this model with experimental data has proven challenging because the two model parameters, V and C, are difficult to measure. We propose a novel consumer-resource model that overcomes these difficulties, and we explore the dynamical behavior of the model. Furthermore, by studying a series of consumer-resource models with interactions based on the Hawk–Dove game, we make new predictions for how the level of aggression may change with the richness of the environment, animal mortality, and the amount of time spent fighting.

1 Introduction

The Hawk–Dove model [22] postulates evolution of aggression among consumers that compete for a resource. The model, presented as a game, considers a population consisting of two behavioral types called Hawks and Doves. Hawks are aggressive individuals that are ready to fight for the resource while Doves are non-aggressive and avoid fighting. Thus, only meetings between two Hawks result in a fight that is costly, and Hawks always win the contest over Doves. The model assumes that the resource level is fixed and it is contested only when two individuals pair. So the model is a prototype of contest competition [20]. The model then predicts that when the cost of fighting for the resource is low, the Hawk is the only evolutionarily stable strategy (ESS), while if the cost is high both Hawks and Doves coexist in the population. The model has two parameters: the cost of fighting and the value of the resource. These parameters are difficult to link to real biology in the context of resource-consumer models, because the model does not make a clear mechanistic link between the measurable quantities (i.e., resource level and mortality rate) and the two model parameters.

Auger et al. [3] advanced toward linking the Hawk–Dove model and the biology by extending this model to consider the resource explicitly. In particular, these authors considered a prey–predator Lotka–Volterra type model where predators play the Hawk–Dove game. They assumed that the equilibrium of this game tracks current prey and predator population densities, and they showed that predators play Hawk when the prey population density is high and predator population is low. This is a counterintuitive result as it might seem that aggressivity should increase with either a decrease in prey density or an increase in predator density, because in both cases the average amount of the resource obtained by a single predator will decrease [4, 7], but see Lach [18]].

In this article, we introduce three theoretical models to study further the link between resource density and aggressivity. The first one (Sect. 2) is the classic Hawk–Dove model where we assume the resource is fixed and we interpret V as the amount of the fixed resource and C as the mortality among Hawks due to fighting. In this model, the evolution of the proportion of Hawks is purely frequency dependent. It is described by the replicator dynamics where the total consumer population growth is exponential. Thus, the model describes contest competition among Hawks and Doves for the resource.

The second model (Sect. 3) considers resource dynamics explicitly. Changes in proportion of Hawks are again described by the replicator dynamics. By modifying the first model to allow resource levels to change in response to consumer behavior, this second model combines scramble competition for resource with contest competition between Hawks and Doves. Both of these two models assume that Hawks and Doves compete for the resource only when they are paired, i.e., individuals do not gain fitness by foraging as a single consumer. This is in line with the assumptions of the classic Hawk–Dove game.

The third, more mechanistic model (Sect. 4) overcomes this assumption by allowing both Hawks and Doves to gain fitness as single foragers. This model then results in a resource-Hawk–Dove consumer model that is similar to the Rosenzweig–MacArthur resource-consumer model, for which, according to the competitive exclusion principle [9, 19], two consumers cannot co-exist with a single resource at equilibrium, unless there is sufficient heterogeneity. This heterogeneity can take many forms [6], for example, spatial heterogeneity [25] or other limiting factors [19]. In the Hawk–Dove game, Hawks are more aggressive than Doves. When Hawks meet Doves, Hawks obtain the resource; when one Hawk meets another Hawk, only one of the Hawks obtains the resource. As we assume that Hawks fight for the resource between themselves and Hawks steal resource that is handled by another Dove, we are also interested to learn whether aggressivity among members of one population provides sufficient heterogeneity to permit coexistence at an equilibrium.

In this article, we illustrate the development of increasingly sophisticated dynamical consumer-resource models motivated by the Hawk–Dove game. With each subsequent model, we re-interpret the game within consumer-resource model frameworks. We explain why a consumer-resource model motivated by the Hawk–Dove game leads logically to the counterintuitive result about the evolution of aggression given by Auger et al. [3]. With the final model, we establish connections with the Rosenzweig–MacArthur model and intraguild predation models, and we produce novel predictions about the dynamics and evolution of aggressive behavior.

2 The Hawk–Dove Model with Fixed Resource

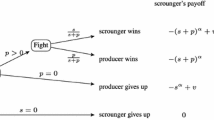
The standard payoff matrix for the symmetric Hawk–Dove game [22] is

(1)

where $V>0$ is the benefit that the winner of a contest obtains, and $C>0$ is the cost of the fight between two Hawks. When $p=H/(H+D)$ is the proportion of Hawks in a population of size $N=H+D$,¹ the payoffs of Hawks and Doves are, respectively,

$$\begin{aligned} W_{H}&=p\frac{V-C}{2}+(1-p) V \end{aligned}$$

(2a)

$$\begin{aligned} W_{D}&=(1-p)\frac{V}{2}. \end{aligned}$$

(2b)

Assuming that Hawk and Dove per capita growth rate is proportional to payoffs, population dynamics are

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}H}{\textrm{d}t}&=(W_{H}-m)H\\ \frac{\textrm{d}D}{\textrm{d}t}&=(W_{D}-m)D \end{aligned} \end{aligned}$$

(3)

where m is the per capita rate of mortality caused by other reasons than resource competition. Competition between Hawks and Doves appears in (3) in the frequency-dependent payoffs $W_H$ and $W_D$. Model (3) can be rewritten using variables that correspond to the proportion of Hawks, p, and the total population size, N, as

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}p}{\textrm{d}t}&=p (W_{H}-m-(\overline{W}-m))=\frac{1}{2} (V-C p)p(1-p)\\ \frac{\textrm{d}N}{\textrm{d}t}&=N(\overline{W}-m)=\frac{1}{2}(V-C p^2-2 m)N \end{aligned} \end{aligned}$$

(4)

where $\overline{W}=p W_H+(1-p)W_D$ is the average payoff.

System (4) is a replicator equation [26] with added mortality m. When we rewrite model (3) as model (4), this dynamical system decouples. We can obtain results about the global stability of equilibria of model (4) by analyzing the dp/dt equation first to determine the dynamics of the distribution of Hawks and Doves and applying that to dN/dt to determine the dynamics of N. The dynamics of model (4) predict that the proportion p of Hawks in the population converges to 1 when $C<V$, or to V/C when $C>V$. Because the population dynamics are density-independent, which is a feature of the replicator dynamics, depending on the relative values of V, C, and m, the population, generically, exponentially grows or decays to zero.

We begin to connect the Hawk–Dove game with classical and novel consumer-resource models by interpreting the game’s payoffs and strategies within this ecological context. Consumers can be aggressive or non-aggressive. Consumers foraging for resources gain a benefit, V, when they encounter and consume the resource. Aggressive consumers pay a cost, C, when they encounter another aggressive consumer and the resource. We interpret the parameters V and C as quantities that add to or detract from a consumer’s growth rate due to the resource competition.

Following the classic HD model of contest competition, we assume that the resource density is fixed and equal to the environmental carrying capacity K, and we assume that V is directly proportional to the density of available resource, i.e., $V=e \lambda K$. This is appropriate when the resource is rapidly renewing. Here, $\lambda$ is the search rate of a consumer for the resource, and e is the efficiency with which a consumer transforms resource uptake to reproduction (see Table 1 for reference). The parameter C measures a cost in terms of additional mortality suffered by two Hawks fighting for the benefit. As in the Hawk–Dove game, V and C are assumed to be constant. After substituting for V and C, model (4) becomes

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}p}{\textrm{d}t}&=\frac{1}{2} (e \lambda K-C p)p(1-p)\\ \frac{\textrm{d}N}{\textrm{d}t}&=\frac{1}{2}(e \lambda K-C p^2-2 m)N. \end{aligned} \end{aligned}$$

(5)

Table 1 Variables and parameters for the models analyzed in this article

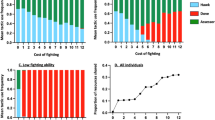
Equilibria of model (5) and conditions for their global stability are given in Table 2. The dependence of the dynamics of model (5) in (m, K) parameter space is shown in Fig. 1a. As mentioned above when describing model (4), the population described by model (5) either grows or decays exponentially to zero.² Although a population that grows without bound does not approach an equilibrium, we will label $\infty$ as an equilibrium value of N in Table 2 and Fig. 1 to facilitate comparisons of this model with the other models we consider below.

Table 2 Equilibria of model (5) and conditions for their feasibility and global stability

As seen in Table 2, there is a unique equilibrium of model (5) for each choice of model parameters $e, \lambda ,K,m,$ and C. First, we observe that the proportion of Hawks at the stable equilibrium $p=V/C=e \lambda K/C$ when $V<C$ corresponds to the ESS of the Hawk–Dove game [10, 22]. When $V>C$, the proportion of Hawks at equilibrium corresponds to the ESS $p=1$. Interpreted biologically, the population will contain both aggressive and non-aggressive animals when the environmental carrying capacity is small relative to the additional mortality cost suffered by two aggressive individuals. When the environment is rich (i.e., $e\lambda K>C$), all animals will be aggressive. This result is qualitatively similar to that of Auger et al. [3].

Fig. 1

Bifurcation diagrams for model (5) (Panel a), model (6) (Panel b), and model (7) (Panel c). For panels (a, b), the stable equilibria showing the proportion of Hawks and overall consumer population density, for models (5) and (6), respectively, are shown in each subset of (m, K) parameter space. For Panel (a) (respectively, Panel b), resources are fixed at K (respectively, resources are at a positive equilibrium given in Table 3). For Panel (c), the global dynamical attractors of model (7) are shown. There are three regions in which the dynamical attractors are equilibria (labeled (K, 0, 0) when both Hawks and Doves go extinct, (R, H, 0) where only Doves go extinct, and (R, H, D) where both Hawks and Doves coexist) and two regions where the dynamical attractors are limit cycles (labeled $(R,H,D)_{osc}$ where both Hawks and Doves coexist along a limit cycle and * where resource and Hawks coexist along a limit cycle while Doves are extinct). Parameters used in these simulations are given in Table 1. In panels (a, b), mortality due to fighting $C=2$. In Panel (c), fighting time $\tau _{HH}=1$

3 The Hawk–Dove Model with Resource Dynamics

The Hawk–Dove game is a prototype of contest competition [21], where the winner monopolizes the contested resource. For example, this game can describe the situation where individuals compete for a fixed number of breeding sites, or males compete for females. However, to connect the Hawk–Dove game to dynamic consumer-resource models, we want to consider both contest competition and scramble competition for a resource [21]. In this section, we remove the assumption of the previous model that the benefit V is constant by including resource dynamics. This is appropriate when the changes in the abundance of resources and the population dynamics of consumers occur on similar time scales. In what follows, we assume that, without consumers, the resource growth rate is logistic and that the consumer growth rate due to resources is directly proportional to the abundance of resources, i.e., $V = e \lambda R$.

From (4), we obtain the following resource-consumer dynamics

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}R}{\textrm{d}t}&=rR\left( 1-\frac{R}{K}\right) -\lambda R N\\ \frac{\textrm{d}p}{\textrm{d}t}&=\frac{1}{2} (e \lambda R-C p)(1-p)p\\ \frac{\textrm{d}N}{\textrm{d}t}&=\frac{1}{2}(e \lambda R-C p^2-2 m)N. \end{aligned} \end{aligned}$$

(6)

In model (6), unlike models (4) and (5), the equations are now coupled. This makes the analysis more complicated and provides a richer dynamical system. Using Mathematica (Appendix A), we calculated the equilibria of model (6) and their local stability. The results are summarized in Table 3, and the stable equilibria in (m, K) parameter space are shown in the bifurcation diagram Fig. 1b. When the consumer mortality rate not due to competition is high (specifically, $m>C/8$) or $m<C/8$ and resource carrying capacity is small (specifically $K<(C+ \sqrt{C(C-8m)})/2$), there is a unique stable equilibrium. This locally stable equilibrium is similar to the unique globally asymptotically stable equilibrium of Sect. 2 in these regions of parameter space (cf. Figure 1a for fixed resource level K) except that, when the consumer population grows exponentially in Sect. 2, now this population size evolves to a positive equilibrium value (either $N_1$ or $N_2$ as given in Table 3). The logistic growth of the resource limited by consumers in model (6) restricts the consumer population size.

For the remainder of parameter space (i.e., $m<C/8$ and $K>(C+ \sqrt{C(C-8\,m)})/2$), there are two stable outcomes for model (6). That is, including resource dynamics as in model (6) can lead to bistability when the mortality rate due to causes other than resource competition is low enough. We did not observe any other dynamical attractors in our simulations. We observe that this bistability occurs in two different ways. In the regions denoted $(1,0), (p_2,N_2)$ and $(p_0,0),(p_2,N_2)$, either the consumer population goes extinct or to a mixed equilibrium of both Hawks and Doves. In the region denoted $(1, N_1), (p_2,N_2)$, the consumer population does not go extinct but it may consist either entirely of Hawks or of both Hawks and Doves. This bistability was also observed by Auger et al. [3]. This demonstrates that when the resource carrying capacity and the cost of fighting are large enough, the population may not go extinct. In the parameter regions where bistability exists, we notice in general that a larger initial population and a larger initial proportion of Hawks leads to the model converging to the Hawk-only equilibrium.

Table 3 Equilibria of model (6) and conditions for their feasibility and local stability

4 The Hawk–Dove Model Embedded in a Mechanistic Consumer-Resource Model

The previous models followed the replicator dynamics framework. The benefit, V, and the cost, C, accrues to the players at the same time. This is precisely why it is difficult to estimate these parameters. For example, if the benefit is a food item, it may take an animal some time to handle the food in order to consume it. Additionally, when animals confront each other over resources, they use non-aggressive or aggressive tactics [8] which may take different amounts of time, as in territorial disputes [12]. To ease parameter estimation while remaining faithful to the core elements of the classical Hawk–Dove game, we create a mechanistic consumer-resource model that includes the salient properties of the Hawk–Dove game, namely, when players meet they may acquire a benefit through sharing or stealing resources from another player, or they may pay a cost for fighting.

To account for the time to handle a food item and to resolve antagonistic encounters, we separate Hawks into three distinct groups: searching for resources, handling resources, and fighting over resources being handled by another Hawk. Similarly, we have two groups for the Doves: searching for resources and handling resources [24]. Motivated by the classic Hawk–Dove model, we assume that when a searching Hawk meets a handling Dove, the Hawk steals the handled resource and immediately becomes a handling Hawk while the handling Dove becomes a searching Dove. When a searching Hawk meets a handling Hawk, a fight occurs. The cost of this fight can be measured temporally in two ways, time spent in an activity that reduces the potential for resource gain and reduced lifespan due to the additional mortality resulting from a fight [15]. We assume that a fight is time consuming and takes time $\tau _{HH}.$ Fighting Hawks experience additional mortality at the rate $m_f$, on average. Once the fight concludes, the winning Hawk handles the resource and the losing Hawk returns to searching for resources.

The dynamical equations that reflect these processes are

$$\begin{aligned} \dot{R}&=\bigg (r(1-\frac{R}{K})- \lambda H_{s}- \lambda D_{s}\bigg )R \end{aligned}$$

(7a)

$$\begin{aligned} \dot{H}_s&= \bigg [ - \lambda H_s R - \lambda H_sD_h-\lambda H_s H_h+\frac{1}{h}H_h+\frac{H_f}{\tau _{HH}}\bigg ] + \frac{e}{h} H_{h}-m H_{s} \end{aligned}$$

(7b)

$$\begin{aligned} \dot{H}_h&= \bigg [ \lambda H_sR+ \lambda H_sD_h+\frac{H_f}{\tau _{HH}}- \lambda H_sH_h-\frac{1}{h}H_h\bigg ] -m H_{h} \end{aligned}$$

(7c)

$$\begin{aligned} \dot{H}_f&= \bigg [2 \lambda H_sH_h-2\frac{H_f}{\tau _{HH}} \bigg ]-m H_{f}-m_{f}H_{f} \end{aligned}$$

(7d)

$$\begin{aligned} \dot{D}_s&= \bigg [- \lambda D_sR+ \lambda D_hH_s+\frac{1}{h}D_h\bigg ] + \frac{e}{h} D_{h}-m D_{s} \end{aligned}$$

(7e)

$$\begin{aligned} \dot{D}_h&= \bigg [ \lambda D_sR- \lambda D_hH_s-\frac{1}{h}D_h\bigg ] -m D_{h}. \end{aligned}$$

(7f)

The bracketed terms account for the aforementioned distributional dynamics which describe the rates at which Hawks and Doves transition from searching, handling, and, for Hawks only, fighting. The terms outside the brackets describe demographic changes described by resource consumption, natural mortality, and additional mortality due to fighting, for Hawks only. Definitions of each variable and parameter are given in Table 1.

Using Mathematica command Solve, we solve for equilibria of model (7). We obtain nine equilibria and, using command Reduce, we search for those that are positive (by assuming that all parameters are positive), i.e., all variables are greater than zero. We obtain that there is no more than one such interior positive equilibrium. Conditions on parameters for this equilibrium to exist are given by quite complex formulas as are the expressions for the equilibrium, so we do not give them here. We are unable to calculate analytically the conditions for the linear stability of this equilibrium, so we analyze model (7) numerically. A numerical bifurcation analysis (Fig. 1c) shows attractors in (m, K) parameter space. Since we are interested in learning more about the stability of aggressive and non-aggressive strategies, we sum across the three groups of Hawks to obtain Hawk abundances (H) and similarly across the two groups of Doves to obtain Dove abundances (D). First, we observe that the two competitors, Hawks and Doves, can stably coexist at this equilibrium for certain parameter values. Second, as the environmental carrying capacity, K, increases, there are two or three thresholds, depending on the mortality rate, where resources may coexist with Hawks at equilibrium or in oscillations, or resources, Hawks, and Doves coexist. Below the lowest threshold (the bottom curve in Fig. 1c), no consumers exist. At low mortality rates (e.g., $m=0.1$), Hawks invade the resource-only equilibrium when the first threshold is met. Hawks exist at an equilibrium with resources at this equilibrium. At the second threshold, this equilibrium loses its stability and Hawks coexist with the resource along a stable limit cycle (this region is denoted as “*”in Fig. 1c). At the highest threshold, Doves invade and Hawks, Doves, and Resource coexist along a stable limit cycle. At higher mortality rates (e.g., $m=0.4$), Hawks and Doves invade simultaneously the resource-only equilibrium at the first threshold. At the next threshold (not shown in Fig. 1c), the coexistence equilibrium destabilizes and Hawks, Doves, and Resources stably coexist along a limit cycle.

To allow us to make comparisons of these models’ results with previous studies of the Hawk–Dove game, we calculate numerically the average proportion of Hawks in the regions in (m, K) parameter space where Hawks and Doves coexist.³ We observe that, at low values of m (e.g., $m=0.1$, Fig. 2a), as the environmental carrying capacity K decreases, the average proportion of Hawks increases. At higher mortality rate values (e.g., $m=0.7$, Fig. 2a), the dependence on K of this proportion is non-monotonous. In fact, as K decreases from 15, the average proportion of Hawks decreases first. The white region of the figure corresponds to parameter values at which the consumer population goes extinct, i.e., p is undefined.

Fig. 2

Panel (a) shows average proportion of Hawks as a function of m and K when $\tau _{HH}=1$. Panel (b) shows average proportion of Hawks as a function of m and $\tau _{HH}$ when $K=10$. Other parameters as listed in Table 1. The white region in Panel (a) corresponds to the extinction of both Hawks and Doves

Hawks pay two types of costs when they fight, represented by $m_f$ and $\tau _{HH}$. Additional mortality due to fighting, $m_f$, is a direct cost. Time spent fighting, $\tau _{HH}$, is an opportunity cost, since neither Hawk gains any payoff during this fighting time. These combine to contribute to the cost C paid by Hawks in the context of the Hawk–Dove game (1). When the time that two Hawks fight over the resource is small, Doves go extinct and Hawks survive along with the resource. For longer fighting times, Hawks and Doves coexist with the resource. We discovered that the level of aggression depends on m. As seen in Fig. 2b, once the fighting time exceeds a threshold that depends on m, the level of aggression decreases with increases in fighting time. This is consistent with the Hawk–Dove game where increased costs tend to lead to a lower proportion of Hawks.

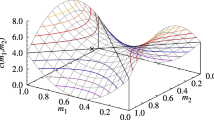
It is well known [e.g.,  14, 17] that the number and stability of equilibria can change when the amount of time that individuals are paired while fighting differs from the amount of time they are paired for other activities. Our numerical results can be seen in the bifurcation diagram, Fig. 3. As before, we sum Hawk groups and Dove groups to obtain Hawk and Dove abundances.

Contrary to the aforementioned results cited above as well as the results of Sect. 3, we did not observe bistability for any of the m and $\tau _{HH}$ values we used. When mortality m is large, Hawks and Doves go extinct. For smaller values of m, we observe Hawks or both Hawks and Doves surviving with the resource, either at an equilibrium or along a limit cycle.

In sum, as the mortality rate changes and as the amount of time that two Hawks fight changes, the stable equilibrium can change (see Fig. 3). We conjecture that the mechanism that causes each equilibrium to become unstable is similar to that of the Rosenzweig–MacArthur model with Holling type II functional response.

Fig. 3

Bifurcation plot for model (7) in $(m, \tau _{HH})$ parameter space. Equilibria where Hawks and Doves coexist are denoted as (R, H, D), equilibria where only Hawks exist are (R, H, 0), and equilibria where both Hawks and Doves are extinct are (R, 0, 0). In the region $(R,H,D)_{osc}$, Hawks and Doves coexist along a limit cycle while in the region $(R,H,0)_{osc}$ only Hawks coexist along a limit cycle with resources. Other parameters as listed in Table 1, and $K=10$

5 Discussion

The Hawk–Dove game [22] predicts that the level of aggression (i.e., the proportion of Hawks) in a population of individuals competing for some resource equals the ratio of the resource value and the cost of a fight between two aggressive individuals who compete for the resource.⁴ This shows that as the value of the resource increases, the proportion of Hawks in the population increases too. Thus, if the value of the resource is thought to be proportional to the environmental carrying capacity, the level of aggression increases with the environmental enrichment. Auger et al. [3] remarked “[t]his result is rather counter-intuitive as... we have expected an increase of contest competition in low prey accessibility.” This game also serves as a prototype model of contest competition. In this article, we show that combining contest competition with scramble competition changes this “counterintuitive” trend as the proportion of Hawks can increase as the environmental carrying capacity decreases.

The Hawk–Dove game is valuable in helping understand why animals may not use lethal force against conspecifics; however, it is too general to serve as a predictive model because the two parameters V and C are not defined well enough to be measured from biological data. To resolve this, we recast the Hawk–Dove game as a model system of two types of consumers competing for a single type of resource. This permits us to represent the benefit V as a renewable food resource and the cost C as additional mortality due to fighting, as in models (5) and (6) of Sects. 2 and 3, respectively. These models are closely related to the models studied by Auger et al. [3] except that these authors (i) assumed that the proportion of Hawks was at the ESS, and (ii) did not relate consumer per capita growth rate to the resource level, i.e., they assumed that the consumer per capita growth rate was fixed and equal to V. Assumption (i) is consistent with fast game dynamics relative to demographic dynamics. Although the transient dynamics of their model should differ slightly from ours, the equilibrium points and their stability (and bistability) are the same.

Indeed, when we focus on the regions in (m, K) parameter space where Hawks or Hawks and Doves are present, it appears in Fig. 1a, b that richer environments (i.e., those with a higher carrying capacity) promote aggression. This is easy to see because when resource abundance is low, the evolutionarily stable proportion of Hawks in the consumer population is directly proportional to the amount of available resource, independent of whether or not the resources are dynamic. This is evident for model (5) of Sect. 2, since in Table 2 the proportion of Hawks at the equilibrium labeled $E_1$ is $e \lambda K/C$, which is directly proportional to K. Furthermore, in our second model (i.e., (6) of Sect. 3) at the equilibrium labeled $(p_2, N_2)$, the proportion of Hawks, p, is again directly proportional to R, as seen in Table 3. Thus, we conclude that the counterintuitive result about aggressivity obtained in Auger et al. [3] and replicated here is not due to their time scale separation. Rather, this counterintuitive result derives from representing the benefit as a quantity directly proportional to the abundance of resource.

When we remove the assumption that the value of the resource is directly proportional to the amount of available resource, as in model (7) of Sect. 4, we obtain results about aggressivity that are more in line with our intuition. For instance, in the region where Hawks and Doves coexist and the dynamics are oscillatory, the average proportion of Hawks decreases with increases in K when m is not too large (e.g., $m=0.2$ in Fig. 2a). Larger values of K increase the abundance of available resources. Thus, searchers can more easily encounter resources which appears to have a proportionally larger positive effect on Doves. For larger values of m, the relationship between the average proportion of Hawks and K is more complicated. When $m=0.5$, for example, the proportion of Hawks tends to decrease until the carrying capacity K exceeds 5.5, beyond which point this proportion increases and then decreases slightly. In sum, we conclude that aggressivity can evolve in environments with low resource carrying capacity, consistent with intuition about scramble competition.⁵

We expect aggressivity in model (7) to decrease with increases in fighting time between Hawks since fighting time is a type of opportunity cost, where time spent fighting reduces the amount of time available to forage for resources. It is less clear that aggressivity will also decrease with increases in the natural mortality rate, m. As m increases, the consumer population gets smaller, but this has a disproportionate impact on the abundances of Hawks, thereby reducing aggressivity. Numerical explorations reveal that the proportion of searchers decreases when m increases (the proportion of handlers increases and the proportion of fighters increases then decreases). Since Hawk searchers benefit from encountering resources and Dove handlers, fewer searchers leads to a lower effective growth rate that is not offset by reduced fighting costs. In conclusion, aggressivity decreases with increases in both fighting time, $\tau _{HH}$, and natural mortality, m, as confirmed in Fig. 2b.

As we embed the Hawk–Dove model into progressively more sophisticated consumer-resource model frameworks starting in Sect. 2 and ending in Sect. 4, we observe that the regions of extinction of both Hawks and Doves shrink, the regions of exclusion of Doves and coexistence of Doves are transformed, and new dynamics emerge. Model (5) has a unique equilibrium whereby the consumer population either grows without bound or goes extinct, depending on the parameter values used. When we include resource dynamics limited by an environmental carrying capacity in models (6) and (7), the consumer abundance does not tend to infinity, as seen in Fig. 1 panels b and c, respectively. The resource limitation predictably limits the growth of the higher trophic level. In model (6), we observe only equilibrium dynamics. Quite unexpectedly, including resource dynamics leads to bistability in three regions in (m, K) parameter space. Similar bistability is observed in intraguild predation models.⁶ In the two sub-regions in Panel b where consumers go extinct in model (5) (for example, where $(m,K)=(0.2, 1.75)$ and $(m,K)=(0.2, 2.25), cf. Panel\, a\, vs. Panel\, b)$, Hawks and Doves can coexist or go extinct. In a third sub-region (for example, where $(m,K)=(0.2, 3.0)$), either Hawks and Doves coexist or Hawks survive alone. Within these sub-regions, the initial proportion of Hawks and the initial number of consumers determine whether the consumer population will go extinct.

In the consumer-resource model (7), we did not observe bistability, but Hawks or Hawks and Doves may coexist with resources at an equilibrium or along a limit cycle. Figures 1c and 3 display the regions of (m, K) and $(m, \tau _{HH})$ parameter space where these behaviors were observed numerically. These figures indicate that in general, a sufficient reduction in m tends to cause dynamical instability as in the Rosenzweig–MacArthur resource-consumer model. Stable equilibrium points become unstable and are replaced by stable oscillatory dynamics when m is reduced. As K is reduced, this instability occurs at lower values of m. When Hawks and Doves coexist with resource, this instability similarly occurs at lower values of m when $\tau _{HH}$ is smaller. In contrast, when only Hawks exist along with resource, this instability occurs at higher values of m as $\tau _{HH}$ is reduced

Hawks and Doves coexist at equilibrium with finite population abundances in models (6) and (7). At first glance, this appears to violate the competitive exclusion principle which states that without sufficient heterogeneity, two consumers cannot co-exist with a single resource at equilibrium. For example, the Rosenzweig–MacArthur model, when applied to a single resource and two competing consumers, only admits coexistence of two consumers on a single resource when there is variation in population densities [2]. According to Amarasekare [1], competitive trade-offs may provide sufficient heterogeneity to allow two consumers foraging on a single resource to co-exist at equilibrium. Specifically, “when interference involves mechanisms that provide a benefit to the interacting species, coexistence is possible provided competing species exhibit an interspecific trade-off between exploitation and interference”⁷[1]. Models (6) and (7) include both scramble competition and contest competition. Scramble competition is modeled by Hawks and Doves consuming the same resource, and contest competition is modeled by Hawks fighting over the resource and Hawks stealing the resource from Doves. Scramble competition exerts an equal effect on both Hawks and Doves. The effects of contest competition differ for Hawks and Doves due to the differences between Hawk–Hawk and Hawk–Dove interactions, as in the Hawk–Dove game (1). The parameters $m,\,K,$ and $\tau _{HH}$ affect the impact that contest competition has on the relative growth rates of Hawks and Doves. When K is larger, searching Doves can more easily encounter resources, and the proportion of Hawks that are searching is reduced. Taken together, Doves experience less contest competition when K is larger. This reduction of competition pressure facilitates coexistence. Within our consumer-resource framework, the different antagonistic interactions among and between Hawks and Doves provides the necessary heterogeneity for Hawks and Doves to co-exist at equilibrium.

Future work includes studying more closely the functional response that can be obtained from the consumer-resource model of Sect. 4. It would also be interesting to explore an analogous extension of the Hawk–Dove model for sexual selection where the resources are not food items but mates.

A Model (6) analysis

First, we reparametrize model (6). This reparametrization is important in stability analysis given below because it allows us to derive in Mathematica conditions for local equilibria stability analytically. This is not possible for the original parametrization of the model given in the article.

Let $R = \alpha \tilde{R},\,N=\gamma \tilde{N}, t = \delta \tau$. Then,

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}\tilde{R}}{\textrm{d}\tau }&= \delta \left[ r\tilde{R}\left( 1-\frac{\alpha }{K}\tilde{R}\right) -\lambda \gamma \tilde{R} \tilde{N}\right] \\ \frac{\textrm{d}p}{\textrm{d}\tau }&=\frac{\delta }{2} (e \lambda \alpha \tilde{R}-C p)(1-p)p\\ \frac{\textrm{d}\tilde{N}}{\textrm{d}\tau }&=\frac{\delta }{2}(e \lambda \alpha \tilde{R}-C p^2-2 m)\tilde{N}. \end{aligned} \end{aligned}$$

(8)

Letting $\delta = \frac{1}{C},\,\gamma =\frac{C}{\lambda },$ and $\alpha = \frac{C}{e\lambda }$, we obtain after simplification,

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}\tilde{R}}{\textrm{d}\tau }&= \frac{r}{C}\tilde{R}\left( 1-\frac{C}{e \lambda K}\tilde{R}\right) - \tilde{R} \tilde{N}\\ \frac{\textrm{d}p}{\textrm{d}\tau }&=\frac{1}{2} (\tilde{R}- p)(1-p)p\\ \frac{\textrm{d}\tilde{N}}{\textrm{d}\tau }&=\frac{1}{2}\left( \tilde{R}- p^2-\frac{2}{C} m\right) \tilde{N}. \end{aligned} \end{aligned}$$

(9)

Now we reparametrize with $\tilde{r} = \frac{r}{C},\,\tilde{K} = \frac{e\lambda K}{C},\,\tilde{m}=\frac{2}{C} m$ to yield

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}\tilde{R}}{\textrm{d}\tau }&= \tilde{r}\tilde{R}\left( 1-\frac{\tilde{R}}{\tilde{K}}\right) - \tilde{R} \tilde{N}\\ \frac{\textrm{d}p}{\textrm{d}\tau }&=\frac{1}{2} (\tilde{R}- p)(1-p)p\\ \frac{\textrm{d}\tilde{N}}{\textrm{d}\tau }&=\frac{1}{2}(\tilde{R}- p^2-\tilde{m})\tilde{N}. \end{aligned} \end{aligned}$$

(10)

Finally, we can drop the tildes to obtain the system

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}R}{\textrm{d}\tau }&= rR\left( 1-\frac{R}{K}\right) - R N\\ \frac{\textrm{d}p}{\textrm{d}\tau }&=\frac{1}{2} (R- p)(1-p)p\\ \frac{\textrm{d}N}{\textrm{d}\tau }&=\frac{1}{2}(R- p^2-m)N. \end{aligned} \end{aligned}$$

(11)

The new state variables correspond to the old ones by $\tilde{R} = \frac{e \lambda }{C}R,\,\tilde{N} = \frac{\lambda }{C}N$.

The advantage of model reparametrization is that model (11) can be analyzed using Mathematica. First, we calculated equilibria and then, using the Routh-Hurwitz criterion we derived conditions for the theoretical local asymptotic stability using command Reduce of Mathematica 12. The results are given in Table 4.

Table 4 Equilibria and their stability of system (11)