Optimal Evading Strategies and Task Allocation in Multi-player Pursuit–Evasion Problems

Abstract

Pursuit–evasion problems involving multiple pursuers and evaders are studied in this paper. The pursuers and the evaders are all assumed to be identical, and the pursuers are assumed to follow either a constant bearing or a pure pursuit strategy, giving rise to two distinct cases. The problem is simplified by adopting a dynamic divide and conquer approach, where at every time instant each evader is assigned to a set of pursuers based on the instantaneous positions of all the players. In this regard, the corresponding multi-pursuer single-evader problem is analyzed first. Assuming that the evader knows the positions of all the pursuers and their pursuit strategy, the time-optimal evading strategies are derived for both constant bearing and pure pursuit cases for the pursuers using tools from optimal control theory. In the case of a constant bearing strategy, and assuming that the evader can follow any strategy, a dynamic task allocation algorithm is proposed for the pursuers. The algorithm is based on the well-known Apollonius circle and allows the pursuers to allocate their resources in an intelligent manner while guaranteeing the capture of the evader in minimum time. For the case of pure pursuit, the algorithm is modified using the counterpart of the Apollonius circle leading to an “Apollonius closed curve.” Finally, the proposed algorithms are extended to assign pursuers in the case of a problem with multiple pursuers and multiple evaders. Numerical simulations are included to demonstrate the performance of the proposed algorithms.

1 Introduction

Coordination strategies for unmanned aerial vehicles (UAVs) have been an active area of research especially in the realm of multi-agent systems over the past decade [5, 13, 17, 32, 55], having numerous applications, including agriculture, aerial surveying, fire detection, disaster management, weather monitoring, and commercial product delivery. Recent analyses of the commercial UAV market show that their use is expected to grow manyfold over the coming years, as aerial drones are becoming a household product, used for recreational and industrial purposes alike.¹ These advancements suggest an urgent need to explore designs for airspace safety systems that can regulate the traffic and usage of UAVs in a large scale. Similarly, UAVs already play a major role in military engagement scenarios, and their use as part of swarm tactics (encirclement, coordinated attack, search and rescue, perimeter defense) promises to change future battlefield operations. It should therefore come as no surprise that a great amount of work has been devoted over the past decade to study coordination strategies of multi-agent UAV problems [42]. To this end, UAV coordination strategies that formulate the problem as a multi-player pursuit–evasion (PE) game offer solutions that address many of the challenges involving multi-agent systems such as of collision avoidance, surveillance and target acquisition [12, 14, 22, 26, 31, 34, 45, 46]. A recent survey of zero-sum PE games with multiple agents can be found in Ref. [25]. Several other prior works dealing with multi-pursuer single-evader (MPSE) PE problems can be found in the literature, and some of the proposed solution techniques have been extended to the associated multi-pursuer multi-evader (MPME) problem with a “divide and conquer” approach in mind.

Evasion from a group of pursuers is a classical MPSE problem that has received a great deal of attention in the literature. Sufficient conditions for successful evasion from a group of identical pursuers were given by Pshenichnyi [39]. These results were later extended by Blagodatskikh and Chernous’ko [7, 10]. The MPSE problem has also been investigated in a differential game setting subject to fixed terminal time, integral and geometric constraints, and different pay-off models [18,19,20]. Obtaining closed-form optimal strategies for all the players for this class of games using Hamilton–Jacobi–Isaacs (HJI) equation formulations is elusive, however, owing to the well-known curse of dimensionality. In this regard, an approach based on value functions to arrive at sub-optimal solutions was proposed by Jang and Tomlin [23]. Zak extended the result to evaders that are more agile compared to the pursuers [56]. Oyler et al. [33] studied planar PE games in the presence of obstacles by constructing the dominant regions for each player. Limitations for capturing a faster evader were provided by Makkapati and Kothari [40], along with a heuristic group pursuit strategy. Additional versions of the group pursuit problem include the problem involving a group of faster, yet less agile, pursuers against a slower, but more agile, evader [8], and the problem with constraints on observations and allowable flying zones [28, 37].

Group pursuit problems involving general dynamics have also been studied in [6, 11, 35, 38]. A probabilistic variant of group pursuit problems has been investigated in [16] using a greedy policy. The analysis was later used to study some heuristic strategies in the case of games with incomplete information [1]. More recently, Bakolas and Tsiotras used dynamic Voronoi diagrams to study MPSE problems in a relay group pursuit setting [2, 4]. Finally, two-pursuer one-evader problems were studied by Makkapati et al. [29].

The literature for multi-pursuer multi-evader (MPME) problems, where there are players from two teams encountering each other with conflicting motives [43, 44, 53], is rather limited compared to its MPSE counterpart. In most cases, some form of heuristic is introduced in order to make the problem tractable. Ge et al. [15] proposed three approaches, which include hierarchical decomposition, moving horizon hierarchical decomposition, and cooperative control. Li et al. [27] also explored a hierarchical approach, while Jin and Qu [24] proposed a heuristic task allocation algorithm. Extensions to the MPME problem include problems with incomplete information [1], nonlinear dynamics [49], and a mix of continuous and discrete observations [48]. However, finding scalable algorithms which can be implemented in real-life MPME scenarios is still an open problem [36, 52].

This paper aims at extending current solution techniques for MPME games involving large teams of UAVs by developing implementable, scalable solutions based on a decomposition of the original MPME problem to a sequence of simpler MPSE problems. A major enabler for this decomposition is a new result that allows us to characterize each pursuer as relevant or redundant for each evader. Only the relevant pursuers participate in the MPSE pursuit of each evader. The identification and classification of each pursuer as relevant or redundant makes use of the classical tool of the Apollonius circle (in the case when the pursuers follows a constant bearing strategy) or its extension, termed herein as Apollonius curve, (in the case when the pursuers follows a pure pursuit strategy). The efficacy of the approach is demonstrated using an illustrative example involving ten pursuers and five evaders.

After this brief introduction, we are now ready to formulate the problem we are interested in solving in this paper.

1.1 Motivating Example

Consider a group of n agents (pursuers) guarding a given area of interest. The objective of the agents is to pursue and intercept m (where typically $m \le n$) intruders (or evaders) that may be detected in this area. Some of the relevant questions that arise while solving this problem include:

• 1. Which pursuer(s) should go after which evader(s)?

• 2. How many pursuers should chase each intruder (evader) in order to capture it in the shortest time possible?

• 3. What is the shortest time-to-capture, given the fact that the evaders are intelligent and will try to postpone capture indefinitely?

Obtaining the answers to the previous questions in their most general form is elusive at this point. Addressing them involves solving a multi-player dynamic game, eventually demanding the solution to a high-dimensional partial differential equation, with the dimensionality increasing as the number of players ($n+m$). In order to proceed and mitigate this problem, the following assumptions are made in this paper.

• A1: The pursuers are faster compared to the evaders.

• A2: The pursuers follow simple navigation laws (pure pursuit or constant bearing strategies).

The rationale behind these assumptions is as follows. Under assumption A1, a pure pursuit or a constant bearing strategy guarantees capture. Also, these two pursuit strategies highlight the available information to the pursuer in order to capture the evader. A constant bearing (CB) strategy is known to be efficient when the pursuer knows the instantaneous position and velocity of the evader [47]. On the other hand, an individual pursuer that has access only to the evader’s instantaneous position can, at best, employ a pure pursuit (PP) strategy [47]. Furthermore, both of these strategies are easy to execute, and they have been implemented successfully in various aerial defense systems. A more detailed discussion on navigation laws for different information structures can be found in Ref. [3].

A potential approach to solve complicated MPME problems is a dynamic “divide and conquer” approach, where the pursuers are divided into several groups corresponding to the evader they pursue at each instant of time. In essence, such divide and conquer strategies formulate the original MPME problem as a sequence of several (simpler) MPSE problems [15, 50]. This approach leads to decentralized (although likely sub-optimal) solutions, as can be seen later. By analyzing the associated multi-pursuer single-evader (MPSE) problems for the cases of CB and PP, one may arrive at an efficient dynamic task allocation algorithm of pursuers to evaders.

The main contributions of this paper can be summarized as follows:

• 1. Inspired from real-world scenarios, first, we provide problem formulations for MPSE and MPME problems, where the pursuers follow simple navigation laws, constant bearing (CB), and pure pursuit (PP).

• 2. In both cases (CB and PP), we derive the characteristics of the optimal evading strategy in the MPSE setting, and establish that the optimal evading strategy depends only on the initial conditions of those pursuers that finally capture (simultaneously) the evader.

• 3. We provide a framework to characterize the pursuers into relevant and redundant in MPSE settings using Apollonius circles (for CB) and Apollonius curves (for PP).

• 4. We provide an algorithm to identify the status of a pursuer, given the instantaneous positions of all the players in the MPSE settings. This algorithm allows us to perform a dynamic task allocation of the pursuers that ensures the evader’s capture in minimum time, under any evading strategy.

• 5. We extend the task allocation algorithm to MPME settings by enforcing a dynamic divide and conquer approach to solve the problem. The resulting algorithm is scalable for any number of pursuers and evaders.

1.2 Problem Formulation

Motivated by the problem discussed in the previous subsection, we consider a pursuit–evasion problem in the Euclidean plane that involves n identical pursuers and m identical evaders. The pursuers’ objective is to capture all the evaders. Capture occurs when one or more pursuers enter the capture zone of an evader (assumed here to be a disk of radius $\epsilon > 0$ centered at the instantaneous position of the evader). At the same time, each evader aims at avoiding capture indefinitely. Let $P_i$ denote the $i\mathrm{th}$ pursuer and let $E_j$ denote the $j\mathrm{th}$ evader. Let also $\mathcal {P}= \{P_1,P_2,\ldots ,P_n\}$ denote the set of pursuers and, similarly, let $\mathcal {E}= \{E_1,E_2,\ldots ,E_m\}$ denote the set of evaders. With a slight abuse of notation, in the sequel, we will also use the subscript indices to denote the corresponding evader or pursuer.

The equations of motion of all the agents are given below

$$\begin{aligned} \dot{x}_i&= u\cos \theta _i, \quad \dot{y}_i = u\sin \theta _i, \quad i \in \mathcal {P}, \end{aligned}$$

(1)

$$\begin{aligned} \dot{x}_j&= v\cos \theta _j, \quad \dot{y}_j = v\sin \theta _j, \quad j \in \mathcal {E}, \end{aligned}$$

(2)

where $p_i = (x_i,y_i) \in \mathbb {R}^2$, and $e_j = (x_j, y_j) \in \mathbb {R}^2$ denote the positions of pursuer $P_i$, and evader $E_j$, respectively, and $\theta _i$ and $\theta _j$ denote the heading angles (control inputs) for the pursuers and the evaders, respectively. In (1) and (2), u and v are the speeds of the pursuers and the evaders, which are assumed constant with $u>v$. The number of states is $2(n+m)$, and it increases linearly with the number of players. It is assumed that the pursuers follow a given, known pursuit strategy. The two distinct pursuit strategies investigated in this paper are CB (the pursuers follow a constant bearing strategy) and PP (the pursuers follow a pure pursuit strategy).

The three problems to be addressed in this paper are listed below.

Problem 1

For both cases CB and PP with $m=1$ (MPSE problem), and assuming that the pursuers are unaware of the evader’s strategy, which pursuers should go after the evader to minimize capture time?

Problem 2

For both cases CB and PP with $m=1$ (MPSE problem), and assuming that the evader has complete information of the pursuers’ whereabouts and their strategy, what is the time-optimal evading strategy?

Problem 3

For both cases CB and PP with $m \ge 1$, and assuming that the pursuers are unaware of the evaders’ strategy, which pursuer(s) should go after which evader(s)?

The rest of the paper is organized as follows. Section 2 presents the characteristics of the optimal evading strategies in MPSE problems for both cases, namely CB and PP. Section 3 develops the theory of active/redundant pursuers and presents an algorithm for task allocation in the context of MPSE problems. The algorithm is then extended to dynamically allocate pursuers to the evaders in the MPME setting. This is discussed in Sect. 4. Numerical simulations demonstrating the performance of the algorithms in both MPSE and MPME settings are included in Sects. 3 and 4, respectively. Section 5 provides concluding remarks and some directions for future work.

2 Optimal Evading Strategies in Multi-pursuer Single-Evader Problems

2.1 Constant Bearing Strategy

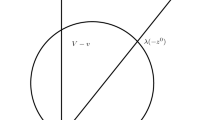
A schematic of the problem geometry with one evader and n pursuers (henceforth, referred to as the MPSE problem) following a constant bearing strategy is shown in Fig. 1a. Since the pursuers are assumed to be following a constant bearing (CB) strategy, the problem can be analyzed by tracking the relative distances between the pursuers and the evader, effectively reducing the number of states from $2(n+1)$ to just n. In this regard, the dynamics can be written in the form,

$$\begin{aligned} \dot{r}_i = v \cos (\theta _{{ E}}- \varphi _i) - u \cos (\theta _i - \varphi _{i}), \qquad i \in \mathcal {P}, \end{aligned}$$

(3)

where $r_i$ is the relative distance between pursuer $P_i$ and the evader, and $\varphi _{i} = \text {atan2}(y_{{ E}}-y_i,x_{{ E}}-x_i)$ is the corresponding line-of-sight (LoS) angle. From now on, we will drop the subscripts for the evader and will use E instead of j to denote the single evader in MPSE settings (i.e., in Sects. 2, 3). Furthermore, we indicate the pursuers using the subscripts directly and the set $\mathcal {P} = \{1,2,\ldots ,n\}$. Note that in the case of a constant bearing strategy, the bearing angle between a pursuer and the evader remains constant until the time-of-capture. Using this fact, the instantaneous heading of pursuer $P_i$ ($\theta _i$, $i \in \mathcal {P}$) can be obtained from the relation,

$$\begin{aligned} u \sin (\theta _i - \varphi _{i}) = v \sin (\theta _{{ E}}- \varphi _{i}), \end{aligned}$$

(4)

which is a function of the instantaneous heading of the evader $\theta _{{ E}}$. The above relation has two possible solutions for each $\theta _i$, given $\theta _{{ E}}$, and the solution for which $\dot{r}_i < 0$ is chosen.

Fig. 1

Schematics of the proposed pursuit–evasion problems

The initial conditions of the problem are

$$\begin{aligned} r_i(0) = \Vert e(0) - p_i(0) \Vert , \qquad i \in \mathcal {P}, \end{aligned}$$

(5)

and the terminal condition is

$$\begin{aligned} \varPsi (r_1(t_{\mathrm{c}}), r_2(t_{\mathrm{c}}),\ldots ,r_n(t_{\mathrm{c}})) = \min _{i \in \mathcal {P}} r_i(t_{\mathrm{c}}) - \epsilon = 0, \end{aligned}$$

(6)

where $t_{\mathrm{c}}$ is the time-of-capture. A formal definition for the time-of-capture is given below.

Definition 1

Given the initial positions of the players (at $t = 0$) in an n-pursuer single-evader problem and assuming that the pursuers follow either a constant bearing or a pure pursuit strategy, and for any evading strategy, the time-to-capture$t_{\mathrm{c}}~(\ge 0)$ is the minimum time so that there is at least one pursuer in the capture zone of the evader.

Since $\theta _i$ is a function of $\theta _{{ E}}$, and by the nature of Assumption A1 ($v < u$), $r_i$ decreases monotonically for all time, and lies in the set $[\epsilon ,r_i(0)]$, $i \in \mathcal {P}$. Also, the time-of-capture is finite for all evader strategies, and is bounded by $t_{\mathrm{c}}^{\max }$, which is the capture time for the farthest pursuer (at the initial time among the n pursuers), assuming the evader follows a pure evasion strategy and none of the pursuers move. Note that the dynamics of the evader is a function of just the control $\theta _{{ E}}\in [0,2\pi ]$, and therefore $\dot{r}_i \in [-(v+u),v-u]$, for all $i \in \mathcal {P}$, at any time and state, which is a convex set. Therefore, from Filippov’s theorem [9], there exists a time-optimal evading strategy. This fact, along with the necessary conditions, given below, ensures that the proposed evading strategy is indeed optimal.

To continue with our analysis, note that since the evader strives to maximize $t_{\mathrm{c}}$ using its control input $\theta _{{ E}}$, the Hamiltonian of the underlying optimal control problem can be written as

$$\begin{aligned} H = -1 + \sum _{i \in \mathcal {P}}\lambda _i \left[ v \cos (\theta _{{ E}}- \varphi _{i}) - u \cos (\theta _i - \varphi _i) \right] , \end{aligned}$$

(7)

where $\lambda _i \, (i \in \mathcal {P})$ are the costates. The corresponding adjoint equations are obtained as

$$\begin{aligned} \dot{\lambda }_i = -\frac{\partial H}{\partial r_i} = 0, \qquad i \in \mathcal {P}, \end{aligned}$$

(8)

and hence the costates are constants, $\lambda _i(t) = c_i, \, t \in [0,t_{\mathrm{c}}]$, for all $i \in \mathcal {P}$. The transversality conditions are

$$\begin{aligned} \lambda _i(t_{\mathrm{c}}) = \nu \frac{\partial \varPsi }{\partial r_i} \Bigg |_{t = t_{\mathrm{c}}}, \quad i \in \mathcal {P}, \quad \text {and} \quad H(t_{\mathrm{c}}) = 0. \end{aligned}$$

(9)

Since the Hamiltonian has no explicit dependency on time, it follows that

$$\begin{aligned} H(t) = 0, \quad t\in [0,t_{\mathrm{c}}]. \end{aligned}$$

(10)

Note that the terminal condition is not differentiable and its partial with respect to each component $r_i(t_{\mathrm{c}})$ can be expressed as

$$\begin{aligned} \begin{array}{ll} \dfrac{\partial \varPsi }{\partial r_i} \Big |_{t = t_{\mathrm{c}}} = 0, &{}\quad \text {if }r_i(t_{\mathrm{c}}) > \epsilon ,\\ \dfrac{\partial \varPsi }{\partial r_i} \Big |_{t = t_{\mathrm{c}}} = 1, &{} \quad \text {if }r_i(t_{\mathrm{c}}) = \epsilon \text { and } r_j(t_{\mathrm{c}}) \ne \epsilon , \quad j \ne i, \\ \dfrac{\partial \varPsi }{\partial r_i} \Big |_{t = t_{\mathrm{c}}} \text { is undefined}, &{} \quad \text {if }r_i(t_{\mathrm{c}}) = \epsilon \text { and } r_j(t_{\mathrm{c}}) = \epsilon , \, \text { for some } j \ne i. \end{array} \end{aligned}$$

(11)

Applying Pontryagin’s minimum principle, with $\dfrac{\partial H}{\partial \theta _{{ E}}} = 0$, yields

$$\begin{aligned} \sum _{i \in \mathcal {P}} \lambda _i \left[ -\,v\sin (\theta _{{ E}}-\varphi _i) + u\sin (\theta _i-\varphi _i)\frac{\partial \theta _i}{\partial \theta _{{ E}}} \right] = 0, \end{aligned}$$

(12)

where from (4),

$$\begin{aligned} \frac{\partial \theta _i}{\partial \theta _{{ E}}}&= \frac{v \cos (\theta _{{ E}}- \varphi _i)}{u \cos (\theta _i - \varphi _i)}, \qquad \cos (\theta _i - \varphi _i) \ne 0. \end{aligned}$$

(13)

Now, the following definition is used to establish the characteristics of the optimal evading strategy.

Definition 2

Consider an MPSE problem and assume that the pursuers follow either a constant bearing or a pure pursuit strategy. For a given strategy of the evader, the capturing pursuer set$\mathcal {P}_{\mathrm{c}} \subset \mathcal {P}$ is the set of pursuers that are in the capture zone of the evader at $t_{\mathrm{c}}$.

Refer to Definition 1 for $t_{\mathrm{c}}$ (time-to-capture), which is always finite since the pursuers follow either a constant bearing or a pure pursuit strategy. Note that at the time-of-capture, one or more pursuers can be in the capture zone of the evader. Therefore, $1 \le \text {card}[\mathcal {P}] \le n$, where $\hbox {card}[\cdot ]$ represents the cardinality of the set. The capturing pursuer set for the optimal evading strategy, given the pursuers follow either a constant bearing or a pure pursuit strategy, is denoted by $\mathcal {P}^*$

Proposition 1

In the case of an MPSE problem with all the pursuers following a constant bearing strategy, the time-optimal evading strategy is dependent only on the initial positions of those pursuers that are in the corresponding capturing pursuer set $\mathcal {P}^*$.

Proof

Let $\hbox {card}[\mathcal {P}^*] = k, \, 1 \le k \le n$ and, without loss of generality, assume that pursuers $P_1, \, P_2,\ldots , P_k$, capture the evader simultaneously at time $t_{\mathrm{c}}$. Therefore, $r_1(t_{\mathrm{c}}) = \cdots = r_k(t_{\mathrm{c}}) = \epsilon$. Then, from (11), $\lambda _i(t) = c_i = 0$, for $i \in \mathcal {P}\backslash \mathcal {P}^*$, and (12) can be written as

$$\begin{aligned} \sum _{i \in \mathcal {P}^*} \lambda _i \left[ -\,v\sin (\theta _{{ E}}-\varphi _i) + u\sin (\theta _i-\varphi _i)\frac{\partial \theta _i}{\partial \theta _{{ E}}} \right] = 0. \end{aligned}$$

(14)

Since $\theta _i \, (i \in \mathcal {P}^*)$ is a function of $\theta _{{ E}}$, and the LoS angles $\varphi _i$ are dependent only on the initial positions of the players, from (14), it is evident that the optimal control input of the evader is only dependent on the initial positions of those pursuers that capture it at the final time $t_{\mathrm{c}}$. $\square$

Substituting (13) in (14), the later can be simplified to

$$\begin{aligned} \sum _{i \in \mathcal {P}^*} \lambda _i \left[ \frac{\sin (\theta _i - \theta _{{ E}})}{\cos (\theta _i - \varphi _i)}\right] = 0. \end{aligned}$$

(15)

The above equation cannot be simplified any further to obtain a closed-form optimal strategy for the evader and hence, the information about the set of pursuers that capture the evader at the time-of-capture, i.e., the set $\mathcal {P}^*$ cannot be obtained in an analytic fashion. Numerical examples indicate that the problem may contain multiple local minima. To tackle this problem and to address the issue of pursuer allocation, the idea of active/redundant pursuers is introduced in the next section. Following the discussion on optimal strategies, its characteristics for the case of pure pursuit is discussed in the following subsection.

2.2 Pure Pursuit Strategy

In the case of a pure pursuit strategy, the velocity vector of the pursuer is aligned along the LoS, as shown in Fig. 1b, i.e., the LoS angles ($\varphi _i$) do not remain constant anymore. Therefore, the dynamics has to include the evolution of both relative distances and the corresponding LoS angles, which can be written as

$$\begin{aligned} \dot{r}_i&= -u + v \cos (\theta _{{ E}}- \varphi _i), \end{aligned}$$

(16)

$$\begin{aligned} \dot{\varphi }_i&= \frac{v}{r_i}\sin (\theta _{{ E}}- \varphi _i), \qquad i \in \mathcal {P}. \end{aligned}$$

(17)

The initial conditions include (5) and

$$\begin{aligned} \varphi _i(0) = \text {atan2}(y_{{ E}}(0)-y_i(0),x_{{ E}}(0)-x_i(0)), \qquad i \in \mathcal {P}, \end{aligned}$$

(18)

with the terminal condition being the same as in (6).

For the case of an MPSE problem where all pursuers follow a pure pursuit strategy, and contrary to the constant bearing case of Sect. 2.1, it is not easy to show existence of an optimal evading strategy using Filippov’s theorem (although a feasible evading strategy always exists trivially). Hence, in the following discussion, we make the implicit assumption that a time-optimal evading strategy exists, and we proceed to characterize this strategy using the necessary conditions for optimality.

The Hamiltonian of the time-optimal control problem in the case of PP can be written as

$$\begin{aligned} H = -1 + \sum _{i \in \mathcal {P}} \left[ \lambda _i \left( -u + v \cos (\theta _{{ E}}- \varphi _i) \right) + \mu _i \frac{v}{r_i}\sin (\theta _{{ E}}- \varphi _i) \right] , \end{aligned}$$

(19)

and the adjoint equations are

$$\begin{aligned} \dot{\lambda }_i = -\frac{\partial H}{\partial r_i}&= -\mu _i \frac{v}{r^2_i} \sin (\theta _{{ E}}- \theta _i), \end{aligned}$$

(20)

$$\begin{aligned} \dot{\mu }_i = -\frac{\partial H}{\partial \varphi _i}&= \lambda _i v \sin (\theta _{{ E}}- \theta _i) - \mu _i \frac{v}{r^2_i} \cos (\theta _{{ E}}- \theta _i), \quad i \in \mathcal {P}. \end{aligned}$$

(21)

The transversality conditions include (9) and

$$\begin{aligned} \mu _i(t_{\mathrm{c}}) = \nu \frac{\partial \varPsi }{\partial \varphi _i} \Bigg |_{t = t_{\mathrm{c}}} = 0, \qquad i \in \mathcal {P}. \end{aligned}$$

(22)

Furthermore, since the Hamiltonian has no explicit dependence on time, it is zero for the entire time interval and (10) holds for this case as well. The partials with respect to $r_i$ are given in (11). Finally, we have

$$\begin{aligned} \sum _{i \in \mathcal {P}} \left[ -\,\lambda _i \sin (\theta _{{ E}}-\varphi _i) + \frac{\mu _i}{r_i}\cos (\theta _{{ E}}-\varphi _i) \right] = 0. \end{aligned}$$

(23)

Proposition 2

In the case of an MPSE problem with all the pursuers following a pure pursuit strategy, the time-optimal evading strategy is dependent only on the initial positions of those pursuers that are in the corresponding capturing pursuer set $\mathcal {P}^*$.

Proof

Let $\hbox {card}[\mathcal {P}^*] = k, \, 1 \le k \le n$ and, without loss of generality, assume that pursuers $P_1, \, P_2,\ldots , P_k$, capture the evader simultaneously at time $t_{\mathrm{c}}$. Therefore, $r_1(t_{\mathrm{c}}) = \cdots = r_k(t_{\mathrm{c}}) = \epsilon$. Then, from (11), $\lambda _i(t) = c_i = 0$, for $i \in \mathcal {P}\backslash \mathcal {P}^*$. Furthermore, from (11), $\lambda _i(t_{\mathrm{c}}) = 0$, for $i \in \mathcal {P}\backslash \mathcal {P}^*$, and from (22), $\mu _i(t_{\mathrm{c}}) = 0$, for $i \in \mathcal {P}\backslash \mathcal {P}^*$. Note that the adjoint equations, (20) and (21), for all $i \in \mathcal {P}$ are affine in their respective costates. Therefore, for $i \in \mathcal {P}\backslash \mathcal {P}^*$, $\lambda _i(t) = 0$, $\mu _i(t) = 0,~t \in [0,t_{\mathrm{c}}]$. Hence (23) can be rewritten as

$$\begin{aligned} \sum _{i \in \mathcal {P}^*} \left[ -\,\lambda _i \sin (\theta _{{ E}}-\varphi _i) + \frac{\mu _i}{r_i}\cos (\theta _{{ E}}-\varphi _i) \right] = 0. \end{aligned}$$

(24)

In (24), $\varphi _i$ is dependent only on its initial conditions and the strategy of the evader. Clearly, the optimal control input of the evader is only dependent on the initial positions of those pursuers that capture it at the final time $t_{\mathrm{c}}$. $\square$

The pure pursuit case does not allow for a closed-form solution of the optimal evading strategy, and as a result, it is difficult to obtain the set $\mathcal {P}^*$ analytically. In this regard, the following section presents sub-optimal solutions for allocating the pursuers for the MPSE problem that can be employed under any evading strategy while guaranteeing capture.

3 Active/Redundant Pursuers

This section presents strategies for the task allocation problem using the tool of Apollonius circles [21]. The Apollonius circle for a pursuer–evader pair is the locus of points where capture occurs, for all possible initial headings of a non-maneuvering evader, given the initial positions of the pursuer/evader pair and assuming that the pursuer follows a constant bearing strategy, see Fig. 2. For the MPSE problem, the Apollonius circle of the pair $P_i$–E is denoted as $\mathcal {A}_i$. It has its center at $O_i\left( \dfrac{x_{{ E}}- \rho x_i}{1 - \rho ^2},\dfrac{y_{{ E}}- \rho y_i}{1 - \rho ^2} \right)$ and radius $d_i = \dfrac{\rho }{1 - \rho ^2}\Vert p_i - e\Vert$, where $\rho = v/u$ (speed ratio) [41]. The Apollonius circles evolve in time as the players move, but the time dependencies will be dropped for the sake of brevity. Let $T_i$ be the closest point to the evader on the Apollonius circle where collision occurs when the evader goes head-on with the pursuer, as shown in Fig. 2. Therefore, the distance of $T_i$ from the evader is ${v\Vert p_i - e\Vert }/{(u+v)}$.

Fig. 2

The locus of capture points for a non-maneuvering evader in the cases CB and PP. Simulation parameters: $u = 1$, $v=0.6$, $p_i(0) = (0,0)$, $p_{{ E}}= (1,0)$

When the pursuer employs a pure pursuit strategy, the locus of all points where capture occurs is a closed curve, represented using $\mathcal {C}_i$ (see Fig. 2), and designated as an Apollonius curve. This Apollonius curve can be obtained from the time taken to capture a non-maneuvering evader

$$\begin{aligned} t_f = \frac{r_o(u + v\cos \phi _i)}{u^2 - v^2}, \qquad v \ne u, \end{aligned}$$

(25)

where $r_o$ is the initial distance between the pursuer-evader pair, and $\phi$ is the evader’s heading measured with respect to the line-of-sight from the pursuer to the evader at the initial time (see Fig. 1b) [47]. Furthermore, and given the heading of a non-maneuvering evader, since the $t_f$-isochrone in the case of a constant bearing strategy always contains the $t_f$-isochrone of a pure pursuit strategy [29, 47], the time-to-capture in the later case is either higher than or equal to the former case. This gives rise to the following lemma.

Lemma 1

Given the positions of the pursuer $P_i$ and the evader E, the corresponding Apollonius circle $\mathcal {A}_i$ is always contained in the area enclosed by the Apollonius curve $\mathcal {C}_i$.

The Apollonius curve is the locus of capture points for a non-maneuvering evader when the pursuer uses a pure pursuit strategy. The Apollonius curve thus generalizes the notion of the Apollonius circle for the case of pure pursuit. Note that the area enclosed by the curve $\mathcal {C}_i$ forms a non-convex set and hence, $\mathcal {C}_i$ is a non-convex curve [51]. Next, the Apollonius circle $\mathcal {A}_i$ and the Apollonius curve $\mathcal {C}_i$ will be used to identify the active and redundant pursuers. The following definitions establish the notions of active and redundant pursuers. Please refer to Definition 2 for $\mathcal {P}_{\mathrm{c}}$ (capturing pursuer set).

Definition 3

Consider an MPSE problem and assume that all pursuers follow either a constant bearing or a pure pursuit strategy. If $P_i \in \mathcal {P}_{\mathrm{c}}$ for some evading strategy, then $P_i$ is an active pursuer. Otherwise, $P_i$ is a redundant pursuer.

Given the instantaneous positions of the pursuers and the evader, it is of interest to find a condition to verify whether a pursuer is active or redundant. In this regard, we first define the instantaneous Apollonius boundary.

Definition 4

Given the positions of the players in an n-pursuer single-evader problem at time $0 \le t < t_{\mathrm{c}}$, and assuming that the pursuers follow a constant bearing strategy, the Apollonius boundary at time t is the set of points $\mathcal {B}_t = \{ X \in \bigcup \nolimits _{i=1}^{n} \mathcal {A}_i ~|~ \mathcal {M}(e, X) \cap \left( \bigcup \nolimits _{i=1}^{n} \mathcal {A}_i \right) = \{X\} \}$, where $\mathcal {M}(e,X)$ denotes the set of points on the line segment with endpoints e (position of the evader) and X at time t.

In other words, the Apollonius boundary is the set of points that belong to the union of all the instantaneous Apollonius circles, and, in addition, each such point is the closest to the evader along its respective line-of-sight originating from the evader. The following lemma establishes an important property of the Apollonius boundary, which will be used in Sect. 4.

Lemma 2

Given the positions of the players in an n-pursuer single-evader problem at time $0 \le t < t_{\mathrm{c}}$, and assuming that the pursuers follow a constant bearing strategy, the Apollonius circle of the closest pursuer is always a part of the Apollonius boundary $\mathcal {B}_t$.

Proof

Without loss of generality, assume $P_1$ is the closest pursuer. It follows that $\mathop {{\mathrm {argmin}}}\nolimits _{i \in \mathcal {P}}~\Vert p_i - e\Vert = 1$, and point $T_1$ (the point closest to the evader on the Apollonius circle $\mathcal {A}_1$, see Fig. 2) is the closest point to the evader along the corresponding line-of-sight originating from the evader. Therefore, the point $T_1$ satisfies the condition $\mathcal {M}(e, T_1) \cap \left( \bigcup \nolimits _{i=1}^{n} \mathcal {A}_i \right) = \{T_1\}$. Hence, the Apollonius circle of the closest pursuer is always a part of the Apollonius boundary. $\square$

Similarly, the Apollonius boundary in the case of pursuers following a pure pursuit strategy can be defined with $\mathcal {C}_i$ replacing $\mathcal {A}_i$ in Definition 4. The Apollonius boundaries in both cases can be visualized in Fig. 3. It can be observed that the region enclosed by the Apollonius boundary in the case of CB is always convex but may be non-convex for the PP case. Note that the Apollonius boundary evolves with time as the Apollonius circles or curves evolve with time as well.

Fig. 3

Apollonius circles, curves, and boundaries for CB and PP cases (simulation parameters: $u = 1$, $v=0.6$)

3.1 Identifying Active/Redundant Pursuers

An algorithm to identify active/redundant pursuers in the case of CB is discussed first, which is based on the following conjecture.

Conjecture 1

Given the positions of all the players in an MPSE problem at time $0 \le t < t_{\mathrm{c}}$, and assuming that the pursuers follow a constant bearing strategy, pursuer $P_i$ is active at time t if $\mathcal {B}_t \cap \mathcal {A}_i \ne \emptyset$, and is redundant otherwise.

The conjecture implies that in the case of CB, a pursuer is active at time $0 \le t < t_{\mathrm{c}}$, if and only if its corresponding Apollonius circle is part of the Apollonius boundary at that instant. The conjecture is inspired from the fact that the region in which the capture point lies in is bounded by the instantaneous Apollonius circle for any strategy of the evader. Note that if a pursuer is active at time $t'$, it need not remain active for all $t > t'$. But if a pursuer is redundant at time $t'$, it will remain redundant for all $t > t'$. The following lemmas based on Conjecture 1 provide simple checks to determine whether a pursuer is active or redundant.

Lemma 3

Given the positions of the players in an n-pursuer single-evader problem at time $0 \le t < t_{\mathrm{c}}$, assume that the pursuers follow a constant bearing strategy. Then, pursuer $P_i$ is the only active pursuer if and only if the conditions

$$\begin{aligned} \mathcal {A}_i \bigcap \left( \bigcup \limits _{j=1,\,j \ne i}^{n} \mathcal {A}_j \right)&= \emptyset , \end{aligned}$$

(26)

$$\begin{aligned} \mathcal {M}(e,T_i) \bigcap \left( \bigcup \limits _{j=1,\,j \ne i}^{n} \mathcal {A}_j \right)&= \emptyset , \end{aligned}$$

(27)

are satisfied, where $T_i$ is the closest point to the evader on the Apollonius circle $\mathcal {A}_i$. Furthermore, if conditions (26) and (27) are not satisfied, then $P_i$ is a redundant pursuer.

Proof

The necessity of the conditions (26) and (27) for $P_i$ to be the only active pursuer is established first. From (26), it can be seen that $\mathcal {A}_i$ does not intersect any other Apollonius circle. Therefore, it is either the case that $\mathcal {A}_i$ contains all other Apollonius circles, or $\mathcal {A}_i$ is contained in every other Apollonius circle. Note that both cases are mutually exclusive. In the later case, the Apollonius boundary is $\mathcal {A}_i$ itself, and $P_i$ is the only active pursuer. Now, if

$$\begin{aligned} \mathcal {M}(e,X) \bigcap \left( \bigcup \limits _{j=1,\,j \ne i}^{n} \mathcal {A}_j \right) = \emptyset , \end{aligned}$$

(28)

where X is any point on $\mathcal {A}_i$, then $\mathcal {A}_i$ is contained in every other Apollonius circle, that is, $P_i$ is the only active pursuer. Since X can be any point on the Apollonius circle $\mathcal {A}_i$, a convenient point to check the condition in (28) is to choose the closest point to the evader on the Apollonius circle $\mathcal {A}_i$. This point has the closed-form expression $T_i\left( \dfrac{x_{{ E}}+ \rho x_i}{1 + \rho },\dfrac{y_{{ E}}+ \rho y_i}{1 + \rho } \right)$, see Fig. 2. Conversely, if $P_i$ is the only active pursuer, then from Conjecture 1, the Apollonius boundary is $\mathcal {A}_i$ itself. In such a case, $\mathcal {A}_i$ does not intersect any other Apollonius circle and it is contained in every other Apollonius circle, which implies (26) and (27) hold. Thus, (26) and (27) become necessary and sufficient conditions for $P_i$ to be the only active pursuer. $\square$

Lemma 4

Given the positions of the players in an MPSE problem at time $0 \le t < t_{\mathrm{c}}$, assume that the pursuers follow a constant bearing strategy, and that the Apollonius circle $\mathcal {A}_i$ intersects at least one of the other Apollonius circles. Then, pursuer $P_i$ is an active pursuer if and only if there exists $X \in \mathcal {I}_i$ such that

$$\begin{aligned} \mathcal {M}(e,X) \bigcap \left( \bigcup \limits _{j=1}^{n} \mathcal {A}_j \right) = \{X\}, \end{aligned}$$

(29)

where $\mathcal {I}_i$ is the set of intersection points between $\mathcal {A}_i$ and the rest of the Apollonius circles.

Proof

The necessity of condition (29) for $P_i$ to be an active pursuer is proven first. Note that $X \in \mathcal {I}_i \subset \mathcal {A}_i$.

Since $X \in \mathcal {B}_t$, and from Conjecture 1, it follows that $P_i$ is an active pursuer at time t. Conversely, if $P_i$ is an active pursuer at time t, from Lemma 4, and since $\mathcal {A}_i$ intersects one or more Apollonius circles, $\mathcal {A}_i$ alone cannot form the Apollonius boundary (see Lemma 3). Therefore, only portion(s) of $\mathcal {A}_i$ [i.e., arc(s) of the circle] can be a part of the Apollonius boundary. The arc(s) which could possibly be a part of $\mathcal {B}_t$ will have one or more of the intersection points as its endpoints. Hence, if $P_i$ is an active pursuer, then there is at least one intersection point $X \in \mathcal {I}_i$ that satisfies the condition in (29). $\square$

The set of intersection points $\mathcal {I}_i$ can be obtained analytically given the instantaneous positions of all the players [54]. The above two lemmas can be used to verify if a pursuer is active or redundant. In this regard, Algorithm 1, named Apollonius circle-based Active Pursuer Check (AAPC), can be employed to check the status of each pursuer. The time complexity of the algorithm is of order $O(n^2)$, since the maximum number of intersections between any two circles is two. Note that by dynamically allocating the task of capturing the evader using AAPC (where at every instant the active pursuers keep pursuing the evader while the redundant pursuers do not react), the pursuers as a group will be able to capture the evader in minimum time. Furthermore, if a pursuer becomes redundant at any point of time $0 \le t < t_{\mathrm{c}}$, it remains redundant after that (i.e., till capture occurs).

The case of PP is more involved because the corresponding Apollonius curve is non-convex. A claim similar to the one given in Conjecture 1 cannot be made and hence, it is difficult to determine the status of a pursuer in this case. In this regard, the convex hull of the area surrounded by the Apollonius curve can be considered. The boundary of this convex hull is used to obtain a refined Apollonius curve, and the active/redundant pursuers can be identified by having checks similar to the ones given in the case of CB. In this case, the active pursuers are simply the ones that keep pursuing the evader. The redundant ones are the ones that remain at rest. At the same time, and since the refined Apollonius curve in the case of PP does not have any closed-form expression, obtaining the intersection points between the refined curves or between the refined curves and a given line segment is computationally more involved. Using an algorithm analogous to AAPC with refined Apollonius curves, numerical simulations obtained in the case of PP are presented in the following subsection. Note that the refined Apollonius curve is a convex curve [51].

Remark 1

The notion of regions of non-degeneracy (RND), discussed in Ref. [29], is taken care implicitly in our approach using the active/redundant pursuers. It can be seen that the RND in [29] was used to check whether a pursuer is active/redundant for the corresponding two-pursuer one-evader problem. These were based on the location of the farther pursuer compared to the closer pursuer. However, when there are more than two pursuers, the approach in [29] no longer works. Therefore, the way the RND was defined in [29] cannot be extended to a general MPSE problem for the cases of CB or PP.

3.2 Numerical Simulations

In this section, simulations of pursuer allocation using AAPC for both CB and PP cases, involving five pursuers and one evader, are presented. The speeds of the pursuers are set to $u = 1$, whereas the speed of the evader is set to $v = 0.6$. The radius of capture is chosen as $\epsilon = 0.1$. The evader follows a form of blind evasion strategy with switching times that are predefined [30]. At each switching time, the evader randomly chooses a heading from a set of allowable headings. The allowable headings set that is specific to the example showcased in this paper is $\{-\,\pi /4,~\pi /2,~3\pi /4\}$.

Fig. 4

Results obtained using AAPC for task allocation in the case of CB

Figure 4 presents the results obtained for the case of CB. Figure 4a shows the initial positions of all the players along with the corresponding Apollonius circles. The triangle denotes the initial position of the evader and the square markers denote the initial positions of the pursuers. It can be observed that at the initial time, the pursuers identified with the colors red, magenta, green, and blue are the active pursuers, as their corresponding Apollonius circles are part of the Apollonius boundary. Figure 4b shows the trajectories of all the players. It can be seen that the green pursuer finally captures the evader, and the rest of the three pursuers, which are initially active, become redundant as time progresses. The cyan pursuer, which is redundant at the initial time, does not move at all. Figure 5 presents the results obtained for the PP case using the refined Apollonius curves. An analysis similar to its CB counterpart can be made by observing Fig. 5a, b, where the cyan pursuer is again redundant at the initial time. The rest of the pursuers, though initially active, eventually become redundant except for the green pursuer, which finally captures the evader, see Fig. 5b.

Fig. 5

Results obtained using AAPC with refined Apollonius curves for task allocation in the case of PP

4 Extension to Multi-pursuer Multi-evader Problems

In this section, the AAPC is extended to solve MPME problems. Given the positions of all the players at some instant of time, the set of evaders for which a pursuer is active can be obtained using AAPC. Note that at a given time instant, a pursuer can be classified as active by more than one evader or no evader whatsoever. In the case where a pursuer is classified as active for more than one evader, one can break the tie by assigning the pursuer to the nearest evader among the ones for which this pursuer is active. Using this idea, the following algorithm can be used for pursuer allocation in MPME problems. Note that the pursuers are assumed to be following a constant bearing strategy.

Apollonius–Voronoi Allocation Algorithm (AVAA) At a given time instant $0 \le t \le t_{\mathrm{c}}$, let $\mathcal {E}_f$ be the set of evaders that are yet to be captured, and let $\mathcal {E}_{\mathrm{c}}$ be the set of evaders that have already been captured. Note that $\mathcal {E} = \mathcal {E}_f \cup \mathcal {E}_{\mathrm{c}}$. Given the current positions of all the players, let $\mathscr {I}: \mathcal {E}_f \rightarrow 2^{\mathcal {P}}$ be the initial allocation function that maps each evader $E_j$ (in $\mathcal {E}_f$) to its set of active pursuers obtained by considering the positions of all the pursuers. That is, for a given $j \in \mathcal {E}_f$, $\mathscr {I}(j)$ is a subset of $\mathcal {P}$. Furthermore, $\mathcal {P}_a = \bigcup \nolimits _{j \in \mathcal {E}_f}\mathscr {I}(j)$ denotes the set of all the active (or assigned) pursuers according to the initial allocation function $\mathscr {I}$. Given the initial allocation function $\mathscr {I}$, let now $\mathscr {J}: \mathcal {P}\rightarrow 2^{\mathcal {E}_f}$ be the dual function defined by $\mathscr {J}(i) = \{ j \in \mathcal {E}_f: \mathscr {I}(j) = i \}$. In other words, $\mathscr {J}$ maps each pursuer to the set of the evaders to which it is allotted as per $\mathscr {I}$. Next, we define the final allocation function$\mathscr {F}$ and the intermediate allocation function$\mathscr {G}$ as follows.

• (a) If $\hbox {card}[\mathscr {J}(i)] \le 1$, for all $i \in \mathcal {P}$, then let $\mathscr {F} = \mathscr {I}$. Otherwise, let $\mathscr {G}: \mathcal {E}\rightarrow 2^{\mathcal {P}}$ be defined as $\mathscr {G}(j) = \Big \{ i \in \mathscr {I}(j) : j = \mathop {{\mathrm {argmin}}}\nolimits _{k \in \mathscr {J}(i)}~\Vert p_i - p_k\Vert \Big \}$. The function $\mathscr {G}$ maps each evader to a set of pursuers in accordance with the mapping $\mathscr {I}$, such that each active pursuer is assigned to the nearest evader among its assigned ones. Note that $\mathscr {G}(j)$ can be an empty set for some j, i.e., an evader can end up be unassigned as per $\mathscr {G}$.

• (b) Let $\mathcal {P}_u = \mathcal {P}\backslash \mathcal {P}_a$ be the set of unassigned pursuers. Now for each evader $E_j$, find the active pursuers considering the positions of the pursuers that are only in the set $\mathscr {G}(j)~\cup ~\mathcal {P}_u$, and obtain an updated allocation function$\mathscr {I}'$ and its corresponding dual $\mathscr {J}'$.

• (c) Repeat steps (a) and (b), by replacing $\mathscr {I}$ and $\mathscr {J}$ with $\mathscr {I}'$ and $\mathscr {J'}$, respectively, until $\mathscr {F}$ is obtained.

Note that in step (a) of the algorithm, ties with multiple assignments of the same pursuer are broken using distance as the metric. Furthermore, if each pursuer is assigned to only one evader or if it remains unassigned, then the initial allocation function $\mathscr {I}$ is also the final one. In any other case, once the intermediate allocation function $\mathscr {G}$ is obtained in step (b) of the algorithm, the set of unassigned pursuers according to $\mathscr {I}$ is obtained. In step (b), an updated allocation function $\mathscr {I}'$ is obtained by checking for active pursuers among the set of unassigned pursuers coupled with the pursuers assigned as per $\mathscr {G}$, for each evader. Because one of the unassigned pursuers (in the set $\mathcal {P}_u$) can become active to the evaders that have lost one or more pursuers during the tie break in step (a). With $\mathscr {I}'$ and its corresponding dual $\mathscr {J}'$, steps (a) and (b) are repeated until each pursuer has only one (or none) assignment. Once an evader is captured, it is removed from the set $\mathcal {E}_f$ and added to the set $\mathcal {E}_{\mathrm{c}}$.

The above algorithm is run at every time instant to obtain the allocation function $\mathscr {F}$, given the players’ current positions, until all the evaders are captured, i.e., until $\mathcal {E}_f$ is empty. The algorithm provides a potentially sub-optimal solution, but it is scalable for any number of pursuers and evaders. The algorithm guarantees capture of all m evaders as is shown in Theorem 2 below. In order to prove this theorem, several preparatory results are needed.

Definition 5

Given the positions of the players in an MPME problem at time $t \ge 0$, the current shortest reach (CSR) is defined by $\mathop {\min }\nolimits _{(i,j) \in \mathcal {P}\times \mathcal {E}_f}~\Vert p_i - e_j\Vert$.

Lemma 5

At a given time instant $t \ge 0$, $i^* \subseteq \mathscr {F}(j^*)$, where $(i^*,j^*) = \mathop {\mathrm {argmin}}\nolimits _{(i,j) \in \mathcal {P}\times \mathcal {E}_f}~\Vert p_i - e_j\Vert$, and $\mathscr {F}$ is the final allocation function of AVAA.

Proof

From Lemma 2, since $i^*$ is the closest pursuer to $j^*$, the Apollonius boundary for $j^*$ contains $i^*$, while considering the positions of all the pursuers (in $\mathcal {P}$). Therefore, $i^*$ will be assigned to $j^*$, as per the initial allocation function $\mathscr {I}$. When $i^*$ has multiple assignments as per $\mathscr {I}$, the intermediate allocation function $\mathscr {G}$ still assigns $i^*$ to $j^*$, as the pursuer is assigned to the closest evader in the case of multiple assignments (as per $\mathscr {G}$). Furthermore, $i^*$ is assigned to $j^*$, as per all the subsequent updated allocation functions $\mathscr {I}'$, owing to the fact $i^*$ is the closest pursuer to $j^*$, and hence as per the final allocation function $\mathscr {F}$. $\square$

Lemma 6

Assuming the pursuers are assigned to the evaders using AVAA, at any given time $t \ge 0$, CSR will converge to zero in finite time, and hence at least one evader will be captured in finite time.

Proof

From Lemma 5, pursuer $i^*$ (corresponding to the CSR) is always assigned to evader $j^*$. Since all the pursuers are faster compared to the evaders, and since they follow a constant bearing strategy, $\hbox {d}(\Vert p_{i^*} - e_{j^*} \Vert )/\hbox {dt} < 0$, for all $t \ge 0$ [47]. Furthermore, as the initial CSR is finite, the CSR converges to zero in finite time. Hence, capture of one evader is guaranteed in finite time. $\square$

Theorem 2

The AVAA algorithm guarantees capture of all the evaders in finite time.

Proof

The result immediately follows from Lemmas 5 and 6. Note that the CSR is updated (from zero) every time a capture occurs, and the captured evader is removed from the list of participating players. Also, the number of evaders are finite. $\square$

Figure 6 demonstrates the performance of AVAA for ten pursuers and five evaders. The simulation parameters remain the same as in Sect. 3.2. In Fig. 6, the red triangles indicate the current positions of the evaders that are not captured and the magenta ones are the evaders that are captured. The blue squares indicate the current positions of the active pursuers and the cyan ones indicate the redundant pursuers. In all three plots, the Voronoi partition of the domain with the pursuers as generators is also included for reference. The animation corresponding to the simulation shown in Fig. 6 can be found on the web.²

Fig. 6

Plots showing the positions and trajectories of the players in a multi-pursuer (squares) multi-evader (triangles) problem at different time instants

5 Conclusion

Under the assumption that the pursuers are faster than the evader(s), and that they follow either a constant bearing (CB) or a pure pursuit (PP) strategy, workable solutions for multi-pursuer single-evader (MPSE) and multi-pursuer multi-evader (MPME) problems are provided. In both CB and PP cases, it has been established that the optimal evading strategy in the MPSE setting depends only on those pursuers that capture the evader simultaneously. Using this insight, a dynamic allocation algorithm for the pursuers, which is independent of the evader’s strategy, has been proposed to solve the MPSE problem. The proposed algorithm is based on the notion of active/redundant pursuers and their classification using the Apollonius cycles (for the case of CB) or the Apollonius curves (for the case of PP). The algorithm is further extended to solve MPME problems for any number of pursuers and evaders. These algorithms ensure capture of all the evaders either in an MPSE or an MPME setting in finite time.

Several extensions of this work are possible. The computational requirements can be reduced by having an estimate of when the assignment can change to avoid unnecessary calculations at every time instant. One of the challenges is extending the notion of Apollonius curves for the cases of CB and PP to also account for turn-radius constraints for all the players. Another possible research direction is to consider the effect of wind fields and other uncertainties in order to allow for a more robust implementation of these algorithms in real-world applications.