Pricing Strategies of Complementary Products in Distribution Channels: A Dynamic Approach

Abstract

This paper investigates the dynamic pricing strategies of firms selling complementary products in a marketing channel. The problem is modelled as a non-cooperative differential game that takes place between decisions makers controlling transfer and retail prices. We computed and compared prices and sales rates of channel members under two scenarios: (i) The first involves a single retailer that sells a unique brand produced by a monopolist manufacturer and (ii) in the second, a complementary product is introduced by an additional manufacturer. We found that in both scenarios, transfer and retail prices decrease over time, but prices decrease faster when the complementary product is introduced into the market. Furthermore, the entry of the complementary product onto the market boosts the sales rate of the existing product. Finally, we found that the retailer in the second scenario always has a non-negative retail margin, meaning that practicing a loss-leadership strategy is not optimal.

1 Introduction

In this paper, we investigate the issue of dynamic pricing in marketing channels in a situation where the products available on the market are complementary. More particularly, the paper aims to characterize channel member prices, sales and profits at the steady state and along the optimal time-paths when both products are available on the market, and compare these results to the case in which only one product is sold. Our objective is to assess the impact of handling complementary products on channel members pricing strategies and on product sales during the planning horizon.

A substantial body of the game theory literature in marketing channels takes a static perspective in the study of firms’ pricing strategies. In most of these studies, the channel structures that were investigated were either bilateral monopolies (i.e. a downstream firm sells the product of a single upstream firm)¹ or competitive channels involving one or more retailers selling substitute products (e.g. [3, 4, 18] and [25]).

The last two decades have seen considerable developments and extensions of this literature to a dynamic setting. Dynamic games, and more precisely differential games, are being used in order to capture the repeated interactions between channel members in a changing environment and the carry over effects of their production and marketing decisions.² Studies focusing on pricing decisions have introduced the dynamic features in different ways: (i) in the cost function, by considering that production costs decrease via learning, or (ii) in the state equation, by considering reference price effects and demand learning. The former captures the impact of past prices on the building of a benchmark (i.e. the reference price) used by consumers to evaluate actual prices,³ while the latter uses a modified version of the Bass diffusion model⁴ to illustrate the process by which past sales impact future sales. The main objectives of these studies are to compare the pricing strategies and the cumulative profits obtained with a dynamic model to their counterparts in a static setting and to investigate whether firms should adopt a skimming or a penetration strategy.

A firm practices a skimming strategy when it fixes a high retail price at the beginning of the planning horizon and then decreases this price in the subsequent time periods. The firm’s objective is to benefit from the high margin associated with the high retail price. Price penetration corresponds to the mirror situation. With this strategy, retail prices are fixed at a low level at the launch of the product and are then increased. Although the margins are lower, the firm benefits in this situation from a larger number of consumers attracted by the low price [6].

The first studies that considered both the cost learning and the diffusion effects (via market saturation and word-of-mouth) in the computation of an open-loop price in a monopoly were Robinson and Lakhani [23] and Kalish [15]. The former found that the optimal pricing strategy was price penetration, while the latter found that the dynamic price was lower than the static one. They proved that the use of a skimming or a penetration strategy depends on the effect of past sales on future sales (i.e. saturation effects) and the level of the word-of-mouth effect. When the saturation effect is negative, or when the word-of-mouth is low (or negative), prices are high at the beginning of the time horizon, then they decrease monotonically over time. The opposite happens in situations where the saturation effects are positive or absent and when the word-of-mouth is high.⁵ These parameters also affect the difference between the profits obtained in a dynamic or a static settings, while Robinson and Lakhani [23] proved that dynamic profits are always higher than static profits.

Extensions of these finding to include competition were explored by Dockner [7], Dockner and Jørgensen [9], Eliashberg and Jeuland [10], and Dockner and Gaunersdorfer [8]. Some of these studies did not include interactions between the competitors’ pricing strategies. In Jørgensen and Zaccour [14], they are denoted by “Demand learning only” models, while the others are classified in the “Competition with price interactions” category.

Dockner [7] belongs to the first category. The author computed open-loop Nash equilibria and found decreasing price trajectories (i.e. skimming strategies). This result was attributed to the demand saturation effect. Eliashberg and Jeuland [10] extended this result to a model of competition with price interactions, in which the competitors were symmetric. Dockner and Jørgensen [9] found that in dynamic demand functions where only price effects were introduced in the model (without any diffusion effect) and firms benefitted from cost learning, prices decreased over time. But when diffusion effects were introduced in the model, they found that the slope of the price trajectory depended on the sign of the diffusion effect: if it was positive, then the pricing strategy increased (i.e. price penetration), and if it was negative, then the price decreased (i.e. price skimming) for both firms and their prices were similar, since firms were assumed to be symmetric.

As mentioned above, all the studies on the issue of dynamic pricing were dedicated to analysing monopolies or competitive channels,⁶ yet none of them investigated the situation where firms interact in a vertical channel structure and the products are complements. The only studies that investigated situations in which products are complements were by Mahajan and Muller [16] and Minowa and Choi [17]. Although these studies did not investigate this issue in a vertical structure, they examined the dynamic pricing strategies of firms in a multi-product context for the particular case of product contingency. The latter corresponds to situations where one or both products (i.e. the contingent product) are useful only if the consumer has the other (i.e. the base product). This case describes the optional contingency relationship. Captive contingency corresponds to the case where none of the products can be used without the other.

In Mahajan and Muller [16], the authors built two dynamic sales functions that captured each form of contingency and computed pricing and sales paths for both situations under two scenarios: one in which both products were controlled by the same firm, and another scenario where separate firms controlled each one of them. The authors found that the pricing strategies of the firms under both scenarios were different: prices of the primary as well as the contingent product were lower when they were produced by the same company with respect to the case where two distinct companies controlled these decisions. This leads to faster diffusion for both products under the centralized scenario, for both cases of product contingencies.

Minowa and Choi [17] concentrated on captive contingency and considered a situation where each firm in an oligopoly sold a base and a contingent product. Under the assumptions of symmetry and zero discounting, the firms’ pricing strategies were found constant. The authors also found a set of conditions under which prices could be decreasing.

The research done by Mahajan and Muller [16] provides the closest reference for our study. However, as for most of the papers that examined the issue of dynamic pricing in the literature, the authors did not investigate the problem from the channel’s perspective. Hence, we have not been able to discern whether manufacturers and retailers should adopt the same dynamic pricing strategies or not, or what the impact on retailer’s margins would be. Furthermore, in all these papers,⁷ the authors computed the open-loop Nash equilibria (OLNE) which involve that firms set prices for the whole period at the beginning of the planning horizon, and these prices are not affected by the sales rate.

In order to fill this gap, this paper contributes to the dynamic pricing literature by adding the following features:

• We examine the dynamic pricing strategies of firms in a vertical channel structure when demand obeys to learning effects (via saturation),

• We consider that products sold in the channel are complements,

• We model the problem by taking into account the interactions in channel members’ pricing decisions, and

• We compute feedback strategies, while most of the papers have used an open-loop information structure. Computing feedback strategies is a challenging task because of tractability problems, but this information structure is more adapted for capturing market realities, particularly in the study of pricing problems, where we expect firms to fix their prices by considering the sales level.

This work also relates to the literature on product-mix pricing. The latter refers to pricing strategies that take into account the interactions existing between demands for different products or brands. The managerial recommendations for firms handling complementary products were summarized in Simon et al. [24]. The authors suggested that managers:

• fix lower retail prices, with respect to the retail prices of a single product sold on the market;

• decrease the product’s price when the level of complementarity between products increases; and

• sacrifice the profit margin on one of the products and increase the profit margin on the other. This strategy is called loss-leadership pricing and is often practiced in the market, especially when both products are controlled by the same firm.

In this paper, we investigate whether these managerial recommendations hold true when the problem is investigated from a game theory perspective. Our main objective is to provide answers to the following research questions:

• (i) What are the firms’ price trajectories over time in a decentralized vertical channel when the retailer holds complementary products?

• (ii) How does the presence of a complementary product affect product prices and sales (w.r.t prices and sales of a unique product sold in a dyad)?

The rest of the paper is organized as follows: Sect. 2 introduces the model. Sections 3 and 4 are devoted to the analytical results and the numerical simulations, respectively. Section 5 provides the conclusion.

2 The Model

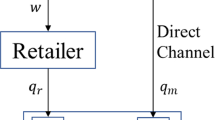
We consider a game that takes place in a vertical channel structure and examine two scenarios: a bilateral monopoly where a monopolist manufacturer sells its single product through an independent retailer, and a channel where two manufacturers sell their complementary products via a unique retailer (i.e. a one-retailer–two-manufacturers channel). To illustrate this setting, one can think of a firm (e.g. a car dealer) selling either a single product or brand (e.g. GM cars) or offering two complementary products (e.g. GM cars and a car insurance).

The manufacturer(s) control(s) the transfer prices, and the retailer controls the retail price(s). We consider a dynamic game with an infinite time horizon where the retailer is a follower and the manufacturer(s) the leader(s). We compute equilibria by adopting feedback information structures. In both scenarios, we consider a dynamic sales response model where we introduce two effects: (i) the effects of retail prices, and (ii) the effects of demand learning via market saturation. In the scenario where two products are sold on the market, we take into account the interactions existing between both firms’ pricing strategies. Put differently, we consider that the sales rate of each product is affected by the price of both products.

The sales rate functional forms and the channel members objective functionals in both scenarios are presented in the next subsections.

2.1 The Bilateral Monopoly Scenario

Under the bilateral monopoly, the sales rate $\dot{x}\left( t\right)$, which captures the current sales at time t, is expressed as follows:

$$\begin{aligned} \dot{x}\left( t\right)&=a-\kappa p_{R}\left( t\right) +bx\left( t\right) , \nonumber \\ x\left( 0\right)&=x_{0}\ge 0 \end{aligned}$$

(1)

where x(t) represents the cumulative sales from the beginning of the planning horizon until time t, and $p_{R}(t)$ is the product’s retail price. a, b and $\kappa$ are parameters such that $a,\kappa >0;b<0$. The parameter a is the demand intercept. It can be interpreted as the maximum sales that can be realized by the firm at the beginning of the planning horizon if the product is given for free (i.e. market potential). Parameter $\kappa$ is the product’s own-price effect. It indicates that the product’s sales rate decreases when its price increases. The parameter b represents the learning effect (i.e. saturation effect). This parameter captures the proportion of the market that will not buy the product at time t because they already bought it. Saturation effect is widely used in the new-product diffusion literature to capture the evolution in the number of adopters of a durable product that admits a ceiling market potential.⁸ The most popular model is Bass [1], who set equal to 1 the value of this parameter in order to capture only the first purchase (replacement purchases are neglected). According to this model, product’s diffusion is a process by which some innovators adopt the product because of media communications, then these adopters influence the remaining part of the market (i.e. imitators) via word-of-mouth. Hence, product diffusion is influenced only by two key parameters: the innovation effect and the imitation effect, and all these parameters, including the market potential, are not affected by marketing decisions (e.g. price or advertising decisions).

The dynamic sales Eq. 1 used in our study can be considered as a modified version of the Bass model where only saturation effects and price effects are introduced. Imitation effects, due to the interactions existing between innovators and imitators, are ignored. A similar model was used in Kalish [15] as a particular case of their general dynamic model. This model could also be considered as a variation of the Nerlov and Arrow capital accumulation model [21], where the stock is total sales, the instrument is the retail price, and the depreciation is captured by the saturation effect.

Considering a common discount rate $\rho$, and denoting by $p_{M}(t)$ and c the wholesale price and the constant unit production cost respectively, the retailer’s and manufacturer’s objective functionals are:

$$\begin{aligned} \displaystyle J_{R}&=\max \limits _{p_{R}}\int _{0}^{\infty }e^{-\rho t}(p_{R}-p_{M})\dot{x}(t)dt, \end{aligned}$$

(2)

$$\begin{aligned} \displaystyle J_{M}&=\max \limits _{p_{M}}\int _{0}^{\infty }e^{-\rho t}(p_{M}-c)\dot{x}(t)dt, \end{aligned}$$

(3)

subject to (1). By (2) and (3), we have defined a differential game, with one state variable x(t) and two control variables $p_{M}(t)$ and $p_{R}(t)$.

2.2 The One-Retailer–Two-Manufacturers Scenario

Now, let us consider a one-retailer–two-manufacturers game. Denoting by $p_{Mi}(t)$ and $p_{Ri}(t)$ the product i’s wholesale and retail prices, respectively; the dynamic demand function of each product i becomes:

$$\begin{aligned} \dot{x}_{i}(t)&=a_{i}-\kappa p_{Ri}(t)+\gamma p_{Rj}(t)+bx_{i}(t),\nonumber \\ x_{i}(0)&=x_{i0}\ge 0,\forall i=1,2;i\ne j \end{aligned}$$

(4)

where $x_{i}(t)$ represents the product i’s cumulative sales rate, and $a_{i},b,\kappa$ and $\gamma$ are parameters such that $a_{i},\kappa >0,b<0,\gamma <0,$ and $\left| \gamma \right| <\kappa$. Parameters $a_{i},\kappa$ and b have the same interpretations as in the previous scenario, with the particularity that the market potential here is specific to the product i which implies that the two manufacturers are not completely identical. The parameter $\gamma$ is negative. It captures the cross-price effect. Hence, it reflects the complementary relationship between products. The condition $\left| \gamma \right| <\kappa$ is a standard assumption in the economic literature. It states that own-price effects on demand must be higher than cross-price effects.

Remark 1

Notice that our model considers that each product’s sales rate is affected by its own cumulative sales, and not the cumulative sales of the other. The literature on substitute products adopted either this modelling approach or that in which the total cumulative market sales have an impact on each product’s sales rate. Since we are studying the situation of complementary products, only the first approach is applicable.

Retailer’s and manufacturer i’s objective functionals are⁹

$$\begin{aligned} \displaystyle J_{R}&= \max \limits _{p_{Ri}, p_{Rj}}\int _{0}^{\infty } e^{-\rho t} \sum \limits _{i = 1}^{2}(p_{R i} - p_{M i}) \dot{x}_{i}(t) dt, \end{aligned}$$

(5)

$$\begin{aligned} \displaystyle J_{M i}&= \max \limits _{p_{Mi}}\int _{0}^{\infty } e^{-\rho t} (p_{M i} - c) \dot{x}_{i}(t) dt, \end{aligned}$$

(6)

subject to (4). By (5) and (6), we have defined a differential game with two state variables $x_{i}(t)$ and four control variables $p_{Mi}(t)$ and $p_{Ri};\forall i=1,2$

3 Equilibria

This section is devoted to the presentation of the main results obtained under both scenarios: the bilateral monopoly and the one-retailer–two-manufacturers channel.

3.1 Bilateral Monopoly

The monopolistic channel problem is defined by the dynamic optimization problem (2)–(3) and the state Eq. (1). We consider that the game is played à la Stackelberg and that the manufacturer is the channel leader, as is commonly assumed in the distribution-channels literature. We denote by $V_{R}(x)$ and $V_{M}(x)$ the retailer’s and manufacturer’s value functions, respectively.

As a follower, the retailer solves the following Hamilton-Jacobi-Bellman (HJB) Equation:

$$\begin{aligned} \displaystyle \rho V_{R}(x)=\max \limits _{p_{R}}\left\{ \left( p_{R}-p_{M}+\frac{\partial V_{R}}{\partial x}\right) \dot{x}\right\} . \end{aligned}$$

(7)

We calculate the derivative of (7) and set it equal to 0 to get the retailer’s reaction function

$$\begin{aligned} p_{R}^{B}\left( x,p_{M}\right) =\frac{bx+a+\kappa \left( p_{M}-\frac{\partial V_{R}}{\partial x}\right) }{2\kappa } \end{aligned}$$

(8)

An interesting result that can be obtained from this reaction function is related to the strategic dependence between channel members’ pricing decisions. Indeed, by computing the first derivative of $p_{R}^{B}$ with respect to $p_{M}$, we can examine how the retailer reacts to the manufacturer’s increase or decrease of the wholesale price.

$$\begin{aligned} \frac{\partial p_{R}^{B}}{\partial p_{M}}\left( x,p_{M}\right) =\frac{1}{2}>0 \end{aligned}$$

This result indicates that the retailer and the manufacturer in the bilateral monopoly are strategic complements: an increase in the wholesale price is reflected by a 50 % increase in the retail price.

The next step is to compute the manufacturer’s reaction function by substituting (8) into manufacturer’s HJB equation:

$$\begin{aligned} \displaystyle \rho V_{M}(x)=\max \limits _{p_{M}}\left\{ \left( p_{M}-c+\frac{\partial V_{M}}{\partial x}\right) \dot{x}\right\} . \end{aligned}$$

(9)

Performing the maximization of the resulting expression provides the strategy:

$$\begin{aligned} p_{M}^{B}=\frac{bx+a+\kappa \left( c+\frac{\partial V_{R}}{\partial x}-\frac{\partial V_{M}}{\partial x}\right) }{2\kappa }. \end{aligned}$$

(10)

By following the steps described in “Appendix A”, we obtain the results described in Proposition 1.

Proposition 1

The retailer’s and manufacturer’s pricing strategies in the bilateral monopoly are given by the following expressions

$$\begin{aligned} p_{R}^{B}&=\left\{ \begin{array}{ll} \frac{3a+\kappa \left( c-\alpha _{2}-\beta _{2}\right) }{4\kappa }+\frac{\left( 3b-\kappa \left( \alpha _{1}+\beta _{1}\right) \right) x}{4\kappa } &{} \quad \text {if this expression is positive}\\ 0 &{} \quad \text {otherwise,} \end{array} \right. \end{aligned}$$

(11)

$$\begin{aligned} p_{M}^{B}&=\left\{ \begin{array}{ll} \frac{a+\kappa \left( c-\alpha _{2}+\beta _{2}\right) }{2\kappa }+\frac{\left( b-\kappa \left( \alpha _{1}-\beta _{1}\right) \right) x}{2\kappa } &{} \quad \text {if this expression is positive}\\ 0 &{} \quad \text {otherwise.} \end{array} \right. \end{aligned}$$

(12)

The retailer’s and manufacturer’s value functions are given by the following expressions

$$\begin{aligned} \displaystyle V_{R}(x)&=\frac{\beta _{1}}{2}x^{2}+\beta _{2}x+\beta _{0}, \end{aligned}$$

(13)

$$\begin{aligned} \displaystyle V_{M}(x)&=\frac{\alpha _{1}}{2}x^{2}+\alpha _{2}x+\alpha _{0}, \end{aligned}$$

(14)

where $\beta _{1},\beta _{2},\beta _{0},\alpha _{1},\alpha _{2}$ and $\alpha _{0}$ are given by

$$\begin{aligned} \alpha _{1}&=\frac{2\left[ \left( 4\rho -3b\right) \pm 2\sqrt{\rho (4\rho -6b)}\right] }{9\kappa }, \end{aligned}$$

(15)

$$\begin{aligned} \beta _{1}&=\frac{\alpha _{1}}{2}, \end{aligned}$$

(16)

$$\begin{aligned} \alpha _{2}&=\frac{2(a-c\kappa )\left( b+\kappa \left( \alpha _{1}+\beta _{1}\right) \right) }{8\kappa \rho -3\kappa \left( b+\kappa \left( \alpha _{1}+\beta _{1}\right) \right) }, \end{aligned}$$

(17)

$$\begin{aligned} \beta _{2}&=\frac{\alpha _{2}}{2}. \end{aligned}$$

(18)

Proof

See “Appendix A”. $\square$

The first result in this proposition gives the pricing strategies for both firms in the marketing channel. We can clearly see that these strategies are linear in the state variable x.

The value function coefficients $\alpha _{1}$ and $\beta _{1}$ are chosen such that

$$\begin{aligned} b+\kappa \left( \alpha _{1}+\beta _{1}\right) <0 \end{aligned}$$

(19)

ensuring that x(t) will converge asymptotically to its steady state $x^{ss}$ given by¹⁰

$$\begin{aligned} x^{ss}=-\frac{a+\kappa \left( -c+\alpha _{2}+\beta _{2}\right) }{b+\kappa \left( \alpha _{1}+\beta _{1}\right) }. \end{aligned}$$

(20)

With the assumption that the expression $\left( a-c\kappa \right)$ is positive,¹¹ we can conclude that $\alpha _{2}$ and $\beta _{2}$ have negative signs when $\left( b+\kappa \left( \alpha _{1}+\beta _{1}\right) \right) <0$.

Taking into account condition (19) and to ensure that the steady state $x^{ss}$ takes positive values, the expression (20) must satisfy the following condition:

$$\begin{aligned} a+\kappa (-c+\alpha _{2}+\beta _{2})>0. \end{aligned}$$

(21)

The value functions parameters $\alpha _{1}$ and $\beta _{1}$ admit two solutions (i.e. solutions where the square roots are affected by either a positive or a negative signs). For each one of these parameters, both solutions are positive. We select the solution where the square root is affected by a negative sign to ensure that the condition (19) is verified.

Hence, the signs of the different parameters allow us to conclude that the pricing strategies of firms are decreasing in the state variable. This means that, with the increase in the cumulative sales (i.e. when more consumers buy the product), the manufacturer and the retailer reduce their retail and wholesale prices, respectively.

The expression of $p_{R}^{B}$ in Eq. (11) indicates that the coefficient of $x\left( t\right)$ in absolute value is higher than its counterpart in the expression of $p_{M}^{B}$ in Eq. (12). Put differently, we have:

$$\begin{aligned} \left| \frac{dp^{B}_{R}}{dx}\right| >\left| \frac{dp^{B}_{M}}{dx}\right| \end{aligned}$$

This result indicates that the retailer reacts more to an increase in product sales than the manufacturer.

The second result in the proposition is expected.¹² It indicates that channel members’ values functions are linear quadratic in the state variable $x\left( t\right)$.

Notice that expressions (16) and (18)¹³ indicate that the manufacturer gets double the retailer’s outcome. Such result has been reported in similar studies examining decentralized bilateral monopolies where the manufacturer is the channel leader.

By substituting the retailer’s pricing strategy in (11) into the state dynamics given by (1), we can compute the cumulative sales trajectory x(t) under the first scenario. This gives the following expression:

$$\begin{aligned} x(t)= (x_{0}-x^{ss}) e^{\frac{1}{4} t \left( b+\kappa \left( \alpha _{1}+\beta _{1}\right) \right) } + x^{ss}. \end{aligned}$$

(22)

The paths for the pricing strategies $p_{R}(t)$ and $p_{M}(t)$ are obtained by replacing (22) in (11) and (12).

3.2 One-Retailer–Two-Manufacturers Game

This section presents the analytical results obtained under the second scenario, where one retailer distributes the products of two manufacturers, and these products are complements.

We solve the dynamic problem defined by (5)–(6) and the state Eq. (4). As in the previous scenario, we consider a Stackelberg game and start by solving the retailer’s HJB equation given by the following expression:

$$\begin{aligned} \displaystyle \rho V_{R}\left( x_{1},x_{2}\right) =\max \limits _{p_{Ri},p_{Rj}}\left\{ \sum \limits _{i=1}^{2}\left( p_{Ri}-p_{Mi}+\frac{\partial V_{R}\left( x_{i},x_{j}\right) }{\partial x_{i}}\right) [a_{i}+bx_{i}-\kappa p_{Ri}\left( t\right) +\gamma p_{Rj}\left( t\right) ]\right\} \nonumber \\ \end{aligned}$$

(23)

for all $i=1,2$ and $i\ne j$. Maximizing the right-hand side and rearranging terms give the retailer’s reaction functions

$$\begin{aligned} p_{R1}&=\frac{a_{2}\gamma +a_{1}\kappa +b\left( x_{2}\gamma +x_{1}\kappa \right) +\left( \frac{\partial V_{R}}{\partial x_{1}}-P_{M1}\right) \left( \gamma -\kappa \right) \left( \gamma +\kappa \right) }{2\left( \kappa -\gamma \right) \left( \gamma +\kappa \right) }, \end{aligned}$$

(24)

$$\begin{aligned} p_{R2}&=\frac{a_{1}\gamma +a_{2}\kappa +b\left( x_{1}\gamma +x_{2}\kappa \right) +\left( \frac{\partial V_{R}}{\partial x_{2}}-P_{M2}\right) \left( \gamma -\kappa \right) \left( \gamma +\kappa \right) }{2\left( \kappa -\gamma \right) \left( \gamma +\kappa \right) }. \end{aligned}$$

(25)

Here again, we can clearly see that

$$\begin{aligned} \frac{\partial p_{R1}}{\partial P_{M1}}\left( x_{1},x_{2},P_{M1}\right) =\frac{\partial p_{R2}}{\partial P_{M2}}\left( x_{1},x_{2},P_{M2}\right) =\frac{1}{2}>0 \end{aligned}$$

These results indicate that retailer’s reaction to an increase in wholesale prices when he is handling the two complementary products is similar to his reaction when he handles a single product: the retail prices are increased by 50 %.

The remaining computations that lead to the results in the next proposition are displayed in “Appendix B”.

Proposition 2

Transfer and retail prices with the presence of a complementary product are given by the following expressions¹⁴

$$\begin{aligned} p_{M1}(x_{1},x_{2})&=\Delta _{1}x_{1}+\Delta _{2}x_{2}+\Delta _{3}, \end{aligned}$$

(26)

$$\begin{aligned} p_{M2}(x_{1},x_{2})&=\Delta _{4}x_{1}+\Delta _{5}x_{2}+\Delta _{6}, \end{aligned}$$

(27)

$$\begin{aligned} p_{R1}(x_{1},x_{2})&=\Delta _{7}x_{1}+\Delta _{8}x_{2}+\Delta _{9}, \end{aligned}$$

(28)

$$\begin{aligned} p_{R2}(x_{1},x_{2})&=\Delta _{10}x_{1}+\Delta _{11}x_{2}+\Delta _{12}. \end{aligned}$$

(29)

The coefficients $\Delta _{1}$,...$\Delta _{12}$ are displayed in “Appendix B”.

Manufacturer i’s and retailer’s value functions are given by

$$\begin{aligned} V_{Mi}(x_{1},x_{2})&=\frac{h_{i1}}{2}x_{1}^{2}+\frac{h_{i2}}{2}x_{2}^{2}+h_{i3}x_{1}x_{2}+h_{i4}x_{1}+h_{i5}x_{2}+h_{i6}, \end{aligned}$$

(30)

$$\begin{aligned} V_{R}(x_{1},x_{2})&=\frac{R_{1}}{2}x_{1}^{2}+\frac{R_{2}}{2}x_{2}^{2}+R_{3}x_{1}x_{2}+R_{4}x_{1}+R_{5}x_{2}+R_{6}. \end{aligned}$$

(31)

Proof

See “Appendix B”. $\square$

The results in this proposition indicate that the pricing strategies of the retailer and the two manufacturers are state dependent. Both the retail and the wholesale prices are linearly affected by the cumulative sales of the two complementary products, and all channel members’ value functions are linear quadratic and depend on both products’ sales rates.

The differential game studied under this scenario does not allow us to solve the problem analytically and to identify the value functions parameters or comment on their signs. Hence, we cannot make any additional comments on the results of Proposition 2 and must solve the problem numerically.¹⁵

We follow the same steps as those described in the previous scenario and substitute Eqs. (28) and (29) into Eq. (4) then solve the resulting dynamic system in order to compute the sales trajectories for both products. They are given by the following expressions

$$\begin{aligned} x_{1}(t)&=\alpha _{1}e^{\lambda _{1}t}+\alpha _{2}e^{\lambda _{2}t}+x_{1}^{SS}, \end{aligned}$$

(32)

$$\begin{aligned} x_{2}(t)&=\alpha _{3}e^{\lambda _{1}t}+\alpha _{4}e^{\lambda _{2}t}+x_{2}^{SS}. \end{aligned}$$

(33)

where $\alpha _{i},i=1,...,4$ are constants. $x_{1}^{SS} and x_{2}^{SS}$ are the cumulative sales values at the steady state given by

$$\begin{aligned} x_{1}^{SS}&=\frac{{g_{2}}\,{r_{0}}-{g_{0}}\,{r_{2}}}{{g_{1}}\,{r_{2}}-{g_{2}}\,{r_{1}}}, \end{aligned}$$

(34)

$$\begin{aligned} x_{2}^{SS}&=\frac{{g_{1}}\,{r_{0}}-{g_{0}}\,{r_{1}}}{{g_{2}}\,{r_{1}}-{g_{1}}\,{r_{2}}}. \end{aligned}$$

(35)

and $\lambda _{1}$ and $\lambda _{2}$ are the real eigenvalues of the matrix associated with the system of differential Eqs. (68) and (69) such that

$$\begin{aligned} \lambda _{1}&=\frac{(g_{1}+r_{2})-\sqrt{(g_{1}+r_{2})^{2}-4(g_{1}r_{2}-g_{2}r_{1})}}{2}, \end{aligned}$$

(36)

$$\begin{aligned} \lambda _{2}&=\frac{(g_{1}+r_{2})+\sqrt{(g_{1}+r_{2})^{2}-4(g_{1}r_{2}-g_{2}r_{1})}}{2}. \end{aligned}$$

(37)

with $(g_{1}+r_{2})^{2}-4(g_{1}r_{2}-g_{2}r_{1})>0$ to ensure that the two eigenvalues are real. The expressions of $g_{0},g_{1},g_{2},r_{0},r_{1}$ and $r_{2}$ are shown in the “Appendix B”.

If the two eigenvalues are negative, the steady state $(x_{1}^{SS},x_{2}^{SS})$ is globally asymptotically stable. If one eigenvalue is positive and the other one negative, the steady state $(x_{1}^{SS},x_{2}^{SS})$ is a stable saddle point. The values of the parameters are chosen such that the steady state is a saddle point. In other words, the initial conditions $x_{1}(0)$ and $x_{2}(0)$ and other parameters are fixed to ensure that $\lambda _{1}<$ 0 and $\lambda _{2}>0$. Sufficient conditions ensuring this behaviour are as follows: $g_{1}+r_{2}>0$ and $(g_{1}r_{2}-g_{2}r_{1})<0$. More precisely, once we fix $x_{1}(0)$, it can be easily shown from (68) and (69) that

$$\begin{aligned} x_{2}(0)=-\left( \frac{g_{1}-\lambda _{1}}{g_{2}}\right) (x_{1}(0)-x_{1}^{ss})+x_{2}^{ss}. \end{aligned}$$

(38)

Here again, it is not possible to analytically compare the equilibrium strategies in the three cases. Thus, we resort to numerical simulations. The results are presented in the next section.

4 Numerical Results

Under the one-retailer–two-manufacturers game, the model parameters are $a_{i},b,\kappa ,\gamma ,c$ and $\rho$. The parameter $\kappa$, which captures the direct price sensitivity, takes positive values. The cross-price sensitivity $\gamma$ must be negative for the products to be complements. And to capture the saturation effects, we set a negative value for the parameter b, which captures the impact of cumulative past sales on the future sales. The parameter $\rho$ is the discounting factor. Since we solve our problem in an infinite horizon, we consider that it takes low positive values: $\rho \in [0.01,0.1]$.

The parameters $a,a_{i}$ and c are scaling factors that do not qualitatively affect the results. We fix their values at the levels indicated for the benchmark case.

For comparison, we fix the same benchmark values for the baseline sales ($a,a_{i}$ and $a_{j}$) and for the price effects parameters $\kappa$ and b in both scenarios. We use a grid defined by $b\in [-1,0]$ and $\gamma \in ]-1,0]$ such that $\left| \gamma \right| <\kappa$ and $\left| \gamma \right| \ne 2\kappa$, and generate numerical results with a mesh size of 0.2. We retain only parameter values verifying the non-negativity constraints on controls, state variables and sales rates as well as the stability condition of the steady state.

Figure 1 shows that the admissible values in the $(\gamma ,b)$ space under the one-retailer-two-manufacturers game are located in the darker region.

Fig. 1

Admissible values $(\gamma , b)$ space (darker region)

Fig. 2

$x(0) = x_{1}(0)=0.08$, $b=-0.8$, $\gamma = -0.6$

4.1 Comparison

One of the main objectives of this study is to investigate the impacts of introducing a complementary product in the distribution channel on firms’ pricing strategies and sales. To provide answers to these questions, we consider the first scenario where a single product (i.e. product 1) is available in the market, and the second scenario where a complementary product (product 2) is introduced. The impact of the complementary product is then assessed by comparing prices and sales of product 1 under both scenarios.

To do so, we start by computing channel members’ strategies and profits and products’ sales under both scenarios for a benchmark case in which we fix the parameter values as follows:

$$\begin{aligned} a= a_{1}=a_{2} = 10, c = 0,\kappa =1, \rho = 0.08. \end{aligned}$$

Before computing the steady state results, we graphically illustrate the sales rate trajectories as well as the wholesale and retail price trajectories for both scenarios. Figures 2 and 3 illustrate the paths for the pricing strategies and sales rates, respectively. We take $b=-0.8$ and $\gamma =-0.6$ as saturation parameters and level of complementarity baseline.

Fig. 3

$x(0) = x_{1}(0)=0.08$,$b=-0.8$,$\gamma = -0.6$

Figures 2 and 3 call for the following claims¹⁶:

Claim 1

The retailer and the manufacturer(s) practice a skimming strategy under both scenarios, but prices are set initially at higher levels when a complementary product is introduced into the market.

Claim 2

The retail and wholesale prices in both scenarios compare as follows:

• (i) $pR^{B}(0)<pR_{1}^{R2M}(0)$ but $pR_{1}^{R2M}(t)$ decreases faster than $p_{R}^{B}(t)$ such that for t high enough; $p_{R}^{B}(t)>pR_{1}^{R2M}(t)$.

• (ii) $pM^{B}(0)<pM_{1}^{R2M}(0)$ but $pM_{1}^{R2M}(t)$ decreases faster than $pM(t)^{B}$ such that for t high enough; $pM(t)>pM_{1}(t)$

Indeed, Fig. 2 shows that firms start by fixing high initial retail and wholesale price levels and then reduce their prices during the planning horizon, regardless of whether there is a complementary product or not. Previous studies cited in the introduction section found that firms apply a skimming strategy when demand obeys to saturation effects, and this result was valid for situations where there is a unique product sold by a single firm and when two competitive products are sold in an oligopoly. Our results extend this finding to the case where the products are complements.

The price trajectories show that although the retail and wholesale prices of a product are set at a higher level when a complementary product is available in the marketplace, the prices decrease is faster under this scenario, leading to lower retail and wholesale prices in the long-run (i.e. for high values of t).

By comparing the retail price trajectories to the wholesale price trajectories, we find that $p_{R_{i}}^{R2M}(t)>$ $p_{M_{i}}^{R2M}(t)$ and the profit margin of product 2 is greater than the profit margin of product 1. This indicates that the unit profit margins are always positive for both products. Hence, it is not optimal for firms in the one-retailer–two-manufacturers scenario to practice a loss-leadership strategy, as suggested in [24].

Claim 3

The sales time path of the existing product is boosted when a complementary product is introduced into the market.

With $x(0)^{B}=x_{1}^{R2M}(0)$ we have that $x(t)^{B}<x_{1}^{R2M}(t)$ for all t.

Figure 3 indicates that the sales trajectory of the existing product is higher under the one-retailer–two-manufacturers scenario. Furthermore, we can see in the same figure that the slope of the sales curve is higher under this scenario, meaning that sales increase at a higher speed, with respect to the case where a single product is sold into the market.

4.2 Sensitivity Analysis

Besides the base-case described above, we conducted a sensitivity analysis to identify the impact of a variation of two of the key parameters, namely b and $\gamma$. When varying a parameter, the other parameters remain at their base-case values.

Table 1 Sensitivity analysis (One-retailer-two-manufacturers game)

The results in Table 1 indicate that if the level of complementarity between products increases, then the retail price at the steady state of the existing product ($pR_{1}^{ss}$) decreases,¹⁷ while the retail price of the second product ($pR_{2}^{ss}$) increases. Both products’ wholesale prices decrease with the increase of the cross-price effect. Hence, the retailer passes-through to consumers only the decrease in first product’s retail price.

The increase in demand saturation effect leads to an increase of both products’ wholesale prices. The retailer reacts by increasing the first product’s retail price, while reducing its retail margin on the second product.

Finally, the increase in product complementarity leads to an increase in both products’ cumulative sales at the steady state, while an increase in demand saturation effect leads to a decrease in these cumulative sales.

5 Conclusions

This study investigates the dynamic pricing strategies of firms selling complementary products in a vertical channel structure where demand obeys to saturation effects. We use a differential game to model and solve the problems resulting from two scenarios: one in which a single product is sold on the market, and a second in which a complementary product is introduced by a second manufacturer. Our study attempts to answer the following research questions, i.e. (i) What are the firms’ price trajectories over time in a decentralized vertical channel when the retailer holds complementary products? and (ii) How does the presence of a complementary product affect product prices and sales (w.r.t prices and sales of a unique product sold in a dyad)?

Our main results indicate that:

• Firms practice a skimming strategy in both scenarios.

• In the presence of a complementary product:

  (i):

  The firm fixes a higher initial retail price, but it decreases faster than the retail price of a single product sold on the market. Hence, for a t that is high enough, the product’s retail price becomes lower than the retail price practiced by firms in a bilateral monopoly.

  (ii):

  It is not optimal for firms to practice a loss-leadership strategy.

  (iii):

  Sales of the existing product are higher (w.r.t. when this product is the only product sold on the market).

As mentioned in the introduction, managerial studies on the issue of multi-product pricing suggest that retailers handling two competing products should fix lower prices with respect to the retail price of a single product. Our result in (i) indicates that when both products are complements, the initial retail prices are higher than those practiced for a single product. However, in the long-run, the situation is inversed since the firm selling both products starts reducing the retail prices at a higher speed (with respect to the case where a single product is sold).

Furthermore, another practice reported in the managerial literature on multi-product pricing suggests the use of loss-leadership pricing when firms distribute complementary products. Our result in (ii) indicates that this practice is not optimal. This result could be explained by the fact that we examine the issue in a dynamic setting.

Solving a dynamic problem that takes place in a marketing channel where two products are sold and looking for feedback strategies is a challenging task. Most of the studies that examined similar issues used some simplifying assumptions by considering only open-loop information structures, or by solving the problem without discounting (i.e. by fixing $\rho =0$). We chose to allow firms to use feedback strategies, so the model would be closer to reality, but this came with the cost: we were not able to compute analytical solutions for the second scenario, and we had to perform a numerical resolution of our optimization problem. Hence, many results are displayed in the form of claims, rather than propositions.

Furthermore, in our model, we considered that the sales rate evolves according to a modified version of the Bass diffusion model where we introduced only the saturation effects. An extension of this study should examine the impact of adding the imitation effects in the model.

Appendix

1.1 Appendix A

The sufficient condition for a stationary feedback Stackelberg equilibrium requires us to find bounded and continuously differentiable functions, $V_{R}(x)$ and $V_{M}(x)$ for the retailer and the manufacturer, respectively, which satisfy for all $x(t)\geqslant 0$, the HJB equations obtained after the substitution of (10) and (8) into Eqs (7) and (9).

Guided by the model’s linear-quadratic structure, we conjecture that the functions $V_{R}(x)$ and $V_{M}(x)$ are quadratic and given by the expressions (13) and (14) in the proposition. The coefficients $\beta _{1},\beta _{2},\beta _{0},\alpha _{1},\alpha _{2}$ and $\alpha _{0}$ are obtained by identification after replacing $V_{R}(x)$ and $V_{M}(x)$ as well as their first derivatives into the HJB equations.

Finally, plugging the derivatives of these values functions into the expressions (10) and (8) provides the channel members’ pricing strategies at the equilibrium displayed in the proposition.

The terminal conditions

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }e^{-\rho t}V_{R}(x(t))&=0, \end{aligned}$$

(39)

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }e^{-\rho t}V_{M}(x(t))&=0. \end{aligned}$$

(40)

are sufficient conditions guaranteeing that the expressions (13) and (14) are the retailer’s and manufacturer’s value functions and that (11)–(12) are the pricing strategies.

1.2 Appendix B

As in the previous scenario, after computing the retailer’s reaction functions, we move to the manufacturer’s problems. We consider that both manufacturers play à la Nash. In other words, they solve their optimization problems simultaneously. The manufacturer i’s HJB equations are:

$$\begin{aligned} \rho V_{Mi}(x_{1},x_{2})= & {} \max \limits _{p_{Mi}}\left\{ \left( p_{Mi}-c+\frac{\partial V_{Mi}}{\partial x_{i}}\right) [a_{i}+bx_{i}-\kappa p_{Ri}\left( t\right) +\gamma p_{Rj}(t)]\right. \nonumber \\&\left. +\frac{\partial V_{Mi}}{\partial x_{j}}[a_{j}+bx_{j}-\kappa p_{Rj}(t)+\gamma p_{Ri}(t)]\right\} . \end{aligned}$$

(41)

Substituting (24) and (25) into (41), the HJB equations of the leaders, and performing the maximization of the right-hand side provide the strategies:

$$\begin{aligned} p_{M1}&=\frac{\lambda _{1}+bx_{2}\gamma +2bx_{1}\kappa +\gamma ^{2}\left( \frac{\partial V_{M2}}{\partial x_{1}}-\frac{\partial V_{R}}{\partial x_{1}}\right) +2\kappa ^{2}\left( \frac{\partial V_{R}}{\partial x_{1}}-\frac{\partial V_{M1}}{\partial x_{1}}\right) +\gamma \kappa \left( c-\frac{\partial V_{R}}{\partial x_{2}}+2\frac{\partial V_{M1}}{\partial x_{2}}-\frac{\partial V_{M2}}{\partial x_{2}}\right) }{4\kappa ^{2}-\gamma ^{2}}, \end{aligned}$$

(42)

$$\begin{aligned} p_{M2}&=\frac{\lambda _{2}+bx_{1}\gamma +2bx_{2}\kappa \gamma ^{2}\left( \frac{\partial V_{M1}}{\partial x_{2}}-\frac{\partial V_{R}}{\partial x_{2}}\right) +2\kappa ^{2}\left( \frac{\partial V_{R}}{\partial x_{2}}-\frac{\partial V_{M2}}{\partial x_{2}}\right) +\gamma \kappa \left( c-\frac{\partial V_{R}}{\partial x_{1}}+2\frac{\partial V_{M2}}{\partial x_{1}}-\frac{\partial V_{M1}}{\partial x_{1}}\right) }{4\kappa ^{2}-\gamma ^{2}}. \end{aligned}$$

(43)

where $\lambda _{1}=a_{2}\gamma +2\kappa (a_{1}+c\kappa )$ and $\lambda _{2}=a_{1}\gamma +2\kappa (a_{2}+c\kappa ).$

Substituting $p_{Ri}$ and $p_{Mi}$, namely (24), (25), (42), 43), into the HJB Eqs. (23) and (41) leads to conjecture the quadratic value functions in Eqs. (30) and (31).

We replace $V_{Mi}(x_{1},x_{2})$ as well as their first derivatives in the HJB equations. To identify the value function coefficients $h_{ij}$ for $i=1,2$ and $j=1,2,...,6$ for manufacturers, we need to solve the twelve Ricatti equations (not printed here). Their canonical forms are the following, for $i=1,2$; $\forall i\ne j$:

$$\begin{aligned} f_{1} (h_{i1}, h_{i3}, h_{j1}, h_{j3}, R_{1},R_{3})&= 0, \end{aligned}$$

(44)

$$\begin{aligned} f_{2} (h_{i2}, h_{i3}, h_{j2}, h_{j3}, R_{2},R_{3})&= 0, \end{aligned}$$

(45)

$$\begin{aligned} f_{3} (h_{i1}, h_{i2}, h_{i3}, h_{j1}, h_{j2}, h_{j3}, R_{1},R_{2},R_{3})&= 0, \end{aligned}$$

(46)

$$\begin{aligned} f_{4}(h_{i1},h_{i3},h_{i4},h_{i5},h_{j1}, h_{j3}, h_{j4}, h_{j5}, R_{1}, R_{3},R_{4}, R_{5})&= 0 , \end{aligned}$$

(47)

$$\begin{aligned} f_{5} (h_{i2}, h_{i3}, h_{i4}, h_{i5}, h_{j2}, h_{j3}, h_{j4}, h_{j5}, R_{2},R_{3}, R_{4}, R_{5})&= 0, \end{aligned}$$

(48)

$$\begin{aligned} f_{6} (h_{i4}, h_{i5}, h_{i6}, h_{j4}, h_{j5}, h_{j6}, R_{4},R_{5})&= 0. \end{aligned}$$

(49)

The value function coefficients for the retailer, $R_{i}$ for $i=1,2,....,6$, are identified through the six Ricatti equations below.

$$\begin{aligned} s_{1}(R_{1},h_{11},h_{21},h_{13},h_{23},R_{3})&=0, \end{aligned}$$

(50)

$$\begin{aligned} s_{2}(R_{2},h_{12},h_{22},h_{13},h_{23},R_{3})&=0, \end{aligned}$$

(51)

$$\begin{aligned} s_{3}(R_{3},h_{11},h_{12},h_{21},h_{22},h_{13},h_{23},R_{1},R_{3})&=0, \end{aligned}$$

(52)

$$\begin{aligned} s_{4}(R_{4},h_{11},h_{13},h_{14},h_{15},h_{21},h_{23},h_{24},h_{25},R_{1},R_{3},R_{5})&=0, \end{aligned}$$

(53)

$$\begin{aligned} s_{5}(R_{5},h_{12},h_{13},h_{14},h_{15},h_{22},h_{23},h_{24},h_{25},R_{2},R_{3},R_{4})&=0, \end{aligned}$$

(54)

$$\begin{aligned} s_{6}(R_{6},h_{14},h_{15},h_{16},h_{24},h_{25},h_{26},R_{4},R_{5})&=0. \end{aligned}$$

(55)

We compute the pricing strategies of all channel members by substituting the derivatives of the value functions into expressions (42), (43), (24) and (25). where

$$\begin{aligned}&\Delta _{1} = \frac{\kappa \left( -2 b+\gamma \left( -2 h_{13}+h_{23}+R_3\right) +2 h_{11} \kappa \right) -h_{21} \gamma ^2+R_1 \left( \gamma ^2-2 \kappa ^2\right) }{\gamma ^2-4 \kappa ^2}, \end{aligned}$$

(56)

$$\begin{aligned}&\Delta _{2} = \frac{-\gamma \left( b+\gamma \left( h_{23}-R_3\right) \right) +\gamma \kappa \left( -2 h_{12}+h_{22}+R_2\right) +2 \kappa ^2 \left( h_{13}-R_3\right) }{\gamma ^2-4 \kappa ^2}, \end{aligned}$$

(57)

$$\begin{aligned}&\Delta _{3} = \frac{-\gamma \left( a_2+\gamma \left( h_{24}-R_4\right) \right) -2 a_1 \kappa +\gamma \kappa \left( -c-2 h_{15}+h_{25}+R_5\right) -2 \kappa ^2 \left( c-h_{14}+R_4\right) }{\gamma ^2-4 \kappa ^2}, \end{aligned}$$

(58)

$$\begin{aligned}&\Delta _{4} = \frac{-\gamma \left( b+\gamma \left( h_{13}-R_3\right) \right) +\gamma \kappa \left( h_{11}-2 h_{21}+R_1\right) +2 \kappa ^2 \left( h_{23}-R_3\right) }{\gamma ^2-4 \kappa ^2}, \end{aligned}$$

(59)

$$\begin{aligned}&\Delta _{5} = \frac{-2 b \kappa +\gamma ^2 \left( R_2-h_{12}\right) +\gamma \kappa \left( h_{13}-2 h_{23}+R_3\right) +2 \kappa ^2 \left( h_{22}-R_2\right) }{\gamma ^2-4 \kappa ^2}, \end{aligned}$$

(60)

$$\begin{aligned}&\Delta _{6} = \frac{-\gamma \left( a_1+\gamma \left( h_{15}-R_5\right) \right) -2 a_2 \kappa +\gamma \kappa \left( -c+h_{14}-2 h_{24}+R_4\right) -2 \kappa ^2 \left( c-h_{25}+R_5\right) }{\gamma ^2-4 \kappa ^2} , \end{aligned}$$

(61)

$$\begin{aligned}&\Delta _{7} = \frac{\kappa \left( \left( \kappa -\gamma \right) \left( \gamma +\kappa \right) \left( -\gamma \left( h_{23}+R_3\right) -2 \kappa \left( h_{11}+R_1\right) +2 h_{13} \gamma \right) -3 b \left( \gamma ^2-2 \kappa ^2 \right) \right) +h_{21} \gamma ^2 \left( \kappa ^2-\gamma ^2\right) }{2 \left( \gamma ^4-5 \gamma ^2 \kappa ^2+4 \kappa ^4\right) }, \end{aligned}$$

(62)

$$\begin{aligned}&\Delta _{8} = \frac{b \left( 5 \gamma \kappa ^2-2 \gamma ^3\right) -\left( \gamma -\kappa \right) \left( \gamma +\kappa \right) \left( h_{23} \gamma ^2-\kappa \left( \gamma \left( -2 h_{12}+h_{22}+R_2\right) +2 \kappa \left( h_{13}+R_3\right) \right) \right) }{2 \left( \gamma ^4-5 \gamma ^2 \kappa ^2+4 \kappa ^4\right) } , \end{aligned}$$

(63)

$$\begin{aligned}&\Delta _{9} = \frac{\kappa \left( -3 a_1 \left( \gamma ^2-2 \kappa ^2\right) -\left( \gamma -\kappa \right) \left( \gamma +\kappa \right) \left( c \left( \gamma +2 \kappa \right) -\gamma \left( h_{25}+R_5\right) -2 \kappa \left( h_{14}+R_4\right) +2 h_{15} \gamma \right) \right) +a_2 \left( 5 \gamma \kappa ^2-2 \gamma ^3\right) +h_{24} \gamma ^2 \left( \kappa ^2-\gamma ^2\right) }{2 \left( \gamma ^4-5 \gamma ^2 \kappa ^2+4 \kappa ^4\right) },\nonumber \\ \end{aligned}$$

(64)

$$\begin{aligned}&\Delta _{10} = \frac{b \left( 5 \gamma \kappa ^2-2 \gamma ^3\right) -\left( \gamma -\kappa \right) \left( \gamma +\kappa \right) \left( \kappa \left( \gamma \left( -h_{11}+2 h_{21}-R_1\right) -2 \kappa \left( h_{23}+R_3\right) \right) +h_{13} \gamma ^2\right) }{2 \left( \gamma ^4-5 \gamma ^2 \kappa ^2+4 \kappa ^4\right) }, \end{aligned}$$

(65)

$$\begin{aligned}&\Delta _{11} = \frac{\kappa \left( \left( \gamma -\kappa \right) \left( \gamma +\kappa \right) \left( \gamma \left( h_{13}-2 h_{23}+R_3\right) +2 \kappa \left( h_{22}+R_2\right) \right) -3 b \left( \gamma ^2-2 \kappa ^2 \right) \right) +h_{12} \gamma ^2 \left( \kappa ^2-\gamma ^2\right) }{2 \left( \gamma ^4-5 \gamma ^2 \kappa ^2+4 \kappa ^4\right) } , \end{aligned}$$

(66)

$$\begin{aligned}&\Delta _{12} = \frac{\kappa \left( \left( \gamma -\kappa \right) \left( \gamma +\kappa \right) \left( \gamma \left( -c+h_{14}-2 h_{24}+R_4\right) +2 \kappa \left( -c+h_{25}+R_5\right) \right) -3 a_2 \left( \gamma ^2-2 \kappa ^2\right) \right) +a_1 \left( 5 \gamma \kappa ^2-2 \gamma ^3\right) +h_{15} \gamma ^2 \left( \kappa ^2-\gamma ^2\right) }{2 \left( \gamma ^4-5 \gamma ^2 \kappa ^2+4 \kappa ^4\right) }.\nonumber \\ \end{aligned}$$

(67)

The transversality condition

$$\begin{aligned} \lim \limits _{t\rightarrow \infty } e^{- \rho t} V_{Mi}(x_{1}(t), x_{2}(t))= & {} 0 ; \\ \lim \limits _{t\rightarrow \infty } e^{- \rho t} V_{R}(x_{1}(t), x_{2}(t))= & {} 0 \end{aligned}$$

guarantees that the expressions (30), (31); and (26), (27), (28) and (29) are the manufacturer i’s and retailer’s value functions, and the pricing strategies. Notice that $(x_{1}(t),x_{2}(t))$ is the solution of the closed-loop dynamics resulting in substitution of (26), (27), (28) and (29) into the dynamic demand (4). We have to solve the following dynamical system:

$$\begin{aligned} \dot{x_{1}}(t)&=g_{1}x_{1}+g_{2}x_{2}+g_{0}, \end{aligned}$$

(68)

$$\begin{aligned} \dot{x_{2}}(t)&=r_{1}x_{1}+r_{2}x_{2}+r_{0}. \end{aligned}$$

(69)

where

$$\begin{aligned} g_{1}&=b-\kappa \Delta _{7}+\gamma \Delta _{10}, \end{aligned}$$

(70)

$$\begin{aligned} g_{2}&=b-\kappa \Delta _{8}+\gamma \Delta _{11}, \end{aligned}$$

(71)

$$\begin{aligned} g_{0}&=a_{1}-\kappa \Delta _{9}+\gamma \Delta _{12}, \end{aligned}$$

(72)

$$\begin{aligned} r_{1}&=b-\kappa \Delta _{10}+\gamma \Delta _{7}, \end{aligned}$$

(73)

$$\begin{aligned} r_{2}&=b-\kappa \Delta _{11}+\gamma \Delta _{8}, \end{aligned}$$

(74)

$$\begin{aligned} r_{0}&=a_{2}-\kappa \Delta _{12}+\gamma \Delta _{9}, \end{aligned}$$

(75)

The solution gives the expressions for both products’ cumulative sales rate trajectories $x_{1}(t)$ and $x_{2}(t)$ given in the proposition. The paths for the pricing strategies are obtained after replacing $x_{1}(t)$ and $x_{2}(t)$ by their expressions (32) and (33) in (26), (27), (28) and (29).