Abstract
We are concerned with an inverse problem arising in thermal imaging in a bounded domain \(\Omega \subset {\mathbb {R}}^n\), \(n=2,3\). This inverse problem consists in the determination of the heat exchange coefficient q(x) appearing in the boundary of a hyperbolic heat equation with Robin boundary condition. A double-logarithmic stability estimate is developed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The classical model for heat propagation is given by the equations
where uis the temperature (difference to a fixed constant reference temperature), \(\beta \) is a positive physical constant and q is the heat flux vector satisfying the classical the well-known Fourier’s law
where k is the thermal conductivity depending on the properties of the material.
The model using classic Fourier’s law assumes the flux q to be proportional to the gradient of the temperature q at the same time \(\theta \) as in (1.2) leads to the paradox of infinite heat propagation speed. That is, any thermal disturbance at a single point has an instantaneous effect everywhere in the medium. In other words, it is clear that Equation (1.2) together with the energy equation of the heat conduction (1.1) yields the classical heat transport equation (of parabolic type)
that allows an infinite speed for thermal signals.
The model using classic Fourier law exhibits the physical paradox of infinite propagation speed of signals. To eliminate this paradox a generalized thermoelasticity theory has been developed subsequently. The development of this theory was accelerated by the advent of the second sound effects observed experimentally in materials at a very low temperature. In heat transfer problems involving very short time intervals and/or very high heat fluxes, it has been revealed that the inclusion of the second sound effects to the original theory yields results which are realistic and very much different from those obtained with classic Fourier’s law. These models are based on hyperbolic-type equations for temperature and are closely connected with the theories of second sound, which view heat propagation as a wave-like phenomenon. In an idealized solid, for example, the thermal energy can be transported by quantized electronic excitations, which are called free electrons, and by the quanta of lattice vibrations, which are called phonons. These quanta undergo collisions of a dissipative nature, causing a thermal resistance in the medium. A relaxation time is associated with the average communication time between these collisions for the commencement of resistive flow. Although the convergence time for the solutions of the hyperbolic model to that of the parabolic model is small, it may become important when extremely short times are involved. It is under such situations that the assumption of a parabolic heat conduction model may lead to inaccurate modelling of the transient thermal behavior.
First relativistic heat conduction models with second sound were introduced by Cattaneo [6] by proposing a modification of Fourier’s law of heat conduction, i.e. the constitutive relation
where \(\tau \) the relaxation constant that is, describes the time lag in the response of the heat flux to a gradient in the temperature. Cattaneo’s law is perhaps the most obvious, the most widely accepted and simplest generalization of Fourier’s law that gives rise to a finite speed of propagation of heat. Replacing the Fourier’s law (1.2) by the Cattaneo law (1.4) and combining with the law of balance of energy (1.1), we obtain a purely hyperbolic description of heat conduction (called also telegraph equation),
which predicts a finite signal speed equals to \(1/\sqrt{\tau }\). Note that both laws, Fourier and Cattaneo, are dissipative with dissipations strong enough to produce exponential decay of the solutions for their corresponding heat equations.
In paper we investigate an inverse boundary coefficient problem in thermal imaging based on the purely hyperbolic heat equation (1.5). However, from a physical point of view, this equation is physically more realistic than (1.1) one based on Fourier’s law, since it propagates with finite speed. It is worth citing that several papers studying different inverse problems for the parabolic heat equation (1.1) and wave equation (e.g, [1,2,3,4,5, 12, 17, 20,21,22,23,24,25]). The inverse problem under consideration consists in recovering the unknown heat exchange (heat loss) coefficient q(x) appearing in the hyperbolic heat equation with Robin boundary condition. This recovery may be obtained from boundary temperature measurements. Let \(\Omega \) be a bounded domain (that is, a non-empty open connected set) of class \(C^3\) in \({\mathbb {R}}^{n}\); we denote by \(\nu \) the outward unit normal vector to its boundary \(\Gamma \). Let \(\{\Gamma _0, \Gamma _1\}\) be a partition of \(\Gamma \) and let \(g : \Gamma _0\times (0,\infty )\rightarrow {\mathbb {R}}\) such that \(supp(g)\subset \Gamma _0\) and \(q : \Gamma _1\rightarrow {\mathbb {R}}\) be two given functions (q is nonnegative). We consider the problem
In engineering applications, the stationary heat flux g corresponds to an uniform heating of the outer surface. Typically, this is the case when heat or flash lamps are used to provide the input flux g. In this paper, we study separately the two cases: stationary \((g:=g(x))\) and time-dependent heat flux \((g:=h(x,t))\). To be able to get some estimations of the solution, we assume that for a fixed positives constants \(R_0\) and \(R_1\), we have
Furthermore, in order to avoid some difficulties, we shall assume that
In the case of time-dependent heat flux \((g:=h(x,t))\), we assume that
Now, by using the same notations as in [9], we introduce the vector space
equipped with the norm
where \(S'({\mathbb {R}}^n)\) is the space of temperate distributions on \({\mathbb {R}}^n\), \({\hat{y}}\) denotes the Fourier transform of the function y and \(B_{s,r}({\mathbb {R}}^n)\) is a Besov space.
Thereafter, we shall need that the solution to the problem (1.6) has some smoothness. In order to give sufficient conditions on data guaranteeing this smoothness, we may define the following sets of boundary coefficients:
where \(M > 0\) is a given constant. We recall that the function q(x) (heat exchange coefficient) in (1.6) is known as the Robin coefficient with a support in \(\Gamma _1\). So, the introduction of the space \(D_M^0\) is suitable and it will be useful in the rest of the paper.
Now, we introduce \(\gamma \times (0,\infty )\) as a subset of the accessible sub-boundary \(\Gamma _0\times (0,\infty )\). We assume that \(\gamma \) does not meet supp(g) (\(g:=g(x)\) or \(g:=h(x,t)\)) and the following condition holds true:
The inverse problem associated to the problem (1.6) can be formulated as follows: Inverse problem. Determine q, supported on \(\Gamma _1\), from the boundary measurements
where \(\Gamma _0\) is assumed to be a priori known and \(u_q\) is the solution to the problem (1.6) with the coefficient q. In this paper, the error \(q-{\tilde{q}}\) is obtained in the whole \(\Gamma _1\) by a double-logarithmic stability. Following [10] and [9], we modulate the problem of detecting corrosion damage by electric measurements. For this end, we consider the following boundary value problem
Using Theorem 2.3 of [11] and the fact that \(B_{n-1/2,1}(\Gamma )\) is continuously embedded in \(B_{n-3/2,1}(\Gamma )\), we obtain that (for any \(q\in D\)) the problem (1.12) has a unique solution \(v_q\in H^n(\Omega )\) \((n=2,3)\). Moreover, we have
where \(R_1=R_1(\Omega ,g,M)\) denotes a positive constant. In the next of this paper, we need the following Theorem in [ [8], Theorem 2] and Lemma in [ [7], Proposition 4.1].
Theorem 1.1
Let \(\Omega \subset {\mathbb {R}}^n\) be a bounded domain with a \({C}^{1,1}\) (Hölder space) boundary \(\partial \Omega \). Let \(\gamma _0\) be an open domain of \(\partial \Omega \) and P an elliptic operator. For all \(\tau \in (0,1)\), there exist two positive constants c and \(\epsilon _0\) such that, for all \(\epsilon \in ]0,\epsilon _0[\) and for all \( v \in H^2(\Omega )\), we have:
Lemma 1.1
Let \(0<\alpha <1\). Then, there exist three positive constants \(\delta ^{*}\), \(s^*:=\left| \ln \delta ^{*}\right| \) and \(c=c(\Omega ,\Gamma )\) such that for any \(0<\delta <\delta ^{*}\), \(s>s^*\) and for a given \(f\in {C}^\alpha (\Gamma )\) (Hölder space) we have:
where \(v_q\) is the solution to (1.12).
In the following we distinguish the two cases: stationary \((g:=g(x))\) and time-dependent heat flux \((g:=h(x,t))\).
2 Stability of the determination of Robin coefficient in the stationary case
In this section, we establish a double logarithmic stability estimate for the determination of a boundary coefficient appearing in the problem (1.6) in the stationary case \((g:=g(x))\).
Let us denote by \(u_q\) the solution to the problem (1.6) which can be decomposed into the sum
where \(v_q\) is the solution to (1.12) and \(w_q\) is the solution to the following problem
2.1 Well-posedness and exponential stability of the problem (2.2)-(2.5)
We will begin by proving existence, uniqueness, and exponential stability results for the problem (2.2)-(2.5). We first define our solution spaces:
with the norm
By hypothesis (1.8) the last expression defines a norm on V, which is equivalent to the norm induced by \(H^1(\Omega )\); consequently, \(V=H^1_{\Gamma _0}( \Omega )\) is a Hilbert space. Note that for function \(w\in H^1_{\Gamma _0}( \Omega )\) the Poincaré’s inequality remains valid, that is
where \(C_p > 0\) is the Poincaré’s constant. We define the following Hilbert space
endowed with the inner product
In order to find a reasonable definition of the (weak) solution to the problem (2.2)-(2.5) we multiply the equation (2.2) by \(v\in V\) and we integrate by parts. Using the boundary conditions (2.3), (2.4) we obtain that
Introducing the new variable \(v = w_t\), setting \(W (t) = (w(t ), v(t ))^T\), the problem (2.2)-(2.5) can be written as a linear evolution equation in \({\mathscr {H}}\) of the form
where \(W(0) = ( w_0, v_0)^{T} \in {\mathscr {H}}\) and \({\mathscr {A}}:{\mathscr {D}}({\mathscr {A}})\subset {\mathscr {H}}\rightarrow {\mathscr {H}}\) is the linear operator defined by
with domain
Note that \(\mathscr {D(A)} \) is densely defined in \({\mathscr {H}} \). Now, we use the theory of semigroups of linear operators to prove the well-posedness of problem (2.2)-(2.5).
Lemma 2.1
Assume (1.8). The operator \({\mathscr {A}} \) generates a semigroup of contractions in \({\mathscr {H}}\).
Proof
Obviously \(\mathscr {D(A)}\) is dense in \({\mathscr {H}}\) and the maximality of \({\mathscr {A}}\) is easily checked. We show now that \({\mathscr {A}}\) is dissipative. For any \(W (t) = (w(t ), v(t ))^T\) be in \(\mathscr {D(A)}\). From (2.10) and the inner product defined on \({\mathscr {H}}\), it is quite easy to check that
Then \({\mathscr {A}}\) is dissipative. To show that \({\mathscr {A}}\) is maximal we need to prove that \(0\in \rho ({\mathscr {A}}).\) It suffices to find \(W={(w, v)}^T\in \mathscr {D(A)}\) such that \({\mathscr {A}}{W}=F\) for any \(F={(f_{1},f_{2})}^T\in {\mathscr {H}}.\) In terms of the components, we find
By (2.11), we have \(v\in V.\) We conclude that there exists a unique function w satisfying (2.12) such that \(w\in {\mathscr {H}}\cap H^{2}(\Omega ).\) It is also clear from the regularity theory of elliptic systems that \(\Vert W\Vert _{{\mathscr {H}}}\le C \Vert F\Vert _{{\mathscr {H}}},\) for a positive C, and we conclude that 0 belongs to the resolvent of \({\mathscr {A}}.\)
Then we conclude that operator \({\mathscr {A}}\) is m-dissipative in \({\mathscr {H}}\). Since \(\mathscr {D(A)}\) is densely defined in \({\mathscr {H}}\), the lemma follows from the well-known Lumer-Phillips Theorem (e.g. see Pazy, [18]).
Now an application of the theory of semigroups (see Pazy, [18]) gives \(\square \)
Theorem 2.1
Assume (1.8). Given \((w_0, w_1) \in {\mathscr {H}}\) arbitrarily, the problem (2.2)-(2.5) has a unique solution satisfying
The energy \(E : {\mathbb {R}}^+\rightarrow {\mathbb {R}}^+\) of the solution is non-increasing.
Recall the definition of the energy \(E : {\mathbb {R}}^+\rightarrow {\mathbb {R}}^+\) of the solution, defined by
The following result shows in particular that the energy is non-increasing.
Lemma 2.2
Given \((w_0, w_1) \in \mathscr {D(A)}\) arbitrarily, the solution to problem (2.2)-(2.5) satisfies the energy equality
Indeed, \( E(S) \ge E(T)\).
Proof
We multiply equation (2.2) by \(w_t\) and we integrate by parts in \(\Omega \times (S, T)\). Using (2.3)-(2.4) we obtain that
and (2.15) follows from the definition of the energy. \(\square \)
Now we shall prove the exponential stabilization of the problem (2.2)-(2.5) which is based on the following inequality used in Haraux [13] and Lagnese [14].
Theorem 2.2
Let \(E: {\mathbb {R}}_+\rightarrow {\mathbb {R}}^+\) be a non-increasing function and assume that there exists a constant \(T > 0\) such that
Then,
Now, we can cite the following result:
Theorem 2.3
Assume (1.8). Given \((w_0, w_1) \in \mathscr {D(A)}\) arbitrarily, then there exist two positive constant \(C_1\) and \(\eta \) such that the energy of the solution to problem (2.2)-(2.5) satisfies
Proof
Replace v into (2.8) by w and integrate over \([S, T] \times \Omega \), we obtain
Thus, from the definition of E, we deduce
We shall estimate the terms of the right member of the above expression. By using the Young’s and Poincaré’s inequalities, we deduce
Substituting (2.19) into (2.18) yields
Applying Theorem 2.2, hence (2.16) follows for every \((w_0, w_1) \in \mathscr {D(A)}\). \(\square \)
2.2 Double logarithmic stability estimate
In this subsection, we establish a double logarithmic stability estimate for the inverse problem in thermal imaging described above. Here, we require the heat flux on a part of the accessible boundary \(\Gamma _0\) be the same at every time. Moreover, we assume that the boundary function g introduced in the problem (1.6) depends only on the space variable x and \(supp(g)\subset \Gamma _0\). Now, let us consider the following assumption:

where \(k \ge 0\) is an integer. Note that g is not identically equal to zero.
Now, we assume that we have (1.8), (1.11), (\(A_1\)) and (1.10). By applying stationary heat flux, we get the following result.
Theorem 2.4
Let the functions \(u_q\) and \(u_{{\tilde{q}}}\) be solutions to (1.6) with coefficients q and \({\tilde{q}}\), respectively. Let the constants \(\alpha \in (0,1)\) and \(\sigma \in (0,1)\). Then, there exist two positive constants \(A=A(\sigma ,\Omega ,\Gamma _i,\gamma )\) and \(B=B(\Omega ,\gamma )\) such that for any \(q,{\tilde{q}}\in D_M^0\cap {C}^\alpha (\Gamma )\cap C^1(\Gamma )\), we have:
where \({C}^\alpha (\Gamma )\) is the Hölder space, A and B are independent of q and \({\tilde{q}}\).
Proof
Let \(\gamma \subset \Gamma _0\subset \Gamma \) be defined as in (1.10). Let \(u_q\) (resp. \(u_{{\tilde{q}}}\)) be the solution to the problem (1.6) with the coefficient q (resp. with the coefficient \({\tilde{q}}\)). Analogously, we can define the functions \(v_q\) and \(v_{{\tilde{q}}}\) . Using relation (2.1), and the continuity of the trace operator, we can find a constant \(\lambda >0\) such that for all \(t>0\)
By Theorem2.3, we get
Then, we have
Let us define \({\tilde{v}}=v_q-v_{{\tilde{q}}}\) satisfying \(\Delta {\tilde{v}} =0\). Then, we use the interpolation inequality (e.g. [16]), to obtain
By relations (1.13) and (2.20), we obtain
Consequently, we have \(\partial _\nu {\tilde{v}} =\partial _\nu v_q-\partial _\nu v_{{\tilde{q}}}=0\) on \(\gamma \). Using the inequality (2.21) and Theorem1.1, we get
Minimizing (2.22) on \(\epsilon \), we obtain the existence of three positive constants \(A_1\), \(B_1\) and \(\tau \) satisfying
From the interpolation inequality (e.g. [16]), by (1.13), we get:
where \(C_4,C_5,C_6\) are positive constants. By using trace theorem, we get
where \(C_7\) is a positive constant. By (2.23) and (2.24), we get the existence of two positive constants \(A_2\) and \(B_2\) such that
Returning to the definition of \({\tilde{v}}=v_q-v_{{\tilde{q}}} \) and the problem (1.12), we get
Then, we have
Combining (2.25) and (2.26) we obtain the existence of two positive constants \(A_3 \) and \(B_3\) such that
By using Lemma1.1 where \(f=q-{\tilde{q}}\), relation (2.27) and minimizing (1.14) on s ensure the existence of three positive constants A, B and \(\sigma \) satisfying
Using the interpolation inequality, there exist two poisitive constants \(C_8\) and \(\theta <1\) such that:
Using (2.28) and (2.29), we obtain the existence of three positive constants A, B and \({\sigma }\) satisfying
\(\square \)
3 Stability of the determination of Robin coefficient in the time-dependent heat flux
In this section, we establish a double logarithmic stability estimate for the determination of a boundary coefficient appearing in the problem (1.6) for the time-dependent heat flux case \((g:=h(x,t))\).
Let us decompose \(u_q\) the solution to problem (1.6) into the sum
where \(v_q\) is the solution to (1.12), \(w_q\) is the solution to (2.2)-(2.5) and \(u^0_q\) is the solution to the following problem
In the following we need the following result.
3.1 Asymptotic stability of the problem (1.6)
We define the following Hilbert space
endowed with the inner product
By using the same previous argument, it is easy to prove that the operator \({\mathscr {A}} \) generates a semigroup of contractions in \({\mathscr {H}}\) and the problem (1.6) is well posed under the condition (1.9). In the next, we will show an asymptotic behavior result for the unique solution to (1.6) in the state space \({\mathscr {H}}\).
Lemma 3.1
The resolvent operator \((\lambda I-{\mathscr {A}} )^{-1}\ :\ {\mathscr {H}}\rightarrow {\mathscr {H}}\) is compact for any \(\lambda > 0\) and hence the canonical embedding \(\Im :\mathscr {D(A)}\rightarrow {\mathscr {H}}\) is compact, where is equipped with the graph norm.
Proof
We seek \(U=(u, v)\in \mathscr {D(A)}\) such that \(( I-{\mathscr {A}} ){U}=F\) for any \(F=(f_{1},f_{2})\in {\mathscr {H}}.\) In terms of the components, we find
Using Lax-Milgram Theorem (see Brezis (1992)), one can readily show that the above system has a unique solution and thus the operator \((\lambda I-{\mathscr {A}} )^{-1}\) exists and maps \({\mathscr {H}}\) into \(\mathscr {D(A)}\). Finally, by using Sobolev embedding, we deduce that \((\lambda I-{\mathscr {A}} )^{-1}\) is compact. The proof follows then from the well-known result of Kato (1976).\(\square \)
The main result of this subsection is:
Theorem 3.1
Assume (1.8) and (1.9) hold. Given \((u_0, u_1) \in {\mathscr {H}}\) arbitrarily, the solution \(U (t) = (u(t ), v(t ))\) to problem (1.6) tends in \({\mathscr {H}}\) to \((\wp ,0)\) as \(t\rightarrow \infty \), where
Proof
we shall first recall that the set
is called the \(\omega -\)limit set z. Applying LaSalle’s principle [15], we have:
-
i)
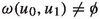 and it is compact set.
and it is compact set. -
ii) \(\omega (u_0,u_1)\) is invariant under the semi-group S(t) of contraction in \({\mathscr {H}}\).
-
iii) Let \((u(t), v(t)) = S(t)(u_0, u_1)\) be a solution to (1.6), then \( \lim _{t\rightarrow \infty }(u(t), v(t))\in \omega (u_0,u_1)\).
-
iv) \(\omega (u_0,u_1)\subset \mathscr {D(A)}\).
-
v) \( t\rightarrow \Vert S(t)\omega \Vert ^2_{\mathscr {H}}\) is a constant function for any \((y,z)\in \omega (u_0,u_1)\).
From (iii), it is sufficient to prove that \(\omega (u_0,u_1)\) contains only element of the form\( (\wp ,0)\). Let \(Y=(y,z)\in \omega (u_0,u_1)\) and \(U(t)=(u(t), v(t))\) the solution to (1.6) corresponding to Y, then we have
Therefore
Thus \(v=u_t=0\) on \(\Omega \), which implies that u is a constant with respect to t. Since \(\Delta u=\tau \partial _{tt}u+\partial _t u\), we deduce that \(\Delta u=0\). Therefore, by Green’s formula and (1.6), we have
Since the three integrals are positive, then we conclude that u is a constant with respect to x on \(\Omega \) and vanishes on \(\Gamma _0\) and \(\Gamma _1\). Finally, \(u=\wp \) on \(\Omega \) where \(\wp \) is a constant and \(u_{|_{\Gamma _0}}=u_{|_{\Gamma _1}}=0\).
Hence the \(\omega -\)limit set contains only elements of the form \((\wp ,0)\), where \(\wp \) is a constant, and we find
To find the expression of \(\wp \), we use \(\Delta u=\tau \partial _{tt}u+\partial _t u\) and we have:
Therefore \(\int _\Omega (\tau u_t+u)udx\) is a constant function. Thus,
Using (3.5) and passing to the limit, we get
\(\square \)
Remark 1
Furthermore, if the initial data \((u_0,u_1)\) satisfies the additional condition
then the constant \(\wp \) of Theorem 3.1 is zero, i.e., \(U(t)=(u(t), v(t))\rightarrow (0,0)\) in \({\mathscr {H}}\) as \(t\rightarrow \infty \).
3.2 Double logarithmic stability estimate
Here, we assume that the boundary function g introduced in the problem (1.6) depends on the space variable x and the time variable t \((g:=h(x,t))\). In this subsection, we suppose that we have the following assumptions
- (\(A_2\)):
-
\({\tilde{h}}=\chi _{\Gamma _a}h\in C((0,\infty ),H^{3/2}(\partial \Omega ))\), and \(\partial _t{\tilde{h}}\in C((0,\infty ),H^{1/2}(\partial \Omega ))\).
Now, we assume that we have (1.8),(1.9), (1.10), (\(A_2\)) and (1.11). By applying time-dependent heat flux, we get the following result.
Theorem 3.2
Let the functions \(u_q\) and \(u_{{\tilde{q}}}\) be solutions to (1.6) with coefficients q and \({\tilde{q}}\), respectively. Let the constants \(\alpha \in (0,1)\) and \(\sigma \in (0,1)\). Then, there exist two positive constants \(A=A(\sigma ,\Omega ,\Gamma _i,\gamma )\) and \(B=B(\Omega ,\gamma )\) such that for any \(q,{\tilde{q}}\in D_M^0\cap {C}^\alpha (\Gamma )\cap C^1(\Gamma )\), we have:
where \({C}^\alpha (\Gamma )\) is the Hölder space, A and B are independent of q and \({\tilde{q}}\).
Proof
Let \(\gamma \subset \Gamma _0\subset \Gamma \) be defined as in (1.10). Let \(u_q\) (resp. \(u_{{\tilde{q}}}\)) be the solution to the problem (1.6) with the coefficient q (resp. with the coefficient \({\tilde{q}}\)). Analogously, we can define the functions \(v_q\) and \(v_{{\tilde{q}}}\) are solutions to (1.12). Using relation (3.1) and trace theorem, we can find two constant \(\lambda >0\) and \({\tilde{\lambda }}>0\) such that for all \(t>0\)
where \(w_q\) and \(w_{{\tilde{q}}}\) are solutions to (2.2)-(2.5), \(u^0_q\) and \(u^0_{{\tilde{q}}}\) are solutions to (3.2). By Theorem2.3 and letting t tends to infinity, we get
Then, by remark 1 and letting t tends to infinity, we get
One can proceed as done in the proof of Theorem 2.4 to get the announced result. \(\square \)
References
Ammari, K., Choulli, M., Logarithmic stability in determining a boundary coefficient in an IBVP for the wave equation. Dyn. Partial Differ. Equ. 14 (2017), no. 1, 33-45.
M. Bellassoued , J. Cheng, M. Choulli, Stability estimate for an inverse boundary coefficient problem in thermal imaging. J. Math Anal. Appl., 343, (2008), 328-336.
K. Bryan, Jr. L. F. Caudill, An inverse problem in thermal imaging. SIAM J. Appl. Math., 56, (1996), 715-735.
K. Bryan, Jr. L. F. Caudill, Uniqueness for a boundary identification problem in thermal imaging. in: J. Graef, R. Shivaji, B. Soni, Zhu (Eds.), Differential Equations and Computational Simulations III, in: Electron. J. Differ. Equ. Conf., 1, (1997), 23-39.
S. Busenberg, W. Fang, Identification of semiconductor contact resistivity. Quar. J. Appl. Math.,49, (1991), 639-649.
C. Cattaneo, Sulla conduzione del calore. Atti. Sem. Mat. Fis. Univ. Modena 3, (1948)(1948), 83-101.
M. Bellassoued, M. Choulli, A. Jbalia, Stability of the determination of the surface impedance of an obstacle from the scattering amplitude. Math. Meth. Appl. Sci., 36, (2013), 2429-2448.
L. Bourgeois, About stability and regularization of ill-posed elliptic Cauchy problems: the case of \(C^{1,1}\) domains. Math.Model. Numer. Anal., 44, (2010), 715-735.
M. Choulli, A. Jbalia, The problem of detecting corrosion by electric measurements revisited. Discrete Contin. Dyn. Syst. Ser. S 9, (2016), 643-650.
M. Choulli, An inverse problem in corrosion detection: stability estimates. J. Inverse Ill-Posed Probl., 12, (2004), 349-367.
M. Choulli, Stability estimates for an inverse elliptic problem. J. Inverse Ill-Posed Probl., 10, (2002), 601-610.
W. Fang, E. Cumberbatch, Inverse problems for metal oxide semiconductor field-effect transistor contact resistivity. SIAM J. Appl. Math., 52, (1992), 699-709.
A. Haraux, Semi-groupes lineéaires et eéquations d’évolution lineéaires peériodiques. Publication du Laboratoire d’Analyse Numeérique No. 78011, Universiteé Pierre et Marie Curie, Paris, 1978.
J. Lagnese, Boundary Stabilization of Thin Plates, SIAM Studies in Appl. Math., Philadelphia, 1989.
J. P.LaSalle, An invariance principle in the theory of stability. Publication du Center for Dynamical Systems. Brown University, April 1966.
J.-L. Lions, E. Magenes, Problèmes aux limites non homogènes et applications, 1, Dunod, (1968) Paris.
G. Inglese, An inverse problem in corrosion detection. Inverse Probl., 13, (1977), 977-994.
A. Pazy, Semigroups of Linear Operators and Applications to Partial Differential Equations, Springer-Verlag, Berlin (1983).
M. Renardy, R.C. Rogers, An Introduction to Partial Differential Equations. Springer-Verlag: New York; 1993.
P. G. Kaup, F. Santosa, M. Vogelius, Method for imaging corrosion damage in thin plates from electrostatic data. Inverse Probl., 12, (1996), 279-293.
Sincich, E., Vessella, S., Wave equation with Robin condition, quantitative es- timates of strong unique continuation at the boundary, Rendiconti dell’Istituto di Matematica dell’Universita di Trieste, 48, (2016), 221-243.
Sincich, E., Smoothness dependent stability in corrosion detection, J. Math. Anal. Appl., 426 (2015), 364-379 .
Z. Sun, Y. Jiao, B. Jin, X. Lu, Numerical identification of a sparse Robin coefficient. Adv. Comput. Math., 41, (2015), 131-148.
Y. Xu, J. Zou, Analysis of an adaptive finite element method for recovering the Robin coefficient. SIAM J. Control Optimiz., 53, (2015), 622-644.
F. M. White, Heat and Mass Transfer: Addison-Wesley, Reading, MA, 1988.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by K Sandeep.
Rights and permissions
About this article
Cite this article
Jbalia, A. Stability estimate for an inverse problem of a hyperbolic heat equation from boundary measurement. Indian J Pure Appl Math 54, 241–252 (2023). https://doi.org/10.1007/s13226-022-00247-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13226-022-00247-4
Keywords
- Inverse problem
- Hyperbolic heat equation
- Robin boundary condition
- Double logarithmic stability estimate





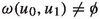 and it is compact set.
and it is compact set.