Magnetized flow of sutterby nanofluid through cattaneo-christov theory of heat diffusion and stefan blowing condition

Abstract

Stefan blowing phenomenon in electrically conducting Sutterby material flow over stretchable rotating disk is demonstrated in this research. Cattaneo-Christov (CC) model of energy diffusion is adopted to analyze the heat transmission. Buongiorno model is carried out to evaluate the involvement of nanoparticles. The formulated system of partial differential expressions is re-structured by the enactment of similarity functions. Runge–Kutta-Fehlberg (RKF) fourth-fifth order process has been executed to communicate the solution of velocity, thermal and solutal fields. The velocity, concentration, thermal fields, skin friction, rate of mass and heat transportations are explored for the embedded non-dimensional parameters graphically. Result reveals that the rise in Stefan blowing factor leads to an enhancement in radial and tangential velocities gradients. The velocity of nanomaterial is reduced by the incrementing material parameter values. The augmenting magnetic parameter values reduced the liquid velocity but improves the temperature. The thermophoretic force and Brownian motion involvement resulted the higher thermal field.

Introduction

Nature comprises a variety of non-Newtonian liquids, according to their different features. There is no combined rheological relationship that can distinguish all non-Newtonian liquids. Therefore, several rheological non-Newtonian liquid models are proposed. Among those, the rheological model of Sutterby liquid is one that defines aqueous solutions that show a high degree of polymer distribution. To date, numerous researchers have paid massive consideration to the flow of Sutterby liquid. Hayat et al. (2020a) scientifically examined the non-Newtonian Sutterby liquid flow past a rotating system. Nawaz et al. (2020) deliberated the thermal properties of Sutterby fluid and Sutterby hybrid nanofluid which consists of two nanoparticles namely Molybdenum disulphide and Silicon dioxide. This research emphasis that the hybrid Sutterby nanofluid is more effective than Sutterby fluid in terms of thermal conductivity. Sajid et al. (2020) utilized an elastic sheet to discuss the influence of activation energy over the Maxwell-Sutterby fluid flow. Mathematical model has been provided here by the researcher for better analysis. Imran et al. (2020) inspected the effect of chemical reactions and transference of heat for the non-Newtonian Sutterby fluid. Implementation of Perturbation method helps in deriving the set of governing equations. Hayat et al. (2021) used a porous constituted medium and described the peristaltic flow of Sutterby fluid. Further the optimization of entropy has been performed here.

Fluid flow through disk rotation is very important in various fields such as geothermal, technological, geophysical, engineering and industries such as rotating equipment, gas or marine propellers, computer storage devices, medical equipments, electrical equipments and heat exchangers. Till today, many scientists have paid massive consideration to the flow of various liquids through rotating and stretchable disks. The rotating disk was taken together with Buongiorno’s model to scrutinize the flow of nanoliquid by Khan et al. (2017). Rauf et al. (2019) used the gyrating disks to study the impact of heat production/absorption on fluid flow. A rotating stretchable disk and moving substrate has been taken by Turkyilmazoglu (2012, 2020a, b) to illustrate the two-phase fluid flow and MHD flow of different fluids. Shehzad et al. (2020) pondered the influence of modified Fourier’s expressions on flow of Maxwell liquid past an isolated gyrating disk with suspended nanoparticles. Gowda et al. (2021a, b) discussed flow of hybrid nanoliquid through moving rotating disks.

However, in most practical applications, depending on the water content of the liquid and temperature, the transfer of species or mass may be noticeable and may result in a ''blowing effect''. This blowing effect stems from the perception of species transfer from Stefan's blowing problem. Lund et al. (2020) reported a model for studying the influence of blowing condition on the Casson nanofluid flow in the occurrence of radiation effect. The significance of Stefan blowing on the Poiseuille nanofluid flow over the parallel plates was schematically depicted by Alamri et al. (2019). Dero et al. (2019) derived a mathematical model which represents the boundary layer flow of fluid with nanoparticles by accounting the Stefan Blowing phenomenon. Amirsom et al. (2019) explicated the Stefan blowing process in forced convected nanomaterial flow induced by the thin needle with microorganisms. The influence of magnetic effect and Stefan blowing condition on the nanofluid flow consists of microorganisms is illustrated by Zohr et al. (2020).

The MHD flow of various non-Newtonian liquids applications can be seen in several manufacturing areas. Therefore, the features of the flow with the impact of magnetic field need to be considered. Krishnamurthy et al. (2016) examined the impact of chemical response on the Williamson liquid flow over a medium which is porous in nature in the occurrence of magnetic effect. The magnetohydrodynamic hyperbolic tangent fluid flow with dust phase through an extending sheet was explored by Kumar et al. (2018). Gireesha et al. (2019) proposed a research that explains the flow of hydromagnetic Casson liquid on taking of viscous dissipation. Doh et al. (2020) considered a spinning disk and analyzed the hydromagnetic nanofluid flow as well as homogeneous and heterogeneous reactions during the flow. Xiong et al. (2021) inspected the boundary layer flow of magneto cross nanoliquid with chemical reaction and mixed convection. Recently, Khan et al. (2021) explored the properties of Maxwell fluid flow through a revolving disk which moves vertically in the existence of magnetic effect. It reveals that rate of transferring heat will increases with the rotation of disk.

Heat transfer is an important factor in the existing environment because of the warmth difference among two bodies or in the same body. To reduce the limitation of parabolic expression of energy, Christov improvised the Fourier’s theory by the inclusion of relaxation stress and named it as “Cattaneo-Christov heat flux model” (CCHFM). Recently, the influence of modified Fourier law on the flow of Burger fluid was elucidated by Waqas et al. (2016). The Darcy-Forchheimer phenomenon of Oldroyd-B material flow through Robin’s conditions and modified Fourier law is represented by Shehzad et al. (2016). Ahmed et al. (2020) used a revolving disk to deliberate the flow of nanofluid under CCHFM. Hayat et al. (2020b) evaluated the hydromagnetic stagnant point Oldroyd-B nanomaterial flow through this theory. Shah et al. (2020) evaluated the governing equations that portrays the mixed convective fluid flow through a plate via modified Fourier law. Ali et al. (2021) addressed the magnetized Oldroyd-B nanomaterial phenomenon through a gyrating frame with CCHFM. Gowda et al. (2021c) explained the flow of nanoliquid caused by a curved stretchy sheet with the help of CCHFM. Reddy et al. (2021) used CCHFM to explain the heat transmission enhancement in micropolar nanofluid flow.

From the aforementioned articles, it is visualized that the aspects of magnetic force in non-Newtonian Sutterby nanofluid flow through stretchable rotating disk under Stefan blowing phenomenon is not evaluated yet. Hence, the main contribution of this research is to examine the boundary layer flow, mass and heat transfer features of a non-Newtonian Sutterby nanofluid flow with Stefan blowing effect by using CCHFM which constitutes the novelty of the current study.

Mathematical formulation

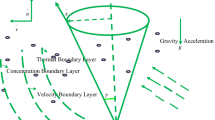
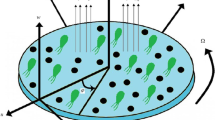
An incompressible hydromagnetic flow of non-Newtonian Sutterby nanofluid generated by the stretchable revolving disk is considered. The disk takes its position at $z = 0$ that stretches along radial direction with stretching rate $a$ and rotates along tangential direction with angular velocity $\Omega$. Cattaneo-Christov heat diffusive theory is incorporated through energy equation. The Stefan blowing phenomenon is elaborated through velocity boundary condition. Magnetic field is carried out along axial direction with uniform strength $\beta_{0}$. The assumption of low Reynolds number is responsible to the omission of induced magnetic field. The electric field is also neglected. The flow is assumed to be axisymmetric and hence the changing is vanishing along the tangential co-ordinate $\theta$. The concentration, temperature and velocity distributions are represented by $C = C\,\left( {z,r} \right),$ $C = C\,\left( {z,r} \right)$ and $\underline{V} = \left( {u\,\left( {z,r} \right),\,v\,\left( {z,r} \right),\,w\,\left( {z,r} \right)} \right)\,,$ respectively. The rotating surface achieves constant concentration $C_{w}$ and temperature $T_{w}$ while ambient fluid concentration and temperature is $C_{\infty }$ and $T_{\infty } ,$ respectively. The illustration of the fluid flow is given in Fig. 1.

Fig. 1

Physical sketch of the flow configuration

The flow model is represented as (Latif et al. (2016) and Khan et al. (2019)):

$$\frac{{\partial w}}{{\partial z}} + \frac{u}{r} + \frac{{\partial u}}{{\partial r}} = 0,$$

(1)

$$\rho \,\left( {w\frac{\partial u}{{\partial z}} - \frac{{v^{2} }}{r} + u\frac{\partial u}{{\partial r}}} \right) = \frac{\partial }{\partial z}\,\left( {\mu \frac{\partial u}{{\partial z}}} \right) - \sigma_{e} \beta_{0}^{2} u,$$

(2)

$$\rho \,\left( {w\frac{\partial v}{{\partial z}} - \frac{vu}{r} + u\frac{\partial v}{{\partial r}}} \right) = \frac{\partial }{\partial z}\,\left( {\mu \frac{\partial v}{{\partial z}}} \right) - \sigma_{e} \beta_{0}^{2} v,$$

(3)

$$\rho \left( {w\frac{\partial w}{{\partial z}} + u\frac{\partial w}{{\partial r}}} \right) = - \frac{\partial p}{{\partial z}} + \frac{\partial }{\partial z}\,\left( {\mu \frac{\partial w}{{\partial z}}} \right),$$

(4)

$$\begin{gathered} \,\left( {w\frac{\partial T}{{\partial z}} + u\frac{\partial T}{{\partial r}}} \right) = \frac{{k_{0} }}{{\rho \,c_{p} }}\left( {\frac{{\partial^{2} T}}{{\partial z^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial r^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \tau_{0} \,\left( \begin{gathered} u\frac{\partial u}{{\partial r}}\frac{\partial T}{{\partial r}} + w\frac{\partial u}{{\partial z}}\frac{\partial T}{{\partial r}} + u\frac{\partial w}{{\partial r}}\frac{\partial T}{{\partial z}} + w\frac{\partial w}{{\partial z}}\frac{\partial T}{{\partial z}} \hfill \\ + 2uw\frac{{\partial^{2} T}}{\partial r\partial z} + w^{2} \frac{{\partial^{2} T}}{{\partial z^{2} }} + u^{2} \frac{{\partial^{2} T}}{{\partial r^{2} }} \hfill \\ \end{gathered} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \tau_{1} \,\left( {\frac{{D_{T} }}{{T_{\infty } }}\left( {\left( {\frac{\partial T}{{\partial z}}} \right)^{2} + \left( {\frac{\partial T}{{\partial r}}} \right)^{2} } \right) + D_{B} \left( {\frac{\partial T}{{\partial z}}\frac{\partial C}{{\partial z}} + \frac{\partial T}{{\partial r}}\frac{\partial C}{{\partial r}}} \right)} \right)\,, \hfill \\ \end{gathered}$$

(5)

$$\,\left( {w\frac{\partial C}{{\partial z}} + u\frac{\partial C}{{\partial r}}} \right) = D_{B} \,\left( {\frac{{\partial^{2} C}}{{\partial z^{2} }} + \frac{1}{r}\frac{\partial C}{{\partial r}} + \frac{{\partial^{2} C}}{{\partial r^{2} }}} \right) + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} T}}{{\partial z^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial r^{2} }}} \right).$$

(6)

The boundary conditions for the above model are prescribed as (Latif et al. (2016) and Khan et al. (2019)):

$$\left\{ \begin{gathered} u = a\,r,\,\,v = r\,\Omega ,\,w = - \frac{{D_{B} }}{{1 - C_{w} }}\left( {\frac{\partial C}{{\partial z}}} \right),\,\,T = T_{w} ,\,\,C = C_{w} , \hfill \\ u \to 0,\,\,v \to 0,\,\,T \to T_{\infty } ,\,\,C \to C_{\infty } . \hfill \\ \end{gathered} \right..$$

(7)

Where $a$ stands for the disk stretching rate.

The Sutterby fluid viscosity is represented as (Khan et al. (2019)):

$$\mu = \mu_{0} \,\left( {\frac{{\sin \,h^{ - 1} b\Lambda }}{b\Lambda }} \right)^{N} ,$$

(8)

in which $\mu_{0} ,\,b,\,\Lambda$ and $N$ represent viscosity at low shear rate, characteristic time, shear rate and dimensionless parameter. For $N = 0$, the fluid model is reduced to the viscous fluid model. The binomial expression of (7) reduces to:

$$\mu \approx \mu_{0} \,\left( {1 - \frac{{\left( {b\Lambda } \right)^{2} }}{6}} \right)^{N} \approx \mu_{0} \,\left( {1 - \frac{{N\left( {b\Lambda } \right)^{2} }}{6}} \right),$$

(9)

The shear rate is defined as:

$$\Lambda = \sqrt {\frac{1}{2}\,tr\,\left( {A_{1}^{2} } \right)} \,,$$

(10)

here $A_{1} = L^{t} + L$ stands for the first Rilvin Erickson tensor, L determines the velocity gradient and t stands for the transpose.

Following similarity functions are considered (Latif et al. (2016) and Khan et al. (2019)):

$$\left\{ \begin{gathered} u = r\Omega f^{\prime}\left( \eta \right),\,\,v = r\Omega g\left( \eta \right),\,\,w = - 2 {\Omega h } f\left( \eta \right),\,\,p = \rho \upsilon \Omega P\left( \eta \right),\, \hfill \\ \,\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\,\,\,\varphi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }},\,\,\,\,\eta = \frac{z} h. \hfill \\ \end{gathered} \right.$$

(11)

Equation (1) is satisfied by the similarity functions. The governing system (2)-(6) in view of (11) attains the following form:

$${f}^{{^{\prime}}{^{\prime}}{^{\prime}}}-2N{\epsilon }^{2}\left(2{{{f}^{{^{\prime}}{^{\prime}}}}^{2}f}^{{^{\prime}}}+{{f}^{{^{\prime}}{^{\prime}}{^{\prime}}}{f}^{{^{\prime}}}}^{2}\right)+Re\left({g}^{2}+2{f}^{{^{\prime}}{^{\prime}}}f-{{f}^{{^{\prime}}}}^{2}\right)-Re{M}^{2}{f}^{{^{\prime}}}=0,$$

(12)

$${g}^{{^{\prime}}{^{\prime}}}-2N{\epsilon }^{2}\left(2{f}^{{^{\prime}}}{{g}^{{^{\prime}}}f}^{{^{\prime}}{^{\prime}}}+{{g}^{{^{\prime}}{^{\prime}}}{f}^{{^{\prime}}}}^{2}\right)-2Re\left(-{fg}^{{^{\prime}}}+g{f}^{{^{\prime}}}\right)-Re{M}^{2}g=0,$$

(13)

$${\theta }^{{^{\prime}}{^{\prime}}}+2RePr{\theta }^{{^{\prime}}}f-4Pr\lambda \left({\theta }^{{^{\prime}}{^{\prime}}}{f}^{2}+{\theta }^{{^{\prime}}}f{f}^{{^{\prime}}}\right)+PrNt{{\theta }^{{^{\prime}}}}^{2}+PrNb{\theta }^{{^{\prime}}}{\phi }^{{^{\prime}}}=0,$$

(14)

$${\phi }^{{^{\prime}}{^{\prime}}}+2ScRef{\phi }^{{^{\prime}}}+\frac{Nt}{Nb}\theta{^{\prime}}{^{\prime}}=0.$$

(15)

Here, $\varepsilon = b\,\Omega ,\,M = \sqrt {\frac{{\sigma_{e} \beta_{0}^{2} }}{\rho \,\Omega }} ,\,\lambda = \tau_{0} \Omega ,\,\Pr = \frac{{\mu \,c_{p} }}{{k_{0} }},\,Nt = \frac{{\tau_{1} \,D_{T} }}{{\upsilon \,T_{\infty } }}\left( {T_{w} - T_{\infty } } \right),\,Nb = \frac{{\tau_{1} \,D_{B} }}{\upsilon \,}\left( {C_{w} - C_{\infty } } \right), \,Re = {\frac{{\Omega h^{2} }}{\upsilon }},$ and $Sc = \frac{\upsilon }{{D_{B} }}$ determine the material parameter, magnetized parameter, thermal stress relaxation constraint, Prandtl number, thermophoresis parameter, parameter of Brownian movement and Schmidt number. The conditions (7) converted into the following patterns:

$$\left\{ \begin{gathered} f^{\prime}\left( 0 \right) = A,\,\,g\left( 0 \right) = 1,\,\,f\left( 0 \right) = \frac{{f_{w} }}{Sc}\varphi^{\prime}\left( 0 \right),\,\,\theta \left( 0 \right) = 1,\,\,\varphi \left( 0 \right) = 1\,\,\,\,\,\,at\,\,\,\,\,\,z = 0, \hfill \\ f^{\prime} \to 0,\,\,g \to 0,\,\,\theta \to 0,\,\,\varphi \to 0\,\,\,\,\,\,as\,\,\,\,\,\,z \to \infty . \hfill \\ \end{gathered} \right..$$

(16)

Here, $A = \frac{a}{\Omega }$ and $f_{w} = \frac{1}{2}\left( {\frac{{C_{w} - C_{\infty } }}{{1 - C_{w} }}} \right)$ stand for the stretching constraint and Stefan blowing factor. Here, it is of worth mentioning that the similarity Eqs. (12)-(15) can be converted into Von Karman viscous fluid pumping problem by ignoring the Sutterby material flow i.e. N = 0. Furthermore, the Stefan blowing influence in (16) must be replaced by uniform injection/suction by considering the porous disk configuration.

Skin-friction in tangential and radial directions is defined as (Hayat et al. (2018) and Khan et al. (2019)):

$$\left\{ \begin{gathered} C_{f\,r} {\text{Re}}_{r}^{\frac{1}{2}} = - \frac{2}{{A_{1}^{2} }}\left( {1 - 2\,\varepsilon^{2} \left( {f^{\prime}\left( 0 \right)} \right)^{2} } \right)\,f^{\prime\prime}\left( 0 \right)\,, \hfill \\ \,C_{f\,\theta } {\text{Re}}_{r}^{\frac{1}{2}} = - \frac{2}{{A_{1}^{2} }}\left( {1 - 2\,\varepsilon^{2} \left( {f^{\prime}\left( 0 \right)} \right)^{2} } \right)\,g^{\prime}\left( 0 \right)\,. \hfill \\ \end{gathered} \right.$$

(17)

Nusselt and Sherwood numbers are elucidated as (Hayat et al. (2018) and Khan et al. (2019)):

$$\left\{ \begin{gathered} Nu_{r} {\text{Re}}_{r}^{\frac{1}{2}} = - \theta^{\prime}\left( 0 \right)\,, \hfill \\ \,Sh_{r} {\text{Re}}_{r}^{\frac{1}{2}} = - \varphi^{\prime}\left( 0 \right)\,. \hfill \\ \end{gathered} \right.$$

(18)

where, ${\text{Re}}_{r} = \frac{{r^{2} \,\Omega }}{\upsilon }$ determines the local Reynolds number.

Numerical method

Reduced expressions are solved numerically by RKF-45 technique by using a high-level language and interactive environment. A sub method called midpoint method is considered to handle the end point singularities with the Richardson extrapolation enhancement scheme. The nonlinear reduced Eqs. 12–15 are re-framed into the first-order differential system by setting the substitutions $y_{1} = f,y_{2} = f^{\prime},$$y_{3} = f^{\prime\prime},$$y_{4} = g,y_{5} = g^{\prime},$$y_{6} = \theta ,y_{7} = \theta^{\prime},$$y_{8} = \phi ,y_{9} = \phi^{\prime},$

$$y^{\prime}_{1} = y_{2} ,$$

$$y^{\prime}_{2} = y_{3} ,$$

$$y^{\prime}_{3} = - \frac{{\left[ { - 2\,N\,\varepsilon^{2} \,Re\left( {2y_{2} \,y_{3}^{2} } \right) - Rey_{2}^{2} + 2Rey_{1} \,y_{3} + Rey_{4}^{2} - M^{2}Re y_{2} } \right]\,}}{{\left( {1 - 2\,N\,\varepsilon^{2} y_{2}^{2} } \right)}},$$

$$y^{\prime}_{4} = y_{5} ,$$

$$y^{\prime}_{5} = - \frac{{\left[ { - 2\,N\,\varepsilon^{2} \left( {2y_{2} \,y_{3} y_{5} } \right) -Re y_{2}^{2} - 2Re\,\left( {y_{2} \,y_{4} - y_{1} \,y_{5} } \right) - M^{2}Re y_{4} } \right]}}{{\left[ {1 - 2\,N\,\varepsilon^{2} y_{2}^{2} } \right]\,}}\,,$$

$$y^{\prime}_{6} = y_{7} ,$$

$$y^{\prime}_{7} = - \frac{{\left[ {2Re\Pr y_{1} \,y_{7} - 4\Pr \,\lambda \,\left( {y_{1} y_{2} \,y_{7} } \right) + \Pr Nt\,y_{7}^{2} + \Pr Nb\,y_{7} y_{9} } \right]}}{{\left[ {1 - 4\Pr \,\lambda y_{1}^{2} } \right]}}\,,$$

$$y^{\prime}_{8} = y_{9} ,$$

$y^{\prime}_{9} = - \left[ {2ReSc\,y_{1} \,y_{9} + \frac{Nt}{{Nb}}y^{\prime}_{7} } \right].$ along with the boundary conditions Eq. 16

$$\left\{ \begin{gathered} y_{2} \left( 0 \right) = A,\,\,y_{4} \left( 0 \right) = 1,\,\,y_{1} \left( 0 \right) = \frac{{f_{w} }}{Sc}y_{9} \left( 0 \right),\,\,y_{6} \left( 0 \right) = 1,\,\,y_{8} \left( 0 \right) = 1\,\,\,\, \hfill \\ y_{2} \to 0,\,\,y_{4} \to 0,\,\,y_{6} \to 0,\,y_{9} \to 0\,\,\,\,\,\,as\,\,\,\,\,\,z \to \infty . \hfill \\ \end{gathered} \right.$$

Here, we select a suitable ${\eta }_{\infty }$ value to justify the far-field conditions asymptotically. Error and mesh selections are depending on the ongoing solution. Further, 1.76 s is the CPU time for estimation of the values. The step-size is adopted as Δη = 0.001 with error tolerance to ${10}^{-6}$ is well-established for the convergence.

Results and discussions

The present study describes the incompressible hydromagnetic non-Newtonian Sutterby nanomaterial flow by a stretchy rotating disk. Modified Fourier theory and magnetic effect is considered in the modelling. Further, Stefan blowing phenomenon is elaborated through velocity boundary condition. This segment explains graphical outcomes of dimensionless parameters on concentration, velocity and thermal fields.

Figure 2 reflects the ${f}_{w}$ nature on the radial velocity profile. A risen in the velocity is detected along radial direction for escalating Stefan blowing parameter values. It is seen that the radial velocity upsurges due to the stretching of the disk which pumps more fluid into the disk. Also, the higher ${f}_{w}$ values improves the radial velocity. Figure 3 portrays the influence of ${f}_{w}$ on tangential velocity. The risen in ${f}_{w}$ values upshots the tangential velocity of the material. Figures 4 and 5 demonstrate the stretching parameter $(A)$ influence on radial and azimuthal velocities, respectively. It is found the higher radial velocity against rising $A$ values as displayed in Fig. 4. As the $A$ values are augmented, the layer of momentum boundary gets thicker. As a matter of fact, the spiral extending rate increases as $A$ upgrades and it quickens outward flow radially. Figure 5 represents the variations of $A$ on tangential velocity. The higher $A$ values diminishes the tangential velocity.

Fig. 2

Velocity $f^{\prime}\left( \eta \right)$ via ${f}_{w}$

Fig. 3

Velocity $\mathrm{g}(\upeta )$ via ${\mathrm{f}}_{\mathrm{w}}$

Fig. 4

Velocity $f^{\prime}(\eta )$ via $A$

Fig. 5

Velocity $\mathrm{g}(\upeta )$ via $A$

Figure 6 displays the variation in $f^{\prime}(\eta )$ for several values of material parameter ($\varepsilon$)$.$ The incremented $\varepsilon$ values decays the radial velocity as portrayed in Fig. 6. Here, the fluid velocity declines due to the fact that the material parameter has direct relation with magnetic field which is accountable for an upsurge in fluid viscosity. Figures 7, 8, 9 reflect the domination of M on the velocity and concentration gradients. The change in radial velocity against dissimilar $M$ values is reflected in Fig. 7. The rising $M$ values declines the radial velocity. Figure 8 portrays the $M$ variations on tangential velocity. The upshoot in values of $M$ declines the tangential velocity as reflected in Fig. 8. This is predictable that the magnetic field working in axial direction affords resistive force which reasons for reducing the fluid velocity radially and tangentially. The existence of a magnetic force in the flow field area slows down the fluid motion. Physically, it arises due to the Lorentz force which creates more struggle to the liquid motion. The Lorentz force comes from the magnetic field that acts as a delaying force. Figure 9 presents the variations of $M$ on concentration. We detected an upsurge in concentration for rising $M$ values. These findings suggest that the magnetization force adds a layer of resistance to flow, lowering the velocity and increases concentration. Lorentz force is induced by the presence of a transverse magnetic field, resulting as a retardation force on nanoparticles and the base fluid velocity. Thermal energy is dissipated as a result of the additional work re-quired to pull the nanofluid toward the magnetic field's operation. This warms the nanofluid which raises temperatures and concentration of the fluid.

Fig. 6

Velocity $f^{\prime}(\eta )$ via $\varepsilon$

Fig. 7

Velocity $f^{\prime}(\eta )$ via $M$

Fig. 8

Velocity $g(\eta )$ via $M$

Fig. 9

Concentration $\phi (\eta )$ via $M$

The change in temperature for diverse ${N}_{t}$ values is portrayed in Fig. 10. Rising ${N}_{t}$ values augmented the temperature. Higher estimation of thermophoretic parameter reasons for stronger thermophoretic force and fluid particles transfer from hot to cooler region which causes the increment in thermal gradient. Figure 11 reflects the sway of ${N}_{t}$ on concentration. The risen in ${N}_{t}$ values enhances the concentration. Here, ${N}_{t}$ is the growing function of concentration gradient.

Fig. 10

Temperature $\theta (\eta )$ via ${N}_{t}$

Fig. 11

Concentration $\phi (\eta )$ via ${N}_{t}.$

Figures 12 and 13 portray the captured variation of ${N}_{b}$ for $\theta (\eta )$ and $\phi (\eta )$. Figure 12 reflects the impact of ${N}_{b}$ over thermal profile. For increasing values of ${N}_{b}$, we detect an increase in thermal gradient as shown in Fig. 12. Physically, the upshoot in ${N}_{b}$ enhances the thermal conductivity of the nano particles present in the fluid, which caused upsurge in temperature of the fluid and resulted an augmentation in temperature. Figure 13 illustrates the ${N}_{b}$ influence on concentration. It is detected that the higher ${N}_{b}$ boost up the collision of fluid particles which resulted in weaker concentration. Figure 14 reflects the $Sc$ effect on concentration. Here, the higher estimation of Schmidt number declines the concentration. Since, $Sc$ depends on the mass diffusion and viscosity. The maximum concentration of nanoparticles corresponds to the smallest Sc. It also shows the thickness of hydrodynamic and nanoparticle species boundary layers. Thus for higher $Sc,$ the viscosity is higher than mass diffusivity that corresponds to weaker concentration.

Fig. 12

Temperature $\theta (\eta )$ via ${N}_{b}$

Fig. 13

Concentration $\phi (\eta )$ via ${N}_{b}$

Fig. 14

Concentration $\phi (\eta )$ via $Sc$

Figure 15 depicts the variations in $Sh{{Re}_{r}}^{-1/2}$ against $Sc$ for dissimilar ${N}_{t}$ values. The growth in ${N}_{t}$ values enhances the mass transmission rate. Figure 16 portrays the influence of ${N}_{t}$ on $Nu{{Re}_{r}}^{-1/2}$ versus ${N}_{b}$. The rising ${N}_{t}$ values declined the heat transmission rate. Figure 17 demonstrates the ${f}_{w}$ influence on skin friction versus $M$ along radial direction. The rise in values of ${f}_{w}$ gradually declines ${C}_{fr}{{Re}_{r}}^{1/2}$. Figure 18 portrays the influence of ${f}_{w}$ on skin friction versus $M$ in tangential direction. The rise in values of ${f}_{w}$ gradually declines ${C}_{f\theta }{{Re}_{r}}^{1/2}$. It is observed from Figs. 17 and 18 that the upsurge in magnetic parameter increases the ${C}_{fr}{{Re}_{r}}^{1/2}$ and ${C}_{f\theta }{{Re}_{r}}^{1/2}$. Table 1 is constructed for the validation of our numerical technique. The numerical results are computed and compared with Hayat et al. (2018) for skin-friction coefficients. Numerical results are observed to be in excellent comparison.

Fig. 15

Sherwood number $(Sh{{Re}_{r}}^{-\frac{1}{2}})$ via ${N}_{t}$

Fig. 16

Nusselt number $(Nu{{Re}_{r}}^{-\frac{1}{2}})$ via ${N}_{t}$

Fig. 17

Skin-friction $({C}_{fr}{{Re}_{r}}^\frac{1}{2})$ via ${f}_{w}$

Fig. 18

Skin-friction $({C}_{f\theta }{{Re}_{r}}^\frac{1}{2})$ via ${f}_{w}$

Table 1 Comparison of the numerical results with published literature by Hayat et al. (2018)

Final remarks

The present study describes the incompressible hydromagnetic non-Newtonian Sutterby nanomaterial flow by a stretchable rotating disk under Cattaneo-Christov heat diffusive theory. Stefan blowing phenomenon is elaborated through velocity boundary condition. The outcomes are probed for the thermal, velocity, and concentration distributions against distinct dimensionless constraints which are reported in the form of graphs. The outcome of the present paper reveals that:

• The escalating values of ${f}_{w}$ upshots the tangential and radial velocities gradients.

• Rise in the values of $A$ diminishes the tangential velocity gradient but upshots the radial velocity gradient.

• The gain values of $\varepsilon$ decays the radial velocity gradient.

• The augmenting M values caused a decay in the liquid velocity but improves the temperature.

• Escalating in the values of ${N}_{t}$ boosts the concentration and thermal gradient.

• Upsurge in ${N}_{b}$ values improves the temperature gradient but decays the concentration.