Introduction

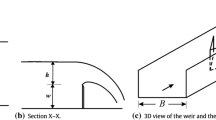
A side weir is an overflow inserted into the main channel laterally to divert part of the flow from the main channel into a side channel. Side weirs are generally used in irrigation, land drainage, urban sewage systems, and sanitary engineering and are also widely used for storm relief and head regulators of distributaries. Like normal weirs, side weirs have diverse styles (labyrinth, sharp, and broad-crested) and forms such as rectangular, trapezoidal, and triangular. Depicted in Fig. 1 is the subcritical flow along the length of a triangular side weir. Where Q1 and Q2 are upstream and downstream discharges, y1 and y2 are the depth of water at upstream and downstream sections, p is weir crest height, B is main channel width, E is the specific energy ((E = y + Q/(2gB2y2)), g is the gravity acceleration, and θ is side weir apex angle.

Fig. 1
figure 1

Subcritical flow over a triangular side weir: a front view, b plan

Full size image

The hydraulic behavior of side weirs in channels has been studied since the turn of the twentieth century. However, many investigations have been based on empirical and experimental work. Other studies implemented theoretical approaches such as specific energy and momentum principle. Almost all experimental work and theoretical investigation are limited to prismatic rectangular channels with a horizontal overflow weir crest.

The flow along a side weir is a typical spatially varied flow with decreasing discharge. The energy equation generally emanates the governing equation for flow over side weirs. The general differential equation of spatially varied flow along a side weir (Fig. 1) with decreasing discharge is expressed as (Henderson 1966):

$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{{S}_{0}-{S}_{\mathrm{f}}-\frac{\alpha Q}{g{A}^{2}}.\frac{\mathrm{d}Q}{\mathrm{d}x}}{1-\frac{\alpha {Q}^{2}T}{g{A}^{3}}}$$
(1)

here α is the kinetic energy correction coefficient, S0 is the main channel slope, Sf is the friction slope, x is the distance along the side weir from the upstream end, dQ/dx is the discharge per unit length of the side weir, A is the cross-sectional area of the flow, and T is top width of the channel. Equation (1) reveals that the longitudinal water surface profile along a side weir under subcritical flow is an ascending curve (Fig. 1). For a horizontal prismatic rectangular main channel, considering the kinetic energy correction coefficient α as unity and ignoring friction losses, Eq. (1) is rewritten as follows:

$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{Qy}{g{B}^{2}{y}^{3}-{Q}^{2}}\left(-\frac{\mathrm{d}Q}{\mathrm{d}x}\right)$$
(2)

De Marchi (1934), by considering constant specific energy E along the length of the side weir, solved the above equation for a rectangular side weir.

The discharge over a triangular side weir Qs is provided by (Kumar 1985):

$${Q}_{\mathrm{s}}=\frac{8}{15}{C}_{\mathrm{m}}\sqrt{2g}{\mathrm{tan}\left(\frac{\theta }{2}\right)\left(y-p\right)}^{2.5}$$
(3)

Differentiating Eq. (3) and considering x (= 2(y − p)tan(θ/2)) leads to (Kumar and Pathak 1987):

$$-\frac{\mathrm{d}Q}{\mathrm{d}x}=\frac{\mathrm{d}{Q}_{\mathrm{s}}}{\mathrm{d}x}=\frac{\mathrm{d}{Q}_{\mathrm{s}}}{\mathrm{d}A}\frac{\mathrm{d}A}{\mathrm{d}x}=\frac{\frac{8}{15}{C}_{\mathrm{m}}\sqrt{2g}{\mathrm{tan}\left(\frac{\theta }{2}\right)\left(y-p\right)}^{2.5}}{2(y-p)\mathrm{tan}\left(\frac{\theta }{2}\right)}=\frac{4}{15}{C}_{\mathrm{m}}\sqrt{2g}{\left(y-p\right)}^{1.5}$$
(4)

where Cm is the De Marchi coefficient. For a triangular side weir located in a rectangular channel, the following equation was introduced by Kumar and Pathak (1987) for Cm:

$${C}_{\mathrm{m}}=\frac{15}{4}\frac{B}{L}({\phi }_{2}-{\phi }_{1})$$
(5)

in which ϕ is the De Marchi function calculated using:

$$\phi =\frac{2E-3p}{E-p}\sqrt{\frac{E-y}{y-p}}-3{\mathrm{sin}}^{-1}\sqrt{\frac{E-y}{E-p}}$$
(6)

where L is the effective length of the triangular side weir calculated by (Balahang & Ghodsian 2021):

$$L=\left({h}_{1}+{h}_{2}\right)\mathrm{tan}\left(\frac{\theta }{2}\right)$$
(7)

here, h1 (= y1 − p) and h2 (= y2 − p) are the depths of water on the weir crest at upstream and downstream sections, respectively. Presuming that E is constant along the side weir, Eqs. (5, 6, 7) are combined to form:

$$\frac{4\left({h}_{1}+{y}_{2}-p\right)\mathrm{tan}\left(\frac{\theta }{2}\right){C}_{\mathrm{m}}}{15B}=\frac{2E-3p}{E-p}\left(\sqrt{\frac{E-{y}_{2}}{{y}_{2}-p}}-\sqrt{\frac{E-{y}_{1}}{{y}_{1}-p}}\right)-3{[\mathrm{sin}}^{-1}\sqrt{\frac{E-{y}_{2}}{E-p}}-{\mathrm{sin}}^{-1}\sqrt{\frac{E-{y}_{1}}{E-p}}]$$
(8)

By the above equation, y2 is obtained by trial-and-error method, provided the values of Cm, B, y1, p, E, and θ are known. Then, the downstream discharge Q2 is calculated by using the energy equation. Then after, the discharge of triangular side weir Qs is calculated by:

$${Q}_{\mathrm{s}}={Q}_{1}-{Q}_{2}$$
(9)

Various researchers have investigated the effect of different variables on Cm of rectangular side weirs. Subramanya and Awasthy (1972), Nandesamoorthy and Thomson (1972), Yu-Tek (1972), Prasad (1976), and Ranga Raju et al. (1979) correlated Cm to upstream Froude number for rectangular side weirs. While Singh et al. (1994) and Jalili and Borghei (1996) correlated Cm with the upstream Froude number and the relative flow head for rectangular side weirs. Additional studies by Borghei et al. (1999) indicated that the ratio of side weir length to main channel width indirectly impacts the discharge of rectangular side weirs.

Unlike rectangular side weirs, only a few studies have been conducted on the discharge coefficient of triangular side weirs. Kumar and Pathak (1987) related the De Marchi coefficient to the upstream Froude number for triangular side weirs, while Ghodsian (2004) linked the De Marchi coefficient to the upstream Froude number and relative head for triangular side weirs. Various equations for the De Marchi coefficient obtained for triangular side weirs with various values of apex angles by Kumar and Pathak (1987) and Ghodsian (2004) are given in Table 1.

Table 1 De Marchi coefficient for triangular side weir
Full size table

As mentioned earlier, De Marchi's approach is based on the trial-and-error method and hence, complicated to obtain triangular side weir discharge. So, it is necessary to examine the capability of other alternatives as introduced in the following:

The traditional triangular weir equation (TWE) is expressed as follows (French, 1985):

$$Q=\frac{8}{15}{C}_{\mathrm{d}}\sqrt{2g}\mathrm{tan}\left(\frac{\theta }{2}\right){h}^{2.5}$$
(21)

where Cd is the discharge coefficient of a sharp-crested triangular weir. Unlike normal weirs, the flow over a side weir is affected by the velocity head (V12/2g) in the main channel. Therefore, TWE for triangular side weirs is defined as follows:

$${Q}_{\mathrm{s}}=\frac{8}{15}{C}_{\mathrm{d}}\sqrt{2g}\mathrm{tan}\left(\frac{\theta }{2}\right){H}_{1}^{2.5}$$
(22)

here H1 (= h1 + V12/2g) is the total upstream head (i.e., in section 1 in Fig. 1). The variation of the flow surface profile along the side weir is not considered in TWE.

Domínguez (1935), based on the following assumptions, introduced a simple method for estimating lateral discharge and water surface profile variations along a side weir:

  1. (1)

    Specific energy is constant along the side weir.

  2. (2)

    The water surface varies linearly along the side weir (h(x) = h1 + (h2—h1(x/L))).

Based on Domínguez, the side weir discharge per unit length of a triangular side weir dQs/dx is expressed as follows:

$$\frac{\mathrm{d}{Q}_{s}}{\mathrm{d}x}=\frac{4}{15}{C}_{\mathrm{dD}}\sqrt{2g}{ (h(x))}^{1.5}$$
(23)

here CdD is Domínguez coefficient. By integrating Eq. (23) with respect to x (x = 0 to x = L), the following equation is obtained for the discharge of a triangular side weir Qs:

$${Q}_{\mathrm{s}}=\frac{4}{15}\left[\frac{2}{5}{C}_{\mathrm{dD}}\frac{\left(\frac{{h}_{2}}{{h}_{1}}+1\right)\left({\left(\frac{{h}_{2}}{{h}_{1}}\right)}^{2.5}-1\right)}{\left(\frac{{h}_{2}}{{h}_{1}}-1\right)}\right]\mathrm{tan}\left(\frac{\theta }{2}\right)\sqrt{2g}{h}_{1}^{2.5}$$
(24)

To consider the velocity head, Eq. (24) is rewritten by substituting h12.5 with H12.5 as follows:

$${Q}_{\mathrm{s}}=\frac{4}{15}\left[\frac{2}{5}{C}_{\mathrm{dD}}^{*}\frac{\left(\frac{{h}_{2}}{{h}_{1}}+1\right)\left({\left(\frac{{h}_{2}}{{h}_{1}}\right)}^{2.5}-1\right)}{\left(\frac{{h}_{2}}{{h}_{1}}-1\right)}\right]\mathrm{tan}\left(\frac{\theta }{2}\right)\sqrt{2g}{H}_{1}^{2.5}$$
(25)

here CdD* is the adjusted Domínguez coefficient.

Bagheri et al. (2014a) and Bagheri et al. (2014b) showed that TWE, Domínguez, and adjusted Domínguez approaches perform better than the De Marchi method for rectangular side weir discharge. They also reported that TWE and adjusted Domínguez coefficients strongly correlate with the approach Froude number for a rectangular side weir, while the Domínguez coefficient weakly correlates with this parameter.

Schmidt (1954), by assuming a linear variation of water surface along a side weir, used (h1 + h2 + h3)/3 instead of h1 to calculate side weir discharge. Based on Schmidt's approach, Eq. (26) is presented to calculate the discharge of triangular side weirs:

$${Q}_{\mathrm{s}}=\frac{8}{15}{C}_{\mathrm{sc}}\sqrt{2g}\mathrm{tan}\left(\frac{\theta }{2}\right){\left(\frac{{h}_{1}+{h}_{2}+{h}_{3}}{3}\right)}^{2.5}$$
(26)

here Csc is the Schmidt discharge coefficient, and h3 is the average flow depths on the side weir crest at upstream and downstream sections. Emiroglu and Ikinciogullari (2016) reported the dependability of the Schmidt procedure for calculating the discharge coefficient of a rectangular side weir for Froude number in the range of 0.75 to 1. Balahang and Ghodsian (2021) proposed the following straightforward equation for calculating discharge Qs of a triangular side weir:

$$\frac{{Q}_{\mathrm{s}}}{{Q}_{1}}=0.637{\left({F}_{r1}\right)}^{-0.937}{\left(\frac{L}{B}\right)}^{1.044}{\left(\frac{L}{{y}_{1}}\right)}^{-0.094}\left[0.345-0.440{\left(\frac{p}{{y}_{1}}\right)}^{1.142}\right]$$
(27)

where L is the effective length of the side weir, which is calculated using Eq. (7). It is clear from Eq. (27) that h2 is essential for calculating Qs.

Researchers have recently focused on using machine learning algorithms to solve engineering problems. Due to its high accuracy, the support vector machine (SVM) has been one of the most prevalent machine learning methods in solving problems of side weirs. Azamathulla et al. (2016) showed that the SVM method is more precise in estimating discharge coefficients than artificial neural network (ANN) and adaptive neuro-fuzzy inference system (ANFIS) techniques. Roushangar et al. (2016) reported that the combined support vector machine with the genetic algorithm (GA-SVR) method has better performance than the gene-expression programming (GEP) method in calculating the discharge coefficient of rectangular and trapezoidal side weirs. Zaji and Bonakdari (2017) illustrated that the SVR technique produces more precise results than the nonlinear regression (NLR) method for estimating a rectangular side weir discharge coefficient. Li et al. (2021) stated that the SVM algorithm produces minor errors in forecasting the rectangular side weir discharge coefficient compared to ANN and extreme learning machine (ELM) methods. Balahang and Ghodsian (2021) reported that the SVR method calculates the discharge of triangular side weirs better than ANFIS, ANN, and gradient-boosted regression trees (GBRT) techniques.

The review of prior studies shows that most investigations have concentrated on forecasting Cm for sharp-crested rectangular side weirs. At the same time, less concentration has been paid to investigate the flow through triangular side weirs. The capabilities of the TWE, Domínguez, adjusted Domínguez, and Schmidt procedures, as an alternative to the De Marchi method, are analyzed to compute the discharge of sharp-crested triangular side weirs, by using a more comprehensive range of values of influencing parameters, compared to earlier researches. Thus, the goals and novelties of the present research are:

  1. (1)

    For the first time, the capabilities of the TWE, Domínguez, adjusted Domínguez, Schmidt, and De Marchi methods are evaluated for calculating triangular sharp-crested side weir discharge.

  2. (2)

    The sensitivity analysis for influencing parameters on the discharge coefficients of triangular sharp-crested side weir (Cm, Cd, CdD, CdD*, and Csc) using a hybrid machine learning approach (PSO-SVR) was implemented for the first time.

  3. (3)

    By using a more comprehensive range of data sets, more accurate equations are introduced for calculating the discharge of triangular sharp-crested side weirs.

Material and methods

Experiments

The experiments were conducted in a prismatic horizontal channel by the second author. The length of the main channel was 9.0 m, its width was 0.5, and its depth was 0.5 m. At the end of the channel, a sluice gate was installed to regulate the water depth. The side channel was perpendicular to the main ones. The sharp-crest side weirs are made of the mild steel plate and installed at the upstream end of the side channel. A supply pipe provided the main channel discharge from an overhead tank with a constant head. A calibrated sharp-crested weir measured the discharges in the main and side channels. Point gauge with ± 0.1 mm accuracy measured the flow depths y1 and y2 (Fig. 1) at the center line of the main channel. Figure 2 shows the laboratory setup used in the present study.

Fig. 2
figure 2

Schematic of the experimental setup

Full size image

Experiments were carried out for various discharges, flow depths, weir heights, and apex angles. All the experiments were performed under subcritical flow conditions. In addition, data obtained by Kumar (1985) and Mohan (1987) are also used for the analysis. Table 2 summarizes the data utilized.

Table 2 Summary of triangular side weir data
Full size table

Dimensional analysis

The discharge coefficient of a sharp-crested triangular side weir is a function of the subsequent geometric and hydraulic variables:

$${C}_{i}=f\left(p,{V}_{1},{y}_{1},g,\theta ,\mu ,\sigma ,\rho ,{S}_{0}\right)$$
(28)

where Ci is the triangular side weir discharge coefficient (including Cm, Cd, CdD, CdD* or Csc), V1 is the mean flow velocity in the main channel at the upstream section, μ is the dynamic viscosity of water, σ is the surface tension coefficient, ρ is the water density, and S0 is the main channel slope. Using the Buckingham Π-theorem Eq. (28) is written as follows:

$${C}_{i}=f\left({\mathrm{Fr}}_{1}, \frac{p}{{y}_{1}}, \theta ,\mathrm{ Re}, {\mathrm{W}}_{e},{S}_{0}\right)$$
(29)

where Fr1 (= V1/((gy1)0.5)), Re (= V1y1/ν), and We (= py1V12/σ) are the Froude number, Reynolds number, and Weber number, respectively, and υ is the kinematic viscosity of water. When the flow is turbulent, the viscosity effect can be neglected compared to the inertial force. For (y1− p) > 30 mm, surface tension influence on the flow over a weir is insignificant (Novák & Čabelka 1981). El-Khashab and Smith (1976) and Borghei et al. (1999) stated that the effect of the main channel slope S0 on the discharge coefficient is nominal. Thus, by ignoring the insignificant variables, Eq. (29) is written as follows:

$${C}_{i}=f\left({\mathrm{Fr}}_{1}, \frac{p}{{y}_{1}} , \theta \right)$$
(30)

Statistical indices

The following statistical indices were utilized to compare the performance of different equations in forecasting the discharge coefficient and the discharge of sharp-crested triangular side weir:

(1) Pearson correlation coefficient (R2) measures the linear correlation between two random variables and is computed by:

$${R}^{2}={\left[\frac{\sum_{i=1}^{N}\left({o}_{i}-\overline{{o }_{i}}\right)\left({e}_{i}-\overline{{e }_{i}}\right)}{\sqrt{\sum_{i=1}^{N}{\left({o}_{i}-\overline{{o }_{i}}\right)}^{2}{\sum }_{i=1}^{N}{\left({e}_{i}-\overline{{e }_{i}}\right)}^{2}}}\right]}^{2}$$
(31)

where oi and ei are the ith observed and estimated values of discharge coefficient or side weir discharge, \(\overline{{o }_{i}}\) and \(\overline{{e }_{i}}\) are the average of observed and estimated values of the discharge coefficient or side weir discharge, respectively, and N stands for the number of data used.

(2) Mean squared error (MSE) for determining the error value and difference between the measured and estimated values expressed as follows:

$$\mathrm{MSE}=\frac{\sum_{i=1}^{N}{({e}_{i}-{o}_{i})}^{2}}{N}$$
(32)

(3) Mean relative error (MRE) is calculated using the following equation:

$$\mathrm{MRE}=\frac{\sum_{i=1}^{N}\frac{\left|{e}_{i}-{o}_{i}\right|}{{o}_{i}}}{N}$$
(33)

(4) Ratio of data in the scope of less than ± 10% error (CP10%) is obtained from the following equation:

$${\mathrm{CP}}_{10}\%=100\frac{{N}_{10}}{N}$$
(34)

here N10 expresses the number of data with error \(({E}_{ri}=\left|{e}_{i}-{o}_{i}\right|*100/{o}_{i}\)) less than 10%.

Particle swarm optimization: support vector regression

A support vector regression (SVR) is a kind of support vector machine for solving regression issues. The main purpose of the SVR model is to discover a function that provides a connection between dependent variable f(x) and independent variables {[x1, …, xn], which is expressed as the following equation (Raschka 2015):

$$f(x)=\sum_{i=1}^{l}{w}_{i}K({x}_{i},x)+b$$
(35)

where xi is n input vector, wi is the weight vector, b is bias, l is the number of samples, and K is the kernel function, which maps xi to linear space if the relationship between f(x) and xi be nonlinear. In the present study, radial basis function is used as kernel, which is expressed as follows:

$$K\left(x,z\right)=\mathrm{exp}\left(\frac{{\Vert x-z\Vert }^{2}}{2{\gamma }^{2}}\right)$$
(36)

here γ determines the radius of the impact of support vectors. Two important SVR parameters besides γ that must be optimized for data training are:

  • C: This parameter adjusts the ratio between the complexity of the model and the required accuracy of the training data and is always greater than zero.

  • ε: This parameter determines the allowable error of the model, which can be a decimal number.

The PSO method is used in this study to get optimal SVR parameters. The details behind of hybrid PSO-SVR algorithm, as shown in Fig. 3, are as follows (Hu et al. 2015):

Fig. 3
figure 3

Flowchart of the PSO-SVR technique

Full size image

Input: train dataset, number of particles n, inertia w, the cognitive element that models the direction of particles to replace to formerly discovered most satisfactory position φ1, a social element that quantifies execution of a particle close to optimal global particle φ2, and the highest iteration number T.

Output: an optimal hybrid of C, ε and γ.

Initialization: Let t = 0, followed by: (1) Initialize \(\mathop{x}\limits^{\rightharpoonup} {}_{i}^{t}\) (position of the ith particle at the tth iteration) with a value in the searching space; (2) Initialize \(\mathop{v}\limits^{\rightharpoonup} {}_{i}^{t}\) (velocity of the ith particle at the tth iteration) as zero or a small arbitrary float number; and (3) Let present historical optimal position \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{b_{i} }}\) be equivalent to \(\mathop{x}\limits^{\rightharpoonup} {}_{i}^{t}\).

Iteration: (1) Let t = 1; (2) Correct the present global historical optimal position of all particles \(\mathop{g}\limits^{\rightharpoonup}\); (3) If t ≥ T, move to step 4; otherwise, end the iteration and output \(\mathop{g}\limits^{\rightharpoonup}\); (4) Update the position and velocity of the n particles, the current historical optimal position of the particles. For this objective, randomly generate \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{U_{1} }}\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{U_{2} }}\) (n × n diagonal matrices in which entries on the major diagonal are arbitrary numbers uniformly dispersed in the gap [0,1]), then, let \(\mathop{v}\limits^{\rightharpoonup} {}_{i}^{t + 1} = w\mathop{v}\limits^{\rightharpoonup} {}_{i}^{t} + \varphi_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{U_{1} }} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{b_{i} }} - \mathop{x}\limits^{\rightharpoonup} {}_{i}^{t} } \right) + \varphi_{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{U_{2} }} \left( {\mathop{g}\limits^{\rightharpoonup} - \mathop{x}\limits^{\rightharpoonup} {}_{i}^{t} } \right)\), and \(\mathop{x}\limits^{\rightharpoonup} {}_{i}^{t + 1} = \mathop{x}\limits^{\rightharpoonup} {}_{i}^{t} + \mathop{v}\limits^{\rightharpoonup} {}_{i}^{t + 1}\). Finally, when one particle passes out of the searching space, it can be controlled by stopping updating the particles fitness value (the MSE of the SVR’s train consequence utilizing this particle) and going to the next step; 5) if MSE (\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{x_{i} }}\)) ≤ MSE (\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{b_{i} }}\)), then, \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{b_{i} }} = \mathop{x}\limits^{\rightharpoonup} {}_{i}^{t}\); and 6) Let t = t + 1.

The present study implements the modeling process using Sklearn, Pandas, and Numpy library in Python 3.8.1. The radial basis function is considered the SVR kernel, and ε is assumed as 0.01 in the modeling process. PSO algorithm is used by setting w = 1.2 and n = 3 to obtain the optimal values of C and γ.

Results and discussion

Sensitivity analysis

The sensitivity analysis was used to study the effect of independent parameters Fr1, p/y1, and θ on Cm, Cd, CdD, CdD*, and Csc. The sensitivity analysis was accomplished using the PSO-SVR technique. Eighty percent of the data is employed to train the models, and the rest is utilized to test the models. Based on Eq. (30), four models are represented for sensitivity analysis by skipping each variable simultaneously, as indicated in Table 3. The sensitivity index is computed for each model to execute the sensitivity analysis. The sensitivity index is the proportion of the model MSE with a skipped parameter to the model MSE in the existence of all the variables. A sensitivity index > 1 means the parameter's significance in the model. The results of the sensitivity analysis are given in Table 3. The number of iterations, values of C and γ, and statistical indices, including R2, MSE, MRE, and CP10% for each model, are also presented in Table 3.

Table 3 Summary of results of PSO-SVR modeling
Full size table

The sensitivity indices in Table 3 indicate that Fr1 is the most influencing variable in determining Cm, Cd, and CdD*. By ignoring Fr1, the MSE index due to Cm, Cd, and CdD* increased by 89.28%, 273.91%, and 304.16%, respectively. Unlike Cm, Cd, and CdD*, CdD and Csc are more influenced by p/y1 than Fr1. In calculating CdD and Csc, the sensitivity index of p/y1 is 1.29 times the sensitivity index of Fr1. By omitting the impact of p/y1 on CdD and Csc, the MSE index increased by 56.76%. According to Table 3, in all the approaches, the side weir angle θ has the least effect on determining the discharge coefficient. By ignoring the effect of θ on Cm, Cd, CdD, CdD*, and Csc, the MSE index increases by 21.43%, 13.04%, 13.51%, 4.69%, and 13.51%, respectively.

Analysis of results

This part aims to study the effect of dimensionless independent variables of Eq. (30) on discharge coefficients obtained from the De Marchi, TWE, Domínguez, adjusted Domínguez, and Schmidt approaches using experimental data introduced in Table 2. The variations of Cm, Cd, CdD, CdD*, and Csc with approach Froude number are shown in Fig. 4.

Fig. 4
figure 4

Discharge coefficient versus Fr1: a Cm, b Cd, c CdD, d CdD* and e Csc

Full size image

The results displayed in Fig. 4a–e confirm that the triangular side weir discharge coefficient decrease by increasing Fr1. Increasing the value of Fr1 is due to increased longitudinal velocity or decreased flow depth. The flow divagation angle and the outflow velocity of a side weir decrease by increasing approach flow velocity (Hager 1987). As a result, the discharge coefficient decreases. The linear water surface profile in terms of the approach Froude number is shown in Fig. 5. Due to the direct relationship between Fr1 and Δh/L, it can be stated that the approach Froude number indirectly affects CdD and Csc. The discharge coefficients CdD and Csc have a similar correlation with Fr1 due to considering the impact of the water surface profile and disregarding the influence of V1 in Domínguez and Schmidt's approaches.

Fig. 5
figure 5

Slope of the water surface profile versus Fr1

Full size image

The scattering of data in Fig. 4 proves that in addition to Fr1, other dimensionless parameters such as p/y1 and θ may affect the discharge coefficients Cm, Cd, CdD, CdD*, and Csc. The lowest percentage of data scatter is observed in Fig. 4b, d, which indicates that Cd and CdD* have the most correlation with Fr1. However, the correlation of CdD* with Fr1 is higher than Cd. It is due to considering the water surface profile variation and V1 in the adjusted Domínguez approach. The data points in Fig. 4c, e show more scatter, which means CdD, Csc, and Fr1 depend on other dimensionless parameters. As observed in the sensitivity analysis results, the dependency of CdD and Csc on p/y1 is greater than the dependency of these two coefficients on Fr1. According to Fig. 4b, d, the variations of Cd and CdD* versus Fr1 is almost linear. The absolute rate of these discharge coefficients versus Fr1 equals 0.511 and 0.554, respectively. In contrast, the variations of Cm, CdD, and Csc versus Fr1 are nonlinear. According to Fig. 4a, c, and e, as Fr1 increase, the absolute rate of Cm, CdD, and Csc increases.

Figure 6 shows the variations of discharge coefficients Cm, Cd, CdD, CdD*, and Csc versus Fr1 for various side weir apex angles. Figure 6a shows that for Fr1 ≥ 0.2, the discharge coefficients Cm, Cd, CdD, CdD*, and Csc increase slightly with the side weir apex angle from 60° to 120°, which confirms the findings of Kumar and Pathak (1987). It is also observed that with increasing Fr1, the variation of Cm, Cd, CdD, CdD*, and Csc increases slightly with the side weir angle. Comparison of Figs. 6a with 6b–e shows that the dependency of Cm with θ at the higher Froude numbers is slightly more than other discharge coefficients. Based on trend lines in Fig. 6, when Fr1 = 0.8, with increasing the side weir apex angle from 60° to 120°, the De Marchi coefficient increases by 0.09, while Cd, CdD, CdD*, and Csc increase by only 0.06, 0.05, 0.03, and 0.05, respectively.

Fig. 6
figure 6

Discharge coefficient versus Fr1 for different side weir apex angles: a Cm, b Cd, c CdD, d CdD* and e Csc

Full size image

According to Eq. (7), the effective length increases with increasing the side weir apex angle. Increasing the side weir's effective length intensifies the flow divagation angle and the outflow velocity. As a result, the discharge coefficient increases. Therefore, it is inferred that with increasing Fr1, the incremental impact of the weir length on discharge coefficients is more prevalent compared to decreasing effect of Fr1.

Another parameter influencing the discharge coefficient is p/y1. Depicted in Fig. 7a–e are the variations of Cm, Cd, CdD, CdD*, and Csc versus p/y1, respectively. It is deduced that the variation of p/y1 with discharge coefficients can be considered linear. According to Fig. 7, CdD and Csc are slightly more correlated with p/y1 than other discharge coefficients, which is logical based on the sensitivity analysis results (Table 3). In contrast, the discharge coefficients Cm, Cd, and CdD* are more influenced by Fr1 than p/y1.

Fig. 7
figure 7

Discharge coefficient versus p/y1: a Cm, b Cd, c CdD, d CdD* and e Csc

Full size image

Based on trend lines demonstrated in Fig. 7, with increasing p/y1, the discharge coefficients Cm, Cd, CdD, CdD*, and Csc increase with the rates of 0.197, 0.113, 0.192, 0.113, and 0.192, respectively. This trend of variations of discharge coefficient with p/y1 is also reported by Singh et al. (1994) and Ghodsian (2004) for rectangular and triangular side weirs, respectively. Other investigators, such as Borghei et al. (1999) and Jalili and Borghei (1996), reported the decreasing effect of p/y1 on the discharge coefficient of rectangular side weir. Therefore, more data are needed to explore this contradiction.

The above analysis indicates a linear variation of p/y1 with the discharge coefficients, while Fr1 has a linear effect on Cd and CdD* and a nonlinear effect on Cm, CdD and Csc. So with these interpretations and employing the dimensionless parameters, Eqs. (37–41) are obtained to predict the discharge coefficients Cm, Cd, CdD, CdD*, and Csc for sharp-crested triangular side weirs. Equations (37–41) are valid for 0.03 ≤ Fr1 ≤ 0.97, 0 < p/y1 < 0.79, and 30 ≤ θ ≤ 120.

$${C}_{\mathrm{m}}=0.518-0.439{{\mathrm{Fr}}_{1}}^{2.814}+0.162\frac{p}{{y}_{1}}$$
(37)
$${C}_{\mathrm{d}}=0.577-0.541{{\mathrm{Fr}}_{1}}^{1.388}+0.045\frac{p}{{y}_{1}}$$
(38)
$${C}_{\mathrm{dD}}=0.528-0.223{{\mathrm{Fr}}_{1}}^{2.143}+0.17\frac{p}{{y}_{1}}$$
(39)
$${C}_{\mathrm{dD}}^{*}=0.581-0.575{{\mathrm{Fr}}_{1}}^{1.304}+0.04\frac{p}{{y}_{1}}$$
(40)
$${C}_{\mathrm{sc}}=0.528-0.223{{\mathrm{Fr}}_{1}}^{2.144}+0.17\frac{p}{{y}_{1}}$$
(41)

Table 4 shows the statistical indices R2, MSE, and CP10% due to the above equations and those introduced by previous studies for predicting the discharge coefficients.

Table 4 Performance of different equations in estimating discharge coefficients
Full size table

The MSE indices due to Eq. (37) for different apex angles indicate the improved performance of this equation compared to previous equations. For the apex angle of 120°, owing to Eq. (37) for calculating Cm, the MSE index is 0.0042, while Eqs. (12) and (10) provide MSE indices equal to 0.0058 and 0.0178, respectively. The values of statistical indices R2, MSE, MRE, and CP10% due to Eq. (37) are 0.410, 0.0045, 0.103, and 66.6 in estimating the De Marchi coefficient and, despite its comprehensiveness, this equation has a good performance compared to earlier equations. The results presented in Table 4 shows that the general Eqs. (38–41) produce suitable statistical indices in estimating the discharge coefficients Cd, CdD, CdD*, and Csc. The MSE indices due to Eqs. (38–41) are 0.0035, 0.0047, 0.0034, and 0.0047, while the MRE indices are 0.097, 0.093, 0.095, and 0.093, respectively.

Figure 8 compares the measured values of Qs with the estimated values of Qs using Eqs. (37–41) and Eq. (27). Figure 8 shows that most of the data points in all approaches fall within the range of ± 10% error lines, except the De Marchi approach. Table 5 compares the performance of Eqs. (37–41) and Eq. (27) in computing Qs based on R2, MSE, MRE, and CP10%.

Fig. 8
figure 8

Estimated versus measured values of Qs

Full size image
Table 5 Performance of different equations in computing triangular side weir discharge
Full size table

According to Table 4, Eq. (37) for apex angle 120° performs better in estimating the De Marchi coefficient than other equations. Table 5 shows improved MSE and CP10% indices due to Eq. (12) in calculating side weir discharge Qs. Therefore, a more accurate estimation of the De Marchi coefficient does not necessarily lead to a more precise calculation of Qs. Equation (37) leads to a lower MSE index in calculating Qs for other values of the side weir apex angle. For example, the MSE index due to Eq. (37), compared to that of Eqs. (13) and (15), in calculating the discharge of a side weir with 60° apex angle, is reduced by 67.10% and 3.88%, respectively. While equations presented by Ghodsian (2004) give a better CP10% in calculating the side weir discharge with apex angles of 60° and 30°. Equation (37) provides the MSE index of 4.581 in calculating the discharge of a triangular side weir.

Table 5 shows that the statistical indices due to the De Marchi coefficients [Eqs. (10)–(20) and Eq. (37)] do not differ much. Thus, due to its comprehensiveness, Eq. (37) is preferred for computing the discharge of a triangular side weir. Table 5 reveals that the MSE index due to Eqs. (27, 38, 39, 40 and 41) reduced by 5.26, 21.20%, 18.40%, 21.22%, and 21.20%, respectively, compared with MSE due to Eq. (37). Also CP10% index due to the above equations increased by 1.04, 8.50%, 8.3%, 10.17%, and 8.3%, respectively.

To compare the accuracy of Eqs. (37–41) in computing the side weir discharge, the Nash–Sutcliffe Efficiency criteria (NSE) were also computed using Eq. (42) and compared with R2, MSE, MRE, and CP10%.

$$\mathrm{NSE}=1-\frac{\sum_{i=1}^{N}{\left({o}_{i}-{e}_{i}\right)}^{2}}{\sum_{i=1}^{N}{\left({o}_{i}-\overline{{o }_{i}}\right)}^{2}}$$
(42)

The obtained NSE due to Eqs. (37–41) and (27) in predicting Qs is 0.968, 0.975, 0.974, 0.975, 0.974, and 0.970, respectively. Therefore, due to the statistical indices R2, NSE, MSE, MRE, CP10%, and NSE, it is clear that the TWE, Dominguez, adjusted Dominguez, Schmidt, and straightforward approaches have better performance than the De Marchi approach. However, it is necessary to mention that in the Dominguez, adjusted Dominguez, Schmidt, and straightforward approaches, the values of flow depths at Sects. "Introduction" and "Material and Methods" and apex angle is required for calculating side weir discharge. While in the TWE approach, only the flow condition at Sect. "Introduction" (Fig. 1) and apex angle are sufficient for calculating side weir discharge. Therefore, using the TWE approach and Eq. (38) with R2 = 0.975, NSE = 0.975, MSE = 3.610, MRE = 0.097, and CP10% = 71.36 for obtaining Qs is more practical and preferred.

Conclusion

This research investigated the effects of dimensionless parameters Fr1, p/y1, and θ on the triangular sharp-crested side weir discharge coefficients obtained from De Marchi (Cm), TWE (Cd), Domínguez (CdD), adjusted Domínguez (CdD*), and Schmidt (Csc) approaches. Sensitivity analysis performed by the PSO-SVR method showed that Fr1 with sensitivity indices equal to 1.89, 3.74, and 4.04 is the most significant parameter for estimating Cm, Cd, and CdD*, respectively. While p/y1 with sensitivity index equal to 1.22 is the most important parameter for predicting CdD and Csc.

The results revealed that Cm, Cd, CdD, CdD*, and Csc decrease with increasing Fr1 and increase with increasing p/y1 and θ. The dependency of Cm on θ was slightly more than the other discharge coefficients (Cd, CdD, CdD*, and Csc). At a constant value of p/y1, Δh/L has a significant correlation with Fr1.

New equations were proposed to estimate Cm, Cd, CdD, CdD*, and Csc for a sharp-crested triangular side weir. Equation (37) showed better performance for calculating triangular side weir discharge than De Marchi coefficients.

As an alternative to the De Marchi approach, all the methods used in this study (TWE, Domínguez, adjusted Domínguez, Schmidt, and straightforward approaches) produced better statistical indices R2, NSE, MSE, MRE (except Balahang and Ghodsian 2021), and CP10%. However, due to the lack of downstream flow depth y2 in the TWE approach (Eq. 38), this method is more practical and introduced as the superior model by producing statistical indices R2 = 0.975, NSE = 0.975, MSE = 3.610, MRE = 0.097, and CP10% = 71.36.

In the present study, it was assumed that the water surface varies linearly along the side weir, while the water surface in the subcritical condition varies as an ascending curve. It is suggested that the performance of the Schmidt approach in calculating triangular side weir outflow be evaluated by considering the nonlinearity of the water surface profile. Although the developed equations estimate the triangular side weir outflow with high precision, the obtained equations must be confirmed at the prototype scale.