1 Introduction

Since the end of 2019, the coronavirus, which is causing the pandemic of the century, has been spreading extremely quickly. After being first discovered in December 2019, it infected a Chinese person in Wuhan, China, on January 30, 2020 (Almendros-Jimenez et al. 2021). On March 11th, the World Health Organisation (WHO) declared this new pneumonia outbreak to be a "global pandemic" and gave it a new name, Covid-19 (Hao and Park 2021; Stoecklein et al. 2022). The term is officially known as "severe acute respiratory syndrome coronavirus 2" (SARS-CoV-2) by the International Committee on Taxonomy of Viruses. Covid-19 has been transferred from animal to human; presently, it is scattered across all continents. The lack of any preventive vaccine proved dangerous to human life.

This global pandemic hardly impacts all sectors, such as education, hospitality, transportation, trading, etc., and many more. As of 13th June 2020, out of a total of 7,553,182 confirmed cases, 423,349 deaths have been confirmed in the whole world. Several scientists from all over the world have been attempting to forecast Covid-19 cases. Utilising both forward prediction and backward inference, epidemic development trends in South Korea, Italy, and Iran were predicted (Chitra and N., R. Shanmathi, and Dr. R. Rajesh. 2015). Handling curve fitting and recurrent neural network future Covid-19 positive cases and confirmed cases were identified in India (Gao et al. 2020).

The statistical forecasting models are helpful in controlling and predicting this global pandemic (Kumar et al. 2023). In this study, ARIMA was used to predict the Covid-19 trend. The Box-Jenkins approach, also referred to as the ARIMA model (Li et al. 2020) engaged in forecasting and analysis (Mohler 1990; N et al.. 2020; Rishabh et al. 2019). We found the ARIMA model applied appropriate forecasting in Covid-19 (Kotlyar et al. 2019; Garcia-Flores et al. 2022; Izquierdo-Pujol et al. 2022; Male 2022) cases in IRAN (Sharma et al. 2021, 2022a, 2016).

2 Related work

Table 1 compares the current research plan with the existing research, which used the ARIMA model to forecast Covid-19.

Table 1 The extant research with the present study
Full size table

India has 28 states and 8 Union Territories (UT), and Covid-19 began to affect those areas on January 30, 2020, when the first case of Chinese origin was noted. Up to 13th June, 35 states and UTs infected in India. Figure 1 shows the red-hot spot on the Indian map due to the maximum deceased. The top 5 states are identified based on the overall death tolls. Due to Covid-19, the highest harmed state is Maharashtra (MH), with 3717 deceased as shown in Fig. 1 (Kumar et al. 2023). The second place of Gujrat (GUJ) state also suffered from a significant loss of human beings with 1415 cases. The capital of India, Delhi (DH) comes in the third position in loss of humans about 1214. Further, Madhya Pradesh (MP) and West Bengal (WB) also have 440 and 451 deceased cases, respectively.

Fig. 1
figure 1

Most infected states on map as of 13 June 2020

Full size image

Figure 2 depicts an increasing number of confirmed, active, recovered, and deceased cases. Until 13th June, there were 301,009 confirmed cases in total; active cases are 137,795, and recovered cases are 154,330 noted. Gradually increasing Covid-19 cases (Rizzo et al. 2022; Tatura 2022; Bungaro et al. 2022; Boudry et al. 2022; Rujen et al. 2023; Sharma et al. 2022b) became matters of anxiety, not only for the government but also for the average human. A total of 8102 deceased cases were reported caused by COVID-19 (Tomar and Gupta 2020).

Fig. 2
figure 2

Cumulative trend of Covid-19 (From1st June to 13th June)

Full size image

Figure 3 visualizes the current scenario of Covid-19 patients having confirmed, active, recovered, and Fig. 3 shows the deceased cases in 35 states/UTs. The highest number of deceased are reported, 3717 in Maharashtra state, which seems to be a red-zone area highly. The second-largest number of deceased, 1415 reported in Gujrat (GJ). The third-largest death count, 1214 cases reported in the capital of India.

Fig. 3
figure 3

State-wise Covid-19 scenario (1st June to 13th June 2020)

Full size image

The primary concepts of this paper are: to discover the impact of active cases on the deceased, identification of active, recovered, confirmed, and deceased cases, state-wise decease predictions based on active and recovered cases, and association of deceased with active and recovered cases.

There are five sections in this paper. Section 1 discussed the Covid-19 introduction theory by concentrating on a recent effect on Indian provinces. Section 2 outlines our contribution to this work. Section 3 focused on objectives with hypotheses, designs conceptual schema with the methodology used. Section 4 is dedicated to experiments performed with discussion. Section 5 discusses the significant limitations of the paper Sect. 6 concludes the study's primary essence, including future work.

3 Contribution

This paper is written to help government officials and policymakers become aware of early detection of cases of Covid-19 in different provinces. They might use these results to prepare future cure and prevention mechanisms to defend against this pandemic. With the online deployment of this model, early detection of deceased, active, recovered and confirmed cases might be estimated. Hence, we need to propose an optimistic model. Using regression, we found useful information that the active and recovered cases positively impacted the deceased rates in each province. For this, the MLR obtained the highest accuracy of 89% in the early detection of the deceased. With a significant R-value of 0.927, we discovered a positive linear association between deceased patients and active cases that demonstrates the acceleration of deaths based on the sharp rise in active cases. We explored that there was a significant linear relationship between deceased patients with recovered cases and active cases. Additionally, we presented regression models that predicted deceased cases (p < 0.05), and we also applied the ARIMA model that identified deceased case cases more accurately than regression. We also demonstrated that the ARIMA model is superior to regression methods for time series data. Additionally, the temporal dynamics behavior of Covid-19 was analyzed with the ARIMA model (Sharma et al. 2016), which forecasted (Sharma et al. 2022a) the 40 days of Covid-19 cases.

4 Research design and methodology

4.1 Objectives

To discover the association of deceased cases with recovered and active cases.

(a)RH0: ρXY = 0 {No association between deceased patient and recovered cases.}

(b)RHa: ρXY ≠ 0{An association between deceased patient and recovered cases.}

(c)AH0: ρXY = 0 {No association between deceased patient and active cases.}

(d)AHa: ρXY ≠ 0{An association between deceased patient and active cases.}

To explore the impact of recovered cases on the deceased.

(e)ERH0: {No effect of recovered cases on the deceased.}

(f)ERHa: {An effect of recovered cases on the deceased.}

To examine the effects of active cases on the deceased.

(g)EAH0: {No effect of active cases on the deceased.}

(h)EAHa: {An effect of active cases on the deceased.}

To estimate the total number of confirmed, active, recovered, and deceased cases over the course of the following 40 days.

To estimate the deceased prediction based on active cases and recovered cases.

4.2 Conceptual design

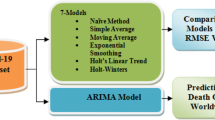
We visualized the present research design in Fig. 4, which presents the schematic diagram with the conceptual idea of the study. This paper analyzed the impact of active and recovered on the deceased. Also, the association of the deceased has been found with the same variable. Regression modelling was used to forecast and examine the covid-19 in this. Based on active and recovered cases, regression analysis (LR and MLR) is applied after the fulfillment of assumptions. Three objectives (Impact, relationship, and prediction) need to be accomplished using regression. We also used the ARIMA forecasting model to predict the trend of all four cases (confirmed, active, recovered, and deceased) for the following 40 days while taking into account the time-series analyses.

Fig. 4
figure 4

Covid-19 out-break detection schema

Full size image

4.3 Dataset description

The present study continually used standard and official data (Tomar and Gupta 2020) from 30th January to 13th June 2020. The five important variables in the dataset are state, confirmed, recovered, active, and deceased. All variables are scale types, with the exception of the state variable. At the end of each day, the data set is updated with the most recent information for 33 Indian states and UTs. Using the Cronbach alpha test, the reliability of data samples is calculated as 0.841. The reliability of data samples is calculated by 0.841 using the Cronbach alpha test. Table 2 shows the recent thirteen days’ data of cases reported, from 1st June to 13th June mid-night. Table 3 stores the cases reported from the 35 states/UTs.

Table 2 Date-wise cases
Full size table
Table 3 State-wise cases
Full size table

4.4 Statistical characteristics of variables

The significant dataset's statistical characteristics are necessary before the analyses. It shows the mean or average (μ) in Eq. (1), dispersion in Eq. (2) properties of data samples.

$$Sum=\sum_{i=1}^{n}Xi$$
(1)
$$Std. Deviation=\surd \frac{{|x-u|}^{2}}{N}$$
(2)

There are N data points in the population, where x is one of the values in the data set, and is the mean (μ) of the data set.

Figure 5 shows the essential statistical properties of confirmed, active, recovered, and deceased variables. 101,141 confirmed cases are the most, with an 8600 deviation value. A less deviation value of 253.8 can be seen in the highest amount of 3717 deceased cases. The standardized values of the four variables are used (Z-score). The term "standard score" is usually used for normal populations; the term "Z score” should only be used for normal distributions. We transformed all variables into the standardized form using Eq. (3):

Fig. 5
figure 5

Statistical characteristics of dataset

Full size image
$$Z=(X-\upmu )/\upsigma$$
(3)

We checked the multicollinearity problem among independent variables with Tolerance (T) (Tran et al. 2020). It is calculated with 1-R2, and the maximum value of T depicts the lowest collinearity. Also, the Variance Inflation Factor (VIF) is calculated by inverting the T. The maximum value justifies low collinearity. Table 4 stores two critical metrics for the multicollinearity problem. For both independent variables, T = 0.18 and VIF = 5 instruct to accept moderate collinearity.

Table 4 Multicollinearity
Full size table

4.5 Regression and correlation

We used the regression methods LR and MLR in the prediction task, which explored influence after modeling. We constructed three predictive models (LR-1, LR-2, and MLR). Below Eq. (5) shows the general equations of LR. During model LR-1, Y is deceased, X is recovered cases, coefficients (a, b) of predictor recovered cases to explain the model, and ε is the error term.

$$Y=\mathrm{b}+\mathrm{a}.\mathrm{X}+\upvarepsilon$$
(4)
$$Y=\mathrm{b}+\mathrm{a}.\mathrm{X}+\upvarepsilon$$
(5)
$$b=\frac{\sum (X-\stackrel{-}{X)} (Y-\stackrel{-}{Y)}}{\sum (X-{\stackrel{-}{X)}}^{2}}$$
(6)
$$a=\overline{Y }-b.\overline{X }$$
(7)
$$\upvarepsilon =\sum ({Y}_{1}- {Y}_{fit })$$
(8)

In the model LR-2, we set Y = deceased, X is active cases, coefficients (a, b) of active predictor cases to explain the model, and ε is the error term. In Eqs. (6) and (7), the regression coefficient indicates the amount by which change in independent variable X must be multiplied to provide an average update in Y. Also, the amount of Y alters for a unit increase in X forces changes in slope. In Eq. (8), The difference between the predicted value and fit value of the dependent variables is used to calculate the total prediction error. The standard error of the slope SE(b) depicted in Eq. (9) and residual standard deviation \({S}_{res}\) is shown in Eq. (10).

$$SE_{{\left( b \right)}} = \frac{{S_{{res}} }}{{\sqrt {\sum X - \bar{X}} }}$$
(9)
$${S}_{res}=\frac{\sum (Y-{{Y}_{fit })}^{2}}{\sum n-2}$$
(10)

In Eq. (11), we fit values for the MLR, where \(\widehat{Y}\) is deceased, \({X}_{1}\) is active cases, \({X}_{2}\) is recovered cases, coefficients (\({b}_{0}\), \({b}_{1}\), \({b}_{2}\)) of predictors active and recovered cases to predict the deceased model, and ε is the error term.

$$\widehat{Y}={b}_{0}+ {b}_{1}{X}_{1}+{b}_{2}{X}_{2}+\varepsilon$$
(11)

Pearson Correlation in Eq. (12) is used to discover the association of deceased cases with recovered and active cases. Where SP is the total deviation score of the deceased, recovered, and later for active cases, and R is the correlation. The sum of the squared deviations for recovered cases is SSy, and the sum of the squared deviations for deceased cases is SSx.

$$R=\frac{SP}{\left(\sqrt{SSx}\right)\left(\sqrt{SSy}\right)}$$
(12)

4.6 ARIMA model

For early detection of covid-19 cases, we used the time-series forecasting ARIMA model in IBM SPSS statistics 25. This model gains information from the dependable variables itself to estimate the trends. A time series, or collection of observations obtained by repeatedly measuring a single variable over time, was used in this model. The ARIMA model predicts future covid-19 cases based on previously known time-series values in the covid-19 dataset (Sharma et al. 2016). The common ARIMA forecasting equation is shown below in Eq. (13).

$${\text{Y}}: \, = {\text{ARIMA}}\left( {{\text{p}},{\text{d}},{\text{q}}} \right)$$
(13)

  • p is no. of lags of the dependent variable,

  • d is no. of differences to become a stationarity variable, and

  • q is no. of lags of the error term.

The base equation of ARIMA is shown in Eq. (14), where moving average parameters (θ’s),

$$\hat{y}_{{\text{t}}} = \mu \, + \, \phi_{{1}} {\text{y}}_{{{\text{t}} - {1}}} + \ldots + \phi_{{\text{p}}} {\text{y}}_{{{\text{t}} - {\text{p}}}} - \theta_{{1}} {\text{e}}_{{{\text{t}} - {1}}} - \ldots - \theta_{{\text{q}}} {\text{e}}_{{{\text{t}} - {\text{q}}}}$$
(14)

We made the following Eq. (15) of the ARIMA model where Y is a confirmed dependent variable and ŷ1, ŷ2…… ŷ40 are days to be identified with forecasting series.

$${\text{Y}}:\hat{y}_{{1}} ,\hat{y}_{{2}} \ldots \ldots \hat{y}_{{{4}0}} = {\text{ARIMA}}\left( {{\text{p}},{\text{ d}},{\text{ q}}} \right)$$
(15)

Our model provides the forecasting model for all four variables, and Eq. (16) depicts the value of p = 0 describes no autoregressive, d = 1 shows difference, and q = 0 states no seasonal moving average parameter,

$${\text{Y}}:\hat{y}_{{1}} ,\hat{y}_{{2}} \ldots \ldots \hat{y}_{{{4}0}} = {\text{ARIMA}}\left( {0,{1},0} \right)$$
(16)

Figure 6 illustrates the five crucial steps that were taken to build ARIMA and forecast Covid-19 cases.

Fig. 6
figure 6

ARIMA process

Full size image

We have tested the component's seasonality and found the stationary data to use ARIMA to forecast. ARIMA model is also used to make data stationaries through differencing in lack of stationaries. Further, using the correlograms, we tested the autocorrelation using Auto Correlation Factor (ACF) and Partial Auto Correlation Factor (PCF). Later, the ARM model was built and validated using appropriate metrics. Figure 7 shows the correlograms with ACF and Partial Auto Correlation Factor PCF of (a) Confirmed (c) Active (e) Recovered (g) Deceased and PCF of (b) Confirmed (d) Active (f) Recovered (c) Deceased against various lags at difference 1. An ACF calculates and displays the average correlation between data points in a four-variable time series and earlier series values calculated with various lag lengths. In contrast to the ACF, the PACF uses correlation to account for any correlation between observations made at shorter lags. The four variables are found stationary because series autocorrelation lies near zero below the lines and insignificant relationships (Wang et al. 2020; Zhang et al. 2020; Yang et al. 2021).

Fig. 7
figure 7

ACF a confirmed b active c recovered d deceased, and PACF e confirmed f active g recovered h deceased

Full size image

5 Results and discussion

This section discussed the experimental findings with validation metrics after using the processed dataset to implement regression models in IBM SPSS statistics 25. To discover the relationship between deceased patients with recovered and active cases, 2–tailed Pearson correlation is applied at a 0.01 level of significance. Figure 8 displays the positive linear correlation between deceased patients and active cases, with a significant R-value of 0.927 reflecting the death enhancement based on the rapid increase of active cases.

Fig. 8
figure 8

Covid-19 case correlation at the 0.01 level (2-tailed)

Full size image

Due to the highest R = 0.988, active cases are increasing with the growth of confirmed. Also, the confirmed and active cases found positively correlated with recovered cases 0.988, and 0.954, respectively. Also, deceased cases are related to active, confirmed, and recovered cases. Enhancement in the deceases can be seen based on recovery caused by R = 0.936. Further, we observed that if cases are increasing actively still, there is a significant recovery of patients (R = 0.954). Thus, the null hypothesis RH0: ρXY = 0 “No association between deceased patient and recovered cases” is failed to accept. Therefore, the alternative hypothesis RHa: ρXY ≠ 0 “An association between deceased patient and recovered cases” is accepted. Thus, a significant linear relationship between deceased patients and recovered cases is observed. To test the null hypothesis AH0: ρXY = 0 “No association between deceased patient and active cases”, a high positive correlation is found R = 0.927, and the cause failed to accept. Its alternative hypothesis AHa: ρXY ≠ 0 “An association between deceased patient and active cases” is accepted. Hence, a significant linear correlation was explored between deceased patients and active cases.

Further, the effect (individual and combined) of both active and recovered cases on the deceased rate is explored. We built three regression models to the standardized value of variables. One side, the LR-1 model’s findings signify the impact of active cases on patient deceased, and contrasted with, the LR-2 model explains the power of recovered cases to predict the deceased.

Table 5 compares the critical parameters of both LR models. We observed the highest correlation R and goodness of fitting by LR-2 model (0.927 < 0.937) (0.859 < 0.877). Therefore, the LR-2 model predicted the deceased higher than the LR-1. The maximum coefficient of determination of LR-2 also proved the predictive strength of the deceased patient model. A significant t-values (P < 0.005) might be useful in hypothesis testing. These metrics demonstrated that active cases predicted the deceased of patients more accurately.

Table 5 Individual impact of active and recovered cases on the deceased
Full size table

Table 6 equates the ANOVA results of LR-1 and LR-2. The residual error of LR-2 lowered as compared to LR-1 (4.1 < 4.8). Both model’s F-values (200.7, 235.5) were found significant (P < 0.005). The LR-2 model significantly reduced the residual error and proved its explanatory power.

Table 6 ANOVA
Full size table

To measure the collective impact (active and recovered cases) on the deceased, the MLR model is built. On one hand, the LR-1 model's findings signify the effect of active cases on the patient deceased, and on the other hand, the LR-2 model explains the power of recovered cases to predict the deceased.

Table 7 depicts the MLR model metrics, which validated the combined predictive strength of recovered and active cases. The residual error was reduced by 0.4. A bit increment in correlation (R) and coefficient of determination (R2) was achieved. The autocorrelation score of 2.3 was determined by the Durbin-Watson test, which is close to 2.5 thresholds and infers acceptable autocorrelation between independent variables and adjusted R2 = 0.882 in the MLR model also significant. Further, the model's F value is also found to be significant (p < 0.005). Therefore, considering both variable active and recovered cases, predictive strength is improved with the new value of R2 = 0.889.

Table 7 MLR model with the impact of active and recovered cases on deceased
Full size table

Three presented models played a vital role in the hypotheses testing, and t values were found significant. In the LR-1, significant t-value is rejected the null hypothesis ERH0: “No effect of recovered cases on patient deceased” and was unable to reject the alternative hypothesis ERHa: “An effect of recovered cases on patient deceased”. As a result, recovered cases had a big effect on patients who passed away. Further, the LR-2 model’s t-value forced to make a decision failed to accept the null hypothesis EAH0: “No effect of active cases on patient deceased” and alternative hypothesis EAHa: “An effect of active cases on patient deceased” is failed to reject. It proved that active cases have a significant impact on the deceased.

Figure 9 plots the standardized predicted values of the deceased provided with the MLR model. Equation Y = 1.87E-16 + 0.93*X is significantly explained with the coefficient of determination R2 = 0.889. Only a few records were observed as far away from the benchmark line. Therefore, active and recovered cases are supported to identify the deceased cases effectively. In other words, the accuracy (89%) or explanation strength (0.889) of predictors towards the target variable is most significant.

Fig. 9
figure 9

Standardized deceased predicted value

Full size image

Figure 10 shows the residual error versus a prediction of the MLR model. The loss curve shows the error points, which does not prove the normal distribution of the residuals because the range does not come in between − 2 and + 2. Hence, the residual is not randomly scattered around zero and linearity achieved. Still, the MLR model is better as compared to the LR-1 and LR-2 of the provinces.

Fig. 10
figure 10

Standardized deceased predicted value

Full size image

Further, the LR-2 model (recovered based) depicted that the MH, Tamilnadu, and DH are the highest deceased-prone provinces. According to this model, less than 100 deceased may have chances in Assam, Kerala, Uttarakhand, and Jammu Kashmir. The MLR model, estimates the deceased based on recovered and active cases. For the MH, it predicted 3411; for Tamilnadu, it estimated 1422; for Delhi, it observed 1148; for Gujrat, it identified 788 deceased cases.

Figure 11 shows the combined predicted values given by the respective regression models. Starting from the actual deceased count in 19 provinces in India reported up to 13th June. The LR-1 model predicted the deceased cases based on active cases. The highest observed deceased affected states are MH, GUJ, and Delhi. According to the LR-1 model, the possibility of more than 3300 deceased in highly red zone state MH and 1504 life of humans lost in Delhi. More than 300 deceased were reported in Gujrat and WB. Tamilnadu state needs to take care too caused of 1235 deceased. Less than 100 deceased cases predicted in the rest of cases.

Fig. 11
figure 11

Regression model’s comparison with real deceased predicted values

Full size image

Figure 12 visualizes the ARIMA Model’s output towards the next 40-days forecasting in India. On the graph, the blue lines signify the forecasting line, red lines show the observed cases, and dotted pink lines denote the UCL and LCL, two control limits: an upper and a lower limit of forecasting. The model predicted the total 753,216 confirmed cases with a lower bound of 704,460 and an upper bound of 801,973 cases. They were forecasting the total number of active cases in the country 331,580 with UCL of 348,581 and LCL of 314,580.

Fig. 12
figure 12

Forecasting with ARIMA

Full size image

Further, the model proved the forthcoming human losses might be encountered 22,411 with UCL of 24,124 and LCL of 20,699. Recovery of infected cases is predicted at 399,225 with UCL of 431,235 and LCL of 367,214. Therefore, based on the observed values, the forecasting graph proved to enhance all four aspects of Covid-19 affected Indians in the next 40- days.

Figure 13 shows the predicted count measured with the ARIMA Model for the next 40 days. The highest number of confirmed cases to be reported was indicated by vertical blue bars, which is 753,216. Among them, the highest active cases are supposed to be 331,580, and the possibility of 399,225 recovered humans until 23rd July. In the next 40 days, the deceased count may arrive up to 22,411. Therefore, we observed that all cases are rising rapidly.

Fig. 13
figure 13

ARIMA Model’s prediction of all cases for next 40 days up to 23rd July 2020

Full size image

Figure 14 compares the deceased predictive strength provided by regression and time series forecast methods. Accordingly, the ARIMA model, India maybe lost the highest number of human lives around 22,411, caused by Covid-19. This forecast value is calculated for 23rd July 2020. The lower number of deceased, 8854 predicted with LR-1 and MLR model identified 9429 deceased not confined to any date.

Fig. 14
figure 14

Total deceased prediction in India suggested by regression and forecasting

Full size image

Table 8 depicts the vital performance measures to prove the strength of forecasting models. All models' goodness of fit (the coefficient of determination) was found significant. The Mean Absolute Percentage Error (MAPE) Eq. (17) of active cases is calculated as very low compared to others. The minimum normalized Bayesian Information Criterion (BIC) is 9.8, calculated for the deceased. According to Eq. (18). All four forecast models are found significant (P < 0.005) due to the computed t-value with Eq. (19).

$$\mathrm{MAPE}=\left\{\frac{\left[\sum_{t-1}^{n} \left|yt-\widehat{y}t\div yt\right|\right]}{n}\right\}\times 100\%$$
(17)
$$BIC = k \, \log \left( n \right) - \, 2\log \left( {L\left( {\hat{\theta }} \right)} \right).$$
(18)
Table 8 ARIMA performance (95% confidence interval)
Full size table
$$t=\widehat{x-\frac{\mu }{s}/\surd N}$$
(19)

Figure 15 displays residuals of predicted values for four cases, including ACF and PACF. It shows UCL and LCL, which create the residual for various lags. For confirm case prediction, 6, 7, and 8 number lag shows significant autocorrelation. Also, this order was approved with the corresponding PACF. The most considerable lag is 7 and 8 for the forecasted active case. For the recovered case, lag 6, 7, and 8 are significant. In deceased forecasting, lag 1, 6, and 7 show the highest autocorrelation in the series.

Fig. 15
figure 15

Residual of ARIMA forecasting

Full size image

6 Conclusion

This study conducted two significant experiments demonstrating regression and time-series forecasting with respect to Covid-19. To estimate the number of Covid-19-infected future human deaths in India, we presented four predictive models. The study's findings looked at the significant correlation between the rate of deceased patients and their recovery and active status. Active cases had an impact on the deceased rate on the one hand, and the recovered patient had an impact on the deceased patient on the other. The ARIMA forecasts the highest deceased in the country. Based on results found with MLR, most deceased may be reported in four provinces (MH, DH, GUJ, Tamilnadu). Overall recovery must be achieved around 400,000, and around 300,000 humans remain active that period. Therefore, profoundly deceased prospects are seen in both cases, even engaged or recovered. Surplus suggestions for recovered patience need to look after more until the pandemic goes down. Additionally, red zone states were warned to take precautions against the epidemic by current models. Observing the government's Covid-19 guidelines and the prohibitions on anticipatory treatment, need to be applied to reduce active and deceased cases, which the model predicted.

Regression models investigated essential elements of the deceased. Based on active and recovered patients, multiple linear regression produced a substantial R2 of 0.89, which predicted that the patient would pass away. Additionally, the timing of Covid-19 was examined using an ARIMA analysis that predicted confirmed, active, recovered, and deceased cases for the following 40 days.

The future study includes applying a Deep Neural network with appropriate optimization methods. The base samples should be consisted of at least one month. The severe future reporting about the huge count of decease and active cases, and forecasting needs to be estimated for the next six months. Additionally, other public datasets can be evaluated and compared with our results.

7 Limitations

The present study is limited to a specific fixed number of hypotheses. The training samples were used only for 13 days. The days for the forecasting are limited up to 40 days. The particular ARIMA model was applied for forecasting purposes with a random walk. Further, we explored the impact of active and recovered cases on deceased cases. Only a state-wise decease was forecasted instead of districts. We have compared regression and ARIMA approaches on the secondary dataset and found that the ARIMA model is more accurate and worth deploying using Flask technology.