Reliability and cost optimization of series–parallel system with metaheuristic algorithm

Abstract

This study looks into the numerous reliability aspects of a series–parallel system. The designed system is made up of the three subsystems A, B, and C that interconnected in a series–parallel manner. Subsystem B has two units, whereas subsystems A and C have a single unit. Here, the system reliability measures such as reliability, availability, and mean time to failure using Laplace transformation and Markov’s process are evaluated. This study deals with minimize cost while system having the maximum reliability as constraining from one of the metaheuristic algorithms i.e., Particle Swarm Optimization (PSO). Lastly, a numerical example and graphical representation has been shown that the proposed methods are effective and efficient for solving reliability measures and cost problems.

1 Introduction

Reliability has vital importance at all stages of all types of industries. In today’s era reliability becomes a major part of our day-to-day life. The user anticipates that the device or system will always operate as expected. (Li, 2012). The series–parallel combination is the basis for the entire system and it is used extensively throughout the world, for instance, refrigerators, air- conditioners, geysers, etc. Hence, a well-designed series–parallel configuration for a system is necessary to be extremely reliable. Today, there has been an overemphasis on the value of complex systems that highly reliable and inexpensive.

Reliability theory has become a highly popular subject in literature and has expanded throughout the technical diagrams. In engineering and mathematics, several authors have worked on system reliability. In the existing literature, various techniques have been used to analyze the series–parallel system’s behavior and determine its reliability measures. Markov models are beneficial when a decision problem entails risk that is continuous throughout time, the event timing is crucial, and decisive events may occur more than once. It can be used to capture the transition probabilities as changes occur. Some extensively used techniques are markov chain, the Markov process regenerative point technology etc. Levitin et al. (2013) analyzed a technique for assessing the reliability and performance distribution of complicated non-repairable multi state systems (MSS). Zhou et al. (2014) studied a model based on the Markov process because of single event disruption, onboard computer systems have a high need for reliability. This work provides a system reliability prediction technique and specifies the main module of system reliability using the Markov model. The graph theory is used to forecast a system’s reliability. Montoro-Cazorla et al. (2018) studied reliability system is susceptible to shocks, internal breakdowns, and audits. The system is governed by a Markov process based on some assumptions. Shocks force several units to fail or be damaged at the same time. Qiu and Ming (2019) discussed a MSS in which each component have random behaviour and must fulfil its demand with shared bus performance. If a unit performs better than its demand, the excess might be distributed to other units in the network units with problems. Jiang et al. (2019) optimized the load in MSSs by standpoint of its collective act and evaluated the collection of various integrals is to evaluate the cumulative performance at failure or a specific time. Kvassay (2019) considered the system topology to determine the structure–function characteristics that may be estimated in both static and dynamic cases. The author also demonstrates the effective use of modular decomposition for these computations. To determine the reliability of the wireless communication system, mean-time-to-failure with variation in failures, sensitivity analysis, Markov process and mathematical modelling are used by Kumar and Kumar (2020). Xie (2020) presented a method to study the effects of cascading failures in systems.

It may be further optimized using various optimization methods once the reliability has been evaluated using the heuristic and metaheuristic methods. The search for the best solution in a complex space is known as an optimization problem, which is a common problem in many engineering fields. Numerical approaches may be useful when a problem cannot be solved analytically or can be solved but takes too much time, although there is no guarantee that the solution will be globally optimized (Şenel et al., 2019). Wang (2007) optimized the configuration of an autonomous hybrid generating system with a variety of power sources, including photovoltaics, storage batteries, and wind turbine generators, which are discussed in this study. Tavakkoli-Moghaddam et al. (2008) proposed a new approach i.e., Genetic Algorithm (GA), due to its intricacy, it is extremely challenging to use conventional optimization tools to solve such a problem optimally. The effectiveness of GA for dealing with difficulties of this nature is shown in this research. A discussion of the suggested algorithm’s resilience follows the presentation of computational results for a representative case. Ouzineb et al. (2008) recommended Tabu Search (TS) heuristic to determine the lowest-cost system design under availability constraints. In most cases, the suggested TS outperforms GA alternatives in terms of, solution execution time and quality. Aghaei (2014) talked about nonlinear formulations to offer a multiobjective technique for the Multi Stage Distribution Expansion Planning (MDEP) when DGs are present. Cost reduction, un-distributed energy, active-power-losses, and a voltage stability index, based on short circuit capacity make up the MDEP’s objective functions. On a typical set of data, the proposed method’s efficacy is evaluated and results of the 33-bus test-system are reported. The evolution of PSO and its applications to optimization are briefly covered in the chapter given by Pant et al. (2017). Mellal (2019) talked about the optimization addresses many objectives, for example- optimizing reliability, decreasing the cost, weight, and volume with the aid of PSO of a multi-objective system. Peiravi et al. (2020) explored the work and developed an exact Markov-based methodology. It is a strong and reliable instrument that has the added benefit of quick computation. The model is solved using GA. The suggested Markov model produces better answers with greater reliability values, according to the findings The warm standby, mixed strategies, model dynamics, and the approach in redundancy allocation problems are all taken into consideration by a newer model for the RAP. PSO and GA are used to find a solution and an example clearly demonstrating the efficacy of the proposed strategy by Saghih et al. (2021). Ling et al. (2021) studied the best subsystem grouping approach to increase system reliability and demonstrated the combined shock process. In terms of major optimization order, several component allocation policies are examined. Marouani (2021) presented to solve reliability-redundancy-allocation issues in series, parallel, and complex systems. This work provided an upgraded and improved PSO method. Results reveal that for all three evaluated scenarios, the total system reliability is significantly higher than that of various systems proposed in earlier studies.

In this article, the authors use Transition State Probabilities (TSP) to determine the upstate and downstate probabilities. The authors have also optimized the system cost using PSO by taking reliability as a constraint. They have also examined the system’s reliability characteristics after graph’s evaluation.

Further, the remainder sections are prearranged as follows: Sect. 2 has a mathematical detail of the system. Section 3 explains the methodology to evaluate the reliability of the series–parallel system. Section 4 discussed some reliability measures. Cost optimization with the help of a metaheuristic algorithm is calculated in Sect. 5. Section 6 provides the result discussion about the whole article. Lastly, Sect. 7 concludes the study with future work.

2 System details

This section provides notations, descriptions, and state-transition diagram of the series–parallel system which are then used to assess the series–parallel system’s performance characteristics like availability, reliability, and MTTF.

2.1 Notations

All the notations used in the modeling of the system are described as.$t$Time variable in year$s$Variable of Laplace transformation$\gamma$System repair rate from a malfunctioning condition to a functional state${\delta }_{A}, {\delta }_{B, }{ \delta }_{C}$Failure rates for subsystem A, B, C${p}_{i}(t)$Transition state probability, where i = 0 to 7${p}_{up}$System upstate probability${p}_{down}$System downstate probability$\overline{p }$ (s)Laplace transformation of p(t)${p}_{i }(q,t)$The probability of the failed stage ${p}_{i}$ Where i = 8 to 11

2.2 System description

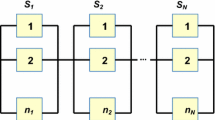
Consider a series–parallel system that contain three sub-systems: A, B, C. Sub-systems A and C are single units while B is a double unit (B₁ and B₂) as shown in Fig. 1. If subsystems A and B fail, the whole system will be in partially working condition with subsystem C. Similarly, after the failure of C, the system will be in partially working condition with subsystems A and B. Failure of A and C or B and C will result as the overall system failure.

Fig. 1

Block diagram of the system

A state-transition-diagram of the system has three states: good, degraded, failed. There are twelve states in which one is good state, seven are degraded states and four are complete failure states. Figure 2 shows the proposed model’s state transition diagram and related states described in Table 1.

Fig. 2

State transition diagram

Table 1 Description of states

3 Model construction and solution

To obtain the following collection of various differential equations that describe the model mathematically. The differential equations of states s₀ to s₇, which are the equations of good and degraded states, are represented by Eqs. (1–9). Equations (10–13) show the differential equations for states s₈ to s₁₁, which are the equations for completely failed states.

$$\left[\frac{\partial }{\partial t}+{\delta }_{A}+2{\delta }_{B}+ {\delta }_{C}\right]{p}_{0}\left(t\right)={\int }_{0}^{\infty }{p}_{11}\left(q,t\right)\gamma dq+{\int }_{0}^{\infty }{p}_{10}\left(q,t\right)\gamma dq+ {\int }_{0}^{\infty }{p}_{9}\left(q,t\right)\gamma dq+{\int }_{0}^{\infty }{p}_{8}\left(q,t\right)\gamma dq$$

(1)

$$\left[\frac{\partial }{\partial t}+{\delta }_{A}+{\delta }_{B}+ {\delta }_{C}\right]{p}_{1}=2{\delta }_{B}{p}_{0}$$

(2)

$$\left[\frac{\partial }{\partial t}+{\delta }_{A}+ {\delta }_{C}\right]{p}_{2}={\delta }_{B}{p}_{1}$$

(3)

$$\left[\frac{\partial }{\partial t}+2{\delta }_{B}+ {\delta }_{C}\right]{p}_{3}={\delta }_{A}{p}_{0}$$

(4)

$$\left[\frac{\partial }{\partial t}+2{\delta }_{B}+ {\delta }_{A}\right]{p}_{4 }= {\delta }_{C}{p}_{0}$$

(5)

$$\left[\frac{\partial }{\partial t}+{\delta }_{B}+ {\delta }_{A}\right]{p}_{5}=2{\delta }_{B}{p}_{4}+ {\delta }_{C}{p}_{1}$$

(6)

$$\left[ {\frac{\partial }{\partial t} + \delta_{B} + { }\delta_{C} } \right]p_{6} = \delta_{A} p_{1} + 2\delta_{B} p_{3}$$

(7)

$$\left[\frac{\partial }{\partial t}+{\delta }_{C}\right]{p}_{7}={\delta }_{A}{p}_{2}+{\delta }_{B}{p}_{6}$$

(8)

$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial q}+\gamma \right]{p}_{j}=0; j=8, 9, 10, 11$$

(9)

Boundary conditions

$${\mathrm{p}}_{8}(0, t)={\delta }_{\mathrm{B}}{\mathrm{p}}_{5}+{\delta }_{\mathrm{C}}{\mathrm{p}}_{2}$$

(10)

$${\mathrm{p}}_{9}(0, t)={\delta }_{\mathrm{C}}{\mathrm{p}}_{3}+{\delta }_{\mathrm{A}}{\mathrm{p}}_{4}$$

(11)

$${\mathrm{p}}_{10}(0, t)={\delta }_{\mathrm{A}}{\mathrm{p}}_{5}+{\delta }_{\mathrm{C}}{\mathrm{p}}_{6}$$

(12)

$${\mathrm{p}}_{11}(0, t)={\delta }_{\mathrm{C}}{\mathrm{p}}_{7}$$

(13)

Initial condition

$${p}_{i}\left(0\right)=\left\{\begin{array}{c}1 \quad i=0 \\ 0 i \quad \ge 1\end{array}\right.$$

(14)

One of the most significant methods for solving linear differential equations is the Laplace transform. In contrast to Fourier transforms, the Laplace transform produces nonperiodic solutions. The nonperiodic function’s Fourier series will always transform into periodic series. The solutions will also be periodic once these series are used to solve differential equations. It is applied in time-domain applications for t ≥ 0. It gives the value on initial condition. Taking the Laplace transformation of Eqs. (1–13) and using Eq. (14), we have

$$\left[s+{\delta }_{A}+2{\delta }_{B}+ {\delta }_{C}\right]{\overline{p} }_{0}\left(t\right)=1+{\int }_{0}^{\infty }{\overline{p} }_{11}\left(q,t\right)\gamma dq+{\int }_{0}^{\infty }{\overline{p} }_{10}\left(q,t\right)\gamma dq+{\int }_{0}^{\infty }{\overline{p} }_{9}\left(q,t\right)\gamma dq+{\int }_{0}^{\infty }{\overline{p} }_{8}\left(q,t\right)\gamma dq$$

(15)

$$\left[s+{\delta }_{A}+{\delta }_{B}+ {\delta }_{C}\right]{\overline{p} }_{1}=2{\delta }_{B}{\overline{p} }_{0}$$

(16)

$$\left[s+{\delta }_{A}+ {\delta }_{C}\right]{\overline{p} }_{2}={\delta }_{B}{\overline{p} }_{1}$$

(17)

$$\left[s+2{\delta }_{B}+ {\delta }_{C}\right]{\overline{p} }_{3}={\delta }_{A}{\overline{p} }_{0}$$

(18)

$$\left[s+2{\delta }_{B}+ {\delta }_{A}\right]{\overline{p} }_{4 }= {\delta }_{C}{\overline{p} }_{0}$$

(19)

$$\left[s+{\delta }_{B}+ {\delta }_{A}\right]{\overline{p} }_{5}=2{\delta }_{B}{\overline{p} }_{4}+ {\delta }_{C}{\overline{p} }_{1}$$

(20)

$$\left[ {s + \delta_{B} + { }\delta_{C} } \right]\overline{p}_{6} = \delta_{A} \overline{p}_{1} + 2\delta_{B} \overline{p}_{3}$$

(21)

$$\left[s+{\delta }_{C}\right]{\overline{p} }_{7}={\delta }_{A}{\overline{p} }_{2}+{\delta }_{B}{\overline{p} }_{6}$$

(22)

$$\left[s+\frac{\partial }{\partial q}+\gamma \right]{\overline{p} }_{j}=0; \quad j=8, 9, 10, 11$$

(23)

Boundary conditions

$${\overline{\text{p}}}_{8} \left( {0, s} \right) = \delta_{{\text{B}}} {\overline{\text{p}}}_{5} + \delta_{{\text{C}}} {\overline{\text{p}}}_{2}$$

(24)

$${\overline{\mathrm{p}} }_{9}(0, s)={\delta }_{\mathrm{C}}{\overline{p} }_{3}+{\delta }_{\mathrm{A}}{\overline{\mathrm{p}} }_{4}$$

(25)

$${\overline{\mathrm{p}} }_{10}(0, s)={\delta }_{\mathrm{A}}{\overline{\mathrm{p}} }_{5}+{\delta }_{\mathrm{C}}{\overline{\mathrm{p}} }_{6}$$

(26)

$${\overline{\mathrm{p}} }_{11}(0, s)={\delta }_{\mathrm{C}}{\overline{\mathrm{p}} }_{7}$$

(27)

solving Eqs. (15) - (23) with the help of Eqs. (24) - (27), we obtain the transition state probabilities as-

$${\overline{p} }_{0}\left(s\right)=\frac{1}{{(s+2\delta }_{B}+{\delta }_{A}+{\delta }_{C})-{S}_{\gamma }\left(s\right)K(s)}$$

$${\overline{p} }_{1}\left(s\right)=\frac{{2\delta }_{B}}{{s+\delta }_{B}+{\delta }_{A}+{\delta }_{C}}{p}_{0}$$

$${\overline{p} }_{2}\left(s\right)=\frac{2{\delta }_{B}^{2}}{({s+\delta }_{B}+{\delta }_{A}+{\delta }_{C})(s+{\delta }_{A}+{\delta }_{C}}{p}_{0}$$

$${\overline{p} }_{3}\left(s\right)=\frac{{\delta }_{A}}{{s+2\delta }_{B}+{\delta }_{C}}{p}_{0}$$

$${\overline{p} }_{4}\left(s\right)=\frac{{\delta }_{C}}{{s+2\delta }_{B}+{\delta }_{A}}{p}_{0}$$

$$\bar{p}_{5} \left( s \right) = \left( {\frac{{2\delta _{B} \delta _{C} }}{{s + 2\delta _{B} + \delta _{A} }} + \frac{{2\delta _{B} \delta _{C} }}{{s + \delta _{C} + \delta _{B} + \delta _{A} }}} \right)p_{0}$$

$$\bar{p}_{6} \left( s \right) = \left( {\frac{{2\delta _{B} \alpha _{A} }}{{s + 2\delta _{B} + \delta _{C} }} + \frac{{2\delta _{B} \delta _{A} }}{{s + \delta _{C} + \delta _{B} + \delta _{A} }}} \right)p_{0}$$

$$\bar{p}_{7} \left( s \right) = \left( {\frac{{2\delta _{B}^{2} \delta _{A} }}{{s + 2\delta _{B} + \delta _{C} }} + \frac{{2\delta _{B}^{2} \delta }}{{s + \delta _{C} + \delta _{B} + \delta _{A} }} + \frac{{2\delta _{B}^{2} \delta _{A} }}{{(s + \delta _{C} + \delta _{B} + \delta _{A} )(s + \delta _{A} + \delta _{C} )}}} \right)p_{0}$$

$$\bar{p}_{8} \left( s \right) = \left( {\frac{{1 - S_{\gamma } \left( s \right)}}{s}} \right)\left( {\frac{{2\delta _{B}^{2} \delta _{A} }}{{s + 2\delta _{B} + \delta _{A} }} + \frac{{2\delta _{B}^{2} \delta _{A} }}{{s + \delta _{C} + \delta _{B} + \delta _{A} }} + \frac{{2\delta _{B}^{2} \delta _{A} }}{{\left( {s + \delta _{A} + \delta _{C} } \right) + (s + \delta _{C} + \delta _{B} + \delta _{A} )}}} \right)p_{0}$$

$$\bar{p}_{9} \left( s \right) = \left( {\frac{{1 - S_{\gamma } \left( s \right)}}{s}} \right)\left( {\frac{{\delta _{C} \delta _{A} }}{{s + 2\delta _{B} + \delta _{C} }} + \frac{{\delta _{C} \delta _{A} }}{{s + 2\delta _{B} + \delta _{A} }}} \right)p_{0}$$

$$\bar{p}_{{10}} \left( s \right) = \left( {\frac{{1 - S_{\gamma } \left( s \right)}}{s}} \right)\left( {\frac{{4\delta _{A} \delta _{C} \delta _{A} }}{{s + \delta _{A} + \delta _{B} + \delta _{C} }} + \frac{{2\delta _{A} \delta _{C} \delta _{A} }}{{s + 2\delta _{B} + \delta _{A} }} + \frac{{2\delta _{A} \delta _{C} \delta _{A} }}{{s + 2\delta _{B} + \delta _{C} }}} \right)p_{0}$$

$$\bar{p}_{{11}} \left( s \right) = \left( {\frac{{1 - S_{\gamma } \left( s \right)}}{s}} \right)\left( {\frac{{2\delta _{B}^{2} \delta _{A} \delta _{C} }}{{s + 2\delta _{B} + \delta _{C} }} + \frac{{2\delta _{B}^{2} \delta _{A} \delta _{C} }}{{s + \delta _{C} + \delta _{B} + \delta _{A} }} + \frac{{2\delta _{B}^{2} \delta _{A} \delta _{C} }}{{(s + \delta _{A} + \delta _{C} )(s + \delta _{C} + \delta _{B} + \delta _{A} )}}} \right)p_{0}$$

$$K\left(s\right)=[{2\delta }_{B}^{2}{\delta }_{c}\left(\frac{1}{s+{\delta }_{A}+2{\delta }_{B}}+\frac{1}{s+{\delta }_{A}+{\delta }_{B}+{\delta }_{c}}+\frac{1}{\left(s+{\delta }_{A}{+\delta }_{C}\right)\left(s+{\delta }_{A}+{\delta }_{B}+{\delta }_{c}\right)}\right)+{\delta }_{A}{\delta }_{C}\left(\frac{1}{s+{2\delta }_{B}{+\delta }_{C}}+\frac{1}{s+{\delta }_{A}+2{\delta }_{B}}\right)+{2\delta }_{B}{\delta }_{A}{\delta }_{C}\left(\frac{1}{s+{\delta }_{A}+2{\delta }_{B}}+\frac{2}{s+{\delta }_{A}+{\delta }_{B}+{\delta }_{c}}+\frac{1}{s+{2\delta }_{B}{+\delta }_{C}}\right)+2{\delta }_{A}{\delta }_{B}^{2}{\delta }_{C}(\frac{1}{s+{\delta }_{A}+{\delta }_{B}+{\delta }_{c}}+\frac{1}{s+{2\delta }_{B}{+\delta }_{C}}+\frac{1}{(s+{\delta }_{A}+{\delta }_{B}+{\delta }_{c})(s+{\delta }_{A}{+\delta }_{C})})]$$

The probability of system’s up-state and down-state are determined as-

$${\overline{p} }_{up}={\overline{p} }_{0}+{\overline{p} }_{1}+{\overline{p} }_{2}+{\overline{p} }_{3}+{\overline{p} }_{4}{+\overline{p} }_{5}+{\overline{p} }_{6}+{\overline{p} }_{7}$$

$${\overline{p} }_{up}=\left[\frac{{2\delta }_{B}}{{s+\delta }_{B}+{\delta }_{A}+{\delta }_{C}}+\frac{2{\delta }_{B}^{2}}{\left({s+\delta }_{B}+{\delta }_{A}+{\delta }_{C}\right)\left(s+{\delta }_{A}+{\delta }_{C}\right)}+\frac{{\delta }_{A}}{\left({s+2\delta }_{B}+{\delta }_{C}\right)}+\frac{{\delta }_{C}}{{(s+2\delta }_{B}+{\delta }_{A})}+\left(\frac{{2\delta }_{B}{\delta }_{C}}{{s+2\delta }_{B}+{\delta }_{A}}+\frac{{2\delta }_{B}{\delta }_{C}}{{s+{\delta }_{C}+\delta }_{B}+{\delta }_{A}}\right)+\left(\frac{{2\delta }_{B}{\delta }_{A}}{{s+2\delta }_{B}+{\delta }_{C}}+\frac{{2\delta }_{B}{\delta }_{A}}{{s+{\delta }_{C}+\delta }_{B}+{\delta }_{A}}\right)+\left(\frac{2{\alpha }_{B}^{2}{\alpha }_{A}}{{s+2\delta }_{B}+{\delta }_{C}}+\frac{2{\alpha }_{B}^{2}{\alpha }_{A}}{{s+{\delta }_{C}+\delta }_{B}+{\delta }_{A}}+\frac{2{\alpha }_{B}^{2}{\alpha }_{A}}{{(s+{\alpha }_{C}+\alpha }_{B}+{\alpha }_{A})(s+{\alpha }_{A}+{\alpha }_{C})}\right)\right]{\overline{p} }_{0}$$

(28)

$${\overline{p } }_{down}={\overline{p} }_{8}+{\overline{p} }_{9}+{\overline{p} }_{10}+{\overline{p} }_{11}$$

$${\overline{p} }_{down}=\left(\frac{1-{S}_{\gamma }\left(s\right)}{s}\right)[(\frac{2{\delta }_{B}^{2}{\delta }_{A}}{{s+2\delta }_{B}+{\delta }_{A}}+\frac{2{\delta }_{B}^{2}{\delta }_{A}}{{s+{\delta }_{C}+\delta }_{B}+{\delta }_{A}}+\frac{2{\delta }_{B}^{2}{\delta }_{A}}{\left(s+{\delta }_{A}+{\delta }_{C}\right)\left({(s+{\delta }_{C}+\delta }_{B}+{\delta }_{A}\right)})+ \left(\frac{{\delta }_{C}{\delta }_{A}}{{s+2\delta }_{B}+{\delta }_{C}}+ \frac{{\delta }_{C}{\delta }_{A}}{{s+2\delta }_{B}+{\delta }_{A}}\right)\left(\frac{4{\delta }_{A}{\delta }_{C}{\delta }_{A}}{{s+{\delta }_{A}+\delta }_{B}+{\delta }_{C}}+\frac{2{\delta }_{A}{\delta }_{C}{\delta }_{A}}{{s+2\delta }_{B}+{\delta }_{A}}+\frac{2{\delta }_{A}{\delta }_{C}{\delta }_{A}}{{s+2\delta }_{B}+{\delta }_{C}}\right)+(\frac{2{\delta }_{B}^{2}{\delta }_{A}{\delta }_{C}}{{s+2\delta }_{B}+\delta }+\frac{2{\delta }_{B}^{2}{\delta }_{A}{\delta }_{C}}{{s+{\delta }_{C}+\delta }_{B}+{\delta }_{A}}+\frac{2{\delta }_{B}^{2}{\delta }_{A}{\delta }_{C}}{(s+{\delta }_{A}+{\delta }_{C}){(s+{\delta }_{C}+\delta }_{B}+{\delta }_{A})}{)]p}_{0}$$

(29)

4 Some measures

4.1 Availability determination

The system’s availability is equal to the sum of maintenance and reliability (Ram and Singh, 2014). Substituting the value of various failure rates ${\delta }_{A}=0.10, {\delta }_{B}=0.004, {\delta }_{C}=0.08, and \gamma =1$ in Eq. (28). Taking an Inverse Laplace Transformation (ILT) of Eq. (28), One can determine the system’s availability in terms of t is-

$$A\left(t\right)=-0.024695{e}^{\left(-0.97650t\right)}+0.027678{e}^{\left(-0.30261t\right)}+0.016715{e}^{\left(-0.18586t\right)}+ 0.017863{e}^{\left(-0.17769t\right)}+0.00012{e}^{\left(-0.98485t\right)}+0.96255{e}^{\left(-0.00683t\right)}$$

(30)

After changing the time t from 0 to 50 with interval 2 in Eq. (29) to determine the nature of the availability of the complex system during long run. The authors obtained Table 2 and the related Fig. 3.

Table 2 Availability of the system

Fig. 3

Availability vs time

4.2 MTTF determination

The MTTF (mean time to failure) of a technological product is the typical interval between non-reparable failures. A system’s MTTF can be founded using its average time between failures (Goyal, 2017a). After using the Laplace variable ‘s’ tends to zero and putting the repair rate $\gamma =0$ in Eq. (28), one can obtain the MTTF as

$$\mathrm{MTTF}=\underset{s\to 0}{\mathrm{lim}}{p}_{up}$$

$$\frac{\begin{array}{c}1+\frac{2{\delta }_{B}}{\left({\delta }_{A}+{\delta }_{B}+{\delta }_{C}\right)}+\frac{2{\delta }_{B}^{2}}{\left({\delta }_{B}+{\delta }_{A}+{\delta }_{C}\right)\left({\delta }_{A}+{\delta }_{C}\right)}+\frac{{\delta }_{C}}{{(2\delta }_{B}+{\delta }_{A})}+\left(\frac{2{\delta }_{B}{\delta }_{C}}{{\delta }_{A}+2{\delta }_{B}}+\frac{2{\delta }_{B}{\delta }_{C}}{{\delta }_{A}+{\delta }_{B}+{\delta }_{C}}\right)+\\ \frac{{\delta }_{A}}{\left({2\delta }_{B}+{\delta }_{C}\right)}+\left(\frac{2{\delta }_{B}{\delta }_{A}}{{\delta }_{C}+2{\delta }_{B}}+\frac{2{\delta }_{B}{\delta }_{A}}{{\delta }_{A}+{\delta }_{B}+{\delta }_{C}}\right)+\\ \left(\frac{2{\delta }_{B}^{2}{\delta }_{A}}{{\delta }_{C}+2{\delta }_{B}}+\frac{2{\delta }_{B}^{2}{\delta }_{A}}{{\delta }_{A}+{\delta }_{B}+{\delta }_{C}}+\frac{2{\delta }_{B}^{2}{\delta }_{A}}{{(\delta }_{A}+{\delta }_{B}+{\delta }_{C})({\delta }_{A}+{\delta }_{C}}\right)\end{array}}{({\delta }_{A}{+2\delta }_{B}+{\delta }_{C})}$$

(31)

Varying ${\delta }_{A}, {\delta }_{B}, and {\delta }_{C}$ respectively as 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and setting ${\delta }_{A}=0.10, {\delta }_{B}=0.004, and {\delta }_{C}=0.08$, one can find the MTTF variance concerning failure rates. The result is shown in Table 3 and related to Fig. 4.

Table 3 MTTF of the system

Fig. 4

MTTF vs variation in failure rate

4.3 Reliability determination

Reliability is the probability that a device will function as intended for a certain amount of time under predetermined circumstances. Reliability is always a function of time (Goyal, 2017b). After fix the value of failure rate as ${\delta }_{A}=0.10, {\delta }_{B}=0.004, {and \delta }_{C}=0.08$ and repair rate equal to zero in Eq. (28), Taking ILT and authors get,

$$R\left(t\right)=0.16080{e}^{(-0.18400 t)}+1.10000{e}^{(-0.18000 t)}+1.00803{e}^{(-0.08800 t)}+ 1.0080{e}^{(-0.10800 t)}-2.27682{e}^{(-0.18800 t)}$$

(32)

Changing the unit time ‘t’ from 0 to 50 with the interval 2 in Eq. (32), obtain Table 4 and Fig. 5 related to the reliability variation of a system.

Table 4 System’ reliability

Fig. 5

Reliability vs time

5 Cost optimization of series–parallel system with PSO

One of the most effective optimization algorithms that is frequently referenced in the literature is the PSO (PSO) algorithm. Due to its ease of use, sparse number of parameters, and quick convergence rate, the PSO algorithm has been successfully used in numerous optimization problems. Authors choose this algorithm because it performs exceptionally well on a variety of problems from various domains.

It is a population-based meta-heuristic optimization approach (Kennedy and Eberhart, 1995a; Eberhart and Kennedy, 1995b). It takes its cues from the way fish school or flock together to find food. In the PSO, the initial population is initially produced at random within the search domain. The best position of the swarm is constantly stored for each particle. when the swarm iterates, the position of each particle update by the given relation:

$$\begin{gathered} v_{d}^{i} \, = \,\,w*x_{d}^{i} + c_{1} *r_{1} *(p_{d}^{i} - x_{d}^{i} ) + c_{2} *r_{2} *(p_{d}^{g} - x_{d}^{i} ) \hfill \\ x_{d}^{i} \, = \,x_{d}^{i} + x_{d}^{i} \hfill \\ \end{gathered}$$

The particle in the swarm is referred to as i in this context. The iteration step is denoted by d, and the random numbers r₁ and r₂ in the range [0, 1], position vector (x), velocity vector (v), and the inertia weight is represented by w. The optimization parameters are represented by the coefficients c₁ and c₂, and they should be non-negative. The best position pⁱ (local best) is obtained by the i^th particle, and p^g gives the global best position of the swarm.

The PSO method substitutes a random position within the search space for the new position and velocity of a particle instead of accepting them with a small likelihood. The objective of this operation is to depart from the local minimums. The process runs till an optimal value is obtained otherwise predefined maximum limit of iterations is attained (Şenel et al., 2019). The flowchart of the PSO algorithm is shown in Fig. 6.

Fig. 6

Flow chart of PSO algorithm

The author uses the PSO to reduce system costs while maintaining the necessary reliability.

The reliability (R) and cost (C) of the Series–Parallel System. (Negi et al., 2021; Tillman, 1970).

$$R={R}_{3}+2{R}_{1}{R}_{2}-{R}_{1}{R}_{2}^{2}-2{R}_{1}{R}_{2}{R}_{3}-{R}_{1}{R}_{2}^{2}{R}_{3} C={K}_{1}{r}_{1}^{{\alpha }_{1}}+2{K}_{2}{r}_{2}^{\alpha 2}+{K}_{3}{r}_{3}^{{\alpha }_{3}}$$

(33)

To obtain the result, the following non-linear programming problem is solved.

Minimize C.

Subject to Constrain

$$0.3\le \, {\text{r}}_{i}\le 1 \quad {\text{i}} = 1, 2, 3$$

$$0.99 \le {R}_{i}\le 1$$

where, K₁ = 200, K₂ = 250, K₃ = 150, and α_i = 0.6, i = 1, 2, 3,

To obtain the minimum cost of the system by using PSO take 200 random particles, cognitive constants c₁ = 20.9 and social constant c₂ = 2.03, and no. of iterations is 1000. By using these values, get the system cost is 481.97.

For the cost optimization of the series–parallel system, the PSO algorithm has been implemented in MATLAB using the simplest penalty functions method for addressing constraints and the result is plotted in the below graph (Fig. 7).

Fig. 7

Cost convergence curve of series–parallel system

6 Result discussion

In this paper, system reliability, availability, MTTF are evaluated using Markov process and minimize cost by PSO technology. The following aspects have been obtained during overall study.

• From Table 2 and corresponding Fig. 3, It is observed that as time goes on, the designed system’s availability gradually declines. The designed system’s availability graph remains constant between 46 to 48 years and after that, it again reduces with time.

• MTTF of the system have been considered with respect to various failure rates shown in Table 3, which represents that with an increment in failure rates${\delta }_{A}, {\delta }_{B} , {\delta }_{C}$., system’s MTTF decreases (Fig. 4).

• Table 5 shows that how the passage of time has an impact on the system’s reliability. As time goes on, the system’s reliability decreases in a curvilinear and uniform manner, as illustrated in Fig. 5.

• Figure 7 represents the relation between iterations and the fitness function and observed that the system’s cost decreases with the growing iterations. However, the system’s optimized cost is 481.97.

7 Conclusion

The current work focuses on a system reliability measure and cost optimization that consists of three components connected in a series–parallel manner. The Markov process is used to calibrate the system’s availability MTTF and reliability. The PSO technique is utilized to optimize the costs.

Series–parallel systems and the Markov process have a large amount of literature (Levitin et al., 2013; Tsumura et al., 2013; Zhou et al., 2014), but metaheuristics have not been used in their research work. It is concluded from the entire study that the series–parallel system’s availability and reliability reduce as time passes on. On examining the MTTF results of the system, it is observed that the MTTF of the system reduces as failure rates increase. When looking at the MTTF graph, one observes that failure rate ${\delta }_{B}$ has a higher degree of variation than failure rates ${\delta }_{A}$ and ${\delta }_{C}$. metaheuristic algorithm has been used to optimize the cost of the proposed system with the consideration of reliability as a constraint and found that cost is reduced efficiently after using this technology. In future, authors try to analyse other parameters such as MTTR, dependability etc. and a hybrid algorithm can be used to optimize the cost.

Appendix

$$\begin{gathered} p_{0} (t + \Delta t) = (1 - 2\delta_{B} \Delta t)\,(1 - \delta_{A} \Delta t)\,(1 - \delta_{C} \Delta t)p_{0} (t + \Delta t) \hfill \\ \quad + \int_{0}^{\infty } {p_{11} (q,t)} \,\gamma (q)\,dq\,\Delta t + \int_{0}^{\infty } {p_{10} (q,t)} \,\gamma (q)\,dq\,\Delta t \hfill \\ \quad + \int_{0}^{\infty } {p_{9} (q,t)} \,\gamma (q)\,dq\,\Delta t + \int_{0}^{\infty } {p_{8} (q,t)} \,\gamma (q)\,dq\,\Delta t \hfill \\ \end{gathered}$$

(34)

$$p_{2} (t + \Delta t) = (1 - \delta_{B} \Delta t)\,(1 - \delta_{C} \Delta t)\,p_{2} (t) + \,p_{0} (t)2\delta_{B} \,\Delta t$$

(35)

$$p_{1} (t + \Delta t) = (1 - \delta_{C} \Delta t)\,(1 - \delta_{A} \Delta t)\,p_{1} (t) + \,p_{2} (t)\delta_{B} \,\Delta t$$

(36)

$$p_{3} (t + \Delta t) = (1 - \delta_{C} \Delta t)\,(1 - 2\delta_{B} \Delta t)\,p_{3} (t) + \,p_{0} (t)\delta_{A} \,\Delta t$$

(37)

$$p_{4} (t + \Delta t) = (1 - \delta_{A} \Delta t)\,(1 - 2\delta_{B} \Delta t)\,p_{4} (t) + \,p_{0} (t)\delta_{C} \,\Delta t$$

(38)

$$p_{5} (t + \Delta t) = (1 - \delta_{B} \Delta t)\,\,p_{5} (t) + \,p_{4} (t)2\delta_{B} \,\Delta t + p_{2} \delta_{C} \Delta t$$

(39)

$$p_{6} (t + \Delta t) = (1 - \delta_{C} \Delta t)\,(1 - \delta_{B} \Delta t)\,p_{6} (t) + \,p_{3} (t)2\delta_{B} \,\Delta t + p_{2} \delta_{A} \Delta t$$

(40)

$$p_{7} (t + \Delta t) = (1 - \delta_{C} \Delta t)\,p_{7} (t) + \,p_{6} (t)\delta_{B} \,\Delta t + p_{1} \delta_{A} \Delta t$$

(41)

$$p_{9} (q + \Delta q,t + \Delta t) = (1 - \gamma \Delta t)\,\,p_{9} (t)$$

(42)

$$p_{8} (q + \Delta q,t + \Delta t) = (1 - \gamma \Delta t)\,\,p_{8} (t)$$

(43)

$$p_{10} (q + \Delta q,t + \Delta t) = (1 - \gamma \Delta t)\,\,p_{10} (t)$$

(44)

$$p_{11} (q + \Delta q,t + \Delta t) = (1 - \gamma \Delta t)\,\,p_{11} (t)$$

(45)

Boundary Conditions

$$p_{9} (0,t) = \delta_{A} \,p_{4} (t) + \delta_{C} \,p_{3} (t)$$

(46)

$$p_{8} (0,t) = \delta_{C} \,p_{2} (t) + \delta_{B} \,p_{5} (t)$$

(47)

$$p_{10} (0,t) = \delta_{A} \,p_{5} (t) + \delta_{C} \,p_{6} (t)$$

(48)

$$p_{11} (0,t) = \delta_{C} \,p_{7} (t)$$

(49)

Initial Condition.

Good Condition $p_{0} = 1$ and all are zero (0).

From Eq. (34)

$$\begin{gathered} p_{0} (t + \Delta t) = (1 - \delta_{C} \Delta t - \delta_{A} \Delta t + \delta_{A} \,\delta_{C} (\Delta t)^{2} - 2\delta_{B} \Delta t + 2\delta_{B} \,\delta_{C} (\Delta t)^{2} \hfill \\ + 2\delta_{B} \,\delta_{A} (\Delta t)^{2} - 2\delta_{B} \,\delta_{C} \,\delta_{A} (\Delta t)^{3} )p_{0} \hfill \\ + \int_{0}^{\infty } {p_{11} (q,t)} \,\gamma (q)\,dq\,\Delta t + \int_{0}^{\infty } {p_{10} (q,t)} \,\gamma (q)\,dq\,\Delta t \hfill \\ + \int_{0}^{\infty } {p_{9} (q,t)} \,\gamma (q)\,dq\,\Delta t + \int_{0}^{\infty } {p_{8} (q,t)} \,\gamma (q)\,dq\,\Delta t \hfill \\ \end{gathered}$$

Neglecting higher order terms of $\Delta t$ since $\Delta t$ is very small. So, authors get-

$$\begin{aligned} p_{0} (t + \Delta t) = & (1 - \delta _{C} \Delta t - \delta _{A} \Delta t - 2\delta _{B} \Delta t)p_{0} (t) \\ & + \int_{0}^{\infty } {p_{{11}} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t + \int_{0}^{\infty } {p_{{10}} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t \\ & + \int_{0}^{\infty } {p_{9} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t + \int_{0}^{\infty } {p_{8} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t \\ \end{aligned}$$

$$\begin{aligned} p_{0} (t + \Delta t) = & p_{0} (t) + ( - \delta _{C} \Delta t - \delta _{A} \Delta t - 2\delta _{B} \Delta t)p_{0} (t) \\ & + \int_{0}^{\infty } {p_{{11}} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t + \int_{0}^{\infty } {p_{{10}} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t \\ & + \int_{0}^{\infty } {p_{9} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t + \int_{0}^{\infty } {p_{8} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t \\ \end{aligned}$$

$$\begin{aligned} p_{0} (t + \Delta t) - p_{0} = & ( - \delta _{C} \Delta t - \delta _{A} \Delta t - 2\delta _{B} \Delta t)p_{0} \\ & + \int_{0}^{\infty } {p_{{11}} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t + \int_{0}^{\infty } {p_{{10}} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t \\ & + \int_{0}^{\infty } {p_{9} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t + \int_{0}^{\infty } {p_{8} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \Delta t \\ \end{aligned}$$

Divide by $\Delta t$ both side

$$\begin{aligned} \frac{{p_{0} (t + \Delta t) - p_{0} (t)}}{{\Delta t}} = & ( - \delta _{C} - \delta _{A} - 2\delta _{B} )p_{0} (t) \\ & + \int_{0}^{\infty } {p_{{11}} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} + \int_{0}^{\infty } {p_{{10}} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \\ & + \int_{0}^{\infty } {p_{9} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} + \int_{0}^{\infty } {p_{8} (q,t)} {\mkern 1mu} \gamma (q){\mkern 1mu} dq{\mkern 1mu} \\ \end{aligned}$$

$$\begin{gathered} \left( {\frac{\partial }{\partial t} + \delta_{C} + \delta_{A} + 2\delta_{B} } \right)\,p_{0} (t) = \int_{0}^{\infty } {p_{11} (q,t)} \,\gamma (q)\,dq\, + \int_{0}^{\infty } {p_{10} (q,t)} \,\gamma (q)\,dq\, \hfill \\ \quad + \int_{0}^{\infty } {p_{9} (q,t)} \,\gamma (q)\,dq\, + \int_{0}^{\infty } {p_{8} (q,t)} \,\gamma (q)\,dq\, \hfill \\ \end{gathered}$$

(50)

Similarly, from Eq. (35) to (41)

$$\left( {\frac{\partial }{\partial t} + \delta_{C} + \delta_{A} + \delta_{B} } \right)\,p_{2} = \,2\delta_{B} \,p_{0}$$

(51)

$$\left( {\frac{\partial }{\partial t} + \delta_{C} + \delta_{A} } \right)\,p_{2} = \,\delta_{B} \,p_{1}$$

(52)

$$\left( {\frac{\partial }{\partial t} + \delta_{C} + 2\delta_{B} } \right)\,p_{3} = \,\delta_{A} \,p_{0}$$

(53)

$$\left( {\frac{\partial }{\partial t} + \delta_{A} + 2\delta_{B} } \right)\,p_{4} = \,\delta_{C} \,p_{0}$$

(54)

$$\left( {\frac{\partial }{\partial t} + \delta_{B} + \delta_{A} } \right)\,p_{5} \, = \,\delta_{C} \,p_{1} + 2\delta_{B} \,p_{4}$$

(55)

$$\left( {\frac{\partial }{\partial t} + \delta_{B} + \delta_{C} } \right)\,p_{6} \, = \,\delta_{A} \,p_{1} + 2\delta_{B} \,p_{3}$$

(56)

$$\left( {\frac{\partial }{\partial t} + \delta_{C} } \right)\,p_{7} \, = \,\delta_{A} \,p_{2} + \delta_{B} \,p_{6}$$

(57)

From Eq. (42), by a Taylor expansion

$$\begin{gathered} p_{9} (q,t) + \Delta q\frac{\partial }{\partial q}p_{9} (q,t) + \Delta t\frac{\partial }{\partial q}p_{9} (q,t) + - - - - - = p_{9} (q,t) \hfill \\ \quad + ( - \gamma \,\Delta t)\,p_{9} (q,t) + \delta_{C} \,\Delta t\,p_{9} (q,t) + \delta_{A} \,\Delta t\,p_{9} (q,t) \hfill \\ \end{gathered}$$

As, $\Delta q \approx \Delta t$, then we get

$$\left( {\frac{\partial }{\partial q} + \frac{\partial }{\partial t} + \gamma } \right)p_{9} (t) = \,0$$

(58)

Similarly, from Eq. (43) to (45)

$$\left( {\frac{\partial }{\partial q} + \frac{\partial }{\partial t} + \gamma } \right)p_{8} (t) = \,0$$

(59)

$$\left( {\frac{\partial }{\partial q} + \frac{\partial }{\partial t} + \gamma } \right)p_{10} (t) = \,0$$

(60)

$$\left( {\frac{\partial }{\partial q} + \frac{\partial }{\partial t} + \gamma } \right)p_{11} (t) = \,0$$

(61)