3D Numerical Modeling of Molten Steel Flow and Inclusion Transports During the Solidification Process of a Large Steel Ingot

Abstract

In this study, a comprehensive three-dimensional model was developed to describe the transport phenomena during ingot solidification. The model couples fluid flow, inclusion distribution, and inclusion trajectories of different sizes. The flow fields were found to be influenced by buoyancy-driven flow and feeding flow, resulting in part circulation. As the solidification of molten steel continues, the capture speed of inclusion particles gradually decreases due to increasing viscosity. The model produced visual representations of inclusions, showing more inclusions at the bottom of the ingot than on the hot-top and fewer inclusions in the central and top areas, consistent with experimental results. Inclusion particle trajectories of different sizes were also simulated during the solidification process, revealing the significant influence of flow fields on inclusion motion.

1 Introduction

Ingot casting is a crucial method for producing high-grade alloy steels and special steels, including high-grade bearing steels and high-grade spring steels, which cannot be substituted with continuous casting. In addition, ingot casting is utilized to manufacture thick plates, seamless tubes, forging pieces, bars, and wires [1].

Ingot casting is an important method that cannot be replaced by continuous casting process for special products, such as thick plates with low compression ratio [1, 2]. Steel products with high performances are increasingly demanded in the world, further reducing the content of inclusions in molten steel has become one of the main objectives in the steelmaking process. Inclusions in steel would result in repairs of slabs/ingots or complete rejection. Moreover, the properties of steel products are largely affected by the inclusions in steel. During molten steel casting process, the flow, heat transfer and solidification impact the inclusion movement in the molten steel, inclusion capture near the solidification front and the inclusion distribution in the ingot. Recently, the capture of particles near the solidified shells is a very complex process and has received extensive attention [3,4,5]. It is difficult to study the behavior of inclusions in the solidification process through experiments. The development of computer technology gives us an opportunity to research this phenomenon by method of numerical simulations. Recently, scholars have been devoting greater attention to the mathematical model that couples the flow, heat transfer, and species transfer in the continuous casting process [6, 7]. The numerical modeling approach has proved to be a significant and efficient tool for forecasting inclusion behavior, including the trajectory of inclusions in the RH [8], tundish [9, 10], and continuous casting mold [11]. Nonetheless, studies in this field primarily focus on the effect of fluid flow on inclusion distribution and removal in molten steel. In this regard, the inclusion motion trajectory analysis is a commonly employed method for studying inclusion behavior [12, 13]. In previous studies, the calculation of the molten steel flow field and the tracking of inclusion in molten steel were not coupled [14,15,16,17]. Moreover, studies of inclusion motion and capture during the solidification process of large steel ingots have not been reported.

Study on inclusion motion and capture during the ingot casting process solidification is very important for the sake of the production of clean steel and the high quality of the final product. This paper developed a 3D numerical model coupling the flow-solidification of molten steel and inclusion transport during the feeding process of a large steel ingot. Moreover, a new feature in the current work is that the non-metallic inclusion movement in molten steel and capture near the solidifying front have been investigated through the developed numerical model. The research results reveal the inclusion removal mechanism during ingot casting and inclusion distribution in a large ingot.

2 Mathematical Model of Fluid Flow and Inclusion Transports

2.1 Assumptions in the Model

To simplify the coupling model, the following assumptions have been adopted in the current work:

• (1) Molten steel is instantaneously filled into the ingot mold. The teemed time of the ingot bottom is remarkably shorter than the solidification time.

• (2) The molten steel is treated as an incompressible Newtonian fluid and the k-ε turbulence model is applied to treat the turbulence effects.

• (3) The non-metallic inclusions are simplified as spherical particles; the density of inclusions is set as 4000 kg/m³; and the density and diameter remain unchanged during the motion.

• (4) The collision and coalescence of small inclusion is ignored. The effects of inclusion motion on molten steel flow and heat transfer are ignored.

• (5) The heat effects of solid-phase transformation reactions are not considered, only the latent heat release is considered.

• (6) Darcy’s law is selected to treat the molten steel flow in the solid–liquid two-phase zone.

2.2 General Governing Equations

The natural convection and thermal convection are determined. The fluid flow rate is small during the molten steel solidification process. The equations are listed as follows [18,19,20]:

• (1) Continuity equation:

  $$\frac{\partial \rho }{{\partial t}} + \frac{{\partial \left( {\rho u_{i} } \right)}}{{\partial x_{i} }} = 0$$

  (1)

where ρ is the molten steel density, kg·m⁻³; t is the time, s; u_i is the x_i direction velocity component, m·s⁻¹.

• (B) Momentum equation (Navier–Stokes equation):

  $$\frac{{\partial \left( {\rho u_{i} } \right)}}{\partial t} + \frac{{\partial \left( {\rho u_{i} u_{j} } \right)}}{{\partial x_{j} }} = - \frac{\partial p}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left( {\mu_{eff} \frac{{\partial u_{i} }}{{\partial x_{j} }}} \right) + \frac{\partial }{{\partial x_{j} }}\left( {\mu_{eff} \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) + \rho g_{i} + \rho g_{i} \beta_{T} (T - T_{r} ) + S$$

  (2)

  where p is pressure, Pa; $\mu_{{{\text{eff}}}}$ is effective viscosity, Pa·s; $\beta_{T}$ is the thermal expansion coefficient; T is temperature, K; T_r is reference temperature, K.

The enthalpy-porosity technique is adapted to treats the solid–liquid phase zone (mushy zone) as a porous medium. In each cell, the porosity is equal to the liquid fraction. The porosity is equal to zero, where the molten steel is fully solidified. Due to the reduced porosity in the mushy zone, the momentum sinks take the following form:

$$S = \frac{{\left( {1 - \beta } \right)^{2} }}{{\left( {\beta^{3} + e} \right)}}A_{{{\text{mush}}}} \left( {v - v_{p} } \right)$$

(3)

where β is the steel liquid fraction, e is a small number (0.001) to prevent division by zero; A_mush is the constant for mushy zone, and $v_{p}$ is the pull velocity. In the present study, the magnitude of $v_{p}$ is zero.

The effective viscosity $\mu_{{{\text{eff}}}}$ can be described as follows:

$$\mu_{{{\text{eff}}}} = \mu_{0} + \mu_{t}$$

(4)

where $\mu_{0}$ is laminar viscosity, Pa·s; and $\mu_{t}$ is turbulent viscosity, Pa·s; The standard k-epsilon turbulence model is adopted to solve the turbulent viscosity.

• (C) Turbulent kinetic energy k equation:

  $$\frac{{\partial \left( {\rho k} \right)}}{\partial t} + \rho u_{i} \frac{\partial k}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{j} }}\left( {(\mu + \frac{{\mu_{t} }}{{\sigma_{k} }})\frac{\partial k}{{\partial x_{j} }}} \right) + G - \rho \varepsilon + S_{k}$$

  (5)

Turbulent energy dissipation rate ε equation:

$$\frac{{\partial \left( {\rho \varepsilon } \right)}}{\partial t} + \rho u_{i} \frac{\partial \varepsilon }{{\partial x_{i} }} = \frac{\partial }{{\partial x_{j} }}\left( {(\mu + \frac{{\mu_{t} }}{{\sigma_{\varepsilon } }})\frac{\partial \varepsilon }{{\partial x_{j} }}} \right) + \frac{{C_{1} \varepsilon G - C_{2} \rho \varepsilon^{2} }}{k} + S_{\varepsilon }$$

(6)

With the k-ε equations, the turbulent kinetic energy production rate is given by

$$G = \mu_{t} \frac{{\partial u_{i} }}{{\partial x_{j} }}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)$$

(7)

The turbulent viscosity is given by $\mu_{t} = \rho C_{\mu } \frac{{k^{2} }}{\varepsilon }$ [21, 22]. Here, $S_{\varepsilon }$ and $S_{k}$ are expressed in the same way to the turbulent kinetic energy k-ε equation:

$$S_{\varepsilon } \left( {S_{k} } \right) = \frac{{\left( {1 - \beta } \right)^{2} }}{{\left( {\beta^{3} + \varepsilon^{\prime } } \right)}}A_{{{\text{mush}}}} \phi$$

(8)

where ϕ represents the turbulence quantity solved (k or ε); k is the fluid turbulent kinetic energy, m²·s⁻²; and ε is the turbulent kinetic energy dissipation rate, m²·s⁻³. The constants of Launder and Spalding are recommended [23], and are currently widely used in the Fluent that are listed in Table 1.

Table 1 Numerical Values used in the k-ε Model

• (D) Energy conservation equation:

  $$\frac{{\partial \left( {\rho H} \right)}}{\partial t} + \frac{{\partial \left( {\rho u_{i} H} \right)}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{i} }}\left( {(\lambda + \frac{{c_{p} \mu_{t} }}{{\Pr_{t} }})\frac{\partial T}{{\partial x_{i} }}} \right)$$

  (9)

In this model, the enthalpy method is used to accurately model the solidification process of the large steel ingot, where H is enthalpy, J·kg⁻¹; $\lambda$ is the thermal conductivity, W·m⁻¹·K⁻¹; c_p is specific heat at constant pressure, which is set as 680 J·kg⁻¹·K⁻¹; $\Pr_{t}$ is turbulent Prandtl number which is 0.85 by default; T is the temperature, K. The enthalpy of the material consists of the sensible enthalpy, h, and the latent heat, $\Delta H$:

$$H = h + \Delta H$$

(10)

$$h = h_{{{\text{ref}}}} + \int_{{T_{{{\text{ref}}}} }}^{T} {c_{p} {\text{dT}}}$$

(11)

where $h_{{{\text{ref}}}}$ is the reference enthalpy, which is set as 25,000 J·kg⁻¹;$T_{{{\text{ref}}}}$ is the reference temperature, which is set as 298 K; and the volume fraction $\beta$ of molten steel is assumed to be linearly proportional to the temperature as follows:

$$\beta = \left\{ \begin{gathered} 0,\quad \quad T < T_{{{\text{sol}}}} \hfill \\ \frac{{T - T_{{{\text{sol}}}} }}{{T_{{{\text{liq}}}} - T_{{{\text{sol}}}} }},\quad \quad T_{{{\text{liq}}}} > T > \hfill \\ 1,\quad \quad T > T_{{{\text{liq}}}} \hfill \\ \end{gathered} \right.T_{{{\text{sol}}}}$$

(12)

where T_liq and T_sol are the liquidus temperature and solidus temperature, which are 1478 K and 1786 K, respectively. The latent heat, L, can be written as follows:

$$\Delta H = \beta L$$

(13)

2.3 Inclusion Transport Equation

Particles are modeled using the Lagrangian approach, which treats them as discrete phases [24]. The Lagrangian particle tracking method is applied to calculate the inclusion trajectories, which solves a force-balance equation for each inclusion in the molten steel [25].

$$\frac{{du_{p} }}{dt} = F_{D} (u - u_{p} ) + \frac{{g_{x} (\rho_{p} - \rho )}}{{\rho_{p} }} + F_{p} + F_{vm} + F_{l}$$

(14)

where u_p is the velocity of inclusion particle, m/s; μ is the dynamic viscosity of molten steel, Pa⋅s;$\rho_{p}$ is the density of inclusion particles, kg/m³;$F_{D} (u - u_{p} )$ is the drag force per unit mass of particles; the second term is the gravitational force; F_p is pressure gradient force; F_vm is virtual mass force; F_l is lift force.

$$F_{D} = \frac{18\mu }{{\rho_{p} d_{p}^{2} }} \cdot \frac{{C_{D} {\text{Re}} }}{24}$$

(15)

where d_p is the diameter of inclusion particle, m; C_D is the drag coefficient, which is solved as follows:

$$C_{D} = \left\{ \begin{gathered} \frac{24}{{{\text{Re}}_{p} }}(1 + 0.15{\text{Re}}^{0.678} ) \, {\text{Re}}_{p} \le 1000 \hfill \\ 0.44 \, {\text{Re}}_{p} > 1000 \hfill \\ \end{gathered} \right.$$

(16)

$${\text{Re}}_{p} = \frac{{\rho d_{p} \left| {u_{p} - u} \right|}}{\mu }$$

(17)

$$F_{p} = \frac{{\rho \pi d_{p}^{3} }}{6}\frac{du}{{dt}}$$

(18)

$$F_{{{\text{vm}}}} = \frac{{\rho \pi d_{p}^{3} }}{12}C_{{{\text{vm}}}} \frac{d}{dt}\left( {u - u_{p} } \right)$$

(19)

$$F_{l} = 1.62d_{p}^{2} (\rho \mu_{eff} )^{1/2} \left| {\nabla \times u} \right|^{ - 1/2} ((u - u_{p} ) \times (\nabla \times u))$$

(20)

where C_vm is the coefficient of virtual mass force, which is set as 0.5 by default.

To consider the turbulent stochastic effect on the particle motion, a random walk model is adapted. The inclusion transient velocity, $u_{p}$, consist of the calculated time-averaged velocity, $\overline{u}_{p}$ and a fluctuating velocity $u^{\prime}_{p}$. Each fluctuation component of the inclusion velocity can be calculated as follows[26]:

$$u^{\prime}_{p} = \varsigma_{i} \sqrt {\overline{{u_{i}^{\prime 2} }} } = \varsigma_{i} \sqrt{\frac{2k}{3}}$$

(21)

where $\varsigma_{i}$ is a random number, k is the local level of turbulent kinetic energy, m²/s².

In the present study, the total amount of oxygen is 10 ppm in the molten steel. The weight of the ingot is 28.7 tons. It is assumed that all the inclusions have a density of 3500 kg/m³, and the total weight of inclusions is obtained. Then, combined with the experimental results of microscopic inclusion index statistics and slime extraction, a different size range of microscopic inclusions and the distribution of large inclusions (> 50 μm) in large steel ingot can be obtained, as shown in Table 2. In this model, the size of inclusions is based on the Rosin–Rammler distribution function, which is distributed to reflect and is equivalent to 2200 particles.

Table 2 Amount ration and mass fraction of different size range inclusions

In this model, the inclusion distribution is based on the Rosin–Rammler distribution function. The exponential relationship is expressed between d and Y_d:

$$Y_{d} e^{{( - d/\overline{d})^{n} }}$$

(22)

where d is the inclusion particle diameter, μm; $\overline{d}$ is the inclusion particle average diameter, μm; and Y_d is the mass fraction of inclusions whose diameter is greater than d.

$$\frac{dx}{{dt}} = u_{p}$$

(23)

The trajectory of each particle is calculated by integrating its local velocity according to formula (23).

2.4 Boundary Condition

Supposing the mold bottom teeming is immediate because the filling time is much shorter than the solidification time, the initial temperature of the large steel ingot is pouring temperature Tg = 1816 K.

For the molten steel flow, a fixed velocity is imposed at the ingot bottom domain inlet, and a pressure outlet is used at the ingot top outlets. Inclusions are injected from the ingot bottom. The inclusion particles are assumed to be trapped when they move to the mold flux-free surface. Additionally, the inclusions captured in the wall adopt the following treatment. According to the literature [27], when the solidification fraction of molten steel is 0.7, the viscosity of molten steel increases suddenly. At this time, inclusions can be easily trapped in the solidification front. This paper solves the trapped inclusions at the solidification front by compiling user defined functions (UDF). Due to the symmetry of the ingot, one-quarter of the large steel ingot is taken as a computational domain. At the free surface and the symmetry planes, the normal gradients of all variables are set to be zero, $\frac{\partial \phi }{{\partial x}} = 0$, and the velocity perpendicular to the surface is set to be zero. A no-slip boundary is adopted so that the wall velocity, pressure, k, and ε are parallel to the wall. The wall adjacent nodes, the velocity component k, and ε parallel to the wall are determined by the wall function.

2.5 Mathematical Model and Numerical Solution Method

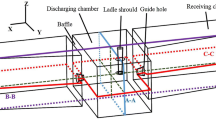
Fluent CFD software has been used for computation. The schematic of the mesh structure and coordinate system are shown in Fig. 1. Due to the symmetry of the computational domain, only one-quarter of the large steel ingot is considered. The mold of ingot casting is complicated in structure, as a result, the hot-top and top of the ingot body are simplified to regular shape to reduce the computing time and improve calculation accuracy. Figure 1 presents the integration schematic diagram after the whole meshing region.

Fig. 1

Geometry (a) and Mesh structure (b)

Commercial Software ANSYS-FLUENT12.0 was used to solve flow equations and accuracy by controlling the number of iterations, ultimately achieving convergence. The computations were conducted under the SIMPLE algorithm. The first-order upwind scheme was adopted to discrete the momentum equations, turbulent kinetic energy equation and the turbulent dissipation rate equation. The convergence criteria of the residuals for each variable are less than 10^–6. The trajectories of inclusion particles are calculated by solving particle motion equations.

3 Experimental Methodology

In order to investigate the inclusion distribution in the ingot and validate the mathematical model, the work has detected inclusions quantitatively in the ingot. After sectioning 1/2 of the surface width of the 28.7-t ingot, samples were taken from the hot-top, top body, central, and bottom areas of the ingot. These samples were then cut into 15 mm × 15 mm × 15 mm test samples, polished and observed by scanning electron microscopy, and 200 fields were counted on each sample 1000 times. The measurements of inclusion distribution in the ingot were used to verify the validation of the mathematical model in the current work.

The inclusion number is measured by the optical microscope and evaluated by the inclusion index statistics. The size that is equivalent to 7.5 μm on the sample size per mm² (106μm²) can be expressed as follows:

$${\text{I}} = \frac{{\sum {n_{i} d_{i} } }}{N \cdot a \cdot b \cdot B} \cdot 10^{6}$$

(20)

where $n_{i}$ is used to observe the number of inclusions of each field under the optical microscope;$d_{i}$ represents the same level of inclusions at an average diameter (0–2.5 μm, 2.5–5 μm, 5–10 μm, 10–20 μm, and > 20 μm); N is the observation field of view (200 fields under the magnification of 1000); and a and b are the actual length and width of observation field respectively,.

A total of 60 specimens were taken from the large steel ingot at the hot-top, top body, central body, and bottom regions.

4 Results and Discussion

4.1 Simulated Flow Field Results

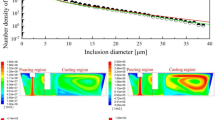
The ingot solidification is a non-steady-state heat transfer process that is accompanied by the liquid metal forced convection, natural convection, the release of latent heat, and convection between molten steel and solidified shell, the solidified shell and the ingot mold, the ingot mold, and the environment, making the solidification of large ingots a very complex physical process [28]. The current study applies Fluent commercial software's solidification/melting module to the simulation. The temperature field coupled with the flow field of a large steel ingot is calculated. The simulated flow field results on the symmetry plane (mid-thickness plane) during the solidification process of the large steel ingot are shown in Fig. 2.

Fig. 2

Velocity vector at different times (0–500 s): a 25 s; b 50 s; c 100 s; d 500 s

From Fig. 2, the flow velocity results of a large steel ingot's temperature distribution and solidification coupled with flow field are simulated at different times. A flow field is formed when the solidification starts. The molten steel viscosity of large steel ingots increases with the decrease in temperature. The buoyancy-driven convection of molten steel occurs because of gravity. Moreover, the feeding flows in the vertical direction appear near the solid–liquid interface resulting from solidification shrinkage. As the solidification continues, the local recirculation flow at the top and bottom of the liquid pool and whole recirculation flow in the liquid pool appear resulting from the buoyancy-driven convection and feeding flow. These can be seen in Figs. 2a–d. The velocity of the molten steel is decreased due to the continuous increase in the molten steel viscosity with the decreasing in temperature.

It can be seen from flow field maps of Figs. 3c and d that flow velocities at the top and bottom regions are higher (quicker) because the natural convection with different density liquid steel occurs in the wide-area ingot. It is also found that the flow velocities of the flow fields in the center zones are quicker than in the other zones. At the final stage of solidification, the circulation of the flow field cannot be formed because a continuous increase of melt viscosity blocks the result of liquid flows.

Fig. 3

Velocity vector at different times (1000–2500 s): a 1000 s; b 1500 s; c 2000s; d 2500 s

The flow field can affect temperature field distribution. The molten steel within the large steel ingot gradually solidifies from the ingot mold to the center of the ingot. When the solidification of a large steel ingot starts at 500 s, a solidified shell is formed due to the temperature gradient between the molten steel near the large steel ingot mold and the environment, where a certain amount of heat is then released, and the density and viscosity of the molten steel increase. The temperature of the molten steel in a large steel ingot becomes uneven during the solidification process. The density of high-temperature molten steel is lower than that of low-temperature molten steel, resulting in thermal convection because of uneven temperatures. Most of the molten steel near the ingot mold sinks along the wall due to gravity. The central part of the molten steel lifts upward along the axis due to the role of a thermal. Therefore, it forms a molten steel circulation, as shown in Fig. 3d.

4.2 Simulated Results of Inclusion Distribution in Large Steel Ingot

Inclusion motion and particle entrapment in an ingot are affected by the steel's fluid flow, heat transfer, and solidification. The inclusion distribution of large steel ingots significantly impacts the final product properties during the rolling process. The solidifying shell may trap particles reaching the mushy zone. It is difficult to directly examine the non-metallic inclusions during the steel ingot solidification process [29]. In the present study, a simulation of the motion for non-metallic inclusions is investigated in detail during the solidification process of a large steel ingot. The distribution of inclusions during the large steel ingot solidification process is visually displayed in Fig. 4 with the help of UDF and post-processing TECPLOT software.

Fig. 4

Distribution of inclusions at different solidification times (0–500 s): a 50 s b 100 s c 300 s d 500 s

The distribution of inclusions before 500 s during the ingot solidification process at different times is shown in Fig. 4. At the beginning of the solidification process, the solidified shell forms as the bottom molten steel comes in contact with the ingot mold bottom, which will capture a large number of inclusions in the solidified shell. By conducting the calculations, 646 inclusions were trapped within the solidification front at 50 s, accounting for 30% of the total. The solidification rate of the large steel ingot decreases after an initial intensity cooling of 50 s, and the speed of inclusion capture within a large steel ingot also declines. Additionally, 143, 285, and 237 inclusions are trapped at the solidification front at 50–100 s, 100–300 s, and 300–500 s, respectively. Overall, in the solidification process of molten steel at the initial 500 s, capturing inclusions in large steel ingots requires a fast speed. A total of 1311 inclusions are trapped, accounting for 60% of the injected inclusions. The inclusion distribution in large steel ingots at the different locations has also been analyzed. It is determined that the number of inclusions trapped by the ingot bottom solidified shell is large. In contrast, a small number of trapped inclusions are at the top body of the large steel ingot.

Figure 5 shows the distribution of inclusions during the ingot solidification process between 1000 and 3000 s. With the solidification development (1000–3000 s), the solidification front captured fewer inclusions due to the floating of inclusions. Furthermore, 441 inclusions are trapped in the molten steel at 500–1000 s, whereas 72 and 93 inclusions are trapped at 1000–1500 s and 2000–3000 s, respectively. With the continuous development of the solidification shell, it is determined that an inclusion gathering area is found at the mold hot-top location due to the cooling intensity at the corner position, so the inclusions become more easily trapped at this location.

Fig. 5

Distribution of inclusions at different solidification times (1000–3000 s) a 1000 s b 1500 s c 2000s d 3000 s

Figure 6 shows the distribution of inclusions during the ingot solidification process between 3000 and 6000 s. The solidification front has been pushed close to the center of molten steel at this stage. Inclusions move for a long time in molten steel. Most inclusions float to the top of the liquid steel and are absorbed by mold flux or trapped by the solidification front. However, very few inclusions still stay within the molten steel. By numerical simulation analysis, only 45 inclusions remain in the molten steel at 3000 s, accounting for 5% of the total number of the injected inclusions. Finally, only five inclusion particles remain in the molten steel at 6000 s.

Fig. 6

Distribution of inclusions at different solidification times (3000–6000 s): a 3500 s b 4000 s c 5000 s d 6000 s

As can be observed from Fig. 6, there are more inclusions at the bottom and top hot locations than at the top and center locations of the ingot. Here, 623 particles are trapped at the bottom of the ingot and accounted for 28.3% of the number of injected particles, 361 particles are in the middle of the large steel ingot and accounted for 16.4% of the number of injected particles, 414 particles are trapped at the mold top and accounted for about 18.8% of the number of injected particles, and 583 particles are at the mold hot-top and accounted for 26.5% of the number of injected particles. The remaining particles are absorbed by mold flux and accounted for about 10% of the number of injected particles.

4.3 Simulation Results of the Inclusion Trajectory with Different Sizes

The inclusion trajectories of varying sizes (5 μm, 10 μm, 20 μm, 50 μm, 100 μm, and 150 μm) are presented in Fig. 7. This work considers these sizes for mathematical model simulation to examine the influence of size on the track of inclusion. The original injection position was on the bottom surface. The injected particles are set with different diameters. Then, 2200 particles were injected into the domain through the inlet, and their trajectories were calculated with a discrete random walk model. The trajectory map for different sizes of inclusions in the molten steel is shown in Fig. 7. Inclusions with a diameter of 100 μm and 150 μm move for a short period of time in the molten steel under the action of the buoyancy of the flow, floating to the top of the molten steel to then be absorbed by the mold flux.

Fig. 7

Trajectories of inclusions with different sizes: a 5 μm b 10 μm c 20 μm d 50 μm e 100 μm f 150 μm

Many small inclusion particles are affected by the circulation within the molten steel, the inclusion motion time is long in molten steel, and the probability of being trapped by the solidification front is also large. Therefore, to improve the effects of removing inclusions in the metallurgical engineering process, appropriate measures should be taken to promote non-metallic inclusions and encourage polymerization.

4.4 Measured Inclusion Distributing Results and Model Validation

Figure 8 shows the morphology and composition of inclusions detected in the central body of the ingot. It can be found that the composition of inclusions in the ingot is mainly Al₂O₃. Moreover, as is shown in Fig. 9, inclusions detected in the hot top, top body and bottom body of the ingot are similar to those detected in the central body of the ingot. Additionally, the size of inclusions detected in the ingot are almost ~ 5 μm or less than ~ 5 μm. Hence, in the current work, the inclusions during the computations are treated as alumina. And the size distribution in the calculation is matched with measured results.

Fig. 8

Morphology and composition of inclusions detected in the central body of the ingot

Fig. 9

Morphology of inclusions detected in the hot top, top body and bottom body of the ingot

Figure 10 shows the predicted and measured local distributions of the entrapped inclusions at different positions of the ingot. The average index statistics of inclusions obtained at different parts of the large steel ingot are 4.58, 3.35, 3.29, and 4.48 mm2, respectively. The aim of this paper is to evaluate the inclusion distribution trend in the ingot. For the numerical simulations, the entrapped inclusions at different positions of the ingot were equivalent to inclusions with 7.5 μm diameter. Then the number of the equivalent inclusions at four positions (hot top, top body, central body and bottom body) were obtained. Subsequently, the ratios of the entrapped inclusions for the four positions were calculated, which were in essence the same as the inclusion index calculated based on the experiments.

Fig. 10

Predicted and measured local distributions of the entrapped inclusions at different positions of the ingot

The numerical simulation results agree with the experimental results, indicating that an established three-dimensional solidification numerical model can be appropriately used to calculate the behavior of inclusion particles during the solidification process. An optimal portion of the top part of the ingot must be cut off, including the rough surface caused by the hot-top location, to ensure that the final product presents good quality. Sometimes, a portion of the bottom is cut off to remove the most inclusion-rich regions from the finished product at the expense of a lower yield.

5 Conclusions

This work investigates the inclusion motion phenomena during the solidification process of large steel ingot casting. Specifically, it examines flow field, inclusion distribution, and inclusion trajectories of different sizes based on a three-dimensional numerical simulation. The results support the following conclusions:

• (1) A flow field is formed when cooling starts. With the development of solidification, the molten steel within the large steel ingot gradually solidifies from the ingot mold to the center of the large steel ingot. The temperature of the molten steel in a large steel ingot becomes uneven during the solidification process. The density increases with the decreasing temperature, and circulation eventually forms within the molten steel.

• (2) At the initial solidification process of molten steel (500 s), the solidified shell is quickly formed, the solidification front also moves quickly to the center of molten steel, and more inclusions are trapped. Then, the rate of the solidification front slows down with time to capture inclusions. At the final stage of solidification, there are more inclusions at the bottom and hot-top locations than at the top and center regions of the ingot, accounting for 28.3%, 26.5%, 16.4%, and 18.8% of the number of injected particles, respectively. The remaining inclusions are absorbed by mold flux, accounting for about 10% of the injected particles.

• (3) Each location's average inclusions index statistics are 4.58, 3.35, 3.29, and 4.48 mm², respectively. Thus, the most important trend in entrapment location is a decrease in inclusions with height up to the ingot. Moreover, the inclusions are again entrapped due to the cooling intensity at the hot-top region. The simulation results of the distribution of inclusions are in good agreement with the experimental observation.

• (4) The trajectory of inclusions of different sizes is different in molten steel. More inclusions with large sizes (100 μm, 150 μm) could be absorbed by the mold flux due to larger buoyancy. In contrast, the floating process of small inclusion particles (5–50 μm) up to the mold flux is longer. Hence, fewer inclusions could be absorbed by the mold flux. The internal flow field of molten steel has a more significant impact on the inclusion’s trajectory.