Equilibrium Versus Paraequilibrium Precipitation of Cementite in Ternary Alloys: Thermodynamic and Kinetic Interpretations

Abstract

The precipitation of cementite on decomposition of austenite is examined by an edgewise layer growth model of the carbide in Fe–1.2C wt% steels. The interface boundary can migrate into the supersaturated matrix isothermally at 400–600 °C, similar to tempering. The present paper thus explores precipitation mechanisms by two different kinetics. Intitially, an equilibrium growth, by the diffusional transport of atoms is simulated with the Dictra package accessing thermodynamic parameters from Thermo-calc. An extremely slow rate for the growth of the carbide platelet seems to be implausible due to the presence of the ternary [M = Mn, Si, Al] of 2 wt%. To overcome this, the investigation then finds an alternative, bringing diffusion constraints of the substitutional atoms under consideration in a paraequilibrium growth study. The SGTE database of the Thermo-calc however lacks paraequilibrium composition of Al in the carbide, thus Thermo-calc cannot be used thoroughly for this study. A first-principles calculation therefore is necessary which  in turn evaluates  the time-lag in equilibrium versus paraequilibrium growth kinetics. It reveals that the paraequilibrium precipitation of cementite is decisive due to Si (or Al) as the ternary, whereas, in the case of manganese steel, an opposite trend can be seen that the equilibrium partition of Mn reduces the Gibbs free energy during the interface study.

1 Introduction

Diffusional transformations of alloys in general involve partitioning of interstitial and substitutional components, as they contribute to the net flux, leading to the dissolution [1], growth [2] or precipitation [3] of a new phase. Experimental investigations in earlier work have demonstrated the fact in steel systems that a reaction rate proceeding at higher temperatures may be influenced by the substitutional alloying element, M [4, 5]. The reason being, diffusivity of M is slower than the interstitial element carbon, thus contributing less in the flux exchange. The thermodynamic condition of equilibrium (local) to prevail at the interface in a γ → α transition is governed by μ ^γ_i  = μ ^α_i , where μ_i is the chemical potential of i, irrespective of the interstitial or substitutional component [6]. If the temperature is reduced further, the volume diffusion of M becomes difficult [7]. Kinetically it may arrive in a situation, such that the precipitation of α from γ near the bainitic transformation temperature provides a uniform chemical potential for the interstitial element carbon, and a uniform site-fraction for the substitutional element M under diffusion constraints across the phase interface [8]. This signifies that the precipitation at lower transformation temperatures may be empowered by the interstitial element carbon, with no partitioning of M at all. Hultgren [9] has called the restricted equilibrium as paraequilibrium; being the central theme of the present study for a comparative analysis vis-à-vis the equilibrium growth of cementite. A key interest may be the time-lag between equilibrium and paraequilibrium growth kinetics which has been reported earlier to be a complex interplay between temperature and alloy chemistry [6].

The concept of paraequilibrium has been introduced by Hillert in connection with the bainitic transformation in steels [7]. He has argued that at intermediate temperatures, when carbon diffuses at an appreciable rate but other alloying elements remain almost immobile relative to iron, the growing phase inherits the alloy content from the parent phase, i.e. a product phase may form with the same alloy content as that in the parent phase. The logic behind this—the interface velocity is greater than the diffusional velocity—allowing substitutional elements to be trapped in [3]. Various authors have demonstrated the phenomenon experimentally in plain carbon and alloy steels [10,11,12,13]. The distribution of the substitutional elements in parent versus product phase is such that the ratio of the substituional element M in both the phases may reach somewhat close to unity [13]. This raises an ambiguity whether the mechanism follows paraequilibrium kinetics as an alternative. The present work intends to scrutinize it with an interface study, such that the distribution of the alloying element in matrix to the carbide may be a key in determining the phase stability through the thermodynamic analysis of the free energy.

It thus seems obvious that whether the phase transformation proceeds under a partition local equilibrium (PLE) or paraequilibrium (PE) at a given temperature is really a question on the magnitude of the alloy diffusivity inside the phase interface. To the knowledge of the present author, the experimental determination is difficult; unless Agren’s [14] treatment for a binary system includes a third mobile component to see if the model is capable of predicting the transition to paraequilibrium growth. Huchinson et al. [15] has initially performed the calculation in Fe–C–Ni for a γ → α transformation; and after an assessment, the model system has been incorporated in the Dictra package [16] in association with Thermo-calc [17]. Ghosh and Olson [6] then have implemented the same model in multicomponent systems for a γ → Fe₃C formation; stating that similar calculation in a ternary alloy, typically with silicon may be difficult, as Thermo-calc lacks the paraequilibrium composition of the latter element in the carbide. Thermodynamic calculations by Kozeschnik and Bhadeshia [18] have also encountered the same problem with silicon; then a compromise has been made, approximating the role of silicon through the thermodynamic contributions of the free energy difference between Fe–1.2C–1.5Mn and Fe–1.2C–1.5Mn–1.5Si alloys (wt%). Ever since, the kinetic investigation in ternary alloys for cementite formation is lacking. Presently, the SGTE database of Thermo-calc has incorporated silicon in it; and for aluminum, still a first-principle calculation in paraequilibrium conditions is necessary. The intention is to establish the role of a ternary element [M = Mn, Al, Si], altering the γ → (Fe,M)₃C formation on the relative basis near bainitic transformation temperature, i.e. at 400–600 °C for an alloy-design. The 2 wt% M in Fe–1.2C may be set as a model system, for which thermodynamic and kinetic interpretations will be provided herewith in turning the hypereutectoid composition into a high-strength and large-ductility bainitic steel [18, 19].

2 Thermodynamic Calculations

The equilibrium calculations were performed with Thermo-calc. Table 1 summarizes the data in wt%, specifying that Si (or Al) remains in austenite (γ), due to a negligible solubility of the latter element in cementite (θ) [12]. The Mn however dissolves in both the phases and preferentially in θ; this is to make the carbide phase thermodynamically more stable with the availability of a larger driving force [20]. The phase fraction of θ in Fe–1.2C may not change significantly with the addition of a ternary element (M). Nevertheless, a key interest is the temperature dependence, indicating that the phase fraction of θ at 600 °C is lower than that at 400 °C. A similar trend may also be seen during a paraequilibrium calculation in Table 2.

Table 1 Equilibrium compositions (wt%) and phase fractions using Thermo-calc calculations

Table 2 Paraequilibrium compositions (wt%) and phase fractions by first-principle’s calculation

The paraequilibrium calculation cannot use Thermo-calc fully for a phase diagram analysis, as the SGTE database lacks aluminum in (Fe,Al)₃C. This compels Jang et al. [21] to calculate phase constituents by using MTDATA [22] as an alternative, in association with first-principles calculations based on the density functional theory [23]. The free energy of cementite is modified as the substitutional solid solution (Fe,Si)₃C, (Fe,Al)₃C or (Fe,Mn)₃C using the same effect of the temperature dependency with Fe₃C. The summary of the result is given in Table 2. Notably, a key difference with the equilibrium calculation (Table 1) is marked by Si or Al-addition in the carbide [12]. The paraequilibrium calculation also states that the precipitation of cementite (PE-θ) is difficult with silicon as the ternary [2]; thus the phase fraction of PE-θ is reduced when Mn (or Al) is substituted by Si at 400 °C, and the carbide phase does not form at all at 600 °C.

3 Growth Model

The precipitation of cementite at 400 − 600 °C initially intends to devise a growth model by the equilibrium transformation in austenite matrix. It allows both interstitial and substitutional elements to take part in the precipitation reaction. The well known Dictra package is incorporated for this purpose, accessing thermodynamic parameters from Thermo-calc. The kinetic data are obtained from the multicomponent diffusion databank, MOB2. As a result, Dictra contains two databanks to model a diffusion controlled transformation in steels. It requires solving diffusion equations and mass balance equations with the Fick’s law of diffusion. The initial condition includes chemical compositions (Table 1) and the cell size following the thermodynamic condition of local equilibrium at the phase interface. A basic assumption is that the cementite precipitate remains initially as an inactive phase, and slowly becomes active once the driving force for a precipitation is assigned to the system. A uniform cell size of 0.8 μm is maintained throughout the calculations irrespective of the alloy compositions, such that sizes of the cementite platelet can be compared on the relative scale, prior to cessation of the precipitation reaction in a closed system. In contrast, the paraequilibrium calculation may not contain any such a restriction in the boundary condition; the platelet can grow without soft impingement as an effect in the mathematical derivations [24]. The phenomenology to obtain the same will be discussed later in Sect. 4.

4 Equilibrium Growth

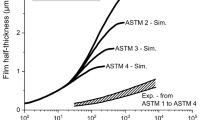
Figure 1 illustrates equilibrium growth of θ in an Fe–1.2C wt% steel; and is superimposed with it, the effect of the ternary element M reducing the platelet-thickness of θ. The experimental work by Miyamoto et al. [2] may find an analogy, stating that Si reduces θ better than Mn, also in the quenched and tempered Fe–0.6C wt% steels. Reportedly at 450 °C, effective contributions of both the elements may remain the same at an early stage of the tempering; it is until 30 s that a larger difference in the rate kinetics can be seen, in an agreement with Fig. 1a. The present work further indicate that the elemental Al may be as effective as Si in delaying the equilibrium growth of θ (Fig. 1a, b); and thus as a possible reason, the latter element has been included in the present calculation. Clearly, Al retards the precipitation of cementite to such an extent that obtaining an equilibrium fraction of θ at 400 °C may be difficult in Fig. 1a. A possible reason is the lack of a driving force [20], causing cessation of the nucleation and growth, until the holding temperature is raised. The interruption of the growth process is still visible at 600 °C by a step-wise manner in Fig. 1b, as Al decreases both the activity and diffusivity of carbon in austenite [25]. The results now will examine a proposal by Leslie and Rauch [20] that the addition of 2 wt% of Al is significant: it may either raise the cementite initiation temperature, or increase the time required for the cementite formation at a given temperature, using concentration-distance profiles (Figs. 2, 3) for a justification with reference to other alloys.

Fig. 1

The role of the substitutional element M [Mn, Si, Al] inhibiting the equilibrium growth of cementite (θ) in Fe–1.2C wt% steels at a 400 and b 600 °C, respectively

Fig. 2

Concentration-distance profiles at 400 °C showing distributions of the substitutional elements: a–d Mn, e–h Si, and i–l Al across the phase interface between θ and γ with time, t

Fig. 3

Concentration-distance profiles at 600 °C showing distributions of the substitutional elements: a–d Mn, e–h Si and i–l Al across the phase interface between θ and γ with time, t

Figure 2a–d indicate that cementite may develop at 400 °C without the redistribution of Mn up to 10⁹ s; because the volume diffusion of Mn is weak, enabling the cementite platelet to grow in size by a non-partition local equilibrium (NPLE). The rate kinetics increases at a higher temperature; thus partitioning stages at 600 °C can be seen clearly in Fig. 3b–d only after 10⁵ s. This agrees with Miyamoto et al. in Fe–0.6C wt% steels that cementite develops initially without the redistribution of Mn, before it gradually enriches into the carbide after a prolonged duration of tempering at 450–650 °C. The role of Si to affect the precipitation kinetics also becomes clearer, using the concentration-distance profiles both at 400 and 600 °C in Figs. 2e–h and 3e–h, respectively. It shows that unlike Mn, Si has a negligible solubility in cementite (Table 1); so it is first rejected by the carbide, due to a negligible partitioning of the later element in cementite. As a result, when the interface penetrates further towards the matrix, the Si concentration in austenite increases from its equilibrium level of 2.41 wt% at 400 °C. The redistribution of Si in austenite in the subsequent stages consumes more than 10¹⁰ s.

A systematic study with Al to delay the equilibrium growth of cementite is lacking. A possible reason is that, the transformation at lower temperatures may deny an extensive diffusion of Al; thus (Fe,Al)₃C will be less stable than Fe₃C owing to a lesser driving force associated with its formation [20]. The concentration-distance profiles thus are available in short durations. It shows that Al has a negligible solubility in cementite; so it gets rejected by the carbide after a negligible partitioning at the interface, both at 400 and 600 °C in Figs. 2i–l and 3i–l, respectively. As the interface penetrates further towards the matrix, the concentration of Al in austenite exceeds the equilibrium limit. The redistribution of Al in austenite in the later stage suffers a considerable delay hindering the growth kinetics. Langer [26] has reported that cementite platelet is difficult to observe in Fe–0.02C wt% steels even after a prolonged duration of ageing at 150 °C. Leslie and Rauch [20] have suggested that the addition of 2 wt% Al in it may further delay the rate kinetics. The cementite platelet thus remains undetected after 11 days (~ 10⁶ s) of ageing at 250 °C and at 375 °C it takes about 3 days (2.6 × 10⁵ s) for the platelet to be seen. A detailed growth kinetics leading to an equilibrium fraction of the carbide in Fe–C–Al has not been reported elsewhere. This makes measured platelet size difficult to fit in the present calculation. A possible reason in Fig. 2 suggests that the time required for completion of the precipitation reaction (in other alloys as well) is greater than 10⁹ s or 32 years. This is unrealistic, unless and until, the systems look for the paraequilibrium kinetics as an alternative.

5 Paraequilibrium Growth

Kinetic factors often prevent transformations from occurring under equilibrium conditions. Various authors [27,28,29] have discussed different kinds of kinetically constrained equilibria that arise naturally. One example of a constrained phase equilibrium is when a phase change is so rapid that one or more of the components may not be able to redistribute among the phases across the interface. In fact, the diffusion coefficients of interstitial and substitutional components differ so greatly that we can often have a situation called ‘paraequilibrium’ in which the interstitial elements can move rapidly and achieve equilibrium [3]. The substitutional elements (M) are constrained in their positions; even the short-range diffusion of the atom is precluded, as if they were kinetically frozen [30]. Thus, paraequilibrium is often regarded as diffusionless transformation with respect to the nearly immobile component M [16].

Ghosh and Olson [8] have simulated precipitation reaction in multicomponent systems. The concept is an extension to the Hultgren’s argument of chemical potentials of substitutional elements under paraequilibrium that if only the mobile element is in thermodynamic equilibrium locally at the phase interface and there is no change in the content of the less mobile elements (substitutional) relative to each other, their individual chemical potentials have no physical meaning and these elements may behave thermodynamically as if they were only a single element [14]. In order to satisfy this, the kinetic investigation thereafter may consider a hypothetical element, for which thermodynamic and mobility parameters are expressed by the weighted average of the thermodynamic parameters and mobility of all the substitutional elements. The implementation of the model has led to a successful calculation of the paraequilibrium growth rate of cementite in Fe–C–Mn–Si and Fe–C–Co–Cr–Mo–Ni alloys [6, 8].

In this respect, an effort to calculate paraequilibrium growth rate of cementite in a ternary alloy is rare. One of the reasons being stated earlier that the SGTE database of Thermo-calc lacks paraequilibrium compositions of Al in cementite. This means the Dictra simulation package for a paraequilibrium precipitation can be utilized only for Mn and Si, and not for Al. In order to draw a comparison, however it is wise adopting a similar procedure (theoretical calculations) for all the alloy compositions which eventually makes us familiar with the formulae behind the paraequilibrium calculation. To start the procedure, the diffusivity of carbon as the only interstitial component in a Fe–C–M is invoked dictating the paraequilibrium growth.

The diffusivity of carbon is sensitive to its concentration gradient in the matrix, and this has to be taken into account in the weighted average diffusivity [3]:

$$\overline{D} = \int_{{X_{\text{C}}^{{{\text{PE}} -\upgamma \uptheta }} }}^{{X_{\text{C}}^{{{\text{PE}} -\upgamma}} }} {\frac{D(x)}{{^{{\left( {X_{\text{C}}^{{{\text{PE}} -\upgamma}} - X_{\text{C}}^{{{\text{PE}} -\upgamma \uptheta }} } \right)}} }}{\text{dx}}}$$

(1)

$$D\left( x \right) = 4.53 \cdot 10^{ - 7} \left( {1 + Y_{\text{c}} \left( {1 - Y_{\text{c}} } \right)\frac{8339.9}{T}} \right)\exp \left[ { - \left( {\frac{1}{T} - 2.221.10^{ - 4} } \right)\left( {17767 - 26436Y_{\text{C}} } \right)} \right]\;{\text{m}}^{ 2} {\text{s}}^{ - 1}$$

(2)

where $X_{\text{C}}^{{{\text{PE}} -\upgamma}}$ is the average carbon concentration in the alloy, $X_{\text{C}}^{{{\text{PE}} -\upgamma \uptheta }}$ the carbon concentration in PE-γ in paraequilibrium with PE-θ at the phase interface. The expression for D(x) as a function of carbon concentration x in mole fraction at a temperature T is given by Ǻgren [31], as:

$$Y_{\text{c}} = x\left( {1 - x} \right)^{ - 1} .$$

(3)

The result of the calculation is given in Table 3. The composition dependence indicates a negligible change in the order of the magnitude, as if diffusion constraints of the substitutional element M make all the ternary alloys virtually a binary one. Bhadeshia [3] had also inferred the same by means of thermodynamic calculations, that the effect of the substitutional element M, influencing the activity of carbon in a solid solution, is very small; when M diffuses under constraints or a kinetically frozen. Meanwhile, the temperature dependence exhibits a larger variation in $\overline{D\,}$ (The weighted average diffusivity of carbon in austenite), with the rise in temperature at 400–600 °C, requiring a further verification of the data with others.

Table 3 The weighted average diffusivity of carbon in austenite, $\overline{D} (x)$, and the thickening rate (α₁) of the paraequilibrium carbide at 400 and 600 °C, respectively for various alloys (wt%)

Ławrynowicz and Dymski [32] have reported that the diffusivity of carbon in austenitic at 400 °C is 3.6 × 10⁻¹⁶ m² s⁻¹; the present calculation finds a good agreement, except a minor difference with silicon making it distinctively different from the other alloys. Thibaux et al. [33] have measured the diffusivity of carbon in austenite at 600 °C to be 4.6 × 10⁻¹⁴ m² s⁻¹ in an Fe–31Ni wt% steel. After the comparison, the present calculation finds a scatter by an order of the magnitude.

The theoretical approach to compute a thickening rate (α₁) of the carbide in one-dimension follows a layer-wise growth. This is in fact true that the formation of cementite at 400–600 °C (near bainitic transformation temperatures) is having a platelet like morphology which satisfies [3]:

$$\left( {\frac{{0.25\uppi}}{{\overline{D} }}} \right)^{0.5} \alpha_{1} \left[ {erfc\left\{ {\left. {\frac{{0.5\alpha_{1} }}{{\left( {\overline{D} } \right)^{0.5} }}} \right\}} \right.} \right]\exp \left( {\frac{{\alpha_{1}^{2} }}{{4\overline{D} }}} \right) = \left( {\frac{{X_{\text{C}}^{{{\text{PE}} -\upgamma}} - X_{\text{C}}^{{{\text{PE}} -\upgamma \uptheta }} }}{{X_{\text{C}}^{{{\text{PE}} -\uptheta \upgamma }} - X_{\text{C}}^{{{\text{PE}} -\upgamma \uptheta }} }}} \right).$$

(4)

The right hand side of the equation is obtained from the first-principles calculation to calculate the α₁ (Table 3) with time t measuring the platelet thickness [3], $Z_{{{\text{PE}} -\uptheta}} =\upalpha_{1} \sqrt t$.

Figure 4 compares paraequilibrium growth rate of the cementite-platelet using both the Dictra simulation package and theoretical calculation in the same alloy. An intention is to find compatibility between both the procedures, such that the theoretical calculation can be an alternative to the Dictra simulation for all the alloy compositions. It turns out that $Z_{{{\text{PE}} -\uptheta}}$ in both the calculations agrees with each other at an early stage of the precipitation. The rate kinetics in the Dictra simulation (firm line) then slows down considerably, when an overlapping of the diffusion fields of the nearby austenite attains a thermodynamic local equilibrium by the soft impingement effect. Goldstein and Randich [24] have also investigated the matter, suggesting that the parabolic nature of such a curve remains intact before the onset of the soft impingement. After that, a delay in the rate kinetics is probable, when a tie-line corresponding to the interface compositions gradually shifts towards the bulk alloy composition. The precipitates can hardly grow at this stage, providing a plateau only in the Dictra simulation. Then, a convenient way to compare the precipitate growth in both the procedures may be by measuring the $Z_{{{\text{PE}} -\uptheta}}$ with a refined precipitate (for the use in Sect. 6). The justification is that, growth curves concern less about the soft impingement as an effect in the early stage of the precipitation [34].

Fig. 4

The paraequilibrium growth of cementite, comparing a theoretical calculation against the Dictra simulation (firm line) in an Fe–1.2C–2Mn wt% alloy at 400 °C, for a validation

Figure 5a demonstrates a variation of the carbon concentrations across the phase interface between PE-θ and PE-γ in an Fe–1.2C–2Mn wt% alloy at 400 °C. The initial and final carbon concentrations in PE-γ are marked as $X_{\text{C}}^{{ 0 ,\upgamma}}$ and $X_{\text{C}}^{{{\text{PE}} -\upgamma}}$ respectively, indicating that a considerable amount of carbon depletion from austenite has resulted in during a decomposition of the matrix phase; as the evidence is put forward by the successive stages in the concentration-distance profile. In this comparison, the partitioning of a substitutional element may not be seen at all in Fig. 5b. In order to reiterate the effect, Table 4 analyzes the ratio of the distribution of various substitutional elements in the matrix to that in the carbide, yielding $(X_{\text{M}} /X_{\text{Fe}} )$ in PE-θ and PE-γ the same, irrespective of the alloy system. This agrees with the experimental observations by Thomson and Miller [13] that the ratio of the substitutional element M in matrix to that in the carbide may be close to unity. The kinetic interpretations may support it accordingly. The diffusivity of carbon in γ-iron at 400 °C from Table 3 is 3.5 × 10⁻¹⁶ m² s⁻¹; in 1 s the mean atomic displacement of a carbon atom, $\sqrt {Dt}$, is 19 nm. On the contrary, the self diffusivity of iron in the γ-iron at 400 °C is 6 × 10⁻²³ m² s⁻¹ [29]; so the equivalent displacement of an iron atom for the same time is 0.08 nm, which is much less than the interatomic spacing of the iron atoms, 0.25 nm. Thus substitutional elements are reported to be configurationally frozen in parent and product sites [6].

Fig. 5

Concentration-distance profiles in paraequilibrium, showing a the partition of carbon, vs. b the distribution of Mn across the phase interface between PE-θ and PE-γ in an exemplary Fe–1.2C–2Mn wt% alloy at 400 °C

Table 4 The ratio of the substitutional element M with respect to iron, $r\,\,( = X_{M} /X_{\text{Fe}} )$ in PE-θ and PE-γ at 400 and 600 °C, respectively for various alloys (wt%)

Thermodynamically, an element i is also said to be trapped when the change in the chemical potential, $\Delta \mu_{\text{i}}$ associated with a phase transition becomes the positive [3]. This necessitates the sharp interface model by Baker and Cahn [28], first in an equilibrium reaction, as follows:

$$\Delta \mu_{\text{i}}^{\uptheta} = \left( {\mu_{\text{i}}^{\uptheta} - \mu_{\text{i}}^{\upgamma} } \right) = {\text{R}}T\ln \left[ {\left( {X_{\text{i}}^{\uptheta} \cdot X_{\text{i}}^{{\upgamma \uptheta }} } \right)/\left( {X_{\text{i}}^{\upgamma} \cdot X^{{\uptheta \upgamma }} } \right)} \right]$$

(5)

where R is the universal gas constant, $X_{\text{i}}^{\uptheta}$ and $X_{\text{i}}^{\upgamma}$ are the concentrations of i in the bulk phases, the $X_{\text{i}}^{{\uptheta \upgamma }}$ and $X_{\text{i}}^{{\upgamma \uptheta }}$ at the interface, when θ and γ are in an equilibrium at a temperature T. In order to satisfy the condition; a solute-concentration in the bulk θ and γ may vary continuously, as an exemplary plot resembles the same in Fig. 3c by the Mn-partitioning. When an equilibrium condition by the redistribution of manganese in cementite is achieved, the concentration gradient within θ disappears fully, i.e. $X_{\text{i}}^{\uptheta} = X_{\text{i}}^{{\uptheta \upgamma }}$, leaving behind a sharp concentration gradient only at the interface in Fig. 3d. This requires further simplification of the model with the partition-coefficient k for the element i, as below:

$$\Delta \mu_{\text{i}}^{\uptheta} = RT\ln \left( {X_{\text{i}}^{{\upgamma \uptheta }} /X_{\text{i}}^{\upgamma} } \right) = {\text{R}}T\ln k.$$

(6)

When k is less than one, $\Delta \mu_{\text{i}}^{\uptheta}$ becomes the negative, allowing the partition of i to be thermodynamically feasible. On the other hand, $\Delta \mu_{\text{i}}^{\uptheta}$ becomes positive when the partitioning of i is to be ruled out; mostly for the substitutional elements during paraequilibrium growth by

$$\Delta \mu_{\text{i}}^{{{\text{PE}} -\uptheta}} = {\text{R}}T\ln \left( {x_{\text{i}}^{{{\text{PE}} -\upgamma \uptheta }} /x_{\text{i}}^{{{\text{PE}} -\upgamma}} } \right).$$

(7)

Table 5 summarizes the data to be particular that the chemical potential (sign) of the substitutional elements in both the transitions in general may be a positive, except Mn having a negative value in equilibrium conditions to take part in the partitioning through the volume diffusion (Fig. 3b–d). The magnitude (for Mn) is however smaller in comparison to the negative value of the chemical potential that is also obtained for the interstitial element carbon. Typically, at a given temperature, the magnitude of the chemical potential of carbon remains nearly the same both in equilibrium and paraequilibrium transitions. This leads to verify an earlier proposal by Bhadeshia that the equilibrium formation of α from γ provides the chemical potential of carbon identical in both phases at the interface, and this remains the case when α forms from γ by a paraequilibrium transition [3]. In this regard, silicon-addition under paraequilibrium condition finds an exception by reducing the magnitude of the chemical potential of carbon (Table 5); henceforth, a less phase fraction of PE-θ against equilibrium fraction of θ at 400 °C is feasible in the Fe–1.2C–2Si (comparing Tables 1 vs. 2).

Table 5 The chemical potential (in kJ mole⁻¹) of Fe, C and the ternary element M at 400 and 600 °C during equilibrium (γ → θ) versus paraequilibrium (γ → PE-θ) transition

The chemical potential of the substitutional elements is now of an interest. Table 5 indicates that the chemical potential of iron (besides carbon) at a given temperature nearly remains the same in equilibrium versus paraequilibrium transition; thereby justifying the necessity to find the role of a ternary element. For an elaboration, Table 5 indicates that $\Delta \mu^{\uptheta}$ for Si (or Al) during equilibrium growth is positive and having the magnitude within 1.24–1.53 kJ mole⁻¹. The paraequilibrium calculation in a similar way indicates that the chemical potential of all the substitutional elements (including Mn) is again positive, with the magnitude 0.14–0.29 kJ mole⁻¹ relatively smaller. Therefore, a positive value of the chemical potential for Si (and Al) does not necessarily mean the trapping of the substituional elements in both the transitions, but may be one of the reasons. Secondly, an extraordinarily large difference in the rate kinetics for a cementite formation in equilibrium versus paraequilibrium cannot be explained by the chemical potential of the individual element (either interstitial or substituional) without deriving free energies in both the transitions.

The Gibbs free energy change ∆G per mole for reactions in a closed system, when an infinitesimal amount of material of composition $\overline{{X_{\text{i}}^{\uptheta} }}$ is transferred from γ of composition $\overline{{X_{\text{i}}^{\upgamma} }}$ to θ of composition $\overline{{X_{\text{i}}^{\uptheta} }}$, is given as [3]:

$$\left| {\Delta G} \right|^{\uptheta} = \left[ {\overline{{X_{\text{Fe}}^{\uptheta} }} \,\Delta \mu_{\text{Fe}}^{\uptheta} + \overline{{X_{\text{C}}^{\uptheta} }} \,\Delta \mu_{\text{C}}^{\uptheta} + \overline{{X_{\text{M}}^{\uptheta} }} \,\Delta \mu_{\text{M}}^{\uptheta} } \right]$$

(8)

where the chemical potentials of the individual element are obtained from Table 5. A similar calculation for a paraequilibrium precipitation also uses the chemical potentials from the same table. The result of the calculation is given in Fig. 6a for a comparison, showing a dramatic reduction in the free energy associated with the paraequilibrium precipitation of cementite when Si (or Al to some an extent) is alloyed as the ternary. The magnitude of the free energy difference between equilibrium and paraequilibrium kinetics is 2.7 and 0.8 kJ mole⁻¹ for Si and Al, respectively; which indicates that the driving force for a paraequilibrium precipitation of cementite will be more intense with (Fe,Si)₃C than (Fe,Al)₃C. Thus, the paraequilibrium precipitation of (Fe,Si)₃C will cease off relatively earlier than (Fe,Al)₃C and in turn, go against the equilibrium kinetics, forcing Si (or Al) to get trapped by the faster moving advancing front of the carbide. In the case of the equilibrium reaction, Si (or Al) despite being slow enough (positive value of chemical potential) cannot get trapped; simply because, the interface mobility is extremely slow in an association with the higher free energy destabilizing the carbide. Interestingly, the magnitude of the free energy difference between equilibrium and paraequilibrium kinetics as mentioned earlier for Al is 0.8 kJ mole⁻¹ which is not very large; hence forth it may not be surprising if someone by chance also observes an initiation of the equilibrium reaction (without completion) in a Fe–C–Al, following Leslie and Rauch [20].

Fig. 6

a The effect of the ternary [M = Mn, Al, Si] of 2 wt% leading to the magnitude of the free of the free energy change $\left| {\Delta G} \right|$ in Fe–1.2C wt% steels during equilibrium versus paraequilibrium precipitation of cementite at 400–600 °C; notably, $\left| {\Delta G} \right|$ for (Fe,Si)₃C is available only at 400 °C, owing to thermodynamic instability at the higher temperature. b The literature data by Kozenthick and Bhadeshia [18] showing a corresponding change in the free energy for Fe–1.2C–1.5Mn–1.5Si wt% alloys, with or without Si addition at 200–700 °C

In the case of manganese steel, an opposite trend of Si (or Al), that is lowering the free energy during the equilibrium precipitation of cementite can be seen (Fig. 6a). The magnitude of the free energy difference between equilibrium and paraequilibrium precipitation is only 0.24 kJ mole⁻¹. This to some an extent agrees with the thermodynamic calculation by Kozeschnik and Bhadeshia [18] in Fig. 6b that the magnitude of the free energy difference between equilibrium and paraequilibrium transition in an Fe–1.2C–1.5Mn may be even closer (0.14 kJ mole⁻¹). It is to be noted here as a key concern that the present calculation in Fe–1.2C–2Mn finds the lowering of the free energy during equilibrium conditions whereas Kozeschnik and Bhadeshia [18] have observed it in Fe–1.2C–1.5Mn during the paraequilibrium precipitation. However, no further comment has been put forward citing the consequences of their outcome.

The aforesaid calculation in Table 6 now will help to understand the effective contribution of carbon to the overall free energy change in both the transitions. It turns out that the interstitial element carbon contributes 92–95% to the calculated $\left| {\Delta G} \right|$ for various alloys; except manganese in equilibrium conditions through partitioning brings down the contribution of carbon by merely a 6% (to 86.5–89.1%). Interface mobility thus is empowered by the volume diffusion of carbon in both the transitions. Most of the driving force available for a phase transition is dissipated in this process alone, in driving the carbon ahead of the interface. Thus, the role of a substitutional element being trapped in a solid solution is to alter the rate kinetics through an indirect way. A possible consequence is reducing the carbon flux across the phase interface. Among the various ternary elements, Si plays a leading role to cause a significant enrichment of carbon in austenite (Table 2). The effective contribution of carbon to the free energy addition in Table 6 thus is bound to decrease.

Table 6 The effective contribution of carbon to the overall free energy change during equilibrium versus paraequilibrium transition at 400 and 600 °C, respectively

Figure 7 investigates a paraequilibrium precipitation of cementite from austenite at 400–600 °C in various alloys. An intention is to verify the effective contributions of the substitutional element M limiting the cementite layer thickness under diffusion constraints. A comparative analysis at 400 °C indicates that the kinetic data tend to be merging with each others, though silicon refines the carbide platelet minutely at this temperature. A similar trend for Si is absent at the higher temperature, due to the thermodynamic instability, allowing the paraequilibrium precipitation of cementite only in the Fe–1.2C–2Mn where M = Mn, Al. An argument by Bhadeshia and Edmonds [35] may reconcile with the present data. It has been suggested that a lattice strain is incorporated by shear when austenite is supercooled near the bainitic transformation temperature. It leads to the formation of extensive dislocation tangles at the bainitic ferrite/austenite interface. When the carbon concentration in austenite is sufficiently high (hereby 1.2 wt%) or beyond a critical limit, it turns into a Cottrell atmosphere. Further decomposition of austenite then is difficult, leaving the residual austenite untransformed even at room temperature. The effect is known as the incomplete transformation phenomena [36] to eliminate the hard, brittle cementite phase completely at 600 °C from the phase mixture. The microstructure however retains a certain volume fraction of PE-θ at 400 °C; the combination of high hardness along with a significant retained austenite is indeed attractive for gear or bearing applications, where a damage tolerance under pitting or contact fatigue conditions is enhanced by austenite that is present in the microstructure [30]. The thermodynamic condition of alloy-design thus prefers a paraequilibrium precipitation of cementite at both the temperatures.

Fig. 7

The paraequilibrium growth rate of cementite in Fe–1.2C wt% steels when the ternary element M is substituted by Mn, Al, or Si at a 400 and b 600 °C, respectively

6 Equilibrium Versus Paraequilibrium Kinetics

This section compares the kinetics of paraequilibrium against the equilibrium transition, in the light of the ternary alloy addition. Assuming a cementite-platelet to grow about 30 nm in size, the time-lag imposed by Si (or Al) in both the transitions is given in Table 7 from Fig. 8. It indicates that paraequilibrium growth is too rapid to be seen and the equilibrium growth may not prevail at all with Si (or Al) in accordance with Fig. 6a; thus measuring the platelet size may be difficult experimentally. For this reason, Ghosh and Olson [6] have performed a Dictra simulation at 350 °C, obtaining a platelet size of 30 nm after 1.4 s in Fe–C–Mn–Si. In comparison, the present calculation at 400 °C obtains the same size after 8.3 s in Fe–1.2C–2Si. A possible reason can be explained from Fig. 6 that the magnitude of $\left| {\Delta G} \right|$ for a Fe–C–Mn–Si is lower than in Fe–1.2C–2Si (0.7 kJ mole⁻¹); thus causing cessation of the precipitation reaction in the quaternary earlier than the ternary.

Table 7 Estimated time duration in equilibrium versus paraequilibrium precipitation, assuming a cementite platelet to grow about 30 nm in thickness at 400 and 600 °C, respectively

Fig. 8

The equilibrium (θ) vs. paraequilibrium (PE-θ) growth of cementite, exhibiting a time-lag due to the ternary element M [Al,Si] of 2 wt% in Fe–1.2C wt% steels at a 400 and b 600 °C, respectively

The effect of Mn can also be seen from Table 7, which exhibits almost zero time-lag between equilibrium and paraequilibrium (PE) kinetics. This raises a speculation that which one of these mechanisms will dominate the growth preferentially during the interface movement. Figure 6a indicates that the magnitude of the free energy difference between equilibrium and paraequilibrium kinetics is 0.24 kJ mole⁻¹, which is very low; thus both the kinetics may be concurrent in Fe–1.2C–2Mn as a novel trend through the following argument. Figure 2a–d indicate that cementite may develop initially without the partition/redistribution of Mn. Thus the paraequilibrium precipitation may take over at this stage with a higher free energy addition. The Mn-concentration in cementite thereby reaches maximum up to 1.89 wt% within few seconds (Fig. 5b). Comparing this with Table 1, the value is still lower than the equilibrium limit of 6.31 wt% Mn in (Fe,Mn)₃C. Thus, the equilibrium-partition of Mn in the next step is mandatory to cause a further reduction in the free energy (Fig. 6a). This makes precipitation of cementite in this alloy a mixed mode type; without compromising much on time. A compelling argument is that if the redistribution of Mn in cementite occurs without paraequilibrium as an aid, the precipitation of (Fe,Mn)₃C would have taken several years (~ 10⁹ s) to complete. Hereby, switching of the mechanisms from PE (paraequilibrium) to PLE (partition local equilibrium) only in the Mn-steel needs a further discussion. The precipitation in a solid state involves a larger activation energy barrier. In order to overcome it, a system often passes through multiple local minima or metastable phases which are difficult to be analyzed by thermodynamic means. One of these kinds may be NPLE (non-partition local equilibrium) mechanism, which may bridge the gap between the initiation (i.e. by PE) and to the completion of the precipitation (i.e. by PLE).

The systems containing Si, on the other hand, may not get such an opportunity. Once the substitutional element is trapped, a dramatic reduction in the free energy causes cessation of the precipitation kinetics. Thus paraequilibrium kinetics appear to be decisive with Si always as the ternary (Fig. 6a). For Al, as the magnitude of the free energy difference between the equilibrium and paraequilibrium kinetics is only 0.8 kJ mole⁻¹, one may by chance observe an initiation of the equilibrium reaction in Fe–1.2C–2Al, before the paraequilibrium mechanism kicks starting.

7 Summary and Conclusions

The effect of the ternary M [Mn, Al, Si] of 2 wt% to alter the precipitation of cementite between equilibrium and paraequilibrium kinetics has been discussed thoroughly in Fe–1.2C wt% steels using thermodynamics and kinetics.

It appears that both Si and Al contain a chemical potential ‘positive’ in equilibrium (1.24–1.53 kJ mole⁻¹) and paraequilibrium (0.14–0.29 kJ mole⁻¹) conditions; this does not necessarily confirm the trapping of the substituional elements in both the transitions, but may be one of the reasons. Again the magnitude of the chemical potentials for Si, Al or C in equilibrium versus paraequilibrium does not differ much. Therefore, an extraordinarily large difference in the rate kinetics cannot be explained by the chemical potentials of either interstitial or substituional component, without deriving free energies in both the transitions.

The paraequilibrium precipitation of cementite is favored by Si (or Al) over the equilibrium kinetics through the energy minimization. The magnitude of the free energy difference between equilibrium and paraequilibrium kinetics is 2.7 and 0.8 kJ mole⁻¹ for Si and Al, respectively. As a result, the driving force for a paraequilibrium precipitation of cementite will be more intense with silicon than aluminium which allows paraequilibrium precipitation of (Fe,Si)₃C to cease off relatively earlier than (Fe,Al)₃C.

In the manganese steel, however an opposite trend of lowering the free energy during the equilibrium precipitation of cementite can be seen. The paraequilibrium kinetics is also mandatory, but at an earlier stage, to offset the time-lag for the redistribution of Mn. This makes precipitation of cementite in this alloy a mixed mode type, as the magnitude of the free energy difference between the two kinetics is only 0.24 kJ mole⁻¹ to make it feasible.

Similarly, the magnitude of free energy difference between the equilibrium and paraequilibrium kinetics for Al is very small, amounting to be only 0.8 kJ mole⁻¹. Therefore, one may by chance observe an initiation of the precipitation reaction in Fe–C–Al under equilibrium mode, before the paraequilibrium kinetics finally prevails.