Rock slope stability assessment based on the critical failure state curve for the generalized Hoek‒Brown criterion

Abstract

The strength reduction method (SRM) based on the generalized Hoek‒Brown (GHB) criterion has become an important and popular topic to analyse the stability of rock slopes. Various reduction strategies have been proposed and applied by the civil and mining engineering community. This paper proposed a new SRM for rock slopes with the GHB criterion based on the critical failure state curve (CFSC). The existence of the CFSC has been proven by theoretical analysis, and the explicit expression of the CFSCs for different parameters m_i and slope angles β, considering the influence of disturbance factor D, has been obtained by curve fitting based on a great deal of simulation data. The new SRM provides a graphic method to determine the parameters at the critical failure state from the initial state by reducing the compressive strength of intact rock σ_ci and the parameter combination s^α with the same ratio and proposes a definition of the factor of safety (FOS) based on the parameters of the two states. This method was applied to nine slope examples to verify its validity and accuracy. The relative errors between the critical state parameters obtained from the graphic method and that from the simulation analysis are less than 10%, which proves the accuracy of the CFSCs. The FOSs obtained by the proposed definition are compared with those obtained by the Bishop simplified method and the local linearization method (LLM), and the results are very close. The relative error is less than ± 5% compared with the LLM, and the stability state predicted is perfectly accurate. However, the calculation procedure is largely simplified, and the calculation speed is largely improved. A practical case of an open pit limestone slope with multiple steps was detailed analysed by the proposed SRM based on CFSC. The FOS results comparison with other existing method has demonstrated its feasibility and reliability in engineering application.

Introduction

The stability assessment and analysis of rock slopes is a significant task for rock engineering projects, such as open pit mining. The strength reduction method (SRM) is widely accepted and used by researchers to analyse slope stability because of its advantage over the traditional limit equilibrium method (LEM) (Zhao et al. 2005; Krahn 2007; Liu et al. 2015; Sari 2019). Presently, SRM research is mainly based on the conventional Mohr‒Coulomb (MC) criterion, which is incapable of explaining the nonlinear deformation and failure characteristics of rock masses. The Hoek‒Brown (HB) criterion, first proposed in 1980 as an empirical nonlinear failure criterion, has developed into a rigorous and complete strength criterion and has been widely applied in rock mechanics and engineering (Hoek and Brown 1980; Hoek et al. 2002). The Generalized Hoek‒Brown (GHB) criterion, as the latest version of the HB criterion presented in 2018 (Hoek and Brown 2019), is capable of estimating the strength and deformation characteristics of homogeneous and isotropic rocks with few discontinuities and heavily jointed rock masses. Combining the advantage of SRM on slope stability analysis and the nonlinear GHB criterion to explore the new strength reduction strategy has become an important and popular research field (Zong and Xu 2008; Melkoumian et al. 2009; Shen and Karakus 2014; Yuan et al. 2020). Due to the complexity of the parameters in the GHB criterion, various reduction strategies have been proposed and applied by many scholars, but none of them has gained wide acceptance in the engineering community. Presently, the representative reduction methods are classified into the following four types:

• (1) Some or all of the GHB parameters are directly reduced by the reduction factor is usually called the “direct reduction method”, and the global safety factor is traditionally defined by the reduction ratio of the original parameters to the reduced parameters at failure. For example, Wu et al. (2006) suggested reducing the uniaxial compressive strength of the intact rock (σ_ci) and the material constant for the intact rock (m_i) with the same ratio. Han et al. (2016) presented the correlation between the three reduction factors of the parameters (mb, s, a) in Hoek–Brown criterion from the softening and hardening regularities of the geomaterial perspective. Song et al. (2012) discussed seven cases of the direct reduction method and found that directly reducing σ_ci and the geological strength index (GSI) could obtain a reasonable global safety factor. However, the direct reduction method could lead to distortion of the GHB failure envelope after the parameters are reduced.

• (2) The integral strength envelope of the GHB criterion is lowered by a reduction factor until the critical failure state, as proposed by Hammah et al. (2005). The determination of the equivalent GHB curve that best approximates the lowered envelope is obtained through the minimization of the total squared error by the simplex method, of which the analysis procedure is complex. Thomas et al. (2008) adopted the spatial mobilized plane (SMP) concept to realize intrinsic material strength factorization. However, this method requires iterative computations to obtain the shear strength at every reduction step, which greatly lowers the calculation efficiency.

• (3) The nonlinear GHB criterion is transformed into the linear MC criterion, and the slope stability is analysed based on the MC criterion, called the equivalent linearization method (Priest 2005; Yang and Yin 2010; Shen et al. 2012). This method was classified into two types: the global approach (Hoek et al. 2002; Zong and Xu 2008) and the local approach (Fu and Liao 2010; Xu and Yang 2018; Wei et al. 2021). The former is to obtain a global linear optimization of the shear strength curve of the GHB criterion; the latter is to obtain the local stress and strength values. Sukanya et al. (2012) believed that the local approach was physically more correct than the global approach. However, the local MC parameters need to be solved by the Newton iterative formula, and the calculation is time-consuming for a complex model.

• (4) Applying stability charts for rock mass slopes satisfying the HB criterion to obtain the safety factor of the slope (Li et al. 2008; Shen et al. 2013; Sun et al. 2016). For example, Shen et al. (2013) and Sun et al. (2016) proposed a slope stability chart for a specified slope angle β = 45° and disturbance factor D = 0 and then combined the weighting factors f_D and f_β to calculate the FOS of a slope assigned various slope angles under different blasting damage. The graph method relies heavily on the accuracy of chart data.

Recently, a new SRM strategy based on the GHB criterion (Yuan et al. 2020), whose core concept is to search for an optimal reduction pathway for the GHB criterion parameters by establishing the critical failure state curves (CFSC) for different slopes. Inspired by its strategy, this paper establishes a more accurate and detailed critical failure state curve equation based on a large amount of numerical simulation data, and an improved parameter reduction scheme and a simpler safety factor definition method are proposed and formed a new SRM based on CFSC. The new SRM allows for rapid determination of the parameters at the critical failure state by a graphic method and a fast and accurate calculation method for the factor of safety (FOS) based on the initial and critical states’ parameters. The advantages of the proposed method over those existing SRMs are that the model establishment and stability numerical analysis based on finite element or finite difference programme which consumes significant computational power and time are not required.

The proposed method is applied to several classical examples to verify the validity and reliability of the parameter reduction scheme and the definition of the safety factor. A practical case of an open pit limestone slope with multiple steps was detailed analyzed by the proposed graphical method to demonstrate its feasibility and reliability in engineering application.

The general Hoek‒Brown criterion and the slope critical failure state curve

The general Hoek‒Brown criterion

The GHB strength criterion is usually given in principal stress space with the following expression.

$$\sigma_{1} { = }\sigma_{3} { + }\sigma_{ci} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha } ,$$

(1)

where σ₁ and σ₃ are the maximum and minimum principal stresses of the rock mass at failure (compressive stress is taken to be positive), and σ_ci is the unconfined compressive strength of the intact rock according to the 2018 edition (Hoek and Brown 2019). m_b, s, and α are empirical parameters reflecting rock mass characteristics related to the fracturing degree of the rock and can be estimated by the functions of the geological strength index (GSI), the disturbance factor D and the material constant of intact rock mi.

$$\left\{ {\begin{array}{*{20}l} {m_{b} = m_{i} \exp \left( {\frac{{{\text{GSI}} - 100}}{28 - 14D}} \right)} \\ {s = \exp \left( {\frac{{{\text{GSI}} - 100}}{9 - 3D}} \right)} \\ {\alpha = \frac{1}{2} + \frac{1}{6}(e^{{ - {\text{GSI}}/15}} - e^{ - 20/3} )} \\ \end{array} } \right.,$$

(2)

where GSI is estimated by the structure (or blockiness) and the surface conditions of the jointed blocky rock masses, of which the maximum value is 100 (for intact rock). D is the disturbance factor subjected to blasting damage and stress relaxation of the rock mass, with a value range of 0.0 (undisturbed) ~ 1.0 (disturbed). m_i is a material constant for the intact rock, which represents the rock type and hardness.

Balmer (1952) proposed that normal stress and shear stress could be expressed as functions of principal stresses as follows:

$$\left\{ {\begin{array}{*{20}l} {\sigma_{n} = \sigma_{3} + \frac{{\sigma_{1} - \sigma_{3} }}{{{{\partial \sigma_{1} } \mathord{\left/ {\vphantom {{\partial \sigma_{1} } {\partial \sigma_{3} }}} \right. \kern-0pt} {\partial \sigma_{3} }} + 1}}} \\ {\tau = (\sigma_{1} - \sigma_{3} )\frac{{\sqrt {{{\partial \sigma_{1} } \mathord{\left/ {\vphantom {{\partial \sigma_{1} } {\partial \sigma_{3} }}} \right. \kern-0pt} {\partial \sigma_{3} }}} }}{{{{\partial \sigma_{1} } \mathord{\left/ {\vphantom {{\partial \sigma_{1} } {\partial \sigma_{3} }}} \right. \kern-0pt} {\partial \sigma_{3} }} + 1}}} \\ \end{array} } \right..$$

(3)

The differential expression ${{\partial \sigma_{1} } \mathord{\left/ {\vphantom {{\partial \sigma_{1} } {\partial \sigma_{3} }}} \right. \kern-0pt} {\partial \sigma_{3} }}$ can be derived from Eq. (1) as follows:

$${{\partial \sigma_{1} } \mathord{\left/ {\vphantom {{\partial \sigma_{1} } {\partial \sigma_{3} }}} \right. \kern-0pt} {\partial \sigma_{3} }} = 1 + \alpha m_{b} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha - 1} .$$

(4)

The expressions of normal stress and shear stress based on the GHB criterion can be obtained by substituting Eqs. (4) into (3), given as follows:

$$\left\{ {\begin{array}{*{20}l} {\sigma_{n} = \sigma_{3} + \frac{{\sigma_{ci} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha } }}{{2 + \alpha m_{b} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha - 1} }}} \\ {\tau = \sigma_{ci} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha } \frac{{\sqrt {1 + \alpha m_{b} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha - 1} } }}{{2 + \alpha m_{b} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha - 1} }}} \\ \end{array} } \right..$$

(5)

As noted in the GHB criterion, the uniaxial compressive strength of the rock mass (σ_cmass) is expressed by setting $\sigma_{3} = 0$, and the tensile strength of the rock mass (σ_tmass) can be obtained by setting $\sigma_{1} = \sigma_{3} = \sigma_{tmass}$, given below:

$$\left\{ {\begin{array}{*{20}l} \begin{gathered} \sigma_{cmass} = \sigma_{ci} s^{\alpha } \hfill \\ = \sigma_{ci} \exp \left( {\left( {\frac{GSI - 100}{{9 - 3D}}} \right)\left( {\frac{1}{2} + \frac{1}{6}(e^{ - GSI/15} - e^{ - 20/3} )} \right)} \right) \hfill \\ \end{gathered} \\ {\sigma_{tmass} = - s\frac{{\sigma_{ci} }}{{m_{b} }}} \\ \end{array} } \right..$$

(6)

Theoretical relationships of slope parameters at the critical failure state

The stability of the slope is determined by the unit weight of the rock mass (γ), the slope height (H), the slope angle (β) and all the parameters involved in the failure criterion of the rock mass. Based on the GHB criterion, a general functional relationship related to all the parameters to describe the critical failure state of any slope could be established. According to the classic definition of the factor of safety (FOS), a slope at the critical failure state indicates an equilibrium between the total resistant shear force and the total sliding force on the potential sliding surface. Thus, this equilibrium state for any slope can be deduced as follows:

$$F = \frac{{\int\limits_{l} {\tau_{s} dl} }}{{\int\limits_{l} {\tau_{m} dl} }} = f_{1} \left( {\frac{{\tau_{s} }}{{\tau_{m} }}} \right) = 1,$$

(7)

where l denotes the potential sliding surface; in each zone, τ_s is the resistant shear stress; and τ_m is the driving shear stress, which greatly depends on the gravity of the overlying rock mass above the potential sliding surface (γH). Thus, Eq. (7) can be expressed as:

$$f_{2} \left( {\frac{{\tau_{s} }}{\gamma H}} \right) = 1.$$

(8)

From the formula in Eq. (5), the following equation can be derived.

$$\left\{ {\begin{array}{*{20}l} {\frac{{\sigma_{n} }}{{\sigma_{ci} }} = \frac{{\sigma_{3} }}{{\sigma_{ci} }} + \frac{{\left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha } }}{{2 + \alpha m_{b} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha - 1} }}} \\ {\frac{{\tau_{s} }}{{\sigma_{ci} }} = \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha } \frac{{\sqrt {1 + \alpha m_{b} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha - 1} } }}{{2 + \alpha m_{b} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{\alpha - 1} }}} \\ \end{array} } \right..$$

(9)

Therefore, the minor principal stress ${{\sigma_{3} } \mathord{\left/ {\vphantom {{\sigma_{3} } {\sigma_{ci} }}} \right. \kern-0pt} {\sigma_{ci} }}$ can be solved by an iteration of ${{\sigma_{n} } \mathord{\left/ {\vphantom {{\sigma_{n} } {\sigma_{ci} }}} \right. \kern-0pt} {\sigma_{ci} }}$ with given m_b, s and α. ${\tau \mathord{\left/ {\vphantom {\tau {\sigma_{ci} }}} \right. \kern-0pt} {\sigma_{ci} }}$ is the function of ${{\sigma_{3} } \mathord{\left/ {\vphantom {{\sigma_{3} } {\sigma_{ci} }}} \right. \kern-0pt} {\sigma_{ci} }}$, m_b, s and α. Thus, ${\tau \mathord{\left/ {\vphantom {\tau {\sigma_{ci} }}} \right. \kern-0pt} {\sigma_{ci} }}$ can be expressed as follows:

$$\frac{{\tau_{s} }}{{\sigma_{ci} }} = f_{3} \left( {\frac{{\sigma_{n} }}{{\sigma_{ci} }},m_{b} ,s,\alpha } \right).$$

(10)

The value of σ_n depends on the gravity of the overlying rock mass γH and the slope angle β only under the condition of gravity. Thus, Eq. (10) can be expressed as:

$$\frac{{\tau_{s} }}{{\sigma_{ci} }} = f_{4} \left( {\frac{{\gamma H}}{{\sigma_{ci} }},\beta ,m_{b} ,s,\alpha } \right),$$

(11)

where the parameters m_b, s and α can be expressed by Eq. (2). Thus, Eq. (11) can be expressed as follows:

$$\tau_{s} = \sigma_{ci} f_{5} \left( {\frac{{\gamma H}}{{\sigma_{ci} }},\beta ,GSI,D,m_i} \right).$$

(12)

According to the equilibrium criterion in Eq. (8), the expression below can be derived:

$$f_{2} (\frac{{\tau_{s} }}{\gamma H}) = f_{2} \left( {\frac{{\sigma_{ci} }}{rH}f_{5} \left( {\frac{{\gamma H}}{{\sigma_{ci} }},\beta ,GSI,D,m_i} \right)} \right) = f_{6} \left( {\frac{{\sigma_{ci} }}{\gamma H},GSI,D,m_i,\beta } \right) = 1.$$

(13)

According to Eq. (6), s^α is the function of GSI and D. Thus, Eq. (13) is finally expressed as:

$$f_{7} \left( {\frac{{\sigma_{ci} }}{{\gamma H}},s^{\alpha } ,m_i,\beta } \right) = 1.$$

(14)

In the literature of Yuan et al.(2020), σ_ci and s^α are combined and replaced by σ_cmass from Eq. (6). In addition, Eq. (14) is deduced below.

$$f_{7} \left( {\frac{{\sigma_{ci} }}{{\gamma H}},s^{\alpha } ,m_i,\beta } \right) = f_{8} \left( {\frac{{\sigma_{ci} s^{\alpha } }}{{\gamma H}},m_i,\beta } \right) = f_{7} \left( {\lambda ,\beta ,m_i} \right) = 1,$$

(15)

where $\lambda = \frac{{\sigma_{ci} s^{\alpha } }}{{\gamma {\text{H}}}}$ is a dimensionless parameter. The parameters λ, β and mi, which satisfy the equilibrium criterion in Eq. (15) at the slope critical failure state, could establish the slope critical failure state curve (CFSC).

Explicit expression of the CFSC by numerical simulation

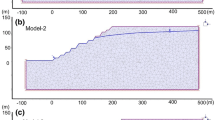
It is a great challenge to establish the explicit expression of CFSC from the implicit function (15) by theoretical analysis. Thus, a numerical simulation method based on FLAC^3D 6.0 software (Itasca Inc., 2016) is used to achieve this goal. Referring to reference (Hammah et al 2005; Fu and Liao 2010), the geometry and grid layout of the slope model used in this numerical simulation is shown in Fig. 1.

Fig. 1

The geometry and grid layout of the slope model

To simplify the simulation procedure, the slope angle is assigned to 45°, 60° and 75°. The height of the slope models is assigned to 10 m, 25 m, 50 m, 100 m and 200 m (the heights are fine adjusted in accordance with the slope angles shown in Table 1). The horizontal displacements of the left and right boundaries are fixed, while both horizontal and vertical displacements are fixed along the bottom boundary. The unit weight γ is set to 25.0 kN/m³. The disturbance factor D is initially set to 0, and its influence on the CFSC is discussed in “The influence of disturbance factor D on the CFSCs”. Only the gravity of the rock mass is considered as an external load in the numerical simulation. The convergence criterion to judge whether the slope has reached a mechanically stable state is setting the maximum unbalance force ratio R to 10⁻⁵. The slope model was considered to be homogeneous and isotropic. Considering the mesh sensitivity, the amount of grids remains the same for different slope models (approximately 4000 ~ 5000 grids).

Table 1 Slope model and values set for the parameters

The elasticity modulus (E) and Poisson’s ratio (ν) of the rock mass remain constant when the GSI, D and σ_ci vary in this study. Because this study pays more attention to the parameters causing plastic failure than the parameters involved in elastic deformation. The simulation results have proven that the changes in the elastic modulus and Poisson coefficient do not affect the parameters of the slope critical failure state.

The procedure of the numerical simulation is as follows:

• (1) Slope models with different slope angles and heights are established, and the rock mass is assigned to be homogeneous and isotropic.

• (2) For each slope model, the unit weight of the rock mass remains the same, and the disturbance factor D is initially set to 0. m_i is fixed as the value in Table 1. GSI is varied with the range of Table 1, and finally, σ_ci is adjusted to lead the slope to the critical failure state. The material parameter values (m_b, s and α) of the slope model are transformed by the Fish function in FLAC^3D with the values of GSI, m_i and D, and σ_ci is repeatedly reduced by an interval of 0.2 until the numerical calculation does not converge, which means that the slope has reached the critical failure state.

• (3) The uniaxial compressive strength of the rock mass σ_cmass and the dimensionless parameter λ are calculated according to the parameters at each critical failure state. The simulation results show that the dimensionless parameter λ at the critical failure state remains constant for different heights and unit weights, while it varies with GSI, m_i and slope angle β. Figure 2 shows the critical failure state curve of the dimensionless parameter λ varying with GSI for different vales of m_i and slope angle β.

Fig. 2

The critical failure state curve of λ varying with GSI for different mi and β

To better represent the theoretical relation, the dimensionless parameter λ can be decomposed as the multiplication of two parameters, ${{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\gamma {\text{H}}}}} \right. \kern-0pt} {\gamma {\text{H}}}}$ and $s^{\alpha }$, as shown in Eq. (16), where ${{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\gamma {\text{H}}}}} \right. \kern-0pt} {\gamma {\text{H}}}}$ was termed the strength ratio (SR) of a rock slope and was strongly related to the safety factor, proposed by Shen et al.(2013), and $s^{\alpha }$ determined by GSI and D, is numerically equivalent to JP(Jointing Parameter) of the Palmström’s RMi system (Russo 2008), which represented the rock mass quality and structure.

$$\lambda = \frac{{\sigma_{cmass} }}{{\gamma {\text{H}}}} = \frac{{\sigma_{ci} }}{{\gamma {\text{H}}}} \cdot s^{\alpha } ,$$

(16)

$s^{\alpha }$ is taken as the x-coordinate, and ${{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\gamma {\text{H}}}}} \right. \kern-0pt} {\gamma {\text{H}}}}$ is taken as the y-coordinate. The points paired by $s^{\alpha }$ and ${{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\gamma {\text{H}}}}} \right. \kern-0pt} {\gamma {\text{H}}}}$ at the critical failure state for different vales of m_i and slope angles β are drawn in the ${\text{s}}^{\alpha } {{ \sim \sigma_{ci} } \mathord{\left/ {\vphantom {{ \sim \sigma_{ci} } {\gamma {\text{H}}}}} \right. \kern-0pt} {\gamma {\text{H}}}}$ coordinate system, which forms the slope CFSC.

The Curve Fitting Tool (cftool) of MATLAB (Mathworks Inc. 2010) was used to fit the CFSC. After comparing various fitting methods, it was found that the fitting type power 2 ($a * x^{b} + c$) had the highest fitting accuracy and the minimal fitting error. The fitting expressions of the CFSCs and fitting accuracy are given in Table 2. The points paired by $s^{\alpha }$ and ${{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\gamma {\text{H}}}}} \right. \kern-0pt} {\gamma {\text{H}}}}$ at the critical failure state and the fitting curve for different slope angles and values of m_i are shown in Fig. 3.

Table 2 The fitting expressions and accuracy of the CFSCs for different m_i and β

Fig. 3

The fitting curves of CFSCs for different m_i and β values

When mi takes values other than 5, 10, 15, 20 and 25, the corresponding CFSCs can be obtained by interpolation. Since the curve of λ varying with mi does not satisfy the linear relation, the CFSCs of other mi values can be obtained by cubic spline interpolation.

The influence of disturbance factor D on the CFSCs

The value of disturbance factor D has a great influence on slope stability (Li et al. 2011). In the latest version of the GHB criterion, the suggested values of D are given for different engineering slopes, that is, D = 0.5 for controlled presplit or smooth wall blasting, D = 0.7 for mechanical excavation effects of stress reduction damage, and D = 1.0 for production blasting. The influence of D on the CFSCs is presented by setting D = 0.5, 0.7, 0.9 and 1.0.

Fixing β and m_i, search for the parameter combination (${\text{s}}^{\alpha } {{ \sim \sigma_{ci} } \mathord{\left/ {\vphantom {{ \sim \sigma_{ci} } {\gamma {\text{H}}}}} \right. \kern-0pt} {\gamma {\text{H}}}}$) of the critical failure state for D = 0.5, 0.7, 0.9 and 1.0. The influence of D on the CFSCs for β = 45° and $m_{i} = 10$ is shown in Fig. 4, from which it can be found that the CFCSs rise with the increase of D. The ratio of the CFSCs (D ≠ 0) to the CFSCs (D = 0) remains almost constant when $s^{\alpha }$ varies, which can be represented by the equation below.

$$R_{D} (D \ne 0) = \left. {\frac{{{{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\gamma {\text{H }}\left( {D \ne 0} \right)}}} \right. \kern-0pt} {\gamma {\text{H }}\left( {D \ne 0} \right)}}}}{{{{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\gamma {\text{H }}\left( {D = 0} \right)}}} \right. \kern-0pt} {\gamma {\text{H }}\left( {D = 0} \right)}}}}} \right|_{{s^{\alpha } }} = \frac{{{{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\gamma {\text{H}} \cdot \, s^{\alpha } \left( {D \ne 0} \right)}}} \right. \kern-0pt} {\gamma {\text{H}} \cdot \, s^{\alpha } \left( {D \ne 0} \right)}}}}{{{{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\gamma {\text{H}} \cdot \, s^{\alpha } \left( {D = 0} \right)}}} \right. \kern-0pt} {\gamma {\text{H}} \cdot \, s^{\alpha } \left( {D = 0} \right)}}}} = \frac{{\lambda \left( {D \ne 0} \right)}}{{\lambda \left( {D = 0} \right)}}.$$

(17)

Fig. 4

The CFSCs with different values of D and the ratio R_D varies with $s^{\alpha }$ for β = 45° and m_i = 10

Therefore, the CFSCs of D ≠ 0 can be obtained by multiplying the CFSCs of D = 0 by the ratio R_D. The estimation of the ratio R_D for different β and $m_{i}$ can be solved by simulation analysis. The procedure is as follows: for β = 45°, mi is set to 5, 10, 15, 20 and 25. The parameters at the critical failure state for D = 0, 0.5, 0.7, 0.9 and 1.0 are searched for the given $s^{\alpha }$, and the dimensionless parameter λ and the ratio R_D for 0.5, 0.7, 0.9 and 1.0 are calculated with Eq. (17). Figure 5 shows that the dimensionless parameter λ varies with m_i for different D at β = 45°, 60° and 75°. Figure 6 shows that the ratio R_D for D = 0.5, 0.7, 0.9, and 1.0 varies $m_{i}$ at β = 45°, 60° and 75°. With the ratio R_D and the CFSCs for D = 0 obtained from “Explicit expression of the CFSC by numerical simulation”, the CFSCs of D = 0.5, 0.7, 0.9, and 1.0 for different mi and β can be obtained.

Fig. 5

The dimensionless parameter λ varies with m_i for different D at β = 45°, 60° and 75°

Fig. 6

The ratio R_D for D = 0.5, 0.7, 0.9, and 1.0 varies with m_i at β = 45°, 60° and 75°

SRM based on the slope CFSC

Reduction strategy for the GHB criterion

With the theoretical existence of CFSC proved and the explicit expression of CFSC obtained, a new reduction strategy based on the compressive strength of rock mass for the GHB criterion was proposed, which can better reflect the physical meaning of strength reduction than the direct reduction of material parameters. In this strategy, the compressive strength of intact rock σ_ci and the parameter combination s^α are reduced by the same ratio, where s^α is numerically equivalent to Jointing Parameter (JP) of Palmström’s RMi system (Russo 2008), which represented the rock mass quality and structure. m_i, as a parameter representing the degree of intact rock hardness, should not be involved in reduction. However, with the decrease in GSI, the parameter of rock mass m_b will decrease correspondingly. According to the GHB criterion of the 2018 edition (Hoek and Brown 2019), the compressive to tensile ratio and the parameter m_i satisfy the approximate relationship in Eq. (18). Thus, the same reduction ratio of the compressive strength and the tensile strength of intact rock can be realized by keeping m_i constant.

$${{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\left| {\sigma_{t} } \right|}}} \right. \kern-0pt} {\left| {\sigma_{t} } \right|}} = 0.81m_{i} + 7.$$

(18)

The disturbance factor D, which is subjected to blast damage and stress relaxation, should not participate in the reduction. The reduction of s^α is only determined by the reduced GSI. The reduction strategy can be expressed by the formula in Eq. (19).

$$K_{r} = \frac{{\sigma_{ci}^{t} }}{{\sigma_{ci}^{r} }} = \frac{{s^{{_{t} \alpha^{{_{t} }} }} }}{{s^{{_{r} \alpha^{{_{r} }} }} }} = \frac{{f(GSI^{t} )}}{{f(GSI^{r} )}},$$

(19)

where K_r is the reduction ratio and $\sigma_{ci}^{t}$, $s^{t}$ and $\alpha^{t}$ are the parameters of the target slope. $\sigma_{ci}^{r}$, $s^{r}$ and $\alpha^{r}$ are the parameters of the reduced slope.

According to the CFSC, the reduction strategy can be replaced by reducing the parameter ${{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\gamma {\text{H}}}}} \right. \kern-0pt} {\gamma {\text{H}}}}$ and the parameter combination s^α by the same ratio represented by the formula in Eq. (20), because γH is constant during the reduction procedure.

$$K_{r} = \frac{{{{\sigma_{ci}^{t} } \mathord{\left/ {\vphantom {{\sigma_{ci}^{t} } {\gamma H}}} \right. \kern-0pt} {\gamma H}}}}{{{{\sigma_{ci}^{r} } \mathord{\left/ {\vphantom {{\sigma_{ci}^{r} } {\gamma H}}} \right. \kern-0pt} {\gamma H}}}} = \frac{{s^{{_{t} \alpha^{{_{t} }} }} }}{{s^{{_{r} \alpha^{{_{r} }} }} }}.$$

(20)

The reduction scheme relative to CFSC can be represented by Fig. 7a, in which the reduction ratios for ${{\sigma_{ci} } \mathord{\left/ {\vphantom {{\sigma_{ci} } {\gamma {\text{H}}}}} \right. \kern-0pt} {\gamma {\text{H}}}}$ and s^α are the same.

Fig. 7

The graphic representation of the reduction strategy and the example for m_i = 5, β = 60°

According to the reduction strategy, when the slope CFSC fitting formula is determined, the slope critical state parameters can be directly determined by mathematical calculation (the point of intersection of the CFSC and the proportional line determined by the target point) without the need for simulation analysis. The parameters ($GIS^{r}$ and $\sigma_{ci}^{r}$) at the critical failure state are determined by the critical state points ($s^{{_{r} \alpha^{{_{r} }} }}$ and ${{\sigma_{ci}^{r} } \mathord{\left/ {\vphantom {{\sigma_{ci}^{r} } {\lambda H}}} \right. \kern-0pt} {\lambda H}}$). The reduction scheme was applied to several slope examples to determine the value of critical state parameters by the MATLAB program. The graph of the example for β = 60° and m_i = 5 by applying this strategy is displayed in Fig. 7b.

To verify the feasibility of this scheme, 15 slope examples with different slope angles β, m_i values and other parameters of initial states (shown in Table 3) were applied by this reduction strategy to predict the critical state parameters. The disturbance coefficient D was assigned to 0 to simplify the procedure. The model numerical analysis was realized by establishing the numerical slope model and continuously reduce the strength parameters by the reduction rule in Eq. (20) until the strength parameters of the critical state are obtained. The parameters predicted by this strategy were compared with those obtained by simulation model analysis. The results are shown in Table 3.

Table 3 The comparison results of the predicted parameters and simulation parameters for the critical state

From the results of Table 3, it can be seen that the relative errors between the parameters of the critical state predicted by the CFSC and the parameters obtained by simulation analysis are lower than 3%, which proves the validity and accuracy of this strategy.

The analysis of the influence of m _i reduction

To determine whether m_i should be reduced, three slope examples given in this paper are reduced and analysed by applying the strength reduction above. The parameters of the three slope examples are shown in Table 4. The parameters at the slope critical failure state are obtained by numerical simulation with the decrease in m_i from the initial value. With the critical state parameters, the curves of shear stress to the normal stress of the slope are drawn to analyse the influence of m_i decreasing on the strength envelope of the GHB criterion.

Table 4 The geometry and material parameters of the three slope examples

The curves of shear stress to the normal stress of the three slopes at the initial state and the critical failure state are shown in Fig. 8a. It can be seen that the strength envelopes are very close with decreasing mi. The shear stress ratio of the initial state to the critical state varies with the normal stress which is shown in Fig. 8b. When the value of mi decreases by Ratio_mi = 1 ~ 1.5 (Eq. 21), the shear stress ratio increases less than 0.12, which means the reduction of m_i has little inference to the shear strength. According to the conservative principle, the strength envelope is the highest and the shear stress ratio is the smallest when m_i is not reduced, corresponding to the lowest safety factor.

$${{{\text{Ratio}}_{mi} = m_{{i{\text{ - initial}}}} } \mathord{\left/ {\vphantom {{{\text{Ratio}}_{mi} = m_{{i{\text{ - initial}}}} } {m_{{i{\text{ - reduced}}}} }}} \right. \kern-0pt} {m_{{i{\text{ - reduced}}}} }}.$$

(21)

Fig. 8

The curves of shear stress and the shear stress ratio of the three slopes

The definition of factor of safety

The definition of a factor of safety (FOS) is the key to slope stability evaluation. In rock slope engineering, the safety factor is often defined by the ratio of anti-sliding force and sliding force on the sliding surface of the slope. This method relies heavily on the determination of the sliding surface, for example, the global safety factor defined by Yuan et al. (2020). Some scholars directly used the reduction ratio of the GHB criterion parameters as the safety factor to simplify the analysis procedure, which is obviously unreasonable. According to the strength reduction strategy in “Reduction strategy for the GHB criterion”, the strength parameters of the initial state and critical state have been obtained, based on which, a new factor of safety (FOS) definition method independent of sliding surface determination was proposed. In this method, the ratio of the average shear strength between the target state and the critical state was taken as the FOS of the slope, where the average shear strength at the critical failure state represents the sliding force per unit area, and the average shear strength at the initial state represents the sliding resistance force per unit area, which satisfies the meaning of strength reserve. The average shear strength with the range of the normal stress shows overall mechanical behaviour.

The specific calculation process is as follows:

• (1) The range of minimum principal stress σ₃ at the critical state is determined by Eq. (22) based on the literature (Hoek et al. 2002)

  $$\left\{ {\begin{array}{*{20}l} {\sigma_{3\max } = 0.72\sigma_{cm} \left( {\frac{{\sigma_{cm} }}{\gamma H}} \right)^{ - 0.91} } \\ {\sigma_{cm} = \sigma_{ci} \cdot \frac{{(m_{b} + 4s - \alpha (m_{b} - 8s))({{m_{b} } \mathord{\left/ {\vphantom {{m_{b} } 4}} \right. \kern-0pt} 4} + s)^{\alpha - 1} }}{2(1 + \alpha )(2 + \alpha )}} \\ \end{array} } \right.,$$

  (22)

  where $\sigma_{cm}$ represents the global “rock mass strength” reflecting the overall behaviour of a rock mass. $\sigma_{3\max }$ is the upper limit of the minimum principal stress for slopes. $\sigma_{ci}$, $m_{b}$, s, and α are the parameters at the critical state.

• (2) The normal stress σ_n and the shear stress τ at the initial state and the critical state, respectively, are calculated with the corresponding parameters by Eq. (5), and the upper limit of σ_n at the initial state and the critical state ($\sigma_{{_{n\max } }}^{t}$ and $\sigma_{{_{n\max } }}^{r}$) were calculated with the upper limit $\sigma_{3\max }$ at the critical state.

• (3) The arithmetic mean value of shear stress τ within the range σ_n obtained by step 2 is taken as the average shear strength, and the ratio of the average shear strength of the target state to the critical state is taken as the FOS. The formula is as follows:

  $$F_{s} = \frac{{\overline{{\tau^{t} }} }}{{\overline{{\tau^{r} }} }} = \frac{{\int_{0}^{{\mathop \sigma \nolimits_{n\max }^{t} }} {\tau^{t} d\sigma_{n} } /\mathop \sigma \nolimits_{n\max }^{t} }}{{\int_{0}^{{\mathop \sigma \nolimits_{n\max }^{r} }} {\tau^{r} d\sigma_{n} } /\mathop \sigma \nolimits_{n\max }^{r} }}.$$

  (23)

The analysis of slope examples

To verify the validity and accuracy of the proposed method in slope stability analysis, several slope examples selected from the published literature were analysed and discussed. These slope examples are the classical examples that have been repeatedly used in the literature of SRM based on GHB criterion and some of them are from practical engineering cases (Example 9). The examples were classified into two groups for D = 0 and D ≠ 0. The slope parameters at the initial state are shown in Tables 5 and 6. First, the parameters at the critical failure state obtained by the graphic method based on CFSCs were compared with those obtained by numerical simulation, of which the results are shown in Tables 7 and 8. From the table, it can be seen that the relative error of dimensionless parameter λ is less than 8% for D = 0 and less than 10% for D ≠ 0. This proves that the CFSCs for D = 0 and mi ≠ 5,10,15,20,25 obtained by cubic spline interpolation have high accuracy, and the CFSCs for D ≠ 0 obtained by the D ratio are relatively accurate.

Table 5 The slope geometry and rock mass parameters at the initial state for D = 0

Table 6 The slope geometry and rock mass parameters at the initial state for D ≠ 0

Table 7 The slope rock mass parameters at the critical failure state for D = 0

Table 8 The slope rock mass parameters at the critical failure state for D ≠ 0

According to the definition of the factor of safety in “The definition of factor of safety”, the FOS of these slope examples can be calculated with the initial and critical parameters. To verify the validity and accuracy of the reduction strategy and the definition of FOS, the results obtained by graphic analysis and simulation analysis were compared with the FOS obtained by the local linearization method and the Bishop simplified (limit equilibrium method). The results are shown in Table 9.

Table 9 The comparison of FOS of slope examples by different methods

The local linearization method (LLM), as a sophisticated SRM, has been applied in FLAC^3D for solving the FOS of the HB criterion slope. This method is physically more correct than the global approach (Sukanya et al. 2012). Among the Limit equilibrium method (LEM), the Bishop simplified method is a well-known technique and widely applied in slope stability analysis of civil engineering. The LEM is limited by the concepts of circular sliding surfaces and slice, while SRM based on finite element analysis can directly obtain the sliding surface of the slope by considering the stress–strain relationship without the shape assumption of the sliding surface, which made SRM more accuracy and reasonable than LEM (Zhao et al. 2002, 2005). The model analysis and the calculation of FOS with LLM were based on the software FLAC^3D 6.0. The model analysis of the FOSs obtained with Bishop’s simplified method were achieved based on the software Slide 6.0.

The FOS obtained by the proposed method (graphic method) is very close to that of the simulation analysis with the same FOS definition (relative error <  ± 5%). Moreover, the error between the proposed method and the local linearization method is also very low (relative error <  ± 5%). The results of the proposed method are usually smaller than that of the Bishop simplified method, with a relative error lower than 20%.

Discussion

The FOSs obtained by the proposed method are very close to the results of the LLM with an absolute relative error smaller than 5%, has an acceptable error compared with the Bishop simplified method. Moreover, the relative error decreases as the FOS approaches 1.0. According to the literature (Du SG 2018), the slope stability state can be classified by FOS in Table 10. By comparing the FOS, it can be found that the proposed method has the same stability state as the other two methods. The calculation speed and efficiency of the proposed method have a large improvement compared with simulation analysis and local linearization method, where searching for an appropriate reduction ratio takes considerable calculation time.

Table 10 The relationship between the FOS and stability state

The analysis of engineering case

The proposed SRM-based GHB criterion was applied to a limestone slope of an open pit mine located at the junction of central Hebei Plain and Taihang Mountain, in Luquan District, Shijiazhuang City, Hebei province, China. The main mineral components of the ore layer are calcite, dolomite and a small amount of clay minerals. The ore layer is thickly layered, with block and porphyritic structure, weak weathering and relatively intact. The mining area is 0.7972 km², and the end slope forms 6 steps (the length for each step is 70 ~ 280 m, the step height is 15 m, the step width is 8-12 m, and the step slope angle is about 65^° ~ 75^°). The final slope height is about 90 m with a 50° slope angle, and the 3D point cloud map is shown in Fig. 9a. To simplify the analysis procedure, a typical section was chosen to establish the slope model, shown in Fig. 9b. Based on geological observations and laboratory experiments, the material parameters of rock mass are obtained and shown below: γ = 27 kN/m³, m_i = 8, σ_ci = 40 MPa, GSI = 45, D = 0.9, E = 50GPa.

Fig. 9

The 3D point cloud map and its typical section of the open pit slope

Although the limestone slope has multiple steps, an equivalent single-step slope based on the final slope height and slope angle (H = 90 m, β = 50^°) can be applied for the proposed graphical method. The detailed analysis procedure was below:

• (1) The fitting expressions of the CFSCs for m_i = 8, β = 45^°, D = 0 and m_i = 8, β = 60^°, D = 0 were deduced by the cubic spline interpolation based on the fitting expressions in Table 2. The expressions of the CFSCs for m_i = 8, β = 50^°, D = 0 was obtained by linear interpolation of two corresponding CFSCs at β = 45^° and β = 60^°.

• (2) The fitting expressions of the CFSCs for m_i = 8, β = 50^°, D = 0.9 are deduced by multiplying the CFSC of m_i = 8, β = 50^°, D = 0 with the corresponding ratio R_D obtained from “The influence of disturbance factor D on the CFSCs”_, and the explicit expression of the CFSCs for m_i = 8, β = 50^°, D = 0.9 was shown in Eq. (24).

  $$y = 0.01496* \wedge ( - 1.279) + 1.609.$$

  (24)

• (3) The parameters of the critical failure state are obtained from the initial state parameters by reducing σ_ci and s^α with the same ratio defined in Eq. (20), and the graphical analysis was shown in Fig. 10, where the red curve represents the CFSC for m_i = 8, β = 50^°, D = 0.9, the green line represents the reduction path, and the intersection point was determined by the critical state parameters, which can be deduced by the reduction strategy in Eq. (25). The critical state parameters are calculated, ($\sigma_{ci}^{r} = 22.8MPa,GSI^{r} = 38.5$), shown in Table 11.

  $$\left\{ {\begin{array}{*{20}l} {{{\sigma_{ci}^{r} } \mathord{\left/ {\vphantom {{\sigma_{ci}^{r} } {\gamma H}}} \right. \kern-0pt} {\gamma H}} = 10.55} \\ {\left. {s^{{_{r} \alpha^{{_{r} }} }} } \right|_{D = 0.9} = \left. {\exp \left( {\left( {\frac{{GSI^{r} - 100}}{9 - 3D}} \right)\left( {\frac{1}{2} + \frac{1}{6}(e^{{ - \frac{{GSI^{r} }}{15}}} - e^{{ - \frac{20}{3}}} )} \right)} \right)} \right|_{D = 0.9} = 0.0067} \\ \end{array} } \right..$$

  (25)

• (4) The FOS of the slope was calculated by the definition of Eq. (24) based on the parameters f the initial and critical states, and the results was shown in Table 12.

Fig. 10

The demonstration of the graphical method of the slope case

Table 11 The parameters of the slope case at initial state and critical failure state

Table 12 The FOSs obtained by different methods and expert analysis report

The slope model based on the typical section is established in FLAC^3D and the parameters of the critical failure state were obtained by constantly reduce the parameters σ_ci and GSI with the same reduction strategy defined in Eq. (20) until the slope reaches the critical failure state, shown in Table 11. The numerical simulation analysis and the maximum shear strain increment contour at the critical failure state is shown Fig. 11a. The numerical analysis based on the local linearization method and the result is shown Fig. 11b. The analysis result of the Bishop simplified method based on the software Slide was shown in Fig. 12.

Fig. 11

The maximum shear strain contour at the critical failure state with numerical simulation analysis and local linearization method

Fig. 12

The results of Bishop’s simplified method with Slide software

The FOSs obtained by different methods were shown in Table 12. The results show that the FOS obtained by the proposed graphical analysis method is between that of the Bishop simplified and simulation analysis. Compared with other methods, the FOS relative error of the Graphical analysis method is less than 10%, and the stability state for different methods are perfectly the same. The results demonstrate the feasibility and validity of the proposed graphical method in the practical engineering slope case with complex slope form. Moreover, the proposed graphical analysis method demonstrates its great advantages in computation amount and time without the model establishment and the multiple numerical analysis of stability.

Conclusions

This paper proposed a new SRM (graphic method) based on the CFSCs. First, the CFSCs are established based on a large amount of simulation data, the influence of m_i and D on the CFSCs are analysed, and the explicit expressions of the CFSCs are determined by curve fitting. Then, the new strength reduction scheme with the same reduction ratio for $\sigma_{ci}$ and $s^{\alpha }$ based on the CFSCs, and the new definition method of FOS was proposed. This new method was applied to nine slope examples and a practical case of an open pit slope to verify its validity and accuracy. The main conclusions are as follows:

• (1) The parameters $\left( {\frac{{\sigma_{ci} }}{{\gamma {\text{H}}}},s^{\alpha } ,mi,\beta } \right)$ satisfy a relationship at the critical failure state by theoretical analysis. For given m_i and β, the relation between $\frac{{\sigma_{ci} }}{{\gamma {\text{H}}}}$ and $s^{\alpha }$ can be represented by an exponential function. These curves are called CFSCs.

• (2) The variations of the CFSCs with m_i and D are analysed. The CFSCs for any value of m_i can be obtained by cubic spline interpolation. The CFSCs for D ≠ 0 can be obtained by multiplying the CFSCs of D = 0 by the ratio R_D.

• (3) A new reduction strategy based on CFSCs is proposed, where $\sigma_{ci}$ and $s^{\alpha }$ are reduced by the same ratio, m_i remains constant to guarantee the same reduction ratio of the compressive strength and the tensile strength of intact rock, and D subjected to blast damage and stress relaxation should not be reduced. The reduction in $\sigma_{ci}$ and $s^{\alpha }$, representing the strength of intact rock and joint parameters (JP) of the rock mass, respectively, can better reflect the strength reduction of the rock mass. The parameters at the critical state can be obtained by the graphic method based on the CFSCs.

• (4) By comparing the critical state parameters obtained by the graphic method and that from the simulation analysis of slope examples, the CFSCs for different m_i and D have a high accuracy.

• (5) A new definition method of FOS, independent of sliding surface, based on the parameters of the initial and critical states, was proposed. By the analysis of nine slope examples, the results showed that FOSs obtained by the graphic reduction method and the new definition of FOS are close to the results of the local linearization method (LLM) and the Bishop simplified method, with ± 5% relative error compared with the LLM. The accuracy of FOS increases when FOS approaches 1.0, and the stability state assessments by the proposed method are perfectly accurate. The results comparison verified the validity and reliability of the SRM and the FOS definition proposed. The proposed method was applied to a practical case of an open pit limestone slope with multiple steps to demonstrate its feasibility and reliability in engineering application.

• (6) The calculation speed and efficiency of the graphic method have a significant improvement compared with the simulation analysis and the LLM, where searching for an appropriate reduction ratio and multiple numerical analysis of stability take considerable calculation time. Under the same computational power, the proposed method based on computation of MATLAB software need less than 30s to search the critical state parameters and calculate the safety factor, while the simulation analysis based on model equilibrium computation of FLAC^3D software takes more than 20 min. The limitation of this proposed method is that the slope must be homogeneous and isotropic and the slope angle is unique. If the slope has multiple steps with different angles, a equivalent slope angle must be determined for the application of the proposed method.