Three-dimensional simulation of hydraulic fracture propagation height in layered formations

Abstract

The prediction of hydraulic fracture (HF) propagation height is of great significance for hydraulic fracturing design and mitigating unfavorable fracture propagation. The height growth of HF in a layered formation is influenced by multiple factors, including in-situ stresses, Young’s modulus, layer interfaces, and their combined effects, in addition to the influence of stress shadows. In this work, the influence of multiple factors on HF propagation was studied using the 3D hydro-mechanically coupled lattice-spring code. Both vertical and lateral HF growth were evaluated quantitatively, and the non-planar propagation of HFs captured. Numerical modeling results show that the HF height decreases with the increment of minimum horizontal principal stress in adjoining layers. As the horizontal stress will be the major principal stress if it exceeds the vertical stress, the HF plane is gradually deflected into the horizontal plane, and the HF crosses the interface into the adjacent layers. Vertical fracture propagation is promoted in high-modulus layers and inhibited in low-modulus layers. Because of fracture tip blunting induced by the shear slip of the interface and fluid leak-off into the interface, HF propagation height is reduced. Multiple mechanisms can be considered together to describe HF propagation in a layered formation. Considering the effect of a weak interface alone, model results may show HF height containment. With a high-modulus or low-stress layer beyond the interface, the HF could cross the interface, leading to further HF height growth. Besides, the stress shadow effect is highlighted as an important mechanism in HF height containment. The HF may reorient itself to become horizontal, thereby resulting in HF height containment. The model results presented allow an improved understanding of the mechanisms of HF height containment in layered formations.

Introduction

Hydraulic fracturing is a proven practice to improve the performance in unconventional reservoirs (Pettitt et al. 2011; Fisher and Warpinski 2012; Lange et al. 2013). It has also been applied to mitigate high abutment stresses in underground mines (Huang et al. 2018). For these applications, the control of hydraulic fracture (HF) propagation height is of major significance in treatment strategy and the mitigation of undesirable HF propagation. Variations in in-situ stresses and properties of the rock mass are often observed in layered formations. As depicted in Fig. 1, multiple factors can influence the HF propagation height, including the in-situ stress regime, Young’s modulus, layer interface characteristics, and fracture toughness(Gu and Siebrits 2008; Wei et al. 2018).

Fig.1

Schematic showing geomechanical parameters that may influence HF propagation height in layered formations

In-situ stress contrast

The stress contrast between adjoining layers is considered as the predominant factor on HF height containment (Teufel and Clark 1984). In laboratory experiments, a stress contrast of 2–3 MPa was found enough to inhibit HF height growth (Warpinski et al. 1982). A distinct element investigation on HF growth in the formation with stress contrast has been presented (Zhang and Dontsov 2018). Reduction in aperture and pinching has been observed when the HF crosses into the high-stress layer. The finite element model results have shown that the direction and shape of HF in a layered formation are strongly influenced by the stress distribution (Salimzadeh et al. 2019). Whether the HF propagates up or down is depends on stress concentration at the layer interface and gravity forces. Most of the previous publications have not, in general, considered the re-orientation of principal stress (i.e., horizontal stress exceeding the vertical stress in the adjacent layer). The influence of re-orientation of principal stress on HF height growth was considered in this work.

Young’s modulus contrast

The modulus contrast can have a noticeable effect on HF height containment. Some researchers investigated the variation of stress intensity factor (SIF) at crack tip based on the theory of linear elastic fracture mechanics (LEFM) (Cook and Erdogan 1972; Simonson et al. 1978). They argued that HF growth would be hindered by the stiff (high modulus) adjacent layer, whereas the soft (low modulus) adjacent layer encourages HF height propagation. However, field observations have shown that soft layers often produce the containment of HFs (Jeffrey et al. 1992; Philipp et al. 2013). Some scholars argued that both stiff and soft adjacent layers could constrain the HF height growth depending on the different mechanisms (Hanson et al. 1980; Gu and Siebrits 2008). The HF height containment due to modulus contrast will be revisited in the following section, and the 3D growth of HF and hydro-mechanical coupling (HMC) effect are incorporated.

Layer interface control HF growth

The presence of modulus contrast and the stress contrast alone is inadequate to stop the HF growth. Blunting of the HF tip due to shear slippage on an interface could stop height growth (Daneshy 1978). The interface strength-focused criterion has been proposed to predict whether the HF will cross an interface (Gu and Weng 2010). The FracT model has been presented to describe the HF crossing conditions, in which the effect of fluid flow and interface permeability were considered (Weng et al. 2018). Zhao et al. (2020) presented a series of simulations of the interaction between interface and HF, which considered the influence of interface strength, fluid properties, and stress difference. Simulation results have shown that the HF crossing behaviors depend on the extent of slippage on a weak interface.

The combined effect of stress contrast, modulus contrast, and interface characteristics

Field evidence has shown that a multiplicity of factors can significantly influence HF growth, including in-situ stress, interfaces, composite layering, and other rock mass heterogeneities (Fisher and Warpinski 2012). Because of the inherent variability in rock characteristics and ground stresses, in addition to the presence of interfaces, these factors should be considered together to describe HF propagation in a layered formation. Many authors have studied the crossing/arrest behavior of HFs intersecting an interface, considering the combination of multiple factors (Yushi et al. 2017; Fu et al. 2018). For instance, Zhang et al. (2007) argued that the HF initiates in a softer layer may be terminated at the interface due to the presence of high stress or injection with a low-viscosity fluid. Fluid pressure is affected by the injection rate and fluid viscosity, as well as coupling with HF width. HF width depends on the stress and Young’s modulus (Gu and Siebrits 2008). Simplified criteria cannot correctly capture the combined effect on HF containment.

Stress shadow effects on HF growth

A stress shadow involves the formation of a zone of compressive stress normal to the HF plane, which may impact the propagation of adjacent HFs. Laboratory experiment results have shown that a stress shadow could either limit propagation or cause divergence of adjacent HFs (Zhou et al. 2018). The boundary element method has been adopted to study multiple parallel HFs interactions. Model results showed that the width of inner HF is restricted by the outer HFs, whereas the outer HFs tended to be more dominant (Castonguay et al. 2013). A Pseudo-3D (P3D) based model simulation showed similar results (Kresse and Weng 2018). Additionally, for HFs in different layers, the HF propagate into the adjacent layer is also restricted due to stress shadow. Alteration of the local stress field attributed to stress shadow may force HFs to move away or towards each other (Bunger et al. 2012; Zhao et al. 2021). The interactions between multiple HFs and the resulting height containment have attracted much attention.

The distinct element method (DEM) has been widely used in rock engineering problems (Elmo et al. 2013; Gao et al. 2019). The opening of contacts between blocks represents the HF propagation pathway. Thus, the HF pathway is constrained to the predetermined contact geometry. The synthetic rock mass (SRM) approach was presented to remove this deficiency (Pierce et al. 2007). XSite is a three-dimensional hydraulic fracturing numerical simulation program based on the SRM and lattice methods (Damjanac et al. 2020). XSite was employed to investigate HF containment, accounting for the influences of stress contrast, and rock brittleness (Wan et al. 2020). XSite has been employed for simulations of lab-scale hydraulic fracture and natural interface interaction (Bakhshi et al. 2019). Stress shadow induced by multi-HFs growth was also investigated by using XSite. The simulation results revealed that the HF dimension and 3D geometry are greatly affected by the stress shadow, depending on in-situ stress differences and spacing (Liu et al. 2019).

In this paper, the lattice-spring code, XSite, was utilized to study HF height growth in the laminated medium. Several simulations were conducted, which considered the effects of stress contrast, modulus contrast, the weak interface, and the combined effect of these factors, in addition to the influence of stress shadows.

Modeling methodology

In the lattice-spring code, XSite, HF propagation is simulated without restricting the HF geometry or HF–joint interaction conditions. Brittle failure of rock is modeled by spring rupture. The opening and slip of joints are described using the smooth joint model (SJM). HF propagates as a combination of intact-rock failure in tension and slip and opening on joints. (Damjanac et al. 2020). The verification of HF propagation in a viscosity-dominated regime and the storage-toughness-dominated regime has been presented by (Damjanac and Cundall 2016 and Fu et al. 2019) respectively.

The lattice-spring mechanical formulation

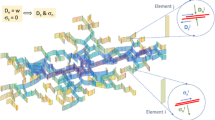
The lattice is a quasi-random three-dimensional array of nodes connected by springs. (Fig. 2a). When the average spacing (i.e., the lattice resolution) is relatively small compared to the length scale of interest, the lattice response is equivalent to that of a continuum. Both the fracturing of intact rock (through spring breakage) as well as rock movement on joints (weak planes) are considered. The joints (weak planes) are inserted into the lattice spring network using an SJM approach, which allows simulation of sliding of a pre-existing joint, unaffected by any artificial joint surface roughness. The springs between the nodes break when their strength (in tension) is exceeded. Breaking of the springs corresponds to the formation of microcracks, and microcracks may link to form macroscopic fractures(Damjanac et al. 2011). The tensile strength is used in the criterion for fracture propagation within intact blocks. The shear criterion is used for pre-existing joints.

Fig. 2

Mechanical model: (a) schematic of a lattice array, with the implementation of a smooth joint [after (Cundall 2011)]; (b) bond strength envelope [after (Itasca Consulting Group 2008)]

The motion law for translational degrees of freedom depends on the following formula (Damjanac et al. 2020):

$$\dot{u}_{{\text{i}}}^{{\left( {t + \Delta t/2} \right)}} = \dot{u}_{{\text{i}}}^{{\left( {t - \Delta t/2} \right)}} + \sum F_{{\text{i}}}^{{\left( {\text{t}} \right)}} \Delta t/m$$

(1)

$$u_{{\text{i}}}^{{\left( {t + \Delta t} \right)}} = u_{{\text{i}}}^{{\left( {\text{t}} \right)}} + \dot{u}_{{\text{i}}}^{{\left( {t + \Delta t/2} \right)}} \Delta t$$

(2)

where $u_{{\text{i}}}^{{\left( {\text{t}} \right)}}$ and $\dot{u}_{{\text{i}}}^{{\left( {\text{t}} \right)}}$ are the position and velocity of component $i$ at time $t$, respectively. m is the mass of node, $\sum F_{{\text{i}}}^{{\left( {\text{t}} \right)}}$ is the sum of all force components i acting on the node with time step Δt.

Spring force variation and relative displacement are calculated by the velocities of the nodes (Damjanac et al. 2020):

$$F^{{\text{N}}} \leftarrow F^{{\text{N}}} + \dot{u}^{{\text{N}}} k^{{\text{N}}} \Delta t$$

(3)

$$F_{{\text{i}}}^{{\text{S}}} \leftarrow F_{{\text{i}}}^{{\text{S}}} + \dot{u}_{{\text{i}}}^{{\text{S}}} k^{{\text{S}}} \Delta t$$

(4)

where F is the spring force, k is the spring stiffness. N represents normal, S represents shear. The spring will break (the microcrack will be formed) if the force exceeds the calibrated spring strength.

The movement on unbonded joints (sliding and opening) is determined by Eq. (5) (Cundall 2011):

$$\begin{gathered} If\; F^{{\text{n}}} - pA < 0\; then\; F^{{\text{n}}} = 0,F_{{\text{i}}}^{{\text{s}}} = 0; \hfill \\ else F_{{\text{i}}}^{{\text{s}}} \Leftarrow \frac{{F_{{\text{i}}}^{{\text{s}}} }}{{\left| {F_{{\text{i}}}^{{\text{s}}} } \right|}}\min \left\{ {\left( {F^{{\text{n}}} - pA} \right)\tan \phi ,\left| {F_{{\text{i}}}^{{\text{s}}} } \right|} \right\} \hfill \\ \end{gathered}$$

(5)

where Fⁿ is the normal force, $F_{i}^{s}$ is the vector of shear force, $\phi$ is the friction angle, p is the fluid pressure, A is the apparent area.

The status of a bonded joint depends on the following logic: if $F^{{\text{n}}} - pA + \sigma_{{\text{c}}} A < 0$ or $\left| {F_{{\text{i}}}^{{\text{s}}} } \right| > \tau_{{\text{c}}} A$ (the bond fails in tension or shear), the joint status follows Eq. (5) ($\sigma_{{\text{c}}}$ is the bond tensile strength, $\tau_{{\text{c}}}$ is the bond shear strength); else, the bond remains intact. Overall fracture depends on both fracture of intact material (bond breaks) as well as yield of joint segments.

Flow in the fractures

The flow in the fractures, both pre-existing (specified as the model input) and newly created (by breaking the lattice springs), is solved within the network of fluid nodes connected by the pipes (one-dimensional flow elements). As depicted in Fig. 3, the fluid pressures are stored in the fluid nodes that act as penny-shaped microcracks located at the broken springs or springs intersected by the pre-existing joints. The geometry of the flow model is a function of the geometry of the fractures in the solid model, and it is automatically generated and updated based on the evolution of the solid model (i.e., generation of new cracks) (Damjanac et al. 2020).

Fig. 3

Schematic representation of the pipe network [after(Damjanac et al. 2016)]

The flow rate along the pipe is calculated based on lubrication theory (Batchelor 1967):

$$q = \beta k_{{\text{r}}} \frac{{a^{3} }}{{12\mu_{{\text{f}}} }}\left[ {p^{{\text{A}}} - p^{{\text{B}}} + \rho_{{\text{w}}} g\left( {z^{{\text{A}}} - z^{{\text{B}}} } \right)} \right]$$

(6)

where a is aperture, $\mu_{{\text{f}}}$ is fluid viscosity, p^A and p^B are hydraulic pressures at nodes “A” and “B”, respectively, z^A and z^B are elevations of nodes “A” and “B” respectively, $\rho_{w}$  is fluid density, and g is gravitational acceleration. k_r is the relative permeability, which depends on saturation, s:

$$k_{{\text{r}}} = s^{2} \left( {3 - 2s} \right)$$

(7)

Calibration parameter β is applied to relate the joint conductivity to the conductivity of a pipe network. The calibrated relation between β and the resolution is built into the code.

The pressure increment with a timestep of Δt can be calculated as:

$$\Delta p = \frac{Q}{V}k_{{\text{f}}} \Delta t$$

(8)

where k_f is the fluid bulk modulus, $V$ is the volume of a fluid element.

$$Q = \mathop \sum \limits_{i} q_{i}$$

(9)

is the sum of all flow rates q_i, from the pipes linked to the fluid element.

Coupling scheme

The coupling of fluid flow and mechanical deformation is incorporated in XSite. The deformation and damage of the solid depending on the loading on it. Fluid pressure is affected by solid deformation. Fracture permeability is determined by the HF aperture and the mechanical deformation (Damjanac et al. 2020).

Fracture propagation criteria

The main lattice model remains as a coarse mesh, the sub-lattice was generated with finer mesh sizes to reach the rock particle scale dimensions. If there is no sub-lattice, the spring tensile strength is calculated based on both tensile strength and toughness of rock(Damjanac et al. 2020).

The criteria for HF propagation are based on a J-integral formulation. The stress intensity factor, K_I, can be calculated as:

$$K_{{\text{I}}} = \sqrt {JE}$$

(10)

where E represents Young’s modulus. If K_I < K_IC (where K_IC is the rock toughness), then the spring tensile strength is utilized to detect spring failure; Otherwise, the K_I is compared to K_IC to detect spring failure.

Model configuration

The dimension of rock was assumed as 5 m × 5 m × 5 m (Fig. 4). The rock mass consists of three layers with different Young’s modulus (E) or minimum horizontal principal stress (σ_x) values for the different model sets. The thickness of the middle layer is 1.5 m. To initiate HF propagation, a starter fracture is positioned at the center of the block. The starter fracture (normal to the x-axis) has a radius of 0.2 m. The fracturing fluid (water) used in hydraulic fracturing has a viscosity of 1 mPa·s. The main lattice is generated here and the model resolution is defined as 0.12 m. The mechanical parameters of rock used in the simulation are listed in Table.1.

Fig. 4

Typical XSite model configuration

Table 1 Mechanical parameters of rock in the XSite model

XSite model results

Effect of stress contrast

For all five simulations, σ_x = 10 MPa in the middle layer, and for all three layers, σ_y = 15 MPa and σ_z = 10 MPa. In each simulation, σ_x was assumed as 5, 7.5, 10, 12.5, and 15 MPa, in the upper and lower layers. The rock has Young’s modulus of 20 GPa. Simulations were conducted under a constant injection rate of 0.002 m³/s for 6 s.

Figure 5 shows the HF geometry with varying σ_x in the upper and lower layers. In general, the main HF is parallel to the max principal stress, which is oriented along y. The height of the HF decreased with σ_x, whereas the length of the HF increased with σ_x. The HF extended farther into the adjacent layers when the magnitude of σ_x was lower compared to the base model (σ_x = 10 MPa). When σ_x was changed from 10 MPa to 15 MP, the HF height was contained, and the lateral growth of the HF was enhanced. The predominant propagation direction of HF changes from the vertical direction to the horizontal direction.

Fig. 5

Hydraulic fracture growth for varying assumed σx in the upper and lower layers: (a) 5 MPa, (b) 7.5 MPa, (c) 10 MPa, (d) 12.5 MPa, and (e) 15 MPa, (σy = 15 MPa and σz = 10 MPa in all three layers)

Figure 6a shows that an increase in assumed σ_x from 5 to 15 MPa resulted in a decrease in the height of the HF (from 4.05 to 2.70 m). Conversely, the length of the HF increased from 2.77 to 4.30 m as assumed σ_x changed from 5 to 15 MPa (Fig. 6b).

Fig. 6

Effects of changes in assumed σx in the upper and lower layers on HF growth: (a) vertical growth (height) and (b) lateral growth (length)

Figure 7 shows the side view of the HF for the case of σ_x = 15 MPa in the adjacent layers showing non-planar HF propagation. Model results show that the HF propagates vertically in the middle layer and then gradually deflects into the horizontal plane as it propagates into the upper and lower layers. Continued HF propagation occurs in a pathway perpendicular to the vertical direction.

Fig. 7

Side view of the HF growth for the case of σx = 15 MPa in the upper and lower layers

Effect of Young’s modulus contrast

For all five models, the assumed modulus was 20 GPa in the middle layer. In the adjacent layers, Young’s modulus (E) value was changed throughout the various simulations (5 GPa, 10 GPa, 20 GPa, 40 GPa, and 60 GPa). The stress field was assumed as: σ_x = σ_y = 5 MPa, σ_z = 7.5 MPa. Simulations were conducted under a constant injection rate of 0.0005 m³/s for 3 s.

Figure 8 shows the geometry of the HF with varying Young’s moduli in the adjacent upper and lower layers. For the case of E = 5 GPa, almost the entire fracture plane was contained within the middle layer. As the assumed modulus increases from 5 to 60 GPa, the HF progressively increases in height propagating within the adjacent layers. For the case of E = 60 GPa, the aperture of the HF in the adjacent layers was smaller than that for the case E = 20 GPa.

Fig. 8

HF growth for varying Young’s modulus in adjacent layers: (a) 5 GPa, (b) 10 GPa, (c) 20 GPa, (d) 40 GPa, and (e) 60 GPa

As shown in Fig. 9a, XSite model results indicate a marked increase in the HF height (from 1.66 to 4.90 m) with an increase in modulus from 5 to 60 GPa. Specifically, as the assumed modulus was changed from 5 to 20 GPa, the height of the HF increased from 1.66 to 3.25 m (an increase of 1.59 m). The simulated height of the HF showed a rise of 1.65 m as the assumed modulus increased from 20 to 60 GPa. In contrast, the length of the HF decreased (from 3.65 to 2.86 m) with an increase in the assumed modulus, Fig. 9b. A marked decrease in length of the HF was simulated as the assumed modulus was increased from 5 to 20 GPa. With a further increase in the assumed modulus from 20 to 60 GPa, the length of the HF did not change significantly.

Fig. 9

Effect of changes in Young’s modulus in the adjacent layers on HF growth: (a) vertical growth and (b) lateral growth

Effect of the weak interface

To simulate the effect of a weak interface on the HF propagation, two parallel square interfaces with dimensions of 5 m × 5 m were symmetrically incorporated in the base model. The spacing between two interfaces was assumed as 1.5 m. The initial interface aperture was assumed to be 1 × 10^–4 m (Note that the interface aperture is varied in the field)(Gudmundsson 2011). Five cases were then simulated with varying assumed interface cohesion of 0.2, 0.6, 1, 1.4, and 1.8 MPa, respectively. The weak interface has a tensile strength of 0.015 MPa and a friction angle of 45 °. The stress field was assumed as σ_x = σ_y = 5 MPa, σ_z = 10 MPa. The rock has a modulus of 20 GPa. Simulations were conducted under the circumstance of treatment with a constant injection rate of 0.0035 m³/s for 4 s.

Figure 10 shows that with the presence of a weak interface, the height of the HF was significantly limited. For the case of c = 0.2 MPa, the HF did not cross the interface, and the interface completely stopped the height growth of the HF. As the assumed cohesion was changed from 0.2 to 1.8 MPa, the HF tends to cross the interface. For crossing cases (c = 1 MPa, 1.4 MPa, and 1.8 MPa), no significant variation in the height of the HF was observed. The aperture of the two interfaces was increased to about 3 × 10^–4 m due to fluid leak-off at the interface.

Fig. 10

HF crossing interfaces with varying assumed cohesion: (a) 0.2 MPa, (b) 0.6 MPa, (c) 1 MPa, (d) 1.4 MPa, and (e) 1.8 MPa

3.4 Combined effects of assumed model inputs

Taking the case c = 0.2 MPa (see Fig. 10a) as a base model, three models were simulated by varying, (i) Young’s modulus in adjacent layers, (ii) the minimum horizontal principal stress in adjacent layers, and (iii) the viscosity of the fluid.

Compared with the case c = 0.2 MPa (see Fig. 10a), Fig. 11 illustrates that the HF can cross the two weak interfaces when the upper and lower layers are stiffer (E = 40 GPa) than the middle layer (E = 20 GPa). The high Young’s modulus in the adjacent layers promoted HF height growth, whereas the interface limited HF growth. In this case, the contribution of the high Young’s modulus on height growth was greater than the containment effect of the weak interfaces. Additionally, the aperture of the HF was reduced when the HF crossed the interface into the stiffer layer (see the color variation of the HF on the two sides of the interface in Fig. 11).

Fig. 11

The combined effect of modulus contrast and the weak interface on HF growth

Compared with the case c = 0.2 MPa (see Fig. 10a), Fig. 11 shows that the HF crossed the two weak interfaces when the assumed σ_x was low (2.5 MPa) in the adjacent layers. The lower minimum horizontal principal stress in the adjacent layers promoted HF height growth, whereas the interface limited HF growth. The contribution of the low minimum horizontal principal stress to HF growth was greater than the containment effect of the weak interfaces. Compared with Fig. 11, no abrupt reduction in the aperture of the HF was observed when the HF crossed the interface into the adjacent layers (see the color variation of the HF on the two sides of the interface in Fig. 12).

Fig. 12

Combined effects of stress contrast and the weak interface on HF growth

Figure 13 presented a simulation of the use of higher viscosity fluid (3 mPa·s) base on the model depicted in Fig. 10a. The rock has a modulus of 20 GPa. Compared with the case of c = 0.2 MPa (see Fig. 10a), Fig. 12 indicates that the increase in fluid viscosity was conducive to the HF crossing the weak interface, leading to the height growth. No abrupt reduction in the aperture of the HF was observed when it crossed the interface into the adjacent layers (see the color variation of the HF on the two sides of the interface in Fig. 13).

Fig. 13

Combined effects of the weak interface and fluid viscosity on HF growth3.5 Effect of the stress shadow

As depicted in Fig. 14a, a rock volume of 6 m × 6 × 6 m was considered to study the stress shadow effects. The thickness of the middle layer was 1.5 m. The three layers were assigned different values of Young’s modulus: 5, 20, and 40 GPa, respectively. An injection point was positioned in each layer. Injection point two was positioned at the center of the block. The lateral and vertical separation distance of the three injection points was 1.5 m. The considered in-situ stress was σ_x = σ_y = 5 MPa, and σ_z = 7.5 MPa. Simulations were conducted under the condition of simultaneous injection with a constant injection rate of 0.001 m³/s for 3 s.

Fig. 14

Stress shadow effect on HF propagation within different layers; (a) model setup, (b) front view, (c) top view, and (d) side view

Figure 14b shows that HF 1 propagated vertically in the soft layer but reoriented itself to the horizontal plane as it propagated into the central, moderately stiff layer, resulting in an L-shaped fracture geometry. Therefore, the height of HF 1 was constrained. Similarly, HF 2 approached HF 3 when it propagated into the stiff layer, also resulting in an L-shaped fracture. In contrast, HF 2 barely crossed into the soft layer from the moderately stiff layer. For HF 3, a slight extension was noted within the moderately stiff layer, and the main part of HF 3 was contained within the stiff layer.

In general, multiple HFs initiated in different horizontal layers tend to move toward each other as they propagate into the same layers, causing the re-orientation of HFs. The dimensions of the HF initiated in the stiff layer are greater than those in the soft layer (see Fig. 14d). The aperture of HF 1 in the soft layer was greater than that in the moderate stiff layer.

Discussion

Effect of stress contrast

HF height containment due to high confining stress was captured in our model, as well as the lateral growth of HF. Height containment is expected to occur if the adjacent layer has higher stress. In contrast, extensive propagation is likely to occur in adjacent layers with lower stress. The over-riding principle for the HF propagation is following the path of least resistance. The lateral growth was relatively enhanced in the middle layer when the adjacent layer has higher stress, and the overall HF tends to be contained in the low-stress layer (refer to Fig. 5). Additionally, the deflection/re-orientation of HFs was also simulated when the re-orientation of the principal stress was incorporated. As the horizontal stress exceeded the vertical stress, the simulated HF was deflected into the horizontal direction, thus the vertical propagation of the HF was contained. The 3D non-planar propagation of the HF limits the applicability of 2D plane strain model approaches. Our model results highlight that the overall propagation of HFs depends on lateral, upward, and downward growth. Three-dimensional investigation of HF growth is hence of major significance in the understanding of HF height containment.

Effect of Young’s modulus contrast

There has been considerable discussion in the published literature concerning the influence of modulus contrast on HF height containment. According to LEFM solutions, the SIF reduces to zero as the HF approaches a stiffer layer, which appears to serve as a barrier preventing the HF from crossing (Simonson et al. 1978; Thiercelin et al. 1987). When an HF approaches a soft layer from a stiff layer, the SIF increases to infinity (Simonson et al. 1978; Ming-Che and Erdogan 1983). Consequently, a soft layer favors HF propagation. However, this argument contradicts both experimental and field data (Daneshy 1978; Philipp et al. 2013). Note that the LEFM solutions have not, in general, accounted for the condition of a fracture spanning boundary. Specifically, the SIF decreases once the HF crosses the boundary into the soft rock, and further HF growth is restricted (Huang et al. 2019). Conversely, the SIF increases after the HF crosses the boundary into the stiff rock (Gu and Siebrits 2008). In summary, HF growth would be enhanced as the HF crosses the interface into the stiff rock. A soft layer limits HF growth when the HF propagates into the soft rock.

The crack-tip tensile stress is magnified in the stiff layer (E = 100 GPa) next to the tip (refer to Fig. 15a). The enhanced tensile stress tends to induce a new fracture in the stiff layer (Gudmundsson and Brenner 2001). In contrast, the soft layer (E = 1 GPa) dissipates the induced tensile stress, which may lead to HF arrest (refer to Fig. 15b).

Fig. 15

HF approaching neighboring layers with different moduli. (The contours truncated at 1 MPa and 10 MPa) [after (Gudmundsson and Brenner 2001)]

Stiff layers restrict the HF width and the fluid flow into the HF tip, thereby inhibit the HF height growth (van Eekelen 1982). However, the opposite conclusion has been drawn by (Gu and Siebrits 2008). Note that HF width and fluid flow is coupled in Gu and Siebrits’s study (the coupling effect was also included in our XSite models), whereas van Eekelen’s research was conducted under an assumption of unchanging fluid pressure in the HF. Because of the hydro-mechanical coupling effect, the aperture of the HF in the stiff rock is smaller than that in the soft rock. Conversely, the dimensions of the HF in the stiff layer are greater than those in the soft layer, under a constant injection rate (refer to Fig. 8).

Effect of the weak interface

Previous studies have shown that the HF height is substantially reduced when the HF encounters weak interfaces (Yushi et al. 2017; Zhao et al. 2020). Two aspects may explain the effect of weak interface on HF height growth.

Tip blunting induced by a shear slip on the interface

High interface strength is conducive to transmitting crack-tip tensile stress into the medium on the opposite side of the interface (Gu and Weng 2010). The crack-tip stress field will remain symmetric if the HF encounters a strong interface, which promotes the HF to cross the interface (Lash and Engelder 2006). Shear sliding is more likely to occur at the weak interface because of its low shear strength. The crack-tip tensile stresses are reduced, and the HF tip becomes blunted as a result of shear slippage (Cooke and Underwood 2001). Consequently, an HF may cease to propagate along its original path when it encounters a weak interface.

Leak-off into the interface

A high-permeability interface could temporarily stop the HF growth when the HF crosses it. After the HF crosses the interface, the HF propagation velocity may decrease due to fluid loss (Chuprakov and Prioul 2015). The interface permeability (in the slippage zone) is a function of the extent of shear slippage (Weng et al. 2018). Depending on the interface permeability and the extent of shear slip, leak-off into the interface may produce a noticeable effect on the HF height growth. A simplified crossing criterion can fail to capture the important effects of interfaces on HF containment in most field cases, and further research is required to address this issue.

Combined effect of model input parameters

The factors mentioned above and others should be considered together to describe HF propagation in layered formations. It is essential to simulate all these related mechanisms when predicting HF growth. For instance, accounting solely for the effect of a weak interface would simulate HF height containment (see Fig. 10a), whereas, with the presence of a modulus contrast or stress contrast, the HF could, in fact, cross the interface, leading to further HF height growth (see Figs. 11 and 12). Treatment with high-viscosity fluid in a formation with a weak interface can lead to contrasting results in HF height growth. Specifically, high-viscosity injection fluid reduces fluid leak-off into the interface, encouraging the HF to cross the weak interface. However, a high-viscosity injection fluid also limits fluid invasion into rock, reducing the overall dimensions of the HF. It is essential to investigate the range of mechanisms that could be involved in a specific case before a reliable conclusion can be reached. The precise analysis of the contributions of such multiple mechanisms is a major challenge, which cannot be fully accomplished by the use of simplified criteria and numerical simulations. As shown in the model results section, this paper has presented a few simple cases to account for such combined effects. However, other possible combinations (e.g., the combination of stress contrast and modulus contrast) and other parameters (e.g., permeability, toughness, and injection rate) were not considered in this work.

Effect of stress shadow

Stress shadow may contribute to or undermine the effectiveness of a fracturing treatment. Multiple HFs amplify the increase in the minimum principal stress in the region between two HFs. One can expect a reduction in the aperture of HFs in the inter-fracture region (Nagel et al. 2013). Thus, the height of HFs would be limited by a high magnitude of the principal stress. Induced stress could locally alter the magnitudes and orientations of the principal stresses, and thus may change the HF height and propagation pathway (Salimzadeh et al. 2017). The effect of 3D stress shadow on HF propagation has been studied based on a P3D model (Kresse and Weng 2018). The results showed that a more accurate prediction on the height growth and width profile could be reached by including the stress shadow effect. However, the P3D model can fail to capture the deflection/re-orientation behavior of HF propagation in a 3D setting (see Fig. 16). A more detailed description of the limitation of the P3D model has been presented (Adachi et al. 2010).

Fig. 16

Effect of stress shadow on HF growth in a P3D model [after Kresse and Weng 2018)]

In the XSite model (see Fig. 14b), the HF deflection behavior induced by stress shadow was simulated and may represent a distinct mechanism of HF height containment. The assumed model stress state was assumed as σ_x = σ_y = 5 MPa and σ_z = 7.5 MPa. When two HFs propagate toward each other, the minimum principal stress (σ_x) in the inter-fracture zone increased (the increased σ_x may exceed the σ_z). In turn, the increased minimum principal stress could exert a significant effect on further propagation paths of the HFs. Therefore, multiple HFs initiated in different horizontal layers tend to move toward each other as they propagate into the same layers, potentially intersecting with each other. The stress shadow is mainly a consequence of the treatment design, implying that different treatment parameters could lead to different extents of the stress shadow effect. Additionally, the stress shadow can be affected by multiple factors, including stress anisotropy, Poisson's ratio, and fluid pressure, among others (Taghichian et al. 2014). Further research is required to fully understand the effect of the stress shadow on HF height containment.

This work aimed to increase awareness of multiple mechanisms that may contribute to HF height containment. In-situ stress, Young’s modulus, layer interfaces, treatment parameters, and various other factors significantly limit the suitability of simplified analytical and numerical tools. Furthermore, hydraulic fracturing is a multi-physics problem requiring a robust simulator that can incorporate solid deformation, fluid flow, HF propagation, and their interaction, in a coupled context. Numerical simulation has made important contributions to the understanding of the mechanisms of HF height containment. Notwithstanding, reliable prediction of HF height growth and propagation path remains challenging because of variations in the stress state, rock mass heterogeneity, spatial variability of the interface properties. Additionally, the model dimension and treatment parameters must be considered seriously in the design of a real system. It is important to perform scaling analysis to properly extrapolate the small-scale model results to real field conditions. It is challenging to apply simplified numerical modeling approaches, and the use of more sophisticated 3D models incorporating the synthetic rock mass approaches is required.

Conclusions

In this paper, a lattice-spring code was adopted to study the hydraulic fracture height growth in layered formations. Several simulations were conducted to account for the effects of stress contrast, Young’s modulus contrast, and a weak interface, as well as their combined effects and stress shadow effects. Both vertical growth and lateral growth were evaluated quantitatively, and the non-planar propagation of hydraulic fracture was captured. The main conclusions are summarized as follows.

• (1) The simulated hydraulic fracture height decreases, and the lateral growth increases, with an increase in the minimum horizontal principal stress in the adjacent layers. If the horizontal stress in the adjacent layers exceeds the vertical stress, the hydraulic fracture plane gradually deflects into the horizontal plane as it crosses the boundary into the adjacent layers.

• (2) An adjacent layer with a high modulus promotes hydraulic fracture growth, whereas an adjacent layer with a low modulus limits hydraulic fracture growth. The containment mechanism involves a variation of the stress intensity factor when the hydraulic fracture crosses the layer boundary as well as the hydro-mechanical coupling effect during the propagation process.

• (3) The increase of interface cohesion leads to the increase of shear resistance at the interface, which contributes to the hydraulic fracture crossing the weak interface. Because of fracture tip blunting induced by the shear slip of the interface and fluid leak-off into the interface, the hydraulic fracture height growth is reduced due to the effect of a weak interface.

• (4) Multiple mechanisms can be considered together to describe hydraulic fracture propagation in a layered formation. The effect of a weak interface alone may lead to simulated hydraulic fracture containment. However, with the presence of a high-modulus or low-stress layer beyond the interface, the simulated hydraulic fracture could cross the interface, leading to further height growth.

• (5) The initiation of multiple fractures from different layers could be subjected to a stress shadow effect, causing deviation of the fracture plane. Moreover, the hydraulic fracture may reorient itself to become parallel to the horizontal plane, resulting in the containment of the vertical growth of hydraulic fracture.