Introduction

The control of gas-induced disaster is still a heavy task in mining industry. With the increase of mining depth, coal mine accidents such as gas-induced disaster still occur frequently although some measures such as mining automation have been made. Different engineering measures (Alonso et al. 2003; Karacan 2007; Liu et al. 2017) have been employed to reduce the gas content near the excavation. These measures can reduce gas accumulation and suppress gas outbursts to some extent, thus avoiding most of gas-induced accidents. It is shown that underground excavation and coalbed methane (CBM) drilling may cause unloading failure of coal seam and increase the emissions of coal seam gas (Yin et al. 2015). Therefore, understanding the accumulation of methane near the coal wall along the borehole is meaningful for the safety evaluation in coal mining industry.

The accumulation of methane near the coal wall along the wellbore is the result of the interaction of rock deformation and gas flow. In rock deformation process, some analytical solutions are available for both stress and displacement. They used different constitutive models such as an elastic–plasticity model after the combination of failure criterion (Carranza-Torres 2004; Guan et al. 2007; Yang and Huang 2010; Zhang et al. 2010; Lu and Yang 2013). For examples, Brown et al. (1983) presented a closed-form solution and an analytical solution for a plastic model by means of a stepwise sequence of calculations. They also proposed a damage variable to take the degradation of materials or the degree of strain softening into accounts. All of these studies ignored the volumetric strain or compaction in the pre-peak deformation stage. When compaction is ignored in this pre-peak deformation stage, it may cause a big error in calculating stress and strain around the borehole. Because coal experiences shear compaction in this pre-peak deformation process, the compaction may affect the distribution of permeability and the accumulation of natural gas near the borehole. Therefore, the compaction in the elastic zone has to be carefully considered when the accumulation of natural gas or permeability distribution around the borehole is computed.

Coal is a typical pore/fracture system (Gilman and Beckie 2000; Clarkson et al. 2007; Booth et al. 2017; Salmachi and Karacan 2017). Coal permeability is due to a set of fractures known as cleats, it is stress and desorption dependent. Coal permeability enhancement due to stress and desorption can be measured by analysis of production data (Salmachi and Yarmohammadtooski 2015). Although coal permeability models have been studied extensively (Cui and Bustin 2005; Palmer and Mansoori 1996; Qu et al. 2014; Salmachi et al. 2016; Shi and Durucan 2004; Li et al. 2017), a fewer publications are available to account for the permeability behaviors of coals at the post-peak unloading failure stage. Chen et al. (2013) measured the permeability of reconstituted coal specimens and investigated the relationship between damage and coal permeability through the observation of coal microstructures by CT scanning. Wang et al. (2013) conducted post-peak permeability experiments to study the coal permeability under different stress and pore pressure. These experiments revealed the influence of fracture on the permeability of coal. Besides the experimental studies, some researchers tried to establish an effective coal permeability model which is applicable in post-failure state. For example, Xue et al. (2017) adopted an exponential relationship between permeability and volumetric strain to calculate the post-failure permeability. Chen et al. (2016) proposed a post-peak permeability model through adding the logistic growth function and a correction factor to the computational formula of the pre-peak permeability. These models were established by fitting the parameters with the experimental data and the parameters in these functions do not have actual physical meaning, thus it cannot essentially reveal the permeability evolution characteristics of coal mass in the post-peak stage. Tang et al. (2002) and Men et al. (2014) analyzed the flow, stress and damage at the post-peak unloading stage by means of brittle–elastic material with residual strength. In their model, the damage is the main factor that causes the growth of fracture and permeability in the post-peak stage. The permeability increases dramatically at the failure of the elements and a permeability jump is given to these elements with sudden damage although the permeability jump is inconsistent with the experimental observation. Based on the work of Tang et al. (2002), Zhu et al. (2016) proposed a new post-peak permeability model, and permeability increased continuously with the growth of damage of coal. Both of these two theoretical models are established based on a clear physical meaning that the increase in permeability is induced by damage. However, because the value of the parameter in these models is obtained based on experience, there may be the deviations between the results of these models and the experimental results. These studies on permeability models in the post-peak unloading stage were meaningful, but the complex seepage mechanism in post-peak stage is still not clear. Therefore, the evolution of permeability in the post-peak unloading failure stage is one of the focuses in this paper.

In this study, an approach is proposed to analyze the interaction among stress, strain and gas flow around a borehole. Main works contain following five components. First, analytical solutions of stress and strain around a borehole are developed after considering the coal compaction in the elastic zone. Then, a new permeability model is proposed for post-peak unloading failure stage. Third, the analytical solutions of stress and strain and the permeability model for post-peak unloading are used to calculate the distribution of stress, strain, and permeability around the borehole. The gas flow equation is numerically solved to obtain the gas distribution. The gas content predicted by this approach is then verified by two sets of field data. Fourth, parametric study is conducted to investigate the effect of the damage enhancement coefficient, initial geo-stress, drilling volume, and uniaxial strength on the gas pressure profile and the permeability around the borehole. Finally, the zoning of permeability and pore pressure is discussed. This study can provide a basis for a fast evaluation of drilling effect on permeability evolution and pore pressure distribution.

Analytical solutions of stress and strain in coal around a borehole

Constitutive model with strain-softening behaviors

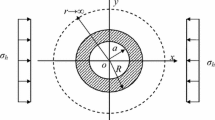
The underground drilling disturbs the rock nearby the newly formed cavity. After drilling, the surrounding rock usually experiences strain softening and forms three stress zones which correspond to the three stages in Fig. 1a. As shown in Fig. 2, R0, Rb and Rp are the radii of the borehole, residual state zone and strain-softening zone, respectively.

Fig. 1
figure 1

Simplified three stepwise curve of rock (Brown et al. 1983)

Full size image
Fig. 2
figure 2

Illustration of three zones due to excavation or drainage drilling

Full size image

At the pre-peak deformation stage, the rock is usually in the elastic stage (I) and few damage is observed (Peng et al. 2015). In the plastic-softening stage (II), the slope of curve \({k_{\text{s}}}\) reflects the softening extent of rock (Brown et al. 1983; Lu and Yang 2013). This slope can be calculated from conventional triaxial compression tests. For an ideal elastic–plastic rock, \({k_{\text{s}}}=0\). If Mohr–Coulomb yield function is applicable, the stresses in the post-peak zone satisfy

$$\sigma _{\theta }^{{\text{p}}}={k_{\text{p}}}\sigma _{{\text{r}}}^{{\text{p}}}+\sigma _{{\text{c}}}^{{\text{p}}},$$
(1)

where \(\sigma _{\theta }^{{\text{p}}}\) and \(\sigma _{{\text{r}}}^{{\text{p}}}\) are the hoop and radial stress components in the strain-softening zone, respectively. \({k_{\text{p}}}={\tan ^2}(45^\circ - \varphi /2)\), where \(\varphi\) is the internal friction angle of coal in that zone. \(\sigma _{{\text{c}}}^{{\text{p}}}\) is the compressive strength. When rock enters the residual stress stage, \(\sigma _{{\text{c}}}^{{\text{p}}}=\sigma _{{\text{c}}}^{{\text{*}}}\). \(\sigma _{{\text{c}}}^{{\text{*}}}\) is the uniaxial residual strength. Generally, the uniaxial compressive strength in the unloading zone can be expressed by

$$\sigma _{{\text{c}}}^{{\text{p}}}={\sigma _{\text{c}}} - {k_{\text{s}}}E\left[ {\varepsilon _{\theta }^{{\text{p}}} - \varepsilon _{\theta }^{{\text{e}}}\left| {_{{r={R_{\text{p}}}}}} \right.} \right],$$
(2)

where \(E\) is the Young’s modulus. The superscripts “p” and “e” refer to plastic and elastic parts, respectively.

The dilatancy of rock is intensive in the post-peak zone. The dilatancy is widely expressed by (Brown et al. 1983; Lu and Yang 2013)

$$\Delta {\varepsilon _{\text{r}}}+m\Delta {\varepsilon _\theta }=0,$$
(3)

where \(\Delta {\varepsilon _{\text{r}}}\) and \(\Delta {\varepsilon _\theta }\) are the increments of radial strain and hoop strain in the strain softening and residual state zones, respectively. The value for \(m>1\) represents the dilatancy extent. m = 1.0 indicates no dilation. As shown in Fig. 1b, the m is denoted as \({m_{\text{p}}}\) in the strain-softening zone and as \({m_{\text{b}}}\) in the residual state zone.

These studies are based on elastic–perfectly plastic or elastic–brittle–plastic or three step–wise models, thus rock is in the elastic zone before peak stress or strength. The volumetric strain curve was shown in Fig. 1c by Brown et al. (1983), but his elastic theory induced zero volumetric strain in this elastic zone. This is not the case for rock because the volumetric compaction is observed in the elastic zone. Volumetric strain is observed to decrease slightly in the elastic zone due to compaction and to increase dramatically in the post-peak zone due to dilatancy (Yin et al. 2013; Wang et al. 2013). This paper will extend Eq. (3) to include the compaction in the elastic zone when the m is specified as \(m<1\). This m is denoted as \({m_{\text{e}}}\). Therefore, the increment of volumetric strain is

$$\Delta {\nu _\varepsilon }=\Delta {\varepsilon _{\text{r}}}{\text{+}}\Delta {\varepsilon _\theta }{\text{=(}}1 - m{\text{)}}\Delta {\varepsilon _\theta }=M\Delta {\varepsilon _\theta },$$
(4)

where \(M=1 - m\) has different value in each zone as shown in Fig. 1c.

Stress and strain in the elastic zone

The equilibrium equation in polar coordinates is

$$\frac{{\partial {\sigma _{\text{r}}}}}{{\partial r}}+\frac{{{\sigma _{\text{r}}} - {\sigma _\theta }}}{r}=0.$$
(5)

For an axisymmetric problem with infinitesimal deformation, strain components can be expressed by radial displacement \({u_{\text{r}}}\) as

$${\varepsilon _{\text{r}}}= - \frac{{{\text{d}}{u_{\text{r}}}}}{{{\text{d}}r}},\;\;{\varepsilon _\theta }= - \frac{{{u_{\text{r}}}}}{r}.$$
(6)

where \(r\) is the radial distance from the center.

The stress in the elastic zone is expressed as (Brown et al. 1983; Lu and Yang 2013):

$$\sigma _{{\text{r}}}^{{\text{e}}}={p_{\text{i}}} - ({p_{\text{i}}} - {\sigma _{{R_{\text{p}}}}}){\left( {\frac{{{R_{\text{p}}}}}{r}} \right)^2},$$
(7)
$$\sigma _{\theta }^{{\text{e}}}={p_{\text{i}}}+({p_{\text{i}}} - {\sigma _{{R_{\text{p}}}}}){\left( {\frac{{{R_{\text{p}}}}}{r}} \right)^2},$$
(8)

where \({p_{\text{i}}}\) is the initial stress, \({R_{\text{p}}}\) is the boundary between the strain softening zone and the elastic zone, \({\sigma _{{R_{\text{p}}}}}\) is the pressure on the boundary between the strain softening zone and the elastic zone and \({\sigma _{{R_{\text{p}}}}}=\frac{{2{p_{\text{i}}} - {\sigma _{\text{c}}}}}{{{k_{\text{p}}}+1}}.\)

Considering the shear stress-induced compaction of rock in the elastic zone, a dilatancy term is introduced into the constitutive law through the maximum shear stress of \(\tau =\frac{1}{2}\left( {\sigma _{\theta }^{{\text{e}}} - \sigma _{{\text{r}}}^{{\text{e}}}} \right)\). The strain in the elastic zone is gotten as

$$\varepsilon _{{\text{r}}}^{{\text{e}}}= \frac{{1 - {\mu ^2}}}{E}\left( {\Delta \sigma _{{\text{r}}}^{{\text{e}}} - \frac{\mu }{{1 - \mu }}\Delta \sigma _{\theta }^{{\text{e}}}} \right){\left( {\frac{{{R_{\text{p}}}}}{r}} \right)^{{m_{\text{e}}} - 1}}+\frac{{1 - {m_{\text{e}}}}}{{1+{m_{\text{e}}}}}\frac{{1+\mu }}{E}\frac{1}{2}(\sigma _{\theta }^{{\text{e}}} - \sigma _{{\text{r}}}^{{\text{e}}}){\left( {\frac{{R_{p}^{{}}}}{r}} \right)^{{m_{\text{e}}} - 1}},$$
(9)
$$\varepsilon _{\theta }^{{\text{e}}}=\frac{{1 - {\mu ^2}}}{E}\left( { - \frac{\mu }{{1 - \mu }}\Delta \sigma _{{\text{r}}}^{{\text{e}}}+\Delta \sigma _{\theta }^{{\text{e}}}} \right){\left( {\frac{{{R_{\text{p}}}}}{r}} \right)^{{m_{\text{e}}} - 1}}+\frac{{1 - {m_{\text{e}}}}}{{1+{m_{\text{e}}}}}\frac{{1+\mu }}{E}\frac{1}{2}(\sigma _{\theta }^{{\text{e}}} - \sigma _{{\text{r}}}^{{\text{e}}}){\left( {\frac{{{R_{\text{p}}}}}{r}} \right)^{{m_{\text{e}}} - 1}}.$$
(10)

The strain is simplified as

$$\varepsilon _{{\text{r}}}^{{\text{e}}}= - {m_{\text{e}}}H{\left( {\frac{{{R_{\text{p}}}}}{r}} \right)^{{m_{\text{e}}}+1}},$$
(11)
$$\varepsilon _{\theta }^{{\text{e}}}=H{\left( {\frac{{{R_{\text{p}}}}}{r}} \right)^{{m_{\text{e}}}+1}},$$
(12)

where \(H=2(1+\mu )[({k_{\text{p}}} - 1){p_0}+{\sigma _{\text{c}}}]/[E({k_{\text{p}}}+1)(1+{m_{\text{e}}})]\).

The volumetric strain \({\nu ^{\text{e}}}\) in this elastic zone is

$${\nu ^{\text{e}}}=\varepsilon _{{\text{r}}}^{{\text{e}}}+\varepsilon _{\theta }^{{\text{e}}}=(1 - {m_{\text{e}}})\varepsilon _{\theta }^{{\text{e}}}=(1 - {m_{\text{e}}})H{\left( {\frac{{{R_{\text{p}}}}}{r}} \right)^{{m_{\text{e}}}+1}}.$$
(13)

The displacement in the elastic zone is expressed as

$${u^{\text{e}}}=H\frac{{R_{{\text{p}}}^{{{m_{\text{e}}}+1}}}}{{{r^{{m_{\text{e}}}}}}}.$$
(14)

Stress and strain in the strain-softening zone

Both elastic zone and strain-softening zone have the same strain at their boundary. The strain in the strain-softening zone is expressed as

$$\varepsilon _{{\text{r}}}^{{\text{p}}}=\varepsilon _{{\text{r}}}^{{\text{e}}}\left| {_{{r={R_{\text{p}}}}}} \right.+\Delta \varepsilon _{r}^{{\text{p}}},\;\varepsilon _{\theta }^{{\text{p}}}=\varepsilon _{\theta }^{{\text{e}}}\left| {_{{r={R_{\text{p}}}}}} \right.+\Delta \varepsilon _{\theta }^{{\text{p}}}.$$
(15)

The solutions for strain and displacement in the strain softening zone are obtained as follows after the combination of Eqs. (15) and (6) with Eq. (3):

$${u^{\text{p}}}=Hr\left\{ {1+\frac{2}{{1+{m_{\text{p}}}}}\left[ {{{\left( {\frac{{{R_{\text{p}}}}}{r}} \right)}^{1+{m_{\text{p}}}}} - 1} \right]} \right\},$$
(16)
$$\varepsilon _{{\text{r}}}^{{\text{p}}}= - H\left\{ {{m_{\text{e}}}+\frac{{2{m_{\text{p}}}}}{{1+{m_{\text{p}}}}}\left[ {{{\left( {\frac{{{R_{\text{p}}}}}{r}} \right)}^{1+{m_{\text{p}}}}} - 1} \right]} \right\},$$
(17)
$$\varepsilon _{\theta }^{{\text{p}}}=H\left\{ {1+\frac{2}{{1+{m_{\text{p}}}}}\left[ {{{\left( {\frac{{{R_{\text{p}}}}}{r}} \right)}^{1+{m_{\text{p}}}}} - 1} \right]} \right\}.$$
(18)

Therefore, the volumetric strain of \({\nu ^{\text{p}}}\) is

$$\begin{aligned}{\nu ^{\text{p}}}&=\varepsilon _{{\text{r}}}^{{\text{p}}}+\varepsilon _{\theta }^{{\text{p}}}=(1 - {m_{\text{e}}})\varepsilon _{\theta }^{{\text{e}}}+(1 - {m_{\text{p}}})\Delta \varepsilon _{\theta }^{{\text{p}}}\hfill \\ &=H\left\{ {1 - {m_e}+\frac{{2(1 - {m_{\text{p}}})}}{{1+{m_{\text{p}}}}}\left[ {{{\left( {\frac{{{R_{\text{p}}}}}{r}} \right)}^{1+{m_{\text{p}}}}} - 1} \right]} \right\}.\end{aligned}$$
(19)

Combining Eqs. (2), (5), (18), (12) with boundary condition \(\sigma _{r}^{e}\left| {_{{r={R_p}}}} \right.=\sigma _{r}^{p}\left| {_{{r={R_p}}}} \right.\), the stress in the strain softening zone is expressed as (Yuan and Chen 1986)

$$\begin{gathered} \sigma _{{\text{r}}}^{{\text{p}}}=\frac{2}{{{k_{\text{p}}}+1}}\left[ {{p_0}+\frac{{{\sigma _{\text{c}}}}}{{{k_{\text{p}}} - 1}}+\frac{{({k_{\text{p}}}+1){k_{\text{s}}}EH}}{{({k_{\text{p}}} - 1)({k_{\text{p}}}+{m_{\text{p}}})}}} \right]{\left( {\frac{r}{{{R_{\text{p}}}}}} \right)^{{k_{\text{p}}} - 1}} \hfill \\ \quad \quad {\kern 1pt} +{\kern 1pt} \frac{{2{k_{\text{s}}}EH}}{{1+{m_{\text{p}}}}}\left[ {\frac{1}{{{k_{\text{p}}}+{m_{\text{p}}}}}{{\left( {\frac{{{R_{\text{p}}}}}{r}} \right)}^{1+m}} - \frac{1}{{{k_{\text{p}}} - 1}}} \right] - \frac{{{\sigma _{\text{c}}}}}{{{k_{\text{p}}} - 1}}, \hfill \\ \end{gathered}$$
(20)
$$\sigma _{\theta }^{{\text{p}}}={k_{\text{p}}}\sigma _{{\text{r}}}^{{\text{p}}}+{\sigma _{\text{c}}} - \frac{{2{k_{\text{s}}}EH}}{{1+{m_{\text{p}}}}}\left[ {{{\left( {\frac{{{R_{\text{p}}}}}{r}} \right)}^{1+{m_{\text{p}}}}} - 1} \right].$$
(21)

Stress and strain in the residual state zone

The strain in the residual state zone is the summation of the strain in the residual state zone and the strain at the boundary between strain-softening zone and residual state zone:

$$\varepsilon _{{\text{r}}}^{{\text{b}}}=\varepsilon _{{\text{r}}}^{{\text{p}}}\left| {_{{r={R_{\text{b}}}}}} \right.+\Delta \varepsilon _{{\text{r}}}^{{\text{b}}},\;\varepsilon _{\theta }^{{\text{b}}}=\varepsilon _{\theta }^{{\text{p}}}\left| {_{{r={R_{\text{b}}}}}} \right.+\Delta \varepsilon _{\theta }^{{\text{b}}}.$$
(22)

Similarly, combining Eqs. (6), (22) with Eq. (3) obtains the strain and the radial displacement in the residual state zone as

$${u^{\text{b}}}=2rH\left\{ {\left\{ {\frac{1}{{1+{m_{\text{p}}}}}+\frac{1}{{1+{m_{\text{b}}}}}\left[ {{{\left( {\frac{{{R_{\text{b}}}}}{r}} \right)}^{1+{m_{\text{b}}}}} - 1} \right]} \right\}{{\left( {\frac{{{R_{\text{p}}}}}{{{R_{\text{b}}}}}} \right)}^{1+{m_{\text{p}}}}}+\frac{{{m_{\text{p}}} - 1}}{{2({m_{\text{p}}}+1)}}} \right\},$$
(23)
$$\varepsilon _{{\text{r}}}^{{\text{b}}}= - 2H\left\{ {\left\{ {\frac{{{m_{\text{p}}}}}{{1+{m_{\text{p}}}}}+\frac{{{m_{\text{b}}}}}{{1+{m_{\text{b}}}}}\left[ {{{\left( {\frac{{{R_{\text{b}}}}}{r}} \right)}^{1+{m_{\text{b}}}}} - 1} \right]} \right\}{{\left( {\frac{{{R_{\text{p}}}}}{{{R_{\text{b}}}}}} \right)}^{1+{m_{\text{p}}}}}+\frac{{{m_{\text{e}}}}}{2} - \frac{{{m_{\text{p}}}}}{{{m_{\text{p}}}+1}}} \right\},$$
(24)
$$\varepsilon _{\theta }^{{\text{b}}}=2H\left\{ {\left\{ {\frac{1}{{1+{m_{\text{p}}}}}+\frac{1}{{1+{m_{\text{b}}}}}\left[ {{{\left( {\frac{{{R_{\text{b}}}}}{r}} \right)}^{1+{m_{\text{b}}}}} - 1} \right]} \right\}{{\left( {\frac{{{R_{\text{p}}}}}{{{R_{\text{b}}}}}} \right)}^{1+{m_E}}}+\frac{{{m_{\text{p}}} - 1}}{{2({m_{\text{p}}}+1)}}} \right\}.$$
(25)

The volumetric strain \({\nu ^{\text{b}}}\) in the residual state zone is

$${\nu ^{\text{b}}}=\varepsilon _{{\text{r}}}^{{\text{b}}}+\varepsilon _{\theta }^{{\text{b}}}=2H\left\{ {\left\{ {\frac{{1 - {m_{\text{p}}}}}{{1+{m_{\text{p}}}}}+\frac{{1 - {m_{\text{b}}}}}{{1+{m_{\text{b}}}}}\left[ {{{\left( {\frac{{{R_{\text{b}}}}}{r}} \right)}^{1+{m_{\text{b}}}}} - 1} \right]} \right\}{{\left( {\frac{{{R_{\text{p}}}}}{{{R_{\text{b}}}}}} \right)}^{1+{m_{\text{p}}}}} - \frac{{{m_{\text{e}}}}}{2}+\frac{{3{m_{\text{p}}} - 1}}{{2({m_{\text{p}}}+1)}}} \right\}.$$
(26)

The Mohr–Coulomb criterion in the residual state zone can be expressed as

$$\sigma _{\theta }^{{\text{p}}}={k_{\text{p}}}\sigma _{{\text{r}}}^{{\text{p}}}+\sigma _{{\text{c}}}^{*},$$
(27)

where \(\sigma _{{\text{c}}}^{*}\) is the uniaxial residual strength.

The stresses in the residual state zone are obtained by solving Eqs. (5), (27) with the boundary condition \(\sigma _{{\text{r}}}^{{\text{p}}}\left| {_{{r={R_{\text{b}}}}}} \right.=\sigma _{{\text{r}}}^{{\text{b}}}\left| {_{{r={R_{\text{b}}}}}} \right.\). They are

$$\begin{gathered} \sigma _{{\text{r}}}^{{\text{b}}}=\{ \frac{2}{{{k_{\text{p}}}+1}}\left[ {{p_0}+\frac{{{\sigma _{\text{c}}}}}{{{k_{\text{p}}} - 1}}+\frac{{({k_{\text{p}}}+1){k_{\text{s}}}EH}}{{({k_{\text{p}}} - 1)({k_{\text{p}}}+{m_{\text{p}}})}}} \right]{\left( {\frac{{{R_{\text{b}}}}}{{{R_{\text{p}}}}}} \right)^{{k_{\text{p}}} - 1}} \hfill \\ \quad \quad {\kern 1pt} - {\kern 1pt} \frac{{2{k_{\text{s}}}EH+(1+{m_{\text{p}}})({\sigma _{\text{c}}} - \sigma _{{\text{c}}}^{*})}}{{({k_{\text{p}}} - 1)({k_{\text{p}}}+{m_{\text{p}}})}}\} {\left( {\frac{r}{{{R_{\text{b}}}}}} \right)^{{k_{\text{p}}} - 1}} - \frac{{\sigma _{{\text{c}}}^{*}}}{{{k_{\text{p}}} - 1}}, \hfill \\ \end{gathered}$$
(28)
$$\sigma _{\theta }^{{\text{b}}}={k_{\text{p}}}\sigma _{{\text{r}}}^{{\text{b}}}+\sigma _{{\text{c}}}^{*}.$$
(29)

Radius of strain-softening zone and residual state zone

According to Eqs. (20), (28), at the boundary between the strain-softening zone and the residual state zone \({R_{\text{b}}}\), \(\sigma _{{\text{r}}}^{{\text{b}}}\left| {_{{r={R_{\text{b}}}}}} \right.=\sigma _{{\text{r}}}^{{\text{p}}}\left| {_{{r={R_{\text{b}}}}}} \right.\), the relationship between \({R_{\text{p}}}\) and \({R_{\text{b}}}\) is obtained as

$${R_{\text{p}}}={R_{\text{b}}}{\left[ {1+\frac{{(1+{m_{\text{p}}})({\sigma _{\text{c}}} - \sigma _{{\text{c}}}^{*})}}{{2{k_{\text{s}}}EH}}} \right]^{\frac{1}{{1+{m_{\text{p}}}}}}}.$$
(30)

The radius of strain-softening zone \({R_{\text{b}}}\) is obtained by Eq. (28) with \(r={R_0}\) and \(\sigma _{{\text{r}}}^{{\text{b}}}={p_{\text{s}}}\), \({p_{\text{s}}}\) is the supporting traction of cavity. The supporting force exists for the roadway when the supporting measures are adopted. The supporting force is \({p_{\text{s}}}=0\) for boreholes during coalbed methane (CBM) drilling. The final expression is

$$\begin{aligned} {R_{\text{b}}} & ={R_0}\Bigg\{ \Bigg\{ \frac{2}{{{k_{\text{p}}}+1}}\left[ {{p_{\text{i}}}+\frac{{{\sigma _{\text{c}}}}}{{{k_{\text{p}}} - 1}}+\frac{{({k_{\text{p}}}+1){k_{\text{s}}}EH}}{{({k_{\text{p}}} - 1)({k_{\text{p}}}+{m_{\text{p}}})}}} \right]{\left[ {\frac{{2{k_{\text{s}}}EH}}{{2{k_{\text{s}}}EH+(1+{m_{\text{p}}})({\sigma _{\text{c}}} - \sigma _{{\text{c}}}^{*})}}} \right]^{\frac{{{k_{\text{p}}} - 1}}{{1+{m_{\text{p}}}}}}} \\ & \quad - \frac{{2{k_{\text{s}}}EH+(1+{m_{\text{p}}})({\sigma _{\text{c}}} - \sigma _{{\text{c}}}^{*})}}{{({k_{\text{p}}} - 1)({k_{\text{p}}}+{m_{\text{p}}})}}\Bigg\} \Bigg/\left( {{p_{\text{s}}}+\frac{{\sigma _{{\text{c}}}^{*}}}{{{k_{\text{p}}} - 1}}} \right){\Bigg\} ^{\frac{1}{{{k_{\text{p}}} - 1}}}}. \\ \end{aligned}$$
(31)

After the radii of the strain softening and the residual state zones are obtained by Eqs. (30) and (31), the stresses around a borehole can be finally obtained by Eqs. (7), (8), (20), (21), (28) and (29) and the volumetric strains can be finally calculated by Eqs. (13), (19) and (26).

Permeability evolution of coal at post-peak failure stage

A brief review of permeability of coal at post-peak failure stage

In the process of coal mining and gas extraction, the fracture of coal changes significantly due to the release of both radial and hoop stresses and thus the permeability of coal seam increases dramatically due to excavation or CBM drilling. According to the experiments conducted by Pan et al. (2014) and Chu et al. (2017), Fig. 3 is drawn to present the change of permeability along four loading paths, where curve 1 presents the loading path and curve 2 denotes the pre-peak unloading path in elastic zone. Both curves 1 and 2 are coincided because of elastic deformation. Curve 3 presents the pre-peak unloading of elastic–plastic materials because plastic deformation is irrecoverable. Finally, curve 4 presents the post-peak unloading path. Obviously, curve 4 has special property compared to other three paths.

Fig. 3
figure 3

Permeability evolution of coal with loading and unloading

Full size image

Each curve represents different physical mechanisms. The permeability changes along curve 1 for loading and along curve 2 for unloading. Due to reversible deformation, curves 1 and 2 are identical. During loading process, permeability decreases with the increase of stress due to coal compaction. The deformation resisting capability of fracture surface is developed and the decreasing trend of permeability slows down. When stress is unloaded, the permeability increases due to the release of whole coal structure. Both curves for loading and unloading are coincided due to elastic deformation. For the coal with elastic–plastic model, permeability increases with unloading (see curve 3). The unloading process is irreversible process. It is difficult for a closed fracture in loading process to be recovered completely in unloading process. Thus the permeability is smaller than that in loading process. It is also noted that the permeability increases very fast when stress is small. As seen in curve 4, the coal swells significantly in the post-peak unloading. This significantly enhances the permeability in this stage. This unloading destructs the coal microstructures and generates a large amount of new cracks. Stress drops until the residual stress state where the coal is seriously damaged. Simultaneously, the permeability is rapidly enhanced. The gas is more easily released from the fractured coal. This causes higher gas emission and thereby increases the gas content to its limit and even induces coal and gas outburst. Therefore, the permeability model is the critical to the control of coal and gas outburst and each loading path has its evolution of permeability.

Evolution of coal porosity and permeability

The bulk volume of the porous medium is \(V={V_{\text{p}}}+{V_{\text{s}}}\) and its porosity is \(\phi ={V_{\text{p}}}/V\). The volumetric strain and the pore-volumetric strain are expressed by

$$\frac{{\Delta V}}{V}= - \frac{1}{K}{\text{(}}\sigma - \alpha p)+{\varepsilon _{\text{s}}},$$
(32)
$$\frac{{\Delta {V_{\text{p}}}}}{{{V_{\text{p}}}}}= - \frac{1}{K}{\text{(}}\sigma - \beta p)+{\varepsilon _{\text{s}}},$$
(33)

where \(\alpha\) is the Biot coefficient and \(\beta =1 - {K_{\text{p}}}/{K_{\text{s}}}\). \({K_{\text{p}}}\) is the modulus of pores. \(\sigma ,p\) are the total hydrostatic stress and pore pressure, respectively. \({\varepsilon _{\text{s}}}\) is the sorption–induced swelling strain.

Thus, the change of porosity is calculated by

$${\text{d}}\phi ={\text{d}}\left( {\frac{{{V_{\text{p}}}}}{V}} \right)=\frac{{{V_{\text{p}}}}}{V}\left( {\frac{{{\text{d}}{V_{\text{p}}}}}{{{V_{\text{p}}}}} - \frac{{{\text{d}}V}}{V}} \right).$$
(34)

Integrating Eq. (34) yields

$$\frac{\phi }{{{\phi _0}}} = {\text{exp}}\left\{ {\left( {\frac{1}{K} - \frac{1}{{{K_{\text{p}}}}}} \right){\text{[(}}\sigma - {\sigma _0}{\text{)}} - {\text{(}}p - {p_0}{\text{)]}}} \right\}.$$
(35)

The permeability change law is obtained by (Cui and Bustin 2005)

$$k={k_0}{\left( {\frac{\phi }{{{\phi _0}}}} \right)^3}={k_0}{\text{exp}}\left\{ {{\text{3}}\left( {\frac{1}{K} - \frac{1}{{{K_{\text{p}}}}}} \right){\text{[(}}\sigma - {\sigma _0}{\text{)}} - {\text{(}}p - {p_0}{\text{)]}}} \right\}.$$
(36)

This formula is more suitable for elastic deformation. The relationship between the permeability and effective stress can be expressed as (Shi and Durucan 2004; Pan and Connell 2011; Salmachi et al. 2013)

$$k={k_0}{e^{ - 3{c_{\text{f}}}(\sigma - {\sigma _0})}},$$
(37)

where \({k_0}\) is the initial permeability; \({c_{\text{f}}}\) is the cleat compressibility. This permeability model describes the permeability evolution of the coal without damage.

Assuming that the length of the fracture traces per unit area of the trace plane is \({P_1}\) and the area of fractures per unit volume of rock is \({P_2}\), the fracture porosity of the coal can be expressed as \(\phi =b{P_2}\). Then, the permeability can be rewritten as

$$k=\frac{{{P_1}}}{{\tau P_{2}^{3}}}\frac{{{\phi ^3}}}{{12}},$$
(38)

where \(\tau\) is the tortuosity parameter; \(b\) is the fracture aperture.

Differentiating the fracture permeability with respect to the effective stress results in

$$\frac{{\partial k}}{{\partial {\sigma _{\text{e}}}}}=\frac{{{P_1}}}{{\tau P_{2}^{3}}}\frac{{{\phi ^2}}}{4}\frac{{\partial \phi }}{{\partial {\sigma _{\text{e}}}}}.$$
(39)

Incorporating Eq. (39) into (38), we have

$$\frac{{\partial k}}{{\partial {\sigma _{\text{e}}}}}=3{D_{\text{f}}}k,$$
(40)

where \({D_{\text{f}}}=\frac{1}{\phi }\frac{{\partial \phi }}{{\partial {\sigma _{\text{e}}}}}\), which denotes the change in the fracture porosity of damaged coal in different stress states.

A damage variable \(D\) was introduced to take into consideration the degeneration of elasticity modulus (Brown et al. 1983; Yang and Baleanu 2013)

$$D=1 - E/{E_0},$$
(41)

where \(E\) is the elastic modulus of coal samples under different stress states, and \({E_0}\) is the initial elastic modulus of the coal samples.

The damage variable \(D\) can be used to describe the development degree of fractures in the coal samples (Peng et al. 2015; Zhu et al. 2013, 2018). Therefore, the following equation can be used to describe the relationship between these two variables

$${D_{\text{f}}}=\gamma D,$$
(42)

where \(\gamma\) is the coefficient, which reflects the sensitivity degree of the fracture development to the effective stress.

Thus, Eq. (40) can be expressed as

$$\frac{{\partial k}}{{\partial {\sigma _{\text{e}}}}}=3\gamma Dk.$$
(43)

When \(\lambda = - \gamma /{c_{\text{f}}}\), Eq. (43) can be expressed as (Xue et al. 2016)

$$k={k_0}{e^{ - 3{c_{\text{f}}}\lambda D({\sigma _{\text{e}}} - {\sigma _{{\text{e0}}}})}},$$
(44)

where \({k_0}\) is the initial permeability, \({c_{\text{f}}}\) is the compression coefficient of fracture, \(\lambda\) is the damage enhancement coefficient, which reflects the influence coefficient of damage to permeability, \({\sigma _e}\) is the effective stress. More detailed description about this equation can be referred in Xue et al. (2016).

An approach for the couplings among stress, strain and gas flow

Gas flow equation

The mass conservation law of gas is

$$\frac{{\partial m}}{{\partial t}}+\nabla \cdot ({\rho _{\text{g}}}{\vec {q}_{\text{g}}})={Q_{\text{m}}}`,$$
(45)

where \({\rho _g}\) is the gas density, \({\vec {q}_g}\) is the velocity, \({Q_m}\) is the source, and m is the gas content which calculated through the Langmuir equation (Saghafi et al. 2007),

$$m={\rho _{\text{g}}}\phi +{\rho _{{\text{ga}}}}{\rho _{\text{c}}}\frac{{{V_{\text{L}}}p}}{{p+{p_{\text{L}}}}},$$
(46)

where \({\rho _{\text{g}}}\) is the gas density, \({\rho _{{\text{ga}}}}\) is the gas density at standard conditions, \({\rho _{\text{c}}}\) is the coal density, \(\phi\) is the coal porosity, VL denotes the adsorption capacity of coal, and PL denotes the Langmuir pressure constant.

After ignoring the gravity, the Darcy velocity of \({\vec {q}_{\text{g}}}\) is given by (Yarmohammadtooski et al. 2017)

$${\vec {q}_{\text{g}}}= - \frac{k}{\mu }\nabla p,$$
(47)

where k is the coal permeability and \(\mu\) is the dynamic viscosity. Substituting Eqs. (46) into (45), the equation of gas flow is

$$\left[ {\phi +\frac{{{\rho _{\text{c}}}{p_{\text{a}}}{V_{\text{L}}}{p_{\text{L}}}}}{{{{(p+{p_L})}^2}}}} \right]\frac{{\partial p}}{{\partial t}}+p\frac{{\partial \phi }}{{\partial t}} - \nabla \cdot \left( {\frac{k}{\mu }p\nabla p} \right)={Q_{\text{m}}}.$$
(48)

Computation procedure of the approach

The deformation and the stress redistribution nearby a borehole and the formation of post-peak failure zone are mainly induced by drilling process while the influence of gas flow within coal seam on these changes is slight (Adhikary and Guo 2015; Borisenko 1985). On the other hand, coal deformation and crack propagation at the post-peak failure stage are mainly governed by stress redistribution. The deformation and stress redistribution have significant impacts on permeability evolution and gas pressure profile. The approach should take this impact of stress redistribution on permeability and gas pressure into account. Based on this understanding, an approach as described in Fig. 4a is proposed in this paper. Particularly, the effect of deformation and stress on porosity and permeability is carefully considered in the calculation of gas flow. In this case, the above analytical solutions of stress and strain are used to calculate their impact on porosity and permeability.

Fig. 4
figure 4

Flowchart for computational procedure of the approach

Full size image

This approach adopts the following computational procedure: First, the analytical solutions of stress and strain are used to compute the stress and strain in each zone and to determine the size of each zone. Then, the permeability model is used to calculate the permeability distribution in each zone. That is, the pre-peak permeability model (Cui–Bustin model) is applied to the elastic zone and the post-peak permeability model is applied to both strain-softening and residual state zones (Fig. 4b). Finally, the gas flow equation is numerically solved based on the porosity and permeability in each zone.

The coal matrix swelling affects the permeability of the undamaged coal mass significantly. We consider the coal matrix swelling in pre-peak stage by adopting the Cui–Bustin model in pre-peak stage. For the fractured coal mass in post-peak failure stage, the gas sorption-induced strain is usually less than 5 × 10−4 (Liu et al. 2010) and the overall volumetric strain is normally larger than 1.5 × 10−2 (Chen et al. 2016). The total volumetric strain of the coal increases substantially due to the excavation-induced damage in the post-failure stage, even with the emergence of macro-fracture and large deformation, while the gas sorption-induced strain accounts for a small percentage of the overall volumetric strain. Therefore, we consider the coal matrix swelling in pre-peak stage and ignore it in the post-peak failure stage, with referring the approach proposed by Chen et al. (2016).

A one-dimensional numerical model is established, as shown in Fig. 5. The length of the model is 100 m. The initial gas pressure in the coal seam is 1.5 MPa and the cavity to represent the borehole is 50 mm in radius. The pressure will remain constant at a large distance from the well, thus the boundary condition may be approximated as follows (Liu et al. 2015):

Fig. 5
figure 5

One-dimensional physical model

Full size image
$$p={p_0}\;{\text{at}}\;r={R_{\text{c}}},$$
(49)

where \(r={R_{\text{c}}}\) is the radius of the whole analyzed zone. The extraction pressure of the borehole is

$$p={p_{\text{a}}}\;{\text{at}}\;r={R_0},$$
(50)

where \(r={R_0}\) is the radius of the borehole.

After the borehole is drilled, the gas flows from coal seam to borehole. Other computational parameters are listed in Table 1. The nonlinear partial differential equation (PDE) solver within the framework of COMSOL Multiphysics is employed to solve the gas flow equation, and the analytical solutions for deformation and stress are input into the COMSOL.

Table 1 Computational parameters for coal and gas
Full size table

Model validation

Verification by field data

This approach is verified through the comparison with the field data obtained from the No.8 seam in Shoushan mine of the Pingmei Corporation, China. The No.8 coal seam has the gas outburst hazard with a gas pressure of 0.32–0.78 MPa and a gas content of 3.26–6.52 m3/t. The validity of the model can be directly verified by measuring the gas pressure at different positions of the coal seam. However, because of the difficulty in measuring gas pressure, we adopted gas content as the comparison parameter instead of gas pressure. We measured the gas content distribution of coal seam at the time of 135 days after roadway excavation according to the determination method for underground gas content (State Administration of Coal Mine Safety of China 2006). The gas content was measured every 1 m along the excavation wall of roadway from the depth of 1 m.

A similar physical model to Fig. 5 is established. The initial gas pressure in the coal seam is 0.78 MPa and the cavity to represent the roadway is 2.7 m in radius. The same boundary conditions are used in the calculation, as show in Fig. 5. Following parameters are used to calculate the gas content distribution of coal seam after excavation. The initial geo-stress is 11.95 MPa. The roadway was supported with bolt mesh and the support pressure is 0.15 MPa. The initial gas pressure is 0.78 MPa; CH4 Langmuir pressure constant is 6.1 MPa; CH4 Langmuir volume constant is 0.02 m3/kg; CH4 Langmuir volumetric strain constant is 0.023. Other parameters are derived from Table 1. Figure 6 presents the comparison between our simulations with the field data. This figure shows that the approach can reliably predict the gas content nearby the newly formed cavity. Therefore, this approach is applicable to gas flow problem around a borehole.

Fig. 6
figure 6

Comparison of simulated gas content and field data

Full size image

Numerical validation

In this section, we further examine the effectiveness of this approach in simulating the gas flow around the cavity. We compared our approach with the fully coupled hydro-mechanical model of Xue et al. (2018). The coupled governing equation for coal seam deformation and gas flow in the model of Xue et al. (2018) are expressed as:

$$G{u_{{\text{i,jj}}}}+\frac{G}{{1 - 2\mu }}{u_{{\text{j,ji}}}} - \alpha {p_{\text{i}}} - K{\varepsilon _{{\text{s,i}}}}+{f_{\text{i}}}=0,$$
(51)
$$\left[ {\phi +\frac{{{\rho _{\text{c}}}{p_{\text{a}}}{V_{\text{L}}}{p_{\text{L}}}}}{{{{(p+{p_{\text{L}}})}^2}}}} \right]\frac{{\partial p}}{{\partial t}}+p\frac{{\partial \phi }}{{\partial t}} - \nabla \cdot \left( {\frac{k}{\mu }p\nabla p} \right)={Q_{\text{m}}}.$$
(52)

The physical model is same as the model in “Computation procedure of the approach” and the same parameters are used in the calculation. A comparison of the pressure distribution and permeability distribution along the radial direction at 107 s is shown in Fig. 7. It can be seen from Fig. 7 that there is a good agreement between these two solutions, which further verifies the effectiveness of the approach proposed in this paper.

Fig. 7
figure 7

Comparison with the numerical solution

Full size image

Parametric study on the approach

The approach is applied to the analysis of stress, strain, gas pressure and permeability distribution around a borehole through parametric study. This study is to understand the accumulation of gas content around the borehole and to explore the mechanism of gas accumulation. The base computation parameters are listed in Table 1. Each time changes only parameter from the base parameters. The effects of following parameters on permeability and gas distribution are investigated: permeability enhancement coefficient, initial geo-stress, drilling size, and uniaxial strength.

Distribution of stress and volumetric strain

Based on the computation parameters in Table 1, the radii are obtained as Rb = 71.83 mm for the residual state zone and Rp = 89.83 mm for the strain softening zone. Figure 8 presents the stress distribution along radial direction after drilling. The distance is measured from the center of circular borehole. The drilling surface is free of traction, thus the radial stress on the wall drops to almost zero. The radial stress gradually increases and approaches towards the initial in situ stress with further distance from the wall of the hole. However, the hoop stress at the coal wall immediately drops to a low stress level (residual state) after drilling. This stress rises with further distance from the wall and approaches to a peak stress at the radius of strain-softening zone Rp. The stress concentration factor at this point is 1.87. This stress concentration factor is the ratio of the mining–induced stress to the pre-mining in situ stress. It is found that this factor is in the range of 1.5–6 (Singh et al. 2011).

Fig. 8
figure 8

Stress distribution around borehole

Full size image

The change of volumetric strain along the radial distance is observed in Fig. 9. The volumetric strain decreases in the elastic zone due to coal compaction. In the plastic zone, dilatancy and damage are observed and the volumetric strain increases substantially. When me = 0.8, the volumetric strain reaches its minimum of \({\nu _\varepsilon }\) = − 0.05% at the radius of strain-softening zone Rp = 89.83 mm. The volumetric strain reaches its maximum of \({\nu _\varepsilon }\) = 0.48% at the coal wall of borehole. If the compaction is not considered, that is me = 1, the volumetric strain in the elastic zone is \({\nu _\varepsilon }\) = 0 but the maximum volumetric strain is still \({\nu _\varepsilon }\) = 0.48% at coal wall. Therefore, coal compaction in elastic zone has some impact on the volumetric strain near the interface between strain-softening zone and elastic zone.

Fig. 9
figure 9

Change of volumetric strain with compaction coefficients around borehole

Full size image

Parametric study on permeability distribution

Effect of the damage enhancement coefficient on permeability

The effect of damage enhancement coefficient \(\lambda\) is observed in Fig. 10. The initial permeability of coal seam is specified as 1 × 10−17 m2. The permeability keeps unchanged in the undisturbed rock which is far away from the borehole. In the elastic zone, the permeability decreases gradually to the minimum of 8.86 × 10−18 m2 at the boundary of strain-softening zone and elastic zone. As the hoop stress increased with the decrease of distance from borehole, cracks close. The closing of cracks blocks flow channels and reduces the permeability. In the strain-softening zone, coal enters the post-peak failure stage. New cracks emerge in a large scale. This induces the rapid increase of permeability and the decline of coal strength. Finally, the coal enters the residual stress state where coal is fully fractured and has the highest permeability. When the damage is not considered, the maximum permeability is 1.11 × 10−17 m2 which is 1.1 times of its initial permeability. When damage enhancement coefficient \(\lambda\) = 1.5, 4.5 and 6.5, the maximum permeability is 1.62 × 10−17 m2, 1.07 × 10−15 m2, and 2.26 × 10−14 m2, respectively. When \(\lambda\) = 4.5, the maximum permeability of coal around borehole increases about 2 orders of magnitude due to drilling.

Fig. 10
figure 10

Effect of the damage enhanced coefficient on permeability

Full size image

Effect of initial geo-stress on permeability

The impact of initial geo-stress on permeability is investigated. Initial geo-stress is assumed to be hydrostatic stress generated by the gravity of overlying strata. Figure 11 presents the permeability profile along the radial distance. This figure shows that the radii of both residual stress zone and strain-softening zone are larger for higher initial geo-stress. The unloading zone is larger and the permeability enhancement is higher. Therefore, higher initial geo-stress has larger unloading zone and higher permeability enhancement. This suggests that the permeability enhancement due to drilling increases with the increase of mining depth and thus the risk of coal and gas outburst is higher.

Fig. 11
figure 11

Effect of initial geo-stress on permeability

Full size image

Effect of drilling size on permeability

The effect of drilling size on the permeability is explored. Figure 12 is the relationship between permeability and normalized distance from center. A unique relationship is observed regardless of drilling radius R0. With the increase of drilling radius R0, both the residual state zone and the strain softening zone are broadened. The ranges of unloading zone and the permeability enhancement zone are widened, too. However, permeability, hoop stress, radial stress and volumetric strain are only function of the normalized radius R/R0 if the gravity is not considered. The permeability enhancement degree is also observed to be independent of drilling radius R0. The drilling size only affects the range of permeability enhancement. The permeability enhancement is closely related to the mechanical property of coal seam and the geological condition of coal mine. In the excavation process of coal mine including gas drainage borehole, the coal around borehole and in front of working face experiences a post-peak failure process. Thus, the permeability in these zones is usually high. This may trigger gas outburst. Of course, gas outburst is a nonlinear dynamic disaster triggered by the combination of in situ stress, gas pressure and the change of mechanical properties of coal (Hu et al. 2015a, b; Jin et al. 2011). In situ stress, gas pressure, the mechanical properties of coal, and energy characteristic are the important factors in considerations when the risk of gas outbursts is evaluated.

Fig. 12
figure 12

Effect of excavation size on permeability

Full size image

Effect of uniaxial strength on permeability

The effect of failure strength of coal on permeability is investigated. Figure 13 presents the influence of uniaxial strength of coal on permeability. This figure shows that uniaxial strength has some impacts on the permeability only at the post-peak failure stage. When uniaxial strength of coal is lower, the zone of post-peak failure is larger and the permeability enhancement is greater. In coal mining, the physical properties of coal vary widely in different districts. Therefore, coal strength is an important factor to the excavation-induced permeability enhancement and the trigger of coal and gas outburst.

Fig. 13
figure 13

Effect of uniaxial strength on permeability

Full size image

Gas pressure profile near borehole

The gas pressure profile is a crucial parameter for coal and gas outburst. Figure 14a presents the gas pressure distribution along radial distance from the borehole at different times. In computation, the coefficient \(\lambda\) = 4.5 and the gas pressure at the coal wall is 0.1 MPa. A high pressure gradient is observed near the boundary between strain-softening region and elastic region. This indicates poor permeability in this small zone. The gas cannot easily flow through this zone (Lin et al. 2010).

Fig. 14
figure 14

Gas pressure distribution in coal mass around borehole

Full size image

The effect of damage enhancement coefficient on gas profile is discussed here. Figure 14b presents the gas pressure profile at t = 1 × 107 s when the coefficient \(\lambda\) = 1.5, 4.5 and 6.5. The gas pressure has a distribution of “slow–steep–slow” shape when \(\lambda\) = 4.5 and 6.5. When the \(\lambda\) is low, the permeability enhancement is not salient in the post-peak failure stage. Its gas velocity does not increase substantially. A smooth transition for the pressure curve is observed in the whole zone. The maximum gradient of pore pressure appears near the coal wall. When the \(\lambda\) is high such as 60 and 100, the permeability is pretty high in the post-peak failure zone. The maximum gradient is observed near the boundary of strain softening zone and elastic zone. This is the difference from those with low \(\lambda\) or no damage enhancement coefficient.

Zoning of permeability and pore pressure

The distributions of stress, strain, permeability, and gas pressure are plotted together in Fig. 15. The data in Fig. 15 are obtained from Figs. 8, 9, 10, 11, 12, 13 and 14. The gas pressure curve is at t = 1 × 107 s. These figures show that drilling leads to the stress redistribution around borehole. Three zones of elastic zone, strain softening zone and residual state zone are formed along the distance from the coal wall. They correspond to the three stages of stress–strain curve. After drilling, the coal wall (location a) is totally unconfined, the horizontal stress \({\sigma _{\text{r}}}\) and the vertical stress \({\sigma _\theta }\) decline to the low value. With the increase of distance from the coal wall, the stress \({\sigma _{\text{r}}}\) and \({\sigma _\theta }\) increase gradually. The coal between the locations a and b is at the post-peak failure stage. The coal has strong volumetric expansion. As the coal is in the post-peak zone, fractures amalgamate to form channels for gas flow. It can greatly enhances the permeability and maintain the permeability at a high level. The maximum permeability (location a) is 2–3 orders higher than its initial permeability. Gas in this zone can flow freely from the high-pressure zone to the low-pressure zone. The gas pressure drops rapidly. This makes the pressure curve at t = 1 × 107 s gentle and gas pressure gradient keeps small. Because of high permeability of coal, the zone I (a–b) is the full flow zone (FFZ) as described in Table 2. After that, the hoop stress \({\sigma _\theta }\) reaches its peak in the stress concentration area (b–c). The stress concentration compacts the coal and the permeability reaches its minimum. This higher vertical stress closes fractures and makes gas flow through this stress-increased zone more difficult. A pretty high pressure gradient is maintained in this zone. This poor permeability zone or II (b–c) forms a flow shielding (FSZ) as classified in Table 2. Beyond the location c, coal is in the elastic zone where the radial stress \({\sigma _{\text{r}}}\) and the hoop stress \({\sigma _\theta }\) approach gradually to the initial stress state. The volumetric strain and permeability are steadily recovered to the in situ state. The zone III (c–d) is the transitive flow zone (TFZ). At last, the coal enters into the zone IV (outside a–d), namely in situ rock flow zone (IRFZ), where the coal is not affected by drilling.

Fig. 15
figure 15

Distribution of stress, strain, permeability and gas pressure around borehole

Full size image
Table 2 Zone division of coal around a borehole
Full size table

The dimension of the four zones can be roughly measured in this example. The full flow zone (FFZ) is nearby coal wall, about 30 mm long, the next is the flow-shielding zone (FSZ), about 20 mm long, then transitive flow zone (TFZ) follows, about 200 mm long, and finally the in situ rock flow zone (IRFZ). Due to stress release, the permeability is 2–3 orders of magnitude higher in the FFZ than in the IRFZ. However, the permeability in the FSZ is approximately 12% lower than that in the IRFZ due to stress concentration. The gas in the FSZ is difficult to flow, thus forming high pressure gradient zone. The permeability in the TFZ gradually increases from the small value in the FSZ to the initial value in the IRFZ. This demonstrated that the current compute approach is applicable to the formation analysis of gas accumulation. These results calculated by the approach can provide a theoretical guidance for gas drainage during the mining procedure.

Conclusions

In this study, analytical solutions of stress and strain and post-peak permeability model are combined to evaluate stress, strain, and permeability distribution of coal around a borehole, and gas flow equation is numerically solved to understand the distribution of gas pressure. Major findings can be drawn:

  1. 1.

    The approach proposed in this study is feasible to analyze the permeability distribution and gas pressure profile. This approach adopts the analytical solutions of stress and strain to describe deformation process and gas flow equation to describe the accumulation of gas content within coal seam. This approach has simpler computational procedure and higher computational efficiency.

  2. 2.

    Coal compaction in the elastic zone has important impacts on the distribution of permeability of a borehole and the accumulation of gas content. When me=0.8, the volumetric strain reaches its minimum of − 0.05% and the permeability decreases gradually to the minimum of 8.86 × 10− 18 m2 at the radius of strain-softening zone. This compaction can make the permeability of coal in the elastic zone be smaller than the initial permeability. This helps the coal seam form a flow-shielding zone near the interface between plastic zone and elastic zone.

  3. 3.

    The evolution of permeability is closely related to the physical properties of coal and the geological condition of coal seam. Higher initial geo-stress and lower failure strength have larger unloading zone and higher permeability enhancement. With the increase of drilling radius, both the residual state zone and the permeability enhancement zone are broadened while the permeability, hoop stress, radial stress and volumetric strain are only function of the normalized radius R/R0.

  4. 4.

    The coal seam around a borehole can be divided into four zones based on their permeability distribution. Because of excavation-induced release of stress, the permeability in the FFZ was 2–3 orders of magnitude higher than the initial value. The permeability of the FSZ was lower than the initial value due to stress concentration, and gas in this zone is difficult to flow due to the stress concentration.