Fully coupled three-dimensional nonlinear numerical simulation of pumping-induced land movement

Abstract

Excessive groundwater extraction can cause aquifer systems to move three-dimensionally. Based on the equilibrium of soil skeleton and continuity of groundwater flow, a fully coupled nonlinear three-dimensional mathematical model has been constructed, which incorporates the prevalent nonlinear mechanical and hydraulic properties of aquifer systems. The horizontal and vertical displacements with regard to nonlinear mechanical properties are obviously less than those results with linear stress–strain relationship, and the discrepancy between them increases with the elapsed time. Compared with the results with regard to the constant hydraulic properties, the horizontal and vertical displacement and the drawdown with nonlinear hydraulic conductivity increase. The discrepancy between the results with and without nonlinear hydraulic properties also increases with the elapsed time. For the ideal aquifer systems addressed in this study, horizontal displacement is predominant when groundwater is pumped from aquifer units. The horizontal strain is compressive within the zone contiguous to the pumping well, and it is tensile beyond that. However, the horizontal strain, especially the tensile strain, is negligible. Such small tensile strain cannot result in tensile stress because there is original compressive stress in soils. The nonlinear mechanical and hydraulic properties of aquifer systems have clear impacts on the numerical simulation of the displacement and the pore water pressure in hydrostratigraphic units, and their impacts increase with pumping time. They should be considered in land movement simulation due to long-term groundwater withdrawal.

Introduction

Excessive groundwater withdrawal from unconsolidated aquifer systems has caused severe land subsidence and/or earth fissures in many areas around the world (Galloway and Burbey 2011; Calderhead et al. 2011; Zhang et al. 2015). Aquifer systems are usually composed of aquifers and aquitards. When groundwater is extracted from an aquifer unit, the pore water pressure in itself and its neighboring units will decrease, resulting in increasing normal effective stress. This will cause soil skeleton to deform, and ground movement ensues. The vertical displacement of ground surface is called land subsidence. Land subsidence and ground movement can cause substantial damage such as loss of ground surface elevation, cracking of building foundations and underground pipelines, and intensification of storm tides in coastal areas.

Traditionally, land subsidence is usually mathematically simulated under such assumptions as (1) soil compaction only occurs vertically; (2) soils deform linearly; (3) hydraulic properties remain constant; (4) fluid flow and soil deformation are uncoupled, thus the groundwater simulation is first performed, and then soil deformation is calculated according to the previous change in pore water pressure (Gambolati et al. 1974).

However, the deformation of soil skeleton often occurs both vertically and horizontally when groundwater is pumped. Wolff (1970) measured the radial strain caused by pumpage from a single well. Su et al. (1998) conducted a field-pumping test in an unconfined aquifer and found that the maximum cumulative horizontal displacement was even of the same order of magnitude as vertical displacement. Horizontal and vertical deformations were also recorded in a controlled aquifer test in the aquifer system in Mesquit, USA (Burbey et al. 2006). Such field measurement indicates that it is necessary to take three-dimensional soil skeletal displacement into account in simulation of land subsidence.

On the other hand, when groundwater is extracted from an aquifer system, decrease in pore water pressure, increase in effective stress, and deformation of soil skeleton are occurring simultaneously and there are mutual causal links between them. Deformation of soil skeleton and change of pore water pressure are physically coupled in the case of land subsidence due to groundwater withdrawal. Real land subsidence should be therefore solved as coupled in principle. Gutierrez and Lewis (2002) also demonstrated that the fluid flow and deformation should be coupled in a deformable fluid-saturated porous media, particularly for problems involving fluid extraction or injection in underground formation.

With the research moving forward, the simulation of land subsidence has been developing from one-dimensional to three-dimensional soil skeletal displacement and from uncoupled (two-step) to coupled mathematical models. Based on Biot’s consolidation theory, Gambolati et al. (2000) analyzed three-dimensional land subsidence caused by water and gas extraction in the Po River basin, Italy and Burbey (2006) simulated three-dimensional deformation and strain induced by pumpage. In their models, both groundwater flow and deformation of soil skeleton are three-dimensional, and the coupling between them is taken into consideration. However, the existing simulations with regard to three-dimensional land subsidence have almost taken soil skeleton of aquifer systems as linear elastic materials (Gambolati et al. 2000; Burbey 2006; Kihm et al. 2007; Castelletto et al. 2015).

Land subsidence due to groundwater withdrawal is related with groundwater flow and deformation of aquifer system, and thus the mechanical and hydraulic properties of soil skeleton are essential for simulation of land subsidence. In the very early period of such studies, soil skeleton was often considered to deform elastically and its hydraulic conductivity was taken as constant (Gambolati et al. 1974). Through one-dimensional simulation of aquifer-system compaction near Pixley, California, however, Helm (1976) proposed that the mathematical model with stress-dependent specific storage and hydraulic conductivity could significantly improve the simulation results of observed compaction. A lot of field and laboratory data have also shown that the fundamental deformation characteristics of soil skeleton are nonlinear and inelastic, meaning soil compressibility is stress-dependent and most part of deformation is irrecoverable (Zhang et al. 2012). In the simulation of land subsidence resulted from groundwater extraction, the nonlinear and inelastic deformation properties of soils were usually represented by skeletal specific storage of aquifer systems, as indicated in Eq. (1) (Calderhead et al. 2011)

$$S^{\prime}_{\text{sk}} = \left\{ {\begin{array}{*{20}c} {S^{\prime}_{\text{ske}} = \frac{{0.434C_{\text{s}} \gamma_{\text{w}} }}{{\left( {1 + e_{0} } \right)\sigma^{\prime}}}} &\quad {\sigma^{\prime} < \sigma^{\prime}_{\text{pre}} } \\ {S^{\prime}_{\text{skv}} = \frac{{0.434C_{\text{c}} \gamma_{\text{w}} }}{{\left( {1 + e_{0} } \right)\sigma^{\prime}}}} &\quad {\sigma^{\prime} \ge \sigma^{\prime}_{\text{pre}} } \\ \end{array} } \right.$$

(1)

where $C_{\text{c}}$ is the compression index; $C_{\text{s}}$ is the recompression index; $\sigma^{\prime}$ is the vertical effective stress; ${\text{kPa}}$; $e_{0}$ is the initial void ratio; $\sigma^{\prime}_{\text{pre}}$ is the pre-consolidation stress, ${\text{kPa}}$; $\gamma_{\text{w}}$ is the unit weight of water, ${\text{kN/m}}^{ 3}$; $S^{\prime}_{\text{ske}}$ is the elastic skeletal specific storage, ${\text{m}}^{ - 1}$; $S^{\prime}_{\text{skv}}$ is the inelastic skeletal specific storage, ${\text{m}}^{ - 1}$. When groundwater level is higher than the historically lowest values (i.e., effective stress is smaller than the pre-consolidation stress), elastic specific storage is adopted; otherwise, inelastic specific storage is applied. However, Eq. (1) is only applicable to one-dimensional deformation because it is deduced from the linear relationship between logarithmic loading and corresponding void ratio under odometer tests. When two- or three-dimensional ground movement is considered, it is not applicable. Although Lewis and Schrefler (1978) proposed a tangential modulus to represent a nonlinear material in a two-dimensional case, they did not do real nonlinear simulation because of the lack of available information concerning the nonlinear behavior of soils. They did not mention how to determine whether the soil skeleton is loaded or unloaded either. On the other hand, most simulations of land subsidence do not consider the change of the hydraulic conductivity with the deformation of soil skeleton. However, when soil skeleton deformation occurs, the porosity will change and so will permeability of soils. With increasing compaction of aquifer systems, the porosity of soil skeleton actually decreases and its hydraulic conductivity reduces accordingly. Kim and Parizek (1999) proposed that the deformation dependencies of the hydraulic properties intrinsically induce hydraulic heterogeneity and nonlinear consolidation. Preisig et al. (2014) also suggested that hydrodynamic parameters depend on effective stresses in regional basin-fill aquifer systems.

On the basis of previous research work, simulation of land subsidence is trending to involve the three-dimensional skeletal displacement and nonlinear mechanical and hydraulic properties in order to better represent real problems. More work has to be done yet. The present paper aims to construct a mathematical model which not only represents the coupling of groundwater flow and soil deformation but also takes three-dimensional skeletal displacement and nonlinear mechanical and hydraulic properties into consideration, and to investigate the effects of skeletal properties on land subsidence, ground movement, and the pore water pressure.

Governing equations and numerical solution

The governing equations are constructed on the basis of the following assumptions: (1) the material is isotropic and continual; (2) the strain is small; (3) the water flows through the soil skeleton according to Darcy’s law. Following the Biot’s formulation and considering the equilibrium of soil skeleton and the continuity of water flow, the coupled three-dimensional model of land subsidence can be obtained (Biot 1941; Zienkiewicz 1982; Gambolati et al. 2000) by the combination of Eqs. (2) and (3)

$$\left\{ \begin{array}{l} \left( {\lambda + G} \right)\frac{{\partial \varepsilon_{v} }}{\partial x} + G\nabla^{2} u = \alpha \frac{\partial p}{\partial x} \hfill \\ \left( {\lambda + G} \right)\frac{{\partial \varepsilon_{v} }}{\partial y} + G\nabla^{2} v = \alpha \frac{\partial p}{\partial y} \hfill \\ \left( {\lambda + G} \right)\frac{{\partial \varepsilon_{v} }}{\partial z} + G\nabla^{2} w = \alpha \frac{\partial p}{\partial z} + \gamma \hfill \\ \end{array} \right.$$

(2)

$$\frac{1}{{\gamma_{\text{w}} }}\nabla \cdot \left( {K\left( {\nabla p - \left\{ g \right\}} \right)} \right) + Q = \left[ {n_{v} \beta_{\text{w}} + M_{\text{s}} \left( {\alpha - n_{v} } \right)} \right]\frac{\partial p}{\partial t} + \alpha \frac{{\partial \varepsilon_{v} }}{\partial t}$$

(3)

where $\alpha = 1 - \frac{{M_{\text{s}} }}{M}$ is the Biot’s coefficient; $M_{\text{s}}$ is the volumetric compressibility of soil grain, ${\text{m}}^{ 2} / {\text{kN}}$; $M = \frac{1 - 2\nu }{E}$ is the volumetric compressibility of soil skeleton, ${\text{m}}^{ 2} / {\text{kN}}$; $\lambda = \frac{\nu E}{{\left( {1 - 2\nu } \right)\left( {1 + \nu } \right)}}$ is the Lame constant, ${\text{kPa}}$; $G = \frac{E}{2(1 + \nu )}$ is the shear modulus of soil skeleton, $kPa$; $E$ is the elastic modulus of soil skeleton, ${\text{kPa}}$; $\nu$ is the Poisson’s ratio of soil skeleton; $\varepsilon_{v} = - \frac{\partial u}{\partial x} - \frac{\partial v}{\partial y} - \frac{\partial w}{\partial z}$ is the volumetric strain of soil skeleton, and it is positive for compression and negative for expansion; $u$, $v$, and $w$ are the displacement in parallel with the axes $x$, $y$, and $z$, respectively, and they are positive in the corresponding positive axis direction, $m$; the axes $x$, $y$, and $z$ constitute a three-dimensional Cartesian coordinate system and the positive direction of axis $z$ is upward; $p$ is the pore water pressure, ${\text{kPa}}$; $t$ is the time, $s$; $\gamma$ is the unit weight of soil, ${\text{kN/m}}^{ 3}$; $\gamma_{w}$ is the unit weight of water, ${\text{kN/m}}^{ 3}$; $K$ is the hydraulic conductivity of soil, ${\text{m/s}}$;$Q$ is the source or sink, ${\text{m}}^{ 3} / {\text{s}}$; $n_{v}$ is the porosity of soil skeleton; $\beta_{w}$ is the volumetric compressibility of water, ${\text{m}}^{ 2} / {\text{kN}}$; $\nabla$ is the gradient operator; $\nabla^{2}$ is the Laplace’s operator; $\left\{ g \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \gamma_{w} } \\ \end{array} } \right]^{T}$. Soil skeletons are typically much more compressible than the individual soil grains. This means that the value of $M_{s} /M$ is much smaller than 1.0, thus the value of $\alpha$ approximately equals 1.0.

The elastic modulus and Poisson’s ratio in the coupled three-dimensional model are originally constant, indicating that the soil is assumed to be a linear elastic material. However, soils are hardly ideal elastic materials, and nonlinearity and inelasticity are their fundamental characteristics. In order to take these basic properties into consideration in the simulation of land subsidence, we adopt the empirical expression proposed by Duncan and Chang (1970) to represent the nonlinear deformation characteristics of soils. In the empirical expression, the relationship between stress and strain is hyperbolic, which was constructed on the basis of a great number of laboratory consolidated-drained tests. As such, soils can be regarded as elastic materials within each small stress increment, but their elastic modulus and Poisson’s ratio are both stress-dependent. Accordingly, the stress-dependent tangential modulus $E$ can be expressed as (Duncan and Chang 1970)

$$E = \left[ {1 - R_{\text{f}} s} \right]^{2} \cdot k \cdot p_{\text{a}} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{n}$$

(4)

and

$$s = \frac{{\sigma_{1} - \sigma_{3} }}{{\left( {\sigma_{1} - \sigma_{3} } \right)_{f} }} = \frac{{\left( {1 - \sin \phi } \right)\left( {\sigma_{1} - \sigma_{3} } \right)}}{{2c \cdot \cos \phi + 2\sigma_{3} \cdot \sin \phi }}$$

(5)

where $R_{\text{f}}$ is the failure ratio, and $R_{f} = \left( {\sigma_{1} - \sigma_{3} } \right)_{f} /\left( {\sigma_{1} - \sigma_{3} } \right)_{u}$; $c$ is the effective cohesion, ${\text{kPa}}$; $\phi$ is the effective internal friction angle, degree; $\sigma_{3}$ is the minor effective principal stress, ${\text{kPa}}$; $\sigma_{1}$ is the major effective principal stress, ${\text{kPa}}$; $p_{\text{a}}$ is the atmospheric pressure, ${\text{kPa}}$; $k$ and $n$ are the dimensionless parameters of soils; $\left( {\sigma_{1} - \sigma_{3} } \right)_{f}$ is the deviatoric stress at failure, ${\text{kPa}}$; $\left( {\sigma_{1} - \sigma_{3} } \right)_{u}$ is the ultimate deviatoric stress, ${\text{kPa}}$; $s$ is the stress level, representing the extent to which the soil element is close to failure. Mohr–Coulomb criterion is used for shear failure criterion. If the stress level of an element is no less than 1.0, the element has shear failure. The stress-dependent Poisson’s ratio $\nu$ is expressed as (Duncan and Chang 1970)

$$\nu = \frac{{G - F\lg \frac{{\sigma_{3} }}{{p_{\text{a}} }}}}{{\left( {1 - A} \right)^{2} }}$$

(6)

in which, $A = \frac{{D\left( {\sigma_{1} - \sigma_{3} } \right)}}{{k \cdot p_{\text{a}} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{n} \left[ {1 - R_{\text{f}} s} \right]}}$; $D$, $G$, and $F$ are the dimensionless parameters of soils.

In order to consider the irrecoverable deformation under unloading, Duncan and Chang (1970) replaced the tangential modulus with the resilient modulus of soil when unloading, which is given as

$$E_{ur} = k_{ur} p_{\text{a}} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{{n_{ur} }}$$

(7)

where $E_{\text{ur}}$ is the resilient modulus, ${\text{kPa}}$; $k_{\text{ur}}$ and $n_{\text{ur}}$ are the dimensionless parameters of soils. All parameters in Eqs. (4)–(7) can be determined through the consolidated-drained compression tests conveniently. If the values of parameters $R_{\text{f}}$, $n$, $n_{ur}$, $F$, and $D$ are zero and $k = k_{ur}$, the tangential modulus and Poisson’s ratio will be independent on stress and identical for loading and unloading like those for linear elastic materials.

Besides, with soil skeleton deforming, the void ratio changes, and thus the hydraulic conductivity of the aquifer system changes correspondingly. Here the relationship between hydraulic conductivity and void ratio developed by Lambe and Whitman (1979) is adopted as following

$$K = \left\{ {\begin{array}{*{20}l} {K_{0} 10^{{\left( {e - e_{0} } \right)/m}} } \hfill & {{\text{for}}\;{\text{clay}}} \hfill \\ {K_{0} \left( {\frac{e}{{e_{0} }}} \right)^{3} \left( {\frac{{1 + e_{0} }}{1 + e}} \right)} \hfill & {{\text{for}}\;{\text{sand}}} \hfill \\ \end{array} } \right.$$

(8)

where $K_{0}$ is the initial hydraulic conductivity, ${\text{m/s}}$; $K$ is the current hydraulic conductivity, ${\text{m/s}}$; $e_{0}$ is the initial void ratio; $e$ is the current void ratio; $m$ is the slope of $e - \log K$ plot, which is related to the properties of soil.

Through Eqs. (4)–(8), the nonlinear deformation characteristics and nonlinear hydraulic conductivity of aquifer systems can be incorporated into Eqs. (2) and (3), and then a fully coupled three-dimensional nonlinear land subsidence model has been constructed. In order to solve the mathematical land subsidence model (Eqs. 2 and 3) under given initial and boundary conditions, the finite element method (FEM) is employed. The simulated domain is discretized into hexahedron isoparametric elements. The discretization of Eqs. (2) and (3) is as following

$$\begin{aligned} \left[ K \right]\left\{ {\Delta \delta_{t} } \right\} + \left[ {K^{\prime}} \right]\left\{ {\Delta \beta_{t} } \right\} & = \left\{ R \right\} - \left[ K \right]\left\{ {\delta_{t - 1} } \right\} - \left[ {K^{\prime}} \right]\left\{ {\beta_{t - 1} } \right\} \\ \left[ {K^{\prime}} \right]^{T} \left\{ {\Delta \delta_{t} } \right\} + \left[ {\tilde{K}} \right]\left\{ {\Delta \beta_{t} } \right\} & = \left\{ Q \right\}\Delta t - \left[ {\tilde{K}} \right]\left\{ {\beta_{t - 1} } \right\} \\ \end{aligned}$$

(9)

in which, $\left[ K \right]$ is the stiff matrix; $\left[ {\tilde{K}} \right]$ is the permeability matrix; $\left[ {K^{\prime}} \right]$ is the matrix which represents the interaction between nodal displacement and nodal pore water pressure; $\left[ {K^{\prime}} \right]^{T}$ is the transposed matrix of $\left[ {K^{\prime}} \right]$; $\left\{ {\Delta \delta_{t} } \right\}$ is the nodal incremental displacement vector at the current time step; $\left\{ {\Delta \beta_{t} } \right\}$ is the nodal incremental pore water pressure vector at the current time step; $\left\{ {\delta_{t - 1} } \right\}$ is the nodal displacement vector at the preceding time step; $\left\{ {\beta_{t - 1} } \right\}$ is the nodal pore water pressure vector at the preceding time step; $\left\{ R \right\}$ is the nodal loading vector; $\left\{ Q \right\}$ is the nodal flow rate vector; $\Delta t$ is the time step.

It is necessary to decide whether an element expands (unloading) or compacts (loading) in the numerical simulation through the finite element method. On the condition of one-dimensional land subsidence, it is convenient to decide whether the soil skeleton is loaded or unloaded according to the increasing or decreasing pore water pressure, as given in Eq. (1). In the case of two- or three-dimensional skeletal deformation, however, whether the soil skeleton is loaded or unloaded cannot be simply determined according to the pore water pressure decreasing or increasing, because the effective horizontal and vertical stresses often do not change proportionally at the occurrence of lateral deformation. Thus, the combination of principle stresses is needed to be taken into account. The stress state of an element can be represented by a Mohr’s circle (circle A), as shown in Fig. 1, in which the Mohr–Coulomb failure criterion is also indicated by a straight line (failure line). The failure line is given as

$$\tau_{f} = c + \sigma tg\phi$$

(10)

where $\tau_{f}$ is the shear strength on a plane, ${\text{kPa}}$; $\sigma$ is the normal effective stress on the corresponding plane, ${\text{kPa}}$. If the pore water pressure in an element decreases in the condition of constant total major and minor stresses, the major and minor effective stresses will increase equally and the Mohr’s circle will move to the right (circle B), and the mean effective stress increases. In this case, the element is loaded. However, increase in pore water pressure does not always indicate the element is unloaded. For example, when the pore water pressure in an element increases in the condition of constant total major and minor stresses, the major and minor effective stresses will decrease equally and the Mohr’s circle will move to the left (circle C). Although the mean effective stress decreases, the Mohr’s circle becomes closer to the failure line, meaning the element is not unloaded but loaded. The actual stress state of an element is much complex due to three-dimensional deformation caused by groundwater withdrawal, and the corresponding Mohr’s circle of the element changes both in position and size in the coordinate system in Fig. 1. According to triaxial consolidated drainage tests, it can be empirically determined that a soil element is unloaded if its current stress state satisfies the following condition (Qian and Yin 1994)

$$\left\{ {\begin{array}{*{20}l} {\left( {\sigma _{1} - \sigma _{3} } \right) < \left( {\sigma _{1} - \sigma _{3} } \right)_{{\max }} } \hfill \\ {s < s_{{\max }} } \hfill \\ \end{array} } \right.$$

(11)

where $\left( {\sigma_{1} - \sigma_{3} } \right)_{\hbox{max} }$ is the historically maximal values of the deviatoric stress of the element; $s_{\hbox{max} }$ is the historically maximal values of the stress level of the element; $\left( {\sigma_{1} - \sigma_{3} } \right)$ is the current deviatoric stress of the element; $s$ is the current stress level of the element. In the case of one-dimensional skeletal deformation, the set of in equation (11) is equivalent to the condition $\sigma^{\prime} < \sigma^{\prime}_{\text{pre}}$ or that the current pore water pressure is greater than its historically maximal value. For the unloaded elements, the resilient modulus is applied; otherwise, the tangential modulus is applied for loaded elements. The flowchart of the implement of numerical simulation is shown in Fig. 2.

Fig. 1

Mohr’s circle and failure line

Fig. 2

Flowchart depicting overall structure of the implement of numerical simulation

Model verification

In order to verify the numerical model, two simplified cases with known analytical solutions are presented here: One is the one-dimensional Terzaghi’s consolidation under a uniform load, and the other is the infinite aquifer unit with a single pumping well.

One-dimensional Terzaghi’s problem

Figure 3 is the sketch of one-dimensional consolidation problem. The uniform load is applied instantaneously on the upper boundary at time $t = 0$ and remains constant afterward. Drainage is only allowed through the upper boundary, and the pore water pressure on it keeps zero all the time $t > 0$. The other boundaries are no flow and no normal displacement. The analytical resolutions of pore water pressure and the settlement of the top surface are (Lambe and Whitman 1979)

$$p\left( {z,t} \right) = \frac{4}{\pi }p_{0} \sum\limits_{m = 1}^{\infty } {\frac{1}{2m - 1}\exp \left( { - \frac{{\left( {2m - 1} \right)^{2} \pi^{2} Ct}}{{4H^{2} }}} \right)} \sin \frac{{\left( {2m - 1} \right)\pi \left( {H - z} \right)}}{2H}$$

(12a)

$$s_{p} = C_{M} p_{0} H\left[ {1 - 4\sum\limits_{m = 1}^{\infty } {\frac{1}{{\left( {2m - 1} \right)^{2} }}\exp \left( { - \frac{{\left( {2m - 1} \right)^{2} }}{{4H^{2} }}Ct} \right)} } \right]$$

(12b)

where $p\left( {z,t} \right)$ is the pore water pressure, ${\text{kPa}}$; $s_{p}$ is the settlement of the top surface, $m$;$C_{M} = \left( {\lambda + 2G} \right)^{ - 1}$ is the vertical uniaxial compressibility, ${\text{kPa}}^{ - 1}$; $C = K/\gamma_{w} /C_{M}$ is the consolidation coefficient, ${\text{m}}^{ 2} / {\text{s}}$; $t$ is the time, $s$; $H$ is the thickness of the soil layer, $m$; $p_{0}$ is the initial pore water pressure, ${\text{kPa}}$;$z$ is the vertical axis, which origin is at the bottom boundary, $m$. The column domain is discretized into 80 cubic elements (Fig. 3). In the numerical simulation, the uniform load $q = 200\;{\text{kPa}}$, the elastic modulus $E = 5\;{\text{MPa}}$, the Poisson’s ratio $\nu = 0.35$, the thickness of soil layer $H = 10\;{\text{m}}$, and the hydraulic conductivity $K = 3 \times 10^{ - 4} \;{\text{m/day}}$. Figure 4 is the distribution of pore water pressure along the $z$ axis at different time. Figure 5 indicates the change of settlement of the top surface with the elapsed time. A good agreement exists between the analytical and numerical pore water pressure and top displacement.

Fig. 3

Schematic illustration of Terzaghi’s consolidation problem and discretized domain

Fig. 4

Numerical and analytical solutions of the pore water pressure for Terzaghi’s problem

Fig. 5

Numerical and analytical solutions of the vertical displacement at the top for Terzaghi’s problem

A single pumping well in an infinite aquifer unit

A fully penetrating well is set in an aquifer unit which infinitely extends horizontally, as shown in Fig. 6. Groundwater is pumped from the well at a constant rate. The top and bottom boundaries of the aquifer unit are no flow and the bottom boundary is no normal displacement. By averaging the three-dimensional model over the thickness of the aquifer, Bear and Corapcioglu (1981) obtained analytically averaged piezometric head (drawdown) and horizontal displacement, and land subsidence for the case of a single well pumping from an infinite homogeneous isotropic aquifer. These variables are zero at the initial time and at the sufficiently remote external boundary. The analytical solutions are

$$s = - \frac{{Q_{w} }}{4\pi T}W\left( u \right)$$

(13a)

$$\Delta_{z} = - \frac{{Q_{w} }}{{8\pi C_{v} }}W\left( u \right)$$

(13b)

$$U_{r} = - \frac{{Q_{w} t}}{4\pi Br}\left[ {uW\left( u \right) + 1 - e^{ - u} } \right]$$

(13c)

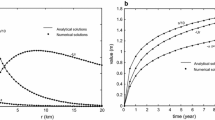
in which, $u = \frac{{r^{2} }}{{4C_{v} t}}$; $s$ is the averaged drawdown, m; $Q_{w}$ is the constant pumping rate,${\text{m}}^{ 3} / {\text{day}}$; $T$ is the transmissivity of the aquifer, ${\text{m}}^{ 2} / {\text{day}}$; $W\left( u \right) = \int_{u}^{\infty } {\frac{1}{x}e^{ - x} {\text{d}}x}$ is the well function; $r$ is the horizontal distance from the center of discharge well, $m$; $C_{v} = \frac{T}{S}$ is the consolidation coefficient of the aquifer, ${\text{m}}^{ 2} / {\text{day}}$; $S$ is the storativity; $t$ is the time, day; $U_{r}$ is the averaged horizontal displacement, $m$; $\Delta_{z}$ is the vertical displacement at the top of aquifer unit, $m$; $B$ is the thickness of the aquifer unit, $m$. A numerical simulation is done to the case shown in Fig. 6. The thickness of the aquifer unit is 50 m. The distance of the external boundary from the discharge well is 20 km. The domain is discretized into hexahedron isoparametric elements, as shown in Fig. 7. There are two model layers. The total elements are 22,088 and the total nodes are 34972. The parameters in this case are: $Q_{w} = 1440\;{\text{m}}^{ 3} / {\text{day}}$, $E = 3.6\;{\text{MPa}}$, $\nu = 0.25$, $K = 5\;{\text{m/day}}$, $C_{v} = 1440\;{\text{m}}^{ 2} / {\text{day}}$, $T = 250\;{\text{m}}^{ 2} / {\text{day}}$. The compaction, the averaged drawdown, and the averaged horizontal displacement at the distance of 3 km from the discharge well are indicated in Fig. 8. They show that there is a good agreement between the numerical and analytical solutions. The numerical results at the elapsed time of 1 year are indicated in Fig. 9, which are also in good agreement with the analytical solutions.

Fig. 6

Schematic illustration of an infinite aquifer unit with a single pumping well

Fig. 7

A quarter of discretized simulated domain of an infinite aquifer. a Discretization of the top surface. b Discretization of the volume

Fig. 8

Numerical and analytical solutions at a distance of 3 km from the discharge well. a Averaged horizontal displacement over the aquifer thickness. b Averaged drawdown over the aquifer thickness. c Land subsidence

Fig. 9

Numerical and analytical solutions at a time of 1 year. a Averaged horizontal displacement over the aquifer thickness. b Averaged drawdown over the aquifer thickness. c Land subsidence

Model application and discussion

In order to comprehensively understand how the nonlinear mechanical and hydraulic properties of aquifer systems affect the simulation results of ground movement, an ideal aquifer system with four hydrostratigraphic units is proposed (Fig. 10). The domain is 20 km in longitude, 20 km in width, and 105 m in height. It consists of one unconfined unit, one confined unit, and two aquitard units. The system is in a steady state before pumpage. Water is pumped from the well that penetrates through the hydrostratigraphic units at the center of the area and only perforates the confined unit. The initial pore water head and displacement are zero. Except for the part that is perforated, there is no flow on the well wall. There is no horizontal displacement on the whole well wall. The top surface is unrestricted and no traction. The head in the unconfined unit keeps constant. The bottom boundary has zero vertical displacement and no flow. The lateral boundaries have zero horizontal displacement and keep a fixed head. The domain is discretized into hexahedron isoparametric elements. A quarter of the discretized domain is shown in Fig. 11. There are five model layers, two of which are within the pumped aquifer unit. The total elements are 17,640 and the total nodes are 23,328. The parameters of the model are selected on the basis of the references (Zhang et al. 2008a, 2015), as given in Table 1.

Fig. 10

Schematic illustration of an ideal aquifer system

Fig. 11

A quarter of discretized simulated domain of an ideal aquifer system

Table 1 Parameters of aquifer and aquitard units used in numerical simulation

Linear versus nonlinear mechanical properties

Considering the nonlinear stress–strain relationship, the numerical results with nonlinear mechanical properties (NMP) are indicated in Fig. 12. Figure 12 shows the horizontal and vertical displacement and the pore water pressure on the top of the aquifer along the line y = 0 at different time. The figures show that the nonlinear mechanical properties have clear impacts on the ground movements. Compared with the results with linear stress–strain properties (LMP), the horizontal and vertical displacements with regard to nonlinear mechanical properties decrease obviously. The discrepancy between the results with LMP and NMP increases with pumping time. However, the impact of nonlinear mechanical properties on the change in pore water pressure (drawdown) is relatively small. The drawdown increases slightly when considering nonlinear mechanical properties. Unlike linear elastic materials, the tangential modulus and Poisson’s ratio of soils with NMP vary with the effective stress state of individual elements. Therefore, the soil elements often have different modulus and Poisson’s ratio even though they are within identical aquifer units. This results in that the variation of displacement of NMP with the distance from the discharge well is gently rolling and not as monotonous as that with LMP. Figure 13 shows the variation of the tangential modulus and Poisson’s ratio of element 2206, which is in the upper part of the aquifer and which center is 532 m away from the discharge well horizontally. This element is within the compaction zone, and its effective stress increases with pumping time, leading to increasing tangential elastic modulus and decreasing Poisson’s ratio.

Fig. 12

Numerical results with and without nonlinear mechanical properties. a Horizontal displacement. b Vertical displacement. c Drawdown

Fig. 13

Variation of tangential elastic modulus and Poisson’s ratio of element 2206. a Tangential elastic modulus. b Poisson’s ratio

Linear versus nonlinear hydraulic properties

The numerical simulation results considering nonlinear hydraulic properties (NHP) of soils are indicated in Fig. 14. When compared with the simulated results considering the constant hydraulic properties (LHP), the horizontal displacement increases in the vicinity of the zone where the maximum is reached, and vertical displacement and the drawdown increase slightly in the zone contiguous to the discharge well. The discrepancy between the results with NHP and LHP increases with time. Figure 15 shows the variation of the hydraulic conductivity of element 2206. With the groundwater pumped, aquifer compacts and its void ratio decreases, leading to the decrease in hydraulic conductivity.

Fig. 14

Numerical results with and without nonlinear hydraulic properties. a Horizontal displacement. b Vertical displacement. c drawdown (the inset is the enlargement of the enclosed area with dashed lines)

Fig. 15

Variation of hydraulic conductivity of element 2206

Distribution of stress and strain on the top of the system

Groundwater withdrawal results in ground movement, accompanied by the strain and the change in stress state in soils. When the stress state of an element satisfies the maximum tensile stress criterion or Mohr–Coulomb failure criterion, tensile failure or shear failure will occur in the element, and a failure plane initiates. The failure plane may propagate then. Earth fissure is the visible failure plane on the ground surface. In the studied case, no shear failure occurred in any elements. Figure 16 indicates the horizontal displacement vector on the top ground surface after 3-year pumping. The directions of pumping-induced horizontal displacement are primarily toward the discharge well. In the vicinity of the discharge well, the horizontal displacement increases rapidly. Beyond that, it decreases gently with the increasing distance from the well. Although the magnitude of the displacement is great, the strain is small. The area with radial tensile strain is relatively great, but the magnitude is less than 0.0004 in this case (Fig. 17). The weight of the aquifer system gives rise to the vertical and horizontal geostatic stresses, and there exists therefore radial compression stress before pumping. Instead of converting the original radial compression stress into tensile stress, such small tensile strain induced by pumping can only cause it to decrease (Fig. 18). Thus, tensile earth fissures scarcely occur in the area where the individual hydrostratigraphic units in the aquifer system primarily distribute homogeneously in the horizontal direction (Zhang et al. 2008b).

Fig. 16

Horizontal displacement vectors on ground surface (unit: cm). a Horizontal displacement on the top surface. b Horizontal displacement on the top surface in the area enclosed by dashed lines in (a)

Fig. 17

Contours of radial strain on ground surface

Fig. 18

Contours of radial stress on ground surface (unit: kPa)

Conclusions

Excessive groundwater extraction can cause aquifer systems to move three-dimensionally, during which groundwater flow and soil deformation are fully coupled. Based on the equilibrium of soil skeleton and continuity of groundwater flow, a fully coupled nonlinear three-dimensional mathematical model has been constructed, which incorporates the prevalent nonlinear mechanical and hydraulic properties of aquifer systems. The model has been used to numerically simulate an ideal aquifer system with a pumping well.

The horizontal and vertical displacements with regard to nonlinear mechanical properties are obviously less than those results with linear stress–strain relationship. The discrepancy between them increases with the elapsed time. With groundwater exploited, aquifer systems compact, and the tangential elastic modulus increases while the tangential Poisson’s ration decreases in the vicinity of the discharge well. However, the drawdown just increases slightly when considering nonlinear mechanical properties. Compaction of aquifer systems result in the decrease in hydraulic conductivity. Compared with the results with regard to the constant hydraulic properties, the horizontal and vertical displacement and the drawdown increase. Comparatively, the effect of nonlinear hydraulic properties on the simulated results is less than that of nonlinear mechanical properties.

For the ideal aquifer system addressed in this study, horizontal displacement is predominant when groundwater is pumped from aquifer units. The horizontal strain is compressive within the zone contiguous to the pumping well, and it is tensile beyond that. However, the horizontal strain, especially the tensile strain, is negligible. Such small tensile strain is not enough to convert the original compressive geostatic stress in soils into tensile stress.

The nonlinear mechanical and hydraulic properties of aquifer systems have clear impacts on the numerical simulation of the displacement and the pore water pressure in hydrostratigraphic units, and their impacts increase with pumping time. They should be considered in land movement simulation due to long-term groundwater withdrawal.