Production rate analysis of multiple-fractured horizontal wells in shale gas reservoirs by a trilinear flow model

Abstract

Most multiple-fractured horizontal wells experience long-term linear flow due to the ultralow permeability of shale gas reservoirs. Considering the existence of natural fractures caused by compression and shear stresses during the process of tectonic movement or the expansion of high-pressure gas, a shale gas reservoir can be more appropriately described by dual-porosity medium. Based on the assumption of slab dual-porosity, this paper uses the trilinear flow model to simulate the transient production behavior of multiple-fractured horizontal wells in shale gas reservoirs, which takes the desorption of adsorbed gas, Knudsen diffusion and gas slippage flow in the shale matrix into consideration. Production decline curves are plotted with the Stehfest numerical inversion algorithm, and sensitivity analysis is done to identify the most influential reservoir and hydraulic fracture parameters. It was found that the density and permeability of the natural fracture network are the most important parameters affecting the production dynamics of multiple-fractured horizontal wells in shale gas reservoirs. The higher the density and permeability of the natural fractures are, the shorter the time is required to exploit the same amount of reserve, which means a faster investment payoff period. The analytical model presented in this paper can provide some insight into the reserve evaluation and production prediction for shale gas reservoirs.

Introduction

Shale gas reservoirs have become an important source of natural gas supply worldwide. Because of their low permeability, shale gas reservoirs are developed for production by horizontal drilling and hydraulic fracturing stimulation. In addition, shale gas reservoirs are naturally fractured reservoirs (Curtis 2002), in which the matrix serves as the primary storage space and natural fractures provide the main flow channels. Gas flow within the shale matrix, natural fractures and hydraulic fractures are controlled by different mechanisms. Understanding the production decline dynamics of fractured horizontal wells in shale gas reservoirs is of great significance to efficiently develop a shale gas reservoir and accurately predict its future production.

For fractured horizontal wells in shale gas reservoirs, different conceptual models have been proposed to analyze well production performance. The models can be divided into two types. One type is source function models (Zhao et al. 2013, 2014, 2016a, b; Wang 2014; Zhang et al. 2015), and the other is linear flow models (Medeiros et al. 2008; Ozkan et al. 2009; Brown et al. 2009; Bohi et al. 2011). Based their work on trilinear models for fractured vertical wells (Lee and Brockenbrough 1986; Olarewaju and Lee 1989; Azari et al. 1990), some researchers (Medeiros et al. 2008; Ozkan et al. 2009; Brown et al. 2009; Bohi et al. 2011) took advantage of trilinear flow models to investigate the production performances of fractured horizontal wells in unconventional gas reservoirs. In their models, the whole reservoir was divided into three different regions, and gas flow in all those regions was assumed to be linear. Based on their models, the production dynamics of fractured horizontal wells were analyzed. The derivation of the proposed trilinear model is relatively easy, and the solution can reflect the primary characteristics of the production dynamics of fractured horizontal wells. However, in their models only the regions between hydraulic fractures were assumed to be naturally fractured. Also, desorption, diffusion and slippage effects of shale gas due to small pore size were not taken into consideration (Zhang et al. 2016).

Considering both diffusive and Darcy flows in shale gas reservoirs, Ozkan and Raghavan (2010) presented a dual-porosity model to study the pressure dynamics of fractured horizontal wells in shale gas reservoirs. In his model, the stress sensitivity of the natural fracture system was also taken into account, but the effects of adsorbed gas and slippage flow were ignored.

From the above analysis, we know that most researchers used the Warren Root model to represent the natural fractures and fracture networks to analyze well performance, and some of them did not consider the special transport mechanisms of shale gas in porous media. Based on a transient slab dual-porosity model, this paper presents an analytical model to simulate production dynamics of fractured horizontal wells in shale gas reservoirs, taking into account desorption, Knudsen diffusion and the slippage effect. Based on the solution, the production decline dynamics of fractured horizontal wells are analyzed in shale gas reservoirs.

Shale gas transport mechanisms

Desorption

As a special self-sourcing and self-storage reservoir type, shale gas reservoirs contain a large amount of adsorbed gas on the surface of organic matter or minerals (Fig. 1), which may desorb and become free gas during production. As the reservoir pressure decreases during production, the originally adsorbed gas desorbs from the pore surfaces. To describe this desorption process, the Langmuir isotherm theory is adopted.

Fig. 1

Gas transport mechanism in shale gas reservoir (Zhao et al. 2013)

Knudsen diffusion and slippage flow

Most pores in shales are on a nanometer scale, thus gas flow in a shale matrix is assumed to be diffusive flow caused by concentration differences and slippage flow near the surface of nanopores (Fig. 2). When the pore diameter is small enough, the average gas molecule mean-free path is comparable to the pore size. In that case, gas molecular collisions dominate, and the gas flows under the concentration gradient, which can be described by the Knudsen diffusion formula. According to Bird (1994), Roy et al. (2003) and Zhao et al. (2016b), the mass flux of gas flow caused by diffusive flow can be expressed as

$$J_{\text{D}} = D_{\text{k}} \frac{M}{ZRT} \cdot \nabla p$$

(1)

where D _k is the Knudsen diffusion coefficient derived by Javadpour et al. (2007).

Fig. 2

Schematic of gas flow in shale gas reservoir with Knudsen diffusion (Zhao et al. 2016b)

With the equation of state, Eq. (1) can be rewritten as

$$J_{\text{D}} = D_{\text{k}} \nabla \rho_{\text{g}}$$

(2)

The mass flux of gas flow caused by viscous flow accounting for the slippage effect can be expressed as

$$J_{\text{a}} = \rho_{\text{g}} Fu$$

(3)

where u is the Darcy’s flow velocity and F is a coefficient used to correct for the gas slip velocity, the expression is $F = 1 + \sqrt {\frac{8\pi RT}{M}} \frac{{\mu_{\text{g}} }}{{p_{\text{avg}} R_{\text{m}} }}\left( {\frac{2}{\alpha } - 1} \right)$. α is the tangential momentum accommodation coefficient, whose value varies theoretically in a range from 0 to 1, depending on wall surface smoothness, gas type, temperature and pressure.

Trilinear flow model

Physical model

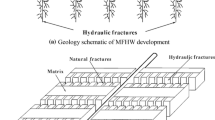
Figure 3 is a schematic of a multiple-fractured horizontal well in a shale gas reservoir.

Fig. 3

Schematic of a fractured horizontal well in a shale gas reservoir

• 1. A horizontal well intercepted by n _F hydraulic fractures is in the center of a rectangular shale gas reservoir. The length of the horizontal wellbore is L _e . The hydraulic fractures, which are perpendicular to the horizontal wellbore, are assumed to fully penetrate the entire reservoir thickness and have identical properties.

• 2. The reservoir is divided into three contiguous regions: the outer region outside the stimulated reservoir volume region, the inner region between the hydraulic fractures and the hydraulic fractures. Gas flow in each region is assumed to be linear.

• 3. Unfractured regions in the shale gas reservoirs are represented by a dual-porosity media model, which is composed of a shale matrix and natural fractures. The natural fractures are assumed to be uniformly distributed in the reservoir, and the total number of natural fractures is n _F.

• 4. Shale gas is assumed to flow into the horizontal wellbore through hydraulic fractures only, and the flow at the tips of the hydraulic fractures is negligible.

• 5. The gas flow rate from each hydraulic fracture is assumed to be identical, and the sum of the flow rates from all hydraulic fractures is the total flow rate of the fractured horizontal well.

• 6. Viscous flow diffusive flow and slippage flow are assumed to occur in the shale matrix.

• 7. Single-phase isothermal flow and negligible gravity and capillary effects are assumed.

Definitions of parameters

Dual-porosity parameters

The dual-porosity model proposed and analyzed by Kazemi (1968) is used to represent the original shale gas reservoir in this paper. The matrix system is represented by rectangular slabs, divided by a set of parallel horizontal natural fractures, as shown in Fig. 4.

Fig. 4

Conceptualization of dual-porosity model

Because of the symmetry of the dual-porosity model, the centers of the rectangular slabs can be considered as impermeable boundaries, and the gas flow in the matrix is linear from the centers of the slabs to the adjacent natural fractures.

In this dual-porosity model, two characteristic parameters, the elastic storativity ratio and the interporosity flow coefficient, are defined by Kazemi (1968) as

$$\omega = \frac{{\left( {\phi c_{\text{t}} } \right)_{\text{mi}} }}{{\left( {\phi c_{\text{t}} } \right)_{\text{fi}} }}\frac{{h_{\text{mt}} }}{{h_{\text{ft}} }}$$

(4)

and

$$\lambda = \frac{{12k_{\text{m}} \theta_{\text{mi}} }}{{k_{\text{f}} }}\frac{{h_{\text{mt}} }}{{h_{\text{ft}} }}\frac{{x_{\text{F}}^{2} }}{{h_{m}^{2} }}$$

(5)

Dimensionless parameters

For convenience in calculation and derivation, the mathematical model in this paper is established and solved in terms of dimensionless forms. The definitions of the relevant dimensionless parameters are as follows:

The dimensionless pseudo-pressure and time are defined by Brown et al. (2009) and Ozkan et al. (2009) as

$$m_{\text{D}} = \frac{{\pi k_{{ 2 {\text{f}}}} h_{\text{ft}} T_{\text{sc}} \left( {m_{i} - m} \right)}}{{p_{\text{sc}} q_{\text{F}} T}}$$

(6)

and

$$t_{\text{D}} = \frac{{k_{{2{\text{f}}}} }}{{\left( {\phi_{\text{i}} c_{\text{ti}} \mu_{\text{gi}} } \right)_{{2{\text{f}}}} x_{\text{F}}^{2} }}t_{\text{a}},$$

(7)

respectively.

Where, the expressions of pseudo-pressure and pseudo-time are $m_{\xi } (p_{\xi } ) = 2\int\limits_{0}^{{p_{{_{\xi } }} }} {\frac{{p^{\prime } }}{{\mu_{\text{g}} z}}} {\text{d}}p^{\prime }$ and $t_{\text{a}} = \left( {c_{\text{t}} \mu_{\text{g}} } \right)_{{\xi {\text{i}}}} \int\limits_{0}^{t} {\frac{1}{{\left( {c_{\text{t}} \mu_{\text{g}} } \right)_{\xi } }}} {\text{d}}t$.

The dimensionless reservoir and hydraulic fracture conductivities are defined by

$$F_{\text{RD}} = \frac{{k_{{ 2 {\text{f}}}} x_{\text{F}} }}{{k_{{ 1 {\text{f}}}} y_{e} }}$$

(8)

and

$$F_{\text{FD}} = \frac{{k_{\text{F}} w_{\text{F}} }}{{k_{{ 2 {\text{f}}}} x_{\text{F}}^{2} }},$$

(9)

respectively.

The dimensionless distances are defined by

$$x_{\text{D}} = \frac{x}{{x_{\text{F}} }},\quad y_{\text{D}} = \frac{y}{{x_{\text{F}} }},\quad z_{\text{D}} = \frac{z}{{{{h_{\text{m}} } \mathord{\left/ {\vphantom {{h_{\text{m}} } 2}} \right. \kern-0pt} 2}}},\quad x_{\text{eD}} = \frac{{x_{e} }}{{x_{\text{F}} }},\quad y_{\text{eD}} = \frac{{y_{e} }}{{x_{\text{F}} }},\quad w_{\text{D}} = \frac{{w_{\text{F}} }}{{x_{\text{F}} }}$$

(10)

The dimensionless diffusivity ratio is defined by

$$\eta_{{\varsigma {\text{D}}}} = \frac{{\eta_{\varsigma } }}{{\eta_{{ 2 {\text{f}}}} }}$$

(11)

where η is the diffusivity and $\eta_{\varsigma } = \frac{{k_{\varsigma } }}{{\left( {\phi_{\text{i}} c_{\text{ti}} } \right)_{\varsigma } \mu_{\text{gi}} }} \, \left( {\varsigma = 1 {\text{f}}, 2 {\text{f}},{\text{F}}} \right)$.

Mathematical model

In this section, the trilinear flow model is derived and solved. Because of the symmetry of the well-reservoir configuration, it is enough to consider one-quarter of a hydraulic fracture in a rectangular drainage region as shown in Fig. 5 (Brown et al. 2009; Ozkan et al. 2009).

Fig. 5

One-quarter of a hydraulic fracture in a rectangular drainage region (Ozkan et al. 2009)

Mathematical models describing the gas flow in each region are first established separately, and then coupled and solved together by the continuity conditions on the interfaces between different regions.

Outer region flow model

Based on the assumption of a linear gas flow in the x-direction in the outer region, the following governing equation and corresponding boundary conditions can be obtained in the Laplace domain.

The governing equation for the shale matrix system in the outer region is

$$\frac{{\partial^{2} \bar{m}_{{ 1 {\text{mD}}}} }}{{\partial z_{\text{D}}^{2} }} = s\omega_{1} \frac{1}{{\eta_{{ 1 {\text{fD}}}} }}\frac{3}{{\lambda_{1} }}\left( {1 + \sigma_{1} } \right)\bar{m}_{{ 1 {\text{mD}}}}$$

(12)

(see “Appendix 1” section for details).

The corresponding boundary conditions for the shale matrix system in the outer region can be given by analyzing the flow state in box-shaped shale matrix slabs.

Because the matrix system is connected with fracture networks, the pressure at the cohesion surfaces should be equal, which serves as the outer boundary condition and is written as

$$\left. {\bar{m}_{{ 1 {\text{mD}}}} } \right|_{{z_{\text{D}} = 1}} = \left. {\bar{m}_{{ 1 {\text{fD}}}} } \right|_{{z_{\text{D}} = 1}}$$

(13)

Because the gas flow in each of the slabs is symmetrical about the centers of the blocks, the middle surfaces of the slabs in the z direction can be seen as no-flow boundaries. Therefore, the inner boundary conditions can be given as

$$\left. {\frac{{\partial \bar{m}_{{ 1 {\text{mD}}}} }}{{\partial z_{\text{D}} }}} \right|_{{z_{\text{D}} = 0}} = 0$$

(14)

The governing equation for the natural fracture system in the outer region is

$$\frac{{\partial^{2} \bar{m}_{{ 1 {\text{fD}}}} }}{{\partial x_{\text{D}}^{2} }} - \frac{{\lambda_{1} }}{3}\left. {\frac{{\partial \bar{m}_{{ 1 {\text{mD}}}} }}{{\partial z_{\text{D}} }}} \right|_{{z_{\text{D}} = 1}} = \frac{s}{{\eta_{{ 1 {\text{fD}}}} }}\bar{m}_{{ 1 {\text{fD}}}}$$

(15)

(see “Appendix 2” section for details).

The corresponding boundary conditions for the natural fracture system in the outer region are

$$\left. {\frac{{\partial \bar{m}_{{ 1 {\text{fD}}}} }}{{\partial x_{\text{D}} }}} \right|_{{x_{\text{D}} = x_{\text{eD}} }} = 0$$

(16)

and

$$\left. {\bar{m}_{{ 1 {\text{fD}}}} } \right|_{{x_{\text{D}} = 1}} = \left. {\bar{m}_{{ 2 {\text{fD}}}} } \right|_{{x_{\text{D}} = 1}}$$

(17)

The solution of Eqs. (12)–(17) gives the relation between the pressure distributions of the outer and inner regions:

$$\bar{m}_{{ 1 {\text{fD}}}} = \frac{{\cosh \left[ {\sqrt {sf_{1} \left( s \right)} \left( {x_{\text{eD}} - x_{\text{D}} } \right)} \right]}}{{\cosh \left[ {\sqrt {sf_{1} \left( s \right)} \left( {x_{\text{eD}} - 1} \right)} \right]}}\bar{m}_{{ 2 {\text{fD}}}}$$

(18)

where $f_{1} \left( s \right) = \frac{1}{{\eta_{{ 1 {\text{fD}}}} }} + \frac{{\lambda_{1} }}{3s}\sqrt {s\alpha_{1} } \tanh \left( {\sqrt {s\alpha_{1} } } \right)$ and $\alpha_{1} = \frac{1}{{\eta_{{ 1 {\text{fD}}}} }}\frac{3}{{\lambda_{1} }}\omega_{1} \left( {1 + \sigma_{1} } \right)$.

Inner region flow model

Assuming that linear gas flow takes place in the inner region, the following governing equation and corresponding boundary conditions in the Laplace domain can be obtained.

The governing equation for the shale matrix system in the inner region is

$$\frac{{\partial^{2} \bar{m}_{{ 2 {\text{mD}}}} }}{{\partial z_{\text{D}}^{2} }} = s\frac{3}{{\lambda_{2} }}\omega_{2} \left( {1 + \sigma_{2} } \right)\bar{m}_{{ 2 {\text{mD}}}}$$

(19)

And the corresponding boundary conditions for the shale matrix system in the inner region are

$$\left. {\bar{m}_{{ 2 {\text{mD}}}} } \right|_{{z_{\text{D}} = 1}} = \left. {\bar{m}_{{ 2 {\text{fD}}}} } \right|_{{z_{\text{D}} = 1}}$$

(20)

and

$$\left. {\frac{{\partial \bar{m}_{{ 2 {\text{mD}}}} }}{{\partial z_{\text{D}} }}} \right|_{{z_{\text{D}} = 0}} = 0$$

(21)

The governing equation for the natural fracture system in the inner region is

$$\frac{{\partial^{2} \bar{m}_{{ 2 {\text{fD}}}} }}{{\partial y_{\text{D}}^{2} }} + \frac{1}{{y_{\text{eD}} F_{\text{RD}} }}\left. {\frac{{\partial \bar{m}_{{ 1 {\text{fD}}}} }}{{\partial x_{\text{D}} }}} \right|_{{x_{\text{D}} = 1}} - \frac{{\lambda_{2} }}{3}\left. {\frac{{\partial \bar{m}_{{ 2 {\text{mD}}}} }}{{\partial z_{\text{D}} }}} \right|_{{z_{\text{D}} = 1}} = s\bar{m}_{{ 2 {\text{fD}}}}$$

(22)

The corresponding boundary conditions for the natural fracture system in the inner region are

$$\left. {\frac{{\partial \bar{m}_{{ 2 {\text{fD}}}} }}{{\partial y_{\text{D}} }}} \right|_{{y_{\text{D}} = y_{\text{eD}} }} = 0$$

(23)

and

$$\left. {\bar{m}_{\text{FD}} } \right|_{{y_{\text{D}} = {{w_{\text{D}} } \mathord{\left/ {\vphantom {{w_{\text{D}} } 2}} \right. \kern-0pt} 2}}} = \left. {\bar{m}_{{ 2 {\text{fD}}}} } \right|_{{y_{\text{D}} = {{w_{\text{D}} } \mathord{\left/ {\vphantom {{w_{\text{D}} } 2}} \right. \kern-0pt} 2}}}$$

(24)

According to the solution of the outer region flow model, the following formula can be obtained,

$$\left. {\frac{{\partial \bar{m}_{{ 1 {\text{fD}}}} }}{{\partial x_{\text{D}} }}} \right|_{{x_{\text{D}} = 1}} = - \beta_{1} \bar{m}_{{ 2 {\text{fD}}}}$$

(25)

where $\beta_{1} = \sqrt {sf_{1} \left( s \right)} \tanh \left[ {\sqrt {sf_{1} \left( s \right)} \left( {x_{\text{eD}} - 1} \right)} \right]$.

Taking Eq. (25) into Eq. (22) and then combining it with Eqs. (23) and (24), the relation between the pressure distributions in the inner region and the hydraulic fractures is

$$\bar{m}_{{ 2 {\text{fD}}}} = \frac{{\cosh \left[ {\sqrt {\beta_{2} } \left( {y_{\text{eD}} - y_{\text{D}} } \right)} \right]\bar{m}_{\text{FD}} }}{{\cosh \left[ {\sqrt {\beta_{2} } \left( {y_{\text{eD}} - {{w_{\text{D}} } \mathord{\left/ {\vphantom {{w_{\text{D}} } 2}} \right. \kern-0pt} 2}} \right)} \right]}}$$

(26)

where $\beta_{2} = \beta_{1} \frac{1}{{y_{\text{eD}} F_{\text{RD}} }} + sf_{2} \left( s \right)$, $f_{2} \left( s \right) = 1 + \frac{{\lambda_{2} }}{3s}\sqrt {s\alpha_{2} } \tanh \left( {\sqrt {s\alpha_{2} } } \right)$ and $\alpha_{2} = \frac{3}{{\lambda_{2} }}\omega_{2} \left( {1 + \sigma_{2} } \right)$.

Hydraulic fracture flow model

Considering linear gas flow in hydraulic fractures, the following governing equation describing gas flow in the hydraulic fractures can be obtained

$$\frac{{\partial^{2} \bar{m}_{\text{FD}} }}{{\partial x_{\text{D}}^{2} }} + \frac{2}{{F_{\text{FD}} }}\left. {\frac{{\partial \bar{m}_{\text{IfD}} }}{{\partial y_{\text{D}} }}} \right|_{{x_{\text{D}} = {{w_{\text{D}} } \mathord{\left/ {\vphantom {{w_{\text{D}} } 2}} \right. \kern-0pt} 2}}} = \frac{s}{{\eta_{\text{FD}} }}\bar{m}_{\text{FD}}$$

(27)

The inner and outer boundary conditions for flowing problems in the hydraulic fractures are

$$\left. {\frac{{\partial \bar{m}_{\text{FD}} }}{{\partial x_{\text{D}} }}} \right|_{{x_{\text{D}} = 1}} = 0$$

(28)

and

$$\left. {\frac{{\partial \bar{p}_{\text{D}} }}{{\partial x_{\text{D}} }}} \right|_{{x_{\text{D}} = 0}} = - \frac{\pi }{{sF_{\text{FD}} }}$$

(29)

The expression for pressure distribution in hydraulic fractures is obtained by solving Eqs. (27)–(29):

$$\bar{m}_{\text{FD}} \left( {x_{\text{D}} } \right) = \frac{\pi }{{s \cdot F_{\text{FD}} }}\frac{{\cosh \left( {\left( {1 - x_{\text{D}} } \right)\sqrt {s\beta_{\text{F}} } } \right)}}{{\sqrt {{\text{s}}\beta_{\text{F}} } \sinh \left( {\sqrt {s\beta_{\text{F}} } } \right)}}$$

(30)

where $\beta_{\text{F}} = \frac{1}{{\eta_{\text{FD}} }} + 2\frac{{\alpha_{\text{F}} }}{{sF_{\text{FD}} }}$ and $\alpha_{\text{F}} = \sqrt {\beta_{2} } \tanh \left[ {\sqrt {\beta_{2} } \left( {y_{\text{eD}} - {{w_{\text{D}} } \mathord{\left/ {\vphantom {{w_{\text{D}} } 2}} \right. \kern-0pt} 2}} \right)} \right]$.

Setting x _D = 0 in Eq. (30) yields the dimensionless bottomhole pressure expression for a fractured horizontal well with a constant production rate in the Laplace domain:

$$\bar{m}_{\text{wD}} \left( {x_{D} } \right) = \frac{\pi }{{s \cdot F_{\text{FD}} \sqrt {s\beta_{F} } \tanh \left( {\sqrt {s\beta_{F} } } \right)}}$$

(31)

According to Van Everdignen and Hurst (1949), the dimensionless production rate for a fractured horizontal well with a constant bottomhole pressure can be obtained by the equation:

$$\bar{q}_{\text{D}} = \frac{1}{{s^{2} \bar{m}_{\text{wD}} }}$$

(32)

With Eq. (32), the production rate decline of fractured horizontal wells in shale gas reservoirs can be analyzed.

Sensitive analysis

Based on the above theory, the production rate decline curves of a horizontal well with multiple hydraulic fractures in shale gas reservoirs were plotted and analyzed. The input parameters used in the calculation are listed in Table 1.

Table 1 Input data for production rate decline analysis

Figure 6 shows the production decline curves for a fractured horizontal well in a shale gas reservoir. Three linear flow periods can be identified based on the characteristics of the decline curves, the linear flow periods in the hydraulic fractures (Stage I), in the inner region (Stage IV) and in the outer region (Stage VI). However, it should be pointed out that the linear flow period in hydraulic fractures is usually very short and may not be observed in the actual production decline curves. In addition, because of the ultralow permeability of shale gas reservoirs, it takes a long time to observe the linear flow in the outer region (Stage VI). Therefore, most of the observed linear flow behavior is actually in the inner region (Stage IV).

Fig. 6

Production decline curves for a fractured horizontal well in a shale gas reservoir

Stage III is the bilinear flow period, in which linear flows in hydraulic fractures and the inner region occur simultaneously in the reservoirs, but the duration of this period is also very limited and may not be observed.

Other flow periods in Fig. 6 are as follows: Stage II is the transition flow period; Stage V is the boundary controlled flow period of the inner region; and Stage VII is the boundary controlled flow period of the outer region.

Note that, many of the flow regimes described above cannot be observed in real test data, such as the bilinear flow period, because the fracture network is not always large enough and interference between fractures will deviate the curve. In field practice, the characteristic equation of linear flow is always used to interpret the reservoir parameters.

Figures 7 and 8 show the effects of the parameters related to the hydraulic fractures on the production decline curves. It can be observed that the value of hydraulic fracture permeability affects mainly the early-time production dynamics. The greater the permeability of the hydraulic fractures, the higher the early-time production rate will be. Intermediate-and late-time production dynamics are not affected by the permeability of the hydraulic fractures. Greater fracture permeability allows a higher gas flow capacity from the inner fracture network system into hydraulic fractures. When the pressure wave transports outside the inner fracture network, the well production rate is controlled mainly by the formation properties of the outer region. Therefore, during the later flow period, all rate curves coincide (Fig. 7).

Fig. 7

Effect of hydraulic fracture permeability on well production rate

Fig. 8

Effect of hydraulic fracture number on well production rate

The number of hydraulic fractures has a marked effect on the behavior of the entire production decline period. The more hydraulic fractures there are, the higher the production rate. With an increase in hydraulic fracture numbers, the stimulation effect slows for each fracture. To reduce hydraulic fracturing costs, an optimal number of hydraulic fractures can be determined.

Figures 9 and 10 show the effects of parameters related to the natural fractures in the inner region on the production decline curves. It can be seen that the permeability and number of natural fractures in the inner region have a primary effect on production decline dynamics. A higher permeability and number of natural fractures leads to a higher production rate at early-and intermediate-production times, indicating that less exploitation time is needed to develop the same amount of reserves.

Fig. 9

Effect of natural fracture permeability in the inner region on well production rate

Fig. 10

Effect of the number of natural fractures in the inner region on well production rate

Figures 11 and 12 show the effects of parameters related to natural fractures in the outer region on the production decline curves. It can be seen that the permeability and number of natural fractures in the outer region have an effect on mainly the late-time production dynamics. Higher fracture permeability and more natural fractures in the outer region lead to a higher production rate at later production stages. However, because of the generally ultralow permeability of shale gas reservoirs, the reflection of gas production from the outer region usually takes quite a long time.

Fig. 11

Effect of natural fracture permeability in the outer region on well production rate

Fig. 12

Effect of the number of natural fractures in the outer region on well production rate

Figures 13 and 14 show the effects of diffusion and slippage flow in the inner region on the production decline. It can be seen that the diffusion and slippage flow coefficients affect mainly the early-time production dynamics. Higher values of diffusion and slippage coefficients lead to a higher apparent matrix permeability in the inner region, resulting in a higher interporosity flow rate from the shale matrix to the natural fracture system in the inner region and correspondingly a higher production rate at early production time.

Fig. 13

Effect of the diffusion coefficient in the inner region on well production rate

Fig. 14

Effect of the slippage coefficient in the inner region on well production rate

Figure 15 shows the effect of the horizontal wellbore length on the production decline. It can be seen that the length of the horizontal wellbore affects mainly late-time production dynamics. The longer the horizontal wellbore, the longer the linear flow period in the inner region, and the later the reflection of the boundary controlling effect.

Fig. 15

Effect of the length of horizontal wellbore on well production rate

Figure 16 shows the effect of the half-length of hydraulic fractures on the production decline. It can be seen that the value of the half-length of hydraulic fractures has a marked effect on production dynamics. The greater the half-length, the higher the production rate as longer half-lengths of the hydraulic fractures provide a larger stimulated area around the horizontal wellbore.

Fig. 16

Effect of the half-length of hydraulic fractures on well production rate

Figure 17 shows the effect of the adsorption factor (σ) on the well production rate. The expression of the adsorption factor defined in Eq. (38), it can estimate the content of gas adsorbed on the surface of the shale matrix. The greater the σ, the more adsorbed gas there will be. During the production process, with the decrease in reservoir pressure as free gas is withdrawn from the natural fracture system, the adsorbed gas will be desorbed from particle surfaces. Under the same pressure difference, the greater the σ, the more gas is desorbed, which means the higher the production rate will be. At the beginning time in Fig. 17, because the reservoir pressure does not decrease to the Langmuir pressure, production rates under all adsorption factors coincide.

Fig. 17

Effect of the adsorption factor on well production rate

Conclusions

An analytical trilinear flow model for multiple-fractured horizontal wells in shale gas reservoirs, which takes into consideration desorption, Knudsen diffusion and slippage flow, is presented in this paper, and production decline dynamics are analyzed. Based on the sensitivity analysis, the following conclusions can be made:

• 1. The permeability and the number of natural fractures have a primary effect on the entire production dynamics of fractured horizontal wells in shale gas reservoirs, whereas the permeability of hydraulic fractures affects mainly the early-time production dynamics. Based on this analysis, when conducting hydraulic fracturing stimulation in shale gas reservoirs, the objective should be focused on creating more connected fractures rather than creating highly permeable primary fractures.

• 2. The half-length, and number of hydraulic fractures and the length of the horizontal wellbore have a primary effect on production dynamics. Greater half-lengths, more hydraulic fractures and longer horizontal wellbores will create larger stimulated (highly permeable) areas in shale gas reservoirs. However, considering the cost of drilling and fracturing, there is an optimal combination of these parameters.

• 3. The diffusion and slippage flow in the shale matrix have an effect on the early-time production dynamics of fractured horizontal wells. Higher diffusion and slippage coefficients lead to a higher apparent matrix permeability and thus a higher production rate.

Appendices

Appendix 1: Governing equation in shale matrix

Based on the mass conservation law, and considering Knudsen diffusion and the slippage flow, we can derive the following equation to describe gas flow in a shale matrix:

$$\frac{\partial }{\partial z}\left( {D_{\text{k}} \frac{{\partial \rho_{\text{g}} }}{\partial z} - uF\rho_{\text{g}} } \right) - \frac{{\partial q_{\text{d}} }}{\partial t}\frac{2}{{R_{\text{m}} }} = \frac{{\partial \left( {\rho_{\text{g}} \hat{\phi }_{\text{m}} } \right)}}{\partial t}$$

(33)

where q _d is the mass of gas desorbed per unit rock, and can be expressed as

$$q_{\text{d}} = \frac{{\rho_{\text{bi}} \rho_{\text{gsc}} }}{{SV_{\text{k}} }}\frac{{V_{\text{L}} p}}{{p_{\text{L}} + p}}$$

(34)

For gas reservoirs, gas properties are always functions of reservoir pressure, thus Eq. (33) is a linear partial differential equation. Pseudo-pressure and pseudo-time are adopted to linearize the equation.

With the equation of state and the definitions of pseudo-pressure and pseudo-time, Eq. (33) becomes

$$k_{\text{am}} \frac{{\partial^{2} \Delta m_{\text{m}} }}{{\partial z^{2} }} = \left( {\hat{\phi }c_{\text{t}} \mu_{\text{g}} } \right)_{\text{mi}} \left( {1 + \frac{2}{{R_{\text{m}} }}\frac{{\rho_{\text{bi}} B_{\text{g}} }}{{\phi_{\text{m}} c_{\text{t}} {\text{SV}}_{\text{k}} }}\frac{{V_{\text{L}} p_{\text{L}} }}{{\left( {p_{\text{L}} + p_{\text{m}} } \right)^{2} }}} \right)\frac{{\partial \Delta m_{\text{m}} }}{{\partial t_{\text{a}} }}$$

(35)

where $k_{\text{am}} = \tilde{k}_{\text{m}} \left( {F + \frac{{\mu_{\text{g}} c_{\text{g}} D_{\text{k}} }}{{\tilde{k}_{\text{m}} }}} \right) = \tilde{k}_{\text{m}} \theta_{\text{m}}$ and $\theta_{\text{m}} = F + \frac{{\mu_{\text{g}} c_{\text{g}} D_{\text{k}} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k}_{\text{m}} }}$.

The definitions of pseudo-time and pseudo-pressure are

$$t_{\text{a}} = \left( {c_{\text{t}} \mu_{\text{g}} } \right)_{{\xi {\text{i}}}} \int\limits_{0}^{t} {\frac{1}{{\left( {c_{\text{t}} \mu_{\text{g}} } \right)_{\xi } }}} {\text{d}}t\quad \left( {\xi = 1{\text{m}},\,1{\text{f}},\,2{\text{m}},\,2{\text{f}},\,{\text{F}}} \right)$$

(36)

and

$$m_{\xi } (p_{\xi } ) = 2\int\limits_{0}^{{p_{{_{\xi } }} }} {\theta_{\xi } } \frac{{p^{'} }}{{\mu_{\text{g}} Z}}{\text{d}}p^{'}$$

(37)

If we define the following group of parameters as an adsorption index,

$$\sigma = \frac{{\rho_{\text{bi}} B_{\text{g}} }}{{\phi_{\text{m}} c_{\text{tm}} {\text{SV}}_{\text{k}} }}\frac{2}{{R_{\text{m}} }}\frac{{V_{\text{L}} p_{\text{L}} }}{{\left( {p_{\text{L}} + p_{\text{m}} } \right)^{2} }}$$

(38)

Eq. (35) can be simplified as

$$\frac{{\partial^{2} \Delta m_{\text{m}} }}{{\partial z^{2} }} = \frac{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } c_{\text{t}} \mu_{\text{g}} } \right)_{\text{mi}} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k}_{\text{m}} \theta_{\text{m}} }}\left( {1 + \sigma } \right)\frac{{\partial \Delta m_{\text{m}} }}{{\partial t_{\text{a}} }}$$

(39)

With the definitions of dimensionless parameters given in “Definitions of parameters” section, one can obtain the dimensionless governing equation for a shale matrix.

Appendix 2: Governing equation in a natural fracture system

Based on the mass conservation law, the following equation can be obtained for a natural fracture system in the outer region:

$$\frac{{\partial \left( {\rho \phi } \right)_{{ 1 {\text{f}}}} }}{\partial t} + \frac{{\partial \left( {\rho v_{x} } \right)_{{ 1 {\text{f}}}} }}{\partial x} - \rho q_{{ 1 {\text{m}}}} = 0$$

(40)

where q _1m is the source item, representing the volumetric gas flow rate from a unit of shale matrix to a natural fracture system, and can be expressed as

$$q_{{ 1 {\text{m}}}} = - \frac{2}{{h_{{ 1 {\text{m}}}} }}\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k}_{{ 1 {\text{m}}}} }}{{\mu_{\text{g}} }}\left. {\frac{{\partial p_{{ 1 {\text{m}}}} }}{\partial z}} \right|_{{z = {{h_{\text{m}} } \mathord{\left/ {\vphantom {{h_{\text{m}} } 2}} \right. \kern-0pt} 2}}}$$

(41)

Substituting Eq. (41) into Eq. (40), and with the equation of state and the definitions of pseudo-pressure and pseudo-time, we can obtain the final expression of a governing equation for a natural fracture system in the outer region:

$$\frac{{\partial^{2} \Delta m_{{ 1 {\text{f}}}} }}{{\partial x^{2} }} - \frac{2}{{h_{\text{m}} }}\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k}_{{ 1 {\text{m}}}} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k}_{{ 1 {\text{f}}}} }}\left. {\frac{{\partial \Delta m_{1m} }}{\partial z}} \right|_{{z = {{h_{\text{m}} } \mathord{\left/ {\vphantom {{h_{\text{m}} } 2}} \right. \kern-0pt} 2}}} = \frac{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } c_{\text{t}} \mu_{\text{g}} } \right)_{{ 1 {\text{f i}}}} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k}_{{ 1 {\text{f}}}} }}\frac{{\partial \Delta m_{{1{\text{f}}}} }}{{\partial t_{\text{a}} }}$$

(42)

Similarly, the final expression of a governing equation for a natural fracture system in the inner region can be obtained as follows:

$$\frac{{\partial^{2} \Delta m_{{ 2 {\text{f}}}} }}{{\partial y^{2} }} - \frac{2}{{h_{\text{m}} }}\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k}_{2m} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k}_{{ 2 {\text{f}}}} }}\left. {\frac{{\partial \Delta m_{2m} }}{\partial z}} \right|_{{z = {{h_{\text{m}} } \mathord{\left/ {\vphantom {{h_{\text{m}} } 2}} \right. \kern-0pt} 2}}} + \frac{1}{{x_{F} }}\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k}_{{1{\text{f}}}} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k}_{{ 2 {\text{f}}}} }}\left. {\frac{{\partial \Delta m_{{ 1 {\text{f}}}} }}{\partial x}} \right|_{{x = x_{\text{F}} }} = \frac{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } c_{\text{t}} \mu_{\text{g}} } \right)_{{ 2 {\text{f i}}}} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k}_{{ 2 {\text{f}}}} }}\frac{{\partial \Delta m_{{ 2 {\text{f}}}} }}{{\partial t_{\text{a}} }}$$

(43)

With the definitions of dimensionless parameters given in “Definitions of parameters” section, one can obtain the dimensionless forms of Eqs. (42) and (43).