Introduction

In deep geothermal, tight and shale gas reservoirs, the hydraulic fracturing technique is commonly applied to enhance the strata permeability, and further the heat and gas recovery. On the other hand, hydraulic fracturing is under the intense public and government scrutiny in some countries due to its potential impact on environment such as contamination of the groundwater and induced seismicity. Therefore, analysis of the related coupled hydromechanical process during the pressurized fluid injection is essential. Due to the geological complexity caused by invisibility, and the challenge and high cost in field investigations, numerical modeling becomes an alternative.

Hydraulic fracturing in tight reservoirs with no natural fractures has been well studied over last century, and many semi-analytical and numerical tools were developed, such as P3D, PL3D, and 3D models (Adachia et al. 2007; Economides and Nolte 2000; Zhou and Hou 2013). In these models, a single fracture is preset and oriented in the direction perpendicular to the minimum horizontal stress, indicating that the mechanical mechanism is tension as there is no shear stress involved along the principal direction. This assumption is valid when the rock formation is relatively intact with few natural fractures. It is also proved by in situ seismicity measurement and laboratory experiments, e.g., the seismicity mapping during the hydraulic fracturing in a tight gas reservoir in Cotton valley (Dinske et al. 2010) and the laboratory experiment by the Petroleum Engineering Department at Colorado School of Mines (Casas et al. 2006).

Conversely, deep geothermal and shale gas reservoirs, however, contain natural fractures or faults on engineering scale which have dominating influences on the process of fluid injections because the existing fractures are easier to open and hence provide an effective escape flow channel for the injected fluid. In such cases, the artificial fracture can only be created at the early beginning. When the tip of the newly developed crack meets the existing natural fractures, its propagation is slowed down or even ceases, and the fluid pressure decreases as the injected fluid escapes through the natural fractures. This phenomenon had been confirmed by in situ seismic monitoring and field experiments, e.g., the seismic mapping during the fracturing operation in the hot wet geothermal reservoir Basel (Häring et al. 2008) and the fracturing experiment at Northparkes Mine E48 (Jeffrey et al. 2010). The orientation of the natural fractures has a certain deviation from the principal stress direction. Thus, shear stress exists on the fracture surface, and a mixed mechanical mechanism including shear and tension can occur, rather than tension alone.

The coupled hydromechanical behavior of the fluid flow in rock fractures is complex because the mechanical deformation and the fluid injection are closely interdependent. On one side, the fluid injection causes rise in the pressure within the fracture, tending to prop up and enlarge the fracture. On the other side, the fracture deformation results in variation in the fracture conductivity and further the pressure distribution. The coupling effects are extremely strong. Generally, a monolithic coupling formulation is used to solve the problem numerically.

In the last 10 years, many numerical models were developed to handle the coupled hydromechanical problem in fractured rock formations. However, most models are two-dimensional (2D) based on the assumption of plain strain state. Interface elements are used to describe the mechanical behavior of the fracture. Olson (2008) solves the problem using the boundary integral method, yet with imposed pressure on the fracture boundary, while Réthoré et al. (2007) and Watanabe et al. (2012) use the extended finite element method. In these models, the governing equations are monolithically formulated in an implicit schema. However, due to the large dimension of the coefficient matrix and the great difference in the diagonal elements between the mechanical and the hydraulic part, extra time-consuming iteration steps are needed. Furthermore, it may cause divergence problem with a large volume of matrix elements, especially when extending the problem into three dimension (3D). Besides, these models have only considered the contact situation where the fluid pressure is smaller than the normal stress, and have not considered the shear failures or the related shear dilation. It is also recognized that 2D models are limited for the investigation of the fluid injection on the field scale. There are also 3D models from previous studies. Based on the P3D model (a semi-analytical solution in Adachia et al. 2007), Kresse et al. (2011) developed a model named unconventional fracture model (UFM) for vertical fractures. However, the flow and mechanical computations in the model are simplified and not fully solved numerically, which cannot represent the hydromechanical behavior occurred in real fractures. Using the explicit schema, the commercial software 3DEC (Itasca 2007) considers fracture contact and separation, as well as shear failure and dilation. However, the computational efficiency is limited due to the explicit formulation with sub-iterations to remain mass conservation. The time step of the hydraulic computation is strongly dependent on the mesh size and the hydraulic parameters. According to rule of thumb, the fluid time step is generally below 1.0e−4 s to remain numerical stability. In field applications, the operations could last several hours or even several days. Thus, the application of 3DEC is impractical for a long-term running (Itasca 2007). Nagel et al. (2011) used 3DEC to investigate the hydraulic fracturing in a shale gas reservoir, but the modeled time is only 13.82 s and the computational time is not reported. Due to the limitations of the models mentioned previously, there are still no full 3D numerical models, which not only considers the whole process of fracture opening, shear failure, and dilation during fluid injection, as well as fracture closure in the post-injection phase, but also can be applied to investigate the related hydromechanical mechanism of a single natural fracture on the field scale.

In this study, a 3D numerical model to simulate the coupled hydromechanical behavior of a natural fracture during the fluid injection is developed. In the model, the mechanical behavior of the fracture including fracture opening, closure, shear failure, and dilation is described by a newly developed constitutive model. The numerical solution uses a sequential coupling schema with a special implicit formulation. Using this model, the hydromechanical mechanism of the fluid injection in a natural fracture is investigated.

Governing equations

In general, the fluid injection in a natural fracture involves the following physical processes: fracture opening, closure, shear slippage, and dilation due to change in the effective normal stress and the tangential stress on the fracture plane; change in the porosity and the permeability due to change in the pore pressure; and fluid flow in fractures and pores, including their interactions (leak-off). To describe the mechanical behavior of the rock formation, the linear elasticity theory is used, including the force equilibrium equation (Eq. 1), the geometrical equation (Eq. 2), and the Hook’s law (Eq. 3):

$$\sigma_{ij,j} + \rho_{m} \left( {b_{i} - \frac{{{\text{d}}v_{i} }}{{{\text{d}}t}}} \right)$$
(1)
$$\Delta \varepsilon_{ij} = \frac{1}{2}\left( {\frac{{\partial\Delta u_{i} }}{\partial j} + \frac{{\partial\Delta u_{j} }}{\partial j}} \right)$$
(2)
$$\begin{aligned} & \left\{ {\Delta \varepsilon_{x} ,\Delta \varepsilon_{y} ,\Delta \varepsilon_{z} ,\Delta \varepsilon_{xy} ,\Delta \varepsilon_{yz} ,\Delta \varepsilon_{xz} } \right\}^{\text{T}} \\ & \quad = D\left\{ {\Delta \sigma_{x} ,\Delta \sigma_{y} ,\Delta \sigma_{z} ,\Delta \sigma_{xy} ,\Delta \sigma_{yz} ,\Delta \sigma_{xz} } \right\}^{\text{T}} \\ \end{aligned}$$
(3)

where σ is the stress (MPa); ρ m is the rock density (kg/m3); b i is the gravity acceleration (m/s2); v i is the velocity (m/s); Δε is the strain increment (−); u is the displacement (m); D is the physical matrix; i, j ∊ (x, y, z) and expressed as follows; E is the Young’s modulus (MPa); G is the shear modulus (MPa); v is the Poisson’s ratio (−).

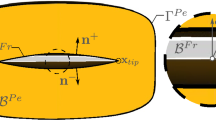
$$D = \left\{ {\begin{array}{*{20}c} {1/E} & { - v/E} & { - v/E} & {} & {} & {} \\ { - v/E} & {1/E} & { - v/E} & {} & {} & {} \\ { - v/E} & { - v/E} & {1/E} & {} & {} & {} \\ {} & {} & {} & {\frac{1}{2G}} & {} & {} \\ {} & {} & {} & {} & {\frac{1}{2G}} & {} \\ {} & {} & {} & {} & {} & {\frac{1}{2G}} \\ \end{array} } \right\}.$$

Because of the displacement discontinuity on the fracture interface, the mechanical behavior must be specially considered. Under high compaction stress, the fracture cannot be fully closed even at zero fluid pressure (P f) as the fracture surface is rough. Hence, there exists a residual fracture aperture w res (Fig. 1a). In the contact condition, the fracture contact area is much smaller than that of the whole fracture surface. This determines that the stiffness of the fracture surface is smaller than that of the rock matrix. Therefore, the deformability of the fracture is greater. The terms “normal stiffness” and “shear stiffness” are used to describe the amount of the normal displacement and the shear displacement with respect to the stress change on the fracture plane (Goodman et al. 1968).

$$\left\{ {\begin{array}{*{20}l} {\Delta w_{\text{un}} =\Delta \sigma_{\text{n,eff}} /k_{\text{n}} } \hfill \\ {\Delta w_{\text{us}} =\Delta \sigma_{\text{s}} /k_{\text{s}} } \hfill \\ \end{array} } \right.$$
(4)

where w un and w us are the normal and the shear displacement, respectively (m); σ n,eff = σ n + αP f: is the effective normal stress (Pa); α is the effective stress coefficient (−); σ s is the shear stress (Pa); k n is the normal stiffness (Pa/m); k s is the shear stiffness (Pa/m).

Fig. 1
figure 1

Schematic demonstration of the fracture in the real and the model case in different hydromechanical conditions

Full size image

In the contact condition, the fracture remains a certain strength to bear the shear stress due to the roughness of the fracture surface and the surface friction (Fig. 1b). Coulomb slip model can be used to describe the shear failure behavior of the fracture:

$$\tau_{\hbox{max} } = - \sigma_{\text{n,eff}} \tan \phi + c$$
(5)

where τ max is the shear strength (Pa); ϕ is the frictional angle (°); c is the cohesion (Pa).

If the existing shear stress exceeds the shear strength, shear failure occurs. The shear stress decreases and maintains the level of the shear strength:

$$\tau_{\text{new}} = \tau_{\hbox{max} }$$
(6)

Then, the shear displacement is calculated as follows:

$$\Delta u_{{{\text{us}},{\text{p}}}} = - (\tau_{\text{new}} - \tau_{\text{old}} )/k_{\text{s}}$$
(7)

where u us,p is the shear displacement induced by the shear failure (m).

The shear displacement induced by the shear failure may lead to the dilation in the normal direction:

$$\Delta w_{\text{un,dil}} =\Delta u_{\text{us,p}} \tan \phi$$
(8)

where ϕ is the dilation angle (°); Δw un,dil is the aperture induced by the shear dilation (m).

According to Eqs. (4) and (8), the fracture aperture in the contact condition is the superposition of the normal displacement and the shear dilation:

$$\Delta w_{\text{u}} = \Delta w_{\text{un}} + \left\langle {\Delta w_{\text{un,dil}} } \right\rangle = -\Delta \sigma_{\text{n,eff}} /k_{\text{n}} + \left\langle {\Delta w_{{{\text{us}},{\text{p}}}} \tan \phi } \right\rangle$$
(9)

where \(\left\langle f \right\rangle = \left\{ {\begin{array}{*{20}c} 0 & {\tau < \tau_{\hbox{max} } } \\ f & {\tau \ge \tau_{\hbox{max} } } \\ \end{array} } \right.\).

During the fluid injection, the fluid pressure and the normal stress increase. Due to the different mechanical behavior of the fracture and the rock formation, the fluid pressure increases faster until the fluid pressure is equal to the normal stress. Then, the two fracture halves are propped open and the shear stress releases instantly (Fig. 1c). According to Adachia et al. (2007), the variation in the fracture aperture is a function of the net pressure which is defined as the difference in the fluid pressure and the initial normal stress:

$$C\Delta w_{o} = P_{\text{f}} (x,y,t) + \sigma_{\text{n,ini}} (x,y)$$
(10)

where w o is the fracture aperture in the separation condition (m); σ n,ini is the initial normal stress (Pa); C is the non-local kernel function (Adachia et al. 2007).

To describe the fluid flow in a rock fracture, the modified cubic flow equation (Eq. 11) (Witherspoon et al. 1980) and the mass conservation equation (Eq. 12) are used. The compressibility of the fluid (water, fracturing fluid, etc.) is small; thus, it has greatly smaller influences on the fracture storage capacity than the variation in the fracture aperture. Therefore, it can be neglected in the mass conservation equation. The effective fracture conductivity factor f reflects the influence of the roughness on the tortuosity of the flow. For smooth or separated fracture faces, f is approximately 1. For mismatched fracture faces, f has a value smaller than 1.

$$v_{{{\text{f}}i}} = - \frac{{(fw)^{2} }}{12\mu }\frac{{\partial (P_{\text{f}} + \rho_{\text{f}} gh)}}{{\partial x_{i} }}$$
(11)
$$\frac{\partial w}{\partial t} + \nabla \cdot (v_{\text{f}} w) + wQ_{\text{s}} = 0$$
(12)

where v fi is the fluid velocity in the i-direction (m/s); f is the effective fracture conductivity factor (−); μ is the viscosity (Pa s); Qs is the source term (1/s); t is the time (s); ρ f is the fluid density (kg/m3); h is the hydrostatic height (m).

The porous flow in the rock formation is described by the transport equation (Eq. 13) derived from the Darcy law and the mass conservation equation for small compressible fluids. The impact of the matrix deformation on the fluid storage is also considered.

$$\frac{{K_{m} }}{\mu }\left( {\frac{{\partial^{2} P_{\text{p}} }}{{\partial x^{2} }} + \frac{{\partial^{2} P_{\text{p}} }}{{\partial y^{2} }} + \frac{{\partial^{2} P_{\text{p}} }}{{\partial z^{2} }}} \right) + Q_{\text{s}} = \frac{1}{{M_{\text{b}} }}\frac{{\partial P_{\text{p}} }}{\partial t} + \alpha \frac{\partial e}{\partial t}$$
(13)

where K m is the permeability (m2); P p is the pore pressure (Pa); Qs is the source term (1/s); M b is the Biot-modulus (Pa); α is the Biot-coefficient (−); e is the volumetric strain (−).

Numerical formulation

In this section, a sequential coupling schema will be introduced to solve the governing equations. The conventional sequential coupling schema with the explicit pressure–width iteration strategy (Fig. 2) requires under-damping to ensure the computational convergence and can take up to 20–30 sub-iterations at each time step. The quantity of the sub-iterations depends on the length of the time step. This coupling concept is adopted by the commercial software 3DEC (Itasca 2007). The default time step is generally below 1.0e−4 s. Therefore, it is difficult for numerical investigation of an in situ operation.

Fig. 2
figure 2

Illustration of the conventional sequential coupling concept with an explicit formulation

Full size image

Regarding numerical computations, the current research efforts are made to find an efficient and stable solution due to the strong hydromechanical coupling effects, especially for 3D problems. In this paper, a sequential coupling concept formulated in a special implicit numerical schema is proposed. The basic idea comes from Zhou and Hou (2013) and Zhou et al. (2014), in which a numerical approach is developed to model the hydromechanical behavior of a tensile opening fracture, but the two halves of the rock fracture are not in contact at all. In this coupling schema, the variation in the fracture aperture in a time step is not estimated by the mechanical computation but by the hydraulic computation with the help of a constitutive equation involving stresses. Then, the strain incremental induced by the aperture change is used to calculate the mechanical response.

In the developed model, hexahedron elements and quadrilateral elements are used to discretize the rock matrix and the rock fracture, respectively (Fig. 3). Figure 4 shows the flowchart of the sequential coupling concept. The computation begins with calculation of the exchange source terms of the fluid flow in fractures and pores. In a time step, a stationary Darcy flow is used to describe the exchange behavior, in which the flow direction is assumed as perpendicular to the fracture surface. The flow equations (Eqs. 14a, 14b) are formulated in an explicit form, indicating that the source term is calculated by the pressure at the pervious step. An empirical infiltration factor is introduced to minimize the impact of the element size perpendicular to the fracture.

$$Q_{{{\text{sf}}(t + 1)}}^{{}} = \frac{{K_{m} \cdot S}}{{\mu \cdot V_{\text{f}} }} \cdot I \cdot \left( {P_{m(t)}^{{}} - P_{f(t)}^{{}} } \right)$$
(14a)
$$Q_{{{\text{s}}m(t + 1)}}^{{}} = \frac{{K_{m} \cdot S}}{{\mu \cdot V_{m} }} \cdot I \cdot \left( {P_{f(t)}^{{}} - P_{m(t)}^{{}} } \right)$$
(14b)

where S is the fracture area of a fracture element (m2); I is the infiltration factor (1/m); V f is the fracture volume of a fracture element (m3); V m is the volume of a rock element including a fracture (m3).

Fig. 3
figure 3

Demonstration of the rock mass element, the fracture element, and the flow direction on the fracture

Full size image
Fig. 4
figure 4

Flowchart of the sequential coupling concept

Full size image

After computation of the source terms, the hydraulic calculation in the fracture and pores is conducted independently. The transport equation (derived from Eqs. 11 and 12) in the fracture is linearized using the finite volume method (Zhou and Hou 2013; Zhou et al. 2014) and formulated in an implicit schema:

$$\begin{aligned} & L_{l(t)}^{{}} P_{{{\text{f}}l(t + 1)}}^{{}} + L_{r(t)}^{{}} P_{{{\text{f}}r(t + 1)}}^{{}} + L_{b(t)}^{{}} P_{{{\text{f}}b(t + 1)}}^{{}} + L_{t(t)}^{{}} P_{{{\text{f}}t(t + 1)}}^{{}} \\ & \quad - \left( {L_{l(t)}^{{}} + L_{r(t)}^{{}} + L_{b(t)}^{{}} + L_{t(t)}^{{}} + \frac{{l_{\text{c}} }}{{\alpha_{1}\Delta t}}} \right)P_{{{\text{f}}o(t + 1)}}^{{}} = w_{(t)} Q_{{{\text{sf}}(t + 1)}} - \frac{{\Delta w}}{{\Delta t}} \\ \end{aligned}$$
(15)

where \(L_{i(t)}^{{}} = \frac{{(fw_{i(t)}^{{}} )^{2} }}{{12\mu s_{i} }}\) i ∊ {l, r, b, t}; s i is the distance between the center of two adjacent flow elements (m); l, r, b, t are the indexes of the neighbor elements; o is index of the central element.

The aperture variation in Eq. (15) is substituted by Eqs. (9) and (10) for the contact and separated fracture, respectively. However, special considerations must be taken here. Let us consider a rock mass element within a fracture element at first (Fig. 3). The fracture element is assumed to go through the middle part of the rock mass element. The stresses on the fracture plane are assumed to be constant and equal to the stresses at the middle point of the rock mass element. All eight grid points of the rock mass element are considered to be fixed in the three coordinate directions during the hydraulic computation.

When the fracture is in the contact condition, the aperture variation induced by tension is described by Eq. (4):

$$\begin{aligned}\Delta w_{\text{un}} & =\Delta \sigma_{\text{n,eff}} /k_{\text{n}} = \frac{{\Delta \sigma_{{{\text{no,eff}}(t +\Delta t)}} -\Delta \sigma_{{{\text{no,eff}}(t)}} }}{{k_{n} }} \\ & = \frac{{\alpha (P_{{{\text{f}}o(t +\Delta t)}} - P_{{{\text{f}}o(t)}} ) + (\sigma_{{{\text{n}}o(t +\Delta t)}} - \sigma_{{{\text{n}}o(t)}} )}}{{k_{\text{n}} }} \\ \end{aligned}$$
(16)

On the other side, the aperture variation can be calculated through variation in the normal stress using the elasticity theory:

$$\Delta w_{\text{un}} = - \frac{{\sigma_{{{\text{n}}o(t +\Delta t)}} - \sigma_{{{\text{n}}o(t)}} }}{{e_{1} }} \cdot l_{\text{c}}$$
(17)

where e 1 = K + 4G/3 is the elastic parameter (Pa); K is the bulk modulus (Pa); G is the shear modulus (Pa); l c is the characteristic length of the rock mass element (Fig. 2) (m).

Substituting Eq. (17) into Eq. (16) yields the following equation:

$$\Delta w_{\text{un}} = \frac{{k_{\text{n}} + (1 - \alpha )e_{1} /l_{\text{c}} }}{{k_{\text{n}} + e_{1} /l_{\text{c}} }} \cdot \frac{{P_{{{\text{f}}o(t +\Delta t)}} - P_{{{\text{f}}o(t)}} }}{{k_{\text{n}} }}$$
(18)

The shear dilation is difficult to obtain in an implicit schema because the effective normal stress used for the calculation of shear strength is unknown before the hydraulic calculation. Therefore, the shear dilation calculated at the previous time step (t) is used:

$$\left\{ {\begin{array}{*{20}l} {\Delta u_{{{\text{us,p}}(t)}} = - (\tau_{\hbox{max} (t)} - \tau_{(t)} ) /k_{\text{s}} } \hfill \\ {\Delta w_{{{\text{un,dil}}(t)}} =\Delta u_{{{\text{us,p}}(t)}} \tan \phi } \hfill \\ \end{array} \quad {\text{if}}\quad \tau_{ (t )} \ge \tau_{{{\text{max(}}t )}} } \right.$$
(19)

Substituting Eqs. (18) and (19) into Eq. (15), Eq. (15) becomes a linear equation system with the unique variable fluid pressure. It can be solved by using iteration methods, i.e., the generalized minimal residual method (GMRES).

When the fracture is in the separation condition and the grid points of the rock mass element are fixed, the variation in the fracture aperture is described as follows:

$$\Delta w_{o(t + 1)} = - \frac{{\sigma_{{{\text{n}}o(t + 1)}} - \sigma_{{{\text{n}}o(t)}} }}{{e_{1} }} \cdot l_{\text{c}} = \frac{{P_{{{\text{f}}o(t + 1)}} - \sigma_{{{\text{n}}o(t)}} }}{{e_{1} }} \cdot l_{\text{c}}$$
(20)

Substituting Eq. (20) into Eq. (15), the variable pressure at time t + Δt (in the separation condition) is implicitly formulated and can also be solved using iteration methods.

After computation of the pressure field, the fracture aperture can be estimated using Eqs. (18), (19), and (20) in different situations (contact and separation), implying that the fracture aperture is not calculated in the mechanical computation. It should be also noted that the fracture cannot bear shear stress in the separation condition. Then, the shear displacement induced by the shear stress redistribution is calculated as follows:

$$u_{l /m(t + 1)} = - \tau_{{{\text{n}}l/{\text{n}}m(t)}} /k_{\text{s}}$$
(21)

With the updated normal and shear displacement of the fracture, the new stress state of the rock mass element within a fracture element can be calculated through the elastic constitutive equations (Eq. 22). Then, it will be further used in the mechanical calculation.

$$\left\{ \begin{array}{l} \sigma_{{{\text{n}}(t + 1),{\text{old}}}} = \sigma_{{{\text{n}}(t)}} - \frac{{\Delta w \cdot e_{1} }}{{l_{\text{c}} }} \hfill \\ \sigma_{{l/m(t + 1),{\text{old}}}} = \sigma_{l/m(t)} - \frac{{\Delta w \cdot e_{2} }}{{l_{\text{c}} }} \hfill \\ \tau_{{{\text{n}}l/{\text{n}}m(t + 1),{\text{old}}}} = \tau_{{{\text{n}}l/{\text{n}}m(t)}} + \frac{{u_{l/m,p(t)} \cdot G}}{{l_{\text{c}} }} \hfill \\ \end{array} \right.$$
(22)

where e 2 = K − 2G/3 is the elastic parameter (Pa); l, m are the indexes of other two local coordinates.

The solution of the mechanical part is mainly with the help of the commercial software FLAC3D (Itasca 2008). In the software, Eq. (1) is dynamically reformulated using the FVM and the linear shape function. Finally, the relationship among the external forces, the internal forces calculated by the stresses, and the velocity at each discrete grid point is obtained (Eq. 23). According to Eq. (23), the change in the stresses in the fracture elements (Eq. 22) causes force unbalance at the grid points and further the movement of the grid points.

$$m^{l} \left( {\frac{{{\text{d}}v_{i} }}{{{\text{d}}t}}} \right)^{l} = \left( {\frac{{T_{{{\text{d}}_{i}^{l} }} \left( {\sigma_{{(t + 1),{\text{old}}}} } \right)}}{a} + m^{l} bi + f_{i}^{l} } \right) + F_{{{\text{d}}_{i}^{l} }} = F$$
(23)

where i is the index of grid points; T d is the force derived from stresses (N); f is the external force (N); F is the total force acting on a grid point (N); m is the mass belongs to a grid point (kg); \(F_{{{\text{d}}_{i}^{l} }} = - \alpha \left| {F_{i}^{l} } \right|{\text{sign}}(v_{i}^{l} )\) is the damping force (N); sign is the signum function; a is the form factor (−).

Equation (23) can be rewritten and linearized using the semi-implicit FDM. After solving the linear equation system, the grid point velocities at each time step are estimated. Then, the obtained velocities are used to calculate the displacements, strains, and stress increments (including the stress increments in the fracture elements) at this time step. It should be noted that the mechanical time is a virtual physical time which is just for the mechanical damping from the dynamic state to the quasi-static state. The mechanical calculation terminates when the maximum unbalanced force from all grid points meets the given error tolerance.

After the mechanical calculation, the stresses of the fracture elements have been changed. The pressure of the fracture elements should be corrected to ensure that the aperture at each fracture element will not change due to change in the stress in this time step. Thus, the following correction is used according to Eqs. (16) and (20):

$$P_{{{\text{f}}(t +\Delta t),{\text{new}}}} = P_{{{\text{f}}(t +\Delta t),{\text{old}}}} - \frac{{(\sigma_{{{\text{n}}(t +\Delta t),{\text{new}}}} - \sigma_{{{\text{n}}(t +\Delta t),{\text{old}}}} )}}{\alpha }$$
(24)

A problem using Eq. (24) for the pressure correction is that the stress change is different from one element to another, and therefore, the velocity field calculated by the corrected pressure field is different from that calculated by the old one, implying that the computation is inconsistent. However, when the stress change in a time step is greatly small, the difference in the stress changes between two neighbor elements becomes negligible. Thus, the error of the velocity field can be ignored. The stress change is caused by the aperture variation in a time step. Therefore, a small time step for the strong aperture variation can be set, while a large time step fits for the small variation. The aperture variation depends on how much fluid flows in or out from a fracture element in a time step. At the beginning of the fluid injection in a natural fracture, a small time step is necessary. During the injection, the rate of the aperture variation becomes smaller with the injection time, as the area of the flow channel with high conductivity increases. Fox example, a high conductive fracture area of 1000 m2 with an injection rate of 6 m3/min indicates an average aperture variation in 0.1 mm/s. Thus, a large time step can be used.

The advantage of this numerical schema is that the two coupled processes are solved separately and only one sub-iteration is needed. Thus, the solution is efficient and stable than that formulated in a monolithic coupling. Besides, the implicit formulation of the flow equation makes it possible to set a relative large time step.

The transport equation of the porous flow (Eq. 13) is also linearized through the FVM in an implicit form (Eq. 25). It can be solved by iteration methods.

$$\sum\limits_{l = 1}^{l = n} {L_{l}^{{}} P_{{{\text{p}}(t + 1)}}^{l} } - \left( {\sum\limits_{l = 1}^{l = n} {L_{l}^{{}} } + \frac{1}{{M_{\text{b}}\Delta t}}} \right)P_{{{\text{p}}(t + 1)}}^{o} = Q_{{{\text{sp}}(t + 1)}} - \frac{{P_{{{\text{p}}(t)}}^{o} }}{{M_{\text{b}}\Delta t}} + \alpha \frac{{e_{(t + 1)} - e_{(t)} }}{{\Delta t}}$$
(25)

where \(L_{l}^{{}} = \frac{{K_{m} }}{{\mu s_{l}^{2} }}\); n is the number of neighbor element; s l is the distance to the lth neighbor element (m).

Model verification

Example 1: Shear displacement through shear failure of a fracture

Example 1 considers a rock sample with an initial shear stress (σ yz ) of 10 MPa (σ xx  = 0, σ yy  = 0, σ zz  = 0, σ xy  = 0, σ xz  = 0). The sample has a geometry of 0.1 m (x) × 0.1 m (y) × 0.2 m (z) within a fracture at the middle of the sample perpendicular to z-direction as illustrated in Fig. 5. The bottom and the top of the sample are fixed in y-direction, and all of the grid points are fixed in z-direction. The parameters are listed in Table 1. According to Eq. (5), the 10 MPa shear stress on the fracture plane is beyond its 5 MPa shear strength, indicating that shear failure will occur. Therefore, the shear stress must be reduced below the shear strength. The decrease in the shear stress is through the shear displacement of the rock sample. The shear displacement of the upper and the lower part of the rock sample can be estimated using the elasticity theory (Eq. 23).

$$u_{y} = \frac{{\Delta \sigma_{yz} }}{G}z + {\text{const}} .$$
(23)

Figure 6 shows the shear displacement along z-direction. The shear displacement increases linearly from the bottom to the middle part of the rock sample. After the displacement jump, it decreases to 0 at the model top. The numerical results show a good agreement with the analytical solution as illustrated in Fig. 6, proving the capability of the method to model the shear displacement through shear failure of a fracture.

Fig. 5
figure 5

Example 1: geometry of the sample and the boundary conditions

Full size image
Table 1 Parameters for the verification examples 1 and 2
Full size table
Fig. 6
figure 6

Example 1: shear displacement along z-direction

Full size image

Example 2: Fluid injection and production in a rock sample within a fracture

Example 2 considers the same rock sample (Fig. 7) as that in example 1, however, with no shear stress but an initial normal stress (σ zz ) of 30 MPa (σ xx  = 0, σ yy  = 0, σ yz  = 0, σ xy  = 0, σ xz  = 0) and an initial fluid pressure of 10 MPa in the fracture. The bottom and the top of the sample are fixed in z-direction. The parameters used in the calculation are the same as those in example 1. In the first 50 s, the fluid is uniformly injected into the fracture at a rate of 5.e−8 m3/s (Fig. 8), indicating an aperture variation rate of 5e−6 m/s. Thus, the aperture is enlarged by 0.25 mm after the 50 s’ injection. Then, a production rate of 5.e−8 m3/s is applied for the next 50 s, implying that the fracture will close until its initial state is achieved.

Fig. 7
figure 7

Example 2: geometry of the sample and boundary conditions

Full size image
Fig. 8
figure 8

Example 2: temporal development of the total aperture, the induced aperture under contact and separation condition

Full size image

Figure 8 shows the temporal development of the total aperture. It increases linearly from 0.1 to 0.35 mm in the first 50 s and then decreases linearly from 0.35 to 0.1 mm in the posterior 50 s. The results show a good agreement with the statements mentioned above. It should be noted that the total aperture consists of the induced aperture in the contact and separation conditions. At the beginning, the fracture is in the contact condition, in which the normal stress is larger than the fluid pressure. Due to the fluid injection, both fluid pressure and normal stress increase. However, the increasing of the fluid pressure is faster until the fluid pressure is equal to the normal stress. At this instant, the two halves of the rock fracture are separated. The critical state of the fracture separation can be estimated analytically. According to Eq. (14), the aperture variation from the beginning to the state of the fracture separation is 0.2 mm. Therefore, 40 s is needed for the fracture separation. According to Eq. (15), the normal stress at the critical state is 55 MPa. The numerical results are in a good agreement with the analytical solution (Fig. 9). With this example, the capability of the method to continuously model the fracture opening and closure, either from the contact to the separation or from the separation to the contact conditions, is proved.

Fig. 9
figure 9

Example 2: temporal development of the fluid pressure in the fracture and the normal stress on the fracture plane

Full size image

Example 3: Hydromechanical coupled fluid flow in a fracture

Example 3 considers a hydromechanical coupled fluid flow in a fracture (Fig. 10). The example was demonstrated in Watanabe et al. (2012). A semi-analytical solution for this problem can be found in Wijesinghe (1968). The model has a geometry of 25 m (x) × 1 m (y) × 1 m (z). A compression stress of 55 MPa is applied on the top of the model, whereas the bottom side is fixed in the normal direction. The fracture has an initial pressure of 11 MPa. The fluid is injected from the left side at a constant pressure of 11.9 MPa; meanwhile, a constant pressure of 11 MPa is applied at the outlet. All parameters used in the calculation are listed in Table 2. The calculation uses a time step of one second.

Fig. 10
figure 10

Example 3: geometry of the model and boundary conditions

Full size image
Table 2 Parameters for the verification example 3
Full size table

Figures 11 and 12 illustrate the pressure and the aperture distribution along the x-coordinate at different times (500 and 2000 s). The numerical results from the developed method and 3DEC show a good agreement with the semi-analytical solution. Figure 13 illustrates the comparison of the fracture aperture using the developed numerical solution with different time steps. With a time step of 5 s, the results have still high precision. Even with a time step of 25 and 50 s, the error is acceptable for field applications. Table 3 shows the computational time with different time steps. The default time step in 3DEC for this example is 1.15e−5 s. Therefore, more than ten thousand seconds is needed for the computation. Conversely, the new approach needs 59 s with a time step of one second. According to this example, the plausibility and the efficient of the approach to model the hydromechanical coupled flow in a fracture is proved.

Fig. 11
figure 11

Example 3: comparison of the fluid pressure calculated using the semi-analytical solutions, numerical models in this study, as well as the commercial software 3DEC at different time points

Full size image
Fig. 12
figure 12

Example 3: comparison of the fracture aperture calculated using the semi-analytical solutions, numerical models in this study, as well as the commercial software 3DEC at different time points

Full size image
Fig. 13
figure 13

Example 3: comparison of the fracture aperture (t = 500 s) calculated using the numerical models in this study with different time steps

Full size image
Table 3 Comparison of the computation time with different time steps for the verification example 3
Full size table

Numerical investigation of fluid injection in a fictive reservoir within a natural fracture

Model generation

In this section, a numerical study on the hydromechanical response of a natural fracture in a fictive reservoir is conducted. The reservoir model is illustrated in Fig. 14. It is located at the depth of 3000 m and with a dimension of 700 m (x) × 400 m (y) × 200 m (z). The model contains three layers: cap rock (50 m thickness), pay zone (100 m thickness), and base rock (50 m thickness). The cap rock and the base rock are intact, whereas a vertical nature fracture lies at the middle of the pay zone and perpendicular to y-direction (Fig. 14). The fracture has an initial aperture of 0.1 mm. All parameters are summarized in Table 4. As boundary conditions, the four lateral sides are fixed in x- and y-directions; meanwhile, the bottom side is also fixed, yet only in vertical direction. An overburden stress of 70 MPa is applied vertically on the top boundary of the model. The coordinate stresses and the primary pore pressure along the depth are shown in Fig. 15.

Fig. 14
figure 14

Demonstration of the geometrical model

Full size image
Table 4 Parameters used in the numerical investigation
Full size table
Fig. 15
figure 15

Normal stresses in the coordinate direction and primary pore pressure along the depth

Full size image

Base case

In the base case, an initial shear stress (τ xy ) of 2.5 MPa is applied in the reservoir, indicating that the fracture bears a 2.5 MPa shear stress. The freshwater with a viscosity of 0.001 Pa s is designed to be injected at the middle of the fracture. The injection rate is 3 m3/min, and the injection lasts 30 min. During the numerical computation, the time step is set to increase from 0.1 to 1 s automatically.

The hydraulic computation in the fracture is based on the mass conservation of an incompressible Newtonian fluid. Therefore, the volume of the injected fluid must be equal to that of the fracture in the case of no leak-off. Figure 16 shows the comparison of the fracture and the injected fluid volume. They match well. The maximum relative error is 0.04 %.

Fig. 16
figure 16

Comparison of the fracture and the injected fluid volume during the injection

Full size image

Figure 17 shows the fluid propagation with the width distribution at different times. At the early beginning, the fluid propagates radially away from the injection point. After it achieves the top barrier, there is no more height growth. The propagation form changes from a circle to an ellipse.

Fig. 17
figure 17

Fluid propagation with width distribution at different times in the base case

Full size image

Figure 18 shows the temporal development of the fluid pressure and the comparison of the primary normal and secondary normal stress at the injection point. At the beginning, the fluid pressure increases rapidly, but then decreases gradually to a nearly constant level. It is greater than the primary normal stress and equal to the secondary normal stress, indicating that the fracture at the injection is all along in the separation condition and no shear dilation occurs. However, due to the shear stress acting on the fracture plane, the hydromechanical behavior of the fracture away from the injection is different. Figure 19 shows the fluid pressure in comparison with the normal stress along line a–a at the end of the injection. It can be concluded from the relationship between the fluid pressure and the secondary normal stress that the fracture near the injection is in the separation condition, and far from the injection is in the contact condition with shear dilation. This conclusion can also be confirmed from Fig. 20, which shows the comparison of the total aperture, tension aperture in the separation condition, shear dilation, and tension aperture in the contact condition at the end of the injection.

Fig. 18
figure 18

Temporal development of the fluid pressure and comparison with the primary and the secondary normal stresses at the injection

Full size image
Fig. 19
figure 19

Comparison of the pressure and the normal stress at the end of the injection along line a–a

Full size image
Fig. 20
figure 20

Comparison of the total aperture, tension aperture in the separation condition, shear dilation, and tension aperture in the contact condition at the end of the injection

Full size image

Figure 21 illustrates the shear displacement on the horizontal plane at the depth of the injection. The displacement discontinuity due to the shear stress redistribution is clear to obtain. Figure 22 shows the shear stress distribution on the fracture plane. The minimum value is 0 and locates at the injection, because the fracture elements near the injection are in the separation condition and cannot bear any shear stress. In the horizontal direction, the shear stress increases gradually to its initial value from the injection to the propagation front; meanwhile, the shear stress at the vertical front is higher than the initial value because of the propagation resistance from the top and the bottom barriers.

Fig. 21
figure 21

Shear displacement on the horizontal plane within the injection point at the end of the injection

Full size image
Fig. 22
figure 22

Shear stress distribution on the fracture plane in the base case

Full size image

Variation of the shear stresses

In this variation, different shear stresses (τ xy  = 0, 2.5, and 10 MPa) are applied. The comparison of the total aperture and the shear dilation at the end of the injection is shown in Fig. 23. In general, the fracture aperture decreases with increase in the shear stress because the propagation length and the fracture area are greater. In the case of no shear stress, the whole fracture is in the separation condition and the tension mechanism dominates during the fluid injection. With the increase in the shear stress, the fracture area in the separation condition strongly shrinks (τ xy  = 2.5 MPa) or even disappears (τ xy  = 10 MPa), indicating that the mechanism is dominated by shear. Figure 24 shows the temporal development of the fluid pressure at the injection. In the case of τ xy  = 0 and 2.5 MPa, the injection pressure is all along above the primary normal stress, whereas the pressure in the case of τ xy  = 10 MPa is first above and then below the primary normal stress, implying that the state of the fracture changes from contact to separation, and then from separation to contact. Because the tension aperture in the separation condition can be reversibly reduced, the maximum value of the total aperture is not at the injection due to the strong decline in the injection pressure.

Fig. 23
figure 23

Comparison of the total aperture and the shear dilation at the end of the injection in the case of different shear stresses

Full size image
Fig. 24
figure 24

Temporal development of the fluid pressure at the injection in the case of different shear stresses

Full size image

Variation of the injection rates

In this variation, different injection rates (q f = 1.5, 3, and 6 m3/min) but the same injection volume are applied. Figure 25 shows the comparison of the total aperture and the shear dilation at the end of the injection. With decrease in the injection rate, the fracture aperture is reduced, the fluid propagation length increases, and the area in the separation condition shrinks. The reason is different pressure responses caused by different injection rates. In general, a high injection rate causes a high pressure response (Fig. 26), hence different pressures cause different mechanical mechanisms.

Fig. 25
figure 25

Comparison of the total aperture and the shear dilation at the end of the injection in the case of different injection rates

Full size image
Fig. 26
figure 26

Comparison of the pressure at the end of the injection along line a–a in the case of different injection rates

Full size image

Variation of the fluid viscosities

In this variation, two fluid viscosities (0.001 and 0.01 Pa s) in the case of τ xy  = 10 MPa are applied. A high fluid viscosity causes a high pressure response and a slow fluid velocity; therefore, the fluid propagation is slower, and the fracture aperture is greater (Fig. 27). With a high viscosity, the state of the fracture near the injection rapidly changes from contact to separation; meanwhile, the shear stress is simultaneously released. Thus, almost no shear dilation occurs even that the fluid pressure is smaller than the primary minimum stress (Fig. 28).

Fig. 27
figure 27

Comparison of the total aperture and the shear dilation at the end of the injection in the case of different viscosities

Full size image
Fig. 28
figure 28

Comparison of the pressure at the end of the injection along line a–a in the case of different viscosities

Full size image

Variation of the injection forms

In this variation, the injection form varies from a point to a 100-m injection section in the case of τ xy  = 10 MPa. Figure 29 shows the comparison of the total aperture and the shear dilation at the end of the injection. The fracture aperture and the fluid propagation of the two cases are nearly the same. The different is the fracture aperture near the injection. With a 100-m injection section, the maximum aperture is at the injection because the injection pressure at the beginning is lower (Fig. 30) and below the primary normal stress. Thus, the main mechanism is the irreversibly shear dilation in the contact condition.

Fig. 29
figure 29

Comparison of the total aperture and the shear dilation at the end of the injection in the case of different injection forms

Full size image
Fig. 30
figure 30

Temporal development of the fluid pressure at the injection in the case of different injection forms

Full size image

Conclusions

An integrated 3D numerical model was developed to simulate the hydromechanical behavior of a natural fracture during the fluid injection. In the developed model, the mechanical behavior of the fracture including the fracture opening, closure, shear failure, and dilation is described by constitutive equations. The hydraulic process is simplified as a fluid flows between two parallel planes. The two processes are coupled together but sequentially solved in a special implicit formulation. The precondition for a plausible computation is a small aperture change in a time step. The advantages of this numerical formulation are that the solution is relative stable and efficient; meanwhile, the mass conservation is strictly obeyed.

Three numerical examples were conducted to verify the developed model, through which the capability of the model to simulate the shear failure and its induced shear displacement discontinuity, the fracture opening and closure from contact to separation and conversely from separation to contact, the hydromechanical coupled behavior of the flow in a fracture and the efficient are proved.

With the developed model, a numerical study on the fluid injection in a fictive reservoir and the related sensitivity study were conducted. It is found that the hydromechanical behavior of the natural fracture during fluid injection is complex, especially when shear stresses acting on the fracture plane. The mechanism in the far field is mainly dominated by shear dilation in contact condition, whereas the mechanism near the injection could be mixed shear–tension in either the contact or the separation conditions, depending strongly on the in situ conditions and the operation parameters such as shear stresses, injection rates, fluid viscosities, and injection forms. With the increase in the shear stress and the injection length, decrease in the injection rate and the fluid viscosity, the fracture state near the injection will change from separation to contact, the injection pressure will decline below the primary normal stress, and the dominated mechanism is shear dilation.

To extend the capabilities of the model, further work will consider natural fracture networks and faults for the coupled fluid flow problem in naturally fractured geothermal and shale gas reservoirs.